Abstract
Sequence data from a series of homologous DNA segments from related organisms are typically polymorphic at many sites, and these polymorphisms are the result of evolutionary processes. Such data may be used to estimate the substitution rates as well as the variability of these rates. Careful characterization of the distribution of this variation is essential for accurate estimation of evolutionary distances and phylogeny reconstruction among these sequences. Many researchers have recognized the importance of the variability of substitution rates, which most have modeled using a discrete gamma distribution. Some have extended these methods to explicitly account for the correlation of substitution rates among sites using hidden Markov models; others have proposed context-dependent substitution rate schemes. We accommodate these correlations using a composite likelihood method based on a bivariate gamma distribution, which is more flexible than hidden Markov models in terms of correlation structure and more computationally tractable compared to the context-dependent schemes. We show that the estimates have good theoretical properties. We also use simulations to compare the maximum composite likelihood estimates to those obtained from maximum likelihood based on the independence assumption. We use data from the mitochondrial DNA of ten primates to obtain maximum composite likelihood estimates of the mean substitution rate, overdispersion, and correlation parameters, and use these estimates in a parametric phylogenetic bootstrap to assess the impact of serial correlation on the estimates of substitution rates and branch lengths.
Keywords: bivariate negative binomial distribution, composite likelihood, substitution rate, phylogeny, parametric bootstrap
1 Introduction
It is well known that the nucleotide substitution rate in DNA varies from site to site due to a variety of functional or structural constraints (see, for example, Gu and Zhang, 1997), and this rate variation impacts the estimation of phylogenetic trees. The need to characterize the distribution of these substitution rates led Yang (1993) to use the gamma distribution, since the shape parameter α (or, equivalently, the heterogeneity parameter ξ = 1/α) can effectively index the variability. Yang (1994) showed that a discrete gamma distribution, obtained by dividing a continuous gamma random variable into K discrete categories, also effectively accommodates this variation but with less computational burden than is required by the continuous gamma distribution. Thorne, Kishino, and Felsenstein (1992), in an alternative approach to substitution rate heterogeneity, proposed a relatively simple model with two varieties of fragments: one with a low substitution rate and one with a faster substitution rate. They used a suitable parameterization of these rates to develop a likelihood-based sequence alignment procedure.
While most of the methods that use the gamma or discrete gamma distribution to model substitution rates treat these substitutions as independent at different sites, a few researchers have attempted to model correlations among sites. Yang (1995) and Felsenstein and Churchill (1996) both proposed hidden Markov chain models that have similar structure but that model rate dependence in different ways. Both models assume that substitution rates are determined by a latent process with K states corresponding to the K components of the discrete gamma distribution, and that the latent process on these states follows a Markov model. Both models require that the substitution rates at any two sites are independent when conditioned on the rates at sites between these positions. Felsenstein and Churchill (1996) put the hidden Markov structure on the components of the discrete gamma distribution, using a transition probability matrix for the K discrete states to control the correlation. Its autocorrelation parameter is defined as the probability that the rate at that site is the same as at the previous site. Thus, the transition probability and associated mean “patch length” (the mean number of adjacent unchanged components in a sequence) depend directly on K. Yang’s method (Yang 1995) assumes that the distribution of the substitution rate at site n is specified fully given the substitution rate at site n − 1 and the correlation is defined as the correlation of substitution rates at two directly neighboring sites. Yang’s method also works with a transition probability between states of the discrete gamma, but the transition probabilities among the K states are determined by a discrete bivariate gamma distribution. Since the correlation coefficient is calculated based on the rates of all K categories and the transition probabilities for a Markov chain of these rate categories, it is less dependent on the choice of K than is the Felsenstein and Churchill method.
A more complex model, based on context-dependent substitution rates, was proposed by Jensen and Pedersen (2000). In this model, the substitution rate at a site may depend on the states of sites in the neighborhood of the site. In particular, the method allows for substitution rates at a particular position in a codon to depend on the other two positions, and on neighboring codons. By deriving the stationary distribution of the substitution process and the ratio of the transition probabilities between two sequences, they can use a numerically intensive Monte Carlo Markov Chain procedure to perform a maximum likelihood analysis. They extended their model to accommodate overlapping reading frames in Pedersen and Jensen (2001). A quite different approach was developed by Morozov (2000) and Lake (1998), who used orthogonal basis functions based on Fourier and/or wavelet decompositions to determine site-specific rate profiles. These decompositions are numerically very intensive, and are most useful when the objective is to determine which regions of a gene evolve faster or slower than the sequence average.
In this paper, we propose to use composite likelihoods based on a bivariate gamma distribution (Lindsay, 1988; Varin and Vidoni, 2005; Henderson and Shimakura, 2003) to accommodate much more complex correlation structures of substitution rates at any neighboring sites using the number of substitutions at sites inferred from either known or estimated phylogenetic relationships (Felsenstein, 1981; Nei and Kumar, 2000) and to provide a direct estimate of these correlation parameters. The correlation of substitution rates at sites addressed in this paper is similar to the one described by Yang (1995) except that this paper considers a more general and flexible correlation structure. Composite likelihoods are pseudo-likelihoods that are typically more tractable than full likelihoods when modeling non-independent data. Fearnhead and Donnelly (2002) explored their use in estimating recombination rates, and Fearnhead (2003) studied the consistency of recombination rate estimates obtained in this fashion. Here we use composite likelihoods to develop a tractable method to study correlated substitution rates. Following Henderson and Shimakua (2003), we construct a pseudo-likelihood based on a product of bivariate negative binomial probability density functions (p.d.f.s), with one such factor for each pair of sites that may be correlated. We extend their work by allowing more complex correlation structures, and we show that estimates obtained by maximizing the resulting pseudo-likelihood (which is not a full likelihood since it ignores three-way and higher correlations) are consistent and asymptotically normal under reasonable conditions.
This paper is organized as follows. The bivariate negative binomial composite likelihood is presented in Section 2, as well as a description of how we generate correlated substitution rates. We study the performance of the method by simulation in Section 3 and apply the method to data from mitochondrial DNA from ten primates in Section 4. In this section we also use a parametric phylogenetic bootstrap to assess the impact of the serial correlation on the estimates of branch lengths. The last section summarizes the results.
2 Methods
2.1 Notation and assumptions
Yang (1995) showed that the substitution rate at a site is not only related to the rates at its directly neighboring sites but also to other adjacent sites. Here we make the simplifying assumptions that the substitution rates at neighboring sites are correlated and the rates at two sites are independent if these two sites are separated far enough. This results in a banded correlation matrix. Suppose that N denotes the length of the DNA sequence under consideration. Let ri and yi denote, respectively, the relative substitution rate and number of substitutions at site i so the absolute substitution rate at site i can be expressed as μri where μ denotes the average substitution rate. Furthermore, we suppose that the marginal distribution of ri is gamma(1/ξ, ξ) with mean 1 and yi | ri ~ Poisson(μri). Marginally, the yi follow a negative binomial distribution with mean μ and overdispersion parameter ξ. The band-matrix correlation structure is defined by
where ρi,i+l is the correlation of substitution rates between sites i and i+l and B denotes the maximum distance of correlated sites. When B = 0 the correlation matrix of substitution rates reduces to a diagonal matrix, which represents the independent case. When B > 0, the correlation matrix is a band matrix with bandwidth 2B + 1. Under independence models, different sites are assumed to evolve independently and the substitution rate at each site is distributed as an independent univariate gamma distribution. When correlation exists, a natural extension from the independent to the correlated case is that the substitution rates ri, ri+1, …, ri+B are jointly distributed as a (B + 1) -variate gamma distribution with correlation matrix RB for any 1 ≤ i ≤ N − B, where
Suppose that given ri, ri+1, …, ri+B, yi and yk are independent for any j ≤ i and k > (i + B), so that unconditionally, the yi, yi+1, …, yi+B are distributed as a multivariate negative binomial, with marginal mean μ, overdispersion parameter ξ, and correlation determined by RB. The overall correlation matrix for substitution rates r = (r1, r2, …, rN) can be written as follows:
| (2.1) |
In practice the correlation structure might be much more involved than the one in (2.1) due to the functional and structural properties. The composite likelihood can be directly extended to accommodate more complex correlation structures, but the asymptotic properties of the estimates obtained from them may be more difficult to determine.
2.2 Composite likelihood for correlated numbers of substitutions
Under the assumptions in Section 2.1, the number of substitutions at the adjacent sites follows a multivariate negative binomial distribution. The multivariate negative binomial distribution becomes unwieldy when the dimension is greater than 2. However, the p.d.f. for the 2-dimensional case is manageable, and we can use a product of bivariate negative binomial p.d.f’s to form a pseudo-likelihood function known as a composite likelihood. Composite likelihood methods were proposed by Lindsay (1988) and further developed by Cox and Reid (2004) and by Varin and Vidoni (2005). Henderson and Shimakura (2003) used a pairwise composite likelihood based on the bivariate negative binomial distribution for longitudinal count data. In this section we construct a composite likelihood function based on the correlation structure given in Section 2.1, and we extend the asymptotic properties to the situation of a long sequence of count data. The bivariate negative binomial p.d.f. is given by
where
Following Henderson and Shimakura (2003), we denote the correlation of substitution rates between sites j and k as ρjk, and we have
| (2.2) |
That is, the correlation between yj and yk (the number of substitutions at sites j and k, respectively) is less than ρjk (the correlation between the corresponding substitution rates at these two sites). Let ρ = (ρ1, ρ2, …, ρB) denote all the nonzero correlation parameters of adjacent substitution rates. The pairwise composite log likelihood for the serial correlated count data can be written as
| (2.3) |
where
| (2.4) |
Pr(yi, yi+k | θ) denotes the bivariate negative binomial p.d.f, and θ = (μ, ξ, ρk). Let P denote the total number of unknown parameters, Θ = {θ = (θ1, θ2, …, θP)} denote the parameter space, and denote the true parameter value. Then the composite-likelihood estimator , defined as the estimate that maximizes the composite likelihood (2.3), has the following properties, as the sequence length gets large:
θ̂N is consistent for estimating
-
θ̂ − θ0 is asymptotically normal with mean 0 and variance Λk,k, whereand J(θ0) = {Jl1l2(θ0)}P×P is defined by
where .
K(θ0) = {Kl1l2(θ0)}P×P is defined by
Since the correlation parameter(s) ranges from 0 to 1 and the overdispersion parameter is non-negative, the parameter space is given by
The regularity assumptions underlying these results, as well as the proof, closely follow those given in Cox and Reid (2004) and Fearnhead (2003) and so are omitted here.
2.3. Simulation of serial-correlated count data
In order to compare results from the composite likelihood method to those from the independence model, we need to simulate serial count data that follow the correlated negative binomial distribution. Given initial values of μ (the marginal mean), B (the number of correlation parameters), and N (the sequence length),
- Generate zi, i = 1, …, N + B, from N(0, 1) and compute
Generate yj from Poisson(μrj), j = 1, …, N.
Clearly, for any j = 1, …, N,
rj ~ gamma(1/ξ, ξ) with mean 1 and overdispersion parameter ξ = 2/(B + 1).
.
yj ~ negative binomial with mean μ and overdispersion parameter ξ = 2/(B + 1).
The count data generated by the above procedure are serial count data with a band correlation structure. By selecting B we can control the correlation bandwidth.
2.4 A parametric phylogenetic bootstrap
The re-sampling bootstrap has been used previously in phylogenetics to obtain the confidence limits of estimated phylogenies (Felsenstein, 1985; Efron, Halloran, and Holmes, 1996). Goldman (1993) proposed a phylogenetic parametric bootstrap, which involves repeated sampling of sequences using a specified parametric distribution. Wang, Salter and Pearl (2002) provided estimates of the parameters in the underlying evolutionary model jointly with the tree and obtained estimates of their standard errors using a bootstrap approach. All these methods assume that the sequence sites are independent. Since we need to obtain repeated sequence sites with a pre-specified correlation structure of substitution rates at neighboring sites, we modified the Goldman (1993) parametric bootstrap by using replicated sequences based on the substitution rates from a correlated gamma distribution.
To carry out the bootstrap, we first need a phylogenetic tree for the original set of sequences, which we obtain using the maximum likelihood program “dnaml” in the PHYLIP package developed by Felsenstein (2005) which is based originally on Felsenstein (1981). We chose this program because it provides the topology of the sequence relationships and the branch lengths and it is convenient to use. We then simulate DNA sequences under the independence substitution rate assumption based on a pre-specified evolutionary model and phylogenetic relationship using the computer program Seq-Gen (Rambaut and Grassly, 1997). The substitution rate portion of the program does the following:
Step 1: Simulate the relative substitution rate from a gamma distribution for each site, ri ~ gamma(1/ξ, ξ), i = 1, …, N. The rates at different sites are independent and the substitution rate at an individual site is μri, where μ is average substitution rate.
Step 2: Simulate nucleotides for each site based on pre-defined evolutionary models and the corresponding substitution rates.
To generate DNA sequences with correlated substitution rates, we adjust Step 1 of the above procedure; no changes are needed for Step 2:
Adjusted Step 1: Simulate the relative substitution rate from a gamma distribution gamma(1/ξ, ξ) for each site, such that substitution rates at neighboring sites are dependent with the following correlation:
where ρmax is the pre-specified maximum correlation of substitution rates among sites and B is the number of correlation parameters, which also indexes the bandwidth of correlation matrix. In order to do this, we first simulate wi ~ gamma(ρmax/(ξB), 1), i = 1, …, N + B − 1 and vi ~ gamma((1 − ρmax)/ξ, 1), i = 1, …, N, then calculate and ri = ξ(vi + ui) for i = 1, …, N. Clearly, ui ~ gamma(ρmax/ξ, 1) and r ~ gamma(1/ξ, ξ). Then the simulated ri, i = 1, …, N, have above specified correlation structure.
By using above adapted version of Seq-Gen (using the adjusted Step 1), the correlation between substitution rates at two nearby sites will decrease with increasing site distances, and the correlations will reduce to zero for sites separated by more than B bases. By re-estimating the maximum likelihood tree for each simulated sequence, which is generated based on the maximum composite likelihood estimates of mean substitution rate, overdispersion, and correlation structure of a original sequence, we obtain parametric bootstrap estimates of the branch lengths and their standard errors.
3. Simulation Results
We simulated serial count data for μ = 0.35 or 0.7, B = 2 or 5, and N = 300 or 600 using the simulation procedure defined in Section 2.3. For each combination of above values 350 simulations were done. The estimates based on maximum likelihood (independence case) and on maximum composite likelihood (correlated case) were used to estimate the corresponding unknown parameters (Table 1). The simulation results show that
Table 1.
For Simulation A count data were generated for the serially correlated case using B = 2, ξ = 2/3, ρ1 = 2/3, and ρ2 = 1/3. For Simulation B, similar data for the serially correlated case used B = 5, ξ = 1/3, ρ1 = 5/6, ρ2 = 2/3, ρ3 = 1/2, ρ4 = 1/3, and ρ5 = 1/6. For the independence cases, the correlation parameters were set to zero. The mean parameters μ took the values 0.7 and 0.35, and the sequence lengths N were 300 and 600. The “mean” and “model se” were the average of the model-based sample mean and standard error, and the “empirical se” was the standard error of the estimated means from the simulations. The simulations consisted of 350 replications. All fitted models for composite method were based on estimating parameters: μ, ξ, and ρj, j = 1, …, B.
| μ = 0.7 | μ = 0.35 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N = 300 | N = 600 | N = 300 | N = 600 | |||||||
| independence | composite | independence | composite | independence | composite | independence | composite | |||
| Simulationl A | μ | mean | 0.698 | 0.698 | 0.703 | 0.703 | 0.351 | 0.351 | 0.348 | 0.348 |
| model se | 0.058 | 0.072 | 0.041 | 0.052 | 0.038 | 0.044 | 0.027 | 0.032 | ||
| empirical se | 0.078 | 0.079 | 0.055 | 0.055 | 0.045 | 0.045 | 0.030 | 0.033 | ||
|
| ||||||||||
| ξ | mean | 0.661 | 0.670 | 0.660 | 0.660 | 0.655 | 0.669 | 0.676 | 0.680 | |
| model se | 0.209 | 0.212 | 0.146 | 0.150 | 0.363 | 0.323 | 0.258 | 0.245 | ||
| empirical se | 0.225 | 0.223 | 0.149 | 0.148 | 0.390 | 0.369 | 0.261 | 0.235 | ||
|
| ||||||||||
| ρ1 | mean | – | 0.653 | – | 0.669 | – | 0.668 | – | 0.665 | |
| model se | – | 0.196 | – | 0.148 | – | 0.313 | – | 0.256 | ||
| empirical se | – | 0.216 | – | 0.162 | – | 0.310 | – | 0.249 | ||
|
| ||||||||||
| ρ2 | mean | – | 0.344 | – | 0.337 | – | 0.397 | – | 0.384 | |
| model se | – | 0.216 | – | 0.145 | – | 0.437 | – | 0.275 | ||
| empirical se | – | 0.218 | – | 0.148 | – | 0.323 | – | 0.265 | ||
|
| ||||||||||
| Simulationl B | μ | mean | 0.703 | 0.703 | 0.702 | 0.701 | 0.353 | 0.355 | 0.346 | 0.347 |
| model se | 0.054 | 0.073 | 0.038 | 0.052 | 0.036 | 0.044 | 0.025 | 0.032 | ||
| empirical se | 0.081 | 0.073 | 0.052 | 0.053 | 0.047 | 0.048 | 0.033 | 0.033 | ||
|
| ||||||||||
| ξ | mean | 0.331 | 0.343 | 0.338 | 0.341 | 0.351 | 0.392 | 0.338 | 0.354 | |
| model se | 0.164 | 0.146 | 0.115 | 0.115 | 0.309 | 0.248 | 0.216 | 0.187 | ||
| empirical se | 0.173 | 0.145 | 0.122 | 0.115 | 0.284 | 0.267 | 0.203 | 0.196 | ||
|
| ||||||||||
| ρ1 | mean | – | 0.748 | – | 0.769 | – | 0.674 | – | 0.745 | |
| model se | – | 0.201 | – | 0.193 | – | 0.482 | – | 0.291 | ||
| empirical se | – | 0.285 | – | 0.214 | – | 0.346 | – | 0.313 | ||
|
| ||||||||||
| ρ2 | mean | – | 0.641 | – | 0.659 | – | 0.593 | – | 0.675 | |
| model se | – | 0.268 | – | 0.239 | – | 0.515 | – | 0.351 | ||
| empirical se | – | 0.313 | – | 0.259 | – | 0.369 | – | 0.334 | ||
|
| ||||||||||
| ρ3 | mean | – | 0.523 | – | 0.501 | – | 0.498 | – | 0.537 | |
| model se | – | 0.310 | – | 0.245 | – | 0.617 | – | 0.410 | ||
| empirical se | – | 0.325 | – | 0.256 | – | 0.373 | – | 0.358 | ||
|
| ||||||||||
| ρ4 | mean | – | 0.396 | – | 0.362 | – | 0.399 | – | 0.427 | |
| model se | – | 0.350 | – | 0.263 | – | 0.712 | – | 0.462 | ||
| empirical se | – | 0.325 | – | 0.266 | – | 0.371 | – | 0.366 | ||
|
| ||||||||||
| ρ5 | mean | – | 0.268 | – | 0.202 | – | 0.261 | – | 0.296 | |
| model se | – | 0.393 | – | 0.270 | – | 0.830 | – | 0.569 | ||
| empirical se | – | 0.305 | – | 0.229 | – | 0.337 | – | 0.356 | ||
The estimates of μ and ξ from these two methods are asymptotically unbiased;
The standard error of μ and ξ from the independence model are underestimated while the composite likelihood method provides unbiased estimates;
The estimates of correlation parameters from the composite likelihood method are asymptotically unbiased and robust;
When the correlation is close to 1 or 0 in short sequences, the estimate of the correlation parameter and the corresponding standard error might be biased due to the restriction of the correlation parameter space to the interval (0,1). These biases are particularly noticeable when the average substitution rate μ or substitution rate heterogeneity ξ is small. This is because corr(yj, yk) becomes small (Equation 2.2) and the correlation among substitution rates cannot be estimated effectively through the number of substitutions at neighboring sites. These biases are reduced for larger N or larger values of μ or ξ.
4 Application to Primate Mitochondrial DNA
To illustrate our methods, we used the protein-coding region ND5 (NADH dehydrogenase subunit 5) of mitochondrial DNA from 10 primates. The ten primates we considered are human, chimpanzee, gorilla, orangutan, gibbon, barbary ape, hamadrya baboon, pygmy chimpanzee, lemur and western tarsier. This choice of coding region and series of species is similar to one studied by Yang (1995) using current sequence data from the National Center for Biotechnology Institute; details may be found in the Appendix. Since the substitution rates at the three codon positions are different, here we estimate the corresponding parameters for codon position 2 of ND5, so we use a total of 604 (codon 2) nucleotides sites; Codon positions 1 and 3 yield similar trees but somewhat different rate parameter estimates (details not shown).
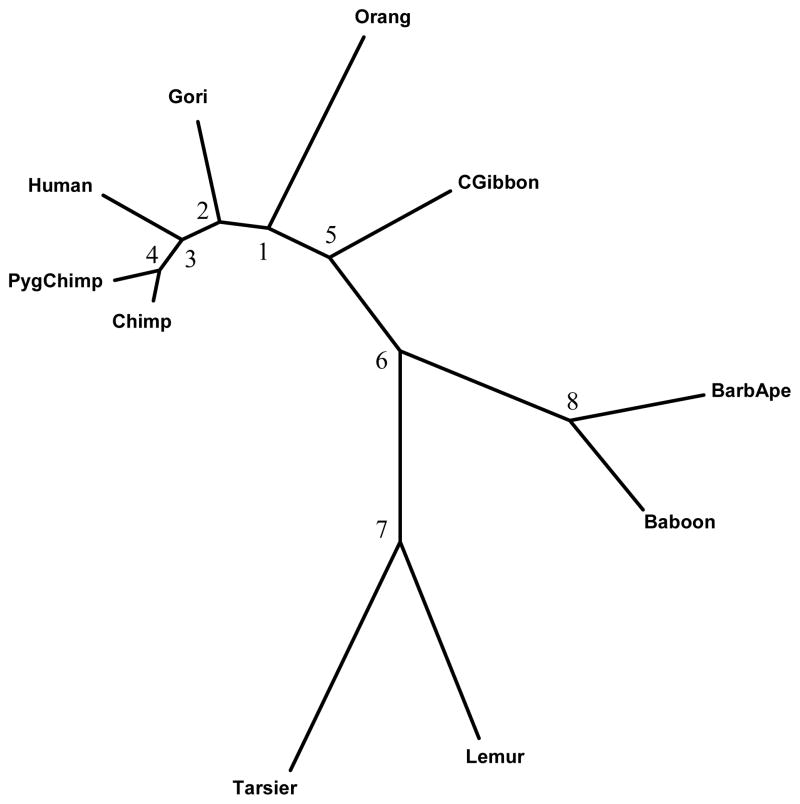
The estimated phylogenetic relationships among these 10 species were generated using the PHYLIP program DNAML (Felsenstein, 2005) under the independence rate assumption, and the estimated branch lengths are given in Table 3. The plot in Figure 1 was generated using the program MEGA (Tamura et al. 2007).
Table 3.
Parametric bootstrap estimates of the branch lengths based on ND5 codon position 2 under the independence and correlated rates assumptions. Sequences with 600 sites were simulated based on the phylogeny shown in Figure 1 using the branch lengths specified in parentheses in the first column. For the correlated rate case, B = 27, ρmax = 0.73, and in both cases, ξ = 1.26. The total number of simulations = 6,000. Of these, 76.1% produced a tree topology identical to the given tree for both independence and correlated cases.
| Branch (Length) | Correlation Type | Mean (Se) | Se Increase (%) | Median (95% CI) |
|---|---|---|---|---|
| 1, 2 (0.0050) | IND | 0.0061 (0.0032) | - | 0.0057 (0.0016,0.0120) |
| CORR B27 | 0.0062 (0.0035) | 9.0 | 0.0056 (0.0015,0.0126) | |
| 1, Orangutan (0.0533) | IND | 0.0488 (0.0095) | - | 0.0486 (0.0339,0.0649) |
| CORR B27 | 0.0496 (0.0132) | 38.8 | 0.0487 (0.0294,0.0730) | |
| 2, 3 (0.0084) | IND | 0.0084 (0.0039) | - | 0.0081 (0.0030,0.0154) |
| CORR B27 | 0.0084 (0.0040) | 3.1 | 0.0079 (0.0029,0.0158) | |
| 2, Gorilla (0.0252) | IND | 0.0240 (0.0066) | - | 0.0238 (0.0137,0.0353) |
| CORR B27 | 0.0242 (0.0079) | 19.6 | 0.0237 (0.0119,0.0379) | |
| 3, 4 (0.0076) | IND | 0.0076 (0.0035) | - | 0.0070 (0.0025,0.0140) |
| CORR B27 | 0.0076 (0.0040) | 11.9 | 0.0069 (0.0017,0.0149) | |
| 3, Human (0.0217) | IND | 0.0208 (0.0062) | - | 0.0205 (0.0116,0.0316) |
| CORR B27 | 0.0210 (0.0073) | 17.2 | 0.0204 (0.0101,0.0343) | |
| 4, Chimpanzee (0.0068) | IND | 0.0067 (0.0035) | - | 0.0067 (0.0017,0.0131) |
| CORR B27 | 0.0068 (0.0036) | 5.3 | 0.0067 (0.0017,0.0135) | |
| 4, Pygmy Chimp (0.0100) | IND | 0.0098 (0.0041) | - | 0.0097 (0.0034,0.0170) |
| CORR B27 | 0.0099 (0.0046) | 11.3 | 0.0098 (0.0033,0.0182) | |
| 5, 1 (0.0133) | IND | 0.0127 (0.0051) | - | 0.0123 (0.0050,0.0217) |
| CORR B27 | 0.0130 (0.0056) | 9.8 | 0.0125 (0.0050,0.0232) | |
| 5, Gibbon (0.0302) | IND | 0.0282 (0.0073) | - | 0.0278 (0.0170,0.0408) |
| CORR B27 | 0.0285 (0.0089) | 22.1 | 0.0280 (0.0151,0.0436) | |
| 6, 5 (0.0252) | IND | 0.0235 (0.0072) | - | 0.0231 (0.0122,0.0361) |
| CORR B27 | 0.0240 (0.0086) | 19.9 | 0.0233 (0.0113,0.0392) | |
| 6, 7 (0.0491) | IND | 0.0428 (0.0097) | - | 0.0425 (0.0273,0.0589) |
| CORR B27 | 0.0430 (0.0123) | 27.4 | 0.0421 (0.0247,0.0647) | |
| 7, Lemur (0.0474) | IND | 0.0433 (0.0093) | - | 0.0429 (0.0284,0.0590) |
| CORR B27 | 0.0442 (0.0124) | 32.4 | 0.0435 (0.0252,0.0661) | |
| 7, Tarsier (0.0626) | IND | 0.0561 (0.0109) | - | 0.0556 (0.0392,0.0747) |
| CORR B27 | 0.0569 (0.0149) | 37.0 | 0.0555 (0.0344,0.0832) | |
| 8, 6 (0.0456) | IND | 0.0404 (0.0091) | - | 0.0400 (0.0262,0.0560) |
| CORR B27 | 0.0409 (0.0116) | 27.6 | 0.0400 (0.0236,0.0613) | |
| 8, Baboon (0.0267) | IND | 0.0255 (0.0071) | - | 0.0252 (0.0145,0.0376) |
| CORR B27 | 0.0258 (0.0086) | 21.4 | 0.0252 (0.0126,0.0409) | |
| 8, Barbary Ape (0.0302) | IND | 0.0285 (0.0076) | - | 0.0281 (0.0168,0.0412) |
| CORR B27 | 0.0288 (0.0093) | 22.3 | 0.0282 (0.0149,0.0451) |
Figure 1.
Phylogenetic relationship among 10 primates based on ND5 Mitochondrial DNA sequences (Codon position 2). In the text, we refer to Clade 1 as the subtree consisted of human, chimpanzee, and pygmy chimpanzee, and Clade 2 as the subtree consisted of gibbon, barbary ape, hamadrya baboon, lemur, and western tarsier.
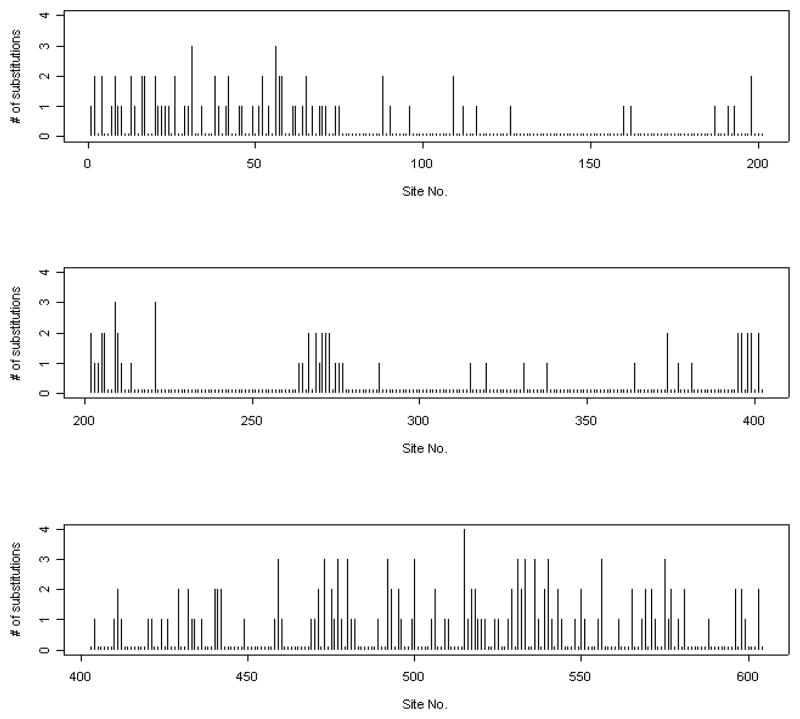
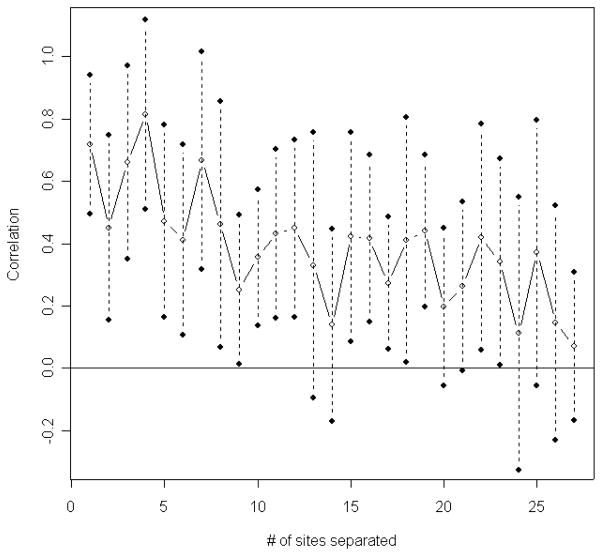
Suppose the estimated tree in Figure 1 represents the true phylogenetic relationship among these species. The number of substitutions at each site was counted using the DNAPARS (DNA parsimony) program in PHYLIP (Felsenstein, 2005). Since DNAPARS estimates the minimum number of substitutions, this number is generally an underestimate. The numbers of substitutions at codon position 2 of ND5 are displayed in Figure 2. This plot illustrates that one effect of the serial correlation is to induce clusters of sites with substitutions interspersed with regions with conserved regions (regions with no substitutions). Figure 3 displays the relationship between the estimated correlation parameter and the distance between sites, and shows that the serial correlation decreases from approximately 0.73 for neighboring sites to zero when two sites are 27 sites apart. Our choice of B = 27 for the mitochondrial data is thus based on the empirical observation that sites separated by 27 or more base pairs show little correlation. Model selection methods (Varin and Vidoni, 2005) may provide alternative methods for selecting B.
Figure 2.
Number of substitutions vs. site number DNA codon position 2 of ND5, 10 primates.
Figure 3.
Correlation vs. the number of sites apart DNA codon position 2 of ND5, 10 primates.
Estimates of the average substitution rate, heterogeneity parameter, and correlation of substitution rates between sites using maximum likelihood methods (for the independence assumption) and composite likelihood methods (for the correlated assumption) are listed in Table 2. Also given in Table 2 are corresponding estimates from the hidden Markov model of Yang (1995) under two evolutionary models where the number of rate categories is chosen as four. The JC69 (Jukes-Cantor) model ignores the type of substitution, and corresponds most closely to our model. Estimates from the HKY model (Hasegawa et. al., 1985), which includes a parameter κ that indexes the transition/transversion ratio, are also included, since this is the model used by Yang (1995). The estimates for the mean substitution rate μ are similar across all methods, while the estimates for the overdispersion parameter ξ are higher for Yang’s methods (2.325 and 2.650 for the JC69 and HKY models, respectively) than for ours (1.213 and 1.260 for the independence and correlated models, respectively). The estimates for the correlation parameter for Yang’s methods (0.935 and 0.897, respectively) are somewhat higher than for the corresponding parameter ρ1 (0.73) from the correlated model.
Table 2.
Parameter estimates from the primate ND5 mitochondrial DNA sequences, codon 2. Estimates on the left (“Yang JC69” and “Yang HKY”) are from the “baseml” program in the PAML package (Yang 2008), using the JC69 and HKY85 evolutionary models based on Yang’s hidden Markov chain approach (1995). Estimates in the center (“Independence”) are parameter estimates and standard errors for the maximum likelihood of the independence model while estimates on the right (“Correlated Rates”) are estimates from the correlated composite likelihood. The parameter estimates for ρi, i = 1, …, 27 are obtained from one composite likelihood model, with the correlation for sites separated by i sites modeled by ρi. The PAML package did not produce standard errors for the parameter estimates.
| Yang JC69 Est |
Yang HKY Est |
Independence | Correlated Rates | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||
| Est | se | Est | se | Est | se | ||||||
| μ | 0.433 | 0.494 | μ | 0.445 | 0.034 | μ | 0.444 | 0.099 | |||
|
| |||||||||||
| ξ | 9.395 | 9.650 | ξ | 1.213 | 0.285 | ξ | 1.260 | 0.480 | |||
|
| |||||||||||
| ρ | 0.935 | 0.897 | ρ1 | 0.73 | 0.11 | ρ15 | 0.42 | 0.17 | |||
|
|
|
||||||||||
| κ | – | 4.902 | ρ2 | 0.45 | 0.15 | ρ16 | 0.42 | 0.13 | |||
|
|
|
||||||||||
| ρ3 | 0.66 | 0.16 | ρ17 | 0.27 | 0.11 | ||||||
|
|
|||||||||||
| ρ4 | 0.81 | 0.15 | ρ18 | 0.41 | 0.20 | ||||||
|
|
|||||||||||
| ρ5 | 0.47 | 0.15 | ρ19 | 0.44 | 0.12 | ||||||
|
|
|||||||||||
| ρ6 | 0.42 | 0.15 | ρ20 | 0.20 | 0.13 | ||||||
|
|
|||||||||||
| ρ7 | 0.67 | 0.17 | ρ21 | 0.26 | 0.14 | ||||||
|
|
|||||||||||
| ρ8 | 0.47 | 0.20 | ρ22 | 0.42 | 0.18 | ||||||
|
|
|||||||||||
| ρ9 | 0.25 | 0.12 | ρ23 | 0.35 | 0.16 | ||||||
|
|
|||||||||||
| ρ10 | 0.35 | 0.11 | ρ24 | 0.11 | 0.22 | ||||||
|
|
|||||||||||
| ρ11 | 0.43 | 0.14 | ρ25 | 0.37 | 0.21 | ||||||
|
|
|||||||||||
| ρ12 | 0.45 | 0.14 | ρ26 | 0.14 | 0.19 | ||||||
|
|
|||||||||||
| ρ13 | 0.33 | 0.21 | ρ27 | 0.08 | 0.12 | ||||||
|
|
|||||||||||
| ρ14 | 0.14 | 0.16 | |||||||||
Note: “Est”=parameter estimate; “se” = model standard error.
As discussed earlier, the assumptions underlying Yang’s hidden Markov model likelihoods differ somewhat from those underlying the substitution rate likelihood and composite likelihood models based on the inferred number of substitutions at sites. Both methods provide estimates of the correlation of substitution rates at two directly neighboring sites. Furthermore, Yang’s method does not provide a standard error or confidence interval for ρ.
An important difference between the independence and correlated models is that the standard errors are underestimated in the independence as compared to the correlated model (0.034 vs. 0.099 for μ, and 0.285 vs. 0.480 for ξ, respectively), which underscores the importance of accounting for correlation in substitution rate models.
To set up the parametric bootstrap, we used the topology given in Figure 1 with branch lengths given in Table 3. DNA sequences were simulated using the evolutionary HKY model under both the correlated rate and independence assumptions with ξ = 1.26, transition-transversion rate 2.5 and base frequencies for A, C, G, T = 0.21, 0.28, 0.11, 0.40, respectively. For the correlated rate case, ρmax (the correlation of substitution rates between two directly neighboring sites) was chosen as 0.73 and B (the number of correlation parameters) was chosen as 27. The simulated sequence length was set at 600 and a total 6,000 simulations were carried out. The transition-transversion rate and base frequencies in the above evolutionary model were chosen to match the corresponding empirical value of codon position 2 of the primate ND5 sequences and the values of ξ, ρmax, and B were chosen to match the corresponding estimates from the composite likelihood approach for the codon position. Phylogenetic relationships among these species were then re-constructed using DNAML based on the simulated DNA sequences with either independent or correlated substitution rates. Among the 6,000 simulations, 76.1% produced a tree topology exactly identical to the given tree for both independence and correlated cases; 88.9% and 88.5% correctly identified both Clade 1 and Clade 2 while 96.0% and 95.8% produced only Clade 2, 92.6% and 92.2% produced only Clade 1 in the given tree for the independence and correlated cases respectively, where the clades are specified in Figure 1. The proportion of correctly identified phylogenetic relationships and summary statistics of each branch length are presented in Table 3. Simulations show that there is not much difference in terms of the proportion of correctly identified topologies and the estimates of branch lengths for this particular case between two types of rate assumptions. Nevertheless, ignoring the rate correlation will cause underestimation of the standard error of branch length. In addition, the branch lengths are somewhat underestimated for both cases, with this underestimation increasing with branch length. This underestimation is due to the fact that the number of observed substitutions is generally less than the number of substitutions that actually occurred and the bias gets larger when branch length increases. Summary statistics based on Clades 1 and 2 were very similar with the ones in Table 3, so details are not presented.
5 Discussion
We have shown that a composite likelihood can be constructed to model complex correlation structures in serial count data arising from comparable DNA sequences. When the correlation matrix is a band matrix, the parameter estimates are consistent and asymptotically normal under reasonable conditions as the sequence length gets large. Failure to accommodate serial correlations had little effect on estimates of the substitution rate, tree topology, or branch lengths, but it results in underestimates of standard errors and confidence intervals of these quantities. The methods we have described can be applied to any set of comparable DNA sequences from related organisms, including those from bacteria or viruses as well as from higher organisms, provided that the sequences can be accurately aligned. The methods can also be applied to protein amino acid sequences. The impact of mis-specifying the correlation pattern or B needs further research.
Acknowledgments
The authors are grateful to two anonymous reviewers for their very valuable comments and to Shili Lin for editorial and formatting assistance.
Appendix
Accession Numbers of Mitochondrial DNA From NCBI
The gene sequences may be obtained from the Entrez Gene website of the National Center for Biotechnology Institute at http://www.ncbi.nlm.nih.gov. To obtain the DNA sequence for the ND5 segment of a particular species, search “Gene” for the relevant accession number, and then select “ND5.” On the Summary page for ND5, click on the Accession Number, and select “FASTA.” This will return the ND5 sequence for that species. Here are the accession numbers that we used:
Contributor Information
Ling Deng, Johnson & Johnson.
Dirk F. Moore, University of Medicine and Dentistry of New Jersey
References
- Cox DR, Reid N. A note on pseudolikelihood constructed from marginal densities. Biometrika. 2004;91:729–737. [Google Scholar]
- Efron B, Halloran E, Holmes S. Bootstrap confidence levels for phylogenetic trees, correction. Proc Natl Acad Sci USA. 1996;93:13429–13434. doi: 10.1073/pnas.93.23.13429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Excoffier L, Yang Z. Substitution rate variation among sites in mitochondrial hypervariable region I of humans and chimpanzees. Molec Biol Evol. 1999;16:1357–1368. doi: 10.1093/oxfordjournals.molbev.a026046. [DOI] [PubMed] [Google Scholar]
- Fearnhead P. Consistency of estimators of the population-scaled recombination rate. Theoret Pop Biol. 2003;64:67–79. doi: 10.1016/s0040-5809(03)00041-8. [DOI] [PubMed] [Google Scholar]
- Fearnhead P, Donnelly P. Approximate likelihood methods for estimating local recombination rates (with discussion) J Roy Statist Soc Ser B. 2002;64:657–680. [Google Scholar]
- Felsenstein J. Evolutionary trees from DNA sequences: A maximum likelihood approach. J Mol Evol. 1981;17:368–376. doi: 10.1007/BF01734359. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. Confidence limits on phylogenies: An approach using the bootstrap. Evolution. 1985;39:783–791. doi: 10.1111/j.1558-5646.1985.tb00420.x. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. Distributed by the author. Department of Genome Sciences, University of Washington; Seattle: 2005. PHYLIP (Phylogeny Inference Package) version 3.6. http://evolution.genetics.washington.edu/phylip.html. [Google Scholar]
- Felsenstein J, Churchill GA. A hidden Markov model approach to variation among sites in rate of evolution. Mol Biol Evol. 1996;13(1):93–104. doi: 10.1093/oxfordjournals.molbev.a025575. [DOI] [PubMed] [Google Scholar]
- Goldman N. Statistical tests of models of DNA substitution. J Mol Evol. 1993;36:182–198. doi: 10.1007/BF00166252. [DOI] [PubMed] [Google Scholar]
- Gu X, Zhang J. A simple method for estimating the parameter of substitution rate variations among sites. Molec Biol Evol. 1997;14(11):1106–1113. doi: 10.1093/oxfordjournals.molbev.a025720. [DOI] [PubMed] [Google Scholar]
- Hasegawa M, Kishino H, Yano T. Dating of human-ape splitting by a molecular clock of mitochondrial DNA. J Mol Evol. 1985;22:160–174. doi: 10.1007/BF02101694. [DOI] [PubMed] [Google Scholar]
- Henderson R, Shimakura S. A serially correlated gamma frailty model for longitudinal count data. Biometrika. 2003;90 (2):355–366. [Google Scholar]
- Jensen JL, Pedersen AMK. Probabilistic models of DNA sequence evolution with context dependent rates of substitution. Adv Appl Prob. 2000;32:499–517. [Google Scholar]
- Lake JA. Optimally recovering rate variation information from genomes and sequences: Pattern filtering. Mol Biol Evol. 1998;15:1224–1231. doi: 10.1093/oxfordjournals.molbev.a026030. [DOI] [PubMed] [Google Scholar]
- Lindsay BG. Composite likelihood methods. In: Prabhu NU, editor. Statistical Inference from Stochastic Processes. Providence: American Mathematical Society; 1988. pp. 221–39. [Google Scholar]
- Morozov P, Sitnikova T, Churchill G, Ayala FJ, Rzhetsky A. A new method for characterizing replacement rate variation in molecular sequences: Application of the Fourier and wavelet models to drosophial and mammalian proteins. Genetics. 2000;154:381–395. doi: 10.1093/genetics/154.1.381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nei M, Kumar S. Molecular Evolution and Phylogenetics. Oxford University Press; 2000. [Google Scholar]
- Pedersen AMK, Jensen JL. A dependent-rates model and an MCMC-based methodology for the maximum-likelihood analysis of sequences with overlapping reading frames. Mol Biol Evol. 2001;18(5):763–776. doi: 10.1093/oxfordjournals.molbev.a003859. [DOI] [PubMed] [Google Scholar]
- Rambaut A, Grassly NC. Seq-Gen: An application for the Monte Carlo simulation of DNA sequence evolution along phylogenetic trees. Comput Appl Biosci. 1997;13:235–238. doi: 10.1093/bioinformatics/13.3.235. http://tree.bio.ed.ac.uk/software/seqgen/ [DOI] [PubMed] [Google Scholar]
- Tamura K, Dudley J, Nei M, Kumar S. MEGA4: Molecular Evolutionary Genetics Analysis (MEGA) software version 4.0. Molec Biol and Evol. 2007;24:1596–1599. doi: 10.1093/molbev/msm092. http://www.megasoftware.net. [DOI] [PubMed] [Google Scholar]
- Thorne JL, Kishino H, Felsenstein J. Inching toward reality: An improved likelihood model of sequence evolution. J Molec Evol. 1992;34:3–16. doi: 10.1007/BF00163848. [DOI] [PubMed] [Google Scholar]
- Varin C, Vidoni P. A note on composite likelihood inference and model selection. Biometrika. 2005;92:519–528. [Google Scholar]
- Wang Q, Salter LA, Pearl KDK. Estimation of evolutionary parameters with phylogenetic trees. J Molec Evol. 2002;55:684–695. doi: 10.1007/s00239-002-2364-7. [DOI] [PubMed] [Google Scholar]
- Yang Z. Maximum likelihood estimation of phylogeny from DNA sequences when substitution rates differ over sites. Mol Biol Evol. 1993;10:1396–1401. doi: 10.1093/oxfordjournals.molbev.a040082. [DOI] [PubMed] [Google Scholar]
- Yang Z. Maximum likelihood phylogenetic estimation from DNA sequences with variable rates over sites: approximate methods. J Mol Evol. 1994;39:306–314. doi: 10.1007/BF00160154. [DOI] [PubMed] [Google Scholar]
- Yang Z. A space-time process model for the evolution of DNA sequences. Genetics. 1995;139:993–1005. doi: 10.1093/genetics/139.2.993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Z. PAML: Phylogenetic analysis by maximum likelihood version 4.1. Distributed by the author. 2008 ( http://abacus.gene.ucl.ac.uk/software/paml.html)