Stable three-dimensional metallic carbon with interlocking hexagons

Significance

Carbon is an amazing material: it not only forms the chemical basis for all known life but also, because of its rich physics and chemistry, displays an array of structures: from the age-old graphite and diamond to more recent C₆₀ fullerene, 1D nanotube, and 2D graphene. One of the unsolved issues in carbon science has been to find a 3D form of carbon that is metallic under ambient conditions. This paper addresses this important challenge. Using state-of-the-art theoretical calculations, we predict the existence of such a phase that is formed from interlocking hexagons and is dynamically, mechanically, and thermally stable. It is suggested that this new form of carbon may be synthesized chemically by using benzene or polyacenes molecules.

Abstract

Design and synthesis of 3D metallic carbon that is stable under ambient conditions has been a long-standing dream. We predict the existence of such phases, T6- and T14-carbon, consisting of interlocking hexagons. Their dynamic, mechanical, and thermal stabilities are confirmed by carrying out a variety of state-of-the-art theoretical calculations. Unlike the previously studied K₄ and the simple cubic high pressure metallic phases, the structures predicted in this work are stable under ambient conditions. Equally important, they may be synthesized chemically by using benzene or polyacenes molecules.

From the age-old graphite and diamond to more recent C₆₀ fullerene (1), nanotube (2), and graphene (3), carbon displays an amazing array of physical and chemical properties and plays a leading role in science and technology. Among all of the hotly pursued research topics in this field, metallic carbon has attracted considerable attention. It has been demonstrated that metallic carbon, due to its high density of states (DOS) at the Fermi level, can be more effective as a catalyst (4). It was also found that metallic carbon exhibits phonon–plasmon coupling (5) and displays negative differential resistance (6) and superconductivity (7, 8). In addition, metallic carbon can become magnetic when Stoner-like criterion (9, 10) is satisfied. Therefore, metallic carbon structures can possess properties even more novel than the semiconducting carbon structures. Unfortunately, the synthesis and characterization of metallic carbon structures has been very challenging. In 1D systems, armchair carbon nanotube is metallic (11), but during synthesis it is very difficult to separate it from other semiconducting structures (12). In 2D graphene (13), the π-bonding of p_z orbitals makes the sheet metallic-like in the plane, but the DOS at the Fermi level is zero. Thus, in the strictest sense, graphene is semimetallic, and defects are needed to make it metallic (14, 15). In the 3D structure, diamond is a semiconductor. Synthesis of 3D metallic carbon under ambient conditions has been elusive. In 2009, Itoh et al. (16) proposed a metallic carbon allotrope named K₄ phase, but subsequent analysis of its phonon dispersion (17) and mechanical properties (18) revealed that the reported metallic K₄ phase is both dynamically and mechanically unstable. Other structures including dense cold compressed graphite (19) and porous T-carbon (20), L-carbon (21), Y-carbon (22), and cubane-based porous carbon (23) have been proposed, but they all are nonmetallic. Recently, it was reported that a simple cubic phase of carbon under 3-TPa pressure could be metallic, but it becomes unstable when pressure is removed (24). In this work, we show that the unique phases of carbon (T6 and T14) formed from interlocking hexagonal rings are metallic under ambient conditions. The dynamic, thermodynamic, and mechanical stability of these unique phases are confirmed by a series of state-of-the-art theoretical calculations.

Our search for a 3D metallic carbon began by examining the two forms of carbon that are metallic, i.e., 1D armchair nanotube and 2D graphene sheet. Both share the common feature that they have hexagons as the building blocks. In fact, it has been reported that carbon nanotubes can be synthesized by directly using benzene molecules that, on dehydrogenation, leave hexagonal C₆ (25, 26). When a nanotube is unzipped by catalysts, it becomes a graphene sheet. We wondered if a similar route could be followed to construct a 3D carbon structure using hexagons as the building block. Our calculations show that it is not only possible to construct such a metallic structure, but it is also stable at ambient temperature and pressure.

Results and Discussion

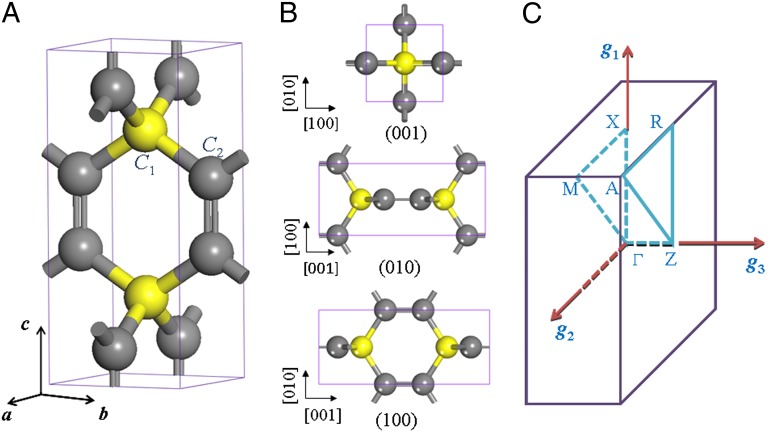
Fig. 1 shows the optimized crystal structure of the unique carbon allotrope investigated in this work. With a high symmetric space group P4₂/mmc (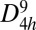, 131), this structure has a simple tetragonal primitive cell containing six C atoms. Hence, we refer to it as T6-carbon. Although this unique allotrope possesses a lower density than that of diamond and cold compressed graphite (19), it is denser than some previously reported porous phases such as T-carbon (20) and L-carbon (21). Therefore, the T6-carbon can be viewed as a nanoporous phase. There are two chemically nonequivalent atomic Wyckoff positions in this structure: one is the 2f (1/2, 1/2, 1/4) site occupied by the sp³ hybridized C atoms (denoted as C1, colored yellow in Fig. 1A), and the other is the 4i (1/2, 0, 0.1118) site occupied by sp² hybridized C atoms (denoted as C2, colored gray in Fig. 1A). The detailed structural information of the T6-carbon and other carbon allotropes are given in Table S1. The bond lengths between C1-C2 and C2-C2 atoms are, respectively, 1.54 and 1.34 Å, showing clear signatures of elongated single σ bonds and double (σ + π) bonds, respectively. The first Brillouin zone in the reciprocal space is displayed in Fig. 1C with a space group of P4/mmm (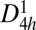, 123). The high symmetry K point paths that we use to describe the dispersions of electron bands and phonon frequencies are also denoted.

Fig. 1.

Crystal structure of T6-carbon: (A) perspective view and (B) polyhedral view from three axial directions. (C) Corresponding first Brillouin zone and the high symmetry K point paths: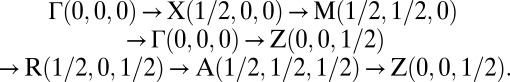

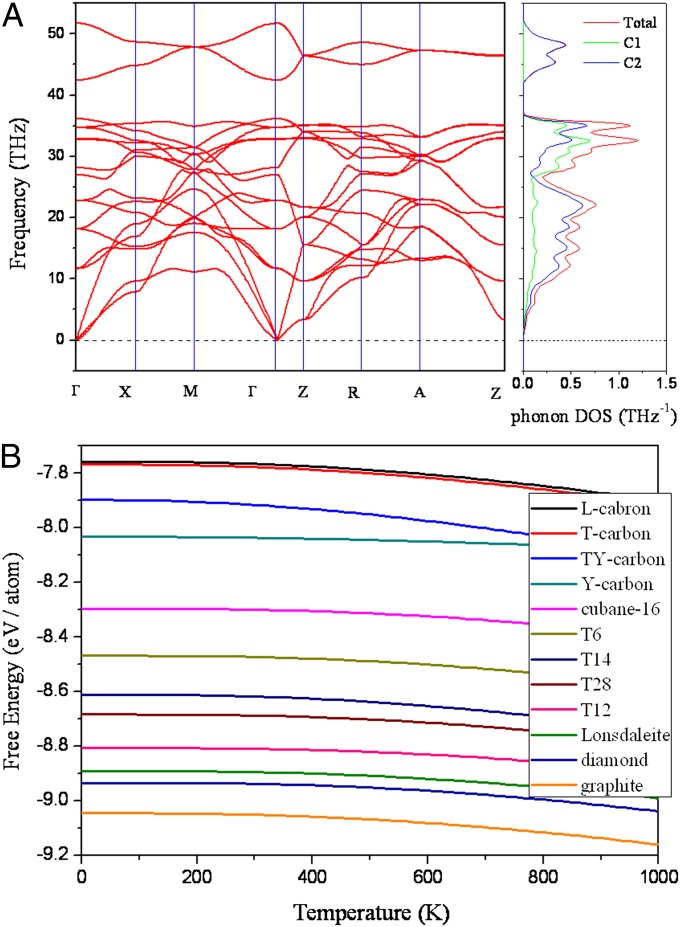
We first examine the dynamical stability of the T6-carbon by calculating the phonon spectra. Phonon dispersion and the frequency DOS are displayed in Fig. 2A. All vibrational modes are found to be real, confirming that this structure is dynamically stable. Unlike the dynamically unstable K₄ phase that lacks high-frequency modes (17), we note that in the phonon spectra of T6-carbon, the highest frequency reaches about 50 THz, comparable to that in diamond. We resolve the frequency DOS into two parts contributed by C1 and C2 atoms, respectively. The partial frequency DOS in Fig. 2A explicitly shows that the high-frequency modes originate from the vibrations of the sp² bonding C2 atoms. This character is distinct from diamond and graphite in which the high-frequency modes are attributed to the sp³ single bonds and the conjugate sp² π bonds, respectively. Furthermore, by projecting the partial DOS (PDOS) of C2 atoms into three Cartesian directions, we find the high-frequency mode to be associated with the stretching of double bonds (Fig. S1).

Fig. 2.

Stability of T6 carbon. (A) Phonon dispersions and the corresponding total and partial frequency DOS. (B) Comparison of Helmholtz free energy vs. temperature for T6-carbon with some other nanoporous carbon allotropes.

Next we examine the mechanical stability of the T6-carbon. In the linear elastic range, the elastic constant tensor forms a symmetric 6 × 6 matrix with 21 independent components. For the tetragonal lattice, only C₁₁, C₁₂, C₁₃, C₃₃, C₄₄, and C₆₆ are independent (27). According to Born criteria (27), the elastic constants of a tetragonal crystal have to satisfy

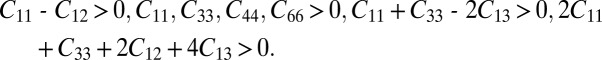To study the elastic properties of the carbon allotropes, six finite distortions of the lattice are used to calculate the elastic constants from the strain–stress relationship (27). The calculated elastic constants of the tetragonal T6-carbon and other carbon allotropes are listed in Table 1. These constants obey all of the conditions listed above, indicating that the T6-carbon structure is mechanically stable. In the previously reported metallic K₄ phase, C₁₁-C₁₂ > 0 criterion could not be satisfied (The K₄ phase has a cubic lattice. Therefore, it has three independent elastic constants C₁₁, C₄₄, and C₁₂. Its mechanical stability, according to Born criteria, has to be subject to C₁₁ > 0, C₄₄ > 0, C₁₁-C₁₂ > 0, C₁₁ + 2C₁₂ > 0). Hence, the K₄ phase is mechanically unstable (18). The bulk modulus calculated from fitting the energy–volume relationship (SI Methods) agrees very well with that estimated from the Voigt–Reuss–Hill approximation (28). The magnitude of the bulk modulus is fairly large (337.4 GPa); it is more than three quarters of that of diamond (433.1 GPa) (29) but comparable to that of cubic boron nitride (30). This indicates that T6-carbon is resistant to hydrostatic compression. The calculated mechanical properties of the T6 and other carbon allotropes are listed in Table S2.

Table 1.

Calculated elastic constants of some cubic and tetragonal carbon allotropes (GPa)

Structure	Diamond	T-carbon	T6	T12
C11	1,078.0	228	730.3	1,012.8
C33			1,164.5	1,001.7
C44	578.9	89	80.5	500.0
C66			68.3	607.9
C12	138.6	141	25.4	214.1
C13			88.8	152.7
B0	451.7	169	336.8	451.8
G0	535.2	70	196.6	422.1

To check the thermal stability, we need to take into account the contribution from lattice vibration. Helmholtz free energies of the T6-carbon and some other recently reported new phases of nanoporous carbon calculated by using the quasi-harmonic approximation (31) are plotted in Fig. 2B. In a wide temperature range, the T6-carbon is thermodynamically metastable compared with diamond and graphite but more stable than many other carbon allotropes including T-carbon (20), L-carbon (21), Y- and TY-carbon (22), and cubane-16 (23). To examine whether the T6-carbon is thermally stable at room temperature, we performed ab initio molecular dynamics (MD) simulations at 300 K with a 4 × 4 × 2 supercell. The geometry of T6-carbon remains nearly intact after heating for more than 6 picoseconds, and the total energy remains almost invariant. These results indicate that the T6-carbon, once synthesized, can be stable at room temperature.

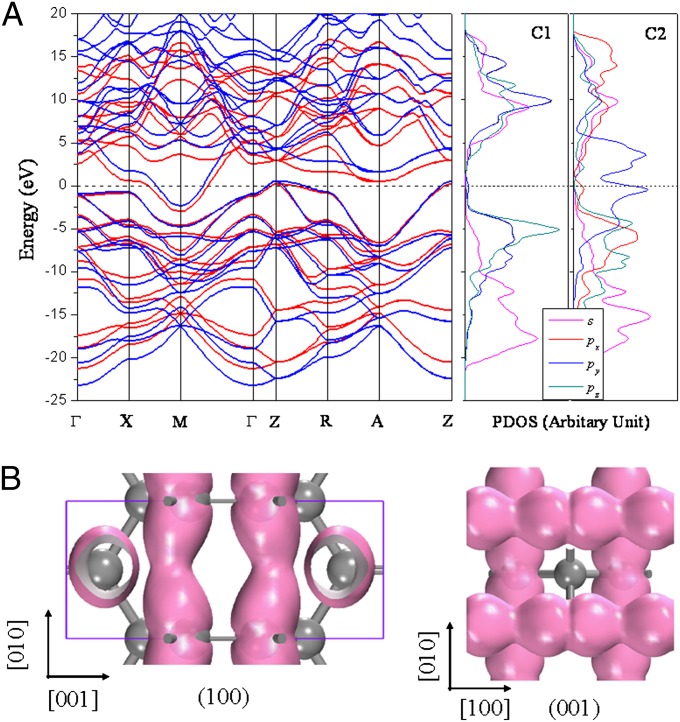
The metallic properties of T6-carbon are studied by calculating the electronic band structure. The results are plotted in Fig. 3A. The Fermi level crosses the highest occupied band in the vicinity of the M point in the Brillouin zone, indicating that T6-carbon is metallic. To further confirm this feature, we recalculated the electronic structure of the system using the screened Coulomb hybrid density functional developed by Heyd, Scuseria, and Ernzerhof (HSE06) (32, 33), which is known to be more accurate in describing the exchange-correlation energy of electrons in solids. The calculated band structure is also plotted in Fig. 3A, in which a modest systematic shift of the highest occupied band can be observed compared with the Perdew–Burke–Ernzerhof (PBE) results within generalized gradient approximation (GGA). However, the metallicity remains unaltered at the HSE06 level, suggesting that the metallic feature of T6-carbon is robust. The projected electron DOS for C1 and C2 atoms in Fig. 3A shows that the dominant contribution to the DOS at the Fermi level comes from C2 atoms.

Fig. 3.

(A) Electronic band structures of T6-carbon calculated using DFT-GGA/PBE (red lines) and HSE06 hybrid functional (blue lines), and projected DOS for C1 and C2 atom at DFT-GGA/PBE level. (B) Charge density isosurface (0.05 e/ų) of the partially occupied band of T6-carbon along the [100] and [001] directions.

To understand the origin of metallicity displayed in the unique phase of carbon, the band decomposed charge density was calculated to visualize the charge distribution in the partially occupied band near the Fermi level. We find that the main contribution to the charge density comes from the C2 atoms, and the electrons in their p_y orbitals form a delocalized network respectively along the [100] and [001] directions (Fig. 3B). These conducting channels are reminiscent of the metallic wires in graphene with 558 topological line defects (15). Referring to the PDOS in Fig. 3A, we can conclude that metallicity of T6-carbon originates from the delocalization of electrons in 2p orbitals of C2. Unlike the unstable K₄ phase where the metallicity comes from the twisted π bonds that lead to soft modes in the phonon spectra (17), the double bonds in T6 phase help avoid the dynamical instability.

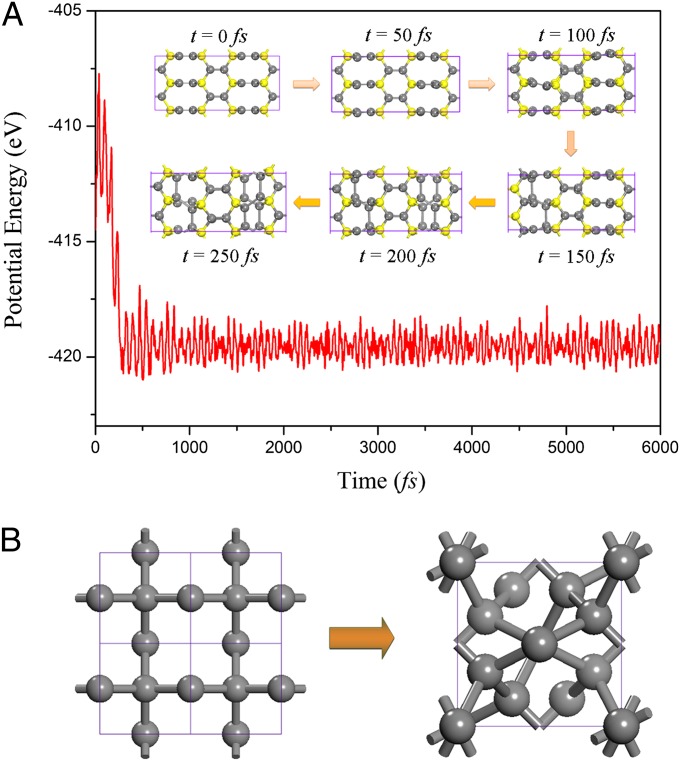
Based on MD simulations, we demonstrated that T6-carbon can withstand temperature up to 300 K. The question is: what is the highest temperature that the T6 phase can withstand? We found that when heated to 500 K, the sp² hybridized C2 atoms deviate from their original positions along the direction perpendicular to the hexagonal rings, resulting in the breakage of the double bonds. After 250 fs, these C2 atoms form single σ bonds with their next nearest neighbor C2 atoms, leading to a new phase with all C atoms in sp³ bonding mode. Snapshots of the structure at different simulation times are given in Fig. 4A. To see if the 500-K structure would remain stable down to 0 K, we reoptimized this structure at 0 K using density functional theory. The relaxed geometry led to a √2 × √2 × 1 reconstruction, which is identical to the recently reported T12 phase (29) (Fig. 4B). This thermal-induced phase transition indicates that the T6 phase could be a possible precursor of the T12 phase. From the T6- to T12-carbon, the density changes from 2.95 to 3.34 g/cm³. To aid experimentalists in identifying the T6-carbon phase, we calculated its Raman spectrum and compared it with graphite. The results are plotted in Fig. S2. We note that the Raman line is blue-shifted compared with graphite. Our results on graphite agree well with experiment (34), providing confidence on the predicted spectra for T6 carbon.

Fig. 4.

(A) Potential energy fluctuation of T6-carbon in MD simulation at 500 K. (Inset) Snapshots depict the process of phase transition. Yellow and gray spheres refer to C1 and C2 atoms, respectively. (B) The (001) view of T6 and T12 phases. The primitive cells are marked by purple squares.

We recall that the metallic T6 phase is stable at room temperature and zero pressure. To see if additional phases of carbon can be designed such that their stability and the metallic properties can be further enhanced over that of T6-carbon, we designed a unique structure by replacing the hexagon units in T6-carbon with fused hexagons. This phase could be synthesized experimentally by using acene molecules or polyacenes (like C₁₀H₈, C₁₄H₁₀, C₁₈H₁₂) instead of benzene molecules (C₆H₆). Fig. 5A shows the geometry containing 14 atoms in the primitive cell (labeled as T14-carbon). Its dynamical stability is also confirmed from the phonon spectra, as shown in Fig. 5B. The calculated electronic band structure clearly shows that the T14-carbon is even more metallic than the T6-carbon (Figs. 3A and 5C). MD simulations at T = 500 K suggest that the T14-carbon undergoes a √2 × √2 × 1 reconstruction yielding a new phase containing 28 atoms per cell, labeled as T28-carbon (Fig. S3A). Here double bonds between the sp² atoms still exist; thus, metallicity remains. The free energy curves of the T14- and T28-carbon are also presented in Fig. 2B, indicating that both the T14 and T28 phases are thermodynamically more stable than the T6 phase. The dynamic stability of the T28 phase is confirmed by calculating the phonon spectrum (Fig. S3B).

Fig. 5.

The T14-carbon consisting of interlocking fused hexagons: (A) optimized geometry, (B) phonon dispersions, and (C) electronic band structure.

In summary, we showed that the rich physics and chemistry of carbon got even richer with the demonstration that 3D carbon structures formed of interlocking hexagons are metallic under ambient conditions. These studied metallic 3D carbon structures are systems with hybridized sp³ and sp² bonding. They have the unique feature that sp³ bonded C atoms guarantee their stability and the sp² bonded C atoms ensure their metallicity. This magic combination results in the following desired properties: (i) unlike previously reported structures, our designed structures are metallic and stable at ambient thermodynamic conditions; (ii) unlike high pressure techniques that require 3 TPa to make carbon metallic, our studied structures may be chemically fabricated using benzene or polyacenes molecules that have already been used in the synthesis of carbon nanotubes; and (iii) at 500 K, the metallic T6 phase changes to the recently identified T12 phase, whereas the metallic T14 phase changes to the metallic T28 phase. The displayed metallicity, high stability, porosity, and ultralightness of the unique carbon phases could usher new technologies. We hope that the present study will stimulate experimental effort in this direction.

Methods

Our studies are based on density functional theory (DFT) and the projector augmented wave (PAW) method (35) as implemented in the Vienna ab initio Simulation Package 5.2 (VASP 5.2) (36). The valance electron wave functions of C (2s²2p²) are expanded using plane-wave basis sets with a kinetic energy cutoff of 500 eV. The electronic exchange-correlation functional prescribed by PBE (37) is used except as otherwise stated. The integration in the reciprocal space is replaced by the summation over K points sampled by the Γ-point-centered Monkhorst-Pack scheme (38) with a grid density of 2π × 0.02 Å⁻¹. A conjugate gradient algorithm is used to optimize the lattice constants and the atomic configurations. Convergence criteria for total energy and Hellmann–Feynman force components are set at 10⁻⁴ eV and 10⁻³ eV/Å, respectively. Phonon dispersions and frequency DOS are calculated using finite displacement method (39) implemented in the Phonopy code (40). The accuracy of this method is carefully checked by recalculating the phonon dispersion of T6-carbon using density functional perturbation theory (DFPT) (41), yielding consistent results. The Canonical (NVT) ensemble is used for MD simulations with the Nosé thermostat (42). A 4 × 4 × 2 supercell is used for the MD simulation to ensure accuracy. Each simulation lasted for 6 ps, with a time step of 1 fs. Elastic constants of carbon allotropes are determined by the finite distortion formalism (27), and bulk modulus is obtained by fitting the equation of states (SI Methods).

For calculations of lattice properties, the Helmholtz free energy is given by

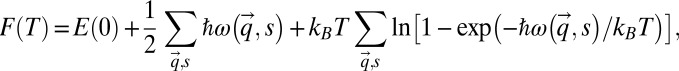where 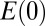is the static lattice energy at 0 K. The second and third terms in the above formula correspond to the zero point energy and vibrational energy at finite temperature, respectively. 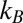and 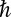are the Boltzmann constant and Planck’s constant, respectively, and 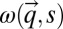stands for the sth phonon frequency with a wave vector 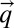at 0 K. The variations in the temperature-dependent electron occupation and electron-phonon coupling are neglected.