Group testing regression model estimation when case identification is a goal

Abstract

Group testing is frequently used to reduce the costs of screening a large number of individuals for infectious diseases or other binary characteristics in small prevalence situations. In many applications, the goals include both identifying individuals as positive or negative and estimating the probability of positivity. The identification aspect leads to additional tests being performed, known as “retests,” beyond those performed for initial groups of individuals. In this paper, we investigate how regression models can be fit to estimate the probability of positivity while also incorporating the extra information from these retests. We present simulation evidence showing that significant gains in efficiency occur by incorporating retesting information, and we further examine which testing protocols are the most efficient to use. Our investigations also demonstrate that some group testing protocols can actually lead to more efficient estimates than individual testing when diagnostic tests are imperfect. The proposed methods are applied retrospectively to chlamydia screening data from the Infertility Prevention Project. We demonstrate that significant cost savings could occur through the use of particular group testing protocols.

1 Introduction

Pooling specimens to screen a population for infectious diseases has a long history dating back to Dorfman’s (1943) proposal to screen American soldiers for syphilis during World War II. Today, testing individuals in pools through group testing (also known as “pooled testing”) has been successfully adopted in many additional areas, including entomology (Gu et al. 2004), veterinary medicine (Muñoz-Zanzi et al. 2000), DNA screening (Berger et al. 2000), and drug discovery (Kainkaryam and Woolf 2009). When compared to testing specimens individually, group testing can provide considerable savings in time and costs when the overall prevalence of the disease (or some other binary characteristic of interest) is low. This makes the use of group testing particularly desirable in applications where there are limitations in resources.

Group testing is generally used for two purposes: case identification and prevalence estimation. The goal of case identification is to identify all individuals as being positive or negative. Individual specimens are initially pooled into groups, and these groups are tested. Individuals within positive testing groups are then retested in some prior specified way to distinguish positive individuals from those that are negative. The goal of prevalence estimation is to estimate the prevalence of positivity in a population. Retesting is not needed in this case because initial group test responses alone can be used to estimate the prevalence. However, when prevalence estimation and case identification are simultaneous goals, the additional retesting information can be used for estimation as well. Intuitively, one would expect statistical benefits (e.g., in terms of efficiency) from including retest outcomes as part of the estimation process. Our paper examines how to include retests while also quantifying the benefits from their inclusion.

The majority of group testing estimation research has focused on inference for an overall prevalence p using only the results from the initial group tests (e.g., Swallow 1985; Biggerstaff 2008; Hepworth and Watson 2009). A few papers, such as Sobel and Elashoff (1975) and Chen and Swallow (1990), discuss including retests to estimate p, but under the restriction of perfect testing and without positive case identification. More recently, estimation research has focused on regression modeling to obtain an estimate of individual positivity, given a set of risk factors. The seminal papers in this area, Vansteelandt et al. (2000) and Xie (2001), both propose likelihood-based estimation and inference using binary regression models, but their approaches differ. Vansteelandt et al. (2000) use a likelihood function written in terms of the initial group responses, and standard techniques for generalized linear models are used to find the parameter estimates that maximize this function. Xie (2001) uses a likelihood function written in terms of the true latent individual statuses and then employs the expectation-maximization (EM) algorithm to maximize the likelihood function. The main advantage of Xie’s approach is that it allows for the inclusion of retests.

Given the large number of ways to retest individuals within positive groups (see Hughes-Oliver (2006) for a review), it is important to determine if there are benefits from including retest outcomes when estimating a group testing regression model. The purpose of our paper is to determine first if benefits truly exist, and then to determine which group testing protocol (algorithm used for the initial testing and subsequent retesting) is the most efficient. This is especially important because group testing is typically applied in settings where cost and time considerations are a primary concern. Ideally, one would want to apply a protocol that results in the fewest number of tests while also producing the most efficient regression estimates. Also, model estimation plays a significant role in the application of informative retesting procedures for case identification (e.g., see Bilder et al. (2010) and Black et al. (2012)). These identification procedures rely on group testing regression models to identify which individuals are most likely to be positive, so having the best possible estimates is crucial.

Our research is motivated by the Infertility Prevention Project (IPP; http://www.cdc.gov/std/infertility/ipp.htm) in the United States, where both prevalence estimation and case identification are important. The purpose of the IPP is to prevent complications from chlamydia and gonorrhea infections in humans. Testing individuals for these diseases is a central part of the IPP, and over 3 million screenings are reported to the IPP annually. In addition to being tested, each individual provides demographic background information and risk history, and healthcare professionals provide clinical observations on each individual. The specific information available on each individual varies by the state in which the individual is tested. Using this information, probabilities of positivity can be estimated to obtain a better understanding of disease positivity for a particular state. In our paper, we will focus on the testing performed by the Nebraska Public Health Laboratory (NPHL), which completes all tests for people screened in Nebraska. This laboratory has an interest in adopting group testing–not only to reduce the number of tests, but also to estimate risk factor - specific probabilities of infection. Using past individual diagnoses, we will assess which group testing protocol provides the most cost effective approach.

The order of our paper is as follows. Section 2 reviews three commonly used group testing protocols. None of these protocols were examined specifically in Xie (2001), so this is the first time that the EM algorithm details have been formally presented for them. In Section 3, we use simulation to investigate the benefits from including retests and to determine which protocol is the most efficient. This section also shows that group testing can actually be more efficient than individual testing when estimating regression parameters. In Section 4, we examine these protocols with respect to chlamydia screening in Nebraska. Finally, Section 5 summarizes our findings and discusses extensions of this research.

2 Estimation of group testing regression models

Define Ỹ_ik = 1 if the i^th individual in the k^th initial group is truly positive and Ỹ_ik = 0 otherwise, for i = 1, …, I_k and k = 1, …, K. Our goal is to estimate E(Ỹ_ik) = p̃_ik, conditional on a set of covariates x_1ik, …, x_g-1,ik, using the regression model

$$f({\tilde{p}}_{ik})={\beta }_0+{\beta }_1{x}_{1ik}+\cdots +{\beta }_{g-1}{x}_{g-1,ik},$$ (1)

where f(·) is a known monotonic, differentiable function. The log-likelihood function can be written as

$$\text{log}[L(\mathit{\beta })]=\sum _{k=1}^K\sum _{i=1}^{I_k}{\tilde{y}}_{ik}\text{log}({\tilde{p}}_{ik})+(1-{\tilde{y}}_{ik})\text{log}(1-{\tilde{p}}_{ik}),$$ (2)

where β = (β₀,…,β_g−1)′ and we assume that the Ỹ_ik’s are independent Bernoulli(p̃_ik) random variables. If the true individual statuses Ỹ_ik were observed, likelihood-based estimation for the model would proceed in a straightforward manner.

In group testing applications, the individual statuses Ỹ_ik are unknown because only group responses may be observed and because groups and/or individuals may be misclassified due to diagnostic testing error. To fit the model, Xie (2001) proposed the use of an EM algorithm to find the parameter estimates that maximize the likelihood function. The algorithm works by replacing the unobserved outcomes ỹ_ik in Equation (2) by (ω_ik ≡ E(Ỹ_ik | ℐ), where ℐ denotes all information obtained by group tests and retests under a particular group testing protocol. The expectation and maximization steps of the algorithm alternate iteratively until convergence is reached to obtain the maximum likelihood estimate of β, denoted by β̂. The estimated covariance matrix of β̂ is obtained by standard methods; e.g., see Louis (1982) and Xie (2001, p. 1960).

The most difficult aspect of the EM algorithm application is to obtain the conditional expectations ω_ik. Xie (2001) provides details only for the protocol outlined in Gastwirth and Hammick (1989), which involves testing individuals in non-overlapping groups and performing one confirmatory test on groups that test positive. While this protocol can be extremely useful for estimation purposes, it can not be used to identify positive individuals. In this paper, we consider three group testing protocols commonly used in practice for case identification. The following subsections elaborate on how to calculate the conditional expectations ω_ik for each protocol. Given these details, the EM algorithm for estimating the model in Equation (1) becomes straightforward to implement.

2.1 Initial group tests from non-overlapping groups

Initial tests from groups that are non-overlapping (i.e., each individual is within only one group) do provide enough information to estimate Equation (1), although not as efficiently as other case identification protocols to be discussed shortly. We begin by describing how models can be fit under this setting to motivate model fitting when retests are included.

Define Z_k as the response for initial group k, where Z_k = 1 denotes a positive test result and Z_k = 0 denotes a negative test result. Because diagnostic tests are likely subject to error, we define the true status of a group by Z̃_k where a 1 (0) again denotes a positive (negative) status. The sensitivity and specificity of the group test are given by η = P(Z_k = 1 | Z̃_k = 1) and δ = P(Z_k = 0 | Z̃_k = 0), where we assume these values are known and do not depend on group size. These assumptions are consistent with most research for group testing regression, including Vansteelandt et al. (2000) and Xie (2001). When only the initial group responses are observed, ω_ik is easily found as

$${\omega }_{ik}=\{\begin{array}{ll}P({\tilde{Y}}_{ik}=1|Z_k=0)=(1-\eta ){\tilde{p}}_{ik}/(1-{\theta }_k),\hfill & \text{if}{Z}_k=0\hfill \\ P({\tilde{Y}}_{ik}=1|Z_k=1)=\eta {\tilde{p}}_{ik}/{\theta }_k,\hfill & \text{if}{Z}_k=1,\hfill \end{array}$$ (3)

where

$${\theta }_k=P(Z_k=1|{\tilde{Z}}_k=1)P({\tilde{Z}}_k=1)+P(Z_k=1|{\tilde{Z}}_k=0)P({\tilde{Z}}_k=0)=\eta +\phi \prod _{i=1}^{I_k}(1-{\tilde{p}}_{ik})$$

is the probability that group k tests positive and φ = 1 − η − δ.

2.2 Dorfman

After initially testing individuals in non-overlapping groups, Dorfman (1943) proposed to individually retest all specimens within the positive testing groups. Individuals within negative testing groups are declared negative. Because of its simplicity, Dorfman’s protocol is the most widely adopted protocol for case identification, and its applications include screening blood donations (Stramer et al. 2004), chlamydia testing (Mund et al. 2008), and potato virus detection (Liu et al. 2011).

Because specimens are retested, ω_ik is no longer the same as given in Equation (3) when a group tests positive. Let Y_ik denote the retest outcome for individual i in group k and assume that the same assay for group tests is also used for individual retests (thus, η is the sensitivity and δ is the specificity for properly calibrated tests). For observed positive groups (Z_k = 1), we have calculated

$${\omega }_{ik}=P({\tilde{Y}}_{ik}=1|Y_{1k}=y_{1k},\dots ,Y_{I_{k}k}=y_{I_{k}k},Z_k=1)=\frac{\eta {\tilde{p}}_{ik}P(Y_{ik}=y_{ik}|{\tilde{Y}}_{ik}=1)\prod _{i\prime \ne i}\sum _{{\tilde{y}}_{i\prime k}=0}^{1}P(Y_{i\prime k}=y_{i\prime k}|{\tilde{Y}}_{i\prime k}={\tilde{y}}_{i\prime k})P({\tilde{Y}}_{i\prime k}={\tilde{y}}_{i\prime k})}{\phi \prod _{i\prime =1}^{I_k}P(Y_{i\prime k}=y_{i\prime k}|{\tilde{Y}}_{i\prime k}=0)(1-{\tilde{p}}_{i\prime k})+\eta \prod _{i\prime =1}^{I_k}\sum _{{\tilde{y}}_{i\prime k}=0}^{1}P(Y_{i\prime k}=y_{i\prime k}|{\tilde{Y}}_{i\prime k}={\tilde{y}}_{i\prime k})P({\tilde{Y}}_{i\prime k}={\tilde{y}}_{i\prime k})}.$$

Derivation details are provided in Web Appendix A of the Supporting Information for this paper.

2.3 Halving

As its name suggests, halving works by first splitting a positive testing initial group into two equally (or as close to as possible) sized subgroups for retesting. Whenever a subgroup tests negative, all of its individuals are declared negative and no further splitting is performed. Whenever a subgroup tests positive, continued splitting occurs in the same manner until only individuals remain. Early origins of the halving protocol go back as far as Sobel and Groll (1959). More recently, halving and its close variants have been used in a number of infectious disease screening applications, including Litvak et al. (1994) and Priddy et al. (2007). Halving has even been described in the product literature for high throughput screening platforms (Tecan Group Ltd. 2007).

For a group of size I_k = 2^s, there are s possible hierarchical splits that contain a particular individual specimen, where the last split results in individual testing. For practicality reasons, all possible hierarchical splits are rarely implemented. Instead, individual testing is performed on subgroups at a pre-determined t^th split, where t ≤ s. For this reason, we will only consider the t = 2 case, so that an individual can be tested at most three times (twice within a group and once alone).

To derive ω_ik under halving, we continue to define Z_k as the initial group response for group k, k = 1, …, K. If the initial group tests positive (Z_k = 1), it is split into two subgroups that we denote by k1 and k2. The two subgroups are subsequently tested and provide the corresponding binary responses Z_k1 and Z_k2. If either subgroup tests positive, the third and final step is to individually test all members within a subgroup, where we continue to define Y_ik as the individual retest outcome for individual i from initial group k. To denote the true statuses for the groups, subgroups, and individual tests under halving, we again use a tilde over the respective letter symbol. We also continue to assume constant sensitivity and specificity for each test regardless of the group size.

For the halving protocol outlined above, there are five possible testing scenarios involving the initial group and its two subgroups. These scenarios are:

1. Z_k = 0: Group k tests negative,

2. Z_k = 1, Z_k1 = 0, Z_k2 = 0: Group k tests positive, but both subgroups test negative,

3. Z_k = 1, Z_k1 = 1, Z_k2 = 0: Group k tests positive, subgroup k1 tests positive leading to individual testing for its members, and subgroup k2 tests negative,

4. Z_k = 1, Z_k1 = 0, Z_k2 = 1: Group k tests positive, subgroup k1 tests negative, and subgroup k2 tests positive leading to individual testing for its members,

5. Z_k = 1, Z_k1 = 1, Z_k2 = 1: Group k tests positive and both subgroups test positive leading to individual testing for members of both subgroups.

In Table 1, we provide expressions for ω_ik in each of these scenarios. Derivations are similar to those for the Dorfman protocol in Section 2.2, but they are much more tedious due to the additional split in the testing process. We present the derivations in Web Appendix B of the Supporting Information for this paper.

Table 1.

The numerator and denominator of ω_ik for the halving protocol described in Section 2.3. To simplify the expressions, q̃_ik =1−p̃_ik and ${\lambda }_{ik}^{({\tilde{y}}_{ik})}=P(Y_{ik}=y_{ik}|{\tilde{Y}}_{ik}={\tilde{y}}_{ik})$ are used, and we assume individual i is within subgroup k1.

Scenario	Numerator	Denominator
1	(1−η)p̃ik	1−θik
2	$\eta (1-\eta ){\tilde{p}}_{ik}[\delta \prod _{i\prime \in k2}{\tilde{q}}_{i\prime k}+(1-\eta )(1-\prod _{i\prime \in k2}{\tilde{q}}_{i\prime k})]$	$$\begin{gathered} {\delta }^2(1-\delta )\prod _{i\prime =1}^{I_k}{\tilde{q}}_{i\prime k}+\delta \eta (1-\eta )(\prod _{i\prime \in k1}{\tilde{q}}_{i\prime k})(1-\prod _{i\prime \in k2}{\tilde{q}}_{i\prime k})+\delta \eta (1-\eta )(1-\prod _{i\prime \in k1}{\tilde{q}}_{i\prime k})(\prod _{i\prime \in k2}{\tilde{q}}_{i\prime k})+ \\ \eta {\left(1-\eta \right)}^2(1-\prod _{i\prime \in k1}{\tilde{q}}_{i\prime k})(1-\prod _{i\prime \in k2}{\tilde{q}}_{i\prime k}) \end{gathered}$$
3	$$\begin{gathered} {\eta }^2{\tilde{p}}_{ik}{\lambda }_{ik}^{(1)}\sum _{{\tilde{y}}_{-1,k1}}(\prod _{i\prime \in k1,i\prime \ne i}{\lambda }_{i\prime k}^{({\tilde{y}}_{i\prime k})}P({\tilde{Y}}_{i\prime k}={\tilde{y}}_{i\prime k}))\times \\ [\delta \prod _{i\prime \in k2}{\tilde{q}}_{i\prime k}+(1-\eta )(1-\prod _{i\prime \in k2}{\tilde{q}}_{i\prime k})] \end{gathered}$$	$$\begin{gathered} \delta {\left(1-\delta \right)}^2(\prod _{i\prime \in k1}{\lambda }_{i\prime k}^{(0)}{\tilde{q}}_{i\prime k})(\prod _{i\prime \in k2}{\tilde{q}}_{i\prime k})+(1-\delta )\eta (1-\eta )(\prod _{i\prime \in k1}{\lambda }_{i\prime k}^{(0)}{\tilde{q}}_{i\prime k})(1-\prod _{i\prime \in k2}{\tilde{q}}_{i\prime k})+ \\ \delta {\eta }^2\sum _{{\tilde{y}}_{k1}\ne 0}(\prod _{i\prime \in k1}{\lambda }_{i\prime k}^{({\tilde{y}}_{i\prime k})}P({\tilde{Y}}_{i\prime k}={\tilde{y}}_{i\prime k}))(\prod _{i\prime \in k2}{\tilde{q}}_{i\prime k})+{\eta }^2(1-\eta )\sum _{{\tilde{y}}_{k1}\ne 0}(\prod _{i\prime \in k1}{\lambda }_{i\prime k}^{({\tilde{y}}_{i\prime k})}P({\tilde{Y}}_{i\prime k}={\tilde{y}}_{i\prime k}))(1-\prod _{i\prime \in k2}{\tilde{q}}_{i\prime k}) \end{gathered}$$
4	$$\begin{gathered} \eta (1-\eta ){\tilde{p}}_{ik}[\eta \prod _{i\prime \in k2}(\sum _{{\tilde{y}}_{i\prime k}=0}^1{\lambda }_{i\prime k}^{({\tilde{y}}_{i\prime k})}P({\tilde{Y}}_{i\prime k}={\tilde{y}}_{i\prime k}))+ \\ \phi \prod _{i\prime \in k2}{\lambda }_{i\prime k}^{(0)}{\tilde{q}}_{i\prime k}] \end{gathered}$$	$$\begin{gathered} \delta {(1-\delta )}^2(\prod _{i\prime \in k2}{\lambda }_{i\prime k}^{(0)}{\tilde{q}}_{i\prime k})(\prod _{i\prime \in k1}{\tilde{q}}_{i\prime k})+(1-\delta )\eta (1-\eta )(\prod _{i\prime \in k2}{\lambda }_{i\prime k}^{(0)}{\tilde{q}}_{i\prime k})(1-\prod _{i\prime \in k1}{\tilde{q}}_{i\prime k})+ \\ \delta {\eta }^2\sum _{{\tilde{y}}_{k2}\ne 0}(\prod _{i\prime \in k2}{\lambda }_{i\prime k}^{({\tilde{y}}_{i\prime k})}P({\tilde{Y}}_{i\prime k}={\tilde{y}}_{i\prime k}))(\prod _{i\prime \in k1}{\tilde{q}}_{i\prime k})+{\eta }^2(1-\eta )\sum _{{\tilde{y}}_{k2}\ne 0}(\prod _{i\prime \in k2}{\lambda }_{i\prime k}^{({\tilde{y}}_{i\prime k})}P({\tilde{Y}}_{i\prime k}={\tilde{y}}_{i\prime k}))(1-\prod _{i\prime \in k1}{\tilde{q}}_{i\prime k}) \end{gathered}$$
5	$$\begin{gathered} {\eta }^2{\tilde{p}}_{ik}{\lambda }_{ik}^{(1)}\sum _{{\tilde{y}}_{-1,k1}}(\prod _{i\prime \in k1,i\prime \ne i}{\lambda }_{i\prime k}^{({\tilde{y}}_{i\prime k})}P({\tilde{Y}}_{i\prime k}={\tilde{y}}_{i\prime k}))\times \\ [\eta \prod _{i\prime \in k2}(\sum _{{\tilde{y}}_{i\prime k}=0}^1{\lambda }_{i\prime k}^{({\tilde{y}}_{i\prime k})}P({\tilde{Y}}_{i\prime k}={\tilde{y}}_{i\prime k}))+\phi \prod _{i\prime \in k2}{\lambda }_{i\prime k}^{(0)}{\tilde{q}}_{i\prime k}] \end{gathered}$$	$$\begin{gathered} {\left(1-\delta \right)}^3\prod _{i\prime =1}^{I_k}{\lambda }_{i\prime k}^{(0)}{\tilde{q}}_{i\prime k}+(1-\delta ){\eta }^2(\prod _{i\prime \in k1}{\lambda }_{i\prime k}^{(0)}{\tilde{q}}_{i\prime k})\sum _{{\tilde{y}}_{k2}\ne 0}(\prod _{i\prime \in k2}{\lambda }_{i\prime k}^{({\tilde{y}}_{i\prime k})}P({\tilde{Y}}_{i\prime k}={\tilde{y}}_{i\prime k}))+ \\ (1-\delta ){\eta }^2\sum _{{\tilde{y}}_{k1}\ne 0}(\prod _{i\prime \in k1}{\lambda }_{i\prime k}^{({\tilde{y}}_{i\prime k})}P({\tilde{Y}}_{i\prime k}={\tilde{y}}_{i\prime k}))(\prod _{i\prime \in k2}{\lambda }_{i\prime k}^{(0)}{\tilde{q}}_{i\prime k})+ \\ {\eta }^3\sum _{{\tilde{y}}_{k1}\ne 0}(\prod _{i\prime \in k1}{\lambda }_{i\prime k}^{({\tilde{y}}_{i\prime k})}P({\tilde{Y}}_{i\prime k}={\tilde{y}}_{i\prime k}))\sum _{{\tilde{y}}_{k2}\ne 0}(\prod _{i\prime \in k2}{\lambda }_{i\prime k}^{({\tilde{y}}_{i\prime k})}P({\tilde{Y}}_{i\prime k}={\tilde{y}}_{i\prime k})) \end{gathered}$$

2.4 Array testing

Both Sections 2.2 and 2.3 describe protocols where individuals are initially tested in non-overlapping groups. Phatarfod and Sudbury (1994) proposed a fundamentally different protocol where specimens are arranged into a two-dimensional array. Samples from specimens are combined within rows and within columns so that each individual is tested twice in overlapping groups. Specimens lying outside of any positive rows and columns are classified as negative. Specimens lying inside a positive row and/or column are potentially positive. This protocol is known as array (matrix) testing, and it is widely applied in high throughput screening applications, such as infectious disease testing (Tilghman et al. 2011), DNA screening (Berger et al. 2000), and systems biology (Thierry-Mieg 2006).

Because individuals are initially tested within one row and one column, we must modify our notation to reflect this. Define Ỹ_ij as the true binary status (0 denotes negative, 1 denotes positive) for the individual whose specimen is located within row i and column j, for i = 1, …, I and j = 1, …, J. With this slight change in notation, our group testing regression model now can be rewritten as

$$f({\tilde{p}}_{ij})={\beta }_0+{\beta }_1{x}_{1ij}+\cdots +{\beta }_{g-1}{x}_{g-1,ij},$$

where the Ỹ_ij’s are independent Bernoulli(p̃_ij) random variables, and the full-data log-likelihood function can be rewritten as

$$\text{log}[L(\mathit{\beta })]=\sum _{i=1}^I\sum _{j=1}^J{\tilde{y}}_{ij}\text{log}({\tilde{p}}_{ij})+(1-{\tilde{y}}_{ij})\text{log}(1-{\tilde{p}}_{ij}),$$

if the true individual statuses were observed. In most screening applications, there will be more than IJ individuals, so more than one array will be needed. In those cases, we could add a third subscript to Ỹ_ij to denote the array and include a third sum over the arrays in log[L(β)]. We avoid doing this for brevity.

As before, because the individual statuses are not observed directly, the EM algorithm is used to fit the regression model. Define R = (R₁, …, R_I)′ and C = (C₁, …, C_J)′ as vectors of row and column binary responses, respectively, for one array. If identification of positive individuals is of interest, specimens lying at the intersections of positive rows and columns are retested individually. Additionally, specimens in positive testing rows without any positive testing columns in the array, which can occur when there is testing error, should be retested as well. The same is true when columns test positive without any rows testing positive. Without loss of generality, we denote the collection of all potentially positive individual responses by Y_Q = (Y_ij)_{(i, j)∈Q} where Q is the index set pertaining to the individual tests, that is

$$Q=\{(s,t)|R_s=1,C_t=1,1\le s\le I,1\le t\le J\text{or}{R}_s=1,C_1=\cdots =C_J=0,1\le s\le I\text{or}{R}_1=\cdots =R_I=0,C_t=1,1\le t\le J\}.$$

If there are no individual tests performed, we simply let Q = Ø, the empty set.

Using all available test responses, we need to obtain the conditional expected value ω_ij ≡ E(Ỹ_ij | ℐ); however, when array testing is used as described above, there is no longer a closed form expression for it. Therefore, as suggested by Xie (2001), we implement a Gibbs sampling approach to estimate ω_ij. This involves successive sampling from the univariate conditional distribution of Ỹ_ij given R = r, C = c, Y_Q = y_Q, and all of the other true individual binary statuses in the array, and this sampling is performed for each i and j. After a large set of samples, the simulated ỹ_ij values for each i and j can be averaged to find an estimate of ω_ij. Implementation details are described next.

For a given row and column combination (i, j), define Ỹ_−i,−j = {Ỹ_i′,j′:i′ = 1,…,I,j′ = 1,…,J,(i′,j′) ≠(i,j)} i.e., all true individual statuses excluding Ỹ_ij. The conditional distribution for Ỹ_ij | ỹ_−I,−j,r,c,y_Q is Bernoulli(γ_ij), where γ_ij ≡ P(Ỹ_ij = 1 | Ỹ_−i,−j = ỹ_−i,−j,R=r,C=c,Y_Q=y_Q) which we derive in Web Appendix C of the Supporting Information for this paper. With these conditional distributions, we generate samples ${\tilde{y}}_{11}^{(b)},\dots ,{\tilde{y}}_{IJ}^{(b)}$ for b = 1, …, B, using the most updated ỹ_−i,−j. The estimate for ω_ij is then taken to be ${\widehat{\omega }}_{ij}={\left(B-a\right)}^{-1}{\sum }_{b=a+1}^B{\tilde{y}}_{ij}^{(b)}$, where a is a sufficiently large number of burn-in samples. The EM algorithm proceeds as usual where ω̂_ij replaces ω_ij in each E-step. The negative information matrix can be estimated using these B Gibbs samples (e.g., see Xie (2001, p. 1961)).

3 Simulation study

We use simulation to evaluate the regression estimators resulting from the group testing protocols described in Section 2. To begin, we consider the model logit(p̃_ik) = β₀ + β₁x_ik, which is equivalently logit(p̃_ij) = β₀ + β₁x_ij for the array testing protocols. We let β₀ = −7 and β₁ = 0.1 and simulate covariates from a gamma(17, 1.4) distribution. The regression parameters and covariate distribution are chosen to produce a realistic group testing setting where most individuals have low risks of being positive and a few individuals have higher risks. Web Appendix D in the Supporting Information provides a histogram of the true individual probabilities for one simulated data set under these settings. Note that the overall mean prevalence is approximately 0.01.

Based on the logit model, we obtain the true probability of positivity p̃_ik (p̃_ij for array testing), which in turn is used to simulate a true individual status Ỹ_ik (Ỹ_ij for array testing). Individuals are then randomly assigned to groups of size I(I×I arrays are used for array testing). Group, subgroup, and individual test responses for each protocol are simulated next by using η and δ as Bernoulli success probabilities. Group testing regression models are fit to these resulting responses. For comparison purposes, we also fit a model to individual testing data when testing error is present using the methodology outlined in Neuhaus (1999). We repeat the same simulation process for each simulated data set of size 5000 individuals. Large sample sizes such as this are common in high volume clinical specimen settings, including the example in Section 4, where group testing is commonly used.

3.1 Estimator accuracy and variance estimation

Table 2 presents results on the accuracy of the parameter estimators and their standard errors for group sizes I= 4, 12, 20 and η = δ = 0.99. The mean rows give each regression parameter estimate averaged over 1000 simulated data sets. The SE/SD rows examine the accuracy of the standard error estimates, where SD denotes the sample standard deviation of estimates across all simulated data sets, and SE denotes the corresponding averaged standard errors. Thus, a SE/SD ratio close to 1 suggests that the true standard errors are being estimated correctly on average. Note that because Gibbs sampling is used for array testing, the EM algorithm is much slower, so our array testing results are based on 300 simulated data sets.

Table 2.

Parameter estimates and standard errors based on 1000 (300 for array testing) simulated data sets with β₀ = −7, β₁ = 0.1, and η = δ = 0.99. The mean row includes the averaged estimate across all simulated data sets. The SE/SD row gives the averaged standard error over all simulated data sets (SE) divided by the sample standard deviation of the estimates across all data sets (SD).

		I = 4		I = 12		I = 20
Protocol		β̂0	β̂1	β̂0	β̂1	β̂0	β̂1
Individual	Mean	−7.003	0.099	−7.013	0.099	−7.016	0.099
	SE/SD	0.983	0.977	0.970	0.966	1.002	0.987
IG	Mean	−6.918	0.096	−6.840	0.091	−6.628	0.081
	SE/SD	0.961	0.948	0.886	0.854	0.861	0.840
Dorfman	Mean	−6.995	0.099	−7.013	0.100	−6.983	0.099
	SE/SD	1.002	1.008	0.982	0.982	0.978	0.980
Halving	Mean	−7.000	0.099	−7.015	0.099	−7.021	0.098
	SE/SD	1.016	1.020	0.982	0.982	0.978	0.973
Array w/o retesting	Mean	−7.024	0.099	−6.984	0.099	−7.023	0.099
	SE/SD	1.007	1.044	0.981	0.997	0.989	0.991
Array w/ retesting	Mean	−7.022	0.100	−7.010	0.100	−7.018	0.099
	SE/SD	0.982	1.017	1.001	1.011	0.979	0.979

We see from Table 2 that using non-overlapping initial groups (IG; Section 2.1) results in comparatively poor estimates of the parameters and their standard errors. These estimates and standard errors become increasingly worse as the group size grows. In contrast, all of the other protocols perform similarly to individual testing, where averaged parameter estimates are close to corresponding true values and SE/SD ratios are close to 1. As these results show, there are important benefits by including retesting information from the Dorfman and halving protocols.

3.2 Improvements in variance estimation from including retests

As the results in Section 3.1 demonstrate, parameters and corresponding standard errors can be estimated well when retests are included. In this subsection, we investigate directly the benefits of including retest information and how this extra information affects the slope estimator precision. Define the relative efficiency for β̂₁ as

$$\mathrm{R}\mathrm{E}({\widehat{\beta }}_{1,\text{Retest}}\text{to}{\widehat{\beta }}_{1,\text{No retest}})=\frac{1}{B}\sum _{b=1}^B\frac{\mathit{\text{Var}}({\widehat{\beta }}_{1,b,\text{No retest}})}{\mathit{\text{Var}}({\widehat{\beta }}_{1,b,\text{Retest}})},$$ (4)

where B denotes the number of simulations, β̂_1,b,Retest denotes the estimator for β₁ when retests are included in the b^th simulated data set, and β̂_{1,b,No retest} is defined similarly when retests are not included. Note that we use the true variances in Equation (4), rather than estimated variances, due to the length of time it takes to fit a model for array testing. For Dorfman and halving, we compare their variances to IG. For array testing, we compare variances with and without retests.

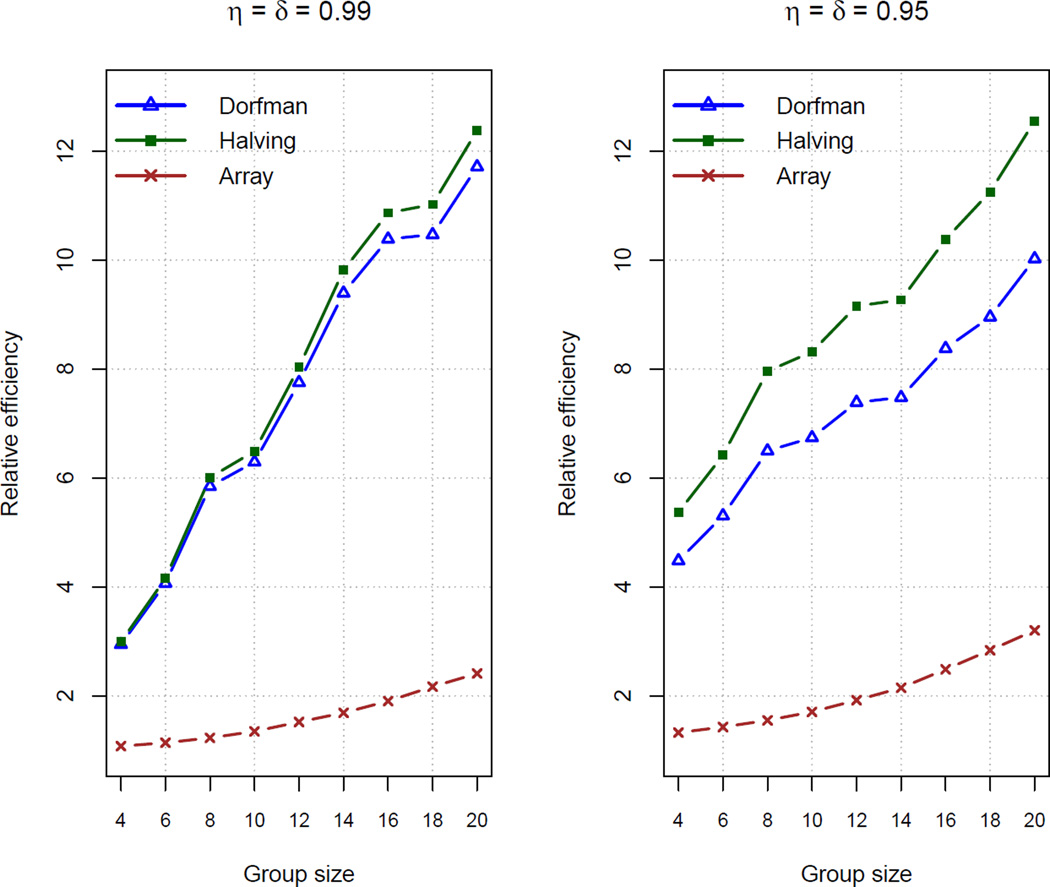
Figure 1 displays the relative efficiencies from B = 500 new simulated data sets for group sizes I = 4, 6, …, 20 when η = δ = 0.99 and η = δ = 0.95. Overall, we see very large efficiency gains from including retesting information. Array testing has the smallest gain, but this is not surprising because each individual is tested initially in two groups already; this is unlike IG where each individual is tested initially in one group. Halving results in larger gains than Dorfman, where the differences between them are more pronounced for smaller η and δ. This occurs because halving will usually result in a lower classification error rate than Dorfman (e.g., see Black et al. 2012), which then leads to less uncertainty in the parameter estimates under halving. Overall, the efficiencies for all protocols grow as the group size does. This is explained by the fact that protocols without retests observe less information as the group size increases. In contrast, retesting will moderate the amount of information lost for larger group sizes.

Figure 1.

Relative efficiencies calculated by Equation (4) based on 500 simulated data sets. Dorfman and halving protocols are compared to IG. Array testing is compared with and without retests.

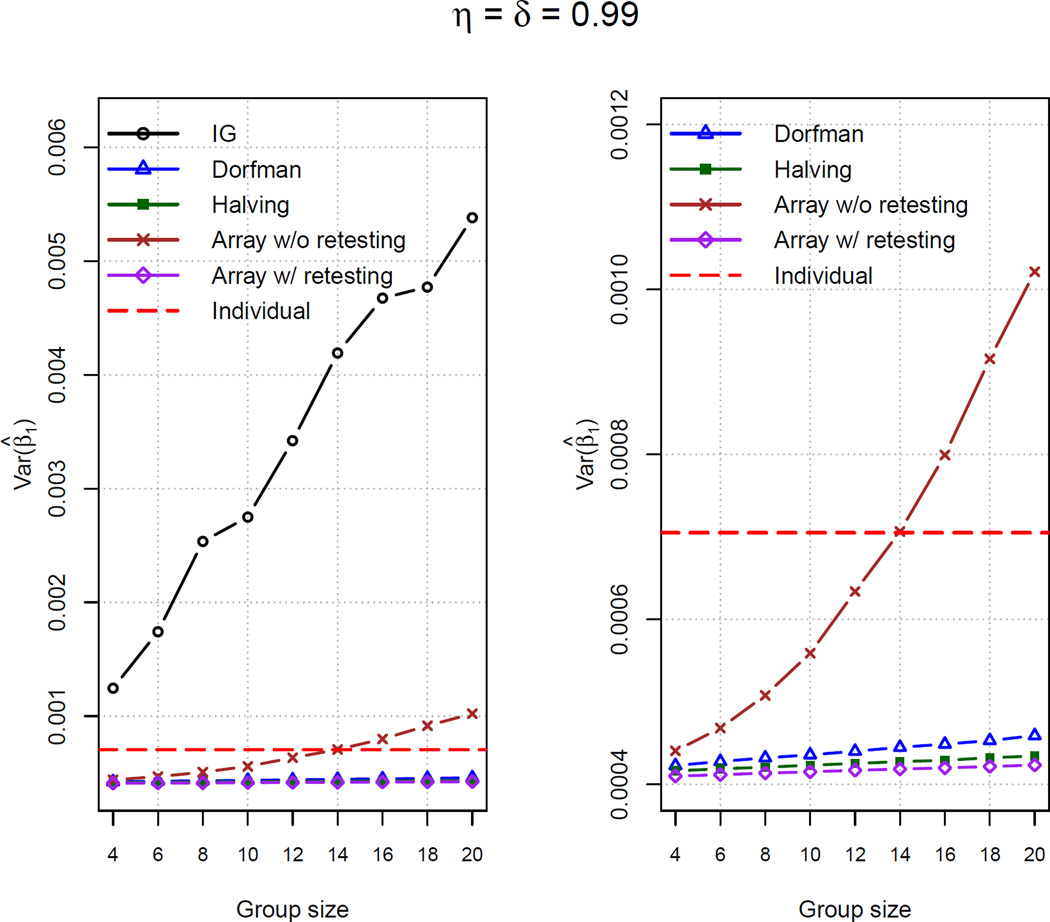
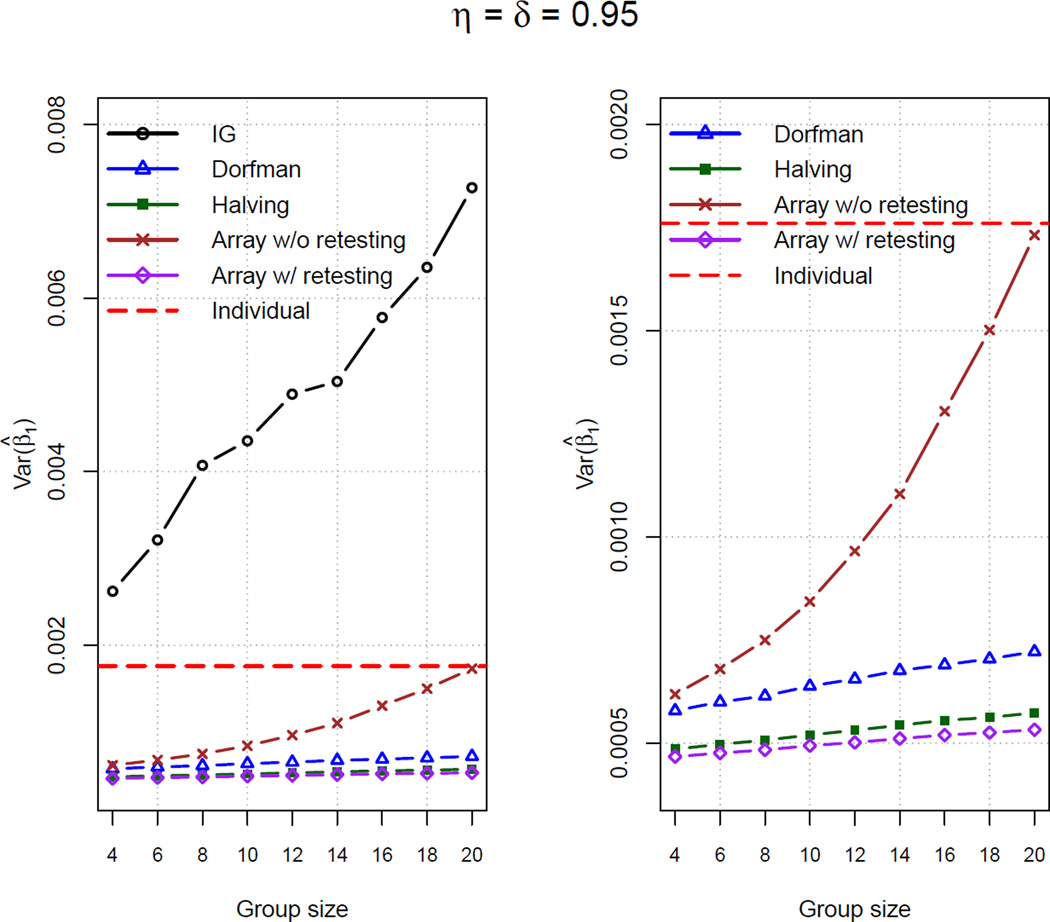
Figure 2 provides plots of the averaged Var(β̂₁) for all simulated data sets. One will note that the averaged Var(β̂₁) for the two testing protocols without retests increases as the group size increases. This is similar to Figure 1 where RE(β̂_1,Retest to β̂_{1,No retest}) increases as a function of the group size. Conversely, when retests are included in a protocol, the averaged Var(β̂₁) changes very little across the group sizes because positive individuals are still identified (subject to testing error).

Figure 2.

Averaged Var(β̂₁) for 500 simulated data sets. The dashed horizontal line corresponds to Var(β̂₁) from individual testing. The right-side plots are the same as those on the left-side except we omit IG in order to reduce the y-axis scale.

Ordered by their averaged Var(β̂₁), we can informally write Dorfman > halving > array testing with retests. Interestingly, each of these protocols (and also array testing without retests for smaller sensitivity, specificity, and group size levels) has a smaller variance than that found through individual testing, while also resulting in a smaller number of tests (see Web Appendix E in the Supporting Information). In other words, not only do these protocols have the potential to drastically reduce the costs needed for classification, but these protocols provide better regression estimates! Note that Liu et al. (2012, Theorem 2) has recently observed this same phenomenon in the absence of covariates. Through additional simulations (not shown), we have seen that the gains from group testing in estimation efficiency (over individual testing) do diminish as the assay sensitivity and specificity both approach 1. This is an expected result because both individual and group testing are likely to find all positive and negative individuals when assays are perfect or nearly perfect.

3.3 Average number of tests per unit of information

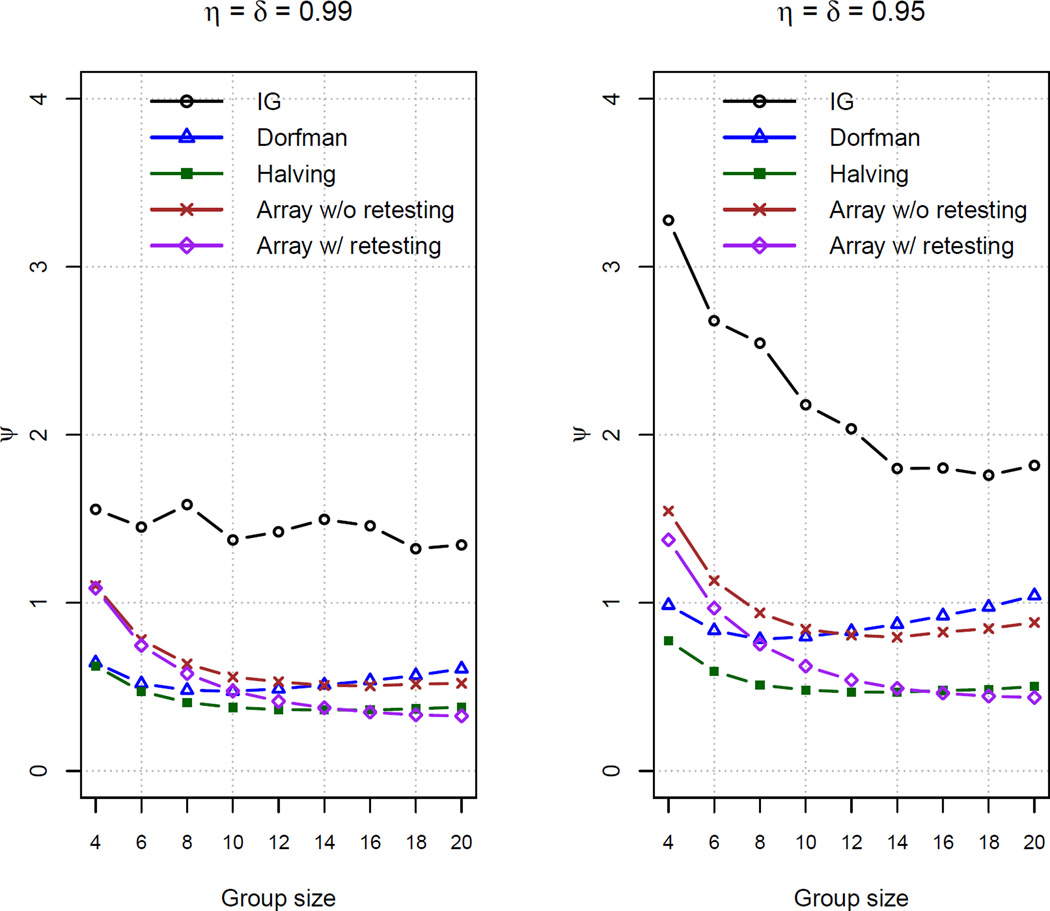
Each protocol uses a different number of tests to estimate the regression parameters. To take this aspect into account, we define the average number of tests per unit of information for β₁ to be

$$\psi =\frac{1}{B}\sum _{b=1}^B\frac{n_b}{1/\mathit{\text{Var}}({\widehat{\beta }}_{1,b})}=\frac{1}{B}\sum _{b=1}^B{n}_b\mathit{\text{Var}}({\widehat{\beta }}_{1,b}),$$ (5)

where n_b is the total number of tests performed for a protocol and β̂_1,b is the estimated β₁ for the b^th simulated data set. The smaller that ψ is, the fewer the number of tests are needed comparatively to obtain the same amount of information about β₁. A similar measure was used by Chen and Swallow (1990, p. 1037) when evaluating the benefits of retesting for overall prevalence estimation.

Figure 3 plots values of ψ for all group testing protocols for the same simulations as in Section 3.2. Individual testing results in ψ = 3.53 for η = δ = 0.99 and ψ = 8.80 for η = δ = 0.95; these values were excluded from the figure to avoid distorting the plots. Comparing between the plots, we see that ψ is larger for η = δ = 0.95 than for η = δ = 0.99, which is a byproduct of increased uncertainty when η and δ are smaller. Within each plot, we again see the benefits of including retests in the estimation process. Dorfman, halving, and array testing with retests have smaller ψ values than their corresponding protocols that do not include retests. Among those that include retests, halving always provides a smaller ψ than Dorfman’s protocol. Also, array testing with retests provides values of ψ close to that of halving for larger group sizes.

Figure 3.

Average number of tests per unit of information calculated by Equation (5) based on 500 simulated data sets.

Of course, the cost of implementation is also a very important consideration when comparing protocols. Group testing is typically performed in situations where the cost of testing is the most dominant consideration. Provided that initial tests and retests cost the same, which would be expected if the same assay is used for both, ψ provides a constant multiple of the cost, so it can be used in the same way as above to judge which protocol is preferred.

3.4 Additional simulations

We have performed a number of additional simulations at a different overall prevalence level and with a smaller number of individuals screened. In summary, we have found that the same conclusions hold in these other situations. Some of these additional simulation results are included in Web Appendix F of the Supporting Information.

4 Infertility Prevention Project in Nebraska

We focus retrospectively on the 6,139 males who had their urine individually tested for chlamydia in 2009 at the NPHL. At this time, the NPHL used the BD ProbeTec ET CT/GC Amplified DNA Assay, where the sensitivity and specificity values were η = 0.93 and δ = 0.95, respectively. The laboratory estimates that each urine test costs approximately $16, so that total expenditures for these individuals were about $98,000. The high volume of clinical specimens combined with their high testing costs is why the NPHL is interested in exploring the use of group testing. In addition to positive or negative chlamydia diagnoses, information available on each individual includes age, race (four levels), symptoms, urethritis, multiple partners in the last 90 days, new partner within the last 90 days, and prior contact with someone who had a sexually transmitted disease (STD). Except for age and race, we use a binary coding (1 = yes, 0 = no) with this information.

Because this is a retrospective analysis involving individual disease responses, it is essential to emulate how group testing would be performed in practice. To begin, we need to choose an appropriate initial group size. This is typically done by using a prior estimate of the overall prevalence p and minimizing the expected number of tests based on this estimate (Kim et al. (2007) provides these expected value formulas). We do this here by using the 2008 observed prevalence of 0.077 to obtain group sizes of 5 for IG and Dorfman and 8 for halving and array testing. Individuals who were tested in 2009 are placed into groups of these sizes in chronological order based on when their specimen arrived at the NPHL. We form groups in this manner because it is convenient for high volume situations when specimens arrive in succession over time.

Once individuals are placed into initial groups, the corresponding group responses are needed. These are not available because the NPHL used individual testing, so we instead simulate group responses by the following methodology. The actual, observed individual responses are treated as the true statuses Ỹ_ik (Ỹ_ij for array testing). Using a Bernoulli distribution with the appropriate probability of η or δ, a response is then simulated for a group containing a set of individuals. For example, if a group of size 5 has negative true statuses for all its members, the group response is simulated from a Bernoulli(1-δ) distribution. If instead at least one member is positive, a Bernoulli(η) distribution is used to simulate the group response. This same process is repeated for each group testing protocol to acknowledge the possibility of testing error.

First-order logit regression models are fit to the responses from each protocol. For comparison purposes, we fit the same model to the individual responses (simulated as well to enable fair comparisons with group testing) while incorporating testing errors by using the methodology of Neuhaus (1999). Table 3 gives the parameter estimates from all fitted models and the number of tests required for each protocol. Overall, all estimates are similar to each other for the same corresponding covariates. Each group testing protocol that includes retests has similar or smaller standard errors than those for the individual testing model, consistent with our findings in Section 3. Using a level of significance of 0.05 with Wald hypothesis tests, individual testing and group testing protocols with retests agree on the same set of important covariates.

Table 3.

Parameter estimates and estimated standard errors for the chlamydia screening data. The “p-value” column gives Wald test p-values for testing whether or not a regression parameter is equal to 0. Note that an overall test is performed for all levels of the variable Race. The number of tests performed by each protocol is in parentheses after the protocol name.

	Individual (6139)			IG (1228)			Dorfman (3458)
Term	Estimate	SE	p-value	Estimate	SE	p-value	Estimate	SE	p-value
Intercept	−2.46	0.24	<0.001	−2.52	0.36	<0.001	−2.16	0.20	<0.001
Age	−0.03	0.01	<0.001	−0.03	0.01	0.061	−0.04	0.01	<0.001
Race level #1	0.79	0.15	<0.001	0.79	0.26	0.017	0.67	0.12	<0.001
Race level #2	0.80	0.32		0.88	0.50		1.08	0.25
Race level #3	0.44	0.26		0.43	0.50		0.37	0.22
Symptoms	0.45	0.16	0.004	0.32	0.30	0.285	0.69	0.14	<0.001
Urethritis	1.29	0.33	<0.001	1.40	0.51	0.006	0.95	0.33	0.004
Multiple partners	0.44	0.19	0.019	0.56	0.33	0.090	0.53	0.16	0.001
New partner	0.17	0.20	0.407	0.11	0.40	0.782	0.10	0.18	0.567
Contact to a STD	1.04	0.15	<0.001	1.12	0.27	<0.001	1.10	0.14	<0.001
	Halving (2898)			Array w/o retesting (1541)			Array w/ retesting (3097)
Term	Estimate	SE	p-value	Estimate	SE	p-value	Estimate	SE	p-value
Intercept	−2.39	0.22	<0.001	−2.56	0.34	<0.001	−2.27	0.21	<0.001
Age	−0.04	0.01	<0.001	−0.03	0.01	0.013	−0.04	0.01	<0.001
Race level #1	0.64	0.14	<0.001	0.94	0.23	<0.001	0.87	0.13	<0.001
Race level #2	0.47	0.34		0.28	0.59		0.77	0.30
Race level #3	0.68	0.22		0.24	0.44		0.50	0.22
Symptoms	0.63	0.15	<0.001	0.64	0.23	0.005	0.84	0.14	<0.001
Urethritis	1.07	0.34	0.002	0.61	0.53	0.254	1.09	0.33	<0.001
Multiple partners	0.35	0.16	0.029	0.56	0.30	0.062	0.44	0.17	0.010
New partner	0.11	0.20	0.600	0.22	0.36	0.549	0.06	0.19	0.745
Contact to a STD	1.16	0.15	<0.001	1.26	0.21	<0.001	1.03	0.15	<0.001

The model fitting time for IG, Dorfman, and halving is no more than a few seconds. However, the model fitting time for the array testing protocols can be exceptionally long due to the Gibbs sampling. In particular, there are 6,139 conditional expectations–one for each individual–that need to be estimated through simulation. Also, simulation variability compounds among these estimates which can lead to a non-uniform descent to the convergence criterion. For example, we used 20,000 Gibbs samples when fitting the model to array testing data with retests. The convergence criterion used was the maximum absolute relative difference between successive regression parameter estimates, say d, needing to be less than 0.005. Convergence was obtained in approximately 15.8 hours with eight complete iterations (3.2GHZ processor was used). However, there was no longer a completely uniform descent to 0.005 by d. By using 40,000 Gibbs samples, there was a uniform descent in five iterations, but the process took approximately 21.5 hours. We have found that this same behavior occurs with other high volume clinical specimen data sets as well.

Overall, the results clearly illustrate the potential advantages of using group testing at the NPHL–not only in terms of estimation and the resulting large-sample inference, but also because of the opportunity to drastically reduce the number of tests needed. For example, halving requires 2898 tests overall, which is a 52.7% reduction from individual testing. Even the simpler Dorfman protocol requires only 3458 tests overall, a 43.7% reduction in tests when compared to individual testing. To put this into a total expenditure perspective, the estimated costs are: $55,328 for Dorfman, $46,368 for halving, and $49,552 for array testing with retests. Given there are over three million screenings for the IPP annually across the United States, one can see that significant savings could occur if group testing was adopted throughout the country. A few states, such as Iowa and Idaho, have already at least partially implemented group testing using Dorfman’s protocol, but even more cost savings could be obtained using halving or array testing with retests.

5 Discussion

In this paper, we have outlined how to estimate a group testing regression model when case identification is a goal. Our work shows that including retests leads to large reductions in estimator variability while also improving accuracy. Overall, halving and array testing with retests are the best protocols when considering the number of tests and estimator variability. We also showed that group testing can lead to more efficient estimates of regression parameters than individual testing. This is an extremely important finding, because it shows that more information can be gained while doing less in terms of testing. To disseminate our research, we have made available new functions in R’s binGroup package (Bilder et al. 2010) which implement the model fitting methods outlined in this paper. Examples of model fitting with these functions are included in the Supporting Information for this paper.

Group size selection is an important consideration in most applications where group testing is used (e.g., see Swallow (1985)). Aside from assay considerations, the optimal group size is the one that leads to the smallest number of tests while still providing as much information as possible. Our research shows the average number of tests per unit of information stays relatively stable over a large range of group sizes when retests are included. Thus, protocols with retests are somewhat robust to the group size used, which makes its choice not as critical as when retesting is omitted.

The EM algorithm proposed by Xie (2001) can be used to fit models for data arising from any group testing protocol. While our paper focused on three commonly used protocols for case identification, other protocols are available. In particular, array testing can be implemented with a master group for each array and/or in more than two dimensions (Kim et al. 2007; Kim and Hudgens 2009). Future research could examine these other protocols to determine if more estimation benefits result from their implementation. In the case of array testing, all protocols will likely need to use the Gibbs sampling approach outlined in Section 2.4 to estimate a conditional expectation for every cell within an array. As shown in Section 4, this can be time consuming depending on the size of the arrays and how many arrays there are. Potentially, parallel processing could be used with one core processor per array to reduce the model fitting time.