Modeling Protein Association Mechanisms and Kinetics

Abstract

Substantial advances have been made in modeling protein association mechanisms and in calculating association rate constants (k_a). We now have a clear understanding of the physical factors underlying the wide range of experimental k_a values. Half of the association problem, where k_a is limited by diffusion, is perhaps solved, and for the other half, where conformational changes become rate-limiting, a number of promising methods are being developed for k_a calculations. Notably, the binding kinetics of disordered proteins are receiving growing attention, with “dock-and-coalescence” emerging as a general mechanism. Progress too has been made in the modeling of protein association kinetics under conditions mimicking the heterogeneous, crowded environments of cells, an endeavor that should ultimately lead to a better understanding of cellular functions.

Introduction

The association of proteins with small molecules and other macromolecules constitute the key steps of all cellular functions. In addition to the structures of the complexes formed and their binding affinities, association mechanisms and rate constants uniquely contribute to the characterization of cellular functions. Association processes are often under kinetic, rather than thermodynamic, control [1], e.g., when several macromolecules compete for the same binding site [2] or when a protein is faced with alternative pathways [3]. Understanding the physical principles governing association mechanisms and rate constants and furthermore, realistically modeling them, are thus of paramount importance.

In many cases, convincing arguments can be made that rapid association, not just high affinity, is essential for biological function. For example, some bacteria produce enzymes (e.g., barnase in Bacillus amyloliquefaciens and nuclease colicins in Escherichia coli; Fig. 1) that are exported to rapidly kill off competitor cells by cleaving their nucleic acids. However, these enzymes can also potentially cleave the host cell’s own nucleic acids. This ill fate is prevented by co-producing inhibitors (i.e., barstar and immunity proteins), and rapid enzyme-inhibitor association here is obviously crucial to ensure the self-defense of the host cell.

Fig. 1.

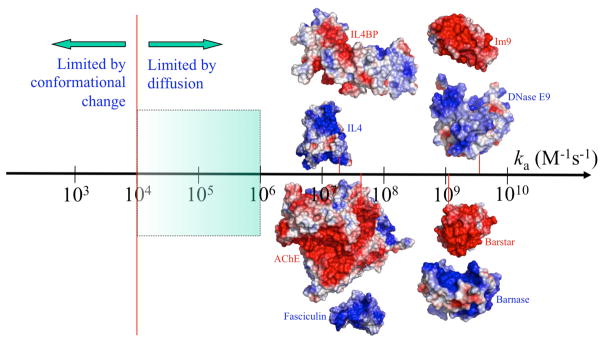
The wide spectrum of experimental values for the rate constants of protein-protein association. The conformational change-limited regime and diffusion-limited regime are generally separated around k_a = 10⁴ M⁻¹s⁻¹ (indicated by a vertical line). In the diffusion-limited regime, if there is no long-range force to bias the diffusion, k_a usually falls between 10⁴ and 10⁶ M⁻¹s⁻¹ (shaded region). Proteins that associate with k_a > 10⁷ M⁻¹s⁻¹ invariably feature strongly complementary electrostatic surfaces (as shown for four complexes; blue and red represent positive and negative electrostatic potentials, respectively); k_a values for the four systems measured at ionic strengths of 150, 50, 15, and 25 mM (from left to right) are indicated by short lines touching the k_a axis.

Various cellular functions rely on altering association (k_a) and dissociation (k_d) rate constants. Translation initiation, putatively the rate-limiting and most highly regulated phase of bacterial protein synthesis, provides a good example. Crucial to translation initiation is the binding of the initiator tRNA (i.e., fMet-tRNA^fMet) to the ribosome 30S subunit [2]. This binding, in the absence of initiation factors (IF1-3), has the same low k_a and low k_d as the binding of noncognate, elongator tRNAs [4•]. Pre-binding of IF1-3 to the 30S subunit results in increases in k_a of as much as 400-fold for the initiator tRNA but by only ~10-fold for noncognate tRNAs, as well as significant, uniform increases in k_d for all the tRNAs. The resulting disparity in k_a is essential for the accuracy of initiator tRNA selection.

Post-translational modifications such as phosphorylation present a different mechanism for altering k_a. A recent study [5] found that response levels in cellular signaling correlated with the phosphorylation-dependent binding affinities of a linker peptide on a kinase for the SH2 domain of an effector protein. However, as the phosphorylation in this case affected k_a but not k_d, a similar correlation can be argued if k_a, instead of the association constant (i.e., K_a = k_a/k_d), is used. Even if K_a was the determinant for the cellular function in this study, it remains important to point out that the increases in K_a upon phosphorylation were achieved through increases in k_a, as opposed to decreases in k_d. The latter might not be a viable option for signaling proteins, as the complexes formed with their targets generally have to be short-lived. It has been proposed that structural disorder allows signaling proteins to bypass the requirement for maintaining high k_a, without sacrificing specificity [6].

The question of whether K_a or k_a is the better predictor of cellular response in signaling was specifically addressed by Kiel and Serrano [7]. They introduced c-Raf mutations that were expected to change either only K_a (by changing k_d) or only k_a (by compensatory changes in k_d) for association with Ras. The effects of these mutations on MAP kinase signaling correlated better with predicted k_a than with predicted K_a. While signaling networks may not generally be dictated by single protein-protein association steps, this study does highlight the importance of considering association kinetics, not just equilibrium, in predicting the outcome of signaling.

The association constant is determined by the end states of the binding process, namely the unbound state, in which the two subunits separately reside in the solvent environment, and the bound state, in which the subunits form specific, noncovalent interactions. In contrast, to determine the association rate constant one has to consider the whole binding process. This process involves both overall translational and rotational diffusion of the molecules, which brings the binding sites on the two molecules into proximity, and internal conformational changes, which allow the molecules to achieve their native stereospecific fit. There is a long history of deriving theoretical results for k_a by formulating the diffusional and internal motions of simple molecular models [1] and in developing algorithms for computing k_a through simulating the motions of realistically represented protein molecules [8–12].

The past few years have seen major progress in modeling protein association mechanisms and in calculating association rate constants. In highlighting this progress below, we will focus on association between protein molecules, but will occasionally include examples where the subunits are nucleic acids, small molecules, and multi-component complexes.

An overview on the wide spectrum of protein association rate constants

The observed k_a values for protein-protein association range from ~1 to 10¹⁰ M^–1s^–1 (Fig. 1). It is now clear that this 10 orders of magnitude spectrum involves two different rate-limiting mechanisms [13,14]. The binding process between two proteins, A and B, can be modeled by the reaction scheme [6,13]

$$\text{A}+\text{B}\underset{k_{\text{D}-}}{\overset{k_{\text{D}}}{\rightleftarrows }}\text{A}·\text{B}\underset{k_{\text{c}-}}{\overset{k_{\text{c}}}{\rightleftarrows }}\text{C}$$ (1)

where A · B denotes an initial complex in which at least a portion of the binding site on A forms near-native contact with the cognate portion of the binding site on B, and C denotes the final, native complex. The formation of the initial complex predominantly involves the translational and rotational diffusion of the molecules, whereas the subsequent step predominantly involves the conformational changes of the molecules. The overall rate constants for association and dissociation are

$$k_{\text{a}}=k_{\text{D}}{k}_{\text{c}}/(k_{\text{D}-}+k_{\text{c}})$$ (2)

$$k_{\text{d}}=k_{\text{D}-}{k}_{\text{c}-}/(k_{\text{D}-}+k_{\text{c}})$$ (3)

Both the diffusional step and the conformational step can be rate-limiting for association. The former regime occurs if k_c ≫ k_D− (e.g., when structural differences are small between the bound and unbound states). Then k_a ≈ k_D Recent calculations for over 100 protein-protein complexes found that, in the absence of any biasing force in the diffusional step, diffusion would set an upper bound of 10⁴ to 10⁶ M⁻¹s⁻¹ for k_a [15••]. Electrostatic attraction can bias the diffusional step and push up k_D by 3 or more orders of magnitude. Indeed, proteins that associate with rate constant higher than 10⁷ M⁻¹s⁻¹ always have highly complementary electrostatic surfaces (Fig. 1).

When large-scale structural differences exist between the bound and unbound states, the conformational step can become rate-limiting. In this regime, k_a ≈(k_D/ k_D−) k_c k_D/k_D− is the association constant for forming the initial complex and probably has a lower bound of 10² to 10³ M⁻¹, similar to those for low-affinity protein-protein complexes. k_c could be compared to the rate of transition from a folding intermediate to the native state of a protein, which can be as low as 10⁻² to 10⁻³ s⁻¹ [16,17]. Therefore, a lower bound of 1 M⁻¹s⁻¹ is expected when association is rate-limited by conformational changes.

The diffusion-limited regime

In general, k_a values higher than 10⁴ M⁻¹s⁻¹ can be proposed to be diffusion-limited. Most k_a calculations have been restricted to this regime [11]. Here, the initial complex can be placed very close to the native complex, and its precise location can be determined by sampling near the bound state in the 6-dimensional translational and rotational space [18]. This and other developments culminated in the transient-complex theory for protein association [13]. The transient complex specifically refers to the initial complex in the diffusion-limited regime, in which the two proteins have near-native separation and relative orientation but have yet to form most of the stereospecific native contacts. The association rate constant is predicted as

$$k_{\text{a}}=k_{\text{a}0}exp(-\mathrm{\Delta }{G}_{\text{el}}^{\ast }/k_{\text{B}}T)$$ (4)

where k_a0 is the “basal” rate constant, i.e., the rate constant at which the two proteins reach the transient complex by free diffusion, and the Boltzmann factor captures the rate enhancement by inter-protein electrostatic attraction. Applications to structurally similar proteins show that different degrees of electrostatic complementarity across the binding interface can produce orders of magnitude disparities in k_a [19]. Differences in sizes and shapes of the interface can also contribute to variations in k_a by modulating the basal rate constant, which is dictated by the extent of the orientational restraints between the subunits in the transient complex [15••,20••]. The orientational restraints themselves may result in preferred pathways for reaching the transient complex [21]. Pre-binding of a third protein near the interface can modify the placement of the transient complex, potentially contributing to a dramatic increase in k_a [22].

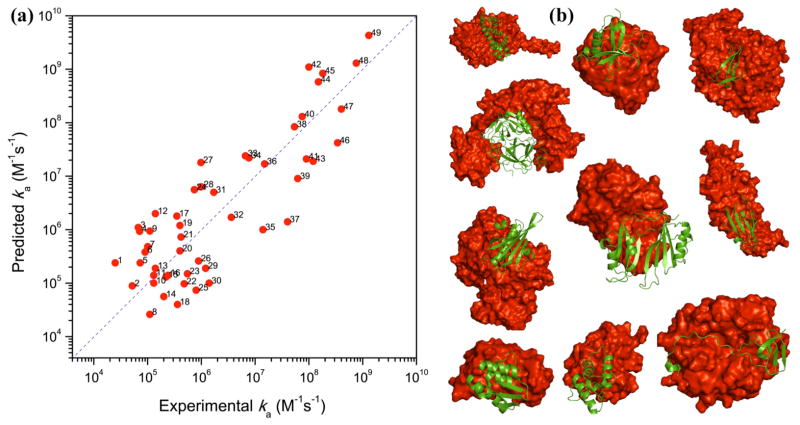
Another important development is the automated implementation of the transient-complex theory, resulting in the TransComp web server (http://pipe.sc.fsu.edu/transcomp/) for k_a prediction [15••]. To illustrate the level of accuracy of the server predictions a comparison to experimental results for 49 diverse protein-protein complexes is shown in Fig. 2. In an intriguing application, extensive TransComp calculations suggested that a conserved cationic surface on the kinesin motor domain enhances the association rate with, and contributes to, the directional movement on microtubules [23•].

Fig. 2.

Level of accuracy of TransComp k_a predictions. (a) Comparison of predicted and experimental k_a values for 49 protein-protein complexes. (b) Structures of 10 of the 49 complexes, illustrating the structural diversity. Adapted from Qin et al. [15••].

Recently machine-learning protocols have also been employed to predict kinetic parameters from atomic coordinates [24,25]. The benefit of these approaches is that they too are able to identify, from diverse training sets, which structural and energetic features are the more powerful predictors, with solvent mediated hydrogen bonding and surface complementarity identified as being particularly important for the prediction of k_a [25].

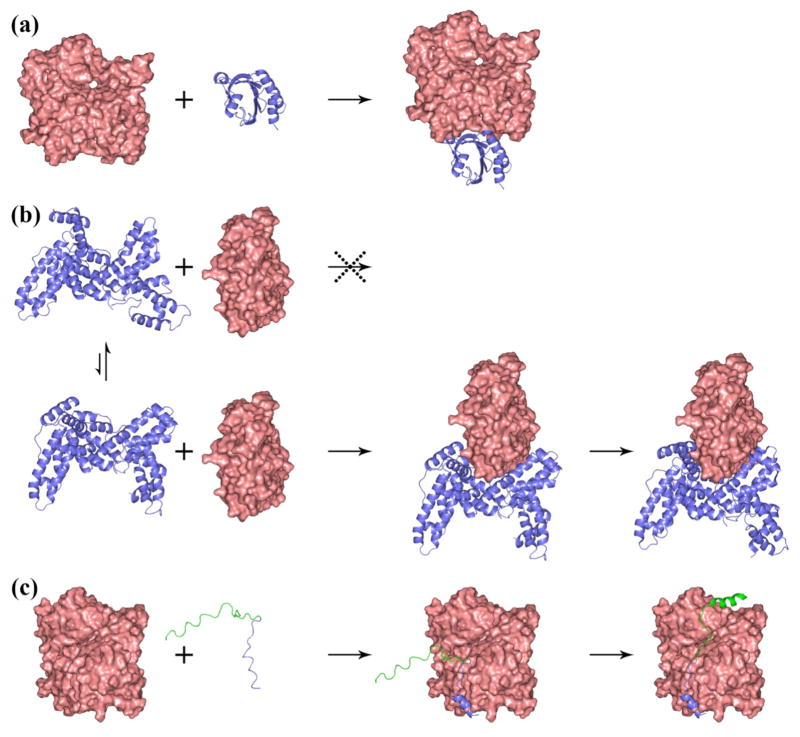
Structural and dynamic differences of proteins result in a variety of association mechanisms [15••,20••]. The association of many proteins that fall in the diffusion-limited regime can be viewed as rigid docking of the subunits accompanied by fast local conformational adjustments (Fig. 3a). In other cases the docking of one subunit may require a larger scale breathing motion of the other subunit to open the binding site (Fig. 3b). As long as the breathing motion is fast on the timescale of the diffusion approach between the subunits, the overall association process is still diffusion-limited [26].

Fig. 3.

Three different mechanisms of protein association, illustrated by three proteins binding to G-actin (shown as pink surface) [20••]. (a) Profilin reaches the transient complex (not shown) with G-actin by diffusion and then quickly forms the native contacts all at once to produce the native complex. (b) Vitamin-D binding protein must undergo breathing motion to transiently widen the opening between its domains 1 and 3 to allow G-actin to enter. (c) The Wiskott-Aldrich syndrome protein has a disordered actin-regulatory region. The binding of this regulatory region to G-actin follows the dock-and-coalesce mechanism: the WH2 segment (in blue) docks to the cleft between subdomains 1 and 3 of G-actin, allowing the remaining segment (in green) to sample conformations and coalesce to its cognate subsite in the cleft between subdomains 2 and 4 of G-actin.

Modeling conformational changes during association

When conformational changes are slow on the timescale of the diffusion approach between the subunits, they become rate-limiting. In this regime, internal motions have to be explicitly modeled during the association. A few such simulation studies, on binding of small molecules to proteins, have been published over the years [27,28]. Using algorithms originally designed for calculating the association rate constants of rigid molecules [8,9] to calculate the association of flexible molecules presents the formidable challenge of having to simulate internal motions over the length of time required for achieving successful association.

Recently a new algorithm was developed [29], based on breaking the association process into two problems confined to either the outer region, where the molecules can be modeled as rigid, or the inner region, which covers the binding site but is small enough such that modeling of internal motions can be affordable. The algorithm has been tested on the binding of small molecules to proteins [Qin, Greives, & Zhou, to be published]. Another interesting approach is based on long, extensive molecular dynamics simulations, from which a Markov state model of the binding process was constructed [30•]. Application of either approach has yet to be made to study protein-protein association.

Association of disordered proteins with structured targets

Intrinsically disordered proteins (IDPs) represent an extreme form of molecular flexibility [31,32]. Their coupled folding and binding processes have increasingly been investigated experimentally and computationally [33,34••]. When bound to structured targets, they often form open structures with extended interaction surfaces [35]. It is unlikely that an IDP would form its extensive interactions with its target all at once, as the resulting severe orientational restraints would lead to extremely low k_a [6,15••]. Rather, different segments of the IDP have to form contacts with their cognate subsites at different times. A likely scenario, consistent with molecular simulations [36–39], is the sequential formation of these contacts [15••,20••]. In such a “dock-and coalescence” mechanism (Fig. 3c), one particular segment of the IDP first docks to its cognate subsite on the target, thereby allowing the remaining segments to explore conformational space and coalesce around their cognate subsites.

In the simplest case, the docking step is rate-limiting for overall association. Then mutations, either on the docking segment of the IDP or on its cognate subsite, that perturb the docking step would significantly affect the overall k_a, whereas those perturbing the coalescing step or even deletion of the entire coalescing segment would not. Such telltale signs have indeed been observed experimentally [40–43•]. Molecular simulations have suggested that the flexibility of IDPs helps reduce the free energy barrier for the coalescing step [39,44], potentially making the docking step rate-limiting. Importantly, for IDPs that bind to their targets with a rate-limiting docking step, the TransComp method can again be used to predict the association rate constants, by studying just the binding of the docking segments with their cognate subsites [15••]. TransComp calculations have now produced k_a values that are in quantitative agreement with experimental results for a variety of IDPs, suggesting that dock-and-coalesce may be a general mechanism for IDPs binding to their structured targets, often with docking as the rate-limiting step [15••,20••,34••].

Compared to structured proteins, IDPs achieve similar levels of specificity for their targets, but with the specific interactions more widely distributed over space. Therefore during dissociation these interactions do not have to be broken all at once, leading to an increase in k_d. In this way IDPs can form highly specific and yet short-lived complexes with their targets, fulfilling the twin requirements for signaling proteins [6].

Influence of cellular environments on association kinetics

Understanding cellular functions ultimately requires the modeling of protein association processes not in dilute solutions but in solutions mimicking the crowded, heterogeneous cellular environments. It is now recognized that such environments can significantly affect both thermodynamic and kinetic properties of protein association [45]. A reasonable approach to model association kinetics in a crowded solution is by accounting for the effects of the crowder molecules on the interaction energetics and the motional dynamics of the reactant molecules [46]. This approach has been validated by simulations of a simple system in which both reactant and crowder molecules are modeled as hard spheres [47].

For protein association that is rate-limited by the conformational step, the dominant contribution of crowding can be captured by its effect on the free energy of the transition state for the conformational step (relative to the unbound state). If this transition state is structurally similar to the native complex, then the effect of crowding on free energy barrier is close to that on the binding free energy. An efficient method has been developed for calculating the latter quantity [48].

For protein association in the diffusion-limited regime, crowding exerts its dominant effect on the diffusional approach of the subunits toward the transient complex. The presence of crowder molecules slows down the relative diffusion of the associating subunits but also produces an effective interaction energy between them [47]. The transient-complex theory has been modified to account for these effects and predict the association rate constant under crowding as [49•]

$$k_{\text{ac}}=\gamma k_{\text{a}0}exp(-\mathrm{\Delta }{G}_{\text{el}}^{\ast }/k_{\text{B}}T)exp(-\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{c}}^{\ast }/k_{\text{B}}T)$$ (5)

where γ is the factor by which the relative diffusion constant is slowed down by the crowders and $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{c}}^{\ast }$ is the crowding-induced interaction energy between the subunits in the transient complex. Hard-core repulsion from the crowder molecules can lead to apparent attraction between the subunits (i.e., $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{c}}^{\ast }<0$). Then and $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{c}}^{\ast }$ would have opposing consequences on the association rate, leaving a nearly null net effect. Therefore despite the presence of crowders the association would appear unimpeded. This prediction is confirmed by recent kinetic experiments under in vitro crowding and in living cells [50,51•].

Prospects

Over recent years major progress has been made in modeling protein association mechanisms and in calculating association rate constants. For half of the association problem, where k_a is higher than 10⁴ M⁻¹s⁻¹ and limited by diffusion, the determinants for k_a are now well understood and the calculations of k_a are quite accurate. For the other half, where conformational changes become rate-limiting, promising methods are being developed and it will be interesting to see how practical and predictive when these are ready for application to study protein-protein association.

Quantitative modeling of protein association kinetics can provide answers to open questions concerning essential cellular functions. For example, how do initiation factors achieve the substantial rate increase for the binding of the initiator tRNA to the ribosome 30S subunit? Interference with this rate increase may potentially be a new mechanism of antibiotic action. More broadly, modeling of association mechanisms may uncover intermediates along kinetic pathways, which could form a new class of targets for drug design [52].

An area where the progress in k_a calculations reported here could have immediate impact is the modeling of signaling networks. One of the more popular approaches to modeling such networks dynamically is to construct a set of rate equations to monitor key cellular events over time [53]; for example, the nucleocytoplasmic shuttling of proteins associated with the TGF-β pathway [54], and the modulation of disease-associated pathways due to protein missense mutations [7,55]. While some of the kinetic parameters for such equations have been or can be experimentally determined, others may need to be predicted. It is here that the accurate prediction of association rate constants from bound or even unbound protein structures can be extremely valuable.

Highlights.

• Protein association rate constants are essential for cellular functions.

• Half of the problem of modeling association kinetics has a solution.

• Binding of disordered proteins appears to follow a dock-and-coalesce mechanism.

• Crowded cellular environments influence protein association and cellular functions.