Identifying external influences on global precipitation

Significance

This study provides evidence that human activities are affecting precipitation over land and oceans. Anthropogenic increases in greenhouse gases and stratospheric ozone depletion are expected to lead to a latitudinal intensification and redistribution of global precipitation. However, detecting these mechanisms in the observational record is complicated by strong climate noise and model errors. We establish that the changes in land and ocean precipitation predicted by theory are indeed present in the observational record, that these changes are unlikely to arise purely due to natural climate variability, and that external influences, probably anthropogenic in origin, are responsible.

Abstract

Changes in global (ocean and land) precipitation are among the most important and least well-understood consequences of climate change. Increasing greenhouse gas concentrations are thought to affect the zonal-mean distribution of precipitation through two basic mechanisms. First, increasing temperatures will lead to an intensification of the hydrological cycle (“thermodynamic” changes). Second, changes in atmospheric circulation patterns will lead to poleward displacement of the storm tracks and subtropical dry zones and to a widening of the tropical belt (“dynamic” changes). We demonstrate that both these changes are occurring simultaneously in global precipitation, that this behavior cannot be explained by internal variability alone, and that external influences are responsible for the observed precipitation changes. Whereas existing model experiments are not of sufficient length to differentiate between natural and anthropogenic forcing terms at the 95% confidence level, we present evidence that the observed trends result from human activities.

Water is the single most important natural resource, and many societal and natural impacts of climate change will depend on the response of the hydrological cycle to anthropogenic warming. Several large-scale changes in precipitation, inferred from theoretical understanding, observations, and climate model predictions, are expected in a warming world (1). To first order, anthropogenic forcings are expected to influence the hydrological cycle through two basic mechanisms. “Thermodynamic” changes follow from the Clausius–Clapeyron relation, which dictates that saturation-specific humidity increases roughly exponentially with temperature, and from the vertical warming profile (2, 3). In the absence of other changes, this increase in tropospheric water vapor will make wet regions wetter and dry regions drier. Tropospheric water vapor is indeed increasing in response to human activities (4), and there is evidence that this increase has contributed to the moistening of wet regions and drying of dry regions (5–7). Existing large-scale studies (7–9) are constrained over land, and thus neglect the 77% of precipitation that falls over oceans. Thermodynamic changes are expected to be even stronger over ocean, because evaporation is limited over dry land regions, and trends in ocean salinity may indicate an intensification of the global hydrological cycle (10). However, no study has yet detected a signal of climate change in global (land and ocean) precipitation.

“Dynamic” changes result from shifts in atmospheric circulation, which in turn affect the horizontal and vertical transport of water vapor. Numerous observational and model-based studies have detected circulation shifts using various metrics (ref. 11 and references therein). Models indicate that increasing greenhouse gases, in the absence of other external forcing terms, result in a poleward expansion of the tropical Hadley cell and subtropical dry zones (12). However, stratospheric ozone depletion can also lead to similar circulation shifts (13) and is likely the dominant contributor to the observed poleward movement in Southern Hemisphere circulation patterns in austral summer (14).

Any study of anthropogenic influences on global precipitation must therefore consider both thermodynamic and dynamic mechanisms (15). Detection of the climate change signal is complicated by the muted response of global-mean model precipitation to a temperature increase (compared with the increase in water vapor) and the zonal nature of the predicted changes (in both sign and displacement). Additional difficulties exist: first, it is well-known that interannual and interdecadal modes of natural variability such as the El Niño/Southern Oscillation (ENSO) have considerable impacts on precipitation, potentially obscuring any climate change signal. Second, global precipitation climatologies exhibit strong spatial gradients, and model errors in representing the locations of these gradients are common. Consequently, averaging precipitation over latitude bands and over many simulations (as in refs. 7 and 9), which is generally performed to reduce the influence of internal variability, may also obscure physically robust simulated precipitation shifts. Finally, total precipitation is also strongly influenced by orography, cloud formation, and other small-scale processes that may not be well-simulated in climate models.

In this paper, we argue that the presence of two physically robust, interlinked mechanisms necessitates the use of multivariate detection techniques (16). We propose a method to simultaneously detect the intensification and latitudinal redistribution of global precipitation, test these changes against model estimates of natural internal variability, and investigate the roles of various relevant external forcings.

Thermodynamic and Dynamic Indicators

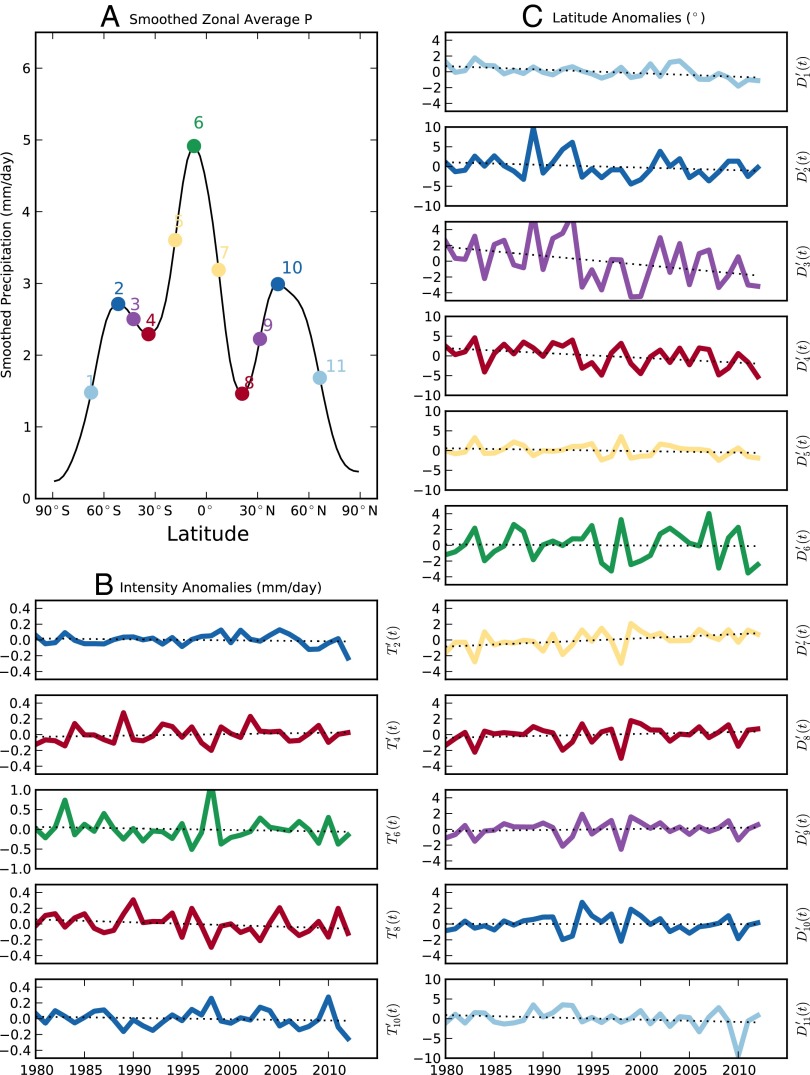
We use the Global Precipitation Climatology Project (GPCP) global observational dataset (17) spanning 1979–2012. In this paper, we focus on boreal winter (December–February; hereafter DJF). We begin by smoothing observed DJF seasonal precipitation climatologies so that spatial structure on scales less than 5° is removed (18). Fig. 1A shows the result of this smoothing process for a single representative year (1990). The smoothed, zonally averaged precipitation field has five local extrema, excluding the polar-most points. Physically, these correspond to (from left), the Southern Hemisphere (SH) midlatitude storm track peak, SH subtropical dry zone trough, equatorial tropical peak, Northern Hemisphere (NH) dry zone trough, and NH storm track peak. In the observations, the zonally averaged smoothed DJF precipitation has exactly five local extrema in every year.

Fig. 1.

Illustration of the methods used to generate thermodynamic and dynamic indicators. (A) Smoothed, zonally averaged boreal winter precipitation in the observational GPCP dataset for 1990. Local extrema are marked in dark blue (midlatitude storm tracks), red (subtropical dry zones), and green (equatorial tropical peak). Cyan, purple, and yellow circles indicate half-max points: latitudes where the smoothed zonally averaged precipitation is equal to the average of neighboring extrema. (B) Observed peak intensity anomalies (mm/d) in the observational dataset. Best-fit trends obtained by linear regression are shown as black dotted lines. (C) Observed peak and half-max point location anomalies in the observational dataset. Best-fit trends are drawn as black dotted lines.

For each year, we calculate the latitude and intensity (i.e., the value of the smoothed precipitation field) at each extremum. We then calculate the six “half-max” latitude points, defined as the latitudes where the smoothed zonally averaged precipitation is equal to the average of the nearest peak and trough. This process yields 1) a dynamic time series 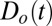with 11 spatial dimensions representing variations in peak, trough, and half-max latitudes, and 2) a thermodynamic time series 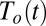with five spatial dimensions representing variations in the intensity at each peak and trough. (The terminology used here represents an oversimplification: dynamical strengthening or weakening of the circulation can also contribute to changes in precipitation intensity, whereas large-scale changes in precipitation may have consequences for atmospheric circulation.) We then calculate the anomalies 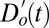(Fig. 1B) and 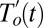(Fig. 1C) relative to 1980–2012 observed time means. This allows us to characterize total changes in zonally averaged precipitation using intensification and shifts simultaneously.

We apply the same methods to climate model precipitation data from the third and fifth phases of the Coupled Model Intercomparison Project (CMIP3/CMIP5). To obtain model data spanning the observational period, we splice “historical” experiments with 21st-century experiments in which changes in greenhouse gas and aerosols are specified according to Representative Concentration Pathway 8.5 (RCP8.5, used in CMIP5) or Scenario A1B (used in CMIP3) (SI Appendix, S2). For each model, we perform the same smoothing and peak detection procedure. Anomalies 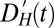and 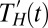are now calculated with respect to the model 1980–2012 average peak/trough and half-max latitude and intensity. This technique effectively preserves and highlights the changes in intensity and displacement that likely would be obscured in the multimodel average of zonal-mean precipitation. The procedure is then repeated for yearly seasonal DJF climatologies in the CMIP5 preindustrial control (PIC) runs, yielding control anomaly time series 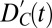and 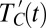, which are then concatenated into a single time series (SI Appendix, S1).

Fingerprints

We estimate the expected response of the dynamic and thermodynamic indicators to external forcing using a leading “fingerprint” method (16, 19). We begin by first averaging the anomaly time series 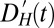and 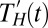over an individual model’s spliced historical and RCP8.5 realizations, and then averaging over all models. Because internal variability is uncorrelated across models, this reduces the effect of climate noise, yielding a clearer picture of the climate system’s response to external forcing: the fingerprint of climate change.

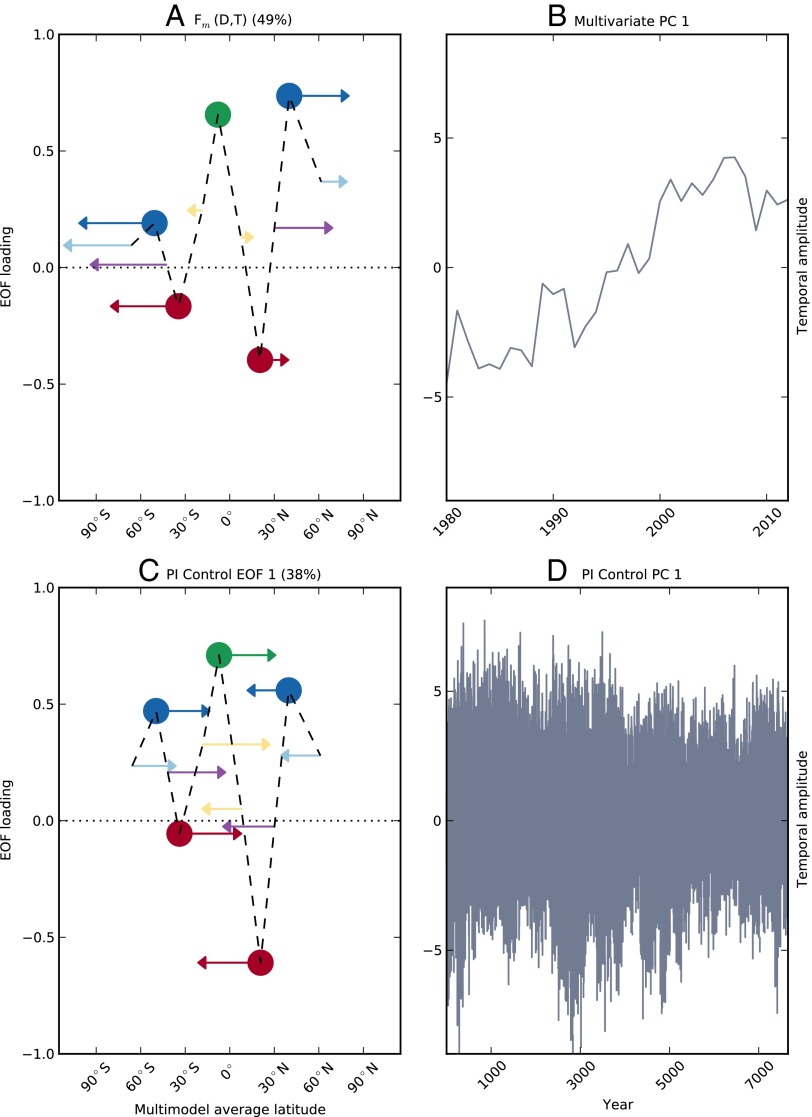
To examine simultaneous thermodynamic and dynamic changes, we calculate the leading multivariate empirical orthogonal function (EOF) 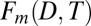, determined from the cross-covariance matrix of the multimodel average 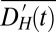and 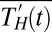(Fig. 2A). This fingerprint reveals that the multimodel response of the climate system to external forcing is characterized by two physical effects: a wet-get-wetter, dry-get-drier pattern in precipitation intensity, and an attendant poleward expansion in both hemispheres in zonal-mean precipitation. The associated first principal component (PC) (Fig. 2B) shows a distinct positive trend over the observational time period. By contrast, Fig. 2C shows the leading noise EOF of the concatenated PIC runs, and Fig. 2D the associated PC. This EOF resembles the fingerprint 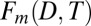except, instead of the poleward expansion observed in the forced case, it displays the equatorial contraction expected in the zonal-mean response to ENSO (20, 21). This suggests that ENSO, the primary mode of natural variability, will not project well onto the multivariate fingerprint 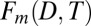. In other words, using this fingerprint will improve signal-to-noise ratios by effectively filtering out climate noise (SI Appendix, S8).

Fig. 2.

Multivariate fingerprint of forced precipitation change and the primary noise mode. (A) Fingerprint 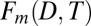, or leading eigenvector of the cross-covariance matrix of the multimodel average 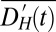and 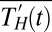. Both time series are scaled to unit variance before input. Thermodynamic EOF loading is plotted on the vertical axis; the direction and magnitude of dynamic EOF loading are displayed as arrows. The horizontal axis is the multimodel average latitude of detected peak/trough and half-max points. For visual clarity the arrows exaggerate the actual shift in latitude by a factor of 50. This EOF explains 49% of the total variance. (B) Principal component associated with the fingerprint 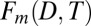. (C) Leading noise eigenvector of the cross-covariance matrix of the concatenated model PIC runs 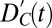and 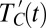. As in A, the y axis shows thermodynamic EOF loading, whereas arrows, scaled by a factor of 50, show dynamic EOF loading. The x axis shows the multimodel average latitude of detected points. This EOF explains 38% of the total variance. (D) Principal component associated with the leading noise EOF.

Even though both thermodynamic and dynamic responses are based in fundamental physics, and therefore robust across multiple independent climate models, model errors may mask even strong responses. The fingerprint, or characteristic response to external forcing, is often obtained by averaging over multiple models to eliminate internal variability. This response may be diluted if models disagree on the locations of important features. For example, two models projecting strong subtropical drying trends may yield a smaller trend when averaged if the model dry zones are sufficiently far apart. Additionally, estimates of internal variability are often obtained by concatenating the preindustrial control runs of multiple models into a single long time series. However, variations in the principal components of the concatenated control runs may reflect model biases, not the amplitude of internal variability in the models. Previous attempts to control for model errors have included coarse zonal averaging (7), focus on a single region (5, 6), the use of a warping function for feature bias correction (22), and the model-by-model approach described in ref. 23. The method we use (SI Appendix, S4) is designed to capitalize on robust model features even in the presence of feature biases. This method allows for the simultaneous detection of dynamic and thermodynamic changes in zonal-mean precipitation and demonstrates that these changes are inconsistent with internal climate variability, as we now show.

Detection of Changes

To determine if these changes in intensity and location are present in the observations, we project the combined observed anomaly fields 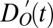and 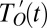, normalized to unit variance, onto the multivariate fingerprint 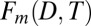. This projection yields the spatial covariance between the observed pattern and the fingerprint at time t and measures the similarity between the observed and fingerprint patterns. If the externally forced fingerprint is present and growing in the observations, then the projection should increase with time and display an overall positive trend (19). By contrast, the fingerprint should not be expressed in precipitation changes originating from climate noise alone, except by chance. We use this characteristic to assess whether observed trends can be explained by internal variability. To do so, we calculate the distribution of 33-y nonoverlapping trends in the concatenated model PIC projections onto the fingerprint 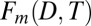. The SD of this distribution, denoted ∈, constitutes a measure of internal climate variability. The signal-to-noise (S/N) ratio is then obtained by dividing the observed trend by ∈.

If observed trends are incompatible with internal variability, we can claim to have detected a signal. To attribute a signal to external forcing, we need to assess whether it is compatible with forced model results. Whereas all models in the CMIP5 archive incorporate the effects of ozone depletion in addition to other human and natural forcings, only half of those in the previous generation (CMIP3) do so (14). This allows us to determine the relative weight of greenhouse gas and ozone depletion contributions to changes in precipitation. We therefore calculate the projections onto the fingerprint for the spliced CMIP5 models (ALL5), and spliced CMIP3 models including (ALL3) or excluding (NoOz3) anthropogenic stratospheric ozone depletion.

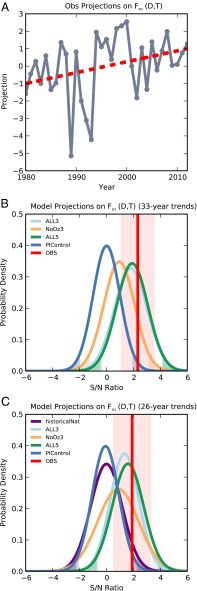
Fig. 3A shows the projection of the observed dynamic and thermodynamic indicators, normalized to unit variance, onto the fingerprint 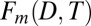. The corresponding S/N ratio is shown in Fig. 3B, as well as fitted probability density functions for the PIC, ALL5, ALL3, and NoOz3 S/N ratios. A strong positive trend is evident in the observed projection. As expected, the distribution of 33-y nonoverlapping control run trends is centered around zero. The observed S/N ratio of 2.4 is well above the 5% significance threshold, suggesting that the observed covariability between location and intensity is incompatible with internal climate noise alone. The ALL3 and ALL5 trends do not differ significantly from each other, nor do they differ from the NoOz distribution (SI Appendix, Table S1). The observed S/N ratio is located near the mean of all three externally forced distributions. This indicates that the combined amplification and shift in zonal precipitation is externally forced and present even in the absence of anthropogenic ozone depletion.

Fig. 3.

(A) Projection (gray) of the observed thermodynamic and dynamic indicators onto the multivariate fingerprint, and best-fit line (red). (B) Best-fit normal probability distribution functions (PDFs) for trends in the projection of model data onto the fingerprint. All trends have been normalized by ∈, the SE of the control distribution to obtain S/N ratios. The blue line shows the PDF of nonoverlapping 33-y trends from the concatenated model PIC runs. The green line shows the PDF for individual CMIP5 historical/RCP8.5 model projection trends. Yellow/cyan lines show the PDF for CMIP3 models excluding/including stratospheric ozone depletion. For all PDFs, the two-sided 95% confidence intervals are shaded. The red line indicates the observed S/N ratio, and the shaded red box ± 1 SE in estimating the trend from assumed independent annual samples. The observed S/N ratio, located near the mean of the forced distributions, is incompatible with internal variability at 95% confidence. (C) As in B, but for 26-y trends and including historicalNat experiments. The observed S/N ratio is located near the mean of the forced distributions and in the tail of both control and historicalNat distributions.

To differentiate between natural and anthropogenic forcing terms, we repeated the analysis over the shorter time period spanned by the “historicalNat” experiments in the CMIP5 database (1980–2005). These experiments incorporate solar variability and volcanic eruptions over the historical period, but contain no anthropogenic forcings. The results, now using 26-y trends, are shown in Fig. 3C. The observed trend lies in the tail of the historicalNat and piControl distributions, but the S/N ratio is not significant at the 95% confidence level. This is likely due to the shortened period over which we calculate trends. However, the similarity between the historicalNat trend distribution and the PIC trend distribution, and the fact that these distributions significantly differ from those obtained using anthropogenically forced models, strongly suggest that natural external forcings alone are unlikely to explain the observed changes.

Modeled Internal Variability

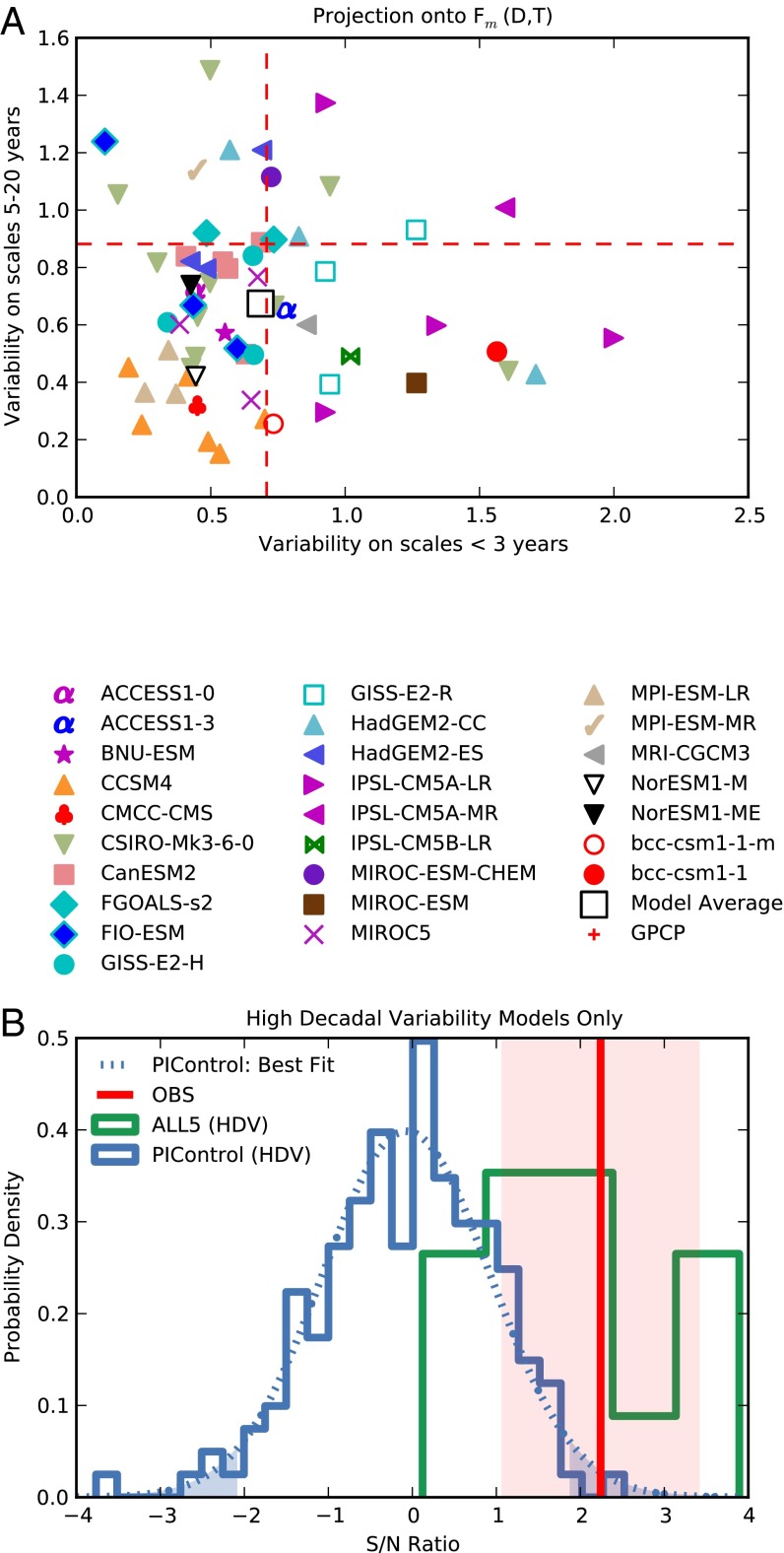
Detection and attribution (D&A) studies rely on credible model estimates of internal variability (24, 25). If models systematically underestimate the amplitude of natural climate noise, this may lead to spurious detection due to artificially low variability inflating the S/N ratio. It is therefore important to compare variability in observations and spliced CMIP5 historical/RCP8.5 runs. We first detrend modeled and observed time series of projections onto the multivariate 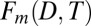fingerprint and then apply a band-pass filter to extract variability on scales between 5 and 20 y, as in ref. 25. We also apply a high-pass filter to extract variability on scales less than 3 y. Fig. 4A shows the performance of models at simulating medium- and high-frequency variability in the projection. Model estimates of decadal variability are more important for D&A applications, and Fig. 4A indicates a systematic underestimate in decadal variability of the multivariate projection. Does this lead to spurious detections by inflating the S/N ratio? To investigate this possibility, we consider only those models (FGOALS-s2 and MIROC-ESM-CHEM; see SI Appendix, Table S2 for full model information) in which the ensemble average over realizations overestimates 5–20-y variability in the multivariate projection. Restricting our analysis to these two models only, we find (Fig. 4B) that the observed trend is still highly unlikely to occur in these model control runs at the 95% confidence level.

Fig. 4.

(A) Comparison of modeled and observed variability in the multivariate projection onto the fingerprint 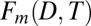. (B) Normalized histograms of trends in the multivariate projection onto the fingerprint 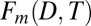for the control runs (blue) and spliced historical and RCP8.5 runs, considering only models that overestimate decadal variability in the projection (high decadal variability or HDV models).

Comparisons with Previous Work

We note that our detection method relies on the covariance matrix measuring the relationship between the dynamic and thermodynamic indicators. To calculate the fingerprint and projection, we normalize each indicator to unit variance, thus removing information about the amplitude of variability in the individual components. Our fingerprint therefore measures the degree of synchronicity between variations in the thermodynamic and dynamic indicators, not their respective amplitudes. This means it is possible to detect a trend in the projection onto 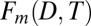in the absence of trends in eithe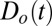r or 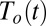, if thermodynamic changes and dynamic changes increasingly occur in tandem.

It is, of course, possible to calculate single-variable fingerprints to examine changes in 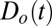(SI Appendix, S6.1) or 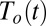(SI Appendix, S6.2) separately. The noise filtering aspect of the multivariate fingerprint is lost in the single-variable cases: natural variability, ENSO in particular, will project onto these fingerprints and decrease the S/N ratio (SI Appendix, Fig. S8). However, considering each variable separately allows for comparisons with previous studies that have detected changes in the hydrological cycle or atmospheric circulation.

We find, considering the dynamical indicator alone, that the observations do show a poleward shift in the main features of global precipitation. As previous authors (14) have found, the observed trend is much larger than the trends found in forced model runs, although including anthropogenic stratospheric ozone depletion reduces the discrepancy.

Although other studies (7, 26) have found evidence for thermodynamic changes in the hydrological cycle, we do not detect a trend in the thermodynamic indicator alone. This is due to differences in datasets and time periods considered (SI Appendix, Figs. S4–S6). Our method is designed to detect changes in the zonal-mean structure of global precipitation; other metrics, designed to capture more local changes, have found evidence for regional thermodynamic changes (27) that exceed model predictions.

Conclusions

In this paper, we have presented a simple method to track thermodynamic and dynamic changes in global precipitation. This method identifies physical effects that are robust across multiple models, even in the presence of model errors. We have identified a fingerprint pattern that characterizes the simultaneous response of precipitation location and intensity to external forcing and acts as a noise filter. Observed changes in this multivariate response are incompatible with our best estimates of natural variability and consistent with model predictions of externally forced change. The synchronicity of these changes is key, however: considering either change in isolation does not lead to detection and attribution (SI Appendix, Fig. S3). By focusing on both the underlying mechanisms that drive changes in global precipitation, and by restricting our analysis to the large scales where we have some confidence in models’ ability to reproduce the current climate, we have shown that the changes observed in the satellite era are externally forced, and likely to be anthropogenic in nature.