Quantifying the dynamic interactions between a clathrin-coated pit and cargo molecules

Significance

Clathrin-mediated endocytosis is the primary pathway of cargo internalization in mammalian cells. However, little is known about the time-dependent interactions between the endocytic machinery and cargo molecules. Nevertheless, these interactions are known to regulate the maturation of a clathrin-coated pit. In this study, we attain a quantitative understanding of the interactions between clathrin-coated pits and cargo using a combination of imaging techniques, single-molecule tracking, and stochastic modeling. We observe that the binding times of cargo molecules are much shorter than the overall endocytic process, albeit they exhibit a very broad distribution. Our modeling explains the measured statistics of cargo captures and binding times. This work further identifies a mechanism for the large diversity in the dynamic behavior of clathrin structures.

Abstract

Clathrin-mediated endocytosis takes place through the recruitment of cargo molecules into a growing clathrin-coated pit (CCP). Despite the importance of this process to all mammalian cells, little is yet known about the interaction dynamics between cargo and CCPs. These interactions are difficult to study because CCPs display a large degree of lifetime heterogeneity and the interactions with cargo molecules are time dependent. We use single-molecule total internal reflection fluorescence microscopy, in combination with automatic detection and tracking algorithms, to directly visualize the recruitment of individual voltage-gated potassium channels into forming CCPs in living cells. We observe association and dissociation of individual channels with a CCP and, occasionally, their internalization. Contrary to widespread ideas, cargo often escapes from a pit before abortive CCP termination or endocytic vesicle production. Thus, the binding times of cargo molecules associating to CCPs are much shorter than the overall endocytic process. By measuring tens of thousands of capturing events, we build the distribution of capture times and the times that cargo remains confined to a CCP. An analytical stochastic model is developed and compared with the measured distributions. Due to the dynamic nature of the pit, the model is non-Markovian and it displays long-tail power law statistics. The measured distributions and model predictions are in excellent agreement over more than five orders of magnitude. Our findings identify one source of the large heterogeneities in CCP dynamics and provide a mechanism for the anomalous diffusion of proteins in the plasma membrane.

Clathrin-mediated endocytosis (CME) is the principal route of cargo internalization in mammalian cells (1, 2). This process occurs through a sequence of tightly regulated molecular events that include the initiation and maturation of clathrin-coated pits (CCPs) mediated by the recruitment of cytosolic clathrin, adaptor proteins, and cargo (3–5). Advances in fluorescence microscopy over the last 10 y have enabled the direct visualization of CCPs and their dynamics in living cells. Total internal reflection fluorescence (TIRF) microscopy is today one of the leading assays in the study of CME (6–9) as it enables the observation of the different stages in the life cycle of CCPs (10). When fluorescently labeled clathrin is used to image the endocytic process, the initial assembly of a CCP is seen as the appearance of a fluorescence spot on the plasma membrane. Similarly, the disappearance of fluorescence indicates the end of a CCP because either the endocytic process aborts and components disassemble or it produces a clathrin-coated vesicle that exits the total internal reflection excitation field.

Several groups have undertaken the formidable task of surveying the concerted recruitment of large numbers of endocytic proteins to the different CCP stages (11, 12). However, little is still known about how this sequence of endocytic events is physically regulated. This unsolved puzzle is further complicated by the broad heterogeneity that characterizes the maturation of CCPs. Even though this process is tightly regulated through a myriad of endocytic signals, it is still largely governed by stochastic events as are most cellular trafficking phenomena (10, 13, 14). To shed light onto the temporal regulation of CME, a deeper understanding of the dynamic interaction between CCPs and endocytic proteins is needed. Undoubtedly, the identification and characterization of binding motifs in endocytic proteins is vital to the understanding of endocytosis regulation (15, 16). However, a quantitative study of these interactions taking into account the heterogeneity and the stochastic nature of CCP growth is currently lacking. As the clathrin coat matures, the interaction with cargo molecules changes. Thus, a fundamental understanding of CCP–cargo interactions requires that temporal evolution of the endocytic machinery is considered and measurements are placed in the context of pit age.

Here, we study the recruitment of cargo into growing CCPs in live mammalian cells. In our previous TIRF-based studies of K⁺ channel diffusion and trafficking, we often observed channels in the plasma membrane alternating between mobile and immobile periods before being internalized by the cell. This finding led us to hypothesize that immobilization events were caused by transient binding to CCPs. We now investigate the dynamics of CCPs in human embryonic kidney (HEK) cells in terms of their lifetimes and growth characteristics and then study the binding affinity of the K⁺ channels and CCPs as a function of the clathrin coat age. We use multicolor TIRF microscopy to simultaneously image individual Kv2.1 or Kv1.4 potassium channels and fluorescently labeled CCPs. A primary finding is that the growth of CCPs is a major contributor to the heterogeneity in endocytic proteins–CCP interactions. From these observations, we can speculate that the intrinsic changes in the recruitment kinetics during the CCP growth play a key role in the temporal regulation of the endocytic process. Our experimental data (35,869 Kv2.1 and 8,412 Kv1.4 binding events longer than 0.5 s) reveal that cargo–CCP interactions involve a broad distribution of dissociation coefficients that emerges from the temporal evolution of cargo affinity during the CCP life cycle. A kinetic model for the binding of cargo within a CCP is derived, taking into account the clathrin coat assembly through the recruitment of adaptor proteins. This model predicts to a remarkable degree the observed properties of cargo catch-and-release processes.

Results

CCP Lifetimes and Growth.

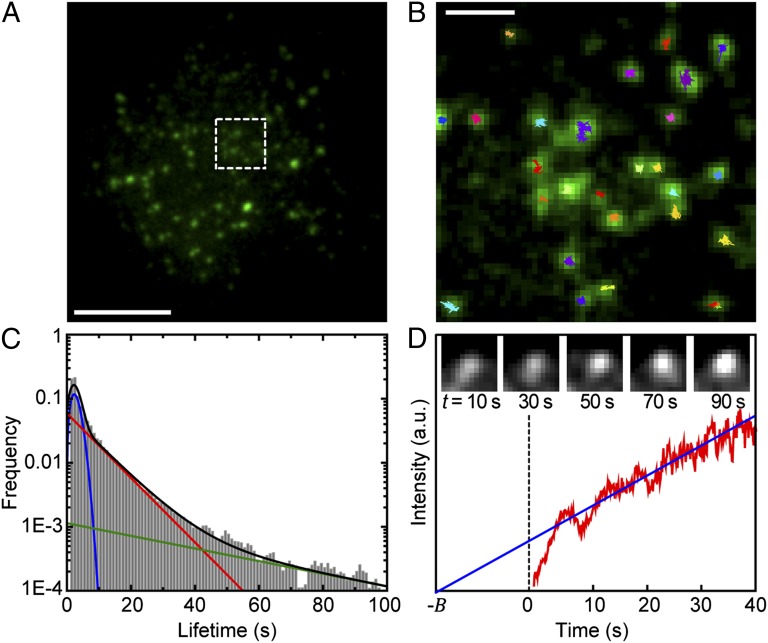
As a first step in the study of CCP–Kv interactions, we obtained the distribution of CCP lifetimes and studied their growth rate. We visualized the dynamics of CCPs in living HEK293 cells expressing GFP-labeled clathrin light chain (CLC) using a TIRF microscopy assay. In this imaging modality, only the region next to the basal plasma membrane is excited, thus enabling the observation of the clathrin coat initiation, maturation, and termination as the pit appears, grows, and, at last, disappears from the excitation field. Fluorescently labeled CCPs appear as diffraction-limited fluorescent puncta on the cell surface (Fig. 1A), which can be detected and tracked by fitting a 2D Gaussian function to each individual spot. This approach provides both the location of the pit with accuracy beyond the diffraction limit and its emission intensity. Fig. 1B shows the CCP tracks obtained from a small region selected from Fig. 1A overlaid on a single frame of GFP–CLC. We acquired 31,492 trajectories containing the CCP spatial localization in real time, the lifetime of each pit (i.e., duration of the tracks), and the evolution of the emission as the pit grows.

Fig. 1.

CCP growth and lifetimes. (A) Fluorescence image of GFP-CLC–labeled CCPs. (Scale bar: 10 μm.) (B) Zoomed image of boxed region in A. CCPs trajectories are overlaid on the fluorescence image of GFP-labeled CCPs. Trajectories were obtained using u-track software. (Scale bar: 2 μm.) (C) Lifetime distribution of n = 31,492 CCPs in control cells. The black line is a fit to the cumulative distribution function, a combination of one Rayleigh distribution (blue) plus two exponential distributions (red and green). (D) Ensemble averaged intensity profile of 4,377 CCPs in 12 different cells. The blue line is a fit to the linear part of the curve. Representative fluorescence time series of a CCP is shown in the Inset.

The lifetime, time between appearance and disappearance of a fluorescently labeled pit within the TIRF illumination field, is an important parameter in the characterization of CCP dynamics. Ideally, a CCP trajectory starts and ends within the imaging time. However, in many instances, the measured trajectories are truncated by either the beginning or the end of the recorded movie. This effect introduces bias in the measured lifetimes by effectively reducing the number of measured long trajectories. To account for trajectories that are not seen in their entirety, the biasing factor was computed and the lifetime distribution corrected (see ref. 10 and SI Text). Fig. 1C shows the corrected lifetime distribution of CCPs. Using Bayesian information criterion for model selection in the same fashion as in ref. 10, we identify three subpopulations of clathrin pits (see SI Text for details). The model that best describes the measured distribution is a combination of one Rayleigh and two exponential distributions. The Rayleigh distribution fits the data arising from the shortest trajectories (blue line in Fig. 1C) and the exponential distributions (red and green lines) model the longer-lived pits. The identification of three kinetically distinct subpopulations agrees with the measured CCP lifetimes in BSC1 cells (10).

The interactions between cargo and a CCP change over time because as the pit matures more adaptor proteins capable of binding cargo molecules are recruited. Thus, a characterization of the CCP growth is necessary to develop a theoretical framework of these interactions. The amplitude found with the tracking algorithm provides the intensity of the GFP–CLC spots, but this approach suffers from certain limitations. The assembly of the clathrin coat is not deterministic, but it is a stochastic process characterized by large fluctuations. In addition, the number of fluorescently labeled clathrin molecules incorporated into a pit is burdened by Poisson statistics, making it very difficult to reliably characterize the growth rate at the single CCP level. Nevertheless, it is possible to use the ensemble average to gather statistical information on the growth (17, 18). The second problem encountered with this approach is that a CCP is not flat on the cell membrane. This introduces bias in the estimated number of fluorophores because the TIRF intensity depends exponentially in the actual distance from the coverslip. To overcome these problems, the recruitment kinetics of clathrin and AP-2 adaptor complex was previously studied using a combination of TIRF and epifluorescence illumination (19). It was found that when ensemble averaging is obtained by aligning the CCP trajectories to their point of appearance, as we report here, strong deviations between fluorescence increase and growth rate are seen at times far from the aligning point. In particular, it was found that, due to a restructuring of the CCP in the axial direction, the TIRF fluorescence decreases at late stages, even though the CCP grows. It was observed that clathrin and AP-2 are recruited at a very fast rate during a short initiation stage, followed by a long slower growth phase. To validate these results in HEK cells, we have reproduced some of these findings. CCPs with lifetimes longer than 10 s were analyzed and an ensemble average was performed over all trajectories by aligning them to their point of appearance. By excluding short-lived pits from the analysis, we also exclude noise due to the disappearance of these short-lived pits. Fig. 1D shows the ensemble-averaged CCP intensity time course. The fluorescence images of a CCP are shown in the Inset of Fig. 1D, to exemplify the growth process. An increase in fluorescence is seen as the pit matures. As expected, both initiation and growth modes are observed. During the initiation stage, the fluorescence intensity increases rapidly, indicating the number of clathrin molecules grows quickly. Our data indicate this initiation stage lasts on average 6.5 s, which is within the range of previous observations (19). As a CCP matures, it enters into a second stage characterized by a slower growth rate. Eventually, the CCP enters a short stage where the signal decreases until it disappears because the pit either dissolves or separates from the plasma membrane. In Fig. 1D, the slower, growing phase is highlighted with a blue line.

The time-dependent size of a CCP during its growth phase can be approximated fairly well by a constant growth rate as observed in Fig. 1D and in figure 1 A and B in ref. 19. Therefore, a simple linear model describes the number of available adaptors:

where 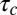is the mean time of recruitment of an additional adaptor molecule and B is introduced to account for the initiation phase, as illustrated in Fig. 1D. By using the fluorescence intensity to estimate the number of adaptor proteins, we can infer the number of available binding sites in a growing CCP as a function of time.

Kv2.1 and Kv1.4 Are Internalized via CME.

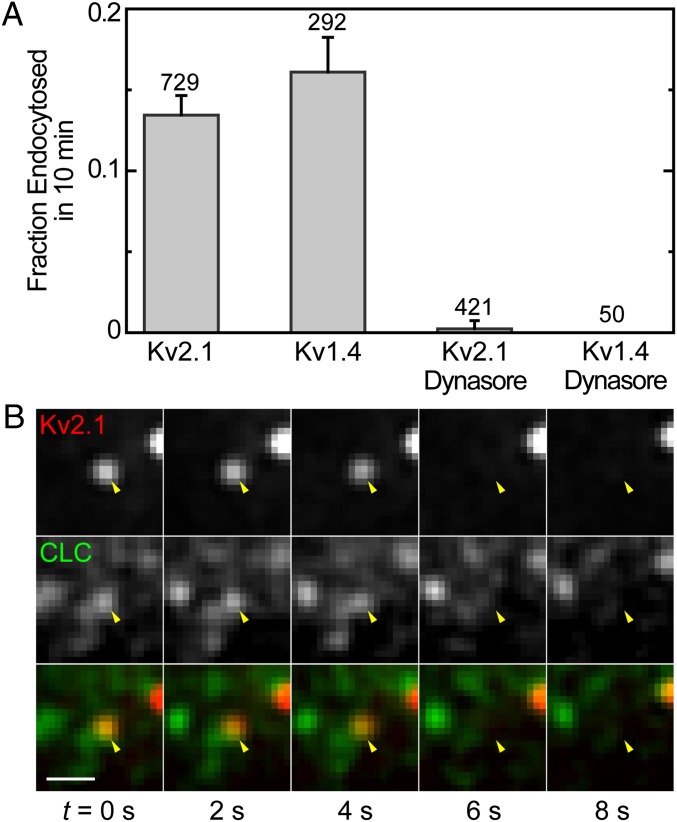
To investigate the interaction between CCPs and the voltage-gated potassium channels Kv2.1 and Kv1.4 (the cargo molecules used here), we established that these channels internalize via clathrin-mediated pathways. First, the rate of endocytosis was determined by imaging quantum dot (QD)-tagged Kv2.1 or Kv1.4 and finding events at which the fluorescent particles leave the plasma membrane. In a TIRF assay, when a molecule is internalized it leaves the excitation evanescent field. So the termination of a QD trajectory is indicative of an endocytic event (20, 21). QDs are particularly suitable for these measurements because they do not display photobleaching. However, their intrinsic blinking behavior, viz., the stochastic switching between bright and dark states, makes them prone to introducing false endocytic events in our data. Therefore, we manually inspected the end of each track to assert that the trajectory terminations were not an artifact of the tracking algorithm, but rare long blinking events may still appear as internalizations. Trajectories that are terminated at the edge of the cell are discarded because they likely represent channels that translocate to the upper membrane. The rate of endocytosis was determined from the number of endocytic events in a 10-min time frame. We find that 13% (n = 729) of Kv2.1 and 16% (n = 292) of Kv1.4 surface channels are internalized in a 10-min time window (Fig. 2A).

Fig. 2.

Kv channels are internalized via CME. (A) Fraction of channels endocytosed in 10 min. The graph shows endocytic fraction for Kv2.1 and Kv1.4 with and without dynamin inhibitor dynasore. (B) Fluorescence time series of Kv2.1 endocytic event. The yellow arrow indicates QD-Kv2.1 (bottom row) and GFP-CCP (middle row) location. Both the fluorescence of the QD and GFP disappear at the same time, marking the endocytic event. (Scale bar: 1 μm.)

As an additional control for the potential adverse effect of QD blinking, we used an alternative approach to ascertain the fluorescence extinction is truly due to endocytosis. If Kv2.1 channels are internalized via clathrin-mediated pathways, inhibition of CME should result in a reduction in the rate of their internalization. Dynasore, an inhibitor of dynamin, was used to hinder CME. Dynasore is a potent inhibitor of endocytic pathways that are dynamin dependent, and it blocks coated vesicle formation within seconds of application (22). Upon application of 80 μM dynasore, the endocytosis of Kv2.1 and Kv1.4 was effectively extinguished completely. As shown in Fig. 2A, the rate of Kv2.1 endocytosis is reduced from 0.013 min⁻¹ in control cells to 0.0002 min⁻¹, with only 1 in 421 trajectories appearing to end in endocytosis. Out of 50 Kv1.4 trajectories, no endocytic events were observed after dynasore application. These dramatic changes reveal that Kv2.1 and Kv1.4 endocytosis is mediated by dynamin and that track terminations are indeed due to channel endocytosis.

We also examined the colocalization and concurrent internalization of QD-labeled channels and GFP–CCPs. Two-color TIRF microscopy was used to simultaneously visualize QD and GFP; their fluorescence was overlaid; and the termination of QD fluorescence was again manually inspected. When the loss of QD–Kv2.1 fluorescence occurred at the same time and location as the loss of a GFP–CLC spot, the event was identified as CME. Fig. 2B shows a representative 8-s time-lapse series of a clathrin-mediated endocytic event where both Kv2.1 and CCP leave the plasma membrane at the same time. In the top panel, the fluorescence of a QD–Kv2.1 channel is marked with a yellow arrow. A GFP-labeled CCP that shares the same location with the QD is seen in the middle panel and is also indicated with a yellow arrow. The bottom panel presents the overlaid images. We manually analyzed 98 Kv2.1 trajectories in 12 different cells and 47 Kv1.4 trajectories in 8 cells that were terminated within the experimental imaging time. Eighty-six percent of disappearing Kv2.1 channels and 87% of disappearing Kv1.4 channels were observed to terminate concurrently with the end of an associated CCP trajectory, providing further evidence that these channels are endocytosed via CME and can be used as cargo model systems for the study of the interaction between cargo molecules and clathrin-coated structures.

Capture into CCPs.

Before endocytosis, cargo proteins must interact with the CCP through the association to adaptor proteins. Given that the endocytic pits remain confined to nanoscale regions (Fig. 1B), the mobility of Kv channels and other cargo proteins is expected to be strongly hindered while bound to a CCP. Kv2.1 and Kv1.4 immobilize within CCPs at some point during the pit life cycle. However, contrary to classic textbook examples, most Kv2.1 and Kv1.4 channels escape from the pit before the life of the endocytic pit is ended for both the abortive and productive populations, i.e., pit dissolution or internalization, respectively. For example, out of 4,066 examined Kv2.1 capture events, we observed that only 17% remain bound until CCP termination (the channel release was considered to be caused by CCP termination when the pit signal disappeared within 0.5 s). This implies that cargo affinity to the pit is not strong enough to maintain it immobilized until endocytosis occurs.

The identification of events where K⁺ channels are captured into CCP indicates these channels alternate between diffusive and immobile states. In our previous work (23), we reported that the motion of Kv channels on the cell surface exhibits frequent, transient immobilization. We identified transient immobilization events by analyzing the statistics of the square displacements between given lag times. While the channel is in the immobile state, it displays square displacements over prolonged periods much smaller than the mean square displacement (MSD) observed during the mobile phase. Thus, we identified immobilization or stalls in the channel trajectory by detecting periods of consecutive lag times over which the square displacement remains below a given threshold (23).

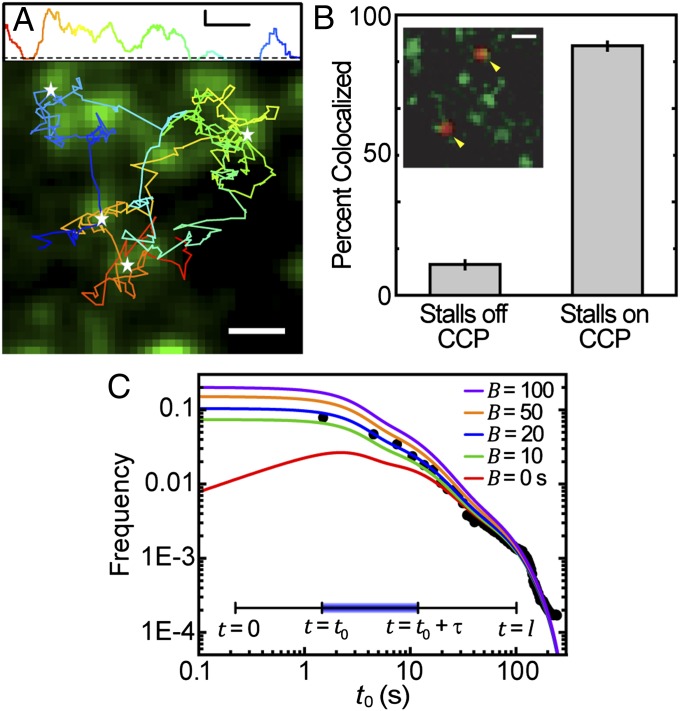
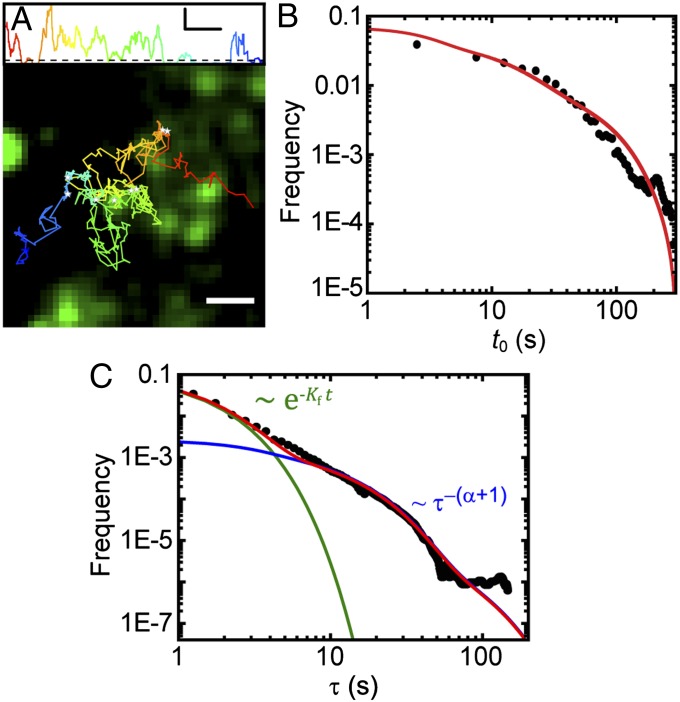
We hypothesize that the observed periods of Kv2.1 immobilization are due to the channel becoming captured within endocytic sites. Fig. 3A shows a trajectory of a QD–Kv2.1 channel overlaid on a GFP–CLC fluorescence image. The instantaneous MSD, calculated with a 20-frame sliding window, of the trajectory is also shown. Immobilization events can be seen as the MSD falls below a threshold of 2,000 nm². Stalls greater than 1 s are indicated with white stars in the image. All of the stalls seen in this example occur within CCPs. A total of 35,869 stalls lasting longer than 0.5 s were found in 2,925 Kv2.1 trajectories. To further confirm that Kv2.1 immobilizations are a consequence of the channel being captured into a CCP, 1,752 of the found transient immobilizations were manually inspected for colocalization to clathrin. Fig. 3B shows that 89% of these Kv2.1 stalling events occurred on a CCP. This fraction is four times higher than the average area fraction covered by clathrin. The Inset of Fig. 3B shows a representative image of two QD–Kv2.1 complexes that colocalize to GFP–CCPs while stalling.

Fig. 3.

Capture of cargo into CCPs. (A) Trajectory of QD–Kv2.1 overlaid on GFP–CLC image. The white stars indicate binding events (stalls) that are longer than 1 s. A sliding window MSD with a window of 20 frames shows the decrease in diffusion, indicative of a stalling event. A threshold (dotted line) of 2,000 nm² indicates stalling events. (Scale bar: 1 μm; MSD scale bar: 20 s and 0.01 μm².) (B) Percentage of stalls greater than 0.5 s within an area of R_TH² = 2,000 nm². Inset is a fluorescence image demonstrating two QD–Kv2.1 (red) stalls, indicated by yellow arrows, occurring in a GFP-labeled CCP (green). (Scale bar: 1 μm.) Eighty-one percent (n = 1,752) of Kv2.1 stalls colocalized with a CCP. (C) Histogram of the times of capture within a CCP (round points) together with the model of the distribution of times of capture P(t₀) for five different values of B between 0 and 100 s (solid lines), which indicate the time shift due to the initiation phase as seen in Fig. 1D. Inset depicts lifetime of a CCP, originating at time t = 0, capturing cargo at t = t₀, cargo dissociating from pit at 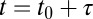, and ending abortively or productively at .

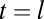By studying the distribution of immobilization times, we observed that it does not obey an exponential decay (23). This complexity may be caused by having different affinities at different stages in the life cycle of a CCP. Within this model, the dissociation coefficient depends on the size of the CCP and the rate of escape of a channel from a pit directly depends on the time of capture within the CCP life cycle. The Inset of Fig. 3C illustrates the Kv2.1–CCP interaction cycle: the life of the pit begins at time t = 0, at a later time t₀ the channel is captured, and it remains in the CCP during a time 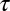. When a membrane protein undergoes a diffusive motion, the probability that it finds a clathrin membrane structure without being actively attracted in that direction is proportional to the structure perimeter. Thus, within a mean-field circular pit approximation, the probability density of a cargo protein being captured into the pit at time t₀ scales as the square root of adaptor proteins, 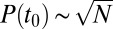. Furthermore, from the law of total probability, the probability that a given binding event occurs at time t₀ is 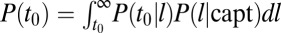, where 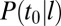is the posterior probability that a binding event occurs at time t₀ given that the lifetime of the pit is 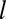. We denote 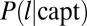as the probability for a pit that captures a channel to have a lifetime 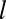. From Eq. 1, the number of adaptor proteins at time t₀ is proportional to 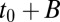. Thus, the law of total probability yields the a priori distribution:

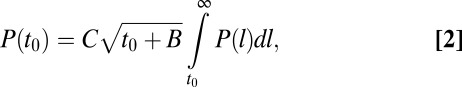where C is a normalization constant and 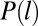is the lifetime distribution of the CCPs, as shown in Fig. 1C. The complete derivation of Eq. 2 is presented in SI Text. Rigorously, the distribution of times of capture can be different for a cargo molecule that returns to the CCP after escaping. In particular, the return times may be affected by the antipersistent characteristics of diffusion in a crowded environment. However, for the sake of simplicity, we neglect the effect of return times in the derivations. Using the measured CCP lifetime probability density, we are able to predict the distribution function of the times of capture with a single unknown, namely the time parameter B related to the initiation stage of the CCP as described in Fig. 1D. We measured the distribution of times of capture for 35,869 stalls using an automated algorithm that matches the Kv2.1 stalls to a CCP trajectory. Note that, throughout the manuscript, “time of capture” refers to the point within the CCP life cycle when a K⁺ channel becomes captured. The measured distribution of times of capture is shown in Fig. 3C along with the model prediction (Eq. 2). We find excellent agreement between our prediction and the measured distribution for B = 20 s.

Modeling the Affinity Between Cargo and CCPs.

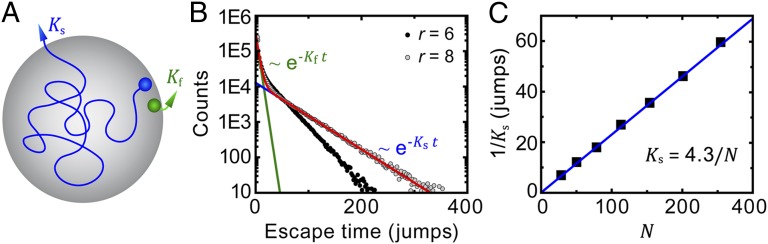
The probability density of dwell times of a two-state, memoryless, Markov process with dissociation constant k_off is an exponential distribution with characteristic time 1/k_off. The case of dissociation from a CCP is more complex because, if a cargo molecule escapes from the binding site of one adaptor protein, it can rebind to an adjacent binding site. Thus, k_off from a CCP depends on pit size and, in turn, on the age of the pit itself. Intuitively, a molecule that binds to the edge of the pit has two different ways to escape from it: It can turn around and step out of the pit or, alternatively, it can explore the pit through a longer random walk by hopping between a large number of binding sites (as illustrated with K_s and K_f in Fig. 4A). The problem of the molecule escaping a pit can be modeled as a random-walk first-passage time. We simulated this process on a square lattice. A tracer representing a cargo molecule is placed at the edge of a circle and it is allowed to jump to one of the four adjacent sites at each time step. Once the tracer reaches a lattice point outside the circle, it escapes. We performed 10⁶ simulations for each radius and built the distributions of escape times. Fig. 4B shows the distributions for the radii r = 6 and r = 8. Two distinctive escape populations are seen, with only the longer-lived one showing a strong dependence on pit size. The characteristic time of this slow-escaping population scales linearly with the area of the circle or, alike, with the number of available binding sites (Fig. 4C).

Fig. 4.

Numerical simulation of the escape of cargo from CCPs. Random walks are simulated on a square lattice inside circles of different radii, and the escape time is computed. From 10⁶ simulations, we find there are two populations of escape times. (A) Schematic of the pathways taken by a random walker to escape from a circle. A particle that escapes fast, K_f, is shown in green, and a particle that escapes slowly, K_s, is shown as a blue trajectory. (B) Escape time for circles with radii equal to six lattice points (black) and eight lattice points (gray). Two populations of escape times are seen and both exponential fits are shown for r = 8 in green (fast) and blue (slow). The red curve is total distribution of escape times shown as the sum of the fast and slow exponential decays for r = 8. (C) Characteristic escape time of the slow population for pits of different number of lattice points. The characteristic escape time is the inverse of the rate of escape, and it is seen to be proportional to the number of lattice points within the circle. This is analogous to a quadratic relation r² ∼ D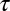 , where r is the radius of the pit and 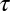is the escape time.

The Cargo–CCP Interaction Displays a Long-Tail Power Law Relaxation.

The escape rate of the population of cargo molecules that escape fast from a circular pit can be approximated to be independent of pit size. Therefore, the binding time does not depend on the time of capture and its probability density scales as 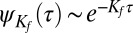. However, the rate of escape of the slow population is time dependent. We can formulate a rate equation for the survival probability, i.e., the probability of a molecule still remaining in a pit a time 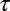after capture, 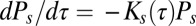. Using Eq. 1 and the simulation results in Fig. 4C, we obtain 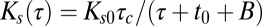for a molecule that is captured at time t₀, yielding power law statistics for the binding times:

where 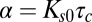, and we have omitted a δ function term due to the finite number of molecules with a binding time that ends at 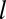, the pit lifetime.

The a priori distribution of binding times 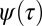can be obtained by using Bayes’ theorem and combining the slow and fast distributions as described in SI Text. Introducing a weight factor w for the fast and slow distributions, 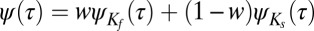, we find

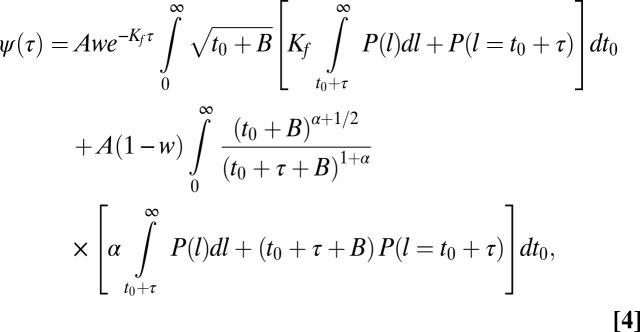where the normalization factor is 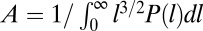and 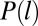is the probability density function of CCP lifetimes. Even though this expression seems formidable, boasting integrals that have to be numerically computed, the unknown parameters are w and K_f, which affect the fast population, and α, which impacts only the slow distribution. As a consequence, the weight w and the fast dissociation rate K_f are relevant only for binding times smaller than 8 s. The nontrivial part of the distribution of binding times is the range of times longer than 8 s and it deals with the long-tail distribution, which depends solely on the exponent α.

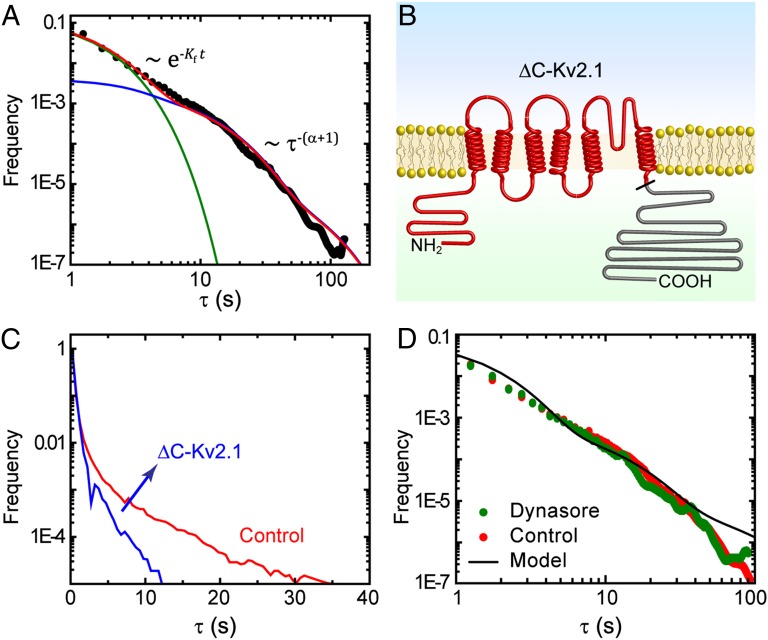
We measured the time Kv2.1 channels remain captured within a CCP by observing the duration of 35,869 immobilization events. Fig. 5A shows the binding-time distribution along with the model prediction (Eq. 4). The individual contributions of the fast and slow escape rates are shown in green and blue, respectively. The lifetime of CCPs displays three subpopulations (Fig. 1C), but we find that the longer population does not contribute to the distribution of slow-escaping binding times. As seen in Fig. 5A, the model holds very well to the measured distribution of binding times when α = 0.85.

Fig. 5.

Binding-time distributions of Kv2.1. (A) Measured binding-time distribution of Kv2.1 into CCPs, round full circles. The contribution of fast-escaping channels is shown as a green solid line and slowly escaping channels in blue, along with the overall distribution in red (Eq. 4). (B) Schematic of ΔC-Kv2.1 mutant channel. The black tick marks where the C terminus (grayed) is removed. (C) Binding-time distribution for ΔC-Kv2.1. Without the C terminus, Kv2.1 becomes captured into CCPs less frequently, and it only remains bound for short times. (D) Binding-time distribution of Kv2.1 after inhibition of the GTPase dynamin with 80 μM dynasore. No statistically significant changes in the binding-time distribution are observed between control cells and dynasore-treated cells.

The Effect of Dynamin and the Interactions with the Channel C Terminus.

Because the C terminus of Kv2.1 contains multiple binding sites for adaptor proteins, we investigated the role of this domain in the affinity between Kv2.1 and CCPs by using a Kv2.1 mutant that lacks the last 318 aa of the C terminus (ΔC-Kv2.1). Previous reports show that this channel traffics to the surface and retains the electrophysiological characteristics of wild-type Kv2.1, but its lateral diffusivity is enhanced due to a lack of interactions with cytoskeletal components (24). A schematic of the ΔC-Kv2.1 is depicted in Fig. 5B. The deletion of the C terminus drastically changes the distribution of binding times (Fig. 5C). We find that ΔC-Kv2.1 never immobilizes within CCPs for longer than 12 seconds (n = 2,683 trajectories), a stark difference to the wild-type channel. Upon deletion of the C terminus of Kv2.1, the channel is internalized less efficiently and no longer exhibits a broad distribution of binding times. These data indicate that the C terminus of Kv2.1 is necessary for long-term capture into CCPs.

We also investigated the role of dynamin in cargo–CCP affinity by using the inhibitor dynasore (22). The binding-time distribution of Kv2.1 after dynasore application was compared with that in control cells (Fig. 5D). No significant changes are seen in the binding times of Kv2.1 between cells treated with dynasore and control cells, even though channels fail to internalize after treatment (Fig. 2A).

Affinity of Kv1.4 to CCP.

We show that our CCP affinity model can be applied to different molecules by studying the behavior of the voltage-gated potassium channel Kv1.4 in the same manner as Kv2.1. The dynamics of Kv1.4 differ from Kv2.1 as it moves more freely across the plasma membrane (23). As shown in Fig. 2A, Kv1.4 is also internalized via CME. In a similar way as seen for Kv2.1, Kv1.4 is often immobilized on the cell surface during prolonged times (23), alternating between periods of high and low diffusivity. Here, using two-color imaging and particle tracking, we find that the Kv1.4 stalling times are also rooted in the channel being captured by a CCP and subsequently released (Fig. 6A). From the analysis of 1,065 immobilizations in 583 trajectories, 82% of these events are colocalized with CCPs.

Fig. 6.

Analysis of Kv1.4 binding to CCPs. (A) Trajectory of an individual Kv1.4 channel together with the stalls of Kv1.4 longer than 1 s (white stars). Stalls for Kv1.4 also colocalize to CCPs, with 82% (n = 1,065) of all stalls occurring within a CCP. Sliding window MSD with a window length of 20 frames is shown above. The dotted line is a threshold indicating portions of the trajectory where the channel is moving (above threshold) or stalling (below threshold). (Scale bar: 0.02 μm²/s and 20 s.) Color of MSD and trajectory represent timescale, beginning at red and ending at blue. (B) Measured times of capture within a CCP together with the analytical probability distribution (Eq. 2) with B = 20 s. (C) Measured binding-time distribution for Kv1.4 shown with the model prediction. Contributions of fast (green)- and slow (blue)-escaping channels are shown along with the overall probability (red) (Eq. 4).

The distribution of times of capture of Kv1.4 within a CCP also agrees well with Eq. 2 (Fig. 6B), indicating that, as Kv1.4 is not actively transported toward endocytic structures, the probability of a channel finding the CCP is proportional to the pit perimeter length. This expresses that the capture of Kv1.4, as that of Kv2.1, is achieved by random encounters between cargo molecules and CCP. Fig. 6C shows the distribution of Kv1.4 binding times found from the distribution of immobilization times. Again, our kinetic model of time-dependent affinity with a CCP derived in Eq. 4 agrees to a remarkable degree with the experimental data. An α value of 0.9 was used for Kv1.4 and the same weight between fast and slow population is used for both Kv2.1 and Kv1.4 channels, which is found from the escape-time Monte Carlo simulations.

Discussion

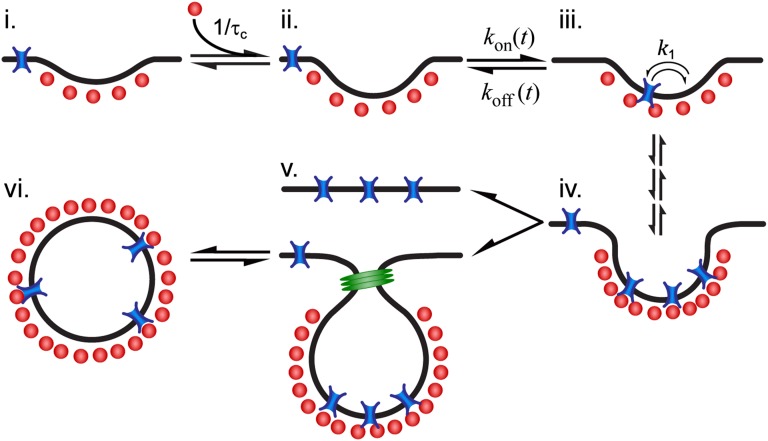
The broadly accepted picture of a clathrin-mediated endocytic process includes cargo molecules that are captured into a CCP and remain within the pit until internalization. This description has the appeal of selective cargo recruitment in a highly efficient manner. Nevertheless, our experiments show this is far from the actual process in live cells. Instead, we observe that captured cargo molecules are often released before completion of the CCP cycle. However, the dissociation relaxation does not obey an exponential decay. This catch-and-release process by CCPs is regulated by the cargo–pit interactions, which in turn depend on the age of the pit and display an extremely broad heterogeneity. In addition, because diffusive membrane proteins are immobilized by binding to a CCP, these proteins are seen to display alternating diffusive/immobile periods (23). We derived a model that describes the capture and release of cargo into CCPs. One of the key features of our observations is that potassium channels “remember” how much time they have spent bound to a CCP. Because of pit growth, the longer the time a channel spends within a CCP, the more difficult it is to escape. Thus, the release of a channel from a CCP is not a Markov process. Fig. 7 illustrates the main aspects of the process involving capture and release of cargo: (i) At time t = 0, a pit nucleates by recruiting adaptor proteins and clathrin (shown as one unit in red) from the cytosol. (ii) The pit enters a linear growth phase where, on average, an additional adaptor protein is recruited every time lapse 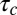. (iii) At some stochastic time t = t₀ within the pit growth stage, cargo that was randomly diffusing in the plasma membrane encounters the pit and it becomes captured. The channel can bind and unbind adaptor proteins within the pit with a dissociation rate k₁, performing a random walk as it hops between different adaptor binding sites. After a random time 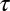, the channel may escape from the pit. However, the escape rate is time dependent. (iv) As the pit matures, more cargo becomes captured until the process is terminated at time t = 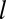, either (v) abortively or productively. Productive pits are cleaved from the membrane via the GTPase dynamin (green) resulting in a (vi) clathrin-coated vesicle.

Fig. 7.

Kinetic model of CCP growth and capture of cargo. (i) Cargo (blue) diffuses laterally in the plasma membrane. Adaptor proteins and clathrin (schematically shown as one unit in red) are recruited to a site of CCP initiation. (ii) The pit grows at a rate of 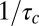, where 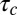is the average time of arrival of an extra adaptor to the pit. (iii) At time t = t₀, a cargo molecule is captured into the pit, it remains there for a time τ, and it escapes from the pit with a rate k_off. The rate of capture k_on and the rate of dissociation k_off are both time dependent. (iv) As the pit matures, additional cargo becomes captured within the pit until the pit is terminated at time t = 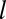, (v) either abortively or productively. Productive pits are pinched off the membrane via the GTPase dynamin (green). (vi) The result of a productive CCP is a clathrin-coated vesicle.

Our kinetic model is built around the growth of CCPs and how pits of different sizes have different affinities for cargo. However, CCP–cargo interactions can also be understood in terms of a static picture by means of a distribution of pit sizes. In the hypothetical situation that the distribution of pit sizes is available instead of the distribution of lifetimes, the same results could be achieved. Given a distribution P(N) of adaptor proteins per CCP, we can infer a distribution of slow dissociation rates using the relation K_s ∼ 1/N. The temporal analysis has the advantage that the distribution of binding times is found from first principles, namely a power law relation. In the spatial analysis, we speculate that a broad distribution of escape rates also gives rise to power law statistics.

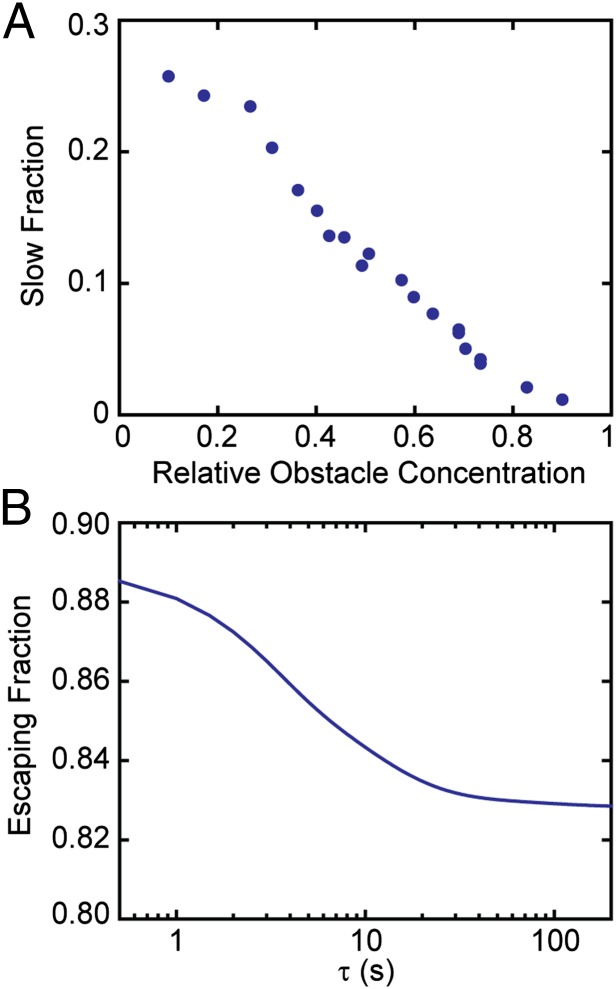
Endocytic cargo displays two catch-and-release populations that are intrinsic to the interaction with the clathrin-coated structure. On one hand, a fast exponential decay is found to have a characteristic time of the same order of magnitude as the escape rate from the individual adaptor (k₁ in Fig. 7). On the other, cargo dissociation exhibits a slow, power law relaxation decay. However, molecules that are captured during the last stages of the productive clathrin coats only show an exponential decay. In other words, cargo that is captured more than 1 min after initiation of the clathrin coat does not display power law dissociation behavior. When a pit gets into the later productive stage, it is most likely saturated with cargo molecules and only newly arriving adaptors leave room for the binding of new molecules. As a consequence, only the exponential decay is seen at this stage as newly bound cargo is not able to explore the core of the CCP. Supporting this hypothesis, we observe that the weights of each population are independent of the type of K⁺ channel as the same values are observed for Kv2.1 and Kv1.4. Therefore, the likelihood of a captured channel to explore the core of the CCP is a property of the pit itself and not the cargo molecule, as long as different cargo binds to the same adaptor. The hypothesis that cargo escapes faster from a mature pit when a large fraction of the adaptor binding sites are occupied at the time of capture can also be tested numerically via Monte Carlo simulations. We modeled this process in a similar way as presented in Fig. 4B, but with the additional complexity that lattice points can be blocked by mobile particles. Initially, a given number of particles is placed at random positions inside the circle, and at each time step both the tracer and all particles are allowed to move to one of the four nearest lattice sites. We use a “blind ant” algorithm, that is, if the chosen site for either an obstacle or the tracer is occupied the particle remains in the same spot but the time increases (25). Because we are interested in how the escape times are modified when the binding sites of the growing pit are occupied, we look at the fraction of tracers that escape via the slow pathway, i.e., the slow-escaping population fraction. Fig. 8A shows the fraction of tracers choosing the slow pathway as a function of the percentage of lattice points occupied by obstacles in a circle with r = 8 (for zero obstacle concentration, this is the normalized area under the blue line in Fig. 4B). It is observed that, when the obstacle concentration increases, the probability of a molecule to explore the interior of a CCP decreases. The transition occurs at a characteristic concentration of 45 ± 15%. Interestingly, this value is close to the percolation threshold in a square lattice (c_p = 0.41). However, the percolation threshold depends on the lattice geometry, e.g., in a triangular lattice c_p = 0.5. So the concentration of obstacles at which a cargo molecule does not explore the interior of a CCP probably depends on the clathrin scaffold structure.

Fig. 8.

Numerical results for CCP–cargo interactions. (A) Fraction of tracers that belong to the slow-escaping population as a function mobile obstacle concentration, as found from Monte Carlo simulations in a circle of radius r = 8. For each obstacle concentration, 100,000 realizations were obtained. When the obstacle concentration increases, more tracers are found to escape via the fast pathway that is described in Fig. 4. (B) Fraction of cargo molecules that escape from a pit before CCP termination up to a time 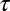, as computed from our model (Eqs. 4 and 5).

Our findings suggest the following fundamental implications related to the relationship between cargo binding and endocytic dynamics. (i) Affinity: Cargo molecules escape from the CCP before pit departure. We do not know at this point whether this is true for all existing cargo molecules. For potassium channels, we observe that 83% of captured molecules escape from the CCP. However, one can postulate that specific nonescaping cargo may exist. (ii) Temporal evolution: Both the probability of cargo being captured and the probability of cargo escaping the pit depend on time. Thus, as the pit grows it becomes more efficient in capturing cargo and keeping it in the CCP. (iii) Selectivity: Given that cargo can escape from the CCP, by increasing the affinity, the endocytic process would increase selectivity to specific cargo molecules. Thus, cargoes with higher affinity accumulate in a CCP more readily than those with lower affinity. (iv) Regulation of endocytic rates: Different adaptor molecules can be present in a CCP. However, multiple cargoes compete for the same adaptor sites and, therefore, the modulation of the affinity of competitive cargoes would cause the regulation of endocytic rates. (v) Heterogeneity: It has been previously shown that the accumulation of cargo molecules stabilizes CCPs, changing the relative distributions and lifetimes of CCP subpopulations (10). Here, we show that, due to its non-Markovian nature, cargo–CCP interactions display a long-tail power law relaxation. Interestingly, such relaxation dynamics have extremely broad distributions; for example, any asymptotic power law distribution 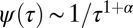with 0 < α < 1 has infinite variance. Therefore, the time spent by each cargo in a CCP can have very large fluctuations, which, in turn, lead to a broad distribution of captured cargo molecules at a given time. Because the number of cargo molecules affects the maturation of the CCP, large fluctuations in the pit lifetime are introduced. In other words, a long-tail distribution in binding times yields large heterogeneities in both the number of captured cargoes and the CCP lifetime.

One of the key findings in this manuscript is that cargo is not “permanently” captured by CCPs before being internalized. Instead, cargo molecules are transiently immobilized at the CCP in a catch-and-release–type situation. This observation allows the development of a model based on the time-dependent affinity between cargo and CCP. From our experimental measurements we find 83% of Kv2.1 channels escape the CCP before pit termination/departure. Remarkably, we can reach this same number from our stochastic model of cargo–CCP interactions using the parameters found above. Fig. 8B shows the fraction of cargo molecules that escape the pit up to a given binding time. To obtain this from our model, we split Eq. 4 in the parts for cargo escaping and cargo remaining within the pit. Explicitly, the fraction of cargo remaining within the pit until termination is as follows:

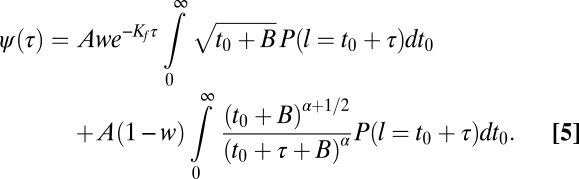It is observed in Fig. 8B that the fraction of cargo that escapes from the pit decreases over time. This is a consequence of the pit growing, thus reducing the chances of escaping and having higher chances of encountering the pit termination time. Again, our model predictions agree with experimental findings.

The tools developed here can be applied to any molecule that is internalized by CME as long as the distribution of CCP lifetimes is measured in the cell under investigation. The fundamental parameter in our model is the exponent 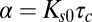, which is basically the product of the dissociation rate from the single adaptor and the average time it takes for a new adaptor molecule to be recruited into the pit. This parameter measures how fast the dissociation coefficient changes as the pit grows: the smaller α, the stronger the impact of changes with time. If 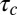is very long compared with 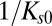, which is proportional to 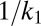as shown in Fig. 7, then the pit does not significantly change size from the time of capture until the time of release. Therefore, the memory effects in the dissociation are lost and the process appears stationary. In the static (spatial) picture, this means k_off does not change substantially within the range of available pit sizes. However, if 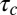is short, the pit grows substantially before the cargo escapes.

Power law distributions can result in self-similar processes with long memory. These systems are intrinsically complex and standard tools such as hidden Markov models cannot be used to unravel the transitions between different (hidden) states. In particular, for power law dwell-time distributions of the form 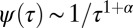, the process displays weak ergodicity breaking when 0 < α < 1, i.e., the temporal averages do not converge to the ensemble average in the long time limit (26). Furthermore, in this case, the average time a molecule spends in a bound state increases with experimental time, so the system also exhibits aging. When the power law is truncated, convergence to ergodicity is expected to be remarkably slow compared with the case when the dwell time is characterized by an exponential decay (27). These intrinsic properties should also give rise to anomalous diffusion in the plasma membrane as observed broadly over the last decade (28–31) and to aging effects as seen recently (23, 32). However, this work does not imply this is the main mechanism for anomalous subdiffusion in the plasma membrane, but that this mechanism certainly contributes to the observed anomalies.

In summary, we found that both Kv2.1 and Kv1.4 channels are endocytosed through clathrin-mediated pathways, but their interactions with CCPs are dominated by a catch-and-release behavior. We show that the binding times of cargo molecules associating to CCPs are shorter than the overall endocytic process. The escape probability from a pit is explicitly dependent on the size of the CCP. We derived a kinetic model that accurately predicts this time-dependent affinity between cargo and CCP. This is shown to be a non-Markovian process characterized by a power law relaxation.

Materials and Methods

Cell Culture and Transfection.

Human clathrin light chain A (CLC) subcloned into the mRFP-C1 and eGFP-C1 expression vectors were kindly provided by Dr. Santiago Di Pietro (Colorado State University). Kv2.1 and Kv1.4 expression vectors have been described previously (24, 33). HEK293 cells (American Type Culture Collection, passages 38–45) were cultured in DMEM (Gibco, Life Technologies) supplemented with 10% (vol/vol) FBS (Gibco) at 37 °C and 5% (vol/vol) CO₂. Cells were transfected to express a Kv2.1 construct with an extracellular biotin acceptor domain (Kv2.1-loop BAD) that, when coexpressed with a bacterial biotin ligase, results in biotinylated Kv2.1 channels on the cell surface. Similarly, we obtain biotinylated Kv1.4 channels. Transfection was performed by electroporation using a Bio-Rad Genepulser Xcell (Bio-Rad Laboratories) in a 0.2-cm gap cuvette with a single 110-V 25-ms pulse with 3 μg of Kv2.1-loop BAD, 1 μg of biotin ligase pSec BirA, along with 200 ng of fluorescently labeled GFP–CLC expressing DNA depending on the experiment. Following electroporation, cells were plated on cover glass-bottom culture dishes that were previously Matrigel-coated (BD Biosciences) and supplemented with DMEM without phenol red (Life Technologies) and 10% (vol/vol) FBS. Cells were used for live-cell imaging within 24 h of transfection. Low GFP–CLC expression levels were used to avoid artifacts and we verified that decreasing the plasmid concentration did not introduce any apparent differences in the morphology or dynamics of fluorescent clathrin on the cell surface.

Live-Cell Imaging.

Before imaging, cells were rinsed three times with a HEK physiological imaging saline (146 mM NaCl, 4.7 mM KCl, 2.5 mM CaCl₂⋅2H₂O, 0.6 mM MgSO₄, 0.15 mM NaH₂PO₄, 0.1 mM ascorbic acid, 8 mM glucose, and 20 mM Hepes). Cells expressing biotinylated Kv2.1 channels were incubated in a 0.1 nM solution of streptavidin-conjugated QDs (Qdot 655; Invitrogen) containing 150 μM BSA (IgG/fatty acid free; Sigma-Aldrich) for 5 min, then the cells were rinsed twice with imaging saline to remove any unbound QDs. Transfected cells were imaged in imaging saline at 37 °C. Imaging was performed in a custom-built, objective-type TIRF microscope described previously (23). For two-color TIRF imaging, a 473-nm laser was used to excite both GFP–CLC and 655QD–Kv2.1. The fluorescence emissions were then optically split (Optosplit; Cairn) onto the two halves of an electron-multiplying charge-coupled device (EMCCD iXon DU-888; Andor). Both the dish and the objective were maintained at 37 °C using a temperature control system (Bioptechs).

Endocytosis Disruption Reagents.

Dynasore was used to disrupt CME. This pharmacological reagent works by inhibiting the GTPase dynamin (22), which is mainly responsible for the scission of vesicular buds from the plasma membrane (34). It has been suggested that dynamin is also involved in the early stages of CCP formation, serving as both a regulator and integrity monitor (10, 35, 36). Dynasore was dissolved in dimethyl sulfoxide (DMSO) (Sigma-Aldrich) and directly added to the imaging dish to a final concentration of 80 μM (22). The final DMSO concentration was 0.2% and showed no effects on its own.

Image Processing and Particle Tracking.

Images were acquired using Andor IQ 2.3 software and saved as 16-bit tiff files. The images were overlaid using the Cairn-Optosplit plugin available in ImageJ, and they were frame averaged using a custom-written algorithm in LabView that averages the intensities of every pair of images, reducing the number of frames to one-half. Then the 2x frame averaged images were filtered using a Gaussian kernel with a SD of 1.0 pixel in ImageJ. Single-particle tracking of GFP–CLC and QD–Kv2.1 was performed using the u-track algorithm developed by Jaqaman et al. (37). To accurately track QDs, this algorithm was modified so that the gap closing cost function accounts for the inherent QD blinking behavior.

Displacement Square and Stalling Analysis.

The instantaneous MSD was found from the detected locations within the QD trajectories using a sliding time-window averaging method (23). The length of the averaging window was set to 20 frames (2 s), 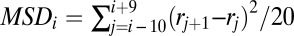. We identified events in which the channel MSD remains below a threshold 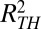= 2,000 nm². The time and location of each stall lasting longer than 0.5 s were recorded to determine where stalls occurred with respect to clathrin. Stalls occurring within 130 nm from the CCP (this distance is due to the accuracy of the image overlay) were considered to be colocalizing with clathrin.