Comminution of solids caused by kinetic energy of high shear strain rate, with implications for impact, shock, and shale fracturing

Significance

Fragmentation, crushing, and pulverization of solids, referred to as comminution, has long been of keen interest for mining, tunneling, explosions, meteorite impact, missile impact, ground shock, terrorist attacks, and various industrial processes. Recently, interest surged in comminution of gas or oil shale as a way to enhance the permeability of shale mass by orders of magnitude. Particularly intriguing is a proposed, environmentally friendlier, alternative to hydraulic fracturing in which the fracturing would be achieved by shock waves from explosions or electrohydraulic pulsed arc in a horizontal borehole. The discharge of contaminated water would, in this case, be negligible. In all these problems the energy dissipation density is a key parameter to predict. Here a theory to do so is outlined.

Abstract

Although there exists a vast literature on the dynamic comminution or fragmentation of rocks, concrete, metals, and ceramics, none of the known models suffices for macroscopic dynamic finite element analysis. This paper outlines the basic idea of the macroscopic model. Unlike static fracture, in which the driving force is the release of strain energy, here the essential idea is that the driving force of comminution under high-rate compression is the release of the local kinetic energy of shear strain rate. The density of this energy at strain rates >1,000/s is found to exceed the maximum possible strain energy density by orders of magnitude, making the strain energy irrelevant. It is shown that particle size is proportional to the −2/3 power of the shear strain rate and the 2/3 power of the interface fracture energy or interface shear stress, and that the comminution process is macroscopically equivalent to an apparent shear viscosity that is proportional (at constant interface stress) to the −1/3 power of this rate. A dimensionless indicator of the comminution intensity is formulated. The theory was inspired by noting that the local kinetic energy of shear strain rate plays a role analogous to the local kinetic energy of eddies in turbulent flow.

The previous studies of high-rate dynamic fracture of rocks, concretes, ceramics, composites, and metals have dealt mainly with the nucleation, propagation, and branching of dynamically propagating cracks, their interference with elastic or shock waves, and the mechanism of development of the zones of densely distributed fractures, called the Mescall zones (1–7). However, a comminution model in the form of a macroscopic constitutive equation that could be used in large dynamic finite element programs for global response of structures is apparently still unavailable.

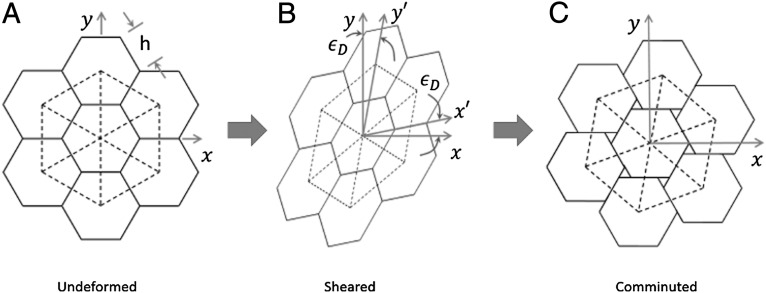
Seeking such a constitutive model, we begin with the analysis of a simple idealized process in which the solid is comminuted to identical particles (Fig. 1). Among simple space-filling regular subdivisions in the plane of maximum shear, regular hexagons are the most likely because they give the smallest surface-to-volume ratio (Fig. 1A) and thus require the minimum energy to form. In the direction normal to the hexagons, we assume the particles to be prismatic.

Fig. 1.

Example of comminution of material into prismatic hexagonal particles; the velocities are shown as infinitesimal displacements (in which case the gaps at the hexagon corners are second-order small and thus negligible). (A) Undeformed material, (B) sheared material, and (C) comminuted material.

Consider that, at a certain moment, the strain rate (shown in Fig. 1B as a displacement regarded as infinitesimal) becomes high enough for the kinetic energy of shear strain rate to suffice for creating the fractures and interface slips that separate the particles of as yet unknown size. As that happens, the particles release their local kinetic energy, slip against each other, and regain their original undeformed shape, while the particle centers conform to the same macroscopic velocity field (Fig. 1C).

For the sake of simplicity and clarity, we will first outline a 2D analysis of comminution in the plane of maximum shear strain rate denoted as 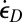, and leave the 3D generalization for later discussion. Before comminution or slip, the displacement velocities in the directions of current (Eulerian) coordinates x and y, whose origin is attached to the particle centroid, are 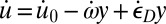and 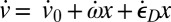, in which the superior dots denote time derivatives. After comminution or slip, these velocities become 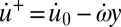and 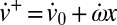. Assuming particle symmetry with respect to axes x and y, we have , and for the drop of kinetic energy of the hexagonal prisms per unit volume we obtain

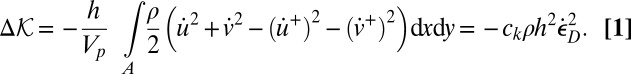Here A = particle area, ρ = mass density, 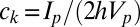, , 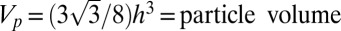and 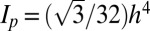= polar moment of inertia of each hexagonal prism of side h and length h. Note that the macroscopic velocities of material rotation ω and displacements 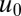and 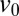have no effect on 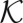, which means that the local kinetic energy density is separable from the kinetic energy density of the macroscopic 2D motion defined by the velocities of particle centroids.

It is interesting that the kinetic energy 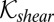of a particle deforming by pure shear at rate 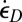happens to be the same as the kinetic energy 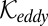of an eddy rotating as a rigid body of the same size at angular rate 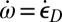(Fig. 2). Thus, we see a partial analogy with turbulence (8), which is what inspired the present theory. In both comminution and turbulence, the microlevel kinetic energy augments the kinetic energy of the macrolevel motion. The microlevel kinetic energy is dissipated by fluid viscosity in the eddies of turbulent flow, or by the energy, Γ, of interface fracture or subsequent frictional slip. However, unlike an eddy, the local shear strain motion cannot continue indefinitely.

Fig. 2.

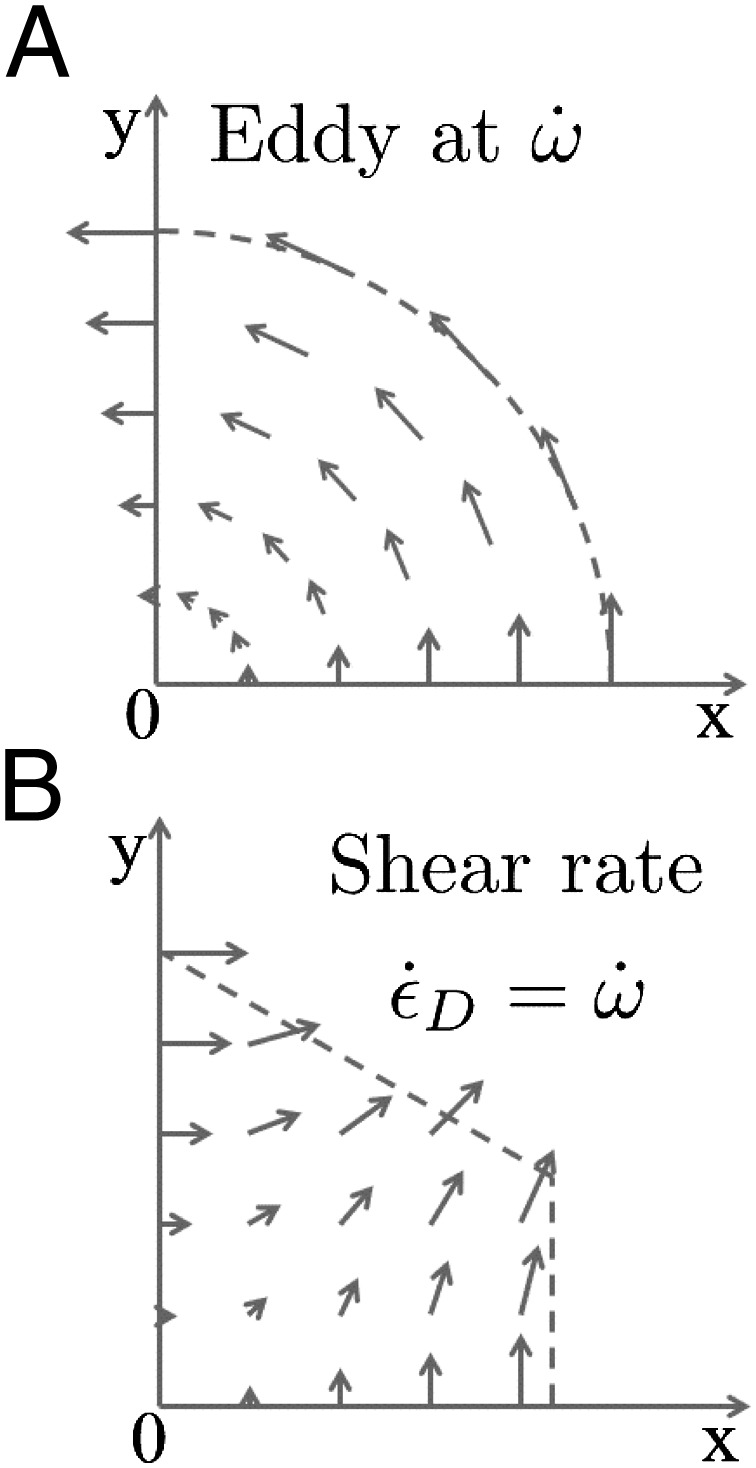
Fields (in the first quadrant) of local velocity vectors giving the same kinetic energy density for (A) rigid body rotation and (B) pure shear deformation of the same magnitude.

In reality, particle sizes h vary randomly, according to a certain distribution, for which the following cumulative distribution [Schuhmann’s power law (9–12)] is adopted:

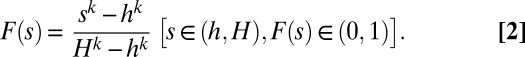Here k = empirical constant 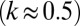, s = variable particle size, and h and H = minimum and maximum particle sizes (usually 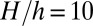to 100). Because the macroscopic quasi-static constitutive law with nonlocalized strain softening includes the energy dissipation corresponding to material crushing into particles of the size d_a of the largest material inhomogeneities, such as the maximum aggregate size in concrete, H should be considered to be one order of magnitude smaller (i.e., about 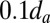). The average particle size is 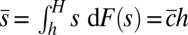, the combined interface area per unit volume is 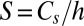, and the loss of kinetic energy of the shear strain rate of the particles of all sizes per unit volume is 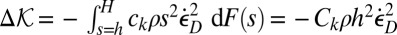, where 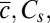and C_k are dimensionless constants. For 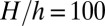and for hexagonal or cubical particles, 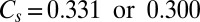, and , respectively (the values for cubical particles are included to show that the particle shape does not make much difference).

Assuming that all of a kinetic energy decrement 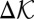is dissipated by an interface fracture energy increment 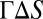, the energy balance condition is 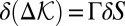; Γ = shear fracture energy or, after break, the work of friction per unit interface area (which is considered as constant because its dependence on the confining pressure and slip velocity is not known. So, the interface fracture (or frictional slip) can occur when

After substitutions into Eq. 3 one gets

where 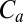is a dimensionless constant. If 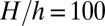, then 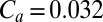for hexagonal prisms and 0.019 for cubical particles. Again, the precise particle shape does not make a major difference.

It should be mentioned that Eqs. 4 and 3 are similar to Grady’s (13) equation, derived and experimentally verified for tensile comminution caused by a high volumetric strain rate driven by explosion within a hollow sphere. Later, Grady (14) verified empirically (although not theoretically) that 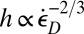holds also for the impact of missiles, in which the role of volume expansion is negligible. This fact serves as one experimental verification of the present theory (Eq. 4).

Note that, more generally, and specifically for a single dynamically propagating crack in two dimensions, the dynamic energy release rate involving both the elastic strain energy 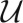and the kinetic energy with inertial effects was rigorously formulated in equations 5.3.2 and 5.3.20 of Freund’s book (7). Eq. 3 may be regarded as a simplification of these equations to the case of negligible 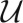and at the same time a generalization and adaptation to a smeared continuum representation of many diffuse cracks characterized by their combined surface S.

Substitution of Eq. 4 into Eq. 1 further yields

where 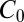is a certain dimensionless constant; 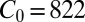for hexagonal prisms and 1,013 for cubical particles. This expression suggests how to implement the energy sink owing to comminution in macroscopic structural analysis. Note that 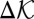has the dimension of stress and can be interpreted as such.

To obtain a 3D generalization, it is convenient to introduce equivalent viscosity 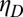such that the viscous stress strain relation 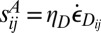would give the same energy dissipation density as Eq. 5 for any deviatoric strain rate tensor 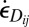, in the variational sense; here 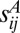is the additional deviatoric stress caused by the comminution. Now we note that the energy density is the same as the stress, that 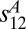must be equal to 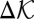when all other tensorial components vanish, and that 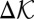must be a tensorial invariant. To satisfy these three conditions, it is necessary that 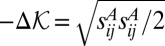. Because 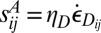in terms of viscosity, we may write 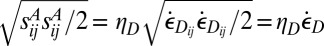, where now 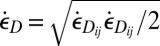, which simplifies to pure shear 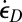when 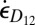is the only nonzero component. Therefore, the energy sink owing to the comminution process may be modeled by the equivalent viscosity

Unlike Eq. 1, this 3D generalization is only approximate because, in three dimensions, the local kinetic energy density of strain rate is not separable from the total kinetic energy density. There is an energy cross-term involving both 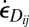and general rotation tensor 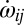, which is here neglected. However, calculations indicate that this cross-term is not important.

Viscosity 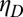can easily be implemented in the constitutive relation in a finite element program. It may be noted that the enhancement of dissipative viscous resistance to shearing is again a feature analogous to the enhancement of viscous resistance caused by eddies in turbulent flow.

In view of the partial analogy with turbulence (Fig. 2), can one formulate a dimensionless indicator analogous to the Reynolds number, which would decide when the comminution dominates the energy dissipation? One can. The strain energy density stored in the material may be expressed as 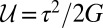, where G is the elastic shear modulus and τ is the shear stress. When 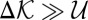, then obviously the comminution cannot be caused by the release of strain energy and the release of kinetic energy is the only possible energy source for the comminution. Therefore, we may define the dimensionless numbe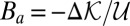r or

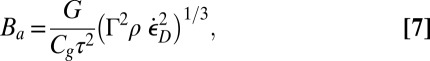which has the property that the comminution is

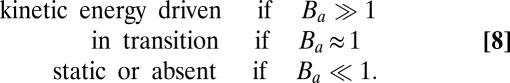Substituting τ = τ₀ = maximum shear stress that can be resisted by the material (i.e., the yield strength), one has the sufficient condition for the comminution to be driven by the kinetic energy release. The equivalent viscosity may also be uniquely expressed in terms of .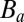

Note that exponent 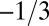in Eq. 6 is only an approximation for constant Γ. Although no relevant data exist at present, Γ as a characteristic of postfracture frictional work is likely to decrease with the slip rate; if it decreases as a power law it would reduce the exponent in Eq. 6 below 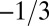. Further note that if, after comminution, 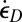further increases, particles already comminuted are getting comminuted to smaller sizes. However, if 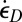decreases while remaining in the comminution range according to Eq. 7, energy balance requires the frictional slip to be concentrated into interfaces between groups of particles moving as virtually rigid bodies (h then represents the size of these groups).

Finite element simulations indicate that, in practical applications such as impact, the rate of expansive volumetric strain rate, 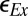, plays no significant role. For explosions in a shale mass, however, the rates of shear strain and of volumetric expansion may both be important. One can show that, in that case, the foregoing theory can be easily generalized; for example, 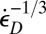in Eq. 6 needs to be replaced by .

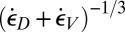Some Results and Discussion

Although a practically most intriguing application of dynamic comminution modeling may be the fracturing of gas or oil shale by electro-hydraulic pulsed arc (15, 16) or by chemical explosion in the pipe of a horizontal borehole, no data on this recently discussed alternative technology exist in the public domain. Nevertheless, a confirmation of the present comminution model can be obtained by fitting the data on the measured exit velocity, 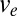, of projectiles penetrating concrete walls of different thicknesses.

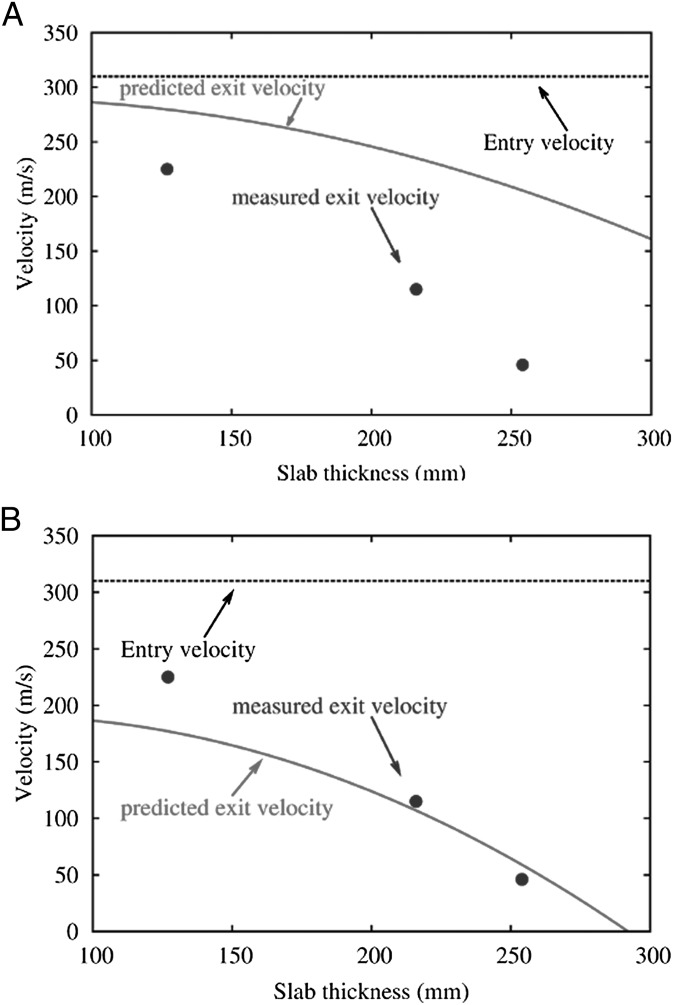
One such set of data is shown in Fig. 3 (17), which shows 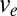as a function of the thickness D of the wall. The entry velocity of the missile is 310 m/s. The 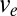values are computed with an explicit dynamic finite element program using the microplane model, first under the assumption that the only rate effects are the quasistatically calibrated rate effects, which consist of viscoelasticity of intact concrete between the cracks and of the rate of bond breakage at the fracture front controlled by activation energy (18). As seen, this simple assumption leads to a gross overestimation of the exit velocities. However, when the presently formulated equivalent viscosity owing to kinetic comminution is included, the data for the two thicker walls are fitted perfectly (in ref. 17, the strength and strain limits of the microplane constitutive laws were elevated horizontally by more than an order of magnitude and vertically by more than three times, with no physical justification, so as to fit these data).

Fig. 3.

Comparison of measured exit velocities and finite element predictions using microplane constitutive model M7 (A) with quasi-static strain rate effects only and (B) with both quasi-static strain rate effects and effect of comminution of concrete (the experimental data points are taken from ref. 17).

For the thinnest wall, the exit velocity is still overestimated (Fig. 3). However, this is likely explained by differences in the specific moisture contents in the nanopores of concrete. For a lower moisture content, Hopkinson bar experiments have shown a lower strength in high-rate shear, and this is the case for the thinner wall because it dries faster. However, analysis of this and many other questions is beyond the scope of this brief article. A detailed discussion is given in a separate extensive report (18).

To release gas or oil from the shale mass by means of shock waves generated by explosions or pulsed arc in a horizontal borehole, the fragmentation would have to be sufficiently fine to achieve a drastic increase of permeability (19). Reports on ongoing dynamic finite element simulations indicate that the shear strain rates produced by such shock waves exceed 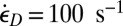(20). Does it suffice for sufficient fragmentation? For a crude assessment, consider that the material parameters of a typical unconfined shale are 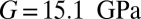, , 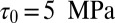, 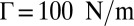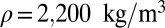(21–23). This yields 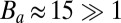, and thus suffices for comminution. However, in real situations the shale is subjected to a large confining pressure, such as 50 MPa, for which one may expect 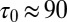MPa. If again 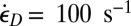, one gets 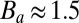, the other parameters remaining the same. So this situation is at the mere inception of dynamic comminution. A more detailed assessment will require taking into account the rate of volumetric expansion behind the pressure shock front, considering shocks due to stronger explosions or pulsed arcs, and examining the interference of shock fronts from different sources.

As a final remark, the dynamic erosion of a solid surface by impinging hard particles (24) is a fundamentally different process to which the present analysis does not apply.