Folding of RNA tertiary structure: linkages between backbone phosphates, ions, and water

Abstract

The functional forms of many RNAs have compact architectures. The placement of phosphates within such structures must be influenced not only by the strong electrostatic repulsion between phosphates, but also by networks of interactions between phosphates, water, and mobile ions. This review first explores what has been learned of the basic thermodynamic constraints on these arrangements from studies of hydration and ions in simple DNA molecules, and then gives an overview of what is known about ion and water interactions with RNA structures. A brief survey of RNA crystal structures identifies several interesting architectures in which closely spaced phosphates share hydration shells or phosphates are buried in environments that provide intramolecular hydrogen bonds or site-bound cations. Formation of these structures must require strong coupling between the uptake of ions and release of water.

Introduction

At the time Biopolymers was founded in 1963, most contributors would have been skeptical of the idea that RNA molecules could fold into compact native structures capable of protein-like functions such as specific ligand recognition or catalysis. One reason for skepticism was the full negative charge of the backbone phosphate: the electrostatic repulsion developed in folding a ‘globular’ RNA could be enormous, and dehydration of ‘buried’ phosphates could be energetically costly as well. It was not obvious whether stabilizing interactions could be sufficiently strong to overcome these barriers to RNA folding. In any case, it seemed obvious that proteins were best suited for shape-based functionality, and outside of the puzzle of why the protein synthetic machinery contained so much RNA, there was little reason to consider the possibility of highly folded RNAs.

It is now well known that RNA is capable of a remarkable variety of functional architectures, many of them surprisingly compact. Near and within a compact RNA structure, the positioning of phosphates, water, and ions must all be energetically coupled. The purpose of this review is to explore what is known of the basic thermodynamic constraints on these arrangements and how those constraints are manifested in the architecture of native RNAs. Fundamental physical principles regarding nucleic acid interactions with water and salt have been illuminated by elegant and rigorous experiments, many of them reported in Biopolymers. The implications of those principles for the folding of RNA tertiary structures are still being explored.

Phosphate hydration in nucleic acids

Water structure near DNA phosphates

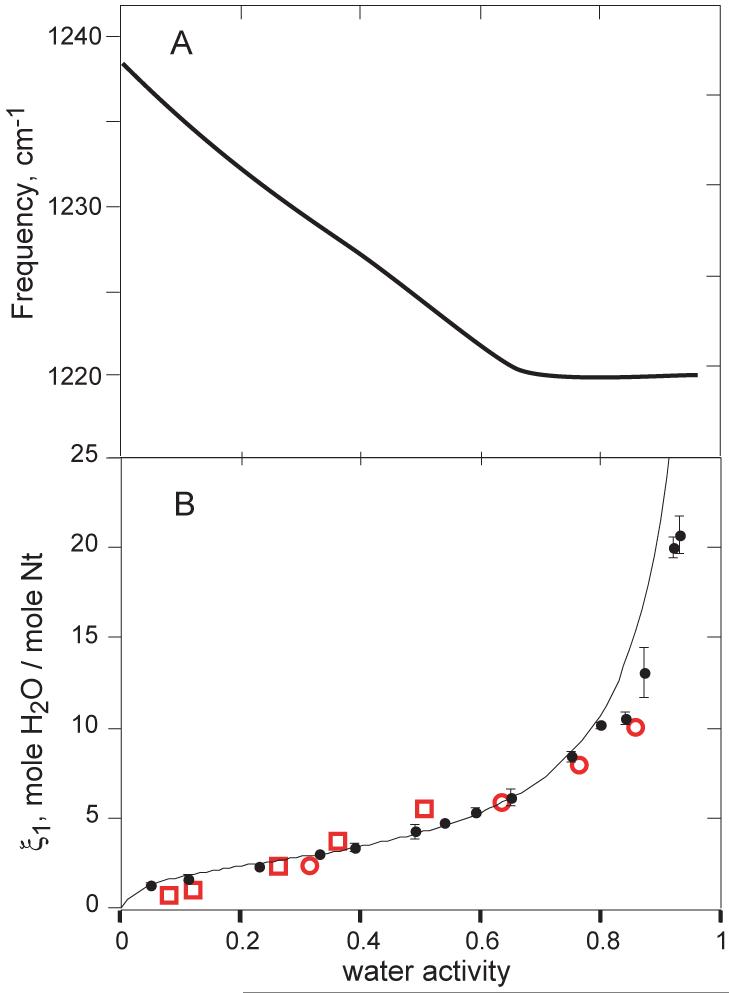
On the surface of a DNA or RNA molecule, the negative charge of the non-bridging phosphodiester oxygens is expected to generate the strongest interactions with water. Indeed, in DNA films held in equilibrium with atmospheres of increasing relative humidity, a band identified as the anionic P-O asymmetric stretch (1240 cm⁻¹) shifts linearly with an increase in water activity from 0 to 0.65 (Figure 1A).¹ About six waters per nucleotide are taken up as the P-O bond is titrated (Figure 1B).² The sodium salt of DNA was used to make the films, and presumably the first waters taken up are bound to a Na⁺ - phosphate ion pair. Further IR studies with deuterated water (HDO) showed that DNA samples hydrated with up to ~9 waters per nucleotide fail to show a characteristic spectral change associated with the formation of ice, even at −150 °C.³ Strong water – phosphate – Na⁺ interactions must present a large energetic barrier to the formation of ice-like hydrogen bonds between water molecules.

Figure 1.

Properties of Na•DNA that has been equilibrated with water atmospheres of varying vapor pressure (21 °C). A, shift in the antisymmetric PO₂ ⁻ band observed in IR spectroscopy of thin (1-5 micron) films. The smooth curve is as drawn through data points in Figure 4 of ¹. B, the number of water molecules per nucleotide in Na•DNA fibers (ξ₁, eq 1) as a function of water activity (closed circles; data points from Table I of ²). The solid line is a least-squares fit of the BET equation for adsorption of gases onto surfaces ⁸ with the parameters v_m (number of molecules adsorbed in a first monolayer) = 2.18 waters/nucleotide and the BET parameter c = exp[(E₁-E_L)/RT] = 22.4, where (E₁-E_L) is the difference in the heat of adsorption between the first (E₁) and subsequent (E_L) adsorbed layers. Open red symbols, data from buoyant density data obtained with DNA in concentrated solutions of various lithium (squares) or cesium (circles) salts.¹²

Crystal structures of short DNA duplexes at high resolution suggest likely arrangements of water around DNA phosphates. As expected from computations of dimethylphosphate solvation,⁴ each anionic oxygen can hydrogen bond with water at three different positions, arranged as a tetrahedron. Of these six potential sites, an average of about 2.5 ordered waters are observed per phosphate.⁵ In A-form DNA and RNA helices, one of the two anionic oxygen atoms points into the major groove spaced about 5.5 Å from the corresponding oxygens of neighboring nucleotides. This distance is short enough that one water hydrogen bonds to two oxygens.^6,7 It may be that some first-shell water of hydration is released when single-stranded polynucleotides pair to make an A-form duplex.

Water – DNA interaction detected by osmotic methods

In experiments similar to the spectroscopic studies described above, the weight of Na•DNA fibers was measured after equilibration with atmospheres of progressively higher water vapor pressure,² an experiment termed isopiestic distillation. The quantity measured is

$${\xi }_1={\left(\frac{\partial mo{l}_1}{\partial mo{l}_2}\right)}_{{\mu }_1,T,P}$$ (1)

where component 1 is water and component 2 is the sodium salt of DNA (Na•DNA). The vapor pressure of water is proportional to its chemical potential (μ₁) or activity (a₁) on a mole fraction scale. ξ₁ is thus the number of moles of water that has been taken up per mole of sodium-nucleotide when the system is in equilibrium with water vapor fixed at μ₁. ξ₁ is plotted as a function of water activity in Figure 1. The shape of the curve, which shows an initial uptake of ~2 waters at a₁ < 0.1, is reminiscent of isotherms obtained for the adsorption of gases onto surfaces.⁸ In those systems, the initial uptake corresponds to coverage of the surface by a single molecular layer of adsorbed gas. The approximately linear region that follows the initial uptake represents adsorption of additional layers of water. Interpretation of the Figure 1 isotherm by a simple multilayer gas-adsorption model ^2,8,9 suggests that two waters are bound directly to each Na•DNA nucleotide, with a binding energy about −1.8 kcal/mol stronger than that of subsequent layers. These numbers should be viewed as approximations, as the surface adsorption model does not capture important aspects of Na•DNA hydration. Hydration of dry Na•DNA is actually an absorption process, in which the water dissociates Na-phosphate ion pairs and separates DNA molecules as the film swells. It should also be noted that up to ~60% humidity DNA is in a disordered conformation with substantially unstacked bases;¹⁰ a transition to A-form helix geometry takes place between 60 and 70% humidity. Nevertheless, the conclusion remains that approximately two waters associate tightly at low water activity, presumably with anionic oxygen – Na⁺ ion pairs.

Other isopiestic distillation experiments have been carried out with solutions of Na•DNA plus a third component, a salt such as NaCl.¹¹ ξ₁ for such three-component systems has also been derived from the buoyant density of DNA in dense salt solutions.¹² The salt concentrations in these experiments is high enough to substantially reduce the water activity. The resulting plots of ξ₁ vs. a₁ are similar to data obtained with Na•DNA as the only solute, though the initial uptake of two waters is not reproduced (Figure 1). Alternatively, equilibrium dialysis experiments look at the distribution of salt between the solution of Na•DNA and salt vs. a salt solution alone.¹³ Here the chemical potentials of both water and salt are held constant, and the quantity usually reported is

$${\xi }_3{\left(\frac{\partial mo{l}_3}{\partial mo{l}_2}\right)}_{{\mu }_1,{\mu }_3,T}$$ (2)

ξ₃ is negative, ranging from approximately −0.1 at low salt to −0.5 at salt concentrations greater than ~ 1 M.¹⁴ This exclusion of salt is a manifestation of the Donnan effect associated with dialysis equilibrium of charged polymers. In a dialysis solution initially composed of Na•DNA and NaCl, some of the Na⁺ ions that originally neutralized the DNA will migrate to the buffer-only chamber, accompanied by an equal number of Cl⁻. The net result is an exclusion of ξ₃ anions per nucleotide and a retention of (1-ξ₃) cations per nucleotide. Compared to the initial solution, ξ₃ anion-cation pairs have migrated out of the Na•DNA solution, an overall exclusion of salt by the DNA.

ξ₁ and ξ₃ have sometimes been interpreted as quantifying water uptake (hydration) or ion exclusion, respectively. As developed in detail by Cohen & Eisenberg in a classic Biopolymers paper,¹³ these two parameters are two sides of the same coin, and are related by

$${\xi }_1=-{\xi }_3\frac{55.5}{m_3}$$ (3)

Each parameter is therefore sensitive to both hydration and salt exclusion. In the isopiestic distillation experiments of Figure 1B, the relation between ξ₁ and ξ₃ is such that the uptake of water at low activity is almost entirely due to water binding directly to the DNA, with little contribution from ion release. At higher water activity, where ξ₁ becomes 20-50 waters per nucleotide, the measurements are primarily detecting the release of ions- the water taken up is diluting released ions, not binding to the DNA surface. Conversely, ξ₃ measures primarily ion exclusion in dilute salt solutions, but at high salt (~5 NaCl), there is probably some contribution to ξ₃ from hydration.¹³ The agreement between isopiestic data with Na•DNA alone, in which salt exclusion is not an issue (Figure 1B, red) and with buoyant density data (black points) is excellent up to a₁≈ 0.8, suggesting that ion exclusion contributes to ξ₁ only at even higher water activities greater than ~ 0.8.

In summary, the experiments shown in Figure 1 suggest that DNA phosphates are the most strongly hydrated part of the molecule, binding two waters with a free energy of at least – 1.8 kcal/mol (−20 kT); the actual value could be much more negative. Perhaps four more waters bind phosphate tightly. Unfortunately the data do not bear on the extent of hydration in the relatively dilute salt (and high water activity) solutions used in most RNA folding studies. An alternative method for assessing water release in RNA folding reactions is described in the next section.

Osmolyte probes of phosphate hydration

A way to measure the hydration of a macromolecule in dilute salt solution is to use small neutral compounds, termed either co-solvents or osmolytes, that compete with water for interactions at the macromolecular surface. If an osmolyte interacts more favorably than water with the surface, the mole ratio of osmolyte to water in the solvation layers will be greater than the mole ratio in the bulk solution. Conversely, if water is the preferred solvent the osmolyte concentration within the solvation shell is decreased. The degree of osmolyte accumulation or exclusion is measured by a preferential interaction coefficient.^16,17 With respect to an equilibrium dialysis experiment in which the chemical potential of the osmolyte is held constant, the coefficient is

$${\Gamma }_{32}={\left(\frac{\partial m_3}{\partial m_2}\right)}_{T,{\mu }_1,{\mu }_3}$$ (4)

The so-called ‘protecting’ osmolytes, which stabilize protein structure, are excluded from protein surfaces (Γ₃₂ < 0); the same osmolytes tend to stabilize RNA tertiary structure as well.¹⁸ It is this class of osmolytes that can help define the volume of hydrating water.

It is convenient to interpret Γ₃₂ in terms of a ‘two-domain’ model.¹⁷ The model supposes that a mole ratio of osmolyte to water, B₃/B₁, applies within a volume around the macromolecule; the ratio in the bulk solution is m₃/m₁ = m₃/55.5 (molal units). The relation

$${\Gamma }_{32}\approx B_3-B_1\left(\frac{m_3}{m_1}\right)$$ (5)

then holds. In the event that B₃ ≈ 0, i. e. osmolyte is entirely excluded from the surface of the macromolecule, then B₁, the moles of water in the hydration domain, can be calculated. (Space does not permit a full discussion of the measurement of Γ₃₂ when a fourth component, excess salt, is present. See ^19,20 for more detail.)

The osmolyte glycine betaine (GB) appears to be so strongly excluded from protein and DNA surfaces that it can be used to measure B₁. Γ₃₂ is difficult to measure by equilibrium dialysis, but it can be calculated from vapor pressure osmometry (VPO) measurements that monitor water vapor pressure as a function of solute concentrations. Measurements of GB exclusion from albumin (BSA) yield a maximum hydration density of 0.14 ± 0.01 H₂O/Ų, which approximately corresponds to a monolayer of water.²¹

Similar measurements have been made with helical DNA.¹⁹ The degree of GB exclusion implies a hydration volume of about 17 H₂O per nucleotide. As the backbone and groove surfaces are quite different in their interactions with water and (potentially) in their exclusion of GB, interpretation of Γ₃₂ is aided by studies with model compounds. Capp et al.,²² based on extensive measurements of GB interactions with small molecules, find that various atomic groups contribute additively to the overall interaction of a compound with GB. The exclusion due to anionic phosphate oxygen is particularly large, 0.27 H₂O/Ų or about three layers of water. Since B-form DNA phosphates have a solvent-accessible surface area of 74 Å, this exclusion implies a hydration of ~20 H₂O per helix phosphate. Thus the GB exclusion from phosphate alone (~20 H₂O) is sufficient to account for the overall exclusion of GB from DNA surfaces. GB has a large dipole moment but is unable to donate a hydrogen bond to anionic oxygen, so it is not surprising that phosphate would far prefer to bind water in a first solvation shell rather than GB. But the Γ₃₂ measurements suggest that much more than a single shell of water is organized around a phosphate in such a way that GB is excluded.

Although the spectroscopic and thermodynamic experiments discussed in this section have been done with DNA, the same conclusions about the strong hydration of backbone phosphate apply to RNA. The only caveat is that some RNA structures may harbor phosphates that share water of hydration (as already mentioned in regard to A-form helices) or are partially inaccessible to solvent (discussed below).

Ion interactions with RNA: general considerations

It is well known that addition of salt, with either mono- or divalent cations, stabilizes helical DNA or RNA over single-stranded forms, and RNA tertiary structures over partially unfolded structures. With respect to RNA, the possible mechanisms at work have been discussed and reviewed.^23-25 There are several reasons why the subject has been difficult to treat, particularly for RNA: physiologically relevant conditions include a mixture of cation valences, K⁺ and Mg²⁺; both long range (coulombic) and short range (e.g., polarization) forces may come into play; and the strong hydration of both ions and the RNA are also relevant. Though the devil is in the (quantitative) details, which are by no means worked out yet, there are a few generalizations that are useful for a qualitative visualization of the factors at work in ion – RNA interactions. These generalizations are presented here in terms of the preferential interaction formalism. Rather than the exclusion of cation-anion pairs used above (eq 2), it is convenient to use a separate interaction coefficient for each ion species, particularly when considering mixed Mg²⁺/K⁺/anion buffers. These single-ion coefficients are defined in reference to dialysis equilibrium, e.g.

$${\Gamma }_{2+}={\left(\frac{\partial m_{2+}}{\partial m_{RNA}}\right)}_{{\mu }_2+{\mu }_1,T}$$ (6)

is the excess of divalent ion present with the nucleic acid, over the bulk solution concentration. Similar expressions apply to monovalent cations and anions, with the proviso that the Γ coefficients are not independent. If expressed as ions per nucleotide, charge neutrality of the solution is satisfied by

$$2{\Gamma }_{2+}+{\Gamma }_{+}-{\Gamma }_{-}=1$$ (7)

Note that Γ₋ is negative; repulsive coulombic forces exclude anions from the vicinity of the RNA. In these terms, the following generalizations may be made:

• A simple quantitative relation between Γ₊, Γ₋, and the linear charge density of a polynucleotide (such as helical DNA) at low concentrations of a 1:1 salt has been derived ²⁶ and confirmed by experiment.^14,27 As charges become more closely spaced along the backbone, the maximum free energy of ion-polynucleotide interaction is obtained by increased retention of cations (Γ₊ increases) and decreased exclusion of anions (Γ₋ also increases, i.e. becomes less negative). Although there is no simple formula to calculate Γ₊ and Γ₋ for RNAs of irregular shape, the general principle still applies, that any conformational change that increases RNA charge density also increases both Γ₊ and Γ₋ in solutions with monovalent ions.

• It is entropically advantageous for RNA to accumulate excess divalent cations in preference over monovalent ions, i.e. the exchange of ~2 excess K⁺ by one excess Mg²⁺ results in the net release of approximately one ion.²⁸ Any increase in RNA charge density tends to draw cations into a smaller volume near the RNA, and increases the entropic advantage of Mg²⁺ - K⁺ exchange. The sensitivity of RNA folding to Mg²⁺ concentration therefore tends to be greatest for the most compact tertiary structures. It is likely that this entropic effect is responsible for the major part of Mg²⁺ - RNA interaction free energies in most RNAs.²⁸

• RNA tertiary folds may incorporate specific ion chelation sites. There is a thermodynamic trade-off in that chelated ions must be partially dehydrated, which is energetically costly, but the very negative electrostatic potential that may develop at chelation sites can more than compensate.^29,30 Though not common, chelation sites specific for either K⁺ or Mg²⁺ are found in a number of RNAs (see below).

• All ion interactions with an RNA are strongly coupled. It may be convenient to distinguish classes of ions whose energetics are amenable to different approximations, but ultimately the classes cannot be manipulated independently.³¹

The influence of ions and osmolytes on partially unfolded RNAs

A number of RNAs, ranging in size from 71 to 1492 nt, show dramatic reductions in the radius of gyration as salt is added at concentrations below those needed to stabilize the complete tertiary structure.^30,32-35 The phenomenon is frequently termed ‘collapse’.³⁶ Most of these studies have looked at the effects of adding MgCl₂ to RNAs in low salt buffers, though in some RNAs high concentrations of monovalent salt have similar effects.³⁷ Since increasing salt concentration (either monovalent ions or Mg²⁺ in the presence of monovalent ion) should favor more compact forms of an RNA, the observation is not entirely a surprise, but a complete quantitative accounting of the forces at work is still in progress. Recent studies have looked at the roles of ion valence, ³⁸ transient tertiary contacts,³⁹ electrostatic repulsion between helices,⁴⁰ and short-range interactions ⁴¹ in promoting collapsed vs. extended states. It is, of course, quite possible that multiple mechanisms are in play.

The effect of protecting osmolyte on RNA unfolded states has been studied in only one case, TMAO (trimethylamine oxide) with the adenine riboswitch aptamer.¹⁸ This 71 nt RNA binds adenine as a ligand in a central pocket formed from a three-way helix junction. In the absence of ligand and at low Mg²⁺ concentrations, the three helices are in an extended, T-shaped conformation. As MgCl₂ is titrated, two of the helical arms become hydrogen-bonded together via bases in their hairpin loops; the radius of gyration decreases substantially during the titration.^30,42 Titration with TMAO (in the absence of Mg²⁺) remarkably mimics the effect of Mg²⁺ in driving formation of the loop-loop interaction and compaction of the RNA. Neither Mg²⁺ nor TMAO affects the radius of gyration of a mutant RNA that is incapable of forming tertiary structure. TMAO is uncharged and cannot screen long-range repulsion between RNA segments, but as proposed in the next section, could stabilize helix-helix packing or junction conformations consistent with compact conformations.

PO₂ ⁻ exposure to solvent in native RNA structures

The compaction that is associated with formation of an RNA tertiary structure generates a much more negative electrostatic potential for the native RNA than found in secondary structure.^43,44 The higher charge density of a compact structure should be favored by added salt, for reasons discussed above. This section will develop the idea that compaction is usually accompanied by changes in phosphate hydration that result in the net release of water. To explore the relation between ions, hydration and native structure formation, a more detailed look at the ways anionic phosphate oxygens are distributed within the native structure is in order.

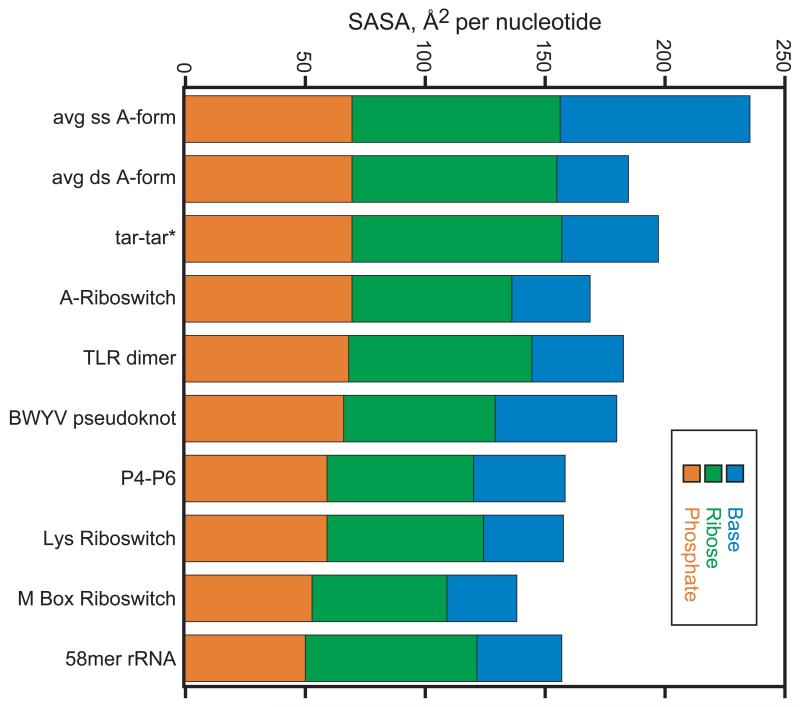
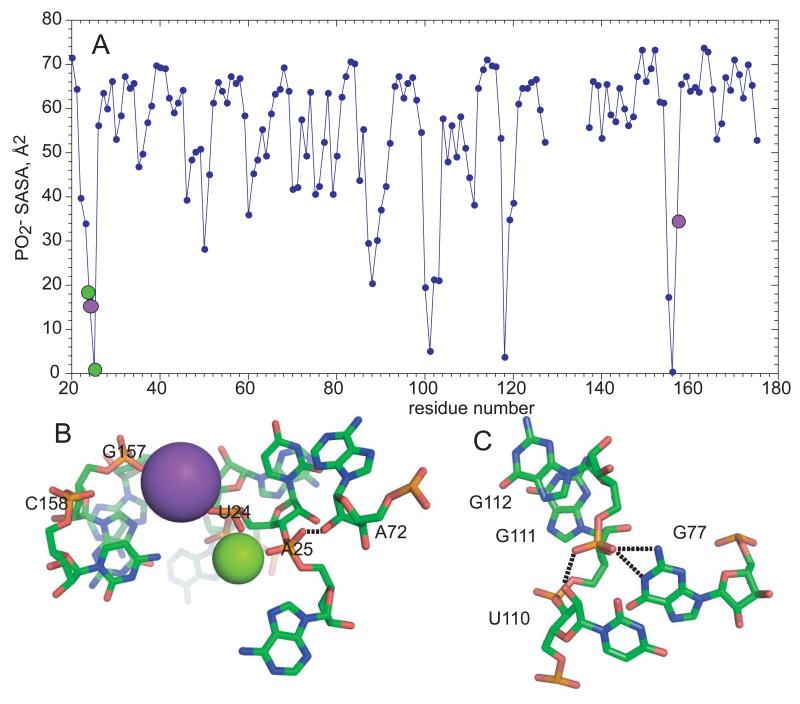
If it is energetically costly to dehydrate anionic phosphates, RNA structures should tend to keep PO₂ ⁻ oriented towards solvent. In fact, the PO₂ ⁻ solvent accessible surface area (SASA) in many native RNA structures is, on average, about the same as that of A-form RNA (~70 Ų, cf. tar-tar* and A-riboswitch RNAs, Figure 2). There are, however, a number of RNAs which bury significantly larger PO₂ ⁻ surface area; each of the four right-most RNAs in Figure 2 has one or more phosphates that is almost completely inaccessible to water (SASA < 16 Ų). The M-box riboswitch is an extreme example in which four PO₂ ⁻ are completely buried and six others leave less than 25 Ų exposed to solvent (Figure 3A). The x-ray crystal structures of these RNAs suggest two mechanisms that help compensate for the unfavorable free energy of burial:

• The anionic oxygen accepts hydrogen bond(s) from bases or ribose 2′ OH. In an example from the lysine riboswitch,⁴⁵ the G112 anionic oxygens are in a pocket formed by two NH donors and a 2‘OH (Figure 3C). While it is uncommon to find both anionic oxygens hydrogen bonded, as many as 6% of nucleotides in RNA tertiary structures have a single such bond.⁴⁶ The widespread U-turn and GNRA tetraloop motifs,^47,48 and some purine-purine base pairs and major groove triple helices ⁴⁶ are also stabilized in this way.

• The buried anionic oxygens form part of a chelation site for K⁺ or Mg⁺. In the M-box RNA, at least 10 anionic oxygens are directly contacted by chelated K⁺ and Mg²⁺ ions; three of these are shown in Figure 3B. The M-box RNA has an unusually large number of chelated ions, and is also unusually compact (Figure 2).

Figure 2.

Solvent accessible surface areas for various RNA structures, normalized per nucleotide. Calculations used a sphere of radius 1.4 Å and the program Surface Racer ⁵⁸ as described.⁵⁹ The surface areas were calculated using the following atomic coordinates: avg ss or avg ds A-form RNA, models of a single or double stranded RNA were generated from ideal A-form helix parameters ⁵⁹; tar-tar*, a ‘kissing loop’ complex, 1KIS; A-riboswitch, an adenine riboswitch aptamer, 1Y26; TLR dimer, an RNA designed to dimerize via a tetraloop – receptor motif, 2ADT; BWYV pseudoknot, 1L2X; P4-P6, a domain of a group I intron, 1GID; Lys riboswitch, aptamer domain of a riboswitch binding lysine, 3D0X; M Box riboswitch, a riboswitch aptamer that senses Mg²⁺, 2QBZ; 58mer rRNA, a fragment of large subunit ribosomal RNA, 1HC8.

Figure 3.

‘Buried’ phosphates in RNA structures. A, solvent accessible surface area of PO₂ ⁻ groups in the M-box riboswitch RNA (2QBZ).⁶⁰ B, Mg²⁺ (green) and K⁺ (purple) ions chelated by the M-box RNA. A hydrogen bond between a phosphate oxygen and 2′OH is marked by a dashed line. Direct contacts to phosphates are denoted by colored circles on the top panel. C, nucleotides from a lysine-riboswitch RNA (3D0U) ⁴⁵ that hydrogen bond to a phosphate (G112) with reduced solvent accessibility (25.6 Ų). The three dashed lines are probable hydrogen bonds (N-O or O-O distances ≤ 3.0 Å).

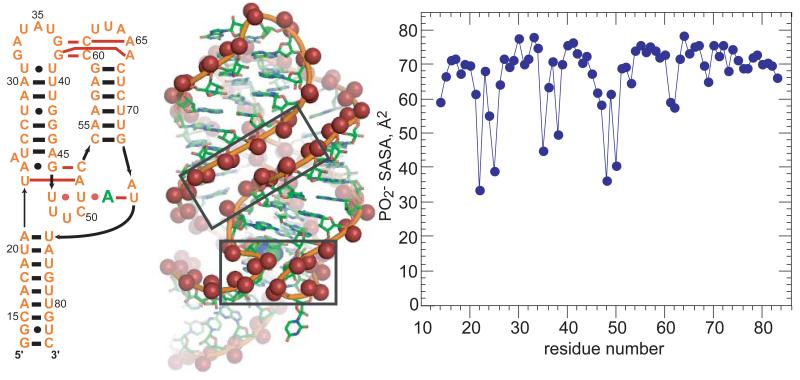
A common feature of RNA tertiary structures is the close juxtaposition of two phosphate oxygens such that one water molecule may hydrogen bond to both, similar to the arrangement previously noted for consecutive phosphates in A-form RNA. The adenine-riboswitch (A-riboswitch), which shows very little protection of phosphates from solvent (Figure 4), provides two sets of examples. First, the complete RNA tertiary structure includes a set of loop-loop hydrogen bonds that brings two short helical segments into approximately parallel alignment. Phosphates from each helix are staggered in such a way that distances between anionic oxygens on different strands are between 5.4 and 7.9 Å. In a high resolution crystal structure of the similar guanine-riboswitch (4FE5), much of this inter-helix space is filled with essentially a single layer of water (Figure 4B). Protecting osmolytes, which favor phosphate dehydration, should stabilize this helix-packing arrangement. In a simpler RNA designed to dimerize via tetraloop – receptor motifs placed at either end of about one turn of helix,⁴⁹ the unusually strong dependence of the dimerization equilibrium on both salt and TMAO concentrations is entirely attributable to the parallel juxtaposition of the helical segments.¹⁸ Short segments of parallel helices are a common theme in large RNAs.^50-52

Figure 4.

Phosphate solvation in the A-riboswitch. Left, secondary structure of an adenine riboswitch aptamer domain.⁶¹ The bound adenine is in green. Red dots or bars indicate tertiary base-base hydrogen bonding. Middle, 1.3 Å resolution crystal structure of a homologous guanine riboswitch (4FE5). The bound guanine is shown as a space-filling model encompassed by the RNA behind the sharp bends within the lower box. Anionic oxygens are displayed as spheres. Oxygens come close enough to share hydrating water in the two boxed regions; a third such region is on the backside of this view of the RNA. Right, PO₂ ⁻ SASA of the A-riboswitch (1Y26).

The second A-riboswitch example is a set of tertiary contacts surrounding the ligand binding site. Two sharp ‘kinks’ in the backbone bring phosphates into close enough proximity (4.8-5.6 Å) to share first shell waters (Figure 4B). All hairpin loops and many junction loops require a reversal in the backbone direction, so there are frequent possibilities for shared waters at sharp bends.

The extent of water release upon folding of the A-riboswitch has been probed by the osmolyte TMAO, which is chemically similar to GB and excluded from phosphate to a comparable extent.¹⁸ The amount of water taken up or released in an RNA conformational transition can be estimated by using the linkage relation

$$\left(\frac{\partial \ln \left(K_{obs}\right)}{\partial a_{Osmolyte}}\right)=\frac{{\Gamma }_{32}^U-{\Gamma }_{32}^N}{a_{Osmolyte}}\approx -\frac{\Delta B_1}{55.5}$$ (8)

where K_obs is the observed equilibrium constant for the transition from N to U, a_osmolyte is the activity of osmolyte, the superscripts U and N refer to unfolded and native RNA conformations, and ΔB₁ is the number of waters taken up or released in the transition.¹⁷ ΔB₁ calculated for folding of the A-riboswitch is ~170 waters, or an average of 2.4 waters per nucleotide. Using the phosphate hydration derived from GB studies mentioned above, 0.27 H₂O/Ų, the release of 170 waters corresponds to 9 A-form phosphates (70 Ų SASA each) becoming entirely dehydrated. Clearly no phosphate has been entirely stripped of water in this RNA, but ~18 retain much less than a full three layers of water.

In summary, folding of an RNA tertiary structure is always accompanied by the uptake of cations, and in instances where it has been examined, the simultaneous release of hydrating water from phosphates. Both phenomena are rooted in the close juxtaposition of phosphates in the native structure. In this case, ion release and water uptake are [thermodynamically] coupled by the folding of the tertiary structure.

Linkage of ion and osmolyte interactions with RNA

The above discussion of phosphate environments in compact RNAs gives reasons to suspect a further link between ions and hydrating water. The parallel helices of the A-riboswitch and TLR RNAs are expected to create a region of more negative electrostatic potential that draws cations (either monovalent or divalent) closer to the RNA surface, where they may well displace water from phosphate hydration layers. (Similarly, K⁺ has been proposed to exchange with ordered water in the minor groove of B-form DNA.⁵³) It is exceedingly difficult to develop a quantitative picture of the water-ion distribution in this critical region near the RNA surface, by either experiment or computation. High resolution crystal structures can reveal ordered water and site-bound ions, but the majority of neutralizing ions remain unresolved. Ion distributions derived from continuum models, which give reasonable estimates of the overall ion excess,⁵⁴ become problematic near RNA surfaces where the size and hydrogen-bonding capacity of water become important factors.

In principle, molecular dynamics simulations can resolve the molecular interplay between ions and water, and have been used in an attempt to account for the effects of group I monovalent ions on the tar-tar* RNA complex.⁵⁵ In this heterodimer, two RNA hairpin loops are bound together by Watson-Crick pairing, a motif known as ‘kissing loops’. Simulations show the expected accumulation of cations in pockets of negative electrostatic potential created by the structure. Those ions closest to the RNA have the most negative RNA interaction free energy and also the smallest average number of waters in a first hydration shell. There is a strong dependence on ion size such that Γ₊ varies inversely with ion radius, as observed experimentally.⁵⁶ A notable example of size-dependence is the positioning of Na⁺ between phosphates at sharp backbone bend; the larger K⁺ and Cs⁺ ions are too large to occupy the same location. The changes in ion hydration must be paralleled by changes in RNA hydration, and the net release of water from a folded RNA may include water that has been displaced by ions.

Concluding remarks

This review has developed the idea that a major factor in the energetics of RNA tertiary folding is the positioning of backbone phosphates. There are two factors at work: electrostatic repulsion and strong interactions with water (hydration). Both factors promote extended conformations of partially unfolded RNA, and work against formation of compact native structures, especially those in which phosphates are buried within the solvent accessible surface. The two factors are almost inextricably linked: any conformational change that increases the charge density of the RNA is very likely to lead to some release of hydrating water, especially if one considers that hydration of anionic oxygens may extend to three layers of water. Although salt (with either monovalent or divalent cations) and protecting osmolytes (such as TMAO or GB) are chemically very different and affect the thermodynamics of RNA folding by distinct mechanisms, the two kinds of solutes have essentially the same effect on RNA in that they both shift conformational equilibria towards more compact conformations.

A large fraction of the effect of mono- and divalent salts on RNA stability can be rationalized in terms of coulombic interactions between an “ion atmosphere” and the RNA, without any explicit accounting for hydration changes;^28,54 for RNAs with buried ion - phosphates and ions, reasonable energies can be derived from a simple Born model of hydration.^29,57 However, a more precise understanding of RNA stability, the evolutionary pressures on RNA architecture, and the binding of RNA to proteins or small molecule ligands will require the development of detailed molecular pictures of both water and ion distributions in the few solvation layers surrounding an RNA. The rapid expansion of the power and sophistication of computational methods is likely to allow these kinds of investigations in the near future.