Predicting the morphology of sickle red blood cells using coarse-grained models of intracellular aligned hemoglobin polymers

Abstract

Sickle red blood cells (SS-RBCs) exhibit heterogeneous cell morphologies (sickle, holly leaf, granular, etc.) in the deoxygenated state due to the polymerization of the sickle hemoglobin. Experimental evidence points to a close relationship between SS-RBC morphology and intracellular aligned hemoglobin polymers. Here, we develop a coarse-grained (CG) stochastic model to represent the growth of the intracellular aligned hemoglobin polymer domain. The CG model is calibrated based on the mechanical properties (Young’s modulus, bending rigidity) of the sickle hemoglobin fibers reported in experiments. The process of the cell membrane transition is simulated for physiologic aligned hemoglobin polymer configurations and mean corpuscular hemoglobin concentration. Typical SS-RBC morphologies observed in experiments can be obtained from the current model as a result of the intracellular aligned hemoglobin polymer development without introducing any further ad hoc assumptions. It is found that the final shape of SS-RBCs is primarily determined by the angular width of the aligned hemoglobin polymer domain, but it also depends, to a lesser degree, on the polymer growth rate and the cell membrane rigidity. Cell morphologies are quantified by structural shape factors, which agree well with experimental results from medical images.

1 Introduction

Sickle cell anemia has been identified as the first “molecular disease”¹ which may cause impaired blood flow and painful episodes in patients. The cause of this disease is the abnormal sickle hemoglobin molecules inside the sickle red blood cells (SS-RBCs). Specifically, the glutamic acid residues at the sixth position of the two β-subchains are replaced by valine in sickle hemoglobin, which results in low solubility in hypoxic conditions. As the oxygen of a SS-RBC is removed, sickle hemoglobin tends to aggregate in the bulk solution through a homogeneous nucleation and further grows into polymer states via a heterogeneous nucleation on the surface of the pre-existing polymers, according to the double nucleation model.^2,3 Due to the intra-cellular sickle hemoglobin polymers, SS-RBCs exhibit substantial increase in the cell rigidity,⁴ elevating the blood flow resistance and potentially triggering vaso-occlusion in the microcirculation. Besides altering the cell rigidity, the growing sickle hemoglobin polymer domain inside the SS-RBC can potentially distort (“sickle”) the cell membrane, and therefore change the cell morphology under certain conditions.

However, unlike the elevation of cell rigidity, only some types of the deoxygenated SS-RBCs undergo apparent morphologic changes. Kaul et al.⁵ investigated the deoxygenated SS-RBC morphology by categorizing the SS-RBCs into four groups according to the mean corpuscular hemoglobin concentration values. While the cell groups with medium mean corpuscular hemoglobin concentration (<35 g dL⁻¹) exhibit apparent cell deformation in deoxygenated conditions, most of the cells with high mean corpuscular hemoglobin concentration values exhibit granular or near biconcave shapes. Moreover, it is found that the SS-RBC morphology also depends on the rate of the deoxygenation procedure.^6,7 SS-RBC suspensions following fast deoxygenation exhibit a large portion of cells with a granular shape. In contrast, most of the SS-RBCs undergo large shape transition to “sickle” or “holly leaf” cells after gradual deoxygenation, see Fig. 1. To explore the mechanism of the cell distortion, the intracellular sickle hemoglobin polymer configuration was visualized by optical birefringence⁸ and differential polarization microscopy⁹ with different cell morphologies and mean corpuscular hemoglobin concentration. It was revealed that the wide variety of SS-RBC morphologies has a close relationship with the intracellular aligned hemoglobin polymer. Although the aligned hemoglobin polymer occupies only about 5% of the total sickle hemoglobin polymer,¹⁰ the cell morphology is mainly determined by the total number of the aligned hemoglobin polymer domains and the configuration of each domain in the cell.^8,9

Fig. 1.

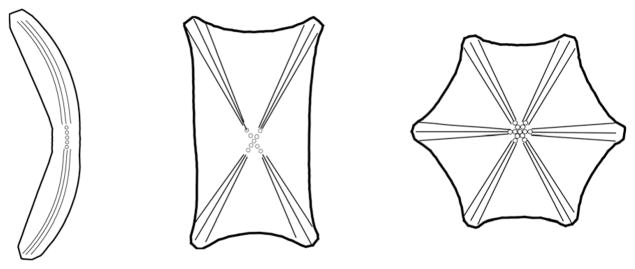
Sketches of typical cell shapes for deoxygenated SS-RBCs observed in experiments.⁹ From left to right, the three sketches represent the “sickle”, “holly leaf” and “granular” shapes of SS-RBCs. The various cell morphologic states are mainly determined by the specific intracellular aligned hemoglobin polymer configurations, represented by the solid lines. The dots represent the post-homogeneous nucleus.

According to the double nucleation theory,^2,3 the formation of a single polymer domain is initialized by the homogeneous nucleation of the sickle hemoglobin molecules in bulk solution and proceeds with explosive growth via polymer elongation and heterogeneous nucleation on the pre-existing polymers. The homogeneous nucleation rate is reported to be concentration dependent with a power of 60 ± 10 (ref. ¹¹). Such extremely high concentration dependence explains the prevalence of single polymer domains in low mean corpuscular hemoglobin concentration cells, and that multiple sickle hemoglobin domains are usually found in high mean corpuscular hemoglobin concentration cells. On the other hand, the structure and amount of aligned hemoglobin polymer for individual domains are mainly controlled by the heterogeneous nucleation and the fiber growth rates.^12–14 With high concentration and fast growth rate, a post-nucleation aggregate of twofold symmetry develops into a spherulitic domain through the growth of heterogeneously nucleated fibers and further deflection from the parent fibers. On the contrary, the angular widening of the polymer domain, originated from the fiber branching, is largely suppressed for smaller heterogeneous nucleation rate as observed in both experiments¹⁴ and numerical simulations.¹⁵ Remarkably, this tendency is also consistent with the inverse relationship between the amount of intracellular aligned hemoglobin polymer and the mean corpuscular hemoglobin concentration values for each class of cells (categorized by the total number of polymer domains) reported in ref. 9.

To study the physical basis of the various SS-RBC shapes observed in experiments, we conducted numerical simulations to systematically investigate the effect of the sickle hemoglobin polymer configurations and SS-RBC membrane rigidity on the final morphologic states. The primary goal of this work is to examine if the various types of distorted cell shapes can be obtained from the different intracellular aligned hemoglobin polymer configurations determined by the different cell mean corpuscular hemoglobin concentration values and deoxygenation rates observed in experiments. Specifically, we employed a previously developed RBC model¹⁶ in combination with a new coarse-grained (CG) stochastic model to represent the growth of the aligned hemoglobin polymer domain inside the cells. We studied the distortion of the cell membrane with aligned hemoglobin polymer domains of different angular widths. The classical elongated cell with “sickle” and “holly leaf” shapes appears to have originated from the single aligned hemoglobin polymer domain with relatively limited angular width, whereas the “mosaic” or the near-biconcave shapes are favored with the near spherulitic configurations. Moreover, for each type of the cell shapes, individual SS-RBCs exhibit various morphologic states as shown in ref. 17 and 18. Therefore, the second goal of this work is to examine if, for each type of the SS-RBC (elongated, sickle, holly leaf, etc.), the various degrees of membrane distortion observed in experiments¹⁷ can be obtained as a result of the typical intracellular sickle hemoglobin growth rates and the cell rigidities without introducing any further ad hoc assumptions. We note that the heterogeneous nucleation events are not explicitly modeled in the present work; instead, we directly consider the different aligned hemoglobin polymers originated from the various heterogeneous nucleation conditions and we investigate the subsequent cell morphological transition with those typical aligned hemoglobin polymer configurations observed in ref. 9 and 10. We note that the current CG modeling may yield limited new physical insight into the details of sickle hemoglobin polymerization; however, it allows us to quantify the complex relationships among the fiber growth rate, cell membrane–polymer interaction and aligned hemoglobin polymer configurations, and identify their effects on the distortion of cell membranes.

The paper is organized as follows. In Section 2, we explain the details of the multiscale RBC model and the coarse-grained model of the intracellular aligned hemoglobin polymer. In Section 3, we study the final shapes of SS-RBC with different intracellular aligned hemoglobin polymer configurations. For each type of the SS-RBC, we study the effect of the cell rigidity on the final morphologic states. Moreover, the various cell morphologies are quantified by both 3D and 2D structure factors and compared with the results obtained from medical images. We conclude in Section 4 with a brief discussion.

2 Numerical model

The physical model for the red blood cell (RBC) membrane and the aligned hemoglobin polymer is developed in the framework of the Dissipative Particle Dynamics (DPD) method.^19,20 It is a particle-based method widely used for simulation of soft matter systems such as polymer solutions²¹ and red blood cell suspensions.²² Each DPD particle represents a virtual cluster of atoms or molecules rather than an individual atom. Different from the Molecular Dynamics (MD) method, additional dissipative and random forces are included in the particle interactions due to the eliminated degree of freedom during the coarse-graining procedure.²³ We refer to ref. 24 for details of this method.

2.1 RBC membrane

In the equilibrium state, the RBC maintains a biconcave shape as described in ref. 25. In the present model, the RBC membrane is represented by a two-dimensional triangulated network with N_v vertices where each vertex is represented by a DPD particle. The vertices are connected by N_s visco-elastic bonds to impose proper membrane mechanics.^16,26 Specifically, the elastic part of the bond is represented by

$$V_{\text{s}}=\sum _{j\in 1\dots N_{\text{s}}}\left[\frac{k_{\text{B}}{Tl}_{\text{m}}\left(3x_j^2-2x_j^3\right)}{4p\left(1-x_j\right)}+\frac{k_{\text{p}}}{(n-1)l_j^{n-1}}\right],$$ (1)

where l_j is the length of the spring j, l_m is the maximum spring extension, x_j = l_j/l_m, p is the persistence length, k_BT is the energy unit, k_p is the spring constant, and n is a power. Physically, the above two terms represent the wormlike chain potential and a repulsive potential, respectively. An equilibrium bond length can therefore be imposed.

The membrane viscosity is imposed by introducing a viscous force on each spring. Following the general framework of the fluid particle model²⁷ and extended dissipative particle dynamics thermostat,²⁸ we can define dissipative $F_{ij}^{\text{D}}$ and random $F_{ij}^{\text{R}}$ forces given by

$$F_{ij}^{\text{D}}=-{\gamma }^{\text{T}}{v}_{ij}-{\gamma }^{\text{C}}(v_{ij}\times e_{ij})e_{ij},$$ (2)

$$F_{ij}^{\text{R}}\text{d}t=\sqrt{2k_{\text{B}}T}\left(\sqrt{2{\gamma }^{\text{T}}}\text{d}\overline{W_{ij}^{\text{S}}}+\sqrt{3{\gamma }^{\text{C}}-{\gamma }^{\text{T}}}\frac{\text{tr}[{\text{d}W}_{ij}]}{3}1\right)·e_{ij},$$ (3)

where γ^T and γ^C are dissipative parameters, v_ij is the relative velocity of spring ends, tr[dW_ij] is the trace of a random matrix of independent Wiener increments dW_ij, and $\text{d}\overline{W_{ij}^{\text{S}}}=\text{d}{W}_{ij}^{\text{S}}-\text{tr}\left[\text{d}{W}_{ij}^{\text{S}}\right]1/3$ is the traceless symmetric part.

To uniquely relate the model parameters and visco-elastic properties of the cell membrane, we extend the linear analysis of ref. 29 for a regular hexagonal network;¹⁶ the derived shear modulus of the membrane μ₀ is given by

$${\mu }_0=\frac{\sqrt{3}{k}_{\text{B}}T}{4{pl}_{\text{m}}{x}_0}\left(\frac{x_0}{2{(1-x_0)}^3}-\frac{1}{4{(1-x_0)}^2}+\frac{1}{4}\right)+\frac{\sqrt{3}{k}_{\text{p}}(n+1)}{4l_0^{n+1}},$$ (4)

where l₀ is the equilibrium spring length and x₀ = l₀/l_m. The membrane shear viscosity is given by

$${\eta }_{\text{m}}=\sqrt{3}{\gamma }^{\text{T}}+{\gamma }^{\text{C}}/4$$ (5)

The bending resistance of the RBC membrane is modeled by

$$V_{\text{b}}=\sum _{j\in 1\dots N_{\text{s}}}{k}_{\text{b}}\left[1-cos({\theta }_j-{\theta }_0)\right],$$ (6)

where k_b is the bending constant, θ_j is the instantaneous angle between two adjacent triangles having the common edge j, and θ₀ is the spontaneous angle. The relation between the model bending coefficient k_b and the macroscopic bending rigidity k_c of p333 the Helfrich model³⁰ can be derived as $k_{\text{b}}=2k_{\text{c}}/\sqrt{3}$ for a spherical membrane.¹⁶

In addition, the RBC model includes the area and volume conservation constraints, which mimic the area-incompressibility of the lipid bilayer and the incompressibility of the interior fluid, respectively. The corresponding energy is given by

$$V_{\text{a}+\text{v}}=\sum _{j\in 1\dots N_{\text{t}}}\frac{k_{\text{d}}{\left(A_j-A_0\right)}^2}{2A_0}+\frac{k_{\text{a}}{\left(A-A_0^{\text{tot}}\right)}^2}{2A_0^{\text{tot}}}+\frac{k_{\text{v}}{\left(V-V_0^{\text{tot}}\right)}^2}{2V_0^{\text{tot}}},$$ (7)

where N_t is the number of triangles in the membrane network, A₀ is the triangle area, and k_d, k_a and k_v are the local area, global area and volume constraint coefficients, respectively. The terms A and V are the total RBC area and volume, while $A_0^{\text{tot}}$ and $V_0^{\text{tot}}$ are the specified total area and volume, respectively. More details on the RBC model can be found in ref. 16.

2.2 Aligned hemoglobin polymer

In the deoxygenated state, the post-homogeneous aggregates grow into a polymer state and further form into bundles of sickle hemoglobin fibers and cross-linked gel through heterogeneous nucleation and branching. A single sickle hemoglobin fiber is composed of seven double strands in the style of a twisted rope with a diameter d₀ of about 21 nm; fully representing the detailed structure of a single sickle hemoglobin fiber is too expensive in the scale of a single RBC (~10 μm). Instead, we employ a CG model to represent a bundle of sickle hemoglobin fibers where the detailed structure of a single fiber is omitted. Each bundle is represented by single DPD particles connected by elastic bond interactions defined by eqn (1) as well as by the dissipative and random force terms defined by eqn (2) and (3).

The bending rigidity of the aligned hemoglobin polymer bundle is modeled by

$$V_{\text{angle}}=k_{\text{a}}{(\theta -{\theta }_0)}^2,$$ (8)

where k_a is the bending coefficient and θ₀ is the spontaneous angle representing the deflection of the aligned hemoglobin polymer. Finally, the aligned hemoglobin polymer model includes an in-plane dihedral potential to represent the fixed growth direction in global scale; the corresponding potential is given by

$$V_{\text{dihedral}}=k_{\text{d}}[1+cos({\phi }_{\mathit{ijkl}})],$$ (9)

where i, j, k and l are four adjacent DPD particles on the modeled aligned hemoglobin polymer, φ_ijkl is the instantaneous angle between the triangle Δ_ijk and Δ_lkj, and k_d is the constraint coefficient such that the growing fiber is in the same plane.

The development of the aligned hemoglobin polymer domain is modeled by the addition of single beads to the end of the polymer as “Brownian Ratchets”.³¹ The growth rate k_t is represented by

$$k_{\text{t}}=k_{\text{on}}{\text{e}}^{-(f_{\text{s}}\widehat{e})\delta /k_{\text{B}}T}-k_{\text{off}},$$ (10)

where k_on, k_off are the polymerization and depolymerization rates, respectively, f_s is the instantaneous stall force exerted on the end of the polymer bead, and ê is the polymer growth direction. We emphasize that δ represents the unit length increase upon the addition of a single sickle hemoglobin monomer rather than the equilibrium length between the CG beads, which is independent of the length scale of the CG model. This is because the sickle hemoglobin polymer growth is driven by monomer addition rather than obligomer addition. A single sickle hemoglobin monomer can join the pre-existing polymers when the energy cost of this reaction overwhelms the energy gain due to the entropy loss. This result is also validated by experimental measurements.³² On the other hand, k_on and k_off represent the growth and dissociation rates in terms of the CG polymer beads and should be adjusted according to the choice of the length scale of the CG model, as discussed in the following section. For each time step Δt, a single DPD particle is added to the polymer end according to the probability P_t = 1 − e^−k_tΔt. Specifically, a random number η is generated between, [0 1], and a DPD particle is added if η < P_t. Details on the choice of the model parameters are discussed in the next section.

2.3 Simulation setup and physical parameters

The unperturbed RBC membrane keeping the biconcave shape in equilibrium is represented by a stress-free triangulated mesh¹⁶ composed of N_v = 1000 vertices. The shear modulus of the healthy RBC membrane is μ₀ = 6.8 μN m⁻¹ and the bending rigidity is k_c = 3.7 × 10⁻¹⁹ J according to the experimental measurements.^25,33,34 On the contrary, the membrane shear modulus of SS-RBC increases sharply in deoxygenated states. Experimental measurements using a micropipette⁴ revealed that the cell rigidity depends on the mean corpuscular hemoglobin concentration values. For SS-RBC with a low value of mean corpuscular hemoglobin concentration, the effective cell rigidity is between 20μ₀ and 100μ₀, while for cells with a higher value of mean corpuscular hemoglobin concentration (>35 g dL⁻¹), the cell rigidity is on the order of O(10²) μ₀. In the current work, we choose the cell shear modulus as described above. Values of the bending rigidity of SS-RBC under different deoxygenated states are unknown; we set its value to be 20k_c in the current study. Sensitivity studies show that the final cell morphologies depend weakly on the bending rigidity within the range from 10k_c to 30k_c.

The growth rate of the sickle hemoglobin polymer was measured by Aprelev et al. in ref. 32 as a function of monomer activity in bulk solution, given by

$$J=k_{+}{\gamma }_{\text{c}}c-k_{-},$$ (11)

where γ_c is the activity coefficient, and c is the monomer concentration; k₊ and k₋ are the monomer addition and subtraction rates. The linear relationship between J and γ_cc reveals that the growth occurs by monomer addition instead of obligomer addition. While k₊ and k₋ are nearly constant for different sickle hemoglobin solutions, γ_cc depends strongly on the intracellular mean corpuscular hemoglobin concentration value. On the other hand, the development of the aligned hemoglobin polymer domain is modeled in a coarse-grained manner in this work, where each single DPD particle is added to the end of the sickle hemoglobin polymer, forming elastic bonds with its adjacent particles with equilibrium length l₀ = 0.15 μm. Moreover, the modeled polymer represents an aligned hemoglobin polymer bundle composed of multiple sickle hemoglobin fibers. Therefore, the unit increase length per bundle δ scales as

$$\delta ={\delta }_0/N_{\text{f}},$$ (12)

where δ₀ ≈ 0.45 nm is a unit increase length per single fiber, and N_f is the number of the sickle hemoglobin fibers of the bundle. In the present coarse-grained model, we consider the interaction between the aligned polymer and a local area of cell membrane with finite size. The polymer beads interact with the cell membrane vertices within a range of 0.2–0.4 μm. Accordingly, it models a bundle of aligned polymers on the order of O(10²). To this end, we choose N_f = 100, and the effective fiber bundle radius scales as $(1/2)\sqrt{N_{\text{f}}}\times 21\text{nm}\approx l_0$. Accordingly, the polymerization and depolymerization rates scale as

$$k_{\text{on}}=\frac{N_{\text{f}}{k}_{+}{\gamma }_{\text{c}}c\delta }{l_0};k_{\text{off}}=\frac{N_{\text{f}}k\_\delta }{1_0}.$$ (13)

The bending rigidity and Young’s modulus of the aligned hemoglobin polymer bundle scale as $\kappa =N_{\text{f}}^2{\kappa }_0$ and Y = Y₀, where κ₀ and Y₀ are the bending modulus and the Young’s modulus of a single sickle hemoglobin fiber. According to the measurements in ref. 35, we choose κ₀ = 1.0 × 10⁻²⁴ Nm² and Y₀ = 0.1 GPa. In the present model, the parameters of elastic bond interaction V_s between the CG polymer beads are determined by

$$Y=\frac{4l_0}{N_{\text{f}}\pi d_0^2}\frac{{\partial }^2{V}_{\text{s}}}{\partial r^2}{\mid }_{r=l_0},$$ (14)

to match the experimental value of Young’s modulus. Similarly, the parameters of the angle potential V_angle are determined by matching the bending rigidities of the aligned hemoglobin polymer bundle using the thermal fluctuation method discussed in ref. 35 and 36

Starting from an intracellular homogeneous nucleation, the sickle hemoglobin polymers grow toward the cell membrane with the growth rate determined by eqn (10) and eqn (13). As the polymer approaches the cell membrane, the polymer end undergoes a repulsive force exerted by the cell membrane, originated from the entropy loss of the cell membrane due to the presence of the adjacent polymer end. To model this effect, we employ a short range repulsive interaction between the polymer end and the cell vertex, as defined by

$$U_{\text{LJ}}(r)=4\left[{\left(\frac{{\sigma }_{\text{LJ}}}{r}\right)}^{12}-{\left(\frac{{\sigma }_{\text{LJ}}}{r}\right)}^6\right],$$ (15)

where σ_LJ = 0.4 μm and the repulsive interaction vanishes for r > 2^1/6σ_LJ. This repulsive force, in turn, results in various distorted cell membranes, as we will discuss in the following section.

3 Results

3.1 Sickle cell morphology

Sickle red blood cells exhibit heterogeneous shapes in deoxygenated conditions due to the variable stress exerted by the growing sickle hemoglobin polymer on the cell membrane. The final cell shape is mainly determined by two factors: (i) the effective sickle hemoglobin polymer growth rate k_t and (ii) the intracellular aligned hemoglobin polymer domain configuration.

The sickle hemoglobin polymer growth rate in bulk solution J depends mainly on the sickle hemoglobin concentrations as shown in eqn (11). In the present work, we consider the polymer growth of SS-RBCs with typical mean corpuscular hemoglobin concentration value from 32 g dL⁻¹ to 38 g dL⁻¹. The corresponding bulk growth rates vary from 1.2 × 10⁴ molecules s⁻¹ to 5.3 × 10⁴ molecules s⁻¹. However, the effective growth rate k_t, different from the bulk value, also depends on the stall force f_s exerted on the polymer ends according to eqn (10). Since f_s depends on the cell membrane rigidity, the effective growth rate k_t is determined by both the cell membrane rigidity and the mean corpuscular hemoglobin concentration values. As the growing fibers approach and distort the cell membrane, k_t decreases due to the increasing stall force. For individual SS-RBCs with specific mean corpuscular hemoglobin concentration value, we can define a threshold for the coarse-grained polymer bead number N_m such that the effective growth rate k_t vanishes as the number of polymer beads exceeds N_m, whereas N_m, in turn, depends on the cell rigidity and the intracellular polymer configuration.

Different from the effective sickle hemoglobin polymer growth rate, the intracellular aligned hemoglobin polymer configuration depends on several inter-related conditions: the mean corpuscular hemoglobin concentration of the sickle cell, the rate of the deoxygenation process, the final gas tension, temperature, etc., which are difficult to be explicitly incorporated into the current model. Instead, we construct four different types of post-homogeneous nucleation in cell populations of different mean corpuscular hemoglobin concentration values, from which the various aligned hemoglobin polymer configurations typically observed in experiments can be obtained.⁹ In the current section, the SS-RBC morphology is investigated for a specific value of N_m (determined by a specific cell membrane shear modulus) for each type of SS-RBC. The influence of the cell rigidity on N_m and final cell morphology will be discussed in Section 3.2.

First, we consider a post-homogeneous nucleation in linear style, where the free monomers can only be added to the “active” beads at both ends of the polymer, as shown in Fig. 2. This configuration implies that the polymer domain develops along a specific direction in the x–y plane as represented by the growth of a single polymer branch, whereas the angular span of the aligned hemoglobin polymer domain is relatively small. This configuration prevails with the physiological conditions of low mean corpuscular hemoglobin concentration value and slow deoxygenation rate, where the sickle hemoglobin heterogeneous nucleation is largely suppressed, as observed in experiments⁹ and predicted by simulations.¹⁵ Accordingly, we choose the mean corpuscular hemoglobin concentration value as 32 g dL⁻¹, where the bulk growth rate is 1.2 × 10⁴ molecules s⁻¹. Moreover, we note that the aligned hemoglobin polymer domain may deflect along the z direction due to the heterogeneous growth.¹⁵ To incorporate this effect, we set the polymer spontaneous angle θ₀ to be 179° and 180° respectively, where the former represents a deflection and the latter corresponds to a straight bundle.

Fig. 2.

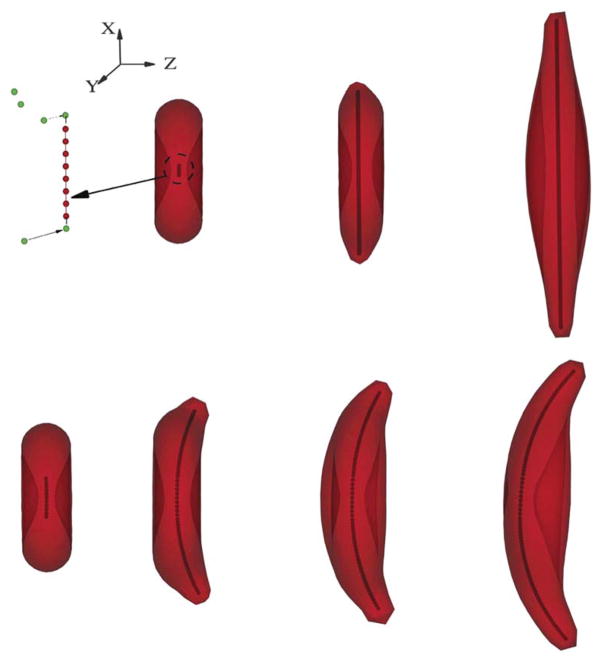
Upper: successive snapshots of the sickle cell membrane in the different development stages of the intracellular aligned hemoglobin polymer domain with “linear” growth in the x-direction. The left sketch demonstrates the coarse-grained model for the aligned hemoglobin polymer domain development: free sickle hemoglobin monomers (green color), represented by the DPD particles, can potentially join with the pre-existing polymers (red color) with the probability defined by the equation of probability, P_t. A linear polymer configuration is adopted in the current case to represent the specific growth direction. Different polymer configurations are adopted to represent the various aligned hemoglobin polymer domains, as shown in Fig. 3 and 4. Lower: successive snapshots of the sickle cell with the growing aligned hemoglobin polymer domain deflected in the z-direction (normal to the cell), resulting in the classical “sickle” shape.

Fig. 2 shows successive snapshots of the cell morphology at different stages of the aligned hemoglobin polymer development. The polymer growth threshold N_m is 80 and 93, respectively. Starting from the post-homogeneous nucleation, the aligned hemoglobin polymer domain develops towards the cell membrane. As the sickle hemoglobin polymer approaches the membrane, two spicules appear on the cell membrane near the interaction points. Moreover, as the length of the aligned hemoglobin polymer domain continuously increases and exceeds the size of the original cell, the cell membrane undergoes subsequent distortion. For a straight sickle hemoglobin bundle free of deflection in the z direction, the distorted membrane exhibits large distortion along the growth direction. In the x–y plane, the original “discocyte” shape transitions into the oval shape where the prolonged diameter is almost twice the value of the original cell. This configuration resembles the sickle cells widely observed in deoxygenated SS-RBCs with low mean corpuscular hemoglobin concentration values.¹⁸ Moreover, for a polymer model with spontaneous angle θ₀ = 179°, the developed sickle hemoglobin fibers exhibit skewed morphology in the y–z plane as well as an elongated state in the x–y plane. Accordingly, the elongated cell membrane follows the spontaneous curvature of the aligned hemoglobin polymer domain, resulting in the classical “sickle” shape of SS-RBC as widely observed under slow deoxygenation.

Next, we consider the aligned hemoglobin polymer domain with finite angular span in the x–y plane. This configuration can be derived from post-homogeneous nucleation composed of multiple sickle hemoglobin fiber branches, as shown in Fig. 3. The angular width of the aligned hemoglobin polymer domain quantified by the angle between the two main polymer branches, varies from 45° to 60°. Free sickle hemoglobin monomers can join the aligned hemoglobin polymer domain at each of the four polymer ends. This configuration corresponds to another type of widely observed aligned hemoglobin polymer domain in SS-RBCs named “central-constriction” according to ref. 9. The polymer domain resembles a dumbbell shape; limited amount of aligned hemoglobin polymer is observed near the center of the nucleation while a large amount of aligned hemoglobin polymer is found in the outer regions. As this type of aligned hemoglobin polymer domain is widely found in SS-RBC with medium mean corpuscular hemoglobin concentration value, we choose the mean corpuscular hemoglobin concentration value as 34 g dL⁻¹ in the present work, and the corresponding bulk growth rate is 1.97 × 10⁴ molecules s⁻¹. Successive snapshots of a SS-RBC with this type of aligned hemoglobin polymer domain are shown in Fig. 3, where the polymer growth threshold N_m and the value of the spontaneous angle θ₀ are set to 120 and 180°, respectively. The growing sickle hemoglobin fiber not only expands the cell along the growth direction but also results in multiple spicules on the cell membrane. The final cell morphology resembles the “holly leaf” shape as widely observed in the SS-RBC with low/medium mean corpuscular hemoglobin concentration value.^5,6,17

Fig. 3.

Successive snapshots of a SS-RBC with the intracellular aligned hemoglobin polymer domain of finite angular width. Two polymer branches are used to represent the angular spanning during the domain development. The final cell morphology resembles a “holly leaf” shape.

Finally, we consider SS-RBCs with the spherulite shape of the aligned hemoglobin polymer domain with the corresponding homogeneous nucleation shown in Fig. 4. In the present work, this configuration represents the polymer domain with spherulite configuration, similar to the polymer configuration observed in sickle hemoglobin solution (ref. ¹⁴), individual cells (ref. ⁹), and through simulation (ref. ¹⁵). It can be viewed as an extreme case of the four arm structure: for a sickle cell with a high value of mean corpuscular hemoglobin concentration, the heterogeneous nucleation rate is large and the polymer domain can transform into spherulite configuration and subsequently develop a radial symmetry. We note that this “radial symmetry” configuration is not the initial configuration of the homogeneous nucleus, but results from the subsequent heterogeneous nucleation events. On the other hand, the development of the polymer network topologies is not considered in the present model. To incorporate the properties of this polymer domain, we start with the post-homogeneous state where the spherulite configuration has already formed, and we study the subsequent development of the polymer domain to explore the effect of the polymer domain on the cell morphologies. The value of “six” arms is kind of arbitrary. This value represents the number of sites where the Hbs polymer can potentially interact with the cell membrane where multiple “spicules” formed. We notice that this type of polymer configuration prevails in cells with a high value of mean corpuscular hemoglobin concentration.⁹ Accordingly, we choose the mean corpuscular hemoglobin concentration value as 38 g dL⁻¹ with the bulk growth rate 5.3 × 10⁴ molecules s⁻¹. The polymer growth threshold N_m and the spontaneous angle θ₀ are 160 and 180°, respectively. With isotropic distribution of sickle hemoglobin polymer branches, free sickle hemoglobin monomers are added to the aligned hemoglobin polymer domain with full angular symmetry. As the sickle hemoglobin fiber approaches the cell membrane, multiple spicules appear on the cell membrane. However, different from the “sickle” and “holly leaf” cells, this type of SS-RBC does not bear further distortion. This is mainly due to two reasons: (i) the growth of the individual sickle hemoglobin arm can be limited due to the depletion of the free sickle hemoglobin monomers. For the spherulite polymer domain, the inner polymer density is relatively high due to the large heterogeneous rate. The polymer domain may run out of free sickle hemoglobin monomer as the domain develops towards the cell membrane. (ii) For deoxygenated SS-RBCs with a high mean corpuscular hemoglobin concentration value, the membrane shear modulus exhibits a much larger value than the cells with low mean corpuscular hemoglobin concentration, resulting in much larger stall force on the growing polymer ends. Moreover, the growth of the spherulite sickle hemoglobin domain expands the cell membrane isotropically. However, the total area of the cell membrane is constrained due to the incompressibility of the lipid bilayer. Therefore, the effective growth rate of the individual sickle hemoglobin fiber is largely suppressed due to the large force exerted on the polymer end. The final stage of the cell resembles the near-biconcave shape with multiple spicules on the cell surface, which corresponds to the granular shape of deoxygenated SS-RBC widely observed in the cells of high mean corpuscular hemoglobin concentration value or with fast deoxygenation procedure.

Fig. 4.

Successive snapshots of a SS-RBC with the intracellular aligned hemoglobin polymer domain of spherulite configuration, where the full domain is filled with sickle hemoglobin polymers due to the high heterogeneous nucleation rate during the growth procedure. The final cell morphology resembles a “granular” shape.

3.2 Quantifying the cell membrane distortion

In the previous section, the final morphology of the sickle cell is obtained for a specific threshold value N_m for the growth of each aligned hemoglobin polymer domain to represent the effect of the stall force exerted on the polymer ends as shown in eqn (10). However, we note that the stall forces on the polymer end depend on the specific cell rigidity, which varies for individual deoxygenated SS-RBCs.⁴ For each type of the SS-RBC discussed above, the bulk growth rate of the intracellular sickle hemoglobin polymer is similar and is determined mainly by the mean corpuscular hemoglobin concentration values.³² However, the deoxygenated cells with different cell rigidities may still end up with different extents of membrane distortion, where the growth rate k_t = k_one^{−f δ=k_BT} − k_off approaches zero. To investigate the effect of cell rigidity on the final cell morphology, we simulate the development of the intracellular aligned hemoglobin polymer domain with different cell membrane shear modulus values according to the experimental measurements.⁴ The detailed choices of the simulation parameters are shown in Table 1.

Table 1.

Simulation parameters for each type of SS-RBC. The symbol “MCHC” represents mean corpuscular hemoglobin concentration values. The symbols “E”, “S”, “H” and “G” represent the elongated, sickle, holly leaf and granular shape of the SS-RBC. μ and μ₀ represent the shear modulus of the deoxygenated SS-RBC and healthy RBC respectively. θ₀ and w represent the spontaneous deflection angle and the angular width of the aligned hemoglobin polymer domains, respectively

	MCHC	μ	θ0	w
E	32 g dL−1	[20μ0,80μ0]	180°	0°
S	32 g dL−1	[20μ0,80μ0]	[178.5°,179°]	0°
H	34 g dL−1	[30μ0,120μ0]	180°	[45°,60°]
G	38 g dL−1	[40μ0,2000μ0]	180°	180°

For each type of the post-homogeneous nucleus discussed above, the development of the aligned hemoglobin polymer domain is simulated with shear modulus shown in Table 1. Instead of terminating the polymer growth with a pre-determined threshold value N_m, the development of the aligned hemoglobin polymer domain is terminated automatically as the effective growth rate k_t approaches 0, therefore defining the final cell morphological states without any ad hoc threshold parameters. Fig. 5 shows the final morphological state of the “sickle” and “holly leaf” cells with different shear modulus values. For a low shear modulus value, both types of SS-RBCs exhibit large membrane distortion; however, the cell shape approaches the undisturbed state as the cell rigidity increases. Sensitivity studies have also been conducted on the elongated and granular types of SS-RBCs, where a similar tendency has been observed. A detailed mathematical description of the various distorted cell membranes is presented in the ESI^†.

Fig. 5.

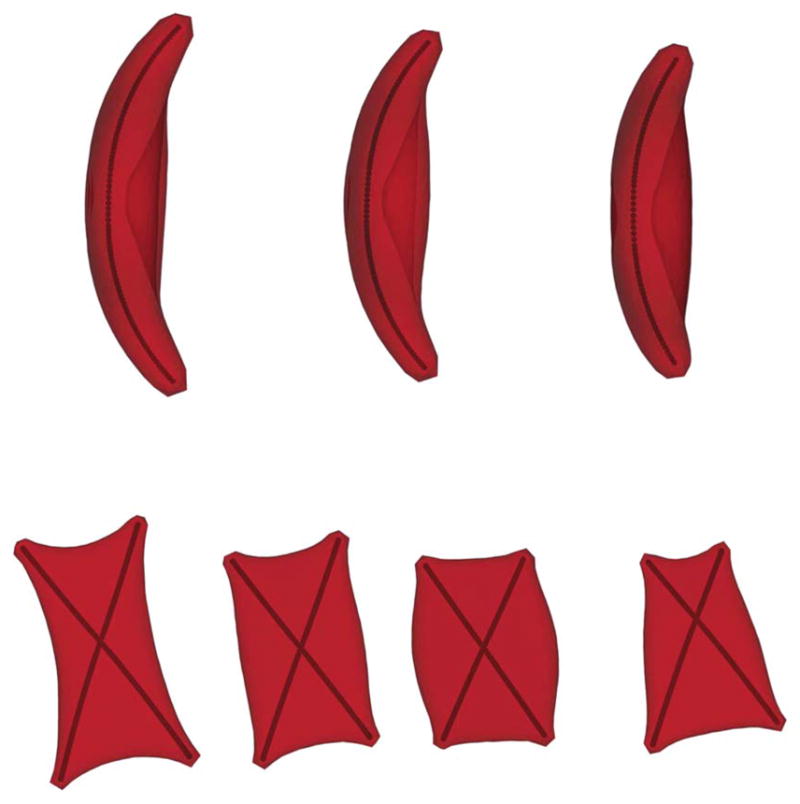
Final morphologies of the “sickle” (upper) and “holly leaf” (lower) shapes of deoxygenated SS-RBC for different values of cell membrane shear modulus. The “sickle” shape of SS-RBC corresponds to low mean corpuscular hemoglobin concentration value (32 g dL⁻¹) and the shear modulus of the cells shown above is set to 20μ₀, 40μ₀ and 70μ₀ according to experimental measurements.⁴ The “holly leaf” shape of SS-RBC corresponds to medium mean corpuscular hemoglobin concentration and the shear modulus is set to 30μ₀, 60μ₀ and 120μ₀. We have also included a non-symmetric case in the fourth plot representing a cell morphology with the post-homogeneous nucleus off the cell center with shear modulus 60μ₀.

To further quantify the membrane distortion, we introduce both 3D and 2D structural factors to characterize the individual SS-RBC as discussed above. The 3D structural factors can be identified by the eigenvalue analysis of the gyration tensor defined by

$$G_{mn}=\frac{1}{N_{\text{v}}}\sum _i\left(r_m^i-r_m^{\text{C}}\right)\left(r_n^i-r_n^{\text{C}}\right),$$ (16)

where rⁱ are the RBC vertex coordinates, r^C is the center-of-mass, and m, n can be x, y, or z. The three eigenvalues obtained from the gyration tensor are denoted by λ₁, λ₂ and λ₃, where λ₁ < λ₂ < λ₃. The asphericity and elliptical shape factors are defined by

$$\begin{array}{l}\text{ASF}=\left({({\lambda }_1-{\lambda }_2)}^2+{({\lambda }_2-{\lambda }_3)}^2+{({\lambda }_3-{\lambda }_1)}^2\right)/2R_{\text{g}}^4\\ \text{ESF}={\lambda }_3/{\lambda }_2,\end{array}$$ (17)

where R_g is the radius of gyration defined by $R_{\text{g}}^2+{\lambda }_1+{\lambda }_2+{\lambda }_3$.

The asphericity shape factor (ASF) measures the deviation of the RBC from a perfect sphere shape while the elliptical shape factor (ESF) measures the degree of distortion on the x–y plane. Fig. 6 shows the instantaneous ASF and ESF for the “sickle” SS-RBC as a function of the development of the aligned hemoglobin polymer domain for two different values of cell rigidity. Starting from the biconcave shape, the structural factors for both cases show rapid changes within the first 0.4–0.5 s, representing the initial fast development of the aligned hemoglobin polymer domain. However, the structural factors show slower change after 0.5 s and converge to specific values due to the decrease of the effective growth rate k_t. The more rigid the cell membrane, the sooner the structural factors begin to converge. Moreover, the asymptotic values of ASF and ESF are larger for less rigid cells. These results are consistent with the theoretical studies in ref. 37 and can be understood by eqn (10). For the same degree of cell distortion, the polymer ends approaching the stiffer cell membrane bear with larger stall (entropy) force,³⁷ resulting in faster decay of the growth rate k_t.

Fig. 6.

Instantaneous values of the asphericity (solid lines) and elliptical shape factor (dash lines) of the “sickle” SS-RBC as the aligned hemoglobin polymer domain develops. The red curves correspond to SS-RBC with membrane shear modulus μ = 30μ₀ and deflection angle θ₀ = 179°. The blue curves represent the SS-RBC with shear modulus μ = 60μ₀ and θ₀ = 178.5°.

To systematically quantify the different cell distortions, the structural shape factors are evaluated for each type of SS-RBC within the physiological region of the cell shear modulus listed in Table 1. As shown in Fig. 7, the granular cells show similar characteristics with a healthy cell for both ASF and ESF. On the contrary, the elongated cells exhibit the largest deviation from the perfect biconcave shape. Compared with the elongated cells, the sickle cells exhibit smaller ASF due to the curvature membrane surface while the holly leaf cells exhibit smaller ESF due to the larger angular width of the intracellular aligned hemoglobin polymer domain.

Fig. 7.

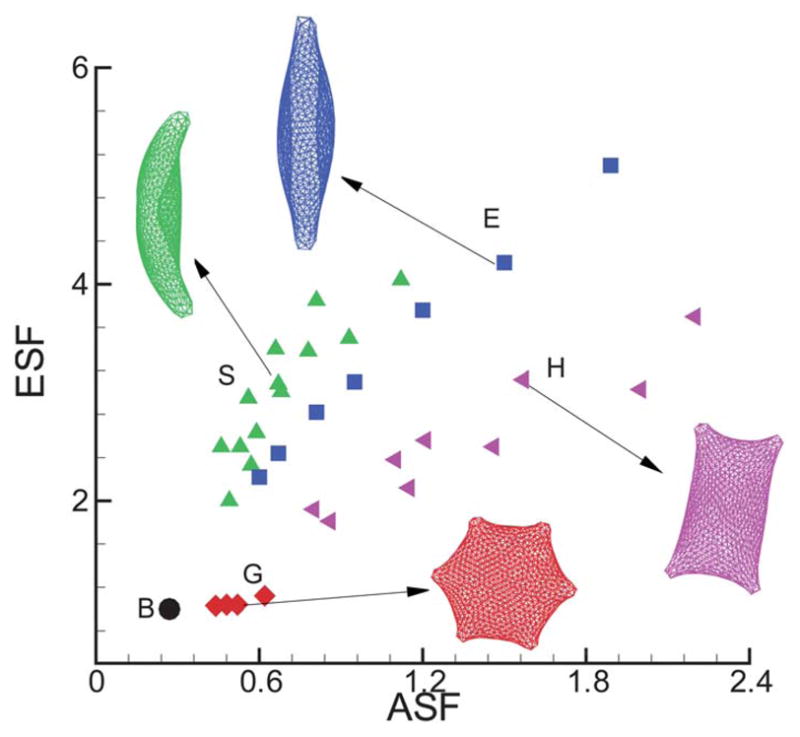
ASF and ESF for the various cell morphologies obtained. The labels “B”, “G”, “S”, “H” and “E” represent the biconcave, granular, sickle, holly leaf and elongated shapes, respectively. The snapshots show the typical cell shapes for each type of SS-RBC morphology obtained in the present study.

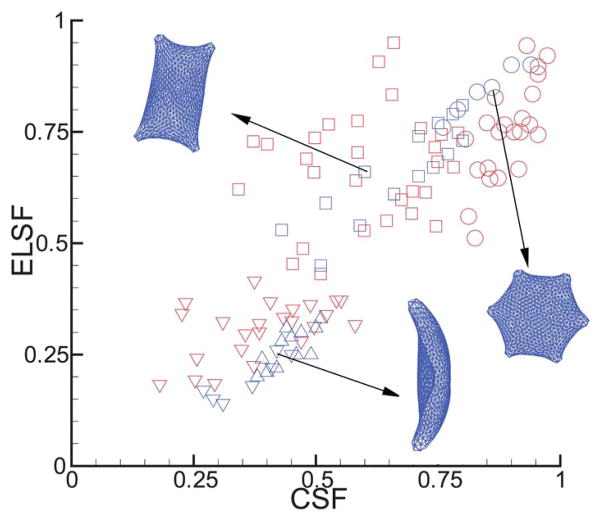
Similar to the 3D structural shape factors, 2D morphological analysis has also been conducted on medical images of different sickle cells, where the circular shape factor (CSF) and 2D elliptical shape factors (ELSF) are used to quantify the various SS-RBC morphologies.^17,18 Accordingly, we analyze the 2D structural properties of the SS-RBC by defining CSF and ELSF as

$$\begin{array}{l}\text{CSF}=4\pi \text{area}/{(\text{perimeter})}^2\\ \text{ELSF}=D_{\text{b}}/D_{\text{a}},\end{array}$$ (18)

where area and perimeter are the in-plane area and perimeter of the close curve defined by the cell. D_a and D_b are the long and short diameters, respectively. CSF and ELSF characterize the deviation of a curve from the circular shape. These two factors are unity for a perfect circle and close to zero for a “line” shape. Similarly, the structural factors are analyzed for each type of the SS-RBC with shear modulus values shown in Table 1. Fig. 8 plots both CSF and ELSF for the various cell membranes obtained from the above simulations. As a comparison, we also show the experimental results of the sickle red blood cells from medical images.¹⁷ The sickle red blood cells are classified into the “sickle”, “holly leaf” and “granular” types according to the cell morphologies under deoxygenated states.¹⁷ As shown in Fig. 8, while the structural factors of sickle red blood cells obtained from the simulation fall within the region of the experimental observations, the simulated results do not cover the entire range of experimental results. The quantitative difference is probably due to the limited knowledge of the physiological conditions for the SS-RBCs in the experiment as the mean corpuscular hemoglobin concentration, rate of deoxygenation and cell membrane deformability are not specified for the individual cell groups of the experiments. Therefore, the physiological conditions specified in Table 1 may not cover the exact region of physiological values adopted in the experiment. This issue requires further experimental and numerical investigations.

Fig. 8.

Circular (CSF) and 2D elliptical shape factors (ELSF) for different cell morphologies obtained from both medical image process¹⁷ (red) and present simulations (blue). The circle and square symbols represent the shape factors of the granular and holly leaf SS-RBC. The red inverted triangle symbols represent both the “sickle” and the “elongated” SS-RBC obtained from the experiment as they are unclassified in the experiment. The blue inverted triangle symbols represent the simulated “elongated” cells while the blue triangle symbols represent the simulated “sickle” cells.

4 Discussion

Starting from a single post-homogeneous nucleation proposed in ref. 3, we investigated the effect of the intracellular growing sickle hemoglobin fiber on the final morphological properties of SS-RBCs. Based on the different sickle hemoglobin configurations typically observed by polarization imaging microscopy, the growth rate of sickle hemoglobin polymer and the mechanical properties of sickle hemoglobin fibers, we constructed a coarse-grained model for the development of the aligned hemoglobin polymer. For individual SS-RBCs, the final morphological state is obtained through the following three steps.

• We choose a specific type of post-homogeneous nucleus according to experimental observations.

• We simulate the development of the aligned hemoglobin polymer domain with the bulk growth rate of the sickle hemoglobin bundles determined by the intracellular mean corpuscular hemoglobin concentration value.

• As the sickle hemoglobin fibers approach the cell membrane, the effective growth rate of the aligned hemoglobin polymer domain decreases with the stall force depending on the cell membrane rigidities. The final morphological state is obtained when the effective growth rate tends to zero.

Using this model, we explored the extent to which the heterogeneous morphologies of deoxygenated SS-RBCs can be obtained without any further knowledge of the detailed structure of the polymer domain at the molecular level. Our simulation results indicate that the various shapes of deoxygenated SS-RBCs are mainly determined by the aligned hemoglobin polymer configuration, which is consistent with the results of ref. 10. Specifically, the polymer domain in SS-RBCs with low mean corpuscular hemoglobin concentration value tends to form an aligned configuration with limited angular width, resulting in the typical “sickle” or “holly leaf” shape. On the other hand, the spherulite polymer domain is favored in SS-RBCs with high mean corpuscular hemoglobin concentration values, resulting in a near-biconcave shape with multiple spicules on the cell surface. This tendency is also consistent with the experimental observation on cell morphology in in vitro blood suspensions in ref. 5 and 6. Within each type of SS-RBC, the cells further show scattered morphological states depending on the individual cell membrane rigidity. Given the membrane shear modulus in the range of physiologic values measured using a micropipette,⁴ the simulated cell morphological states, quantified by the structural factors CSF and ELSF, fall within the range of the experimental results from medical images.

However, we note that several other physical conditions omitted in the current model can potentially also contribute to the heterogeneous distributions of cell morphologies. First, we have assumed that the bulk growth rate is the same at each of the polymer ends. The implicit assumption here is that the rate-limiting process for the aligned hemoglobin polymer domain development is the stall force on the sickle hemoglobin polymers instead of sickle hemoglobin monomer diffusion as discussed in ref. 32. Incorporation of anisotropic fiber growth rates may result in further heterogeneous morphological states. In ref. 6, a non-traditional type of “elongated” cells is obtained after further deoxygenation treatment on the granular cells. They are characterized by elongated projection along a certain direction while the center part keeps the granular shape. It was assumed in ref. 6 that this type of “elongated” cell originates from the further growth of aligned polymer along the elongated direction during the prolonged deoxygenation process. In the present work, we test this idea by imposing an anisotropic growth rate for the intracellular polymer domain. Starting from a granular shape of cell, we impose the polymer growth rate twenty times the original value along the other direction. At the new equilibrium state, as shown in Fig. 9, the cell transforms into an “elongated” shape along that direction while the cell center keeps the granular shape, resembling the non-traditional “elongated” cell observed in ref. 6. We note that the high growth rate value along the specific direction is chosen arbitrarily in this simulation, representing the prolonged incubation of the deoxygenation condition. A complete understanding of the above process requires further investigation. Second, the intracellular post-homogeneous nucleus is assumed to be near the center of the cell. Although this assumption is similar to the experimental observation in ref. 9 and 10 for the “central constriction” cells, the basis of the assumption needs further validation. As a sensitivity study, we have also considered one case for the “holly leaf” cell where the post-homogeneous nucleus is off the cell center, which results in further asymmetry and irregularity on the final cell morphology, as shown in Fig. 5. To the best of our knowledge, there are no experimental results reported on the spatial distribution of the intracellular post-homogeneous nucleus inside a sickle red blood cell. Therefore, it would be interesting to explore if there exist specific spatial preferences/distributions of the intracellular post-homogeneous nucleus by experimental measurements. This information would be important for further systematic exploration of the morphologic transition procedure discussed in the current work. Also, we have assumed that there is only one single post-homogeneous nucleation and polymer domain inside each cell in the present work. In reality, multiple sickle hemoglobin polymer domains can be formed in a single SS-RBC with high mean corpuscular hemoglobin concentration values,^8,9 resulting in multiple irregular spicules on the “granular” cell membrane. Moreover, we note that the intracellular CG polymer model in the present study represents bundles of aligned sickle hemoglobin polymers on a length scale of O(1)μm whereas the detailed configuration of single sickle hemoglobin polymers, which may affect the local cell membrane distortion, is omitted. Finally, we note that the cell morphology transition is a complex procedure where many different physiological factors play important roles, resulting in the well-known “heterogeneous” properties of the sickle cell morphology. While the cell deformability, intracellular polymer configuration and growth rate depend on the intracellular mean corpuscular hemoglobin concentration values, the cell preparation process such as deoxygenation rate can also affect the intracellular polymer configuration and therefore affect the cell morphologies. For the experimental dataset used for comparison in the current work, the sickle cells are collected from blood suspension and classified by the different morphologic characteristics while the mean corpuscular hemoglobin concentration and deoxygenation rate for each cell type are not specified. In the present work, we studied sickle cells with different mean corpuscular hemoglobin concentration values and chose the polymer configuration according to experimental observation⁹ that cells with low mean corpuscular hemoglobin concentration favor the elongated type of polymer and low membrane rigidity while cells with high mean corpuscular hemoglobin concentration favor the spherulite type of polymer and high membrane rigidity. There is no direct mapping between the experimental dataset and the simulation of the present work on the specific physiological conditions. This is a limitation of the present work. Systematic investigation with these effects incorporated would further help to elucidate the cell morphologic transition process.

Fig. 9.

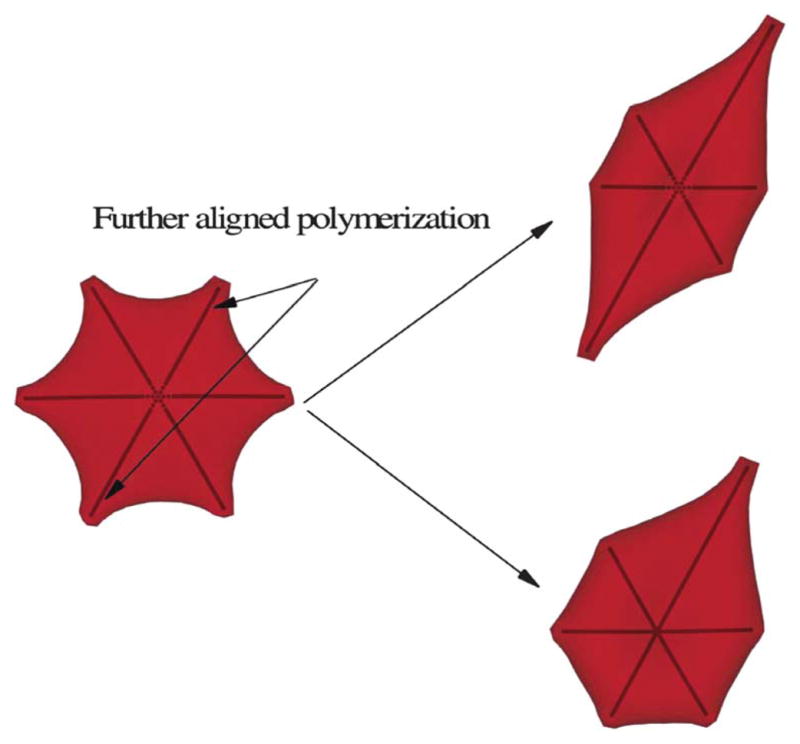
Elongated shapes: with further aligned polymerization along the specific direction, the granular cell (left) transforms into an “elongated” cell with the cell center keeping the granular shape (upper right), resembling the non-traditional “elongated” cell observed in ref. 9. The lower right plot represents the final cell morphology with the high growth rate imposed only on the upper right direction.

The typical time scale of the aligned hemoglobin polymer domain formation in the present work is of the order O(1) s, consistent with the prediction in ref. 32. This process is relatively short as compared to the total time of the “sickling” procedure (O(10)to O(100) s). In microcirculation, we note that the typical time for cell transition in capillaries is around 1–2 s.³⁸ The widespread blood vaso-occlusion originated from the distorted cell membrane is avoided in typical in vivo environments. This is mainly because the homogeneous nucleus formation is omitted in the current work. This procedure is well characterized by a “delay time” before which no sickle hemoglobin polymer can be detected.³⁹ On the other hand, deoxygenated SS-RBCs can get trapped in the post-capillaries due to adhesive interaction with the vessel endothelium.⁴⁰ This procedure may seriously increase the transit time for a SS-RBC to get re-oxygenated, and this results in a vicious in vivo “sickling—occlusion” cycle.