Measuring memory with the order of fractional derivative

Abstract

Fractional derivative has a history as long as that of classical calculus, but it is much less popular than it should be. What is the physical meaning of fractional derivative? This is still an open problem. In modeling various memory phenomena, we observe that a memory process usually consists of two stages. One is short with permanent retention, and the other is governed by a simple model of fractional derivative. With the numerical least square method, we show that the fractional model perfectly fits the test data of memory phenomena in different disciplines, not only in mechanics, but also in biology and psychology. Based on this model, we find that a physical meaning of the fractional order is an index of memory.

Fractional (fractional-order) derivative is a generalization of integer-order derivative and integral. It originated in the letter about the meaning of 1/2 order derivative from L'Hôpital to Leibnitz in 1695¹,²,³, and is a promising tool for describing memory phenomena⁴,⁵,⁶,⁷,⁸. The kernel function of fractional derivative is called memory function⁹,¹⁰, but it does not reflect any physical process. Unclear physical meaning has been a big obstacle that keeps fractional derivative lagging far behind the integer-order calculus. In 1974, the question “what are the physical interpretations of fractional calculus” was put forward as an open problem¹¹. In 2002, a physical explanation was proposed in terms of inhomogeneous and changing time scale by analogy reasoning, but the new time scale has not been validated by any experiment¹¹. Till now there is still no simple answer to the open problem. In fitting the test data of memory phenomena from different fields, we find that the fractional order can be physically explained as an index of memory.

Results

We find that Scott-Blair's model¹², originally a material model, can be a formula for memory phenomena in various disciplines. The model takes the form

where is the fractional derivative which depends on the strain history from 0 to t, and μ is a positive constant. 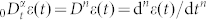if α is an integer n. There are several definitions of fractional derivative. Riemann-Liouville derivative is one of the most popular definitions, described by

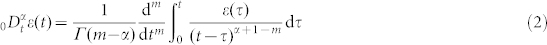where Γ is Euler's Gamma function and m is the integer satisfying m-1 ≤ α < m. The key point of our observation is that a memory process usually consists of two stages: the fresh stage and the working stage. The former is short with permanent retention at the beginning and it cannot be neglected in general, while the latter is governed by the fractional model (1). The critical point between the fresh stage and the working stage is usually not the origin. This observation is quite different from the traditional fractional models of one stage. For example, the fractional Maxwell model¹² is a one-stage model. As the combination of two simple models, it has a more complicated expression than equation (1).

We also find that the order of fractional derivative is an index of memory. This is an answer to the open problem: what is the physical meaning of fractional derivative. The test data in various disciplines fit equation (1) very well, as shown in Fig. 1,2,3Fig. 4. In the recovering or forgetting process (T > 1), the dimensionless form of the solution⁵ of equation (1) is

where T = t/t_M, E(T) = ε(t)/ε_M, and ε_M is the strain at the end instant of creeping t = t_M. The dimensionless retention E increases with an increase of order α. The higher the index, the slower the forgetting is. In particular, E = 0 (nothing memorized) if α = 0, and E = 1 (nothing forgotten) if α = 1. Therefore, we define the fractional-order α as the index of memory.

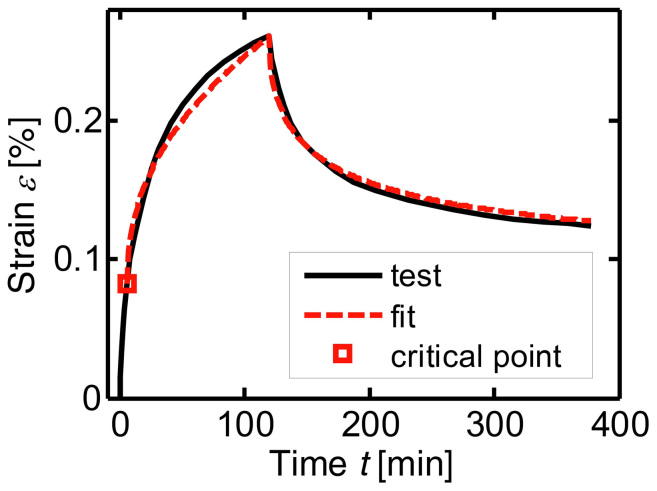
Figure 1. Fitting of the test data¹³ of the third specimen of SiAlYON ceramics.

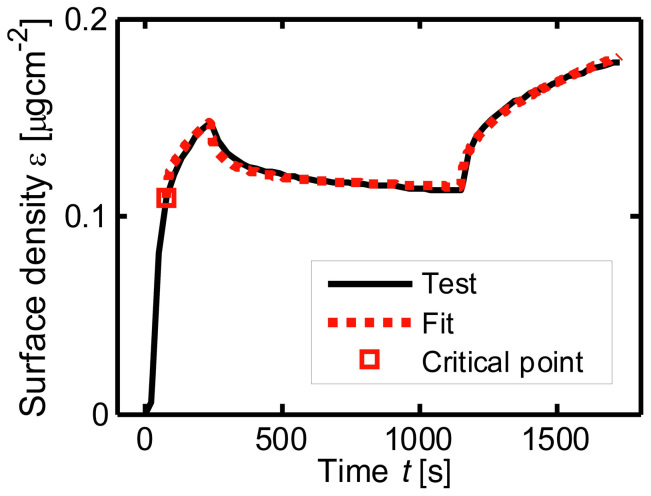
Figure 2. Fitting of the test data¹⁴ of protein adsorption kinetics.

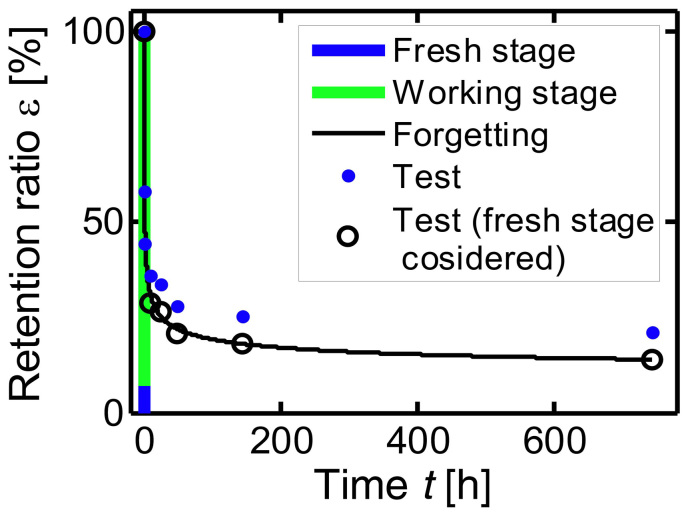
Figure 3. Forgetting curve.

The blue dot markers denote Ebbinghause's forgetting curve¹⁵. The blue line is the fresh stage, the green line is the working stage of learning, the black line is our forgetting curve, and the black circle markers are the test data with fresh stage taken into account. The learning stages are much shorter, and if the horizontal axis scale magnified the shapes of learning curves are like the creeping stage of Fig. 1.

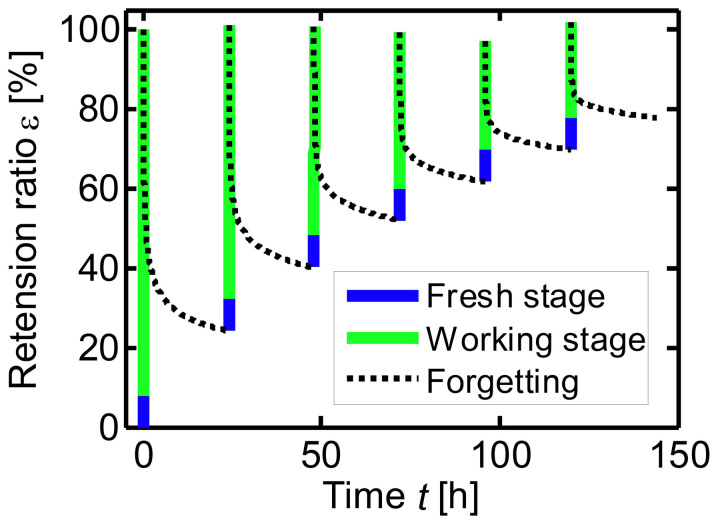
Figure 4. Retention with respect to repeated learning¹⁵.

The blue lines and green lines are the fresh stage and working stage of learning, respectively. The dotted black lines are our forgetting curves. The learning stages are much shorter, and if the horizontal axis scale magnified the shapes of learning curves are like the creeping stage of Fig. 1. The 6 points of test data are not shown in the figure, because their vertical values are all 100%.

Discussion

Firstly, we consider an example in mechanics. The behaviors of viscoelastic materials with memory are usually described by Kevin model, Voigt model, Maxwell model, and so on, in terms of the strain, the stress, and their integer-order derivatives or integrals¹⁶,¹⁷. Comparing with fractional models, such integer-order models reflect memory effects much less accurately¹. Early observations show that viscoelastic materials behave between elasticity and viscosity. It is reasonable, hence, to assume that models of viscoelasticity take the form of equation (1), and it covers two extremes: α = 0 for Hooke's Law of elasticity, and α = 1 for Newton's Law of viscosity. In 1979, equation (1) was successfully used to fit the creep and recovery test data⁵ of nitrocellulose compound at 90°C. Though some generalized fractional models like fractional Kevin, Voigt, and Maxwell models have been established and validated by experiments⁴,¹², works about direct validation of equation (1) are few, to the best knowledge of the authors. For a standard creep and recovery test, the specimen is usually loaded under a constant stress σ(t) = σ₀ from 0 to t_M, and the load is removed at the instant t = t_M, then σ(t) = 0 for t ≥ t_M. Let H(t) be the Heaviside function, then equation (1) takes the following simple form

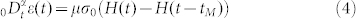where 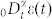is Riemann-Liouville's fractional-order derivative with zero initial condition. The superposition method¹⁸ results in the solution of equation (4) as follows

This is in agreement with the early observations of the behaviors of some viscoelastic materials¹⁹,²⁰,²¹,²². Recently, equation (1) was used¹⁸ to fit the three-point bending test data¹³ of the viscoelastic creep of SiAlYON ceramics at 1200°C and 240 MPa. The model fitted the test data of two specimens very well, but failed to fit the third test curve. To fit the third one, we define the fresh stage and the working stage. In the working stage, equation (5) perfectly fits the third test curve of SiAlYON ceramics specimen. With numerical least square method, we find that α = 0.44, μ = 7.23 × 10⁻⁵ (MPa⁻¹ · s^−α), and the critical point is (6.1455, 0.0828), as shown in Fig. 1. The fresh stage is irrecoverable because equation (5) is positive, i.e., the recovery is always above the critical point. Here and in the next example, the test data are measured from the figures of the corresponding references using the software Origin.

Secondly, we show that equation (1) works not only in modeling viscoelastic materials, but also in modeling biological kinetics with memory. For example, for the protein adsorption kinetics¹⁴, if the symbols of concentration c and the surface density Γ of fibronectin therein are replaced with σ and ε respectively. Then with σ(t) = σ₀[H(t) − H(t − t_M) + H(t − t_N)], where σ₀ = 50 μg/ml, t_M = 240 s, and t_N = 1150 s, the absorbed density is found to be

Using the numerical least square method, we find that α = 0.435, μ = 6.6302 × 10⁻⁵ cm·s^−α, and the critical point is (80, 0.109). Again as shown in Fig. 2, equation (6) fits the test data very well.

Thirdly, we show that equation (1) works well even for the cognitive dynamics in psychology, by fitting the memorizing test data¹⁵ performed by Hermann Ebbinghaus and reported in 1885. The learning tests included different learning materials and learning times of a day. To make the test data comparable, the time for relearning in 11–12 A.M. or 6–8 P.M. was linearly converted to that in 10–11 A.M. The average time of learning is t_M = 994.4 s. The retention ratios of learning ε(%) were 58.2, 44.2, 35.8, 33.7, 27.8, 25.4, and 21.1, respectively after 0.33, 1, 8.8, 1 × 24, 2 × 24, 6 × 24, and 7 × 24 hours, where the retention ratio was obtained by using the ratio of the time of relearning to the original.

By drawing an analogy between learning (forgetting) and loading (unloading), and regarding the retention as the strain, we use equation (1) to fit Ebbinghause's test data. Here we have σ(t) = 1 in the given learning stage from 0 to t_M, which means that for the series of syllables to be learned, the tested person is fully occupied, and σ(t) = 0 when the learning stops after the instant t_M. As the learning efficiencies vary in a day, the test data of at least one day long are used for fitting. The fractional-order α between 0.5 and 1 is assumed, because the linear conversion mentioned above is inadequate for a small order.

Similar to the material tests, at the beginning of learning, one can keep a few syllables quickly in mind and memorize them very well. This is the fresh stage of learning. In the working stage, something is gradually forgotten after the learning stops. We assume that the fresh stage is recovered after one day. Under this assumption, we use the corresponding values of ε minus the vertical value of the critical point respectively to fit the fractional model. By using the numerical least square method and the solution equation (5), we find that α = 0.71, μ = 205.8 h^−α, and the critical point (0, 7.2), where the learning time of fresh stage equals approximately 0. The forgetting curve matches the test data well, as shown in Fig. 3.

Furthermore, we consider Ebbinghause's repeated learning test¹⁵, where 9 series of 12 syllables were learned, and then in the same hour on successive days, relearned to the point of the first possible reproduction. In successive 6 days (n = 1,2,…,6), the times of repetitions for each series averagely are m_n = 16.5, 11, 7.5, 5, 3, and 2.5. As one syllable takes 0.4 s, the learning time equals t_n = m_n × 9 × 12 × 0.4/3600 h. With the test data, the solution of equation (1) for the working stage takes the form

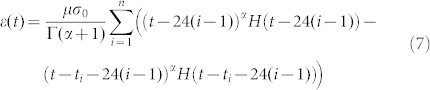Using equation (7) for the working stages and taking the fresh stage into account, the repeated learning and forgetting curves are plotted in Fig. 4. In this case, we find that α = 0.71, μ = 264.5 h^−α, and the height of the fresh stage is 8. Here the fractional-order is the same as that for Fig. 3, as expected. Thus, Ebbinghause's learning and forgetting tests do fit equation (1).

In summary, we divide memory phenomena into fresh stage and working stage, and show that the fractional order is an index of memory by fitting test data of memory phenomena from different fields.

Methods

Let the test data be (t₁, ε₁), (t₂, ε₂), … (t_M, ε_M), (t_{M + 1}, ε_{M + 1}), (t_{M + 2}, ε_{M + 2}), …, (t_N, ε_N), where t_M is the end instance of loading and t_N is the end instance of unloading. The data are fitted by using the numerical least square method, for which the following objective function J is minimized:

At the point (t_M, ε_M), equation (5) gives μ = ε_M/σ₀. Meshing α with uniform grid, with critical point (t_i, ε_i) for 0 ≤ ε_i < ε_N, the minimal value of J can be determined numerically.

Author Contributions

All authors contributed equally to this work. M.D. and Z.W. initialized the study and fitted the fractional models. H.H. derived the numerical least square method. All authors discussed and commented on the manuscript at all stages.