Feature-based Morphometry

Abstract

This paper presents feature-based morphometry (FBM), a new, fully data-driven technique for identifying group-related differences in volumetric imagery. In contrast to most morphometry methods which assume one-to-one correspondence between all subjects, FBM models images as a collage of distinct, localized image features which may not be present in all subjects. FBM thus explicitly accounts for the case where the same anatomical tissue cannot be reliably identified in all subjects due to disease or anatomical variability. A probabilistic model describes features in terms of their appearance, geometry, and relationship to sub-groups of a population, and is automatically learned from a set of subject images and group labels. Features identified indicate group-related anatomical structure that can potentially be used as disease biomarkers or as a basis for computer-aided diagnosis. Scale-invariant image features are used, which reflect generic, salient patterns in the image. Experiments validate FBM clinically in the analysis of normal (NC) and Alzheimer’s (AD) brain images using the freely available OASIS database. FBM automatically identifies known structural differences between NC and AD subjects in a fully data-driven fashion, and obtains an equal error classification rate of 0.78 on new subjects.

1 Introduction

Morphometry aims to automatically identify anatomical differences between groups of subjects, e.g. diseased or healthy brains. The typical computational approach taken to morphometry is a two step process. Subject images are first geometrically aligned or registered within a common frame of reference or atlas, after which statistics are computed based on group labels and measurements of interest. Morphometric approaches can be contrasted according to the measurements upon which statistics are computed. Voxel-based morphometry (VBM) involves analyzing intensities or tissue class labels [1, 2]. Deformation or tensor-based morphometry (TBM) analyzes the deformation fields which align subjects [4, 3, 5]. Object-based morphometry analyzes the variation of pre-defined structures such as cortical sulci [6].

A fundamental assumption underlying most morphometry techniques is that inter-subject registration is capable of achieving one-to-one correspondence between all subjects, and that statistics can therefore be computed from measurements of the same anatomical tissues across all subjects. Inter-subject registration remains a major challenge, however, due to the fact that no two subjects are identical; the same anatomical structure may vary significantly or exhibit distinct, multiple morphologies across a population, or may not be present in all subjects. Coarse linear registration can be used to normalize images with respect to global orientation and scale differences, however it cannot achieve precise alignment of fine anatomical structures. Deformable registration has the potential to refine the alignment of fine anatomical structures, however it is difficult to guarantee that images are not being over-aligned. While deformable registration may improve tissue overlap, in does not necessarily improve the accuracy in aligning landmarks, such as cortical sulci [7]. Consequently, it may be unrealistic and potentially detrimental to assume global one-to-one correspondence, as morphometric analysis may be confounding image measurements arising from different underlying anatomical tissues [9–11].

Feature-based morphometry (FBM) is proposed specifically to avoid the assumption of one-to-one inter-subject correspondence. FBM admits that correspondence may not exist between all subjects and throughout the image, and instead attempts to identify local patterns of anatomical structure for which correspondence between subsets of subjects is statistically probable. Such local patterns are identified and represented as distinctive scale-invariant features [12–15], i.e. generic image patterns that can be automatically extracted in the image by a front-end salient feature detector. A probabilistic model quantifies feature variability in terms of appearance, geometry, and occurrence statistics relative to subject groups. Model parameters are estimated using a fully automatic, data-driven learning algorithm to identify local patterns of anatomical structure and quantify their relationships to subject groups. The local feature thus replaces the global atlas as the basis for morphometric analysis. Scale-invariant features are widely used in the computer vision literature for image matching, and have been extended to matching 3D volumetric medical imagery [14, 15]. FBM follows from a line of recent research modeling object appearance in photographic imagery [16] and in 2D slices of the brain [17], and extends this research to address group analysis, and to operate in full 3D volumetric imagery.

2 Feature-based Morphometry (FBM)

2.1 Local Invariant Image Features

Images contain a large amount of information, and it is useful to focus computational resources on interesting or salient features, which can be automatically identified as maxima of a saliency criterion evaluated throughout the image. Features associated with anatomical structures have a characteristic scale or size which is independent of image resolution, and a prudent approach is thus to identify features in a manner invariant to image scale [12, 13]. This can be done by evaluating saliency in an image scale-space I(x, σ) that represents the image I at location x and scale σ. The Gaussian scale-space, defined by convolution of the image with the Gaussian kernel, is arguably the most common in the literature [19, 20]:

$$I(x,\sigma )=I(x,{\sigma }_0)*G(x,\sigma -{\sigma }_0),$$ (1)

where G(x, σ) is a Gaussian kernel of mean x and variance σ, and σ₀ represents the scale of the original image. The Gaussian scale-space has attractive properties including non-creation and non-enhancement of local extrema, scale-invariance, and causality and arises as the solution to the heat equation [20]. Derivative operators are commonly used to evaluate saliency in scale-space [12, 13], and are motivated by models of image processing in biological vision systems [8]. In this paper, geometrical regions g_i = {x_i, σ_i} corresponding to local extrema of the difference-of-Gaussian (DOG) operator are used [12]:

$$(x_i,{\sigma }_i)=\underset{x,\sigma }{\text{local argmax}}\left\{\right|\frac{dI(x,\sigma )}{d\sigma }\left|\right\}.$$ (2)

Each identified feature is a spherical region defined geometrically by a location x_i and a scale σ_i, and the image measurements within the region, denoted as a_i.

2.2 Probabilistic Model

Let F = {f₁,…, f_N} represent a set of N local features extracted from a set of images, where N is unknown. Let T represent a geometrical transform bringing features into coarse, approximate alignment with an atlas, e.g. a similarity or affine transform to the Talairach space [21]. Let C represent a discrete random variable of the group from which subjects are sampled, e.g. diseased, healthy. The posterior probability of (T,C) given F can be expressed as:

$$p(C,T|F)=\frac{p(F|C,T)p(C,T)}{p(F)}=\prod _i^N\frac{p(f_i|C,T)p(C,T)}{p(F)},$$ (3)

where the first equality results from Bayes rule, and the second from the assumption of conditional feature independence given (C, T). Note that while inter-feature dependencies in geometry and appearance are generally present, they can largely be accounted for by conditioning on variables (C, T). p(f_i|C, T) represents the probability of a feature f_i given (C, T). p(C, T) represents a joint prior distribution over (C, T). p(F) represents the evidence of feature set F.

An individual feature is denoted as f_i = {a_i, α_i, g_i, γ_i}. a_i represents feature appearance (i.e. image measurements), α_i is a binary random variable representing valid or invalid a_i, g_i = {x_i, σ_i} represents feature geometry in terms of image location x_i and scale σ_i, and γ_i is a binary random variable indicating the presence or absence of geometry g_i in a subject image. The focus of modeling is on the conditional feature probability p(f_i|C, T):

$$p(f_i|C,T)=p(a_i,{\alpha }_i,{\gamma }_i,g_i|T,C)=p(a_i|{\alpha }_i)p({\alpha }_i|{\gamma }_i)p(g_i|{\gamma }_i,T)p({\gamma }_i|C),$$ (4)

where the 2nd equality follows from several reasonable conditional independence assumptions between variables. p(a_i|α_i) is a density over feature appearance a_i given feature occurrence α_i, p(α_i|γ_i) is a Bernoulli distribution of feature occurrence α_i given the occurrence of a consistent geometry γ_i, p(g_i|γ_i, T) is a density over feature geometry given geometrical occurrence γ_i and global transform T, and p(γ_i|C) is a Bernoulli distribution over geometry occurrence given group C.

2.3 Learning Algorithm

Learning focuses on identifying clusters of features which are similar in terms of their group membership, geometry and appearance. Features in a cluster represent different observations of the same underlying anatomical structure, and can be used to estimate the parameters of distributions in Equation (4).

Data Preprocessing

Subjects are first aligned into a global reference frame, and T is thus constant in Equation (3). At this point, subjects have been normalized according to location, scale and orientation, and the remaining appearance and geometrical variability can be quantified [22]. Image features are then detected independently in all subject images as in Equation (2).

Clustering

For each feature f_i, two different clusters or feature sets G_i and A_i are identified, where f_j ∈ G_i are similar to f_i in terms of geometry, and f_j ∈ A_i are similar to f_i in appearance. First, set G_i is identified based on a robust binary measure of geometry similarity. Features f_i and f_j are said to be geometrically similar if their locations and scales differ by less than error thresholds ε _x and ε_σ. In order to compute geometrical similarity in a manner independent of feature scale, location difference is normalized by feature scale σ_i, and scale difference is computed in the log domain. G_i is thus defined as:

$$G_i=\{f_j:\Vert x_i-x_j\Vert /{\sigma }_i\le {\epsilon }_x\wedge |\text{log}({\sigma }_j/{\sigma }_i)|\le {\epsilon }_{\sigma }\}.$$ (5)

Next, set A_i is identified using a robust measure of appearance similarity, where f_i is said to be similar to f_j in appearance if the difference between their appearances is below a threshold ε_ai. A_i is thus defined as a function of ε_ai:

$$A_i({\epsilon }_{a_i})=\{f_j:\Vert a_i-a_j\Vert \le {\epsilon }_{a_i}\},$$ (6)

where here ‖ ‖ is the Euclidean norm. While a single pair of geometrical thresholds (ε _x, ε_σ) is applicable to all features, ε_ai is feature-specific and set to:

$${\epsilon }_{a_i}=\text{sup}\{{\epsilon }_a\in [0,\infty ):1\le \frac{|A_i({\epsilon }_a)\cap G_i\cap C_i|}{|A_i({\epsilon }_a)\cap G_i\cap C_i|}\},$$ (7)

where C_i is the set of features having the same group label as f_i, and ε_ai is thus set to the maximum threshold such that A_i is still more likely than not to contain geometrically similar features from the same group C_i. At this point, G_i ∩ A_i is a set of samples of model feature f_i, and the informativeness of f_i regarding a subject group C_j is quantified by the likelihood ratio:

$$\frac{p(f_i|C_j,T)}{p(f_i|{\mathrm{C̅}}_j,T)}=\frac{|A_i\cap G_i\cap C_j|}{|A_i\cap G_i\cap {\mathrm{C̅}}_j|}.$$ (8)

The likelihood ratio explicitly measures the degree of association between a feature and a specific subject group and lies at the heart of FBM analysis. Features can be sorted according to likelihood ratios to identify the anatomical structures most indicative of a particular subject group, e.g. healthy or diseased. The likelihood ratio is also operative in FBM classification:

$$C^{*}=\underset{C}{\text{argmax}}\left\{\frac{p(C_{,}T|F)}{p(\mathrm{C̅},T|F)}\right\}=\underset{C}{\text{argmax}}\left\{\frac{p(C,T)}{p(\mathrm{C̅},T)}\prod _i\frac{p(f_i|C,T)}{p(f_i|\mathrm{C̅},T)}\right\},$$ (9)

where C^* is the optimal Bayes classification of a new subject based on a set of features F in the image, and can be used for computer-aided diagnosis.

3 Experiments

FBM is a general analysis technique, which is demonstrated and validated here in the analysis of Alzheimer’s disease (AD), an important, incurable neurodegenerative disease affecting millions worldwide, and the focus of intense computational research [23, 24, 18, 25]. Experiments use OASIS [18], a large, freely available data set including 98 normal (NC) subjects and 100 probable AD subjects ranging clinically from very mild to moderate dementia. All subjects are right-handed, with approximately equal age distributions for NC/AD subjects ranging from 60+ years with means of 76/77 years. For each subject, 3 to 4 T1-weighted scans are acquired, gain-field corrected and averaged in order to improve the signal/noise ratio. Images are aligned within the Talairach reference frame via affine transform T and the skull is masked out [25]. In our analysis, the DOG scale-space [12] is used to identify feature geometries (x_i, σ _i), appearances a_i are obtained by cropping cubical image regions of side length $4\sqrt{{\sigma }_i}$ centered on x_i and then scale-normalizing to (11 × 11 × 11)-voxel resolution. Features could be normalized according to a canonical orientation to achieve rotation invariance [15], this is omitted here as subjects are already rotation-normalized via T and further invariance reduces appearance distinctiveness. Approximately 800 features are extracted in each (176 × 208 × 176)-voxel brain volume.

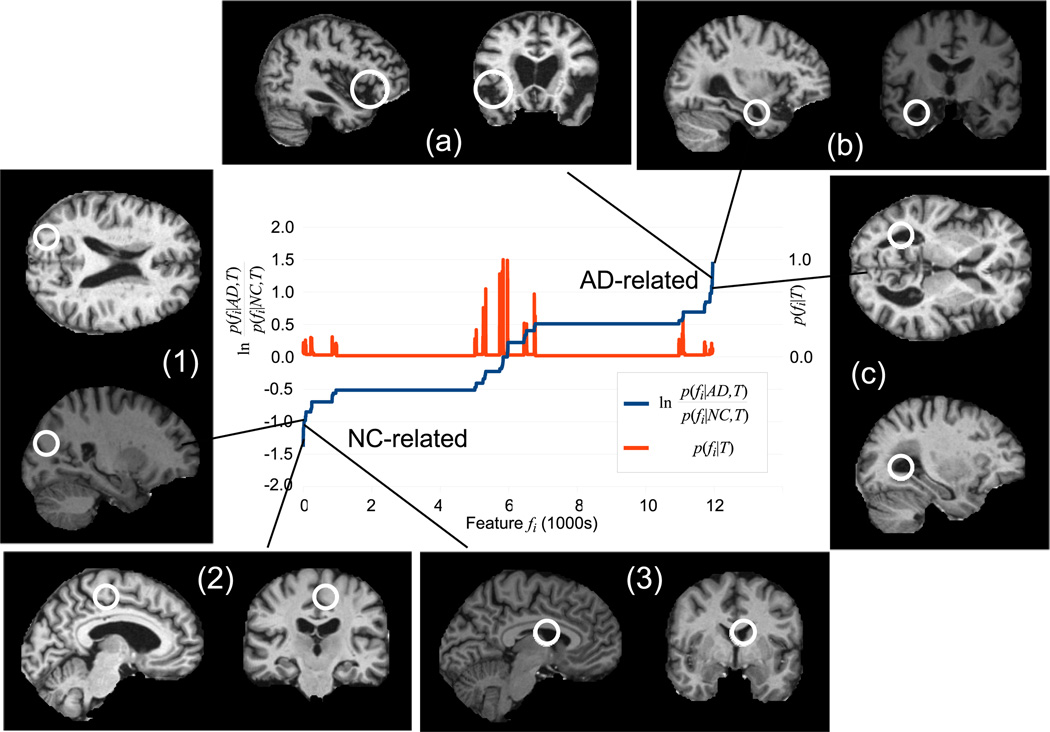
Model learning is applied on a randomly-selected subset of 150 subjects (75 NC, 75 AD). Approximately 12K model features are identified, these are sorted according to likelihood ratio in Figure 1. While many occur infrequently (red curve, low p(f_i|T)) and/or are uninformative regarding group (center of graph), a significant number are strongly indicative of either NC or AD subjects (extreme left or right of graph). Several strongly AD-related features correspond to well-established indicators of AD in the brain. Others may provide new information. For examples of AD-related features shown in Figure 1, feature (a) corresponds to enlargement of the extracerebral space in the anterior Sylvian sulcus; feature (b) corresponds to enlargement of the temporal horn of the lateral ventricle (and one would assume a concomitant atrophy of the hippocampus and amygdala); feature (c) corresponds to enlargement of the lateral ventricles. For NC-related features, features (1) (parietal lobe white matter) and (2) (posterior cingulate gyrus) correspond to non-atrophied parenchyma and feature (3) (lateral ventricle) to non-enlarged cerebrospinal fluid spaces.

Fig. 1.

The blue curve plots the likelihood ratio ln $\frac{p(f_i|AD,T)}{p(f_i|NC,T)}$ of feature occurrence in AD vs. NC subjects sorted in ascending order. Low values indicate features associated with NC subjects (lower left) and high values indicate features associated with AD subjects (upper right). The red curve plots feature occurrence probability p(f_i|T). Note a large number of frequently-occurring features bear little information regarding AD or NC (center). Examples of NC (1–3) and AD (a–c) related features are shown.

FBM also serves as a basis for computer-aided diagnosis of new subjects. Classification of the 48 subjects left out of learning results in an equal error classification rate (EER) of 0.78 ⁴. Classification based on models learned from randomly-permuted group labels is equivalent to random chance (EER = 0.50, stdev = 0.02), suggesting that the model trained on genuine group labels is indeed identifying meaningful anatomical structure. A direct comparison with classification rates in the literature is difficult due to the availability, variation and preprocessing of data sets used. Rates as high as 0.93 are achievable using support vector machines (SVMs) focused on regions of interest [24]. While representations such as SVMs are useful for classification, they require additional interpretation to explain the link between anatomical tissue and groups [5].

4 Discussion

This paper presents and validates feature-based morphometry (FBM), a new, fully data-driven technique for identifying group differences in volumetric images. FBM utilizes a probabilistic model to learn local anatomical patterns in the form of scale-invariant features which reflect group differences. The primary difference between FBM and most morphological analysis techniques in the literature is that FBM represents the image as a collage of local features that need not occur in all subjects, and thereby offers a mechanism to avoid confounding analysis of tissues which may not be present or easily localizable in all subjects, due to disease or anatomical variability. FBM is validated clinically on a large set images of NC and probable AD subjects, where anatomical features consistent with well-known differences between NC and AD brains are automatically identified in a set of 150 training subjects. Due to space constraints only a few examples are shown here. FBM is potentially useful for computer-aided diagnosis, and classification of 48 test subjects achieves a classification ERR of 0.78. As validation makes use of a large, freely available data set, reproducability and comparison with other techniques in the literature will be greatly facilitated.

FBM does not replace current morphometry techniques, but rather provides a new complementary tool which is particularly useful when one-to-one correspondence is difficult to achieve between all subjects of a population. The work here considers group differences in terms of feature/group co-occurrence statistics, however most features do occur (albeit at different frequencies) in multiple groups, and traditional morphometric analysis on an individual feature basis is a logical next step in further characterizing group differences. In terms of FBM theory, the model could be adapted to account for disease progression in longitudinal studies by considering temporal groups, to help in understanding the neuroanatomical basis for progression from mild cognitive impairment to AD, for instance. A variety of different scale-invariant features types exist, based on image characteristics such as spatial derivatives, image entropy and phase. These could be incorporated into FBM to model complementary anatomical structures, thereby improving analysis and classification. The combination of classification and permutation testing performed here speaks to the statistical significance of the feature ensemble identified by FBM, and we are investigating significance testing for individual features. FBM is general and can be used as a tool to study a variety of neurological diseases, and we are currently investigating Parkinson’s disease. Future experiments will involve a comparison of morphological methods on the OASIS data set.