Abstract
Highly networked signaling hubs are often associated with disease, but targeting them pharmacologically has largely been unsuccessful in the clinic because of their functional pleiotropy. Motivated by the hypothesis that a dynamical signaling code confers functional specificity, we investigated whether dynamical features may be targeted pharmacologically to achieve therapeutic specificity. With a virtual screen we identified combinations of signaling hub topologies and dynamic signal profiles that are amenable to selective inhibition. Mathematical analysis revealed principles that may guide stimulus-specific inhibition of signaling hubs, even in the absence of detailed mathematical models. Using the NFκB signaling module as a test bed, we identified perturbations that selectively affect the response to cytokines or pathogen components. Together, our results demonstrate that the dynamics of signaling may serve as a pharmacological target, and we reveal principles that delineate the opportunities and constraints of developing stimulus-specific therapeutic agents aimed at pleiotropic signaling hubs.
Introduction
Intra-cellular signals link the cell’s genome to the environment. Misregulation of such signals often cause or exacerbate disease (Lin and Karin, 2007; Weinberg, 2007) (so-called “signaling diseases”) and their rectification has been a major focus of biomedical and pharmaceutical research (Cohen, 2002; Frelin et al., 2005; Ghoreschi et al., 2009). For the identification of therapeutic targets, the concept of discrete signaling pathways that transmit intra-cellular signals to connect cellular sensor/receptors with cellular core machineries has been influential. In this framework, molecular specificity of therapeutic agents correlates well with their functional or phenotypic specificity. However, in practice, clinical outcomes for many drugs with high molecular specificity has been disappointing (e.g. inhibitors of IKK, MAPK, JNK (Berger and Iyengar, 2010; DiDonato et al., 2012; Roring and Brummer, 2012; Seki et al., 2012)).
Many prominent signaling mediators are functionally pleiotropic, playing roles in multiple physiological functions (Chavali et al., 2010; Gandhi et al., 2006). Indeed, signals triggered by different stimuli often travel through shared network segments that operate as hubs, before reaching the effectors of the cellular response (Bitterman and Polunovsky, 2012; Gao and Chen, 2010). Hubs’ inherent pleiotropy means that their inhibition may have broad and likely undesired effects (Karin, 2008; Berger and Iyengar, 2010; Force et al., 2007; Oda and Kitano, 2006; Zhang et al., 2008) – this is a major obstacle for the efficacy of drugs targeting prominent signaling hubs such as p53, MAPK or IKK.
Recent studies have begun to address how signaling networks generate stimulus-specific responses (Bardwell, 2006; Haney et al., 2010; Hao et al., 2008; Zalatan et al., 2012). For example, the activity of some pleiotropic kinases may be steered to particular targets by scaffold proteins (Berger and Iyengar, 2010; Schrofelbauer et al., 2012; Zalatan et al., 2012). Alternatively, or in addition, some signaling hubs may rely on stimulus-specific signal dynamics to activate selective downstream branches in a stimulus-specific manner, in a process known as temporal or dynamic coding or multiplexing (Behar and Hoffmann, 2010; Chalmers et al., 2007; Hoffmann et al., 2002; Kubota et al., 2012; Marshall, 1995; Purvis et al., 2012; Purvis and Lahav, 2013; Schneider et al., 2012; Werner et al., 2005).
While the importance of signaling scaffolds and their pharmacological promise is widely appreciated (Klussmann et al., 2008; Zalatan et al., 2012), and isolated studies have altered the stimulus-responsive signal dynamics (Purvis et al., 2012; Park et al., 2003; Sung et al., 2008; Sung and Simon, 2004)), the capacity for modulating signal dynamics for pharmacological gain has not been addressed in a systematic manner. In this work, we demonstrate by theoretical means that when signal dynamics are targeted, pharmacological perturbations can produce stimulus-selective results. Specifically, we identify combinations of signaling hub topology and input-signal dynamics that allow for pharmacological perturbations with dynamic feature-specific or input-specific effects. Then, we investigate stimulus-specific drug targeting in the IKK-NFκB signaling hub both in-silico and in-vivo. Together, our work begins to define the opportunities for pharmacological targeting of signaling dynamics to achieve therapeutic specificity.
Results
Dynamic signaling hubs may be manipulated to mute specific signals
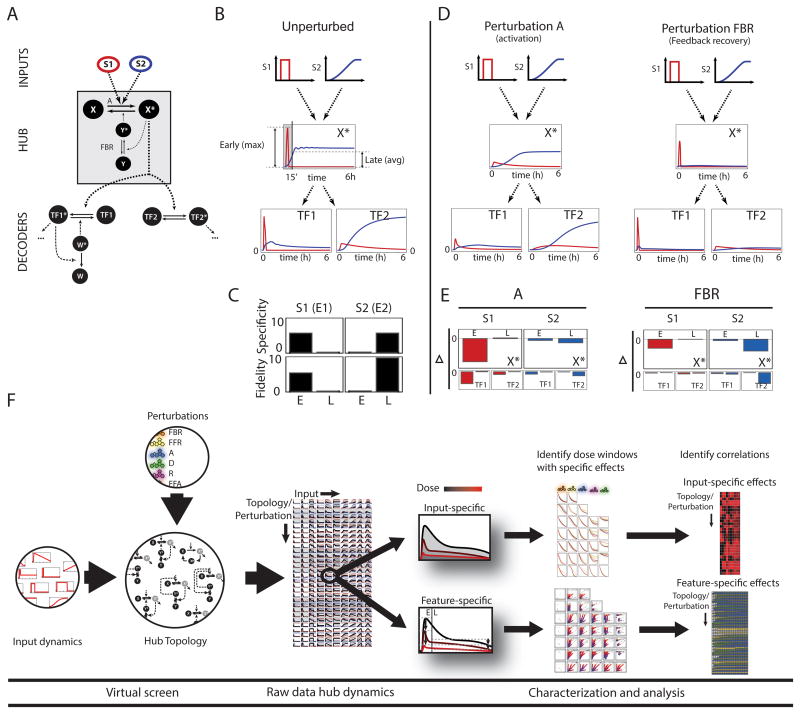
Previous work has shown how stimulus-specific signal dynamics may allow a signaling hub to selectively route effector functions to different downstream branches (Behar et al., 2007). Here, we investigated the capacity of simple perturbations to kinetic parameters (caused for example by drug treatments) to produce stimulus-specific effects. For this, we examined a simple model of an idealized signaling hub (Figure 1A), reminiscent of the NFκB, p53, or MAPK signaling modules. The hub X* reacts with strong but transient activity to stimulus S1 and sustained, slowly rising activity to stimulus S2. These stimulus-specific signaling dynamics are decoded by two effector modules, regulating transcription factors TF1 and TF2. TF1, regulated by a strongly adaptive negative feedback, is sensitive only to fast changing signals, whereas TF2, regulated by a slowly activating two-state switch, requires sustained signals for activation (Figure 1B). We found it useful to characterize the X*, TF1, and TF2 responses in terms of two dynamic features, namely the maximum early amplitude (“E”, time < 15′) and the average late amplitude (“L”, 15′ < t < 6hs). These features, calculated using a mathematical model of the network (see Methods) show good fidelity and specificity (Komarova et al., 2005) (Figure 1C), as S1 causes strong activation of TF1 with minimal cross-talk to TF2, and vice versa for S2.
Figure 1. Pharmacologic perturbations with stimulus-specific effects.
A) A negative feedback module transduces input signals S1 and S2 producing outputs that are decoded by downstream effectors circuits that may distinguish between different dynamics. B) Unperturbed dynamics of X*, TF1*, and TF2* in response to S1 (red) and S2 (blue). Definition of early (E) and late (L) parts of the signal is indicated. C) Specificity and fidelity of E and L for TF1* and TF2*, as defined in (Komarova et al., 2005). D) Partial inhibition of X* activation (A) abolishes the response to S1 but not S2, whereas a perturbation targeting the feedback regulator (FBR) suppresses the response to S2 but not S1. E) Perturbation phenotypes defined as difference between unperturbed and perturbed values of the indicated quantities (arbitrary scales for X*, TF1*, and TF2*). Perturbation A inhibits E and TF1* but not TF2*; perturbation FBR inhibits L and TF2* but not TF1*. F) Virtual screening pipeline showing the experimental design and the two analysis branches for characterizing feature- and input-specific effects. Details in methods and Table S1.
Seeking simple (affecting a single reaction) perturbations that selectively inhibit signaling by S1 or S2, we found that perturbation (A) partially inhibiting the activation of X, was capable of suppressing hub activity in response to a range of S1 amplitudes while still allowing for activity in response to S2 (Figure 1D). Consequently, this perturbation significantly reduced TF1 activity in response to S1 but had little effect on TF2 activity elicited by S2. We also found that the most effective way to inhibit S2 signaling was targeting the deactivation of negative feedback regulator Y (FBR). This perturbation caused almost complete abrogation of late X activity yet allows for significant levels of early activity. As a result, TF2 was nearly completely abrogated in response to S2 but stimulus S1 still produced a solid TF1 response. The early (E) and late (L) amplitudes could be used to quantify the input-signal-specific effects of these perturbations (Figure 1E).
This numerical experiment showed that it is possible to selectively suppress transient or sustained dynamic signals transduced through a common negative feedback-containing signaling hub. Moreover, the dynamic features E and L could be independently inhibited. To study how prevalent such opportunities for selective inhibition are, we established a computational pipeline for screening reaction perturbations within multiple network topologies and in response to multiple dynamic input signals; the simulation results were analyzed to identify cases of either “input signal”-specific inhibition or “dynamic feature”-specific inhibition (Figure 1F).
A computational screen to identify opportunities for input signal-specific inhibition
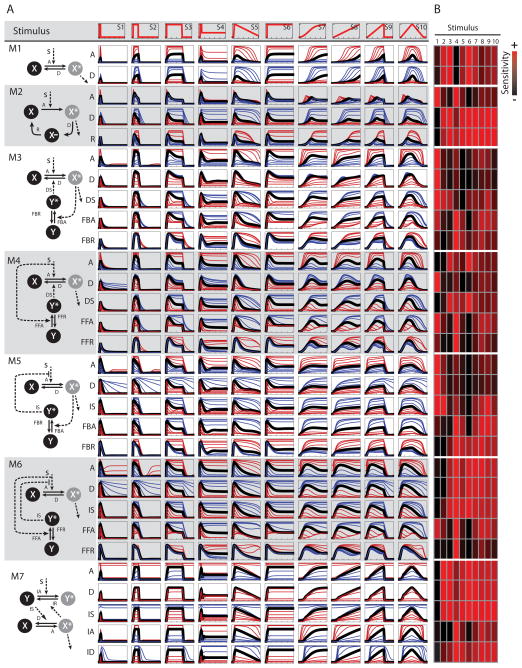
The computational screen involved small libraries of one- and two-component regulatory modules and temporal profiles of input signals (Figure 2A), both commonly found in intra-cellular signaling networks. All modules (M1 to M7, column on left) contained a species X that upon stimulation by an input signal is converted into an active form X* (the output) that propagates the signal to downstream effectors. One-component modules included a reversible two-state switch (M1) and a three state cycle with a refractory state (M2). Two-component modules contained a species Y that upon activation via a feedback (M3 and 5) or feed-forward (M4 and 6) loop either deactivates X (M3 and 4) or inhibits (M5 and 6) its activation. We also included the afore-described topology that mimics the IκB-NFκB or the Mdm2-p53 modules (M7). Mathematical descriptions may be found in “Methods”. While many biological signaling networks may conform to one of these simple topologies, others may be abstracted to one that recapitulates the physiologically-relevant emergent properties.
Figure 2. A virtual screen for stimulus-specificity in pharmacologic perturbations.
A) Signaling modules (left) and input library (top) used in the screen. Dotted lines indicate enzymatic reactions (perturbation names indicated). Time courses of hub activity for each module/input combination for the unperturbed (black) and perturbed cases (blue indicates a decrease, red an increase in parameter value). B) Relative inhibitory effects of perturbations normalized per row (See methods and Figure S1).
The library of stimuli (S1–S10. Figure 2A, top row) comprises ten input functions with different combinations of “fast” and “slow” initiation and decay phases (see Methods). The virtual screen was performed by varying the kinetic parameter for each reaction over a range of values, thereby modeling simple perturbations of different strengths and recording the temporal profile of X* abundance. To quantify stimulus-specific inhibition we measured the area under the normalized dose response curves (time-average of X* vs. perturbation dose) for each module-input combination (Figure 2B and Figure S1. See Methods.).
For many perturbations, we found doses that abrogated the response to some inputs but not others (Figure S1). We also observed that the responses to some input functions are affected similarly in different modules (e.g. inputs S1 and S2, both transient pulses) but others are not. For example, both the responses to inputs S8 and S1 are attenuated by the IS (inhibitor strength) perturbation in M5 but FBA (feedback activation) affects only the former. This indicates that the capacity for selective inhibition is not intrinsic to the specific dynamics of the input signal. Similarly, while some perturbations targeting similar reactions in different topologies had similar “dynamic footprints” (i.e affecting responses to common sets of inputs, for example, FFA -feedforward activation- in modules 4 and 6), most were less consistent and some seemed to have opposite effects (A –activation- in M3/5 and M4/6 for example). Taken together, the results of this screen demonstrate that perturbations with input-dynamics-specific effects are indeed possible, but the specificity is dose- and topology-dependent.
Inhibition of specific dynamic signaling features
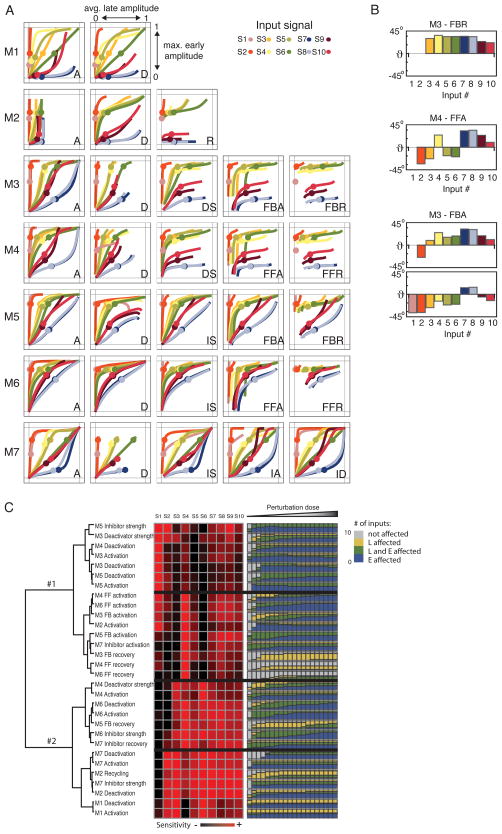
Applying the afore-described E (early maximum) and L (late average) metrics, we found some perturbations to have selectivity for early (E) or late (L) phases of a signal (Figure 3A); for example FBR and to a lesser extent FFR (feedback and feedforward recovery) consistently suppressed the late phase in a module- and largely input-independent manner (shown as the tangent angle at the unperturbed point in the E-L space, Figure 3B, top). Others were less consistent; for example FBA and FFA (feedback and feedforward activation) tended to affect early signaling or late signaling in an input-dependent but module-independent manner (Figure 3B, center). On the other hand, low dose perturbation of the activation reaction (A) inhibited primarily early signaling in the feedback based modules (M3 and M5) and late signaling in the feed forward based modules (M4 and M6) but only for some inputs. Interestingly, the specificity for E or L of some perturbations may be reversed in different dosing regimes (Figure 3B, bottom. Notice horizontal-vertical transition in the corresponding panel in Figure 3A).
Figure 3. Inhibition of specific dynamic signaling features.
A) Feature maps: effect of a perturbation on the maximum early (t<60′) amplitude (y axis) and late (60′<t<300′) average amplitude (x axis) of the X* response. Colored dots mark the unperturbed response to indicated input signals, and curves represent the responses for varying strengths of the indicated perturbation. B) Tangent angle at the unperturbed point in the E-L space (θ<0 E specificity, θ>0 L specificity) Top: Perturbation FBR (M3) suppresses late signaling in an input-independent manner. Center: FFA attenuates early or late signaling in an input-dependent manner. Bottom: E-L specificity switch for two doses of FBA (M3). C) Hierarchical clustering of the inhibitory effects (left) compared to number of input signals showing selective inhibition of early (blue), late (yellow), or both (green) parts of the output. Bars represent different perturbations doses. (See methods and Figure S2).
We then asked whether feature-specific inhibition correlated with stimulus-specific inhibition. Hierarchical clustering the perturbation data (Figure 3C) identified two major groups, characterized by inhibition of the response to very brief (S1 and S2) or sustained inputs. Comparing the clusters and the E or L selectivity (determined from the angle in the E vs. L space, see methods and Figure S2) showed some correlation between a perturbation’s E-L and stimulus-specificity (Figure 3C). We found that perturbations that affect the late phase (e.g. FFR and FBR) affect signaling in response to sustained inputs but had virtually no effect on the response to S1 and S2. The reverse was less clear-cut; perturbations that tend to cause selective suppression of early phases could have an effect on signals without strong early components as well. We also observed that inputs that rise gradually (S7–10) tend to be more sensitive to inhibition than those that rise quickly. However, these correlations are of limited predictive value, as the same perturbation in the same module can affect early signaling for some inputs but late signaling for others. Moreover, E-L selectivity appeared dependent on perturbation dose. Given the complexity of relating perturbations with input and signal dynamics, we decided to study the origin of the phenomenology observed in the screen using the analytical tools of dynamical systems theory.
Phase space analysis reveals underlying regulatory principles
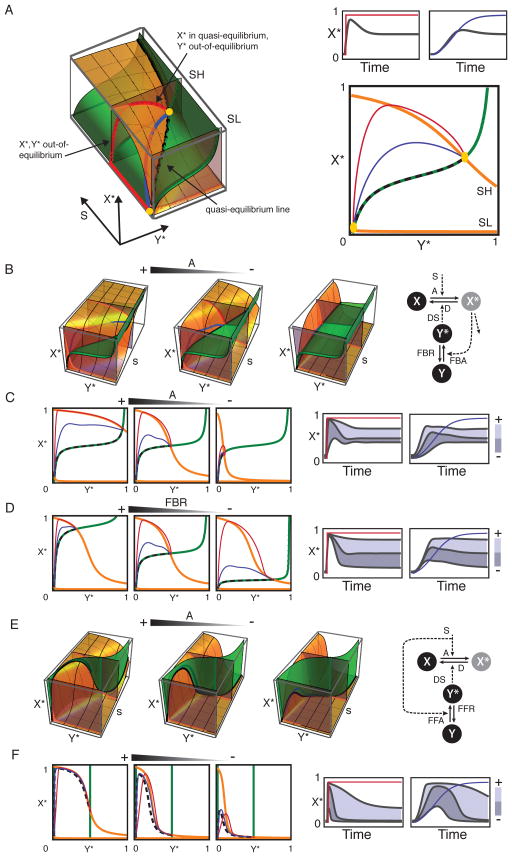
In order to understand the origin of dynamic feature-specific inhibition, we investigated the perturbation effects analytically on each module’s phase space, i.e. the space defined by X* and Y* quasi-equilibrium surfaces (Figures 4 and S4). These surfaces (“q.e. surfaces”) represent the dose response of X* as a function of Y* and a stationary input signal S (“X surface”), and the dose response of Y* as a function of X* and S (“Y surface”)(Figure 4A). The points at which the surfaces intersect correspond to the concentrations of X* and Y* in equilibrium for a given value of S. In the basal state, when S is low, the system is resting at an equilibrium point close to the origin of coordinates. When S increases, the concentrations of X* and Y* adjust until the signal settles at some stationary value (Figure 4A). Gradually changing input signals cause the concentrations to follow trajectories close to the q.e. surfaces (quasi-equilibrium dynamics) following the line defined by the intersection of the surfaces (“q.e. line”) in the extreme of infinitely slow inputs. Fast-changing stimuli drive the system out of equilibrium causing the trajectories to deviate markedly from the q.e. surfaces.
Figure 4. Phase space analysis of signaling modules’ responses.
A) Quasi-equilibrium surfaces for X* (orange) and Y* (green) as functions of stimulus strength s, and 2D projections for low (sL) and high (sH) s levels in feedback-based module M3. The time course of X* in response to a fast (red) and slow gradual (blue) input are indicated. Strict quasi-steady response in black B) Effect of perturbation A in module M3. The arrow indicates whether the perturbation suppresses (−) or enhances (+) the reaction. C) Cross sections of the X* and Y* (orange and green) surfaces for low and high S and the projection of the time-course concentrations of X*-Y* for fast and gradually changing signals (red/blue). Projection of the q.e. line indicated with a dashed black line. Corresponding time courses shown on the right (topmost curve corresponds to higher values of parameter). The perturbation primarily affects steady state levels (transition from left to center panels when the feedback saturates and out-of-equilibrium and quasi-equilibrium dynamics otherwise (transition from center to right panels). D) Effect of perturbation FBR (M3) E) Effect of perturbation A on module M4 and, F) the corresponding two-dimensional projections. Notice how the intersection (black line) of the surfaces defines a peak of activity. Additional details in methods and Figure S3.
Two main principles emerged: 1) perturbations that primarily affect the shape of a q.e. surface tend to affect steady state levels or responses that evolve close to quasi-equilibrium, 2) perturbations that primarily affect the balance of time scales (X*, Y* activation, and S) tend to affect transient out-of-equilibrium parts of the response. These principles reflect the fact that out-of-equilibrium parts of a signal are largely insensitive to the precise shape of the underlying dose response surfaces (they may still be bounded by them) but depend on the balance between the time-scales of the biochemical processes involved. Perturbation of these balances affects how a system approaches steady state (thus affecting out-of-equilibrium and quasi-equilibrium dynamics) but not the steady state levels. To illustrate these principles, we present selected results for modules M3 and M4 and discuss additional cases in the supplement (Figures S3–4).
In the feedback-based modules (M3, M5, M7), the early peak of activity in response to rapidly changing signals is an out-of-equilibrium feature that occurs when the time-scale of Y activation is significantly slower than that of X. Under these conditions, the concentration of X* increases rapidly (out-of-equilibrium) before decaying along the X* surface (in quasi-equilibrium) as more Y gets activated (Figure 4A. Parameters modified to better illustrate the effects being discussed. See Table S2). For input signals that settle at some stationary level of S, Y activation eventually catches up and the concentration of X* settles at the equilibrium point where the X* and Y* curves intersect. Gradually changing signals allow X* and Y* activation to continuously adapt and the system evolves closer to the q.e. line.
In such modules, perturbation A (X* activation) changes both, the shape of the q.e. surface for X* and the kinetics of activation. When in the unperturbed system Y* saturates, perturbation A primarily reduces X* steady state level (Figure 4, B and C, left and center panels). When in the unperturbed system Y* does not saturate, the primary effect are the reduced activation kinetics and therefore the perturbation affects the out-of-equilibrium peak (Fig. 4, B and C, center and right panels) with only minor reduction of steady state levels (especially when Y*’s dose response respect to X* is steep). The transition from saturated to not-saturated feedback (as well as the perturbation strength) underlie the dose-dependent switch from L to E observed in the screen. In both, saturated and unsaturated regimes, the shift in the shape of the surfaces does change the q.e. line and thus affects responses occurring in quasi-equilibrium. In contrast, perturbation FBR (feedback recovery) shifts the Y* surface vertically (Figure 4D), specifically affecting the steady state levels and late signaling; the effect on Y* kinetics is limited because the reaction is relatively slow. Perturbation FBA (feedback activation), also shifts the Y* surface, but the net effect is less specific because the associated increase in the rate of Y* activation tends to equalize X* and Y* kinetics affecting also the out-of-equilibrium peak.
In feed-forward-based modules (e.g. M4), early signaling peaks could arise also under quasi-equilibrium conditions when X and Y have different dose-response curves for S (observe the q.e. line in Figure 4E). In this module perturbation A (activation) primarily changes the shape of the X* surface affecting steady state levels and quasi-equilibrium dynamics. A perturbation dose sufficient to affect early signaling will also completely suppress the late phase of the response, explaining why, in contrast with feedback based modules, perturbation A in feed-forward-based modules (M4 and M6) tended to affect primarily late signaling.
These dynamic response principles (summarized in Table S4) link a perturbation’s feature- and stimulus-specificity. While with simple perturbations, effects on dose-response and kinetics are linked, the particular parameters determine which effect is dominant. Here we have explicitly considered responses to signal input activation, but the same principles apply to the response to signal input termination were there may be specificity based on input decay rates.
Manipulating specific dynamic features of NFκB signaling
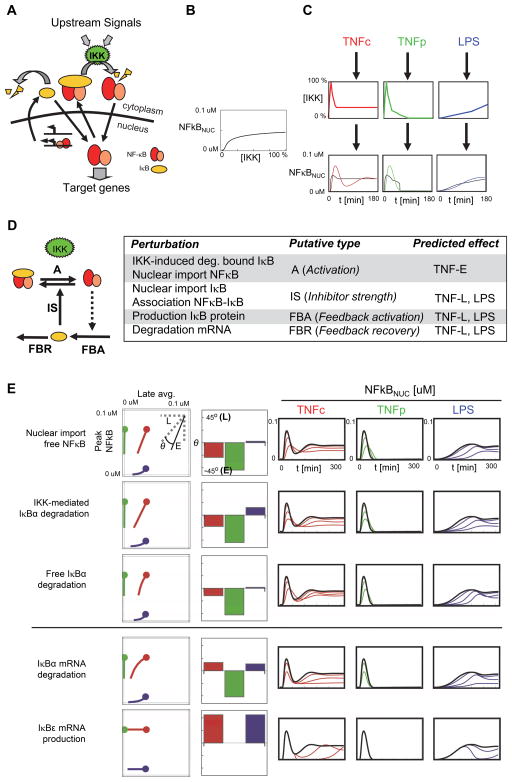
The IKK-IκB-NFκB signaling module functions as a signaling hub for diverse inflammatory, immune and developmental signals (Hoffmann and Baltimore, 2006). Its activity is regulated in a stimulus-specific manner, and stimulus-specific dynamic control of the input kinase IKK was shown to mediate stimulus-specific gene expression programs (Hoffmann et al., 2002; Werner et al., 2005). We examined here how the principles outlined above could be applied to design pharmacological perturbations causing stimulus-specific inhibition of NFκB. We focused on NFκB dynamics typically triggered by Tumor Necrosis Factor (TNF), a pro-inflammatory cytokine, which may mediate chronic (“TNFc”) or pulse (“TNFp”) stimulation, and lipopolysaccharide (LPS), a component of gram-negative bacteria.
In resting cells NFκB is held inactive through its association with inhibitors IκBα, β, and ε. Upon stimulation these proteins are phosphorylated by the kinase IKK triggering their degradation. Free, nuclear NFκB activates the expression of target genes, including IκB-encoding genes, which thereby provide negative feedback (Figure 5A). The IκB-NFκB signaling module is a complex dynamical system, however, by abstracting the control mechanism to its essentials we show below that the above-described principles can be applied profitably.
Figure 5. Modulating NFκB Signaling Dynamics.
A) The IκB-NFκB signaling module. B) Dose response relationship for NFκB vs. IKK C) Three IKK curves representative of three stimulation regimes; TNFc (red), TNFp (green), LPS (blue) function as inputs into the model which computes the corresponding NFκB activity dynamics. The quasi-equilibrium line (black) was obtained by transforming the IKK temporal profiles by the dose response in B. Deviation from the q.e. line for the TNF response indicates out-of-equilibrium dynamics. D) Coarse-grained model of the IκB-NFκB module and predicted effects of perturbations. E) Selected perturbations with specific effects on out-of-equilibrium (top three) or steady state (bottom two). From left to right: feature maps in the E-L space (E: t<60′, L: 120′<t<300′), tangent angle at the unperturbed point (θ>0 indicates L is more suppressed than E and vice versa), and time courses (Green: TNF chronic; Red: TNF pulse; Blue: LPS). Only inhibitory perturbations shown. See Figure S4 for additional perturbations.
We begin by determining whether NFκB activation proceeds out-of- or in quasi-equilibrium using an experimentally validated computational model (Werner et al., 2005) and temporal profiles of IKK inputs determined experimentally for the conditions under consideration. For this we compared the time-dependent concentration of nuclear NFκB with that expected if at each time point the network was in equilibrium with the instant IKK activity level (Figure 5, B and C). Deviations during the early phase of the TNF response indicated that it occurs out-of-equilibrium whereas the response to LPS evolves close to quasi-equilibrium.
Under these conditions our findings suggest it may be possible to selectively attenuate the out-of-equilibrium (early) or steady-state (late) phase of the TNF and LPS response. Selective attenuation of out-of-equilibrium dynamics requires a perturbation that equalizes the activation and feedback time-scales without substantially reshaping the dose-response relationships. Conversely, attenuation of steady sate levels and quasi-equilibrium dynamics requires perturbations that alter the dose-response relationships without substantially affecting the balance of time-scales. We compared the essential control mechanisms of the IκB-NFκB signaling module (Figure 5D, left) with module M3 studied above to infer the effect of perturbations (Figure 5D). We estimated that perturbations classified as A (inhibition of activation), such as inhibition of IKK-mediated IκB degradation or free NFκB nuclear import would primarily affect time-scales and therefore out-of-equilibrium dynamics. These perturbations show E-L switch behavior (Figure 3) but because feedback is not saturated (enough IκB can be produced) we expect them to affect out-of-equilibrium dynamics. In contrast, perturbations classified as IS (inhibitor strength), such as inhibition of IκB import, would unlikely affect the balance of time-scales as the feedback time scale is dominated by slow de-novo protein production. On the other hand, we expected perturbations that enhance the feedback without substantially altering its time scale to cause a reduction in steady state levels and late signaling. Partial inhibition of the feedback recovery (FBR) proved very selective before, suggesting stabilization of IκB mRNA or the protein itself may selectively attenuate the late component of the TNFc response and the LPS response.
We next used the detailed mathematical model to test the predictions (Figure 5E and S4). We found partial inhibition of NFκB nuclear import or IκBα degradation (Figure 5E, top panels) at some doses affected out-of-equilibrium dynamics, attenuating the response to TNFp and the initial peak of the response to TNFc. The response to LPS was delayed but less impacted in terms of sustained amplitude. Unexpectedly, partial inhibition of nuclear export of the NFκB-IκB complex or stabilization of free IκBα produced similar effects. Further analysis revealed that in this network both perturbations effectively act as activation inhibitors: the former causes initial accumulation of the inactive NFκB-IκB complex in the nucleus from which it cannot be directly activated (IKK is cytosolic) whereas the latter generates a basal excess of IκBα that must be degraded before nuclear translocation of NFκB can proceed. Perturbations affecting the time-scale of the feedback (e.g. increase of mRNA production rate) were less selective probably due to the changes they introduced in the IKK-IκB-NFκB dose response relationships. Simulations also confirmed that partial inhibition of IκBα mRNA degradation (protein stabilization affects early signaling as discussed above) attenuates the late phase of the TNFc response and suppresses the response to LPS (Figure 5E, bottom panels), although with some collateral attenuation of the early phase as well. Conversely, destabilization of IκB mRNA impaired post-induction attenuation and significantly extended the response to TNFp. Finally, enhancement of IκBε mRNA production suppresses late TNF-induced signaling in a specific manner. This specificity arises from the delay (~45′) associated with the induction of this gene (Kearns et al., 2006), which also explains why the response to LPS is not affected until late during the signaling event.
The above principles identify conditions necessary but not necessarily sufficient for the existence of perturbations with dynamics, and by extension, stimulus specific effects. Even though the specific effects attained in the IκB-NFκB module are partial (compared to the idealized cases in Figure 4), they demonstrate that perturbations with stimulus-specific effects are indeed feasible within that signaling module.
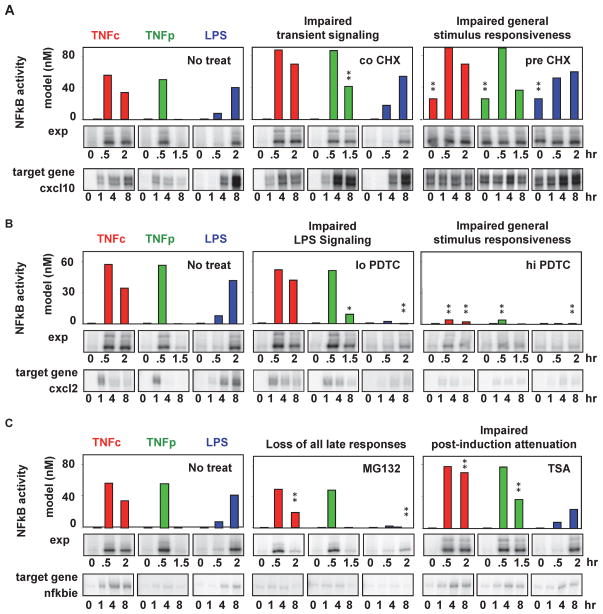
Targeting the NFκB signaling hub to achieve stimulus-specific inhibition
To develop experimentally testable predictions, we simulated the effect of actual pharmacological agents. We focused on agents that target known but ubiquitous biochemical mechanisms (as do some successful therapeutic agents such as aspririn or bortezomib), to test whether they could nevertheless have stimulus-specific effects. Computationally, we simulated the effect of each drug at 11 doses and 3 times of administration and used the feature metric for early and late phases to select treatment conditions from the resulting dataset that had stimulus-specific effects (See Methods). These predictions were tested experimentally in cultures of primary fibroblasts, preparing nuclear extracts and mRNAs at specific time points for subsequent assays of DNA binding activity and target gene expression. We found that co-treatment with the general translation inhibitor cycloheximide (inhibits IκB synthesis) preferentially affected TNFp-responsive signaling resulting in higher target gene expression (Figure 6A, middle panel), whereas pre-treatment with this inhibitor affected NFκB signaling in response to all stimuli (Figure 6A, right panel). Similarly, whereas low doses of the antioxidant pyrrolidine dithiocarbamate (PDTC) (Brennan and O’Neill, 1996), a drug that inhibits NFκB-induced transcription, inhibited NFκB induction and target gene expression by LPS, high doses abrogated signaling in response to all stimuli (Figure 6B). Interestingly, the general proteasome inhibitor MG132 (inhibits IκB degradation) was predicted to specifically inhibit late phase TNFc and LPS-induced NFκB activity but with little effect on early responses characteristic of TNFp stimulations (Figure 6C, middle panel). Consistent with this observation, the expression of the nfkbie gene that is typically induced in the hour-time scale was abrogated by this treatment. In contrast post-induction attenuation of NFκBn - a hallmark of TNF stimulation - was impaired by treatment with the HDAC inhibitor trichostatin A (TSA), a general inhibitor of transcription (and therefore IκB synthesis), whereas LPS-induced NFκB activity was barely affected.
Figure 6. Stimulus-specific pharmacological perturbations of NFκB signaling.
A–C) Simulated and observed effects of pharmacological inhibitors on NFκB activity. Leftmost bar-graph panels show NFκB activity predicted at indicated time points in MEFs in response to TNFc (red), TNFp (green) and LPS (blue) in the absence of pharmacologic inhibitors. Center and right bar graphs show computational predictions in response to the same stimuli under drug treatments. Asterisks indicate effects greater than two fold thought to be experimentally detectable. Upper rows of gel images: electrophoretic mobility shift assays (EMSAs) of NFκB activity. Bottom gel images: RNAse Protection analysis (RPA) revealing the effect on the indicated NFκB target genes (See Table S7).
Discussion
Here we delineate the potential of achieving stimulus-specific inhibition when targeting molecular reactions within pleiotropic signaling hubs. We found that it is theoretically possible to design perturbations that (i) selectively attenuate signaling in response to one stimulus but not another (ii) selectively attenuate undesirable features of dynamic signals, or enhance desirable ones, or (iii) re-modulate output signals to fit a dynamic profile normally associated with a different stimulus.
These opportunities, not all of them possible for every signaling module topology or biological scenario, are governed by two general principles based on time-scale and dose response relationships between upstream signal dynamics and intra-module reaction kinetics (Figure 4, Table S4). In short, a steady state or quasi-equilibrium part of a response may be selectively affected by perturbations that introduce changes in the relevant dose response surfaces. Out-of-equilibrium responses, that are not sensitive to the precise shape of a dose response curve, may be selectively attenuated by perturbations that modify the relative time scales. Dose responses and time-scales cannot in general be modified independently by simple perturbations (combination treatments are required), but as we show in some cases one effect dominates resulting in feature- or stimulus-specificity.
The degree to which specific dynamic features of a signaling profile, or the dynamic responses to specific stimuli, can be selectively inhibited depends on how distinctly they rely on quasi-equilibrium and out-of-equilibrium control. Signals that contain both features may be partially inhibited by both types of perturbation, limiting the specific inhibition achievable by simple perturbations. In practice, this limited the degree to which NFκB signaling could be inhibited in a stimulus-specific manner (Figure 5) and the associated therapeutic dose window (Figure 6). The most selective stimulus-specific effects can be introduced when a signal is heavily dependent on a particular dynamic feature; for example, suppression of out-of equilibrium transients will abrogate the response to stimuli that produce such transients. For a selected group of target genes this specificity at the signal level translated directly to expression patterns (Figure 6B, middle panel). More generally, selective inhibition of early or late phases of a signal may allow for specific control of early and late response genes (Figure 6C), a concept that remains to be studied at genomic scales. While the principles are general, how they apply to specific signaling pathways depends not only on the regulatory topology, but also on the dynamic regime determined by the parameters. As demonstrated with the IκB-NFκB module, analysis of a coarse grained topology in terms of the principles may allow the prediction of perturbations with a desired specificity. Although not studied here, we believe it possible to exploit features such as multi-stability and sustained oscillations to introduce specific effects based on frequency discrimination or through selective alteration of specific stable states. Which dynamic feature to target depends on the downstream effector modules that decode the hub’s dynamic activity and thus determine which dynamic feature is physiologically relevant (Behar and Hoffmann, 2010; Purvis and Lahav, 2013). While we employed simple examples of such decoding circuits in Figure 1 that informed our selection of E and L metrics, future studies (both theoretical and experimental) may uncover diverse topologies and decoding properties that could substantially extend the present work.
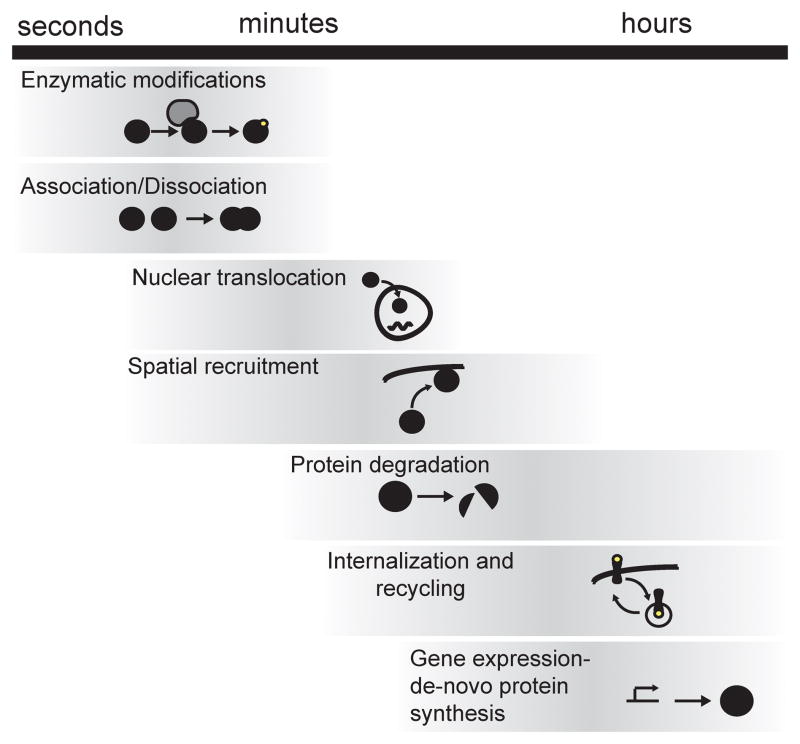
The timescales associated with signaling processes (Figure 7) suggests some are more likely to generate kinetic imbalances that could lead to out-of-equilibrium response dynamics and thus opportunities for achieving specificity based on signaling dynamics. For example, because activation and de-activation mechanisms based on post-translational modifications are typically fast (in the sub-second to second regime), they are more likely to determine dose-response relationships than out-of-equilibrium transients. On the other hand, mechanisms involving protein synthesis and protein degradation are slower (in the sub-hour to hour regime) and are therefore more likely to cause out-of equilibrium dynamic features and thus provide for opportunities for selective drug targeting. The recycling motif (M2), relevant to receptors (Becker et al., 2012) or kinases (Behar and Hoffmann, 2013), can respond with out-of- or quasi-equilibrium signals depending on the specific kinetic rates (Behar and Hoffmann, 2013). In summary, knowing the molecular processes that regulate hub activity can provide clues about signal dynamical features and potential perturbation strategies.
Figure 7. Time scales of cellular processes relevant for signaling.
Order of magnitude timescales associated with intracellular processes that can be combined to produce complex signaling networks. Combinations including processes with different time scales can result in responses with significant out-of-equilibrium components whereas similar time-scales will likely produce quasi-equilibrium dynamics. The time scale difference must be considered in terms relative to the time-scale at which the input signal changes.
Our results warrant a number of other observations. First, the type of pharmacologic interventions discussed here do not require full inhibition of the target. In fact, strong inhibition is undesirable as it suppresses signaling wholesale and tends to degrade the dynamics-selectivity. Thus, drug candidates too weak to be deemed suitable for therapeutic use could become viable for therapeutic applications based on signal-dynamics. This could also allow for lower concentrations, potentially mitigating side effects due to a drug’s polypharmacological footprint (Force et al., 2007; Ma’ayan et al., 2007). Second, perturbations often remain relatively selective for a given dynamic feature or signal input family over a range of doses (often by an order of magnitude or more). This implies that robust effects could be achieved over a wide therapeutic window (notice the pronounced horizontal or vertical segments in Figure 3A). Third, pharmacological intervention does not need to occur concurrently with the stimulus. Thus, particularly for stimuli or conditions involving only short term signaling, the design of perturbations targeting signaling dynamics is largely decoupled from the pharmacodynamic problem. Fourth, what is most relevant for the control of a dynamic signaling feature is the time scale on which a “process” operates and the shape of the overall dose response curves. As processes comprise multiple reactions the result is an expanded list of potential targets. This is exemplified by the role of IκB stability as part of the NFκB “activation” process, where both IκB-degradation and NFκB import reactions emerged as targettable. Taken together, these findings mean that once the corresponding target processes are identified, then there could be a large window of opportunity for finding suitable pharmaceutical approaches for which coarse tuning may suffice. Further, these considerations may suggest a two-step strategy for pharmacological targeting of signaling hubs: first, using a coarse-grained model of regulatory processes to identify opportunities for pharmacological intervention; and second, developing detailed mechanistic reaction model of the key process(es) to be targeted to identify actual molecular drug targets with desired effects.
The approach described here can be used to devise strategies for selective control of signals relevant for particular biological or pathological scenarios even in the absence of a detailed mathematical model. In systems in which temporal control is suspected, the principles outlined here can be used to guide pharmacological design on a trial-and-error basis with signal dynamics as the readout. In this sense, signal dynamics per se (not the signal transducer) may be treated as a pharmacological target.
Methods
Simple computational model
The network in Figure 1 was modeled as (Eq. 1–5).
| (Eq. 1) |
| (Eq. 2) |
| (Eq. 3) |
| (Eq. 4) |
| (Eq. 5) |
Parameters (perturbed and unperturbed) are given in Table S1. Input s was replaced with the functions in eq. 6 and 7 (representing S1 and S2 respectively) with parameters: sl=0, sb=0.0001, sh=1, tr=0.1, td=0, tp1=0.5, j=30, h=0.0085.
| (Eq. 6) |
| (Eq. 7) |
We used the definition of specificity and fidelity in (Komarova et al., 2005) (Eq. 8–11).
| (Eq. 8,9) |
| (Eq. 10,11) |
The quantity TFx|Sy is TFx activity (early or late as defined in the main text) of TFx in response to stimulus Sy.
Virtual screen and phase space analysis
The modules in the virtual screen were modeled with ordinary differential equations using kinetic laws of the form VA, VAI, VD, VDF, and VMA (Eq. 12–17).
| (Eq. 12,13) |
| (Eq. 14–15) |
| (Eq. 16–17) |
In all cases the species were conserved and the total concentration normalized to 1. For the cycle motif, the activation proceeded as in the previous cases but species X* had to undergo deactivation to a refractory species X- which in turn was recycled back to X (Eq. 18).
| (Eq. 18) |
Module equations:
| (Eq. 19) |
| (Eq. 20) |
| (Eq. 21) |
| (Eq. 22) |
| (Eq. 23) |
| (Eq. 24) |
| (Eq. 25) |
The rates for the activation reactions were tuned so they all respond on similar time-scales. Negative regulation was set to operate slower as to generate a wider range of dynamics. The time scale was chosen to be slower than the initial increase rate for “fast” inputs (e.g. S1) but faster than the rate corresponding to gradual inputs (e.g. S8). The Michaelis constants were set to 10% of the total concentration of the corresponding species to represent enzymatic reactions with saturation. The EC50 for the modules were set to roughly correspond to 1 unit of s in order to allow suppression but also enhancement of the responses. Perturbations were simulated by applying multipliers to the kinetic parameters (Table S2). The input curves were generated according to eq. 6 (stepwise) and 7 (sigmoid) with parameters in Table S3:
The global metric (Figure 2A) was calculated as follows: for a given module-perturbation-input signal combination we calculated the AUC (area under the curve) for the X* time course for each perturbation dose. We then generated a dose response curve for AUC (normalized to the unperturbed value) vs. perturbation dose (Figure S1). The relative effect of a perturbation was quantified as the area under the dose-response curves corresponding to different inputs. A smaller number represents higher sensitivity. For Figure 2 the metric was inverted (brighter colors indicate higher sensitivity) and normalized within each row. This dataset was clustered using the function “DendogramPlot” (Mathematica, version 8, Wolfram Inc., Urbana-Champaign, IL) with Euclidean distance and Ward linkage. Selectivity for early or late signaling was quantified by the angle Θ in the E-L space (Figure 3A and S2). We excluded doses that did not substantially change the response (Euclidean distance in the E-L plane < 0.1) and classified the rest as E (Θ≥15°), L (Θ≤15°), or both (−15° <Θ<15°).
NFκB signaling hub
The mass action kinetic model of the NFκB signaling module was taken from an updated version of that in (Werner et al., 2005) See Figure S5 for diagram and Table S5 for reactions and parameters. The model was equilibrated before applying the IKK activity profiles (Table S6). Perturbations were simulated by applying a range of multipliers to groups of related parameters (Table S7).
For modeling the effects of pharmacological inhibitors on the response to LPS stimulation (Figure 5B–D), a simple model to account for TNF feedback was introduced, parameterized by the measured IKK activity profiles in TNF knockout cells (Werner et al., 2005). Specifically, “TNF” is synthesized in an NFκB-dependent manner (0.4 min−1), is added to the IKK scaling factor, and is degraded (0.3 min−1). To simulate pharmacological perturbations, parameters were grouped as described in Table S7 and altered over a wide range (10−0.0625 to 10−2) in three treatment regimens: pre-treatment (during equilibration phase), co-treatment (at start of signaling phase), and post-treatment (at t=60 min).
Simulation and analysis was performed with the package Mathematica 8 (Wolfram Inc., Urbana-Champaign, IL) except for the pharmacological simulations performed with the package MatLab R2007a (The Mathworks, Natick, MA).
Experimental procedures
Primary mouse embryonic fibroblasts (MEFs) were prepared, cultured and stimulated as described (Werner et al., 2005), using either 0.1 μg/ml LPS (Sigma, B5:055), or 1 ng/ml murine TNF (Roche) for the duration of the timecourse (chronic, TNFc) or transiently for 45 minutes (pulse, TNFp). Pharmacological inhibitors (cycloheximide (CHX, Sigma), MG132 (Calbiochem), pyrrolidine dithiocarbamate (PDTC, Sigma), or trichostatin A (TSA, Wako Chemicals) were administered at the concentration indicated 2 hr prior to or coincident with TNF or LPS. Electrophoretic Mobility Shift Assays (EMSA) and RNase Protection Assays (RPA) were performed as described (Werner et al., 2005).
Supplementary Material
Highlights.
Drugs targeting signaling hubs may block specific dynamic features of the signal.
Specific inhibition of dynamic features may introduce pathway-selectivity.
Phase space analysis revealed principles for drug targeting signaling dynamics.
Based on these principles, NFκB dynamics could be manipulated with specificity.
Acknowledgments
We acknowledge helpful discussions with members of the San Diego Center of Systems Biology, critical reading by P. Loriaux (UCSD) and helpful suggestions by an anonymous reviewer. The work presented here was supported by grants from the NIH P50 GM085763, R01 GM 089976, R01 GM072024, R01 CA141722, and a postdoctoral research fellowship from the Cancer Research Institute.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Bardwell L. Mechanisms of MAPK signalling specificity. Biochem Soc Trans. 2006;34:837–841. doi: 10.1042/BST0340837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becker V, Timmer J, Klingmuller U. Receptor dynamics in signaling. Adv Exp Med Biol. 2012;736:313–323. doi: 10.1007/978-1-4419-7210-1_18. [DOI] [PubMed] [Google Scholar]
- Behar A, Hoffmann A. Tunable Signal Processing through a kinase control cycle: the IKK signaling node. Biophys J. 2013;105:231–41. doi: 10.1016/j.bpj.2013.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behar M, Dohlman HG, Elston TC. Kinetic insulation as an effective mechanism for achieving pathway specificity in intracellular signaling networks. Proc Natl Acad Sci U S A. 2007;104:16146–16151. doi: 10.1073/pnas.0703894104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behar M, Hoffmann A. Understanding the temporal codes of intra-cellular signals. Curr Opin Genet Dev. 2010;20:684–693. doi: 10.1016/j.gde.2010.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berger SI, Iyengar R. Role of systems pharmacology in understanding drug adverse events. Wiley Interdiscip Rev Syst Biol Med. 2010;3:129–135. doi: 10.1002/wsbm.114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bitterman PB, Polunovsky VA. Translational control of cell fate: from integration of environmental signals to breaching anticancer defense. Cell Cycle. 2012;11:1097–1107. doi: 10.4161/cc.11.6.19610. [DOI] [PubMed] [Google Scholar]
- Brennan P, O’Neill LA. 2-mercaptoethanol restores the ability of nuclear factor kappa B (NF kappa B) to bind DNA in nuclear extracts from interleukin 1-treated cells incubated with pyrollidine dithiocarbamate (PDTC). Evidence for oxidation of glutathione in the mechanism of inhibition of NF kappa B by PDTC. Biochem J. 1996;320(Pt 3):975–981. doi: 10.1042/bj3200975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chalmers CJ, Gilley R, March HN, Balmanno K, Cook SJ. The duration of ERK1/2 activity determines the activation of c-Fos and Fra-1 and the composition and quantitative transcriptional output of AP-1. Cell Signal. 2007;19:695–704. doi: 10.1016/j.cellsig.2006.09.001. [DOI] [PubMed] [Google Scholar]
- Chavali S, Barrenas F, Kanduri K, Benson M. Network properties of human disease genes with pleiotropic effects. BMC Syst Biol. 2010;4:78. doi: 10.1186/1752-0509-4-78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen P. Protein kinases--the major drug targets of the twenty-first century? Nat Rev Drug Discov. 2002;1:309–315. doi: 10.1038/nrd773. [DOI] [PubMed] [Google Scholar]
- DiDonato JA, Mercurio F, Karin M. NF-kappaB and the link between inflammation and cancer. Immunol Rev. 2012;246:379–400. doi: 10.1111/j.1600-065X.2012.01099.x. [DOI] [PubMed] [Google Scholar]
- Force T, Krause DS, Van Etten RA. Molecular mechanisms of cardiotoxicity of tyrosine kinase inhibition. Nat Rev Cancer. 2007;7:332–344. doi: 10.1038/nrc2106. [DOI] [PubMed] [Google Scholar]
- Frelin C, Imbert V, Griessinger E, Peyron AC, Rochet N, Philip P, Dageville C, Sirvent A, Hummelsberger M, Berard E, et al. Targeting NF-kappaB activation via pharmacologic inhibition of IKK2-induced apoptosis of human acute myeloid leukemia cells. Blood. 2005;105:804–811. doi: 10.1182/blood-2004-04-1463. [DOI] [PubMed] [Google Scholar]
- Gandhi TK, Zhong J, Mathivanan S, Karthick L, Chandrika KN, Mohan SS, Sharma S, Pinkert S, Nagaraju S, Periaswamy B, et al. Analysis of the human protein interactome and comparison with yeast, worm and fly interaction datasets. Nat Genet. 2006;38:285–293. doi: 10.1038/ng1747. [DOI] [PubMed] [Google Scholar]
- Gao C, Chen YG. Dishevelled: The hub of Wnt signaling. Cell Signal. 2010;22:717–727. doi: 10.1016/j.cellsig.2009.11.021. [DOI] [PubMed] [Google Scholar]
- Ghoreschi K, Laurence A, O’Shea JJ. Selectivity and therapeutic inhibition of kinases: to be or not to be? Nat Immunol. 2009;10:356–360. doi: 10.1038/ni.1701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haney S, Bardwell L, Nie Q. Ultrasensitive responses and specificity in cell signaling. BMC Syst Biol. 2010;4:119. doi: 10.1186/1752-0509-4-119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hao N, Zeng Y, Elston TC, Dohlman HG. Control of MAPK specificity by feedback phosphorylation of shared adaptor protein Ste50. J Biol Chem. 2008;283:33798–33802. doi: 10.1074/jbc.C800179200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann A, Baltimore D. Circuitry of nuclear factor kappaB signaling. Immunol Rev. 2006;210:171–186. doi: 10.1111/j.0105-2896.2006.00375.x. [DOI] [PubMed] [Google Scholar]
- Hoffmann A, Levchenko A, Scott ML, Baltimore D. The IkappaB-NF-kappaB signaling module: temporal control and selective gene activation. Science. 2002;298:1241–1245. doi: 10.1126/science.1071914. [DOI] [PubMed] [Google Scholar]
- Karin M. The IkappaB kinase - a bridge between inflammation and cancer. Cell Res. 2008;18:334–342. doi: 10.1038/cr.2008.30. [DOI] [PubMed] [Google Scholar]
- Kearns JD, Basak S, Werner SL, Huang CS, Hoffmann A. IkappaBepsilon provides negative feedback to control NF-kappaB oscillations, signaling dynamics, and inflammatory gene expression. J Cell Biol. 2006;173:659–664. doi: 10.1083/jcb.200510155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klussmann E, Scott J, Aandahl EM. Protein-protein interactions as new drug targets. Berlin: Springer; 2008. [Google Scholar]
- Komarova NL, Zou X, Nie Q, Bardwell L. A theoretical framework for specificity in cell signaling. Mol Syst Biol. 2005;1 doi: 10.1038/msb4100031. 2005 0023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kubota H, Noguchi R, Toyoshima Y, Ozaki Y, Uda S, Watanabe K, Ogawa W, Kuroda S. Temporal coding of insulin action through multiplexing of the AKT pathway. Mol Cell. 2012;46:820–832. doi: 10.1016/j.molcel.2012.04.018. [DOI] [PubMed] [Google Scholar]
- Lin WW, Karin M. A cytokine-mediated link between innate immunity, inflammation, and cancer. J Clin Invest. 2007;117:1175–1183. doi: 10.1172/JCI31537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma’ayan A, Jenkins SL, Goldfarb J, Iyengar R. Network analysis of FDA approved drugs and their targets. Mt Sinai J Med. 2007;74:27–32. doi: 10.1002/msj.20002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marshall CJ. Specificity of receptor tyrosine kinase signaling: transient versus sustained extracellular signal-regulated kinase activation. Cell. 1995;80:179–185. doi: 10.1016/0092-8674(95)90401-8. [DOI] [PubMed] [Google Scholar]
- Oda K, Kitano H. A comprehensive map of the toll-like receptor signaling network. Mol Syst Biol. 2006;2 doi: 10.1038/msb4100057. 2006 0015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park SH, Zarrinpar A, Lim WA. Rewiring MAP kinase pathways using alternative scaffold assembly mechanisms. Science. 2003;299:1061–1064. doi: 10.1126/science.1076979. [DOI] [PubMed] [Google Scholar]
- Purvis JE, Karhohs KW, Mock C, Batchelor E, Loewer A, Lahav G. p53 dynamics control cell fate. Science. 2012;336:1440–1444. doi: 10.1126/science.1218351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purvis JE, Lahav G. Encoding and Decoding Cellular Information through Signaling Dynamics. Cell. 2013;152:945–956. doi: 10.1016/j.cell.2013.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roring M, Brummer T. Aberrant B-Raf signaling in human cancer -- 10 years from bench to bedside. Crit Rev Oncog. 2012;17:97–121. doi: 10.1615/critrevoncog.v17.i1.70. [DOI] [PubMed] [Google Scholar]
- Schneider A, Klingmuller U, Schilling M. Short-term information processing, long-term responses: Insights by mathematical modeling of signal transduction. Bioessays. 2012;34:542–550. doi: 10.1002/bies.201100172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schrofelbauer B, Polley S, Behar M, Ghosh G, Hoffmann A. NEMO ensures signaling specificity of the pleiotropic IKKbeta by directing its kinase activity toward IkappaBalpha. Mol Cell. 2012;47:111–121. doi: 10.1016/j.molcel.2012.04.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seki E, Brenner DA, Karin M. A liver full of JNK: signaling in regulation of cell function and disease pathogenesis, and clinical approaches. Gastroenterology. 2012;143:307–320. doi: 10.1053/j.gastro.2012.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sung MH, Bagain L, Chen Z, Karpova T, Yang X, Silvin C, Voss TC, McNally JG, Van Waes C, Hager GL. Dynamic effect of bortezomib on nuclear factor-kappaB activity and gene expression in tumor cells. Mol Pharmacol. 2008;74:1215–1222. doi: 10.1124/mol.108.049114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sung MH, Simon R. In silico simulation of inhibitor drug effects on nuclear factor-kappaB pathway dynamics. Mol Pharmacol. 2004;66:70–75. doi: 10.1124/mol.66.1.70. [DOI] [PubMed] [Google Scholar]
- Weinberg RA. The biology of cancer. New York: Garland Science; 2007. [Google Scholar]
- Werner SL, Barken D, Hoffmann A. Stimulus specificity of gene expression programs determined by temporal control of IKK activity. Science. 2005;309:1857–1861. doi: 10.1126/science.1113319. [DOI] [PubMed] [Google Scholar]
- Zalatan JG, Coyle SM, Rajan S, Sidhu SS, Lim WA. Conformational control of the Ste5 scaffold protein insulates against MAP kinase misactivation. Science. 2012;337:1218–1222. doi: 10.1126/science.1220683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X, Crespo A, Fernandez A. Turning promiscuous kinase inhibitors into safer drugs. Trends Biotechnol. 2008;26:295–301. doi: 10.1016/j.tibtech.2008.02.008. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.