Multiple Approaches Converge on the Structure of the Integrin αIIb/β3 Transmembrane Heterodimer

Abstract

Integrins link the cytoskeleton to the extracellular matrix and regulate key signaling events that coordinate cellular processes such as secretion, migration, and proliferation. A single integrin molecule can exist in a resting state that does not bind extracellular ligands or in an active state that can engage ligands and form large signaling complexes. Activation signals are transduced between the cytosolic region and the extracellular region by a binary on/off switch in the integrin’s transmembrane (TM) domain; the integrin’s α and β subunits each have a single TM helix that forms an α/β heterodimer in the resting state, and the TM heterodimer separates to transduce an activation signal across the membrane. In this article, two methods used to generate models of the TM heterodimer, both converging on the same structure, are described. The first model was generated by a Monte Carlo algorithm that selected conformations based on their agreement with published experimental mutagenesis results. The second model was generated by threading the integrin’s sequence onto TM helix dimers parsed from the Protein Data Bank and by selecting conformations based on their agreement with published experimental cysteine crosslinking results. The two models have similar structures; however, they differ markedly from some previously published models. To distinguish conformations that reflect the native integrin, we compared the Monte Carlo model, the threaded model, and four published models with experimental mutagenesis and cysteine crosslinking results. The models presented here had high correlation coefficients when compared with experimental findings, and they are in excellent agreement, both in terms of accuracy and in terms of precision, with a recent NMR structure. These results demonstrate that multiple approaches converged on the same structure of the resting integrin’s TM heterodimer, and this conformation likely reflects the integrin’s native structure.

Introduction

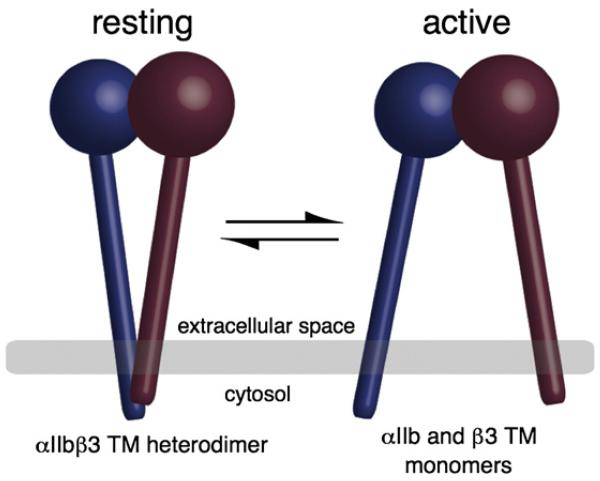
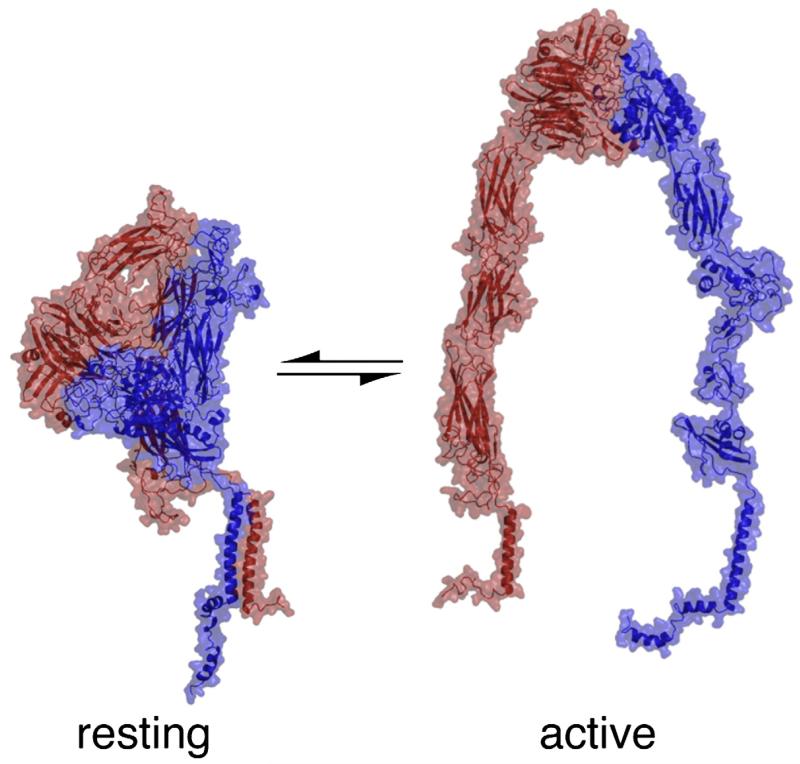
Integrins, the principal cell surface receptors responsible for linking the cytoskeleton to the extracellular matrix, are transmembrane (TM) heterodimers composed of noncovalently associated α and β subunits. Integrin molecules exist in an equilibrium between resting conformations that do not bind extracellular ligands and active conformations that both engage ligands and nucleate large intracellular complexes, which regulate a broad array of signaling pathways.^1,2 Agonist-induced intracellular signals shift integrins from resting conformation to active conformation by exposing extracellular ligand-binding sites. To do so, they must transmit signals across the membrane via the integrin’s TM domain: an integrin is constrained in a resting conformation by the heteromeric association of its α and β subunits’ TM domains. Moreover, disruption of this association is sufficient to induce integrin activation (Fig. 1.^3,4 Thus, the α/β TM heterodimer is a critical structure in regulating integrin function.

Fig. 1.

Integrins exist in equilibrium between resting conformations and active conformations. In the resting conformation, the integrin’s TM helices form an α/β heterodimer and cytosolic domains are held in proximity. In the active conformation, the TM and cytosolic domains separate.

One of the most widely studied examples of regulated integrin function is the platelet integrin αIIbβ3. In its active conformation, αIIbβ3 binds fibrinogen, von Willebrand factor, or fibronectin and mediates platelet aggregation when these αIIbβ3-bound ligands crosslink adjacent platelets.⁵ For prevention of the deleterious formation of intravascular platelet aggregates, αIIbβ3 is maintained in a resting conformation on circulating platelets. However, following vascular injury, αIIbβ3 is rapidly activated, enabling it to mediate the production of a hemostatic platelet plug. The formation and disruption of the αIIbβ3 TM domain heterodimer are key events in shifting αIIbβ3 between resting conformations and active conformations. Thus, there has been considerable effort to produce three-dimensional structural models of the TM domain heterodimer.^6-10 However, each published model is substantially different, and none has accounted well for the consequences of introducing mutations into the αIIb and β3 TM domains. Because of the absence of a satisfactory model for the αIIb/β3 TM heterodimer, we explored two new and fundamentally different strategies to predict its structure.

In the first strategy, we utilized a Monte Carlo algorithm whose scoring function favors conformations that are consistent with published mutagenesis results.¹¹ In the second strategy, we used a threading approach in which the sequences of the αIIb and β3 TM domains were threaded onto a set of TM dimers parsed from high-resolution structures in the Protein Data Bank (PDB). Threaded structures were then scored according to their calculated energy and their agreement with experimental cysteine crosslinking results. Each model was correlated with both experimental mutagenesis and cysteine crosslinking results to assess its agreement with published experimental findings. Additionally, four models selected from the literature were used as reference structures to gauge the quality of the correlations presented here. A more thorough review of prior structural analyses is presented in Discussion.

Finally, while this article was under review, a comprehensive cysteine-scanning analysis was published and an NMR structure depicting an αIIb/β3 TM heterodimer was released, providing a stringent test for our conclusions and for the robustness of the methods.^12,13 Ultimately, the models presented here converged on the same conformation as the NMR structure, and this conformation had the same precision and accuracy as the NMR structure.

Results

Monte-Carlo-based structure prediction of the αIIb/β3 TM domain heterodimer

In the Monte-Carlo-based algorithm that we employed, two straight helices consisting of αIIb amino acids Ile966-Trp988 and β3 amino acids Ile693-Trp715 were docked by randomly altering the six orthogonal parameters that orient two cylinders in space.¹¹ The algorithm’s scoring function was designed to favor conformations that were consistent with published mutagenesis experiments by including a selective advantage for disruptive mutations having higher energies than the wild type and for neutral mutations that are isoenergetic (Fig. 2). Inclusion of mutagenesis information compensates for approximations made during energy calculations and the limited conformational space accessible to the search algorithm.¹⁴ This strategy previously enabled us to accurately predict the structures of the TM homodimers for glycophorin A and BNIP3.^11,15,16

Fig. 2.

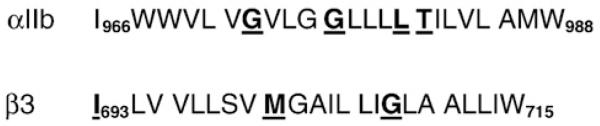
Sequences of the αIIb and β3 TM domains. Amino acids are highlighted if one or more of their mutants activate the integrin.

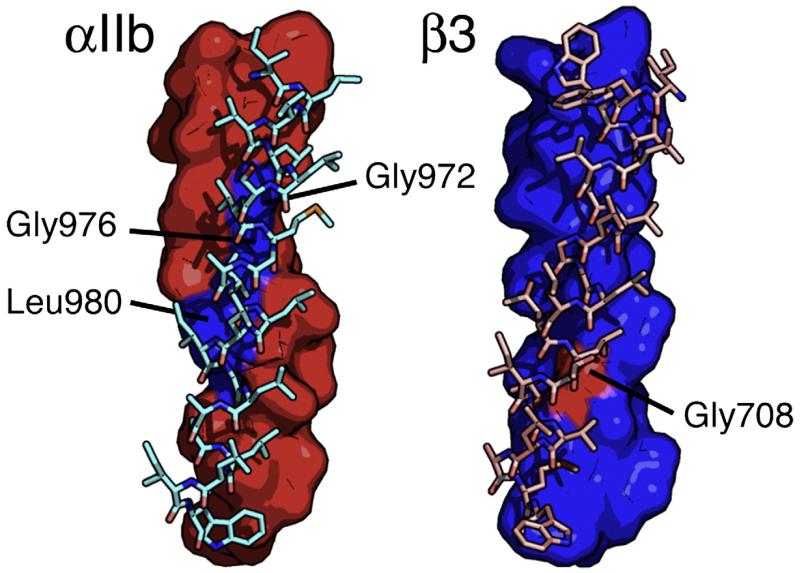
When applied to αIIb and β3, the Monte-Carlo-based algorithm converged on a structure with an angle of 18° between the two helical axes and a right-handed orientation (Fig. 3). This type of interaction occurs frequently in membrane proteins,¹⁷ and its conformation is similar to >100 different TM dimer interfaces reported in the PDB (see Materials and Methods). The heterodimer interface for αIIb consisted of residues Trp968, Val969, Gly972, Gly976, Leu980, Leu983, and Met987, and the β3 interface consisted of residues Ile693, Val696, Leu697, Val700, Met701, Ile704, Gly708, Leu712, and Trp715. This structure is consistent with a published cysteine crosslinking analysis that examined 120 possible pairwise interactions in the αIIb/β3 TM region, even though cysteine crosslinking data were not considered in the modeling procedure (Figs. 4 and 5).¹⁸ The structure is also consistent with mutational analyses of the αIIb and β3 TM domains, with the exception of mutations involving the αIIb residue Thr981 that activate αIIb/β3 expressed in tissue culture cells but reside on the opposite side of the αIIb helix from other activating mutations.^2,3,10,19

Fig. 3.

The Monte Carlo model of the αIIb/β3 TM heterodimer. Left: The αIIb helix is depicted as a surface representation (red), and the β3 helix is shown as a stick representation (cyan). Mutagenesis indicates that Gly972, Gly976, and Leu980 (blue) reside at the heterodimer interface. Right: The β3 helix is depicted as a surface representation (blue). Mutagenesis indicates that Gly708 (red) resides at the heterodimer interface.

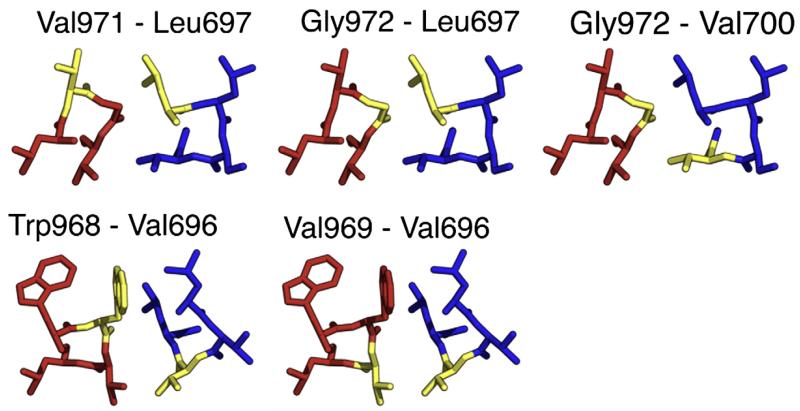
Fig. 4.

Slices through the Monte Carlo model, with amino acids highlighted (yellow), that have a strong propensity to form a disulfide bond when the pair is mutated to cysteine. Leu697 lies between its crosslinking partners Val971 and Gly972. Gly972 lies between its crosslinking partners Leu697 and Val700. Finally, Val696 lies between its crosslinking partners Trp968 and Val969.

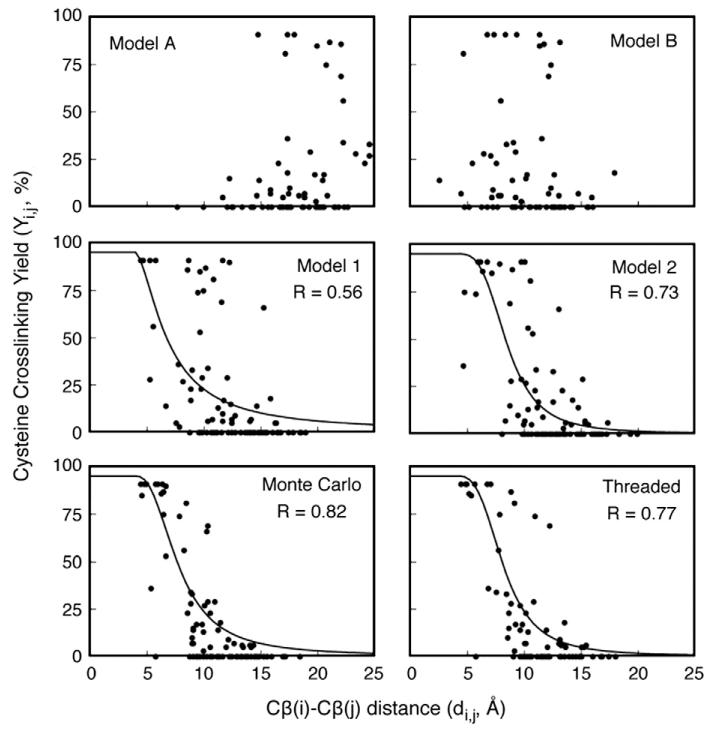
Fig. 5.

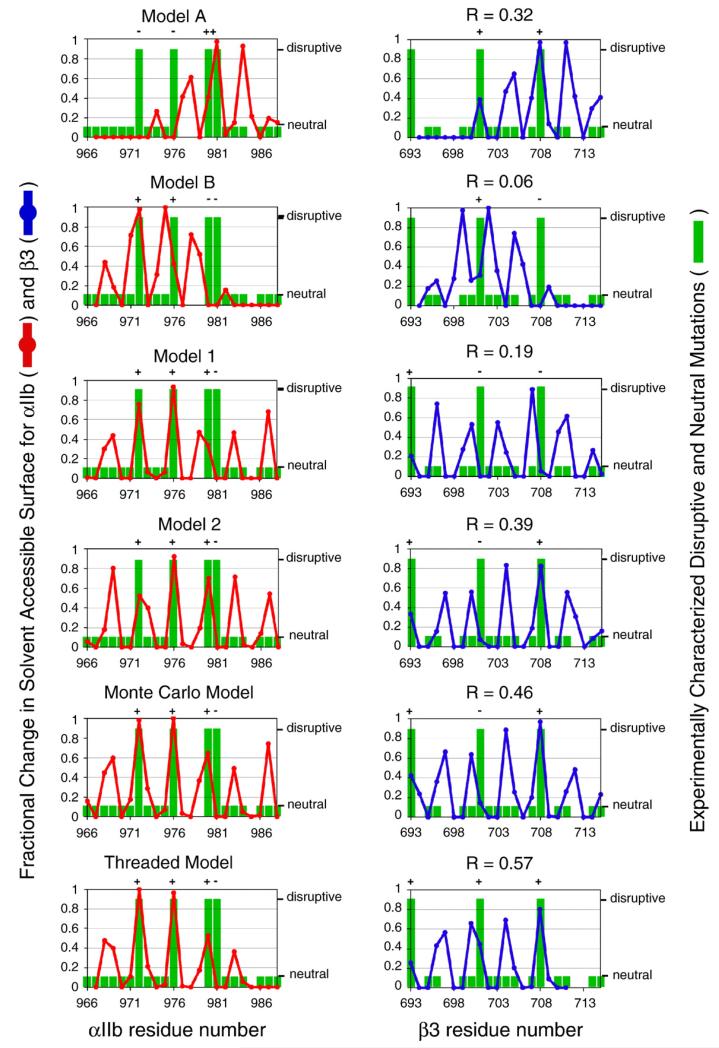
When single-cysteine point mutations are introduced into both the αIIb and β3 TM helices, a disulfide bond can crosslink the integrin subunits. Cysteine crosslinking yield correlates with the distance between two cysteines, and these distances can be measured in a given model. Cβ distances for cysteine mutant pairs were plotted against the experimentally observed cysteine crosslinking yield and fitted to Eq. (2). The correlation coefficient of each fit is reported as R. Literature models A, B, 1, and 2 were used as reference structures to assess the quality of the models presented here.^9,10

In addition to a TM heterodimer, αIIb/β3 function is thought to be constrained by a “clasp” involving membrane-proximal portions of the αIIb and β3 cytoplasmic domains, a notable feature of which is a salt bridge between Arg995 in αIIb and Asp723 in β3.²⁰ Several previous NMR models of the αIIb and β3 cytoplasmic domains predict that Arg995 and Asp723 reside in helices, implying that the αIIb and β3 TM helices might extend into the cytosol, at least through Arg995 and Asp723.^21-25 When our Monte-Carlo-derived model is propagated into the cytosol with straight helices, the distance between Arg995 and Asp723 Cβ atoms is 12 Å, too far to form a salt bridge; however, slight perturbations from a uniform helical structure might allow for an Arg995-Asp723 interaction.

A threaded model of the αIIb/β3 TM domain heterodimer

To verify the Monte Carlo structure, we used threading as a different approach to derive a model for the αIIb/β3 TM heterodimer. In contrast with Monte Carlo-based methods, threading makes use of experimentally determined structures, sampling real protein conformations rather than theoretical geometries.^26,27 Thus, threaded models can account for kinks, bends, coiling, and other deviations from an ideal helical structure with physically accessible conformations.

We threaded the αIIb and β3 TM sequences through 214 parallel TM helix dimers found in high-resolution crystal structures. The sequences were threaded in multiple different frames to generate >50,000 structures. Each conformation was optimized by SCWRL3.0,²⁸ followed by 2000 conjugant gradient steps in NAMD.²⁹ Next, the dimerization energy of each structure—defined as the energy of the optimized model minus the energy of the model’s helices separated by 100 Å and reoptimized—was calculated. The top 1% lowest-energy structures were analyzed to determine whether they were consistent with cysteine crosslinking results, complementing the use of mutagenesis results in the Monte Carlo strategy. Specifically, the distance between the Cβ atoms of five αIIb/β3 residue pairs having a high propensity to form a disulfide bond when the pair is mutated to cysteine was measured.¹⁸ (The remaining 115 experimentally evaluated cysteine mutant pairs were saved for structure validation; see the text below.) The structure with the most consistent average Cβ distance, consisting of αIIb Trp967-Trp988 threaded on chain A residues 392–414 and β3 Ile693-Ala711 threaded on chain A residues 466–484, came from PDB code 1IWG of the crystal structure for the bacterial multidrug efflux transporter AcrB.³⁰

As was the case for the Monte Carlo model, the threaded model has a right-handed crossing. However, due to the nonlinearity of natural helical axes, the interhelix crossing angles in the threaded model range from 48° in the heart of the GXXXG interface to 3.5° near its C-terminus. The steepest crossing angle (48°) occurs between αIIb residues Gly972-Gly975 and β3 residues Ser699-Gly702, and this conformation is characteristic of a canonical GXXXG interaction, which is a dimerization motif found in TM helices.^17,31-33 While the β3 helix is relatively straight, the αIIb helix is kinked by 35° between residues Gly975 and Gly976, extending the αIIb/β3 interface beyond the GXXXG motif and permitting interactions near the membrane–cytosol boundary. Additionally, when the TM helices were propagated into the cytosol, the structure allowed for an interaction characteristic of the putative Arg995-Asp723 salt bridge. The αIIb interface consisted of residues Trp968, Val969, Gly972, Gly976, Leu980, Leu983, and Met987, and the β3 interface consisted of residues Ile693, Val696, Leu697, Val700, Met701, Ile704, and Gly708, essentially identical with the Monte Carlo model and consistent with both additional cysteine crosslinking pairs that were not used to score the model and mutational analyses (Figs. 5 and 6). Finally, the C^α RMSD between the Monte Carlo model and the threaded model is 1.3 Å, indicating similar structures.

Fig. 6.

Point mutations can activate the integrin (large green bars) or can have no effect (small green bars; missing bars indicate positions for which mutagenesis information is not available). Activating mutations are likely to reside at the αIIb/β3 heterodimer interface. The interface of each model was defined using a calculation based on each amino acid’s solvent-accessible surface (red and blue lines; see Eq. (2)). A model is consistent with experimental mutagenesis results if each activating mutation (large green bar) occurs at the model’s interface (large change in solvent-accessible surface). Experimental mutagenesis results were correlated with the fractional change in solvent-accessible surface using linear regression, and each correlation coefficient is reported as R. Literature models A, B, 1, and 2 were used as reference structures to assess the quality of the models presented here.^9,10 See Results for further details.

Comparison of the Monte Carlo model and the threaded model to previously reported models of the αIIb/β3 TM heterodimer

Four three-dimensional models have been reported for the αIIb/β3 TM heterodimer at atomic-level resolution. Two of the models were generated by Monte Carlo methods that did not take into account experimental data (literature models A and B).¹⁰ The other two models were generated from molecular dynamics simulations of integrin homologs that converged on two conformations, with representative structures reported for αIIb/β₃ (literature models 1 and 2).⁹ These four models have substantially different conformations (Table 1), and we used them as reference structures to assess the quality of the models presented here. Additional models of the αIIb/β3 TM heterodimer have been reported but were not considered here because they did not include atomic coordinates³⁴ or because they contain a number of D-amino acids.^6-8 A more thorough review of prior structural analyses is presented in Discussion.

Table 1.

Structural similarity for αIIb/β3 TM models (Cα RMSD in angstroms)

Model	A	B	1	2	MC	T
Model A		6.6	7.5	6.4	6.9	6.7
Model B	6.6		7.8	7.5	7.0	7.1
Model 1	7.5	7.8		2.3	2.4	2.4
Model 2	6.4	7.5	2.3		1.1	1.6
Monte Carlo	6.9	7.0	2.4	1.1		1.3
Threading	6.7	7.1	2.4	1.6	1.3

Literature models A, B, 1, and 2 were used as reference structures to assess the quality of the models presented here.^9,10 The Monte Carlo model, the threaded model, and literature model 2 are structurally similar. Bold denotes the one letter reference code and draws attention to low RMSD models.

First, we considered how well each model correlates with the consequences of introducing disulfide crosslinks between αIIb and β3 TM domains. Luo et al. expressed full-length αIIb/β3 in 293T cells with single-cysteine replacements in both αIIb and β3 TM helices and measured the efficiency of disulfide bond formation, based on the premise that positions forming disulfide crosslinks should be closer in space than positions that do not crosslink the integrin.¹⁸ Thus, the distance between the Cβ atoms of two cysteine residues in a model was correlated with the experimentally determined crosslinking efficiency for the pair (Fig. 5). For a quantitative comparison, it would be ideal to obtain the rates of the crosslinking reactions under carefully controlled conditions. Also, in comparing the experimental data to computational models, it would be ideal to consider not only interatomic distances but also the angular relationship between Cα and Cβ bond vectors and the local dynamics of the structure.³⁵ However, even in the absence of this information, a modest correlation between the extent of disulfide formation and the distance between interacting residues can be observed.³⁶ Therefore, the data were analyzed with Eq. (1), which relates the percent yield (Y_i,j) of the disulfide between the ith residue and the jth residue in a given double mutant to the distance between their Cβ atoms d_i,j in a given model:

$${\gamma }_{i,j}={\gamma }_{\max }\frac{1}{1+{\left(\frac{d_{i,j}-4.0}{d_{50}-4.0}\right)}^n}$$ (1)

where Y_max is the maximal yield observed for the protein of interest (generally slightly less than 100% due to competing side reactions), (d_i,j–4.0) reflects the distance between Cβ atoms with their van der Waals radii subtracted, and (d₅₀–4.0) reflects the distance at which crosslinking is approximately 50%. The value of n reflects the fact that the crosslinking generally has a high order dependence on distance. The data for the Monte Carlo model show a good correlation (0.74); furthermore, the parameters d₅₀ =7.8 Å and n= 2.44 make good physical sense when compared to literature data.³⁵ A similar good correlation was observed for the threaded model (R=0.78; d₅₀=8.2 Å; n=3.1) and for literature model 2 (R=0.73; d₅₀=8.5 Å; n=3.4). A lesser correlation was observed for literature model 1 (R=0.56; d₅₀=6.9 Å; n=1.6), and a poor correlation was observed for literature models A and B.

Next, the models were correlated with the results of mutating either the αIIb or the β3 TM domain, focusing on mutations that induce constitutive αIIb/β3 activation and thus are likely present in the heterodimer interface. A model’s heterodimer interface can be defined by calculating the fractional solvent-accessible surface of each residue f_ASA,i as defined in Eq. (2):

$$f_{\mathrm{ASA},i}=1-\left(\frac{{\text{model}}_{\mathrm{ASA},i}}{{\text{monomer}}_{\mathrm{ASA},i}}\right)$$ (2)

where model_ASA,i is the solvent-accessible surface area of the ith residue in a model of the heterodimer, and monomer_ASA,i is the solvent accessibility of the same residue when the helices are isolated.³⁷ The fractional change in solvent accessibility was correlated with experimental mutagenesis results, as shown in Fig. 6. For this analysis, residues were assigned a value of 1 if at least one of its mutants activates the integrin (large green bar; missing bars indicate points for which data are not available). These positions should reside at the heterodimer interface and have fractional changes in solvent accessibility that approach 1 (peaks in red for αIIb; peaks in blue for β3). Mutations with no significant effect on activation were assigned a value of 0 (small green bar). These positions should cluster away from the heterodimer interface and have fractional changes in solvent accessibility that approach 0 (red/blue minima). Disruptive mutations that occur at a model’s heterodimer interface are marked with “+” and indicate a positive correlation. We also computed a correlation coefficient R for each model(Fig. 6), although we note that a perfectly correlating model would not have an R = 1 because the mutagenesis results were treated in a binary manner. An example of a poorly correlating structure is literature model B, which displays a poor overall correlation (R=0.06) between f_ASA, and the experimental mutagenesis results. The models with the best correlation against experimentation are the Monte Carlo model and the threaded model (R=0.46 and R=0.57, respectively). Overall, the Monte Carlo model and the threaded model correlated with experimental mutagenesis results, while other models correlated to a lesser extent or not at all.

Discussion

Although it has not yet been possible to determine the complete integrin structure at high resolution, partial structural information has been derived from mutagenesis,^2,3,10,19,20 crosslinking,^18,38-41 fluorescence resonance energy transfer experiments,^4,42 electron microscopy,^41,43-45 crystallographic and NMR analyses of integrin fragments,^21-25,46-51 and molecular modeling (Fig. 7).^6-10 Notably, the extracellular portions of the integrins αvβ3 and αIIb/β3 have been crystallized in conformations that are believed to represent their resting and active states.^46,47,49 Additionally, NMR has been used to obtain structures of peptides corresponding to the individual αIIb and β3 TM domains,^50,51 individual cytosolic tails,^21,25 and complexes between the αIIb and β3 cytosolic tails.^22,24 However, the experimental determination of structures for a TM heterodimer has proven to be challenging. Here, we describe two fundamentally different modeling approaches that converged on the same structure for the αIIb/β3 TM heterodimer. This conformation differs from previously published models and favorably compares with experimental data.

Fig. 7.

Models of the full-length resting and active αIIb/β3 integrins. The models were constructed from structures 1txv,⁴⁹ 2rmz,⁵¹ 2k1a,⁵⁰ and 1s4w²¹ and several models kindly provided by Dr. Beau Mitchell.⁵²

Review of published integrin TM heterodimer models

Gottschalk et al.⁷ performed the first structural analysis of the integrin TM heterodimer using a grid/molecular dynamics protocol pioneered by Axel Brunger^53,54 αIIb/β3 was modeled in parallel with homologous integrins in order to identify an evolutionarily conserved structure. Twelve different conformations were identified, and a right-handed structure with a small crossing angle was judged to be in best qualitative agreement with the then-available experimental data. Gottschalk^6,8 has also described slightly different models in two subsequent publications. However, each of Gottschalk’s models contains a number of d-amino acids, possibly because of unfavorable contacts in the starting coordinates, so the resultant models contain a number of inverted stereocenters.

On the basis of reconstructed electron cryomicroscopy images for low-affinity αIIbβ3, Adair and Yeager proposed that the TM domains of resting αIIbβ3 form a coiled coil and modeled it as either a left-handed or a right-handed heterodimer by placing the Arg995-Asp723 salt bridge at the interface.³⁴ They noted that the right-handed coiled coil positioned more conserved amino acids at the heterodimer interface; however, these models were not considered in this analysis.

Substantially different structures were proposed by Partridge et al.¹⁰ Four hundred conformations were generated by Monte Carlo, and representative structures were selected from two heavily populated clusters that passed geometric filters (literature models A and B). One of the conformations predicted the effect of subsequent point mutations (model A).

Finally, Lin et al. performed a grid search of conformational space, followed by molecular dynamics for each grid point, using the sequences of each human integrin homolog in order to identify an evolutionarily conserved structure.⁹ This method is similar to the original work of Gottschalk et al.;⁷ however, proper chirality was maintained. Two conformations (literature models 1 and 2) were identified, and model 2 was predicted to reflect the resting αIIb/β3 TM heterodimer.

Previously, we published a model of the integrin TM heterodimer using a Monte Carlo strategy that included a selective advantage for conformations that were consistent with experimental mutagenesis results, similar to the Monte Carlo method described here.² In our original publication, we were able to identify the same interface reported here, but were unable to distinguish models with “shallow” interhelix crossing angles (−18°) from those with “glycophorin-like” crossing angles (−40°). We have since reparameterized the scoring function,¹¹ and the revised protocol consistently identifies structures with a crossing angle of around −18°. Interestingly, the Monte Carlo algorithm frequently identifies left-handed conformations when mutagenesis data are not used to score the model,¹⁰ similar to the other Monte Carlo implementation described in this article, suggesting that both strategies encounter similar energy landscapes.² Finally, the present article describes an additional threading method used to generate a model that is consistent with experimental cysteine crosslinking results. The resulting model is essentially identical with the Monte Carlo model, except that it introduces a slight kink in the αIIb subunit that allows for a larger crossing angle near the GXXXG interface, similar to a canonical glycophorin-like interaction.

Analysis of different models

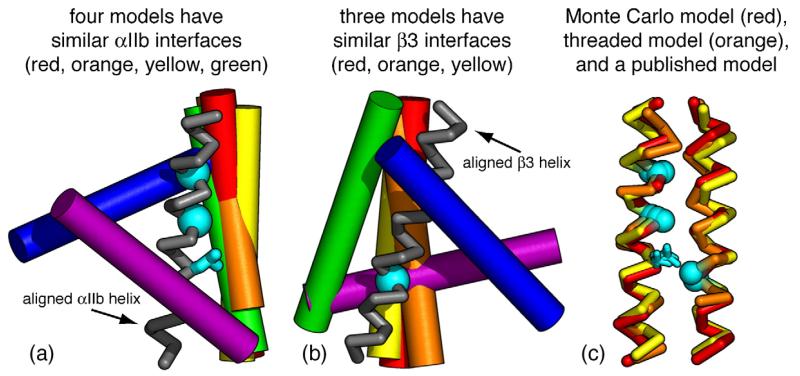
An accurate model successfully predicts experimental results, and each published model of the αIlb/β3 TM heterodimer is buttressed by one or more empirical findings; however, each model has a substantially different structure. To quantitatively assess the accuracy with which a model predicts experimental results, we performed objective measurements on each model and correlated these measurements with published experimental findings. First, fractional changes in solvent accessibility were correlated with published experimental mutagenesis results; the Monte Carlo model and the threaded model reported here had the highest correlation coefficients. Additionally, the distance between different αIIb and β3 residues was correlated with published cysteine crosslinking results; again the Monte Carlo model and the threaded model had the highest correlation coefficients. Among the other models, literature model 2 had the strongest correlation with experimental results, and this model was structurally similar to the Monte Carlo model and the threaded model, with Cα RMSDs of 1.1 and 1.6 Å, respectively. The structural characteristics that cause literature model 2 to correlate slightly less well than the threaded model relate to a small difference in rotation and interhelical distance for the αIIb and β3 helices, particularly evident near residue 701 (Figs. 6 and 8).⁹

Fig. 8.

Different backbone overlays for models of the αIIb/β3 TM heterodimer. (a) The αIIb helices of each model were aligned, and a single αIIb helix is displayed as a gray ribbon. Models have similar αIIb interfaces if their β3 helices overlap (cylinders). (b) The β3 helices of each model were aligned, and a single β3 helix is displayed as a gray ribbon. Models have similar β3 interfaces if their αIIb helices overlap (cylinders). (c) Alignment of the Monte Carlo model, the threaded model, and a previously published model (model 2). These models have similar structures. The αIIb residues Gly972, Gly976, and Leu980, and the β3 residue Gly708 are highlighted in cyan. Mutagenesis indicates that these residues reside at the αIIb/β3 heterodimer interface. The models are color-coded as follows: Monte Carlo model, red; threaded model, orange; model A, purple; model B, blue; model 1, green; model 2, yellow.

Comparison with a recently published NMR structure and other recent results

While this article was under review, two new structures of the αIIb/β3 TM heterodimer were published; in response to reviewers’ comments, we compared the modeling results with these newly published models.^12,13 First, an NMR ensemble of a construct encompassing αIIb residues 958–998 and β3 residues 685–727 was published very recently.¹³ There is an excellent qualitative agreement between the interfaces defined by the Monte Carlo model and the threaded model and the interface described in the NMR publication. Specifically, the αIIb interface contains Gly972 and Gly976 in the NMR structure, and the β3 interface contains Gly708, similar to the interfaces observed in the Monte Carlo model and the threaded model. Also Thr981 does not occur in the interface of the NMR structure, a finding that is consistent with both the Monte Carlo model and the threaded model. The Cα RMSDs for the NMR structure versus the models considered in this article are presented in Table 2. The Monte Carlo model and the threaded model have Cα RMSDs of 1.2 and 1.3 Å with the average NMR model, respectively, demonstrating that they accurately predict the interaction. By comparison, the various models within the NMR structural ensemble have C^α RMSDs ranging from 0.3 to 1.6 Å over the same region considered here. Thus, the Monte Carlo model and the threaded model display precision and accuracy that are comparable to those of the NMR structure.

Table 2.

Structural comparison of αIIb/β3 TM models (C^α RMSD in angstroms)

Model	A	B	1	2	MC	T	R	NMR
NMR	7.3	7.2	2.5	1.5	1.2	1.3	1.7
Rosetta	8.0	6.8	2.8	2.3	1.9	1.4		1.7

The structural similarity of each model to the Rosetta model “R”⁵⁵ and the average structure from the NMR ensemble 2K9J “NMR”⁵⁶ are reported as Cα atom RMSD (in Å). Models are the same as in Table 1. Bold denotes the one letter reference code and draws attention to low RMSD models.

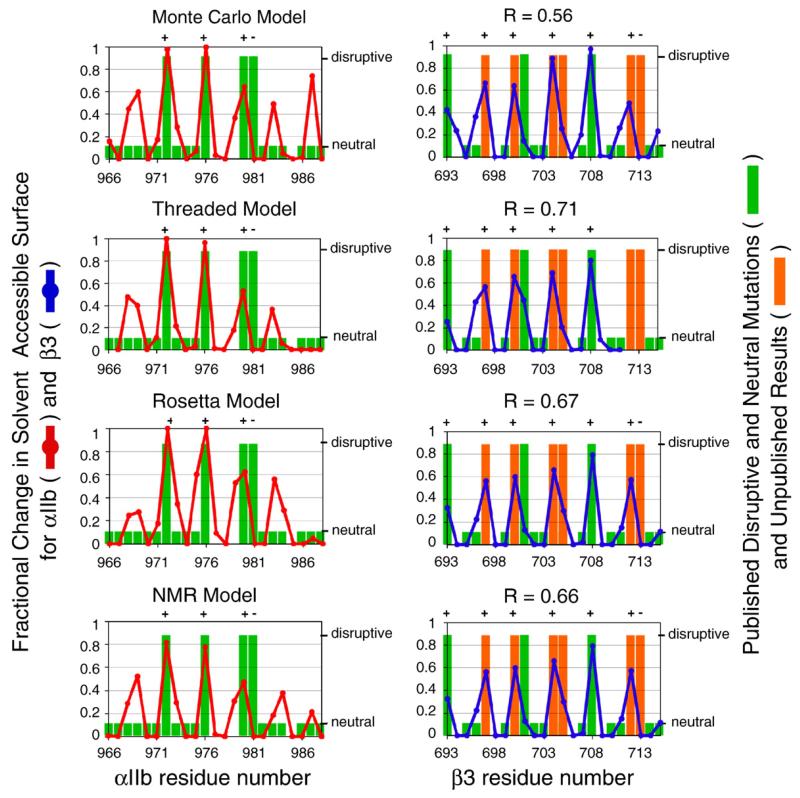
Moreover, a very recent cysteine-scanning analysis encompassing the entire αIIb and β3 TM region correlated extremely well with the Monte Carlo model and the threaded model (Fig. S1). The correlations, now with a more extensive set of disulfide crosslinking data over a wider range of sequence, are similar to those in Fig. 5, again confirming the conclusions of this work. A new model of the αIIb/β3 interaction was also developed using the Rosetta algorithm, with the cysteine crosslinking efficiencies used as modeling restraints.¹² This Rosetta model was in excellent agreement with the threaded model and the Monte Carlo model (Table 2).

Finally, our laboratory has recently characterized the interacting interface of β3 and found a number of TM mutations activating αIIb/β3 that have not been described in the literature (H. Zhu, D. G. Metcalf, W. F. Degrado & J. S. Bennett, unpublished results, 2009). Notably, Ile704 resides at the αIIb/β3 TM interface in a number of models, including the Monte Carlo model and the threaded model, and Ile704Leu had the largest effect on the integrin activation of all the mutants we have considered. (This contrasts with a previous report that assayed transiently transfected Ile704Leu.)¹⁹ Ile704Leu and other unpublished disruptive mutations were considered in additional correlations shown in Fig. 9, which also includes correlations for the Rosetta and NMR models. By contrast, the other models discussed above are in poorer agreement (the correlation coefficients were as follows: model A, 0.30; model B, 0.01; model 1, 0.00; model 2, 0.43; data not shown).

Fig. 9.

Correlations for the Monte Carlo model, the threaded model, the Rosetta model,¹² and the average NMR structure from PDB code 2K9J¹³ with mutagenesis results, including recent unpublished findings. This figure is analogous to Fig. 6. Point mutations can activate the integrin (large green/orange bars; orange bars denote unpublished results) or can have no effect (small green bars; missing bars indicate positions for which mutagenesis information is not available). Activating mutations are likely to reside at the αIIb/β3 heterodimer interface. The interface of each model was defined using a calculation based on each amino acid’s solvent-accessible surface (red and blue lines; see Eq. (2)). A model is consistent with experimental mutagenesis results if each activating mutation (large green/orange bar) occurs at the model’s interface (large change in solvent-accessible surface). Experimental mutagenesis results were correlated with the fractional change in solvent-accessible surface using linear regression, and each correlation coefficient is reported as R.

Conclusion

We generated two models of the αIIb/β3 TM domain heterodimer using fundamentally different methods: a Monte Carlo algorithm that selected conformations based on their agreement with published mutagenesis results, and a threading method that selected conformations based on their agreement with cysteine crosslinking results. The two methods converged on a similar structure and, when compared to previously published models, the Monte Carlo model and the threaded model were most consistent with reported experimental findings, suggesting that they are most likely to reflect the native structure of the αIIb/β3 TM heterodimer.

Materials and Methods

Monte Carlo modeling algorithm

We first modeled the αIIb/β3 TM domain heterodimer using a Monte-Carlo-based structure prediction strategy.¹¹ In the Monte Carlo protocol, two straight helices (φ=−65°; ψ=−40°; ω=180°) consisting of αIIb amino acids Ile966-Trp988 and β3 amino acids Ile693-Trp715 were docked by randomly altering six parameters as follows: at the start of each docking step, the αIIb and β3 backbone atoms were superimposed on top of each other. Then, the helices were rotated between 0° and 360° about their helical axes, specifying the αIIb and β3 interfaces following subsequent translations. Next, the helices were translated between −15 and 15 Å along their axes, defining their point of closest approach following a subsequent rotation. Third, one helix was rotated relative to the other between −90° and 90° to define the interhelix crossing angle. Lastly, the helices were separated between 5 and 9 Å, orthogonal to the interhelix rotation, defining the interhelix diameter. Monte Carlo was implemented during each docking step by changing one or more parameters from the most recent accepted step to a new random value.

After each docking step, side-chain conformations were optimized by dead-end elimination and/or Monte Carlo, as previously described,¹¹ and the dimerization energy was calculated. We define dimerization energy as the potential energy of two helices in a docked conformation minus the energy of the two helices separated by 100 Å. Potential energies were calculated in vacuo with the AMBER united-atom force field for van der Waals interactions.⁵⁵ We softened the potential function to mitigate artifacts from rigid-body docking: favorable interactions were calculated using a 12-6 Lennard–Jones potential with the van der Waals radii scaled to 95%, and repulsive interactions were calculated with a linear ramp from 0 to 10 kcal/mol.⁵⁶ The side-chain optimization and energy calculation steps were then repeated for an array of point mutations in order to compare the conformation with published experimental results. The move was accepted or rejected based on a modified Metropolis criterion that considers the dimerization energies of the wild type and the mutants. Specifically, the energy function was:

$${\text{score}}_{\text{conformation}}=E_{\text{dimerization}}+{\text{penalty}}_{\text{disruptive}}+{\text{penalty}}_{\text{neutral}}$$ (3)

where E_dimerization is the energy of the dimer minus the energy of the monomeric state; penalty_disruptive is a restraint that creates a selective advantage for conformations that are consistent with experimentally characterized disruptive mutations; and penalty_neutral is a restraint that creates a selective advantage for conformations that are consistent with experimentally characterized neutral mutations:

$${\text{penalty}}_{\text{disruptive}}=\frac{{\alpha }_{\text{disruptive}}}{n}\sum _{i=1}^n\ln \left(\frac{1}{1+{\mathrm{e}}^{-\beta \Delta E_i}}\right)$$ (4)

$${\text{penalty}}_{\text{neutral}}=\frac{{\alpha }_{\text{neutral}}}{n}\sum _{i=1}^n{\mathrm{e}}^{\beta \mid \Delta E_i\mid }$$ (5)

where ΔE_i is the computed difference in dimerization energy between mutant i and the wild-type sequence for a given conformation, and n is the total number of mutants considered by the penalty. The α coefficient scales the magnitude of the restraint, and it was set to −60.1 for the disruptive penalty and to 1.02E–2 for the neutral penalty. The β coefficient adjusts the sensitivity of the restraint, and it was set to 0.521 for disruptive penalty and to 9.63 for neutral penalty.

The composite energy function provides selective advantages for conformations in which (1) disruptive mutations have energies higher than that of the wild type and (2) neutral mutations are isoenergetic with the wild type. This procedure ensures that the algorithm converges on conformations that are consistent with experimental mutagenesis results. The αIIb mutants Val969Asn, Leu970Asn, Leu974Asn, Gly975Asn, and Leu983Ala, and the β3 mutants Ser699Asn, Val700Asn, Gly702Asn, Ile704Asn, and Leu705Asn were scored as neutral mutations; the αIIb mutants Gly972Asn, Gly972Ala, Gly972Leu, and Gly976Leu, and the β3 mutants Met701Asn and Gly708Asn were scored as disruptive mutations.^2,3

Ten initial Monte Carlo cycles consisted of 50,000 docking steps, with an exponential temperature decay from 10,000 to 10 K. Regardless of whether a docking step was accepted or rejected, its parameters and score were recorded to restrict conformational space in subsequent Monte Carlo cycles. Following the first 10 cycles, conformational space was restricted to ±2 SD from the mean values for conformations scoring within 10 kcal of the best structure. The Monte Carlo cycles were repeated in the restricted conformational space, and the best-scoring structure was chosen as the final model, which is representative of both the most frequently identified conformation and the best-scoring conformation.

Comparing the Monte Carlo interface with interfaces found in TM crystal structures

In sampling every accessible dimer interface, our Monte Carlo method considers interfaces that are similar to those in published structures and theoretical interfaces that may not occur in nature. The structural similarity between our Monte Carlo model and our threaded model confirms that the Monte Carlo interface can occur in nature. Additionally, the Monte Carlo interface was compared with interfaces observed in the Orientations of Proteins in Membranes (OPM) database.⁵⁷ Specifically, Cα RMSDs were calculated between interfaces consisting of 10 residues from both the αIIb and the β3 helices in the Monte Carlo model and interfaces found in high-resolution crystal structures from the OPM database. Among the parallel helix dimers found in the OPM database, 28% (113 of 400) had Cα RMSDs less than 1.5 Å with the Monte Carlo model over at least 10 residues from both helices, demonstrating that the Monte Carlo interface frequently occurs in nature.

Threading known structures with integrin sequence

Threading is the modeling of an unknown structure based on the experimentally determined structures of other proteins.^26,27 While it is usually applied to problems in which the protein of unknown structure has a sequence that is highly similar to that of a protein of known structure, we thought it could be useful for the prediction of membrane helix pairs due to the limited number of packing motifs found between membrane helices.¹⁷ The αIIb amino acids Ile966-Trp988 and the β3 amino acids Ile693-Trp715 were threaded through 214 parallel TM helix dimers parsed from PDB codes 1c3w, 1e12, 1ehk, 1eul, 1fx8, 1h2s, 1iwg, 1j4n, 1jb0, 1k4c, 1kb9, 1kf6, 1kpl, 1kqf, 1l7v, 1l9h, 1m3x, 1m56, 1msl, 1nek, 1ocr, 1okc, 1pp9, 1pv6, 1pw4, 1q16, 1q90, 1qla, 1rc2, 1rh5, 1u7g, 1xfh, and 1yew, and the Monte Carlo model was threaded as an internal control. Sequences were threaded in all possible combinations such that at least 15 αIIb amino acids and 15 β3 amino acids overlapped at the same depth in the membrane. If the integrin sequence was longer than the template helix, only the portion of the sequence for which a three-dimensional template was available was evaluated. When the template was longer than the integrin sequence, the additional template amino acids were mutated to alanine. The side-chain rotamers of each threaded structure were then optimized with SCWRL3.0,²⁸ and each model was energy minimized in NAMD using the CHARMM force field.^29,58 NAMD minimization consisted of 2000 conjugant gradient steps with a R=10 dielectric constant. This search produced >50,000 models.

Dimerization energies were calculated using the energy function described for the Monte Carlo protocol (see the text above), and the 500 lowest-energy models were filtered based on whether they were consistent with the cysteine crosslinking results of Luo et al.¹⁸ Disulfide bonds crosslink the αIIb/β3 amino acid pairs Gly972-Leu697, Gly972-Val700, Val969-Val696, Val971-Leu697, and Trp968-Val696 when the pair is mutated to cysteine. The distance between the Cβ atoms of each pair was calculated and averaged to determine whether a model was consistent with the observed cysteine crosslinks. Gly972 was mutated to alanine to add its Cβ atom, and any Cβ–Cβ distance closer than 4 Å was set to 4 Å because this distance approaches the maximum yield for cysteine crosslinking. A “best-threaded” structure that had the shortest average distance for the five robust crosslinks was selected.

The best-threaded structure came from PDB code 1IWG of the crystal structure for the bacterial multidrug efflux transporter AcrB³⁰ in which the αIIb TM amino acids Trp967-Trp988 were threaded onto PDB code 1IWG chain A residues 392–413, and the β3 TM amino acids Ile693-Ala711 were threaded onto PDB code 1IWG chain A residues 466–484. The helices were analyzed by HELANAL to characterize deviations from ideal structure and to calculate interhelix crossing angles.⁵⁹

Correlation with cysteine crosslinking experiments

The Monte Carlo model, the threaded model, and four published models were analyzed to determine whether they were consistent with the cysteine crosslinking experiments of Luo et al.¹⁸ For each cysteine mutant pair, the disulfide bond formation efficiency was calculated by sampling its published color density in Adobe Photoshop CS. Next, the distance between the Cβ atoms of each pair was calculated for a given model. Glycine was mutated to alanine to add its Cβ atom. A plot of the Cβ distance versus cysteine crosslinking efficiency was analyzed according to Eq. (1) using a nonlinear least-squares fitting routine implemented in KaleidaGraph (Fig. 5).

Correlation with mutagenesis experiments

The Monte Carlo model, the threaded model, and four published models were analyzed to determine whether they were consistent with published mutagenesis results. TM mutations that activate the integrin cause the αIIb/β3 TM heterodimer to separate, and these positions are likely to reside at the heterodimer interface.^2,3,10,19 The amino acids at a model’s interface can be defined by calculating their fractional changes in solvent accessibility upon docking to form a heterodimer. First, the solvent accessibility of each amino acid was calculated using DSSP.⁶⁰Then the solvent accessibility was recalculated for the separated helices. The fractional change in solvent accessibility f_ASA,i was calculated with Eq. (2) (see Results) and correlated with experimental mutagenesis results using linear regression. For this analysis, a residue was assigned a value of 1 if at least one of its mutants activates the integrin. These positions should reside at the heterodimer interface and have fractional changes in solvent accessibility that approach 1. Other positions that have been probed by mutagenesis were valued at 0. These positions should cluster away from the heterodimer interface and have fractional changes in solvent accessibility that approach 0. Mutations to hydrophilic amino acids were disregarded because they can affect oligomerization and orientation in a membrane, and mutations to threonine were disregarded because threonine can perturb the secondary structure of a helix.^61,62

Assessment of the putative Arg995-Asp723 salt bridge

Reciprocal mutagenesis suggests that an interaction between αIIb Arg995 and β3 Asp723 stabilizes the integrin’s resting state.²⁰ The αIIb and β3 helices in the Monte Carlo model and the threaded model were extended to Arg995 and Asp723 using ideal backbone geometries (φ=−65°; ψ=−40°; ω=180°), and the feasibility of a salt bridge was assessed by manual manipulation of the Arg995 and Asp723 χ angles. Arg995 and Asp723 were proximal in both Monte Carlo and threaded models, but only the threaded model allowed for the formation of a Arg995-Asp723 salt bridge.

Abbreviations used

TM

transmembrane

PDB

Protein Data Bank

OPM

Orientations of Proteins in Membranes