Chiral Colloidal Molecules And Observation of The Propeller Effect

Abstract

Chiral molecules play an important role in biological and chemical processes, but physical effects due to their symmetry-breaking are generally weak. Several physical chiral separation schemes which could potentially be useful, including the propeller effect, have therefore not yet been demonstrated at the molecular scale. However, it has been proposed that complex nonspherical colloidal particles could act as “colloidal molecules” in mesoscopic model systems to permit the visualization of molecular phenomena that are otherwise difficult to observe. Unfortunately, it is difficult to synthesize such colloids because surface minimization generally favors the growth of symmetric particles. Here we demonstrate the production of large numbers of complex colloids with glancing angle physical vapor deposition. We use chiral colloids to demonstrate the Baranova and Zel’dovich (Baranova N. B., Zel’dovich B. Y.Chem. Phys. Lett. 1978, 57, 435) propeller effect: the separation of a racemic mixture by application of a rotating field that couples to the dipole moment of the enantiomers and screw propels them in opposite directions. The handedness of the colloidal suspensions is monitored with circular differential light scattering. An exact solution for the colloid’s propulsion is derived, and comparisons between the colloidal system and the corresponding effect at the molecular scale are made.

Introduction

The interaction potential of spherical colloids can be tuned to mimic the potentials that drive certain atomic and ionic processes. This allows for direct visualization of phase transitions and solid state phenomena difficult to observe at the atomic level, such as crystallization, melting, and dislocation dynamics.² In analogy to “colloidal atoms”³ the term “colloidal molecules” has been suggested⁴ to describe small nonspherical clusters of particles that represent molecules and their interactions at the mesoscale. In addition to being of interest as model systems, the potential applications of these shape-anisotropic particles include functional materials, such as colloidal crystals with novel optical properties⁵ and self-assembly.⁶

Of particular interest in this context are the colloidal counterparts to chiral molecules. Available synthetic approaches for colloids, however, generally yield particles that are either spherical or highly symmetric.^5,7 Assembly of spherical colloid building blocks is generally nonspecific, yielding a range of aggregate sizes and shapes. Only a few methods have been published that can produce large numbers of colloids with uniform, programmable shape, and in enantiopure samples.⁸

Among the approaches for chiral separation that are suitable for study in the colloidal regime are active and passive separation techniques that rely on the hydrodynamic interaction between the particles and the solvent, e.g. in shear flow or using active propulsion mechanisms. The feasibility of using shear flow for enantiomer separation,⁹ which in theory should be possible but has so far not been realized on the molecular scale, has been demonstrated using ∼16 μm-long, right-handed helically shaped Leptospira biflexa flaB bacteria.¹⁰ It has also recently been reported^8b that flow through a chiral microfluidic-channel can be used to separate racemic mixtures of ∼6-μm-sized (chiral) particles produced with photolithography. It is not yet clear whether either effect can be observed at the molecular scale.

In 1978 Baranova and Zel’dovich¹ predicted the “propeller effect” in which a racemic mixture of chiral molecules is separated into left and right fractions when subjected to a radio frequency electric field of rotating polarization. The applied electric field couples to the electric dipole moment of the molecule and causes the molecules to rotate. The sense of rotation is given by the circularity of the electric field. Opposite enantiomers will ‘screw’ in opposite directions and thus separate along the direction about which the electric field rotates. Baranova and Zel’dovich estimated the propeller effect for molecules by assuming a rotating electric field of 0.3 MV/m at 100 MHz and deduced that this should give rise to a 7% enantiomeric excess per centimeter of sample vessel after ∼27 h for molecules with a permanent electric dipole moment of 4 D. The propeller effect has thus far not been demonstrated experimentally.

Herein, we demonstrate the propeller effect with a colloidal model system by separating a racemic mixture of magnetic dipolar chiral colloids. We first describe a refinement of our previously published fabrication process^8c to obtain ∼10¹⁰ chiral dipolar colloids. We verify the handedness of the colloidal solutions with differential circular scattering experiments and then describe the experimental observation of the separation of a racemic mixture via the propeller effect. An exact analytical result that describes the motion of dipolar propeller-shaped colloids as a function of the externally applied torque is given, and we discuss the significance of this study for chiral molecules.

Results and Discussion

Parallel Growth of Chiral Colloids

A number of strategies to produce colloidal molecules have been developed, including geometrical confinement (e.g., by microwells or emulsion droplets), cluster formation through the application of external fields or the inclusion of magnetic patches, controlled surface nucleation or phase separation approaches, and use of molecular scaffolds for selectively forming bonds between particles.^5,7 Most of these approaches tend to yield mixtures of different clusters with high symmetry, due to the fact that colloids, unlike atoms, generally lack directional interactions. Recently, colloids with up to seven chemically functionalized patches that bind selectively to complementarily functionalized particles have been realized.¹¹ Since their production process is based on first assembling clusters of small particles using the emulsion droplet technique, the resulting patches still display the high symmetry characteristic for syntheses employing geometric confinement.

Beyond its original application to clusters of spheres, the term “colloidal molecule” has been applied to monolithic colloids in the form of rods, cubes, and more complicated geometries.^5b,12 To this day however, producing chiral colloidal molecules remains a challenge. Relatively large magnetic dumbbell colloids that self-assemble into helical chains as a mesoscopic counterpart to chiral polymers have been produced,^8a but to our knowledge single chiral micrometer-sized colloidal particles have not been reported as a model for chiral compounds.

In this work we grow billions of colloids with defined chirality, and in-built dipole functionality, via glancing angle deposition (GLAD). GLAD is a physical vapor deposition (PVD) technique that can grow close to micrometer-sized particles with a variety of shapes and allows for the inclusion of a number of different materials, and thus different functionalities, in a one-step process.¹³

This technique has been used before by our group and others to produce magnetically actuated microhelices.^8c,14 In the past however, the magnetic layer was added by first releasing the particles from the wafer, redepositing them on a flat surface and subsequently coating them with a thin layer of cobalt by thermal evaporation. In our current setup we can include a magnetic section during growth, which significantly increases the yield and uniformity and thus leads to reproducible samples of high monodispersity.

We first coat a wafer with a monolayer of silica seed particles. The material that is used to grow the particles is then deposited onto the substrate by (electron beam) physical vapor deposition at grazing incidence with α ≈ 85° (see Figure 1a). The growth of helices is accomplished by azimuthal rotation of the wafer during the deposition process. The chirality and pitch of the particles can be easily varied by adjusting the rotation direction and speed at a given vapor flux. A ferromagnetic material is incorporated by including a nickel section, which is relatively stable in aqueous solution, into the growth of the colloid. Chemical functionality is obtained by growing the colloid from oxides that permit silane coupling chemistry. The number of helices that are produced in one batch in this manner is of the order of 10¹⁰ on a 2-in.-wafer. Sonication of a wafer piece may release the particles from the wafer (into solution). SEM images of the wafer and of released right- and left-handed helices can be seen in Figure 1b–e.

Figure 1.

(a) Schematic of the GLAD technique and (b) SEM images of a wafer containing helices representative of those used in this work, as well as (c) left- and (d) right-handed chiral magnetic particles and (e) the energy-selective backscattered image (lower right) highlights the magnetic Ni inclusion. Scale bar in (b) is 2 μm; (c) and (d) are 0.5 μm; and (e) is 1 μm.

Circular Differential Light Scattering

In order to characterize the handedness of the colloidal solutions, we resort to scattering experiments, as the colloids do not contain a chromophore or color center. The differential scattering of circularly polarized light was first demonstrated experimentally in 1982 by Bustamante et al.¹⁵ who measured the polarization-sensitive scattering of suspensions of helical octopus sperm heads. They showed that the chirality of scatterers clearly manifests itself in circular differential scattering spectra.^15,16 Its measure is the circular differential scattering intensity (CDSI), defined as:

1

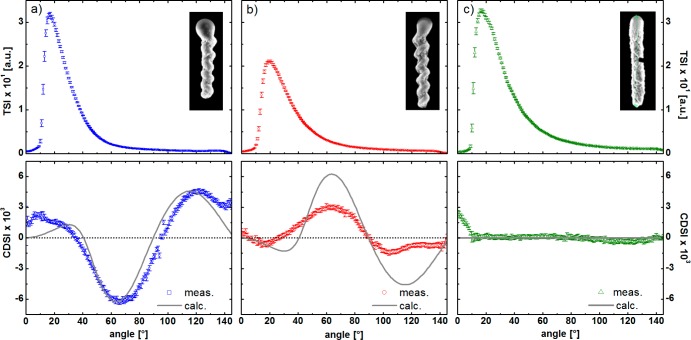
Here I_L,R are the detected scattered intensities when left- and right-circularly polarized light are, respectively, incident upon the sample. TSI is the total scattered intensity. Both CDSI and TSI vary as functions of the scattering angle. Because the circular differential scattering intensity is a chiral observable¹⁷ it can serve as a diagnostic to ensure that colloidal solutions obtained from helices with opposite handedness grown on different wafers are enantiomers. Indeed, since the octopus sperm used in the previous study is only available in one helicity and geometry, CDSI has previously not been validated for pairs of colloidal enantiomers.¹⁸

TiO₂ screws of both helicities were grown on 300 nm SiO₂ beads with a helical pitch of ∼250 nm and with 4 to 5 turns. As an achiral control we also grew TiO₂ rods of the same height but produced with fast azimuthal rotation. The geometrical parameters of the helices were verified by scanning electron microscopy (SEM) images of the samples (Figure 2, details in Table SI1 in the Supporting Information [SI]). The results from the total scattered intensity and the circular differential scattered intensity measurements of the helical colloids are shown in Figure 2. The TSIs decrease monotonically with increasing scattering angles for angles greater than the peak position in all three samples. The differences in the absolute values are mainly due to slight differences in the concentrations. As expected, the total scattering intensity does not differentiate between opposite helicities. In contrast the CDSI signals of the two enantiomers are approximately equal in shape and opposite in sign. The CDSI signal for the achiral rods vanishes for all scattering angles, as expected.

Figure 2.

Total scattering intensity (first row) and the differential scattering signal of circular polarized light of (a) left- and (b) right-handed helices, as well as (c) achiral rod-shaped colloids of the same size; with corresponding SEM images. The dots correspond to the experimental data, whereas the solid lines show the calculation results. Each solution had a concentration of approximatly 0.5 pM.

The solid lines represent theoretical calculations of the scattering intensity and are based on the algorithm proposed by Bustamante et al.^17a which is described in the SI. The calculations are in qualitative agreement with the experimental results for all three samples. Discrepancies between theory and experiment for small angles can be traced back to the fact that, due to experimental limitations at low angle scattering (LAS), the detector observes part of the incident beam,¹⁹ but overall, the CDSI signals are sensitive to the geometry and thus serve as a diagnostic for the chirality of the solutions.^17,20

Chiral Separation via the Propeller Effect

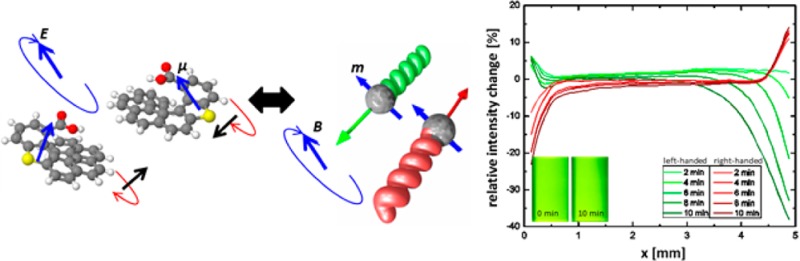
In what follows, racemic colloidal suspensions of magnetic chiral helical colloids are prepared and used for the chiral separation experiments. In our colloidal analogue of the Baranova and Zel’dovich’s proposal,¹ the electric dipolar molecule driven by a rotating electric field is replaced with a magnetic dipolar colloid driven by a magnetic field. The helices are magnetized orthogonally to the helices’ long axes by placing the wafer into a strong electromagnet before the helices are released from the wafer into solution. Figure 3a schematically shows how application of a homogeneous, rotating magnetic field couples to the magnetic moment of the helices and causes them to rotate in solution. The helices translate as they rotate due to shape-induced rotation–translation coupling. Because the drag on the side of the helix is larger, the helices will align to minimize drag, and be propelled along the normal axis of the plane defined by the rotating field. The direction of translation for a helix of a given chirality is the opposite of its enantiomer. For a racemic mixture this results in chiral separation.

Figure 3.

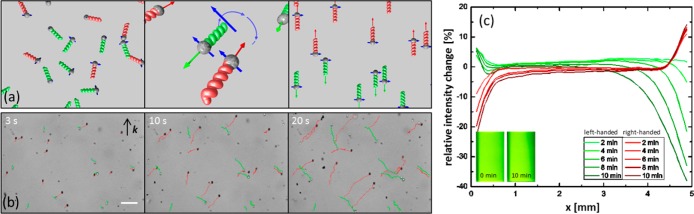
(a) Schematic of magnetic dipolar colloidal helices in the presence of a rotating magnetic field. The opposite enantiomers (red and green) possess a magnetic dipole moment (blue arrow) that aligns and thus rotates with the applied rotating magnetic field. The helices will align such that their drag is reduced, and hence they propel in opposite directions. (b) Tracks of right- (red) and left-handed (green) particles in a magnetic field of 20 G, rotating at a frequency of 20 Hz, over a time interval of 20 s. Scale bar is 20 μm. (c) Relative intensity change with time of the scattering intensity across the width of a 5 mm cuvette filled with a suspension of right- or left-handed colloids in a rotating magnetic field of a strength of 50 G and a frequency of 40 Hz. The colloid concentrations are on the order of 10^–14 M. In the lower left corner are representative images of a cuvette containing left-handed enantiomer after 0- and 10-min field application. There is a clear decrease in intensity at the right of the cuvette as the helices swim to the left.

Tracks of screw propellers are marked in the optical images of Figure 3b. To distinguish both helicities under bright-field illumination, right- and left-handed colloids were made out of different materials with different indices of refraction (silica and titania, respectively), and slightly different geometries were used: the left-handed screws had a slightly smaller diameter and were slightly longer than the right-handed ones. The left- and right-handed diametrically magnetized helices are driven by a magnetic field of 20 G at a frequency of 20 Hz in water. Although the “swimming” behavior of the microhelices has already been demonstrated in previous publications,^8c,14 this is, to our knowledge, the first time that an ensemble of such colloids has been manipulated, thus enabling their application as model colloidal molecules.

The possibility to extend this separation principle to macroscopic sample volumes was demonstrated by tracing the scattering intensity across the width of a cuvette filled with a suspension of either left- or right-handed colloids (for this experiment exact enantiomers were used) which was exposed to a rotating magnetic field that should propel the particles to one side of the cuvette. The result is shown in Figure 3c. It is clearly visible that a reduction in intensity on one side with a simultaneous slight intensity increase on the opposite side takes place within a few minutes and that right-and left-handed helices separate out in opposite directions.

To describe the motion of the helices we introduce the vector k that defines the direction and sense of the driving magnetic field

2

The B field illustrated in Figure 4, rotating in the xz plane such that it moves from +x to +z, has a k that points along the −y direction, out of the page. This choice of k means that right-handed helices will translate parallel to k, while the left-handed particles translate antiparallel to k. In the images, the right-handed colloids (red) move in the direction of k and left-handed enantiomers (green) move in the opposite direction. The movement perpendicular to k is due to interactions with the wall and was not taken into account in the determination of the translational speeds (see Figure 6), since it is a surface effect that causes no enantiospecific separation. The corresponding video of the chiral separation process can be found in the SI. Both the forward velocity and sideways motion agree well with other recent findings.¹⁴

Figure 4.

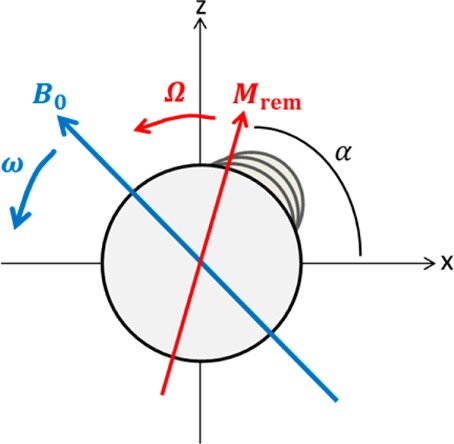
View along the axis of a helix with remnant magnetization M_rem in a magnetic field B₀ rotating at the rotational velocity ω. In this case k points out of the page.

Figure 6.

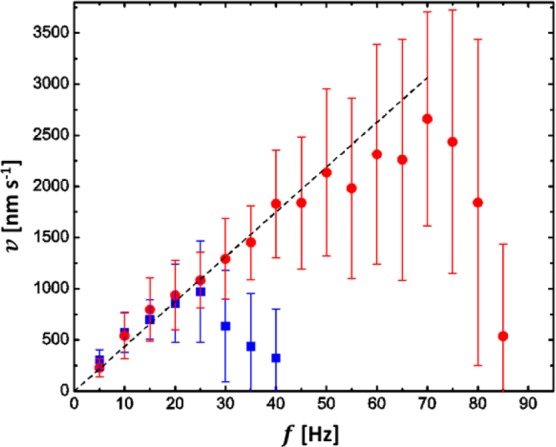
Forward velocity of the chiral colloids with varying frequency of the rotational magnetic field for magnetic field strengths of 20 G (blue squares) and 50 G (red circles). The dotted line is a linear fit of the data below the step-out-frequency (25 Hz for 20 G and 70 Hz for 50 G).

Overall, about 60% of colloids in a batch appear to be functional, i.e. they rotate with the magnetic field and exhibit translation parallel to the axis of rotation. The remaining colloids are either structurally incomplete or are found in clusters of more than one particle. At high concentrations (on the order of 1 pM) the sample tends to agglomerate due to magnetic interactions within less than half an hour, thus it is difficult to determine the efficiency of the chiral separation process over long time scales. Nevertheless, within the field of view (135 μm × 180 μm), 63% of the right-handed enantiomers leave the observed area through the top quarter of the frame and 9% through the bottom quarter, while 54% of the left-handed enantiomer exit the image through the bottom and 19% through the top quarter. Diffusion is negligible in the present colloidal system, and the separation process is limited solely due to structural deficiencies and agglomeration effects in part of the sample, whereas in molecular systems agglomeration would be negligible and diffusion is likely to be a major limiting factor.

The motion of the magnetic chiral colloid is dictated on one hand by the magnetic torque applied by the external magnetic field B acting on the particle’s moment m

3

and on the other hand by the viscous drag force that acts on the particle

4

where R is the colloid’s characteristic size, X is a scale-free geometry factor that depends on the shape (for a sphere X = 8π), η is the fluid’s viscosity, and Ω is its speed of rotation. At low velocities the particle will couple synchronously with the field and maintain constant rotational speed Ω = ω, with the two torques balanced

5

where (ωt – α) is the phase lag between the moment and field (see Figure 4). The rotational speed at which the viscous drag exceeds the magnetic torque is the step-out frequency given by

6

where M_rem is the remnant magnetization. Above the step-out frequency the colloid undergoes a complicated slipping motion with the applied field.

Using the boundary condition

7

in eq 5 one obtains the following analytic expression for the particles’ rotational speed (which is plotted in Figure 5a),

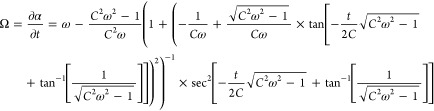8

where C = (Xη)/(M_remB₀). The forward velocity of the colloids is proportional to its angular velocity¹

9

Here ε is the rotation–translation coupling constant or propulsion efficiency and its upper limit is set by the pitch of the helix.

Figure 5.

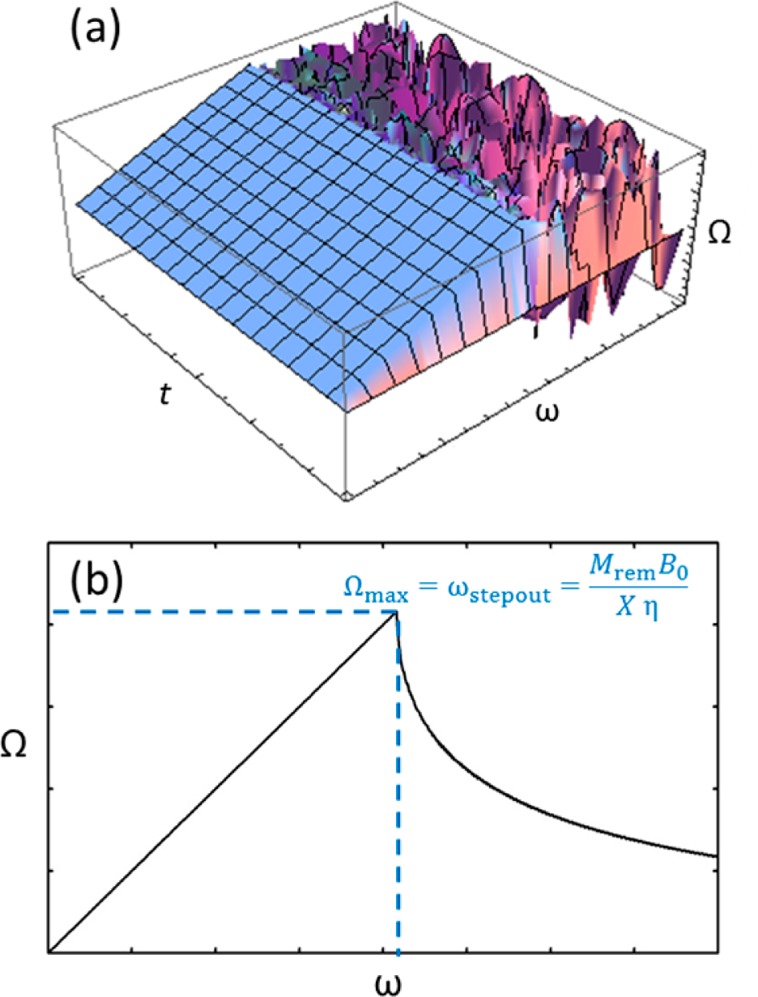
(a) 3D plot of the magnetic particle’s rotational velocity Ω with respect to the field’s rotational velocity ω and time t and (b) plot of the frequency-dependent time-averaged value of Ω.

Figure 5 shows a 3D plot and a time-averaged plot of the particle’s angular velocity dependence on the magnetic field’s rotational frequency. As one can see, Ω is locked to ω up to the step-out frequency, beyond which the average speed decreases rapidly. The result agrees well with a numerical study,²¹ that solved the corresponding problem for higher Reynolds numbers (including a higher-order inertial term).

Figure 6 shows the speed of the particles as a function of the rotational frequency f = ω/2π for two different magnetic field strengths, 20 and 50 G. The experimentally determined velocity distribution is rather broad, especially near (and beyond) the step-out-frequency, as the distance of each colloid to the wall differs in addition to variations of the shape and thus the value for ε. However, overall, the data qualitatively match the theoretical prediction shown in Figure 5. It follows that this colloidal model system can thus be used to determine numerical values for several parameters that Baranova and Zel’dovich could only assume for molecules.¹ For example, from the slope of the line in the linear regime one obtains a propulsion efficiency of ε = 7.0 ± 0.2 nm/rad, which corresponds to about 8% of the theoretical upper limit set by the helices’ pitch.

The geometry factor X can be estimated from the value of the step-out frequency according to eq 6 using the literature value for the remnant magnetization of bulk nickel.²² Taking into account that only about 10% of the particles’ volume is ferromagnetic, this yields a value of approximately X ≈ 600. This value is significantly higher than that for a sphere. A possible explanation for this is that, unlike for spheres and other highly symmetric shapes, for chiral particles X includes a term for the rotation–translation coupling which leads to an additional torque on the colloid. This effect, however, is rather small as the relationship between X and the mobility matrix defined by the relation²³

10

shows:

11

C² defines the magnitude of the translation–rotation coupling and is in all practical cases considerably smaller than DA.²³ Thus, the more likely reason for the discrepancy between the geometry-factor for a sphere and our colloidal helices is the fact that nickel microparticles have a lower remnant magnetization than the bulk metal value that was used in the calculation.

The effect any Brownian motion has on the orientation of the colloids has not been taken into account in eq 8. An estimate of thermal effects is obtained by comparing the strength of the dipolar coupling to kT

12

which is about 10³ in the present experimental system. The corresponding parameter for the propulsion of chiral molecules by an electric field in the Baranova Zel’dovich¹ model is

13

and has a value of 10^–4 for the parameters Baranova and Zel’dovich assume for molecules. The difference highlights the additional challenge faced if the propeller effect is to be used for the separation of chiral molecules.

Conclusions

We have shown that glancing angle physical vapor deposition can be used to produce large numbers of chiral colloids in good yields. These can be used as “colloidal molecules” to investigate physical phenomena that are difficult to observe experimentally at the molecular level. We were able to demonstrate that the differential scattering can be used to characterize chiral colloidal suspensions. The scattering signals of the chiral colloids agree well with theoretical predictions. We report the observation of the propeller effect for chiral colloidal molecules. An analytical solution that describes the motion of dipolar rotors as a function of the externally applied torque is derived. Now, that the propeller effect has been established at colloidal length scales, it is of interest to pursue its realization with chiral molecules. For this, the validity of continuum hydrodynamic models at molecular scales as well as the randomizing force of Brownian motion will have to be considered.

Experimental Section

The helices are grown using GLAD.¹³ In order to obtain well-defined regular helices across entire wafers, the shadowing growth was facilitated by first depositing a seed layer of silica nanoparticles. Monodisperse silica particles with a diameter of about 400 nm were synthesized according to a modified Stoeber Method²⁴ and surface-treated with allyltrimethoxysilane.²⁵ A dispersion of these particles in chloroform was dropped onto the surface of a Langmuir–Blodgett trough, and the monolayer was transferred onto a 2-in. wafer at a surface pressure of about 20 mN/m. The patterned wafer was then transferred into the vacuum system for GLAD electron beam evaporation at 10^–6 mmHg. The deposition angle was ∼85°. For the magnetic colloids a Ni-layer with a thickness of about 200 nm was included in the structure, the helical tail was grown with either silica or titania.

The setup used for differential scattering measurement is shown in Figure 7. A diode-pumped solid-state laser with an optical output power of P = 100 mW (cw) and a wavelength of λ = 532 nm was used as a light source. After passing an optical chopper the light was first linearly polarized and then sent to a photoelastic modulator (PEM), which modulates between left- and right-circular polarization at ∼50 kHz, before it is incident on a cylindrical scattering cell that contains the colloidal solution.

Figure 7.

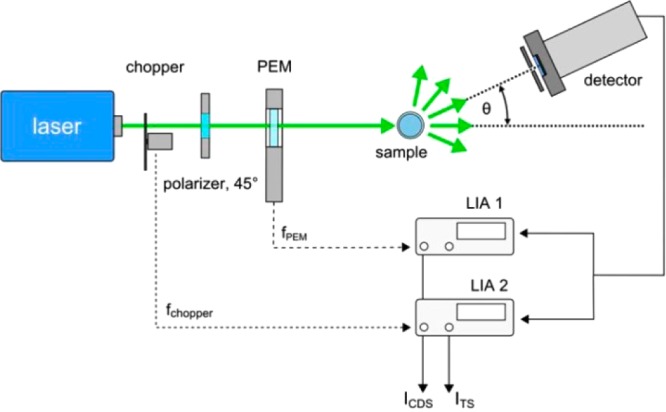
Setup for the differential scattering experiments. Further details can be found in the text.

The scattered light was detected using a photomultiplier tube mounted on a precision goniometer with an angular resolution <1°. The distance between the PMT and the center of the sample cell was d = 10 cm, and together with an entrance aperture of 1.5 mm of the PMT this resulted in an angular resolution of 0.86°.

The detector signal was electronically processed by two lock-in-amplifiers (LIA) locked to the modulation frequency of either the chopper or the PEM. While the PMT moved around the sample in an arc of 1°-steps, 50 data points were taken for every angular position of the detector and averaged. The total scattering intensity (TSI) can be derived from the LIA locked to the chopper frequency, whereas the difference in the scattering between the circular polarization states is detected by the second LIA. The circular differential scattering intensity is calculated according to:²⁶

14

Here α_PEM = π/2 is the retardation introduced by the PEM and j₁(x) the Bessel function of the first kind. R_PEM and R_chopper are the measured amplitudes of the LIAs.

For the measurements of the propulsion speeds and the chiral separation experiments, left- and right-handed colloidal particles, made out of silica and/or titania and including a magnetic nickel strip with a height of about 200 nm, were magnetized diametrically in an electromagnet producing a magnetic field of about 1.8 T. They were dispersed in water by sonicating parts of the wafer for 1 min and mixed in a ratio of 1:1 for separation experiments to produce a racemic mixture. The enantiomers used for imaging the separation process under the microscope were grown from different materials (silica and titania) such that the different refractive indices give rise to a distinguishable brightness under bright-field illumination. For these experiments the colloidal solution (concentration roughly 10^–15 M) was dropped into a gene frame (Thermo Scientific) on a coverslip to minimize drift due to evaporation. The gene frame was then inserted into the center of a custom-built three-axis water-cooled Helmholtz coil which can produce rotating magnetic fields in 3D of up to approximately 100 G. The movement of the particles was observed in a microscope (Zeiss Observer), and the paths of the left- and right-handed particles were analyzed using the software ImageJ.²⁷ For the determination of swimming velocities for each setting at least 18 particles were tracked over a minimum time period of 20 s.

For bulk experiments, enantiopure solutions of colloidal helices with a concentration of roughly 10^–14 M were used. Here left- and right-handed particles resembled true enantiomers and were grown out of titania. A 5 mm cuvette with a clear bottom was filled with the solution and placed inside the Helmholtz coils. It was illuminated through the bottom with a 555 nm LED. While it was subjected to a rotating magnetic field (50 G, 40 Hz), pictures were taken from the side every minute with a Canon EOS 600D camera. To obtain the intensity profiles shown in this work the intensity of the images was integrated over the height of the cuvette for x increments (width) of 0.06 mm and the intensity change relative to the starting value was calculated for each interval.

Supporting Information Available

Theoretical calculation of CDSI signals, geometrical parameters of the colloidal helices, further scattering measurements, chiral separation video. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.