Significance
Repeated modification of a multisite protein plays a key role in cell signaling. After an enzyme catalyzes a reaction at one site, it can modify another site before diffusing away. This physical process, which is amplified in the crowded environment of the cell, has been recently shown by stochastic simulations of hundreds of particles to dramatically change the response of a biochemical network. Here we show that the influence of diffusion on multisite protein modification can be described in a much simpler way, by introducing new connections into the kinetic scheme with rates depending on the probability that an enzyme–substrate pair diffuses apart rather than reacts. Our approach is applicable to complex reaction networks.
Keywords: multisite phosphorylation, escape and capture probabilities, splitting probability, diffusion-influenced rate constants, ultrasensitivity
Abstract
The simplest way to describe the influence of the relative diffusion of the reactants on the time course of bimolecular reactions is to modify or renormalize the phenomenological rate constants that enter into the rate equations of conventional chemical kinetics. However, for macromolecules with multiple inequivalent reactive sites, this is no longer sufficient, even in the low concentration limit. The physical reason is that an enzyme (or a ligand) that has just modified (or dissociated from) one site can bind to a neighboring site rather than diffuse away. This process is not described by the conventional chemical kinetics, which is only valid in the limit that diffusion is fast compared with reaction. Using an exactly solvable many-particle reaction-diffusion model, we show that the influence of diffusion on the kinetics of multisite binding and catalysis can be accounted for by not only scaling the rates, but also by introducing new connections into the kinetic scheme. The rate constants that describe these new transitions or reaction channels turn out to have a transparent physical interpretation: The chemical rates are scaled by the appropriate probabilities that a pair of reactants, which are initially in contact, bind rather than diffuse apart. The theory is illustrated by application to phosphorylation of a multisite substrate.
For bimolecular reactions in solution, the formalism of chemical kinetics is valid only in the limit that the reactants come together many times before reacting. This means that the intrinsic reaction rate must be slower than the rate at which the partners diffuse together. Starting with the seminal work of Smoluchowski (1), it has been shown that the relative diffusion of the reactants, even in a macroscopically homogeneous solution, can lead to deviations from the predictions of conventional chemical kinetics. For example, for reversible reactions, the concentrations decay to their equilibrium values not exponentially, but rather as a power law (2, 3). However, for biochemically relevant concentrations, such effects are small. Even in the crowded environment of a cell, although the total concentration of all macromolecules is of course high, the concentrations of specific molecules that can react with each other are typically low. Although it is interesting and challenging to develop a theory of reversible diffusion-influenced reactions that is accurate at all times and concentrations, in many cases the concentrations are so low that all one has to do is to replace the phenomenological rate constants by their diffusion-influenced values.
In this paper we consider a class of reactions involving macromolecules with multiple sites where, even at low concentrations, it is not enough to replace the rate constants with diffusion-influenced ones. Our interest in such problems was stimulated by the important work of Takahashi et al. (4) on the role of diffusion in a dual phosphorylation–dephosphorylation cycle that can exhibit ultrasensitive (5) and bistable behavior (6). Based on many-particle stochastic simulations, it was shown that slowing down diffusion can speed up response and lead to the loss of ultrasensitivity and bistability (4). These results were attributed to “spatio-temporal correlations between the enzyme and the substrate molecules.” The physical idea is illustrated in Fig. 1 for dual phosphorylation. For the sake of simplicity, we have assumed that the binding and catalytic sites are the same and adopted a reference frame where the substrate is fixed. After modifying the first site, the enzyme dissociates and (i) diffuses away and another enzyme binds and modifies the second site (lower pathway) or (ii) binds to the second site and modifies it (upper pathway). In other words, in the upper pathway both sites are phosphorylated by the same enzyme molecule, whereas in the lower pathway the sites are phosphorylated by different molecules. In the fast diffusion limit, only the lower pathway is in play. In the phosphorylation field, the mechanism is called distributive when the enzyme and substrate dissociate after each modification, whereas in a processive mechanism all sites are phosphorylated before dissociation (7, 8). Thus, when the rate of diffusion is finite, the mechanism inevitably contains both distributive and processive features (4, 9, 10).
Fig. 1.
A substrate S with two sites (yellow) that can be modified (red) by an enzyme E at concentration [E]. Lower pathway: After modifying one site, the enzyme diffuses away and another enzyme binds and phosphorylates the unmodified site. Upper pathway: The enzyme that has just modified one site dissociates, binds to the unmodified site, and then phosphorylates it.
The goal of this paper is to develop a simple theory that can quantitatively describe such phenomena for physically relevant concentration ranges without having to resort to many-particle computer simulations. In a nutshell, not only does one need to replace the existing phenomenological rate constants by their diffusion-influenced counterparts, but also one has to introduce new transitions into the kinetic scheme. The rates of these new reaction channels are determined by the probability that a reactant released from one site binds to another rather than diffusing away. Even for complex geometries, such capture and escape probabilities can be found by numerically solving or simulating only a time-independent, two-particle problem.
The outline of the paper is as follows. We start with arguably the simplest model of multisite modification that can be solved exactly on the many-particle level. In this model, the lifetime of the enzyme–substrate complex is assumed to be so short that a site can be modified when the enzyme simply comes in contact with the substrate. When the enzyme concentration is sufficiently low, it is found that the exact time dependence of the concentrations is well described by ordinary rate equations corresponding to the standard kinetic scheme with the crucial difference that new transitions have been allowed. The corresponding rate constants turn out to have such a simple physical interpretation that the formalism can be readily generalized to treat more realistic cases (e.g., intermediate bound complexes, enzyme reactivation, and binding to inequivalent sites). The rate constants in the modified kinetic schemes can be expressed in terms of the capture and escape probabilities of an isolated pair of reactants. In simple cases, these can be found by solving a time-independent equation subject to the appropriate boundary conditions and, for realistic geometries, by simulating the dynamics of an isolated pair of reactants. Illustrative calculations for dual phosphorylation show that our formalism reproduces the speeding up of the response discovered using stochastic many-particle simulations (4).
Theory
We begin by showing how diffusion leads to the appearance of new reaction channels in the context of a simple exactly solvable model. The final results turn out to be so intuitively plausible that they can be understood without following their derivation. Consider a substrate with N sites that can be irreversibly modified by an enzyme. If the lifetimes of the enzyme–substrate complexes are sufficiently short, this process can be described within the framework of chemical kinetics by the scheme
where  . Here Si denotes the substrate with i modified sites and κi is the phenomenological rate constant for modifying a site on the substrate with i sites already modified. The corresponding rate equations, in matrix form, are
. Here Si denotes the substrate with i modified sites and κi is the phenomenological rate constant for modifying a site on the substrate with i sites already modified. The corresponding rate equations, in matrix form, are
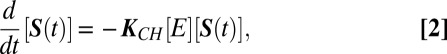 |
where [S(t)] is a vector of concentrations with components [Si(t)],  , and KCH is an (N + 1) × (N + 1) rate matrix whose only nonzero elements are
, and KCH is an (N + 1) × (N + 1) rate matrix whose only nonzero elements are  ,
,  .
.
To see how diffusion influences the kinetics of this reaction, we adopt arguably the simplest nontrivial many-particle model. We consider a single impenetrable spherical substrate uniformly surrounded by M spherical enzymes in volume V. The substrate is static. The enzymes diffuse with diffusion constant D and do not interact with each other. When an enzyme comes in contact with the substrate (i.e., the distance between their centers is R irrespective of orientation), the transition  can occur with the reaction rate constant κi. In this model, modification occurs without forming an enzyme–substrate complex, because we have assumed that the lifetime of such a complex is so short that it can be ignored. Let
can occur with the reaction rate constant κi. In this model, modification occurs without forming an enzyme–substrate complex, because we have assumed that the lifetime of such a complex is so short that it can be ignored. Let  be the probability density that at time t i sites are modified and the enzymes are located at distances
be the probability density that at time t i sites are modified and the enzymes are located at distances  from the substrate. The vector of these probabilities satisfies the M-particle diffusion equation
from the substrate. The vector of these probabilities satisfies the M-particle diffusion equation
 |
where  . The reaction is described by imposing boundary conditions obtained by balancing the diffusive and chemical fluxes at contact:
. The reaction is described by imposing boundary conditions obtained by balancing the diffusive and chemical fluxes at contact:
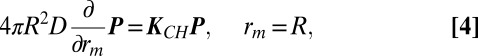 |
where  . The substrate concentrations are given by
. The substrate concentrations are given by 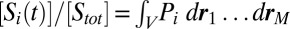 when
when  in such a way that
in such a way that  (i.e., the thermodynamic limit). Here
(i.e., the thermodynamic limit). Here 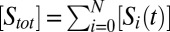 .
.
The different components of P are coupled only by the boundary conditions in Eq. 4. However, by diagonalizing the rate matrix KCH, we can decouple them and reduce the solution of the many-particle problem to N one-particle problems. Let T be the transformation matrix that diagonalizes KCH (i.e., 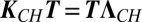 , where
, where 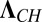 is the diagonal matrix with elements κi,
is the diagonal matrix with elements κi,  and κN = 0). Then it can be shown that (Supporting Information)
and κN = 0). Then it can be shown that (Supporting Information)
 |
where  satisfies
satisfies 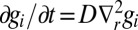 , with the boundary condition
, with the boundary condition 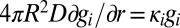 at r = R. Initially,
at r = R. Initially, 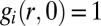 . Differentiating Eq. 5 with respect to time and taking the thermodynamic limit, it can be shown that
. Differentiating Eq. 5 with respect to time and taking the thermodynamic limit, it can be shown that
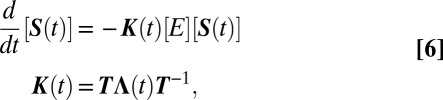 |
where 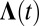 is a diagonal matrix with elements
is a diagonal matrix with elements
 |
where  , kN(t) = 0, dr = 4πr2
dr,
, kN(t) = 0, dr = 4πr2
dr,  ,
, 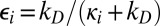 , and kD = 4πDR is Smoluchowski’s diffusion-limited rate constant. As D → ∞,
, and kD = 4πDR is Smoluchowski’s diffusion-limited rate constant. As D → ∞,  , which are in fact the eigenvalues of KCH for the kinetic scheme shown in Eq. 1. Thus, in the fast diffusion limit, Eq. 6 reduces to Eq. 2, as it must. It should be noted that, except when n = 1, the new rate matrix K(t) is not the chemical kinetics rate matrix KCH with κi being replaced by ki(t).
, which are in fact the eigenvalues of KCH for the kinetic scheme shown in Eq. 1. Thus, in the fast diffusion limit, Eq. 6 reduces to Eq. 2, as it must. It should be noted that, except when n = 1, the new rate matrix K(t) is not the chemical kinetics rate matrix KCH with κi being replaced by ki(t).
At times longer than the characteristic diffusion time  , the time-dependent rate coefficients in Eq. 7 approach constant values,
, the time-dependent rate coefficients in Eq. 7 approach constant values,  , and the rate matrix in Eq. 6 approaches a constant matrix, K(∞). In the limit of low concentrations, when the effective volume fraction is much less than unity, the rate equation Eq. 2 with the diffusion-influenced rate matrix K(∞) replacing KCH becomes a good approximation for
, and the rate matrix in Eq. 6 approaches a constant matrix, K(∞). In the limit of low concentrations, when the effective volume fraction is much less than unity, the rate equation Eq. 2 with the diffusion-influenced rate matrix K(∞) replacing KCH becomes a good approximation for  .
.
The crucial point is that K(∞) is not simply KCH with the chemical rate constants κi replaced by the diffusion-influenced ones,  . Rather, is it given by
. Rather, is it given by
 |
where we have used  . The new rate matrix K(∞) has finite elements that were zero in KCH. Consequently, the kinetic scheme that corresponds to the rate matrix K(∞) has new connections (or reaction channels) that were absent in the original chemical kinetic scheme. These new transitions appear due to diffusion and, as shown below, the corresponding rates have a simple physical interpretation.
. The new rate matrix K(∞) has finite elements that were zero in KCH. Consequently, the kinetic scheme that corresponds to the rate matrix K(∞) has new connections (or reaction channels) that were absent in the original chemical kinetic scheme. These new transitions appear due to diffusion and, as shown below, the corresponding rates have a simple physical interpretation.
It should be mentioned that the reversible reaction  can also be solved exactly. All of the above equations hold when KCH contains both forward and reverse rate constants, except Eq. 7, where κi must be replaced by the eigenvalues of the corresponding rate matrix KCH.
can also be solved exactly. All of the above equations hold when KCH contains both forward and reverse rate constants, except Eq. 7, where κi must be replaced by the eigenvalues of the corresponding rate matrix KCH.
Results and Discussion
Consider first how diffusion affects the kinetics of single-site modification, 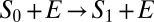 . In this case, the above results are identical to those obtained from the Smoluchowski–Collins–Kimball theory of irreversible diffusion-influenced reactions (11). The decay of the concentration of S0 is not single-exponential, but it is given by
. In this case, the above results are identical to those obtained from the Smoluchowski–Collins–Kimball theory of irreversible diffusion-influenced reactions (11). The decay of the concentration of S0 is not single-exponential, but it is given by 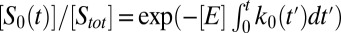 , where the time-dependent rate coefficient k0(t) is given in Eq. 7. At short times
, where the time-dependent rate coefficient k0(t) is given in Eq. 7. At short times 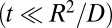 , k0(t) approaches the chemical rate constant κ0. As time increases, the rate coefficient decreases because the enzymes must diffuse to the substrate in order for reaction to occur. When
, k0(t) approaches the chemical rate constant κ0. As time increases, the rate coefficient decreases because the enzymes must diffuse to the substrate in order for reaction to occur. When  , k0(t) approaches the diffusion-influenced (often called steady-state) rate constant
, k0(t) approaches the diffusion-influenced (often called steady-state) rate constant  , where kD = 4πDR is the rate constant in the diffusion-controlled limit when either diffusion is slow
, where kD = 4πDR is the rate constant in the diffusion-controlled limit when either diffusion is slow  or reaction is fast
or reaction is fast  .
.
The diffusion-influenced rate constant, k0(∞), has a simple physical interpretation. Imagine an isolated pair of reactants (e.g., S0 and E), initially in contact, that can irreversibly react. If one waits enough, there are only two possible outcomes: (i) Reaction has occurred (E is “captured” by S0) and (ii) the reactants diffuse apart never to see each other again (E has “escaped” to infinity). For isotropic contact reactivity, the escape probability is  , whereas the capture probability is
, whereas the capture probability is 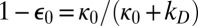 . When diffusion is fast, the substrate and enzyme are much more likely to separate rather than react, so
. When diffusion is fast, the substrate and enzyme are much more likely to separate rather than react, so  . When diffusion is slow, a contact pair is much more likely to react, so
. When diffusion is slow, a contact pair is much more likely to react, so 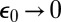 . In terms of this quantity, the diffusion-influenced rate constant can be written either as
. In terms of this quantity, the diffusion-influenced rate constant can be written either as  [the chemical (contact) rate constant is reduced by the escape probability] or, perhaps more intuitively, as
[the chemical (contact) rate constant is reduced by the escape probability] or, perhaps more intuitively, as  (the diffusion-limited rate constant is reduced by the probability that a contact pair eventually reacts). Escape and capture probabilities will play a central role in the rest of the paper. As shown by Onsager (12) in the context of ion recombination, they can be obtained by solving a time-independent problem (13).
(the diffusion-limited rate constant is reduced by the probability that a contact pair eventually reacts). Escape and capture probabilities will play a central role in the rest of the paper. As shown by Onsager (12) in the context of ion recombination, they can be obtained by solving a time-independent problem (13).
The simplest example where diffusion leads to a change in the connectivity of the kinetic scheme is two-site modification, 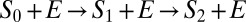 . Naively, it seems that one could just renormalize the chemical rate constants as shown in Fig. 2A [i.e.,
. Naively, it seems that one could just renormalize the chemical rate constants as shown in Fig. 2A [i.e.,  , i = 0, 1]. However, the rate matrix in Eq. 8 actually corresponds to the kinetic scheme shown in Fig. 2B. The “naive” diffusion-influenced rate constant for the transition S0 to S1
, i = 0, 1]. However, the rate matrix in Eq. 8 actually corresponds to the kinetic scheme shown in Fig. 2B. The “naive” diffusion-influenced rate constant for the transition S0 to S1
 is reduced by the escape probability
is reduced by the escape probability 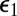 of the S1 and E contact pair. In addition, there is a new direct transition between S0 and S2 with a rate constant equal to k0(∞) times the capture probability,
of the S1 and E contact pair. In addition, there is a new direct transition between S0 and S2 with a rate constant equal to k0(∞) times the capture probability,  , of the S1 and E contact pair. These results can be easily understood. At the instant S0 has been modified, S1 and E are in contact. The probability that the enzyme diffuses away is
, of the S1 and E contact pair. These results can be easily understood. At the instant S0 has been modified, S1 and E are in contact. The probability that the enzyme diffuses away is 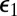 and the probability that it hangs around and modifies the substrate again is
and the probability that it hangs around and modifies the substrate again is 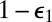 . The first scenario is just the one depicted by the reaction
. The first scenario is just the one depicted by the reaction  in the original scheme. In the second scenario, the same enzyme modifies the substrate twice before diffusing away. This new mechanism, which is only possible because the rate of diffusion is finite, can be approximately treated within the framework of chemical kinetics by allowing the direct transition
in the original scheme. In the second scenario, the same enzyme modifies the substrate twice before diffusing away. This new mechanism, which is only possible because the rate of diffusion is finite, can be approximately treated within the framework of chemical kinetics by allowing the direct transition  . The relative importance of these two channels (i.e., the splitting probability) is determined by the escape probability of the S1 and E contact pair
. The relative importance of these two channels (i.e., the splitting probability) is determined by the escape probability of the S1 and E contact pair  .
.
Fig. 2.
Effect of diffusion on the kinetics of a simple model of dual modification of a substrate by an enzyme. (A) The standard kinetic scheme in which the phenomenological rate constants (κ0, κ1) have been scaled by the escape probabilities of contact pairs. (B) Our kinetic scheme with an additional transition. (C) Comparison of the exact kinetics (red lines, Eq. S21 in Supporting Information) with the predictions of scheme A (black lines, Eq. S23 in Supporting Information with 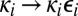 ) and B (dashed blue lines, Eq. S24 in Supporting Information). Time is normalized to
) and B (dashed blue lines, Eq. S24 in Supporting Information). Time is normalized to  .
.  ,
, 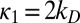 ,
, 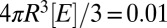 , D = 1, R = 1, [Stot] = 1.
, D = 1, R = 1, [Stot] = 1.
Fig. 2C shows how the new transition in the kinetic scheme influences the time dependence of the concentrations. Because S0 and S2 are now directly connected, the population of S1 is smaller and the concentration of S2 increases faster than that predicted by the “naive” kinetic scheme in Fig. 1A. The faster response of the fully modified substrate becomes more pronounced as the number of sites increases (Fig. S1). For the low concentration used (effective volume fraction  ) it can be seen that the exact kinetics are almost the same as those predicted by the scheme with the extra connection shown in Fig. 2B. As the concentration increases, the difference increases (Fig. S2) so that any theory based on rate equations with time-independent rate constants eventually becomes inadequate.
) it can be seen that the exact kinetics are almost the same as those predicted by the scheme with the extra connection shown in Fig. 2B. As the concentration increases, the difference increases (Fig. S2) so that any theory based on rate equations with time-independent rate constants eventually becomes inadequate.
Two-Site Phosphorylation: Michaelis–Menten Mechanism.
Using the exactly solvable model, we have demonstrated that the effect of diffusion can be accounted for by (i) replacing the bimolecular rate constants by diffusion-influenced ones and (ii) introducing new reaction channels into the kinetic scheme. In the low-concentration limit, for times longer than the diffusion time, the new kinetic scheme describes the kinetics of a simple model of site modification with high accuracy. We will now use physical arguments based on the insights gained from the exactly solvable model to extend these results to more general models of enzyme catalysis. The results presented below are derived in Supporting Information using an approximate low-concentration theory.
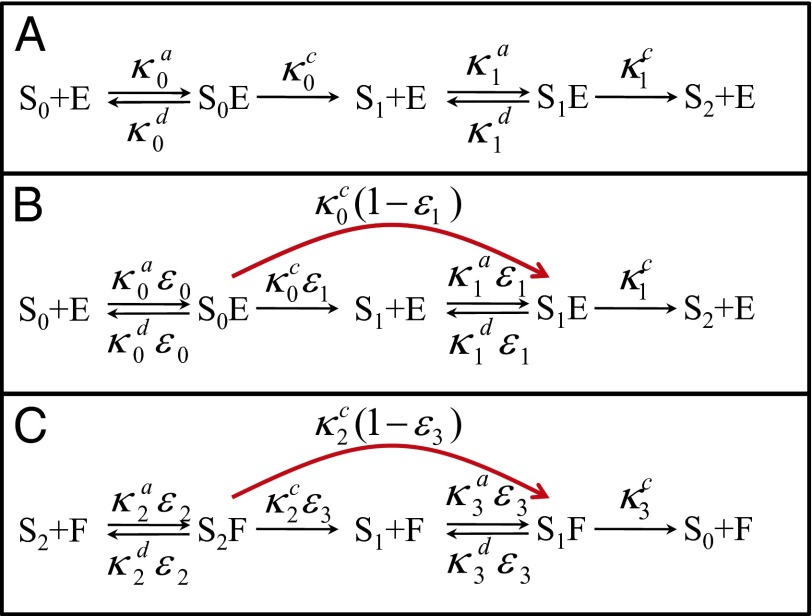
Consider the double phosphorylation of a substrate described by the Michaelis–Menten mechanism (scheme in Fig. 3A). In contrast to the kinetic scheme in Eq. 1, here the enzyme E and the substrate with i modified sites, Si, bind and form the complex SiE, which has a finite lifetime. It is assumed that catalysis and the release of the substrate occur in one step and that no more than one enzyme binds to the substrate. In the microscopic model of this reaction, the enzyme and substrate diffuse with the relative diffusion coefficient D = DE + DS. When they come in contact, the complex SiE can be formed with the association rate constant 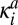 . The complex can dissociate (with the dissociation rate constant
. The complex can dissociate (with the dissociation rate constant 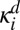 ) and form a contact pair of Si and E. Alternatively, the substrate in the complex can be modified (with the catalytic rate constant
) and form a contact pair of Si and E. Alternatively, the substrate in the complex can be modified (with the catalytic rate constant  ), resulting a contact pair of Si+1 and E. As before, we assume that the molecules are spherical and uniformly reactive, so that the escape probability,
), resulting a contact pair of Si+1 and E. As before, we assume that the molecules are spherical and uniformly reactive, so that the escape probability, 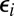 , of the contact pair of Si and E is given by
, of the contact pair of Si and E is given by  .
.
Fig. 3.
Conventional and diffusion-modified kinetic schemes for two-site phosphorylation and dephosphorylation. (A) A substrate S with two sites is phosphorylated by a kinase E via the Michaelis–Menten mechanism. (B) Kinetic scheme that describes the influence of diffusion. Not only are the chemical rates scaled by the escape probabilities (ε’s), but a new transition appears (red arrow) because the same enzyme can phosphorylate the substrate twice before diffusing away. 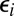 (i = 0, 1) is the probability that an enzyme, initially in contact with a substrate with i modified sites, diffuses away rather than binds to the substrate. (C) Corresponding scheme for dephosphorylation by a phosphotase F.
(i = 0, 1) is the probability that an enzyme, initially in contact with a substrate with i modified sites, diffuses away rather than binds to the substrate. (C) Corresponding scheme for dephosphorylation by a phosphotase F.
We now change the kinetic scheme in Fig. 3A to take diffusion into account (Fig. 3B; the corresponding rate equations, Eq. S42, are given in Supporting Information). The diffusion-influenced rate constant for the association of S0 and E to form S0E is given by  , where
, where  is the escape probability of S0 and E contact pair. The dissociation rate constant of S0E to form S0 + E is the product of the dissociation rate constant
is the escape probability of S0 and E contact pair. The dissociation rate constant of S0E to form S0 + E is the product of the dissociation rate constant  and the escape probability of the S0 and E contact pair,
and the escape probability of the S0 and E contact pair,  . The physical reason for this is that a contact pair cannot be considered to be really dissociated because it can quickly associate again. Full dissociation occurs only when the enzyme and substrate separate completely. It should be noted that the equilibrium constant for binding
. The physical reason for this is that a contact pair cannot be considered to be really dissociated because it can quickly associate again. Full dissociation occurs only when the enzyme and substrate separate completely. It should be noted that the equilibrium constant for binding 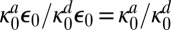 is independent of diffusion, as it must be, because the equilibrium constant is a thermodynamic quantity. These expressions for the renormalized association and dissociation rates have been known at least since the paper of Schurr (14) and their interpretation in terms of escape probabilities at least since the work of Shoup and Szabo (15).
is independent of diffusion, as it must be, because the equilibrium constant is a thermodynamic quantity. These expressions for the renormalized association and dissociation rates have been known at least since the paper of Schurr (14) and their interpretation in terms of escape probabilities at least since the work of Shoup and Szabo (15).
To understand the influence of diffusion on the catalytic step, consider the fate of the contact pair of S1 and E formed from the complex S0E. This pair can separate with probability  or the enzyme can bind again to form the complex S1E with probability
or the enzyme can bind again to form the complex S1E with probability  . Thus, the rate corresponding to the catalytic channel in the scheme shown in Fig. 3A is reduced by
. Thus, the rate corresponding to the catalytic channel in the scheme shown in Fig. 3A is reduced by  and a new channel, which directly connects the two complexes, S0E and S1E, appears with rate constant
and a new channel, which directly connects the two complexes, S0E and S1E, appears with rate constant  . The physical reason for this new connection is that, after modifying the substrate, the enzyme and substrate do not always diffuse apart but can stay close to each other and bind again. Thus, diffusion naturally introduces an element of processivity into a distributive mechanism. No new parameters are needed in this case beyond those that renormalize the rate constants in the original kinetic scheme. When diffusion is fast, all of the escape probabilities approach unity and the modified kinetic scheme in Fig. 3B reduces to that in Fig. 3A. As diffusion slows down, a new transition or reaction channel appears corresponding to the process where after phosphorylating one site the enzyme rebinds and modifies the other.
. The physical reason for this new connection is that, after modifying the substrate, the enzyme and substrate do not always diffuse apart but can stay close to each other and bind again. Thus, diffusion naturally introduces an element of processivity into a distributive mechanism. No new parameters are needed in this case beyond those that renormalize the rate constants in the original kinetic scheme. When diffusion is fast, all of the escape probabilities approach unity and the modified kinetic scheme in Fig. 3B reduces to that in Fig. 3A. As diffusion slows down, a new transition or reaction channel appears corresponding to the process where after phosphorylating one site the enzyme rebinds and modifies the other.
The generalization to more than two sites is straightforward: The rate constant for the catalytic step 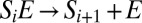 is
is 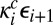 , whereas the new transition between adjacent complexes
, whereas the new transition between adjacent complexes 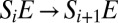 occurs at a rate
occurs at a rate 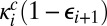 , where
, where  is the escape probability of a contact pair involving E and Si+1.
is the escape probability of a contact pair involving E and Si+1.
Dual Phosphorylation–Dephosphorylation Cycle.
In addition to phosphorylation by a kinase, consider dephosphorylation of a two-site substrate by a phosphotase. The influence of diffusion on the kinetics of this cycle was recently studied using stochastic many-particle simulations based on a clever Green’s function algorithm (4). It was found that slowing down diffusion can speed up response and decrease untrasensitivity.
We now show that the theory developed in this paper predicts this behavior. The diffusion-modified kinetic schemes for this problem are shown in Fig. 3 B and C. The corresponding differential equations for the concentrations are given in Eq. S45 in Supporting Information. The concentration of the doubly phosphorylated substrate relative to its steady-state value is shown in Fig. 4 as a function of time for various diffusion coefficients. It can be seen that the response at first becomes faster as the diffusion constant is decreased. The escape probabilities and the rate constants that appeared in the conventional chemical kinetic scheme all decrease as diffusion slows down because the contact pairs are less likely to separate than bind. This is why one naively expects the response to slow down as the diffusion coefficient becomes smaller. However, the rate constants for the new transitions, because they are proportional to the capture probabilities, increase as diffusion slows down. The competition between these two opposing effects leads to an optimal diffusion coefficient that minimizes the response time.
Fig. 4.
Time dependence of the concentration of the doubly phosphorylated substrate for different diffusion coefficients. The kinetics were obtained by solving numerically the ordinary differential equations (Eq. S45 in Supporting Information) that correspond to the modified schemes in Fig. 3 B and C. Initially, the substrates are in the unphosphorylated form. The diffusion coefficients are (in square micrometers per second) 50 (purple), 10 (blue), 0.5 (green), 0.1 (orange), and 0.025 (red). The other parameters, taken from ref. 4, are  ,
,  ,
, 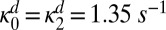 ,
,  ,
,  ,
,  , R = 5nm,
, R = 5nm, 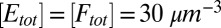 , and
, and  . (Inset) The half-time (i.e., the time at which [S2] reaches half of its steady-state value) as a function of the diffusion coefficient.
. (Inset) The half-time (i.e., the time at which [S2] reaches half of its steady-state value) as a function of the diffusion coefficient.
The kinetic scheme with additional reaction channels in Fig. 3 B and C can also predict the steady-state concentrations of diffusing reactants in a dual phosphorylation cycle. As diffusion slows down, the flux through the new connection increases. Consequently, the steady-state input–output curve becomes more shallow and less sensitive to the variation of the kinase/phosphotase concentration, as shown in Fig. S3 and in agreement with ref. 4.
Enzyme Reactivation Time.
After catalytic modification, an enzyme may be inactive and require some time to become active again. In phosphorylation, kinase reactivation is related to the release of ADP, and binding of ATP and has been shown to play an important role in the kinetics (4, 16). In the framework of chemical kinetics, this effect can be described by replacing the scheme in Fig. 3A by (i = 0, 1):
 |
How does diffusion affect this kinetic scheme? As shown in Supporting Information, when  , for times longer than both the diffusion time
, for times longer than both the diffusion time  and the reactivation time
and the reactivation time  , the diffusion-modified kinetic scheme has the same connectivity as that shown in Fig. 3B with the important difference that the
, the diffusion-modified kinetic scheme has the same connectivity as that shown in Fig. 3B with the important difference that the  ’s that enter the catalytic step [i.e.,
’s that enter the catalytic step [i.e., 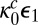 and
and  ] are replaced by
] are replaced by  . This new quantity is the probability that the enzyme, which is initially in the inactive form
. This new quantity is the probability that the enzyme, which is initially in the inactive form 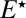 in contact with the singly phosphorylated substrate S1, diffuses away rather than reactivates and binds to the substrate. If the lifetime of
in contact with the singly phosphorylated substrate S1, diffuses away rather than reactivates and binds to the substrate. If the lifetime of 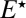 is infinite, then the enzyme always escapes because it cannot react with S1 and thus
is infinite, then the enzyme always escapes because it cannot react with S1 and thus  . Consequently, when the reactivation time is much longer than the diffusion time, the new reaction channel does not contribute and simply renormalizing the rates in the standard kinetic scheme is adequate.
. Consequently, when the reactivation time is much longer than the diffusion time, the new reaction channel does not contribute and simply renormalizing the rates in the standard kinetic scheme is adequate.
For uniformly reacting species, 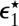 can be found as follows. Let
can be found as follows. Let 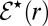 [or
[or 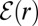 ] be the escape probability of an isolated pair when initially the distance between
] be the escape probability of an isolated pair when initially the distance between  [or E] and S1 is r. We are interested in
[or E] and S1 is r. We are interested in 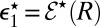 . As
. As 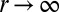 , both
, both 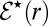 and
and 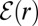 approach unity.
approach unity. 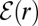 satisfies
satisfies  subject to the partially reactive boundary condition at contact,
subject to the partially reactive boundary condition at contact, 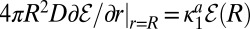 (15).
(15). 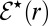 , however, satisfies
, however, satisfies  subject to the reflecting boundary condition at contact,
subject to the reflecting boundary condition at contact,  , because
, because 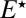 cannot bind to the substrate. Solving these equations, we find
cannot bind to the substrate. Solving these equations, we find
 |
When the lifetime of  is very short
is very short 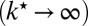 , then
, then 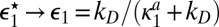 and the diffusion-modified kinetic scheme in Fig. 3B is recovered. However, when
and the diffusion-modified kinetic scheme in Fig. 3B is recovered. However, when 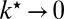 ,
,  and so
and so  always escapes before reactivating and binding to the unmodified site. No new transition appears in the kinetic scheme. Thus, the rate constant of the new reaction channel changes from zero to
always escapes before reactivating and binding to the unmodified site. No new transition appears in the kinetic scheme. Thus, the rate constant of the new reaction channel changes from zero to 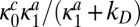 as the ratio of the diffusion time to the reactivation time increases.
as the ratio of the diffusion time to the reactivation time increases.
Anisotropic Reactivity.
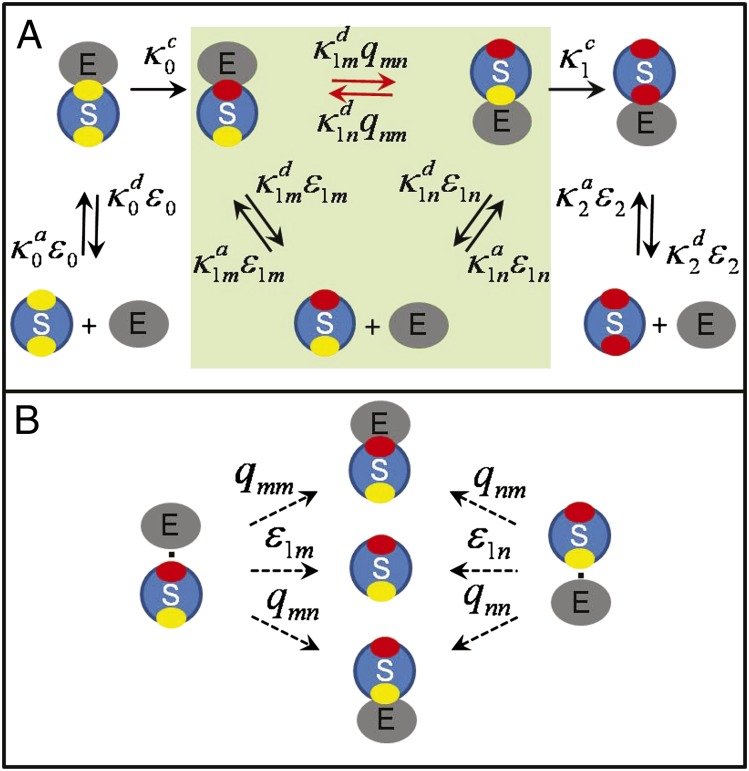
We now generalize the theory to handle two sites that, although equivalent, are located in different places on the surface of the substrate. In addition we remove the assumption in the Michaelis–Menten mechanism that catalysis and product release occur in the same step and explicitly consider the reversible binding of the enzyme to the modified sites. We start, as before, with the conventional chemical kinetics scheme, which is shown in Fig. 5A when all of the ε’s are 1 and the q’s are zero. We denote the nonmodified site (yellow) by “n” and the modified site (red) by “m” so that, for example,  is the association rate constant for binding of the enzyme to the modified site of a substrate with one modified and one nonmodified site.
is the association rate constant for binding of the enzyme to the modified site of a substrate with one modified and one nonmodified site.
Fig. 5.
Two-site modification with anisotropic reactivity. (A) A substrate with nonmodified (yellow or “n”) and modified (red or “m”) sites in the presence of free enzyme (lower row) can form a variety of complexes (upper row). The rate constants in the conventional kinetic scheme (black arrows) are scaled by the escape probabilities, whereas those of the new transitions (red arrows) are proportional to the probability of starting at one site and being captured by the other. (B) Definition of escape (ε’s) and capture (q’s) probabilities. The enzyme, initially in contact with one site, can bind to the same site (qnn, qmm), diffuse away  , or bind to the other site (qnm, qmn). Because of detailed balance,
, or bind to the other site (qnm, qmn). Because of detailed balance,  .
.
The diffusion-modified kinetic scheme for this problem is shown in Fig. 5A. Note that the catalytic rate constants do not change here. The escape probability 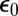 is the probability that the enzyme, initially in contact with one of the sites, escapes rather than binds. The most interesting results are shown in the shaded portion of Fig. 5A and depend on the escape and capture probabilities defined in Fig. 5B. To understand the definition of these probabilities, consider an isolated pair of an enzyme and a substrate in which one of the two sites has been modified. Suppose that the enzyme is initially in contact with the phosphorylated (“m” for modified) site (see the left-hand side of Fig. 5B). Such a pair can have only three fates: (i) The enzyme can rebind to the “m” site with probability qmm, or (ii) it can diffuse away into the bulk with escape probability
is the probability that the enzyme, initially in contact with one of the sites, escapes rather than binds. The most interesting results are shown in the shaded portion of Fig. 5A and depend on the escape and capture probabilities defined in Fig. 5B. To understand the definition of these probabilities, consider an isolated pair of an enzyme and a substrate in which one of the two sites has been modified. Suppose that the enzyme is initially in contact with the phosphorylated (“m” for modified) site (see the left-hand side of Fig. 5B). Such a pair can have only three fates: (i) The enzyme can rebind to the “m” site with probability qmm, or (ii) it can diffuse away into the bulk with escape probability  , or (iii) it can bind to the other (“n”) site with capture probability qmn. Clearly
, or (iii) it can bind to the other (“n”) site with capture probability qmn. Clearly  . The case when the enzyme is initially in contact with the “n” site is analogous (see the right-hand side of Fig. 5B).
. The case when the enzyme is initially in contact with the “n” site is analogous (see the right-hand side of Fig. 5B).
With these definitions, the rate constants in the shaded portion of Fig. 5A have a transparent physical interpretation. The rates corresponding to the new transitions (red arrows) are the product of the dissociation rate constant ( or
or  ) and the probability that the enzyme, starting near one site, binds to the other (qmn or qnm). This new pathway corresponds to the upper mechanism shown schematically in Fig. 1. The association and dissociation rate constants for the transitions that were present in the conventional chemical kinetic scheme (black arrows) are scaled by the appropriate escape probabilities in such a way that the equilibrium constants do not depend on diffusion.
) and the probability that the enzyme, starting near one site, binds to the other (qmn or qnm). This new pathway corresponds to the upper mechanism shown schematically in Fig. 1. The association and dissociation rate constants for the transitions that were present in the conventional chemical kinetic scheme (black arrows) are scaled by the appropriate escape probabilities in such a way that the equilibrium constants do not depend on diffusion.
For anisotropic reactivity, the escape and capture probabilities must be obtained numerically by solving differential equations subject to the appropriate boundary conditions or, for more complex models, by stochastic simulations. Because this is a two-particle problem, it is a lot easier than calculating the time dependence of the concentrations by simulating the reactive dynamics of hundreds of particles. We note for the sake of completeness that for isotropic reactivity simple expressions for these quantities can be found. In the isotropic model, the contact pairs on the left and right sides of Fig. 5B are assumed to be equivalent, so  ,
,  , and
, and  .
.
In the limit that the dissociation rate constants of the complexes between the enzyme and the modified site are very large  , the kinetic scheme in Fig. 5A reduces to that in Fig. 3B with one important difference:
, the kinetic scheme in Fig. 5A reduces to that in Fig. 3B with one important difference:  in the rates
in the rates  and
and  must be replaced by
must be replaced by 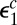 , which is the escape probability of the enzyme initially in contact with the modified site. Because now the enzyme does not bind to the modified site,
, which is the escape probability of the enzyme initially in contact with the modified site. Because now the enzyme does not bind to the modified site, 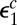 is different from
is different from  that scales
that scales 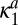 and
and  and is the escape probability of the enzyme initially in contact with the reactive, nonmodified site.
and is the escape probability of the enzyme initially in contact with the reactive, nonmodified site.
Ligand Binding to Inequivalent Sites.
From the shaded portion of Fig. 5A, it is clear that the enzyme E can be regarded as a “ligand” that binds to two inequivalent sites (red and yellow). Thus, our diffusion-modified scheme with extra connections also describes ligand binding when the complexes are distinguishable. The extra transitions describe processes in which a ligand dissociates from one site and binds to another without diffusing away. Although we explicitly considered only two sites, the generalization to many sites is straightforward.
Concluding Remarks
We have shown that the influence of the relative diffusion of the reactants on the kinetics of multisite catalysis can be described by introducing new connections or transitions into the conventional kinetic scheme in addition to using diffusion-influenced rate constants. These new pathways or reaction channels appear because an enzyme, after modifying one site on a substrate, can modify another site before the enzyme–substrate pair diffuses apart. It is remarkable that the rate constants in the new kinetic scheme depend on diffusion only through the escape and capture probabilities of isolated enzyme–substrate pairs. These probabilities depend on the enzyme–substrate interaction potential, the precise definition of the reaction zone, and on other factors such as rotational diffusion, but the connectivity of the diffusion-modified kinetic scheme does not. Thus, the influence of molecular crowding can be treated by solving the pair problem with the appropriate potential of mean force and relative diffusion coefficient. For realistic microscopic models, where the escape and capture probabilities must be found numerically, this is a tremendous simplification because one can now simulate the reactive dynamics of two rather than hundreds of molecules to find the time dependence of the concentrations.
The theory presented here is valid at times longer than the diffusion time when concentrations are low. The fastest relaxation time of the diffusion-modified kinetic scheme must be much longer than the characteristic diffusion time 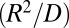 , which is typically on the submicrosecond time scale. When the concentrations are large, so that three-particle correlations are important, or when the lifetime of the bound state is comparable to the diffusion time, one can no longer use the rate equations of chemical kinetics, even in their modified forms. It is possible to extend this theory by using the self-consistent relaxation time formalism that we developed and applied to simple reactions such as
, which is typically on the submicrosecond time scale. When the concentrations are large, so that three-particle correlations are important, or when the lifetime of the bound state is comparable to the diffusion time, one can no longer use the rate equations of chemical kinetics, even in their modified forms. It is possible to extend this theory by using the self-consistent relaxation time formalism that we developed and applied to simple reactions such as  and
and 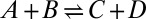 (17), where it is exact at both short and long times. For a substrate with a single catalytic site, this formalism predicts that, as a result of diffusion, the Lineweaver–Burk plot becomes nonlinear at high concentrations (18, 19). When there are multiple sites, the complexity of the theory increases dramatically, and thus there must be compelling reasons for carrying out such a generalization. For the concentrations and parameters used by Takahashi et al. (4) in the many-particle simulations of the mitogen-activated protein kinase cascade, we fully expect that the approach presented here, based on rate equations corresponding to kinetic schemes with renormalized rate constants and additional connections, would accurately describe the influence of diffusion on ultrasensitivity and bistability.
(17), where it is exact at both short and long times. For a substrate with a single catalytic site, this formalism predicts that, as a result of diffusion, the Lineweaver–Burk plot becomes nonlinear at high concentrations (18, 19). When there are multiple sites, the complexity of the theory increases dramatically, and thus there must be compelling reasons for carrying out such a generalization. For the concentrations and parameters used by Takahashi et al. (4) in the many-particle simulations of the mitogen-activated protein kinase cascade, we fully expect that the approach presented here, based on rate equations corresponding to kinetic schemes with renormalized rate constants and additional connections, would accurately describe the influence of diffusion on ultrasensitivity and bistability.
Supplementary Material
Acknowledgments
We thank A. M. Berezhkovskii, H. Qian, S. Y. Shvartsman, and P. R. ten Wolde for their helpful comments and A.R. Panchenko for numerous discussions and stimulating our interest in this problem. This work was supported by the Intramural Research Program of the National Institute of Diabetes and Digestive and Kidney Diseases, National Institutes of Health.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1319943110/-/DCSupplemental.
References
- 1.Smoluchowski M. Versuch einer mathematischen theorie der koagulationskinetik kolloider lösungen. Z Phys Chem. 1917;92:129–168. [Google Scholar]
- 2.Zel’Dovich YB Ovchinnikov AA. Asymptotic form of the approach to equilibrium and concentration fluctuations. JETP Lett. 1977;26(8):440–442. [Google Scholar]
- 3.Gopich IV, Szabo A. Asymptotic relaxation of reversible bimolecular chemical reactions. Chem Phys. 2002;284(1-2):91–102. [Google Scholar]
- 4.Takahashi K, Tănase-Nicola S, ten Wolde PR. Spatio-temporal correlations can drastically change the response of a MAPK pathway. Proc Natl Acad Sci USA. 2010;107(6):2473–2478. doi: 10.1073/pnas.0906885107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ferrell JE, Jr, Bhatt RR. Mechanistic studies of the dual phosphorylation of mitogen-activated protein kinase. J Biol Chem. 1997;272(30):19008–19016. doi: 10.1074/jbc.272.30.19008. [DOI] [PubMed] [Google Scholar]
- 6.Markevich NI, Hoek JB, Kholodenko BN. Signaling switches and bistability arising from multisite phosphorylation in protein kinase cascades. J Cell Biol. 2004;164(3):353–359. doi: 10.1083/jcb.200308060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Patwardhan P, Miller WT. Processive phosphorylation: Mechanism and biological importance. Cell Signal. 2007;19(11):2218–2226. doi: 10.1016/j.cellsig.2007.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Salazar C, Höfer T. Multisite protein phosphorylation—from molecular mechanisms to kinetic models. FEBS J. 2009;276(12):3177–3198. doi: 10.1111/j.1742-4658.2009.07027.x. [DOI] [PubMed] [Google Scholar]
- 9.Aoki K, Yamada M, Kunida K, Yasuda S, Matsuda M. Processive phosphorylation of ERK MAP kinase in mammalian cells. Proc Natl Acad Sci USA. 2011;108(31):12675–12680. doi: 10.1073/pnas.1104030108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Aoki K, Takahashi K, Kaizu K, Matsuda M. A quantitative model of ERK MAP kinase phosphorylation in crowded media. Sci Rep. 2013;3:1541. doi: 10.1038/srep01541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Collins FC, Kimball GE. Diffusion-controlled reaction rates. J Colloid Sci. 1949;4(4):425–437. [Google Scholar]
- 12.Onsager L. Initial recombination of ions. Phys Rev. 1938;54(8):554–557. [Google Scholar]
- 13.Tachiya M. General method for calculating the escape probability in diffusion-controlled reactions. J Chem Phys. 1978;69(6):2375–2376. [Google Scholar]
- 14.Schurr JM. The role of diffusion in bimolecular solution kinetics. Biophys J. 1970;10(8):700–716. doi: 10.1016/S0006-3495(70)86330-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Shoup D, Szabo A. Role of diffusion in ligand binding to macromolecules and cell-bound receptors. Biophys J. 1982;40(1):33–39. doi: 10.1016/S0006-3495(82)84455-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Dushek O, van der Merwe PA, Shahrezaei V. Ultrasensitivity in multisite phosphorylation of membrane-anchored proteins. Biophys J. 2011;100(5):1189–1197. doi: 10.1016/j.bpj.2011.01.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gopich IV, Szabo A. Kinetics of reversible diffusion influenced reactions: The self-consistent relaxation time approximation. J Chem Phys. 2002;117(2):507–517. [Google Scholar]
- 18.Park S, Agmon N. Theory and simulation of diffusion-controlled Michaelis-Menten kinetics for a static enzyme in solution. J Phys Chem B. 2008;112(19):5977–5987. doi: 10.1021/jp075941d. [DOI] [PubMed] [Google Scholar]
- 19.Szabo A, Zhou HX. Role of diffusion in the kinetics of reversible enzyme-catalyzed reactions. Bull Korean Chem Soc. 2012;33(3):925–928. doi: 10.5012/bkcs.2012.33.3.925. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.