Significance
The formation of nanocrystals and cracks in metallic glasses subjected to cyclically varying strains in micro- and nanoscale systems is a topic of scientific and technological interest. However, no real-time studies of such phenomena in fatigued metallic glasses have thus far been reported. Here we present unique observations of nanocrystallization and the onset and progression of fatigue failure in a metallic glass through cyclic straining experiments conducted inside a high-resolution transmission electron microscope. Molecular dynamics simulations were also performed to elucidate the underlying mechanisms. We expect that these techniques and results will provide unique fundamental insights into how crystallization occurs in a wide variety of amorphous materials and will help develop strategies for the design and use of metallic glasses.
Keywords: fatigue crack initiation, fatigue crack growth, fracture, shear diffusion transformation zone
Abstract
Metallic glasses (MGs) exhibit greater elastic limit and stronger resistance to plastic deformation than their crystalline metal counterparts. Their capacity to withstand plastic straining is further enhanced at submicrometer length scales. For a range of microelectromechanical applications, the resistance of MGs to damage and cracking from thermal and mechanical stress or strain cycling under partial or complete constraint is of considerable scientific and technological interest. However, to our knowledge, no real-time, high-resolution transmission electron microscopy observations are available of crystallization, damage, and failure from the controlled imposition of cyclic strains or displacements in any metallic glass. Here we present the results of a unique in situ study, inside a high-resolution transmission electron microscope, of glass-to-crystal formation and fatigue of an Al-based MG. We demonstrate that cyclic straining progressively leads to nanoscale surface roughening in the highly deformed region of the starter notch, causing crack nucleation and formation of nanocrystals. The growth of these nanograins during cyclic straining impedes subsequent crack growth by bridging the crack. In distinct contrast to this fatigue behavior, only distributed nucleation of smaller nanocrystals is observed with no surface roughening under monotonic deformation. We further show through molecular dynamics simulation that these findings can be rationalized by the accumulation of strain-induced nonaffine atomic rearrangements that effectively enhances diffusion through random walk during repeated strain cycling. The present results thus provide unique insights into fundamental mechanisms of fatigue of MGs that would help shape strategies for material design and engineering applications.
Metallic glasses (MGs) possess several unique physical properties, including greater elastic limit and stronger resistance to plastic deformation, compared with crystalline metals and alloys (1–7). For a range of microelectromechanical applications (1, 7–12), the damage tolerance and crack resistance of MGs from thermal and mechanical stress or strain cycling under partial or complete constraint is of significant scientific and technological interest (13–18). Bulk MGs can undergo fully reversible elastic deformation to a strain limit of about 2%, more than an order of magnitude greater than that of coarse-grained crystalline metals, whereupon inelastic deformation commences at stress levels on the order of gigapascals (1, 2). Such high strength, however, is often accompanied by very limited ductility at room temperature. Experiments on MGs in thin-film form or as small-volume structures (typically hundreds of nanometers in linear dimensions) reveal that their elastic strain limit and corresponding strength are further enhanced, to values double those of bulk MGs (7–9). These findings suggest opportunities to use MGs in micro- and nanoscale systems and flexible electronic devices. Such applications, in addition to those in traditional structural components, also inevitably involve service conditions that introduce cyclic variations in thermal stresses and mechanical vibrations, as well as fully or partially constrained deformation. Consequently, the resistance of MGs to the onset and progression of deformation, damage, and cracking under cyclic straining is a topic of research and practical interest (15–22). Despite this need, the fatigue characteristics and mechanisms of MGs are not well understood, and to our knowledge no studies have been performed to date to document real-time, high-resolution observations of cyclic deformation and failure mechanisms of any MG inside a TEM.
Results and Discussion
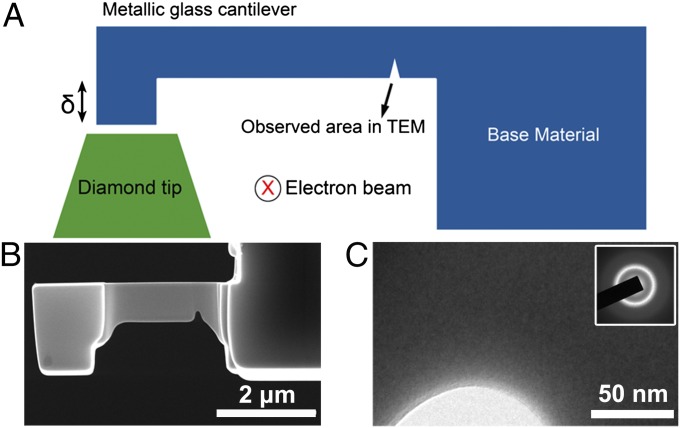
In this work, microbeams of an Al88Fe7Gd5 MG were fabricated through focused ion beam (FIB) machining from a melt-spun ribbon. This microfabrication process introduced a starter notch in the MG test specimen (Fig. 1A) so that fatigue damage and cracking occur within the field of view in the transmission electron microscope (TEM). Fig. 1B is a scanning electron microscope (SEM) image of an actual test specimen (with a total microbeam length of 3,300 nm, a middle section width of 800 nm, a middle section thickness of ∼100 nm, and an initial notch length of ∼220 nm). Cyclic deformation was applied in situ through a Hysitron PI95 deformation device inside a TEM (JEM-2100F; JEOL). Because typical deformation conditions potentially imposed on MGs in microsystems are likely to be displacement/strain controlled rather than stress controlled, cyclic straining was applied under a displacement-controlled mode. Our ability to impose fixed values of cyclic displacements δ (indicated in Fig. 1A) in a well-controlled manner using the in situ deformation stage inside the high-resolution TEM enables us to establish quantitative and mechanistic relationships among microstructure, mechanical deformation, onset, and progression of damage and failure at the atomic scale (5). The imposed displacement was controlled between a minimum value of 160 nm and a maximum value of 400 nm at a constant cyclic frequency of 1 Hz (triangular waveform), and the corresponding strain range was between 0.8% and 2.1%. Fig. 1C is a TEM image of the semicircular notch-tip region where the tip radius is about 25 nm. Selected area diffraction patterns (SADP) of this as-fabricated, untested notch-tip region (Fig. 1C, Inset) confirm a fully amorphous atomic structure.
Fig. 1.
In situ fatigue testing of the metallic glass inside a TEM. (A) Schematic of the experimental setup. Note that the electron beam direction is perpendicular to the plane. (B) SEM image showing a sample fabricated by a FIB. (C) Bright-field TEM image of the notch tip before testing shows that the sample has a fully amorphous structure, as evidenced by the SADP (Inset).
Fig. 2A compares three high-magnification images of the notch-tip region for the untested, cyclically strained, and monotonically strained specimens. Before any mechanical loading, the as-fabricated specimen shown in Fig. 2A, Left reveals a notch-tip region that is “smooth” at the scale of observation. Fig. 2A, Center shows that repeated notch-tip straining caused by 490 displacement cycles results in the “roughening” of the surface of the notch at the nanometer scale. This behavior is analogous to the process of surface roughening introduced by the irreversibility of cyclic slip in crystalline metals whereby initially smooth surfaces of the specimen form “intrusions” and “extrusions”, providing sites for fatigue crack nucleation (23). However, the corresponding SADP found no signs of crystallization as of 490 cycles. If the specimen was subjected to monotonic loading with a maximum strain of ∼12%, no obvious surface roughening was visible at the free surface of the notch (Fig. 2A, Right) or even in the vicinity of a shear band that emanated from the surface under intense strain localization (Fig. S1). It is thus seen from the three images in Fig. 2A that repeated cyclic loading leads to surface damage in the form of atomic scale roughening after several hundred cycles.
Fig. 2.
Microstructure evolution of Al88Fe7Gd5 metallic glass in response to cyclic straining. (A) High-magnification images of the notch-tip region for the untested, cyclically strained (maximum strain ∼2.1%), and monotonically strained (maximum strain >10%) specimens. (B) Fatigue crack morphology after 980, 1,470, and 1,960 cycles, respectively. SADP (Inset) demonstrated the existence of crystalline phase ahead of the crack tip. Note grain growth and crack-tip blunting with cyclic straining. (C) High-resolution TEM observation of two grains (G1 and G2) ahead of the crack tip (Left) and their coalescence after 490 additional cycles (Center). FFT (Left Inset) suggested the initial angle between the two grains was ∼15°. Inverse FFT (Right) of the part framed by the solid white box (Center) revealed that the final “giant” grain contained several dislocations, indicated by the white symbols (Right).
Fig. 2B is a collection of three bright-field TEM images of the notch-tip region after 980, 1,470 and 1,960 cycles, respectively. These images, along with SI Text, reveal the following mechanistic processes. Local cyclic deformation at the roughened surface of the notch tip leads to the initiation of a fatigue crack. Many tiny nanograins are nucleated in this highly strained region. High-resolution video photography of the crack tip shows the growth of a single nanocrystal at the fatigue crack tip with an increasing number of fatigue cycles (Movie S1). By the end of 1,960 cycles, the nanocrystal had grown to a diameter of ∼27 nm. Fig. 2B, Right Inset shows the SADP taken from the corresponding crack-tip area that confirmed the existence of the “giant” grain as well as a few satellite grains in the surrounding amorphous matrix. The grain size and its distribution resulting from cyclic straining are very different from those from monotonic loading (24–27) with similar test geometry. The nanograins formed by monotonic loading are localized in the shear band ahead of the notch and had a grain size of only a few nanometers (for example, Fig. S2). To assess how thermally induced nanocrystallization differs from that mechanically induced by monotonic or cyclic straining, we performed additional experiments. Thermal treatment of an Al-based MG ribbon (heated to 150 °C for about 20 min in the air) produces nanograins of approximately equal size over the entire specimen as shown in Fig. S3. Fig. S3 also indicates that all of the nanocrystals have a face-centered cubic structure irrespective of whether they were induced thermally or by monotonic or cyclic mechanical deformation.
The process of nanocrystal formation and growth is further elucidated by the three high-resolution TEM images in Fig. 2C. Fig. 2C, Left and Center represents the crystalline structure within the amorphous metal matrix after 1,470 and 1,960 displacement cycles, respectively. Fig. 2C, Left and Center shows a larger grain (G1) neighboring a smaller grain (G2); Fig. 2C, Left Inset is based on a fast Fourier transformation (FFT) analysis of an area that contains both G1 and G2, with the orientation mismatch between the grains being ∼15°. This was also confirmed by measuring the lattice fringe in a magnified view. After being subjected to an additional 490 cycles, G1 grew further by consuming G2, as was supported by the FFT image (Fig. 2C, Center Inset) as well as by the corresponding inverse FFT image (Fig. 2C, Right), which revealed that the large grain contained several dislocations.
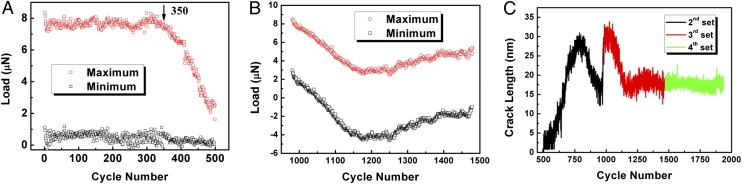
Having established through real-time, high-resolution TEM that cyclic deformation at room temperature leads to nanocrystal formation and growth in the MG, we now show quantitatively how this structure evolution influences the rate of fatigue crack growth (see SI Text, Estimation of Crack Length and Figs. S4–S7 for the definition of crack length). Consider first the variation of the maximum and minimum load during the first 490 fatigue cycles imposed under displacement amplitude control. At the beginning of fatigue loading, the load amplitude corresponding to the fixed displacement amplitude is relatively constant for about 350 cycles, because local cyclic straining produces primarily elastic deformation (Fig. 3A). The initiation of nanoscale roughening of the free surface of the notch tip (as was seen in Fig. 2A, Center), between cycle numbers 350 and 490, appears to have facilitated the onset of inelastic deformation, as supported by the sample edge roughening shown in Fig. 2A, Center. A crack was observed to nucleate at the beginning of the second set of the cyclic loading tests at around 500 cycles. Fig. 3C is a plot of the fatigue crack length, defined as the distance between the advancing tip and the original edge surface position, as a function of the number of cycles, beginning with cycle no. 500. For the subsequent 300 cycles, the crack length increased with fatigue loading. The intense local straining ahead of the advancing sharp fatigue crack, however, leads to a zone of nanocrystals, typically several nanometers in diameter. The coalescence of these nanocrystals (as indicated by the images shown in Fig. 2 B and C), however, produces a large grain that impedes further crack advance. Nanograin growth influences the rate of fatigue crack growth in several distinct and measurable ways. First, with the growth of several nanograins, crack length begins to decrease (between cycle nos. 800 and 980 in Fig. 3C) with an increase in the number of cycles as the presence of a large grain “shields” the crack tip from the severity of cyclic straining. Once the crack tip “breaks free” from the influence of this shielding grain, an abrupt increase in crack length occurs due to a burst of crack growth. However, as the surrounding nanocrystals ahead of this advancing crack front grow further, the apparent crack length decreases once again because of the shielding effect (region between cycle nos. 1,000 and 1,200 in Fig. 3C). This shielding effect is clearly manifested as a distinct load drop between cycle nos. 1,000 and 1,200 in Fig. 3B. Fig. 3B also shows a transition from tension–tension to tension–compression fatigue load, i.e., starting from cycle no. ∼1,050, as a consequence of plastic deformation. The concurrent mechanisms of damage evolution at the crack tip, nanocrystallization, and grain growth thus lead to the anomalous crack growth response shown in Fig. 3C. Another consequence of this anomalous fatigue behavior is the blunting of the crack tip with cyclic loading and grain growth (Fig. 2B).
Fig. 3.
Maximum/minimum loads under a fixed value of imposed displacement amplitude and crack length evolution as a function of fatigue cycles. (A) Load vs. cycle number for the first set of tests spanning 490 cycles. (B) Load vs. cycle number for the third set from 981 to 1,470 cycles. (C) Crack length evolution with increasing cycle number.
Temperature-driven structural disorder-to-order transitions such as the nucleation of crystals in liquid upon cooling have been extensively studied (28–30). However, stress-driven disorder-to-order transitions, such as the one described in this work, are seldom investigated (24, 25). In contrast to scalar temperature, tensorial stress stimuli for crystallization should lead to a preferred texture/directionality. Indeed, our molecular dynamics simulations below show that the nucleated nanocrystals tend to have their crystallographic slip planes parallel to the local shear stress direction. Irrespective of stimulation by temperature or stress, going from structural disorder to order requires “diffusive” reshuffling of atoms. Although the ability of MG to plastically deform under stress by shear transformation zones (STZs) is well known (2, 11), a key question here is how stress enhances “atomic diffusivity” in MG. Prior work (24) on room temperature nanocrystallization during the nanoindentation of a bulk metallic glass also pointed to the possibility of such enhanced atomic diffusivity from severe local stress and flow-induced dilation. To quantify and understand the atomic structure evolution, we carried out molecular dynamics (MD) simulations of cyclic-stress–induced glass–crystal transition. We considered a binary MG Al50Fe50, which shows structure evolution and plastic deformation behavior similar to the MG studied in cyclic loading experiments (details of atomistic simulation can be found in SI Text, Molecular Dynamics Simulation).
The evolution of atomic geometries is analyzed by the following “deformation–diffusion” decomposition (31, 32),
where i is the atom being analyzed, 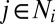 are i’s original neighbors (defined within some cutoff radius) in a reference configuration,
are i’s original neighbors (defined within some cutoff radius) in a reference configuration, 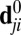 is the original distance between atoms j and i in the reference configuration, and
is the original distance between atoms j and i in the reference configuration, and 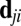 is their current distance vector. The first term in [1] reflects local deformation (shape change), whereas the second term reflects additional atomic movements or shuffling beyond mere shape change. The extent of local diffusion is defined by
is their current distance vector. The first term in [1] reflects local deformation (shape change), whereas the second term reflects additional atomic movements or shuffling beyond mere shape change. The extent of local diffusion is defined by
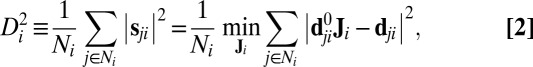 |
where the 3 × 3 local deformation gradient 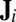 needs to be numerically optimized to minimize
needs to be numerically optimized to minimize 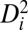 . Although
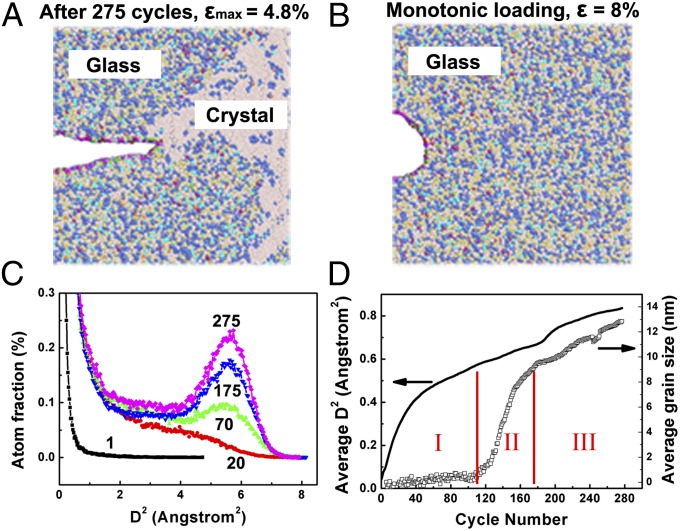
. Although 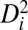 might be small, it accumulates during repeated cyclic mechanical deformation. Fig. 4A shows the atomic configuration of the notch area after 275 cycles of strain (see Fig. S8A for the details of the MD simulation setup): The long-range periodic packing of atoms clearly corresponds to crystallization in the active zone. Statistics of the atomistic
might be small, it accumulates during repeated cyclic mechanical deformation. Fig. 4A shows the atomic configuration of the notch area after 275 cycles of strain (see Fig. S8A for the details of the MD simulation setup): The long-range periodic packing of atoms clearly corresponds to crystallization in the active zone. Statistics of the atomistic 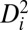 after different cycles are plotted in Fig. 4C. The variation of atom fraction vs.
after different cycles are plotted in Fig. 4C. The variation of atom fraction vs. 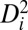 for the first half cycle (representing monotonic loading) showed a sharp decrease. Then it gradually increased to reach a peak value at large diffusional displacement (
for the first half cycle (representing monotonic loading) showed a sharp decrease. Then it gradually increased to reach a peak value at large diffusional displacement (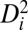 ) as the cycle number increased; e.g., the corresponding
) as the cycle number increased; e.g., the corresponding 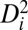 equaled 5.8 Å2 for the peak after 275 cycles (Fig. S8A). Although the peak
equaled 5.8 Å2 for the peak after 275 cycles (Fig. S8A). Although the peak 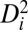 becomes sharper with increasing numbers of cycles, it occurs at an approximately constant square displacement value of about
becomes sharper with increasing numbers of cycles, it occurs at an approximately constant square displacement value of about 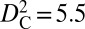 Å2, which characterizes the initiation of crystallization. The root mean square value of this critical threshold,
Å2, which characterizes the initiation of crystallization. The root mean square value of this critical threshold, 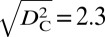 Å, can be regarded as an upper bound to the minimal “glass-to-crystal” distance
Å, can be regarded as an upper bound to the minimal “glass-to-crystal” distance 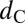 , defined to be the minimal nonaffine displacement per atom necessary to reorder a disordered system, akin to the least number of steps to solve a Rubik’s Cube. The smallness of
, defined to be the minimal nonaffine displacement per atom necessary to reorder a disordered system, akin to the least number of steps to solve a Rubik’s Cube. The smallness of 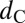 bounded by our simulation trajectories indicates that the glass configurations studied here are not too “far” from their nearest crystal configuration, at least for binary glasses. However, at low temperature T and zero external stress σext = 0, the energy barriers Q are still too high despite the short distance in phase space (33) on the potential energy landscape; thus only when σext is high enough can sufficient atomic shuffling occur, along with local and global shape changes. Our MD trajectories confirm that stress drives both plasticity (shear transformation zone) and diffusion (“diffusion transformation zone”) in metallic glass, the rate of which may be modeled by a generic transition-state theory expression
bounded by our simulation trajectories indicates that the glass configurations studied here are not too “far” from their nearest crystal configuration, at least for binary glasses. However, at low temperature T and zero external stress σext = 0, the energy barriers Q are still too high despite the short distance in phase space (33) on the potential energy landscape; thus only when σext is high enough can sufficient atomic shuffling occur, along with local and global shape changes. Our MD trajectories confirm that stress drives both plasticity (shear transformation zone) and diffusion (“diffusion transformation zone”) in metallic glass, the rate of which may be modeled by a generic transition-state theory expression
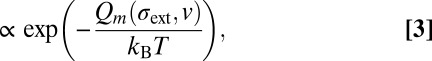 |
where 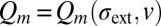 is a microscopic activation barrier; v is the “free volume”, an internal state variable that could change after each event; and m is the event menu option (see figure 1 of ref. 34 for illustration). The shear transformation zone thus can also possess a dual character of diffusion and may be called a “shear diffusion transformation zone” (SDTZ). Note that in [3], stress has both indirect and direct effects on the rate of diffusion. The indirect effects come from a change of v after stress-driven flow [rejuvenation (34, 35) or flow-induced dilation (24)] and later even a possible change of T (32). However, there is a direct effect of stress on diffusion also, as represented by the first dependency of
is a microscopic activation barrier; v is the “free volume”, an internal state variable that could change after each event; and m is the event menu option (see figure 1 of ref. 34 for illustration). The shear transformation zone thus can also possess a dual character of diffusion and may be called a “shear diffusion transformation zone” (SDTZ). Note that in [3], stress has both indirect and direct effects on the rate of diffusion. The indirect effects come from a change of v after stress-driven flow [rejuvenation (34, 35) or flow-induced dilation (24)] and later even a possible change of T (32). However, there is a direct effect of stress on diffusion also, as represented by the first dependency of 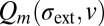 . In [3], increasing σext, increasing v, or increasing T all should lead to an accelerated rate of diffusion in metallic glass, but the functional dependencies on
. In [3], increasing σext, increasing v, or increasing T all should lead to an accelerated rate of diffusion in metallic glass, but the functional dependencies on 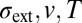 are generally not the same due to inequivalent positions in the fraction
are generally not the same due to inequivalent positions in the fraction 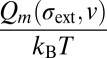 .
.
Fig. 4.
MD simulation on fatigue tests of Al-Fe metallic glass. Two identical specimens were tested under cyclic straining (between strain limits of 3 ± 1.8%) and monotonic loading (strained to 8%). (A) The crystalline phase can be seen clearly after 275 cycles. (B) The sample remained amorphous under monotonic loading even though the strain reached 8%. (C) The distribution of the atom fraction vs. the square of nanoaffine displacement (D2) for cycle nos. 1, 20, 70, 175, and 275. (D) Both the averaged D2 (solid black line) and the average grain size (curve with circles) increased with increasing cycle number.
The averaged 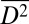 showed a nonlinear increase with increasing strain cycles (Fig. 4D, black solid line). Correspondingly, the average grain size (
showed a nonlinear increase with increasing strain cycles (Fig. 4D, black solid line). Correspondingly, the average grain size (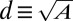 ), where A is the grain area, can be classified into three regimes according to the cycle number. For regime I (cycles ranging from 1 to ∼110), the average grain size remains subnanometer (Fig. 4D, curve with circles). For regime II (cycles ranging from 110 to ∼175), rapid grain growth sets in suddenly following the incubation period in regime I. After the cycle number exceeds 175 (in regime III), the grain growth rate decreases significantly.
), where A is the grain area, can be classified into three regimes according to the cycle number. For regime I (cycles ranging from 1 to ∼110), the average grain size remains subnanometer (Fig. 4D, curve with circles). For regime II (cycles ranging from 110 to ∼175), rapid grain growth sets in suddenly following the incubation period in regime I. After the cycle number exceeds 175 (in regime III), the grain growth rate decreases significantly.
For comparison, atomistic simulation of monotonic deformation (imposed strain ∼8%) of the same sample geometry is shown in Fig. 4B (also Fig. S8B). The active zone was along the plane with maximum shear stress. Neither obvious localization nor long-period packing of atoms (of glassy structure) was observed in these zones (e.g., Fig. 4B). This is further supported by the observation that the fraction of atoms with larger nonaffine displacement remains quite low. We compute a “diffusion-to-shear ratio” 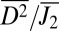 , where
, where 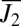 is the mean Mises shear strain invariant from
is the mean Mises shear strain invariant from 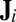 , to quantify the relative diffusive to displacive nature of the structural transformation, based on atomic trajectories. From our simulations, monotonic loading beyond global yielding gives a lower
, to quantify the relative diffusive to displacive nature of the structural transformation, based on atomic trajectories. From our simulations, monotonic loading beyond global yielding gives a lower 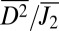 than subyielding cyclic loading. Furthermore,
than subyielding cyclic loading. Furthermore, 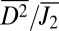 increases with cycle number, due to the cumulative nature of random atomic shuffling displacements that occur by random walk. So it is easier to observe crystallization in small-scale simulations by cyclic deformation than by monotonic deformation. We note that crystallization is still observed experimentally in monotonic loading (24), but the local strains in the shear bands observed in the experimental samples are much larger than what can be easily achieved in simulations. These shear bands cause flow dilatation (24, 36, 37) that triggers more nucleation of nanocrystals inside a mature shear band. In contrast, the relatively lower stress (below the yielding point) under cyclic loading was not high enough to generate a shear band in one cycle. Instead, local accumulation of nonaffine displacements (Fig. S8A) continues with an increase in strain cycles culminating in an amorphous to crystal transition (Fig. 2). It is worth noting that crystallization in our experiments and simulations is a mechanical deformation-driven process without obvious temperature rise, consistent with previous studies (24) of nanocrystal formation at room temperature in a metallic glass subject to nanoindentation.
increases with cycle number, due to the cumulative nature of random atomic shuffling displacements that occur by random walk. So it is easier to observe crystallization in small-scale simulations by cyclic deformation than by monotonic deformation. We note that crystallization is still observed experimentally in monotonic loading (24), but the local strains in the shear bands observed in the experimental samples are much larger than what can be easily achieved in simulations. These shear bands cause flow dilatation (24, 36, 37) that triggers more nucleation of nanocrystals inside a mature shear band. In contrast, the relatively lower stress (below the yielding point) under cyclic loading was not high enough to generate a shear band in one cycle. Instead, local accumulation of nonaffine displacements (Fig. S8A) continues with an increase in strain cycles culminating in an amorphous to crystal transition (Fig. 2). It is worth noting that crystallization in our experiments and simulations is a mechanical deformation-driven process without obvious temperature rise, consistent with previous studies (24) of nanocrystal formation at room temperature in a metallic glass subject to nanoindentation.
The simulated snapshots of the evolution of atomistic configuration in the MG are shown in Fig. S9. Our simulations show that the nucleated crystals tend to have their crystallographic slip or close-packed plane parallel to the local shear stress direction at the nucleation site. Only atoms with coordinate number (CN) ∼14 (the number of atoms perceived as neighbors in the body centered cubic (bcc) crystal that formed in the Al50Fe50 simulation model) are displayed. After 110 cycles, some atoms with CN ∼14 aggregated into a cluster (nanocrystal) on the right side ahead of the propagating crack, and this crystal grew rapidly until it reached the fatigue crack tip. The crystal was not very stable at the beginning and broke up into several pieces during the unloading. Along with increasing strain cycles, the central nucleus gradually became larger and more stable such that its “transient” aggregation with some other tiny clusters became a more permanent structure (Movie S2). The scenario agrees well with the experimental observations depicted in Fig. 2B. The corresponding cyclic load and crack length evolution from MD simulation (Fig. S9 B and C) showed trends similar to those observed in the experiments (Fig. 3 B and C), where a switch from local tension–tension to tension–compression fatigue was noted as a consequence of the shielding of the crack and the attendant retardation of crack growth by nanograin formation and growth.
The abnormal fatigue crack propagation behavior in nanoscale Al88Fe7Gd5 MG could be attributed to several factors. First, from the viewpoint of energy, repeated straining causes sufficient 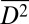 to induce the glass-to-crystal transition near the fatigue crack tip, which dissipates mechanical energy, thereby reducing the effective driving force for crack propagation. Second, MGs at the submicron scale exhibit higher plastic flow stress and more distributed shear transformations than their bulk counterparts (4, 5, 11). Third, for small-volume samples, the phase transition ahead of the fatigue crack could achieve much higher efficiencies (because of a higher concentration of the number of nanocrystals per unit volume) to improve the fatigue tolerance, compared with that in bulk samples. Fourth, cyclic straining-induced crystalline phases near the fatigue crack tip, in conjunction with a plasticity-induced tension-compression fatigue load with displacement-controlled straining, would bridge the wakes of crack and thus extrinsically enhance the fatigue tolerance (38). This is evidenced by the unexpected increase of maximum load in Fig. 3 and by the heavy plastic deformation experienced in the crystalline phase in Fig. 2 (with dislocations inside crystals, as seen in Fig. 2C). In addition, the volume shrinkage [MGs are slightly less dense than their crystalline counterparts (2, 39)] during glass-to-crystal transition might induce additional (residual) compressive stress in the surrounding MG matrix (40), which favors crystallization and grain growth processes in MGs (25, 39). In other words, the fatigue tolerance of the MG beam is self-improved in situ with strain cycles.
to induce the glass-to-crystal transition near the fatigue crack tip, which dissipates mechanical energy, thereby reducing the effective driving force for crack propagation. Second, MGs at the submicron scale exhibit higher plastic flow stress and more distributed shear transformations than their bulk counterparts (4, 5, 11). Third, for small-volume samples, the phase transition ahead of the fatigue crack could achieve much higher efficiencies (because of a higher concentration of the number of nanocrystals per unit volume) to improve the fatigue tolerance, compared with that in bulk samples. Fourth, cyclic straining-induced crystalline phases near the fatigue crack tip, in conjunction with a plasticity-induced tension-compression fatigue load with displacement-controlled straining, would bridge the wakes of crack and thus extrinsically enhance the fatigue tolerance (38). This is evidenced by the unexpected increase of maximum load in Fig. 3 and by the heavy plastic deformation experienced in the crystalline phase in Fig. 2 (with dislocations inside crystals, as seen in Fig. 2C). In addition, the volume shrinkage [MGs are slightly less dense than their crystalline counterparts (2, 39)] during glass-to-crystal transition might induce additional (residual) compressive stress in the surrounding MG matrix (40), which favors crystallization and grain growth processes in MGs (25, 39). In other words, the fatigue tolerance of the MG beam is self-improved in situ with strain cycles.
Conclusion
In summary, glass-to-crystal transition induced by cyclic straining has been demonstrated using quantitative in situ fatigue tests performed on an Al-based MG inside a TEM. It is shown that cyclic straining leads to the nanoscale roughening of an initially smooth surface in the metallic glass. This process is mechanistically analogous to the roughening of surfaces of metallic crystals due to fatigue whereby intrusions and extrusions are created at surfaces, providing preferential sites of stress concentration for fatigue crack nucleation. Such surface roughening is visibly absent if the MG is instead subjected to monotonic straining even to much higher plastic deformation levels. Nanocrystals nucleate around zones of intense deformation produced by mechanical straining. Under cyclic straining, nanocrystals coalesce and grow to average dimensions several times larger than those seen under monotonic straining. Molecular dynamics simulations provide a clear mechanistic basis for these experimentally observed processes. The simulations reveal that the accumulation of local nonaffine displacements, facilitated by stress and assisted by the excess volume that is continuously generated within the shear transformation zones of the MG, leads to the formation and growth of nanocrystals. Our MD results show that the mean square displacement, 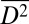 , which is a measure of the extent of the local atomic shuffling needed to achieve a disorder-to-order transition, accumulates with stress cycles. This stress-assisted “effective diffusion” with enhanced “atomic random walk” by SDTZ events resembles the high atomic mobility at elevated temperatures and rationalizes why cyclic straining leads to nanocrystallization at room temperature. The formation of nanograins, which grow to average diameters as large as about 27 nm, causes shielding of the fatigue crack by reducing the effective driving force for crack growth and resisting crack propagation. These results documenting real-time and high-resolution mechanical response provide fundamental insights into the atomic-level mechanisms governing fatigue and crystallization of metallic glasses.
, which is a measure of the extent of the local atomic shuffling needed to achieve a disorder-to-order transition, accumulates with stress cycles. This stress-assisted “effective diffusion” with enhanced “atomic random walk” by SDTZ events resembles the high atomic mobility at elevated temperatures and rationalizes why cyclic straining leads to nanocrystallization at room temperature. The formation of nanograins, which grow to average diameters as large as about 27 nm, causes shielding of the fatigue crack by reducing the effective driving force for crack growth and resisting crack propagation. These results documenting real-time and high-resolution mechanical response provide fundamental insights into the atomic-level mechanisms governing fatigue and crystallization of metallic glasses.
Methods
The submicron-sized cantilever beams were fabricated using a FIB (Helios NanoLab600i) from Al88Fe7Gd5 metallic glass ribbons produced by melt spinning. In situ mechanical testing was conducted inside a JEM-2100F TEM (JEOL) equipped with two CCD cameras, i.e., Model 830 and ORIUS SC200 (Gatan), using a PI95 TEM PicoIndenter (Hysitron) with a time and displacement resolution of ∼0.4 μN and ∼1 nm, respectively. Both the cyclic and the monotonic loading tests were conducted in displacement-control mode, which is more sensitive to transient structure evolution. Fig. S10 shows a typical cyclic displacement loading function with a triangular waveform and a frequency 1 Hz; an initial displacement of 400 nm (∼50% of the middle section sample width) was applied from the initial zero-force configuration followed by cyclic displacements between 400 nm and 150 nm. To obtain detailed structure information (diffraction pattern and high-quality images), the fatigue experiment was terminated after each 490 cycles to perform high-resolution imaging. After the high-resolution image was obtained, another set of fatigue testing was started again on the same specimen with the same displacement-controlled amplitude, while taking the previously unloaded configuration as the reference zero displacement position. Four samples have been cyclically tested and more than 10 samples have been monotonically tested closely under identical conditions. All results shown in this work were repeatable. Details of molecular dynamics simulation are given in SI Text.
Supplementary Material
Acknowledgments
This work was supported by the Natural Science Foundation of China under the following Grants: 50925104, 51231005, 51321003, the 973 Programs of China (2010CB631003 and 2012CB619402), and the 111 Project of China (B06025). J.L. acknowledges support by the US National Science Foundation (NSF) under Grants NSF DMR-1240933 and DMR-1120901, and E.M. acknowledges support from the NSF under Grant NSF-DMR-0904188. M.D. and S.S. acknowledge support from the Singapore–Massachusetts Institute of Technology Alliance (SMA).
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1320235110/-/DCSupplemental.
References
- 1.Greer AL, Ma E. Bulk metallic glasses: At the cutting edge of metals research. MRS Bull. 2007;32(8):611–615. [Google Scholar]
- 2.Schuh CA, Hufnagel TC, Ramamurty U. Overview No.144 - Mechanical behavior of amorphous alloys. Acta Mater. 2007;55(12):4067–4109. [Google Scholar]
- 3.Wang WH, Dong C, Shek CH. Bulk metallic glasses. Mater Sci Eng Rep. 2004;44(2–3):45–89. [Google Scholar]
- 4.Guo H, et al. Tensile ductility and necking of metallic glass. Nat Mater. 2007;6(10):735–739. doi: 10.1038/nmat1984. [DOI] [PubMed] [Google Scholar]
- 5.Shan ZW, et al. Plastic flow and failure resistance of metallic glass: Insight from in situ compression of nanopillars. Phys Rev B. 2008;77(15):155419. [Google Scholar]
- 6.Chen CQ, Pei YT, De Hosson JTM. Effects of size on the mechanical response of metallic glasses investigated through in situ TEM bending and compression experiments. Acta Mater. 2010;58(1):189–200. [Google Scholar]
- 7.Jang D, Greer JR. Transition from a strong-yet-brittle to a stronger-and-ductile state by size reduction of metallic glasses. Nat Mater. 2010;9(3):215–219. doi: 10.1038/nmat2622. [DOI] [PubMed] [Google Scholar]
- 8.Tian L, et al. Approaching the ideal elastic limit of metallic glasses. Nat Commun. 2012;3:609. doi: 10.1038/ncomms1619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wang CC, et al. Sample size matters for Al88Fe7Gd5 metallic glass: Smaller is stronger. Acta Mater. 2012;60(13–14):5370–5379. [Google Scholar]
- 10.Kumar G, Desai A, Schroers J. Bulk metallic glass: The smaller the better. Adv Mater. 2011;23(4):461–476. doi: 10.1002/adma.201002148. [DOI] [PubMed] [Google Scholar]
- 11.Cheng YQ, Ma E. Atomic-level structure and structure-property relationship in metallic glasses. Prog Mater Sci. 2011;56(4):379–473. [Google Scholar]
- 12.Greer JR, De Hosson JTM. Plasticity in small-sized metallic systems: Intrinsic versus extrinsic size effect. Prog Mater Sci. 2011;56(6):654–724. [Google Scholar]
- 13.Wang GY, Liaw PK, Morrison ML. Progress in studying the fatigue behavior of Zr-based bulk-metallic glasses and their composites. Intermetallics. 2009;17(8):579–590. [Google Scholar]
- 14.Wang GY, Liaw PK, Yokoyama Y, Inoue A, Liu CT. Fatigue behavior of Zr-based bulk-metallic glasses. Mater Sci Eng A Struct Mater Prop Microstruct Process. 2008;494(1–2):314–323. [Google Scholar]
- 15.Jang DC, Maass R, Wang GY, Liaw PK, Greer JR. Fatigue deformation of microsized metallic glasses. Scr Mater. 2013;68(10):773–776. [Google Scholar]
- 16.Chuang C-P, et al. Fatigue-induced damage in zr-based bulk metallic glasses. Sci Rep. 2013;3:2578. doi: 10.1038/srep02578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gilbert CJ, Ritchie RO, Johnson WL. Fracture toughness and fatigue-crack propagation in a Zr-Ti-Ni-Cu-Be bulk metallic glass. Appl Phys Lett. 1997;71(4):476–478. [Google Scholar]
- 18.Gilbert CJ, Schroeder V, Ritchie RO. Mechanisms for fracture and fatigue-crack propagation in a bulk metallic glass. Metall Mater Trans A Phys Metall Mater Sci. 1999;30(7):1739–1753. [Google Scholar]
- 19.Menzel BC, Dauskardt RH. Stress-life fatigue behavior of a Zr-based bulk metallic glass. Acta Mater. 2006;54(4):935–943. [Google Scholar]
- 20.Hess PA, Menzel BC, Dauskardt RH. Fatigue damage in bulk metallic glass II: Experiments. Scr Mater. 2006;54(3):355–361. [Google Scholar]
- 21.Wang GY, Liaw PK. Bending-fatigue behavior of bulk metallic glasses and their composites. JOM. 2010;62(4):25–33. [Google Scholar]
- 22.Flores KM, Johnson WL, Dauskardt RH. Fracture and fatigue behavior of a Zr-Ti-Nb ductile phase reinforced bulk metallic glass matrix composite. Scr Mater. 2003;49(12):1181–1187. [Google Scholar]
- 23.Suresh S. Fatigue of Materials. Cambridge, UK: Cambridge Univ Press; 1998. [Google Scholar]
- 24.Kim JJ, Choi Y, Suresh S, Argon AS. Nanocrystallization during nanoindentation of a bulk amorphous metal alloy at room temperature. Science. 2002;295(5555):654–657. doi: 10.1126/science.1067453. [DOI] [PubMed] [Google Scholar]
- 25.Jiang WH, Atzmon M. The effect of compression and tension on shear-band structure and nanocrystallization in amorphous Al90Fe5Gd5: A high-resolution transmission electron microscopy study. Acta Mater. 2003;51(14):4095–4105. [Google Scholar]
- 26.Chen MW, Inoue A, Zhang W, Sakurai T. Extraordinary plasticity of ductile bulk metallic glasses. Phys Rev Lett. 2006;96(24):245502. doi: 10.1103/PhysRevLett.96.245502. [DOI] [PubMed] [Google Scholar]
- 27.Yavari AR, et al. Crystallization during bending of a Pd-based metallic glass detected by x-ray microscopy. Phys Rev Lett. 2012;109(8):085501. doi: 10.1103/PhysRevLett.109.085501. [DOI] [PubMed] [Google Scholar]
- 28.Turnbull D. Formation of crystal nuclei in liquid metals. J Appl Phys. 1950;21(10):1022–1028. [Google Scholar]
- 29.Debenedetti PG. Metastable Liquids: Concepts and Principles. Princeton: Princeton Univ Press; 1996. [Google Scholar]
- 30.Kawasaki T, Tanaka H. Formation of a crystal nucleus from liquid. Proc Natl Acad Sci USA. 2010;107(32):14036–14041. doi: 10.1073/pnas.1001040107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Falk ML, Langer JS. Dynamics of viscoplastic deformation in amorphous solids. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 1998;57(6):7192–7205. [Google Scholar]
- 32.Shimizu F, Ogata S, Li J. Theory of shear banding in metallic glasses and molecular dynamics calculations. Mater Trans. 2007;48(11):2923–2927. [Google Scholar]
- 33.Zhu T, Li J, Lin X, Yip S. Stress-dependent molecular pathways of silica-water reaction. J Mech Phys Solids. 2005;53(7):1597–1623. [Google Scholar]
- 34.Zhao PY, Li J, Wang YZ. Heterogeneously randomized STZ model of metallic glasses: Softening and extreme value statistics during deformation. Int J Plast. 2013;40:1–22. [Google Scholar]
- 35.Shimizu F, Ogata S, Li J. Yield point of metallic glass. Acta Mater. 2006;54(16):4293–4298. [Google Scholar]
- 36.Donovan PE, Stobbs WM. The structure of shear bands in metallic glasses. Acta Metall. 1981;29(8):1419–1436. [Google Scholar]
- 37.Bokeloh J, Divinski SV, Reglitz G, Wilde G. Tracer measurements of atomic diffusion inside shear bands of a bulk metallic glass. Phys Rev Lett. 2011;107(23):235503. doi: 10.1103/PhysRevLett.107.235503. [DOI] [PubMed] [Google Scholar]
- 38.Ritchie RO. The conflicts between strength and toughness. Nat Mater. 2011;10(11):817–822. doi: 10.1038/nmat3115. [DOI] [PubMed] [Google Scholar]
- 39.Ye F, Lu K. Pressure effect on crystallization kinetics of an Al-La-Ni amorphous alloy. Acta Mater. 1999;47(8):2449–2454. [Google Scholar]
- 40.Olsson M, Giannakopoulos AE, Suresh S. Elastoplastic analysis of thermal cycling: Ceramic particles in a metallic matrix. J Mech Phys Solids. 1995;43(10):1639–1671. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.