Movement Variability Near Goal Equivalent Manifolds: Fluctuations, Control, and Model-Based Analysis

Abstract

Fluctuations in the repeated performance of human movements have been the subject of intense scrutiny because they are generally believed to contain important information about the function and health of the neuromotor system. A variety of approaches has been brought to bear to study of these fluctuations, however it is frequently difficult to understand how to synthesize different perspectives to give a coherent picture. Here, we describe a conceptual framework for the experimental study of motor variability that helps to unify geometrical methods, which focus on the role of motor redundancy, with dynamical methods that characterize the error-correcting processes regulating the performance of skilled tasks. We describe how goal functions, which mathematically specify the task strategy being employed, together with ideas from the control of redundant systems, allow one to formulate simple, experimentally testable dynamical models of inter-trial fluctuations. After reviewing the basic theory, we present a list of five general hypotheses on the structure of uctuations that can be expected in repeated trials of goal-directed tasks. We review recent experimental applications of this general approach, and show how it can be used to precisely characterize the error-correcting control used by human subjects.

1 Introduction

Variability from trial to trial is always observed in repeated movement tasks. These fluctuations in movement arise in part from various sources of inherent physiological noise (Faisal et al., 2008; Osborne et al., 2005; Stein et al., 2005), extending even to the genetic level (Eldar & Elowitz, 2010). It is increasingly being recognized that this noise may in fact be critical to enabling and/or enhancing physiological function (Eldar & Elowitz, 2010; McDonnell & Ward, 2011; Stein et al., 2005). Thus, inter-trial movement variability has been the subject of intense scrutiny because it is seen as crucial to our developing understanding of neuromotor health and function, including both motor control (Scott, 2004) and motor learning (Braun et al., 2009; van Beers, 2009). Certainly, this general belief is not new: clinicians concerned with the health of the nervous system have long used movement variability as an important diagnostic indicator.

Our perspective on movement variability is fundamentally dynamical in nature: that is, we take as a general working hypothesis that movement variability is a key characteristic of dynamics of biological perception-action systems. Practically speaking, this means that we analyze variability data in order to extract information about the processes by which observed fluctuations are generated and regulated.

Competing conceptual frameworks have been proposed in the literature to analyze movement fluctuations to this end, each with a primary emphasis on a different aspect of variability. Here, we focus on four of the most prominent of these frameworks: namely, those emphasizing (1) goal equivalence and task manifolds; (2) stochastic optimal control; (3) local dynamic stability; or (4) fractal dynamics. While conceptually there is considerable overlap between these categories, in practice they are represented by specific classes of experimental protocols and data analysis techniques, and have tended to be associated with distinct research groups. Clearly, however, since these methods are all describing the same physical processes, they must in some sense be consistent with each other, even if they are not carried out at the same scale of observation. However, this expectation of an underlying consistency has not always been reflected by the literature. Indeed, in some cases different methods seem to suggest contradictory interpretations. The challenge, then, is how to combine these different conceptual frameworks, and their associated data analysis methods, into a coherent description of task performance, specifically with regard to observed inter-trial fluctuations.

The first aim of this paper is to provide a review of the four conceptual frameworks enumerated above. We then move on to describe how the organization of inter-trial fluctuations can be studied by analyzing only body state variables that interact directly with goal-level performance variables. To do this, the required body-goal interaction is defined for a specific task using goal functions, which can be thought of as a hypotheses on the strategy used to perform a given task. We discuss the fundamental properties of goal functions, principal among them being the possible existence of a goal equivalent manifold (GEM) and its associated sensitivity properties. We then include the idea of “GEM aware” error-correcting optimal control, which closes the perception-action loop at the inter-trial time scale and yields models of the trial-to-trial task dynamics. These models can be used to make theoretical predictions about the structure of goal-level fluctuations, and to show how they are generated by fluctuations at the body-level. We review recent experimental applications of the GEM-based approach, showing how it provides a decomposition of movement fluctuation data that can be used to identify the strategies used to regulate task performance. The GEM framework helps to unify the task manifold, optimal control, local stability and—to a lesser extent—fractal dynamics perspectives on movement variability. It also provides a parsimonious interpretation of fluctuation data that avoids certain paradoxes found in the literature.

2 Current Perspectives on Inter-Trial Fluctuations

2.1 Goal Equivalence & Task Manifolds

Movement variability arises from intrinsic physiological noise expressed through the operation of an inherently redundant neuromotor system (Bernstein, 1967; Scott, 2004; Todorov, 2004). Much work has sought to determine how muscles are organized into functional synergies to resolve the redundancy question (d’Avella et al., 2003; Ivanenko et al., 2007; Lockhart & Ting, 2007). However, these efforts generally characterize average behavior and so provide few insights into movement variability, per se. Redundancy also gives rise to equifinality: i.e., there are many, possibly an infinite number, of ways to perform the same task (Bernstein, 1967). At its core, equifinality, also referred to as goal equivalence, is simply a mathematical consequence of the fact that the space of effective body states needed to generate a movement has significantly greater dimensionality than the space of variables needed to define the task itself.

One approach to addressing this issue experimentally is via uncontrolled manifold (UCM) analysis (Latash et al., 2002, 2007; Schöner & Scholz, 2007). This analysis is based on the fact that equifinality gives rise to a surface in the space of appropriate body-level state variables (e.g., joint angles) such that all states on this task solution manifold correspond to perfect task execution. UCM analysis assumes that such a manifold is defined at each instant along a given movement trajectory, but the independent external goal of the task is typically not considered in defining it. Rather, the task’s goal is represented by the ensemble average movement of some quantity over a set of trials. UCM analysis further postulates that motor control only corrects deviations orthogonal to the task manifold, since only they result in performance error. In contrast, deviations along this manifold are left “uncontrolled”, giving the method its name. These ideas are implemented experimentally by computing ratios of the normalized variances orthogonal to and along a candidate manifold (Latash et al., 2002; Schöner & Scholz, 2007): if a larger variance is found along the candidate manifold than normal to it, the manifold is deemed to be a UCM, indicating that it is being used to organize motor control. This approach has been applied experimentally to many different tasks, including reaching (Freitas & Scholz, 2009), throwing (Yang & Scholz, 2005), sit-to-stand (Reisman et al., 2002), quiet standing (Hsu et al., 2007), hopping (Yen & Chang, 2010), and walking (Robert et al., 2009). The approach has also been used to explore how variance evolves over time during learning (Yang et al., 2007; Yang & Scholz, 2005).

Another approach that makes use of a task manifold is tolerance-noise-covariation (TNC) analysis, which relates performance variability, described in terms of body-level variables, to different goal-level “costs” estimated relative to a specified solution manifold (Cohen & Sternad, 2009; Müller & Sternad, 2004; Ranganathan & Newell, 2010): the tolerance cost, which measures how small body-level perturbations are amplified to produce goal-level error; the noise cost, which measures the effect of overall body-level fluctuation amplitude on goal-level error; and the covariation cost, which measures the extent to which the different variables used to describe body-level fluctuations vary together so that their distribution conforms to the geometry of the task manifold. An important feature of TNC analysis is that its three costs make direct reference to goal-level errors and so characterize how fluctuations at the body and goal levels are related. In contrast with UCM, the TNC approach does not necessarily conceive of the task manifold as existing at each instant of an action, but rather represents it in a minimal space of variables required to specify task execution (e.g., the position and velocity of a ball at release during a throwing task). In practice, the task manifold is determined using numerical simulations, and is used to interpret the statistical analysis results. The TNC approach has been successfully used to demonstrate how humans learn to minimize its three costs to achieve optimal performance.

Both the UCM and TNC approaches are data driven, and primarily describe the distributon of ensembles of body-level data from multiple trials, in particular how this distribution “aligns” with the task manifold. Though defined differently in each method, the task manifold concept provides a theoretical basis for interpreting the geometrical structure of observed variability. However, neither method analyzes the temporal structure of observed inter-trial fluctuations, and so cannot be used to study how goal-level errors are generated, or to quantify the degree of their regulation. While such approaches have successfully been used to identify different motor control strategies and characterize motor learning, the lack of a model describing how fluctuations unfold in time means that these analyses by themselves have limited explanatory and/or predictive capacity.

2.2 Stochastic Optimal Control

Optimality principles have been a major focus for understanding how the central nervous system controls movement (Engelbrecht, 2001; Flash & Hogan, 1985; Hoyt & Taylor, 1981; Rosen, 1967; Srinivasan & Ruina, 2006; Zarrugh et al., 1974). However, most optimization approaches have been used to predict average behavior, not to explain observed variability. In particular, they have not been used to address whether the nervous system merely overcomes variability as an impediment to motor performance (Harris & Wolpert, 1998; Körding & Wolpert, 2004; O’Sullivan et al., 2009; Scheidt et al., 2001), or instead regulates variability in ways that maximize task performance (Cusumano & Cesari, 2006; Dingwell et al., 2010; Todorov & Jordan, 2002) while minimizing control effort and allowing for adaptability.

One means of formally exploring these issues is provided by the minimum intervention principle (MIP), originally proposed as a general theoretical basis for computational movement models (Todorov, 2004; Todorov & Jordan, 2002). The MIP ties the idea of task geometry to stochastic optimal control theory, resulting in a computational framework for predicting how movements are regulated in redundant motor systems (Todorov & Jordan, 2002; Valero-Cuevas et al., 2009). While not the only approach available (Guigon et al., 2008; Yadav & Sainburg, 2011), stochastic optimal control provides computational models that can indeed be both explanatory and predictive.

A variety of experimental investigations based on optimal control ideas have been carried out (Diedrichsen, 2007; Izawa et al., 2008; Liu & Todorov, 2007; Todorov, 2004; Todorov & Jordan, 2002; Trommershäuser et al., 2005; Valero-Cuevas et al., 2009). However, these studies have focused primarily on variability measures for testing the validity of control models, and have largely ignored the role of fluctuation dynamics arising from error-correcting control near the task manifold. However, there is nothing inherent in such models preventing fully dynamical analyses of this nature. On the contrary, given their control-theoretic basis, one expects that the full range of dynamical properties used to characterize dynamical systems, particularly regarding stability and temporal correlation properties of the inter-trial fluctuation time series, to be relevant to future experimental explorations of MIP-inspired models.

2.3 Local Dynamic Stability

Arguably the most fundamental dynamical properties of a system are those related to the local stability of its solutions, defined by how the system responds to sufficiently small (i.e., “local”) perturbations (Full et al., 2002; Hirsch et al., 2004; Verhulst, 1996). In simple terms, if a given steady state behavior persists in the face of local perturbations, it is stable, otherwise it is unstable. In addition to quantifying the stability of steady states, local stability analysis can also be used to signal impending changes in a system’s behavior, or, perhaps most relevant here, to quantify the effectiveness or “strength” of a controller. Measures of variability alone cannot quantify how a system responds to perturbations, and therefore do not provide direct measures of local stability.

Not surprisingly, then, one approach to studying the temporal dynamics of trial-to-trial fluctuations has been to adopt methods from nonlinear time series analysis (Kantz & Schreiber, 1997) for assessing local dynamic stability. In applying such methods, the naturally-occurring physiological noise processes (Faisal et al., 2008) that give rise to inter-trial fluctuations are treated as local perturbations of an otherwise deterministic system.

Lyapunov exponents measure how trajectories that start near to each other in state space diverge exponentially in time, on average, in the double limit as time goes to infinity and the distance between trajectories goes to zero. They have been extensively used to study chaotic systems (Abarbanel, 1996; Kantz & Schreiber, 1997; Rosenstein et al., 1993), and indeed the positivity of the largest Lyapunov exponent is an operational definition of chaotic behavior. However, positive Lyapunov exponents estimated from experimental time series do not “prove” that a system is chaotic if it is not known a priori to be predominantly deterministic, something which definitely cannot be said of the human motor system.

Finite-time Lyapunov exponents (FTLE) (Dingwell & Cusumano, 2000; Dingwell & Marin, 2006), also known as local divergence exponents (McAndrew et al., 2011), local Lyapunov exponents (Abarbanel, 1996), or finite size Lyapunov exponents (Gao et al., 2007), sidestep practical problems associated with the difficult double limit in the definition of true Lyapunov exponents. They are estimated by computing the average exponential rate of divergence of neighboring trajectories over a specified, finite time interval. Thus, while they cannot by themselves be used to identify chaotic behavior, they provide a direct, though time-scale dependent, measure of the sensitivity of a system to local perturbations. Positive exponents indicate local “instability” over the specified time scale, with larger exponents indicating greater sensitivity to local perturbations.

If the system’s behavior is strongly periodic, such as during steady gait or other rhythmic movements, the orbital stability can be conveniently estimated using Floquet stability multipliers (Hurmuzlu & Basdogan, 1994; Su & Dingwell, 2007; Verhulst, 1996). To do this, one defines a Poincaré map (Guckenheimer & Holmes, 1997; Verhulst, 1996) at a reference point, or phase, of the periodic orbit. The Poincaré map shows how deviations away from the orbit evolve in discrete time from one cycle to the next. The eigenvalues of the linearized Poincaré map (Hurmuzlu et al., 1994; Su & Dingwell, 2007; Verhulst, 1996) then give stability multipliers, which give the rates at which small perturbations away from the limit cycle grow or decay. Multiplier magnitudes less than unity indicate stability greater than unity, instability. In experiments, the linearized map is usually estimated directly from data via linear regression.

Such methods have been used to assess the local dynamic stability of walking in both humans (Hamacher et al., 2011; McAndrew et al., 2011; van Schooten et al., 2011) and mathematical models (Bruijn et al., 2011; Roos & Dingwell, 2011). They have also been applied to other tasks, such as lifting (Granata & England, 2006) , unstable sitting (Tanaka et al., 2009), and reaching (Gates & Dingwell, 2011), and have been used to quantify the local stability of stride-to-stride fluctuation dynamics in muscle function (Kang & Dingwell, 2009), as well as kinematics (Kang & Dingwell, 2008b).

Experimental stability analysis is primarily data-driven and so it, too, has limited explanatory or predictive capacity. In addition, these methods are rooted in the study of deterministic dynamical systems, and so their application to fundamentally stochastic biological processes can lead to problems of interpretation. For example, the parallel estimation of both FTLE and Floquet multipliers can lead to apparently contradictory results, with the former suggesting “instability” and the latter “stability” for the same data (Dingwell & Kang, 2007; Su & Dingwell, 2007). Such an apparent contradiction is hypothesized to be due to the inherently multiscale nature of movement time series data, with the FTLEs tending to probe the behavior on smaller, “noisier” time scales, and the Floquet multipliers the behavior at the scale of the observed periodicity. Finally, standard stability analysis makes no reference to goal directedness, and hence cannot by itself identify variability structure arising from goal equivalence.

2.4 Fractal Dynamics

Another family of approaches takes an explicitly stochastic perspective in analyzing observed movement fluctuations, using techniques that have their origin in statistical physics. Fractal dynamics (Goldberger et al., 2002) directly addresses the multiscale nature of motor fluctuations, and examines time series data to, in effect, characterize the type of stochastic process that underlies it, particularly in regard to its temporal scaling and correlation properties.

For many tasks, movements on consecutive trials are correlated (Ganesh et al., 2010; Ranganathan & Newell, 2010), and such dependencies, which cannot be captured by variance measures alone, may be critical to understanding inter-trial control (Dingwell et al., 2010; Scheidt et al., 2001). Auto-correlation based models have shown strong dependence of each consecutive movement on the immediately preceding movement, for both reaching (Gates & Dingwell, 2008; Scheidt et al., 2001) and walking (Dingwell et al., 2010). In many cases, these correlations can persist across many consecutive repetitions of a task (Chen et al., 1997; Delignièeres & Torre, 2009; Hausdorff et al., 1995), even to the point of exhibiting long-range correlations (Hausdorff et al., 1995), also referred to as long-range persistence, long-range dependence, or long memory. A time series is long-range correlated if its autocorrelation decays slowly with the lag, typically according to a power law, so that it does not have a finite correlation time.

Detrended fluctuation analysis (DFA) (Hausdorff et al., 1995; Peng et al., 1992)—or related methods such as rescaled range analysis or spectral estimation (Gao et al., 2006; Rangarajan & Ding, 2000)—has been extensively used to characterize these correlation properties in experimental time series, including those from physiological processes and human movement. The DFA algorithm computes the root mean square deviation from trends in temporal windows of variable length, which is the “fluctuation” in the method’s name. By plotting this fluctuation magnitude against the window size in a log-log plot, linear regression can be used to obtain a DFA scaling exponent α(Hausdorff et al., 1995; Peng et al., 1992).

The DFA exponent gives an easily-computed measure of the statistical persistence in a time series, where “persistence” means that deviations are more likely to be followed by subsequent deviations in the same direction. In contrast, “anti-persistence” means that deviations in one direction are statistically more likely to be followed by deviations in the opposite direction. In either case, the persistence can be of a short or long-range type. However, for a known long-range process, a value of α greater than or less than 1/2 indicates that the time series is long-range persistent or long-range anti-persistent, respectively. When α = 1/2 the time series is commonly said to be “uncorrelated”: more precisely, it indicates that the process in question is short-range correlated, so that over sufficiently long time scales it “looks” uncorrelated. Data-based estimates of exponents with values significantly different from 1/2 have been commonly taken to indicate long-range correlations. Unfortunately, DFA is highly prone to false positive results when used in this way (Delignièeres & Torre, 2009; Gao et al., 2006; Maraun et al., 2004), because non-long-range correlated processes (i.e., processes with finite correlation times) often appear otherwise when evaluated using the DFA exponent alone (Drew & Abbott, 2006; Gisiger, 2001; Maraun et al., 2004; Torre & Wagenmakers, 2009; Wagenmakers et al., 2004, 2005).

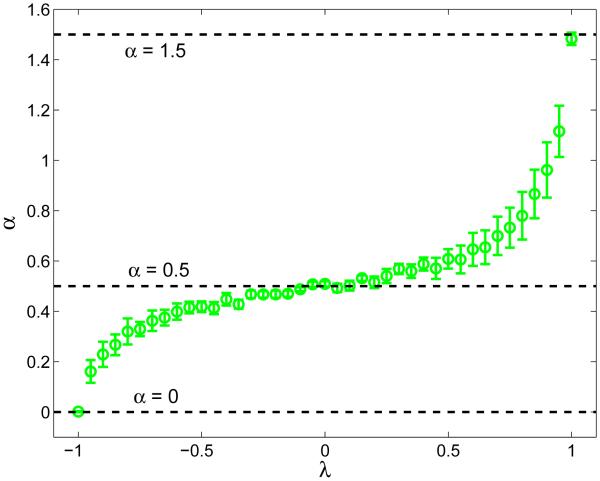
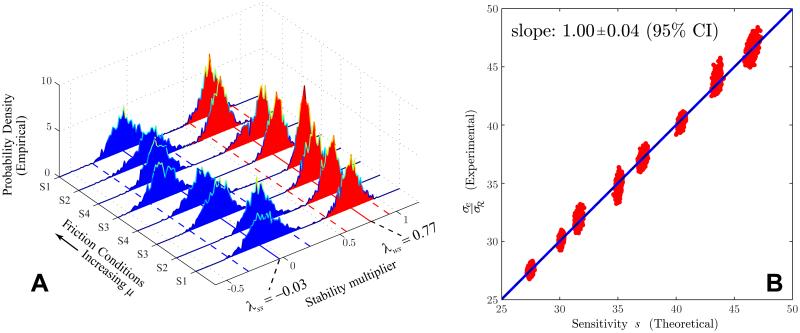
As a simple example, the scalar autoregressive (AR) process given by x_k+1 = λx_k + ν_k, where −1 ≤ λ ≤ 1 and ν is a mean-zero Gaussian random variable, has a finite correlation time for |λ| < 1 and so, under those circumstances, it cannot generate time series that are long-range correlated. Nevertheless, one can apply DFA to estimate α for such a time series, as shown in Fig. 1. The figure shows that as the “stability multiplier” λ is varied, α can take on any value between 0 and 1.5. While the values of α correctly indicate whether or not the given time series is persistent (α > 1/2) or anti-persistent (α < 1/2), to interpret the result as indicating long-range persistence would obviously be wrong. Thus, characterizing long-memory processes from data alone using DFA analysis requires additional information to minimize the chance of false positives (Crevecoeur et al., 2010; Gao et al., 2006). In this work, we will use DFA calculations only as a convenient way to characterize the statistical persistence of our data across multiple lags: we will not use it to make any claims about the presence or absence of long-range correlations in our data.

Figure 1.

Plot of the scaling exponent α vs. λ for the autoregressive (AR) process x_k+1 = λx_k + ν_k, where −]-1 ≤ λ ≤ 1 and ν is a mean-zero Gaussian random variable. For each λ, α was estimated by applying the DFA algorithm to time series of 2 × 10⁴ values of x, with σ_ν = 0.1. The vertical bars show the standard error in the slope estimate used for α. The given AR process is known to have a finite correlation time for |λ| < 1, and hence in this case α ≠ 1/2 does not indicate long-range persistence.

Detrended fluctuation analysis, and related methods, capture fundamental dynamical information about a recorded time series, independent of variability magnitude. However, it is again a purely data-driven method that makes no reference to goal-directedness and so cannot by itself be used to study the organization of control in the presence of equifinality. Indeed, the fact that fractal dynamics has not typically considered goal-equivalent structure in movement fluctuations may underly apparent paradoxes in which different time series from the same phenomenon can yield DFA exponents simultaneously indicating neuromotor “health” and “dysfunction” (Dingwell & Cusumano, 2010; Terrier et al., 2005).

2.5 Summary

The four perspectives on movement variability analysis described above are by no means the only approaches that can be applied to study motor fluctuations. There certainly are other perspectives that have been or could be brought to bear, such as those related to information theory or synchronization, among other possibilities (Davids et al., 2006). However, the four perspectives enumerated here are representative of two fundamental categories: geometrical methods that examine the effect of motor redundancy; and dynamical methods that characterize the processes generating the observed time series. The UCM and TNC approaches fall into the former category; local stability and fractal dynamic analysis falls into the latter. The MIP, which is the only perspective discussed here that is not primarily data-driven, represents a computational framework that can provide a bridge between these two categories by incorporating goal equivalence into models of movement regulation. Such models can, in principle, be used to explain and even predict the geometrical structure of variability and the dynamical properties of observed movement fluctuations.

To date, however, most researchers working from within these perspectives have restricted themselves to either only quantifying measures of variance, on the one hand, or quantifying dynamical properties of uctuation time series, on the other hand. Even the control-theoretic framework of MIP has also so far been tested experimentally using only variability measures that miss much of the uctuation dynamics related to control. Thus, there remains a clear need to develop a combined computational framework and model-based experimental approach that combines the critical ideas and insights from the geometric and dynamical perspectives. In the remainder of this paper, we describe just such a model-based framework, which allows one to study how the human nervous system regulates goal-directed movements in the face of inherent neuromuscular noise and motor redundancy.

3 Goal Equivalence and its Consequences

The goal equivalent manifold (GEM) concept was initially developed (Cusumano & Cesari, 2006) to study the relationship between variability at the body and goal levels using sensitivity analysis, a well-known concept in engineering and other disciplines. The intention was to use accessible laboratory variables to examine precisely how motor performance (as measured by goal level variability) is generated, without necessarily focusing on whether or not the variables represent “true” controlled variables, a frequently stated aim of UCM (Scholz & Schöner, 1999). The GEM approach makes clear distinctions between the goal, the task, and the solution manifold, and it emphasizes that the task manifold exists independent of, and prior to, any specific control scheme. Thus, the GEM framework conceptually separates the task manifold and its associated sensitivity properties, which in control jargon can be considered as part of the “plant”, from the “controller” used to regulate variability, and so can reasonably distinguish between “passive” and “active” properties of a given task.

3.1 Goal Functions and Task Definition

We define a task using a goal function, which expresses the relationship between the goal of the task, the subject, and the environment needed for perfect task execution. We here focus on discretizable tasks with precise, fixed, goal specifications and look at goal functions

$$\mathbf{f}(\mathbf{x};\mathbf{p})=0,$$ (1)

where f is the vector-valued goal function of dimension D_g, and x is the body-level state vector of dimension D_b, The body state x is identified as a minimal vector of variables needed to define task execution. Though it will be suppressed in what follows, here we also include a vector p of parameters (specifying, e.g., the position of a target in a reaching task, or the speed of a treadmill). Typically, the body state x is defined in terms of execution variables, that is, by body-level kinematic quantities the specification of which are sufficient to determine the execution of the task in any given trial. Any value of the body state x that satisfies Eq. (1) will, by definition, exactly attain the goal.

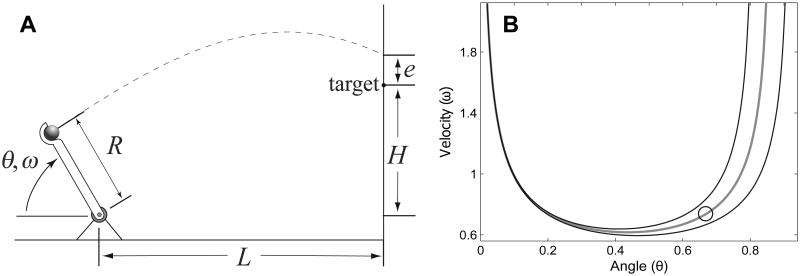
As an example, consider the ball-throwing task (John & Cusumano, 2007) shown in Fig. 2A. We imagine that a human subject drives the manipulandum of length R, which is hinged at its base, and attempts to hit a target at a distance L, elevated above the ground by an amount H. Neglecting air resistance, the elementary mechanics of projectile motion then gives the scalar goal function f ≡ f as:

$$f(\theta ,\omega ;H)=\frac{L+R\cos \theta }{\tan \theta }-\frac{g}{2}{\left(\frac{L+R\cos \theta }{\omega R\sin \theta }\right)}^2+R\sin \theta -H=0.$$ (2)

For this task, then, x = (θ,ω), where the angle θ and angular velocity ω are taken at the release of the ball. Note that D_b > D_g, since here D_b = 2 and D_g = 1. All values of (θ,ω) satisfying Eq. (2) correspond to ball trajectories that exactly hit the target. The goal-level error is e, which has the same dimension as the goal function. In addition to the “environmental” property of the local gravitational acceleration g, the goal function is parameterized by the target positions L and H, and the “body” property R. Assuming that g is a fixed parameter, the complete parameter vector is thus p = (R, L, H): changing any of these parameters will change the goal function and hence its zeros.

Figure 2.

A ball throwing task example (John & Cusumano, 2007). (A) Schematic representation of the task, the goal of which is to hit the target; the body state is x = (θ,ω), so D_b = 2, and the goal-level error is e, so D_g = 1. (B) A typical GEM for the task (gray line), and ±10% error contours (black lines) in the execution variable space. The GEM is the set 𝒢 containing all values of x that satisfy Eq. (2), giving trajectories that exactly hit the target. Angular variables are displayed in radians. The circle is for later comparison with Fig. 3.

3.2 The Goal Equivalent Manifold

Due to motor redundancy, the dimension of the body state variable x is typically greater than the dimension if the goal function f, i.e., D_b > D_g. As a direct result, there will not be a unique solution to Eq. (2), but rather an entire set,

$$\mathcal{G}=\{\mathbf{x}\mid \mathbf{f}\left(\mathbf{x}\right)=0\},$$ (3)

in which for compactness we have not displayed the dependence of fon the parameter vector p. Though it is by no means necessarily the case, it frequently occurs in applications that the set 𝒢 has the structure of a manifold, that is, of a surface in the body state space. In that case, we refer to 𝒢 as the goal equivalent manifold (GEM) for the task.

The GEM for the throwing task example is shown by the grey curve of Fig. 2B. Every point on the GEM represents a strategy x ∈ 𝒢 that perfectly hits the target. Also in the figure are black lines showing ±10% error at the target. Note that the spacing between the error contours is not uniform, indicating that the sensitivity to body-level errors is not uniform along the GEM: the smaller the distance between the error contours, the more sensitive nearby strategies are to body-level errors. For this example, we see that it is better to use strategies involving hard, direct throws, released with relatively large values of θ, rather than lobbed throws, which have small θ.

Our definition of the task manifold is more similar to that conceived of in the TNC approach, described in section 2, than it is to that of the UCM. As with the TNC approach, the body state x in Eq. (1) is a minimal body-level variable that determines the outcome of an individual trial. The dynamics within each trial is not referenced and, indeed, a subject is free to undertake any action whatsoever prior to reaching the GEM. For example, for one trial of the ball throwing task in Fig. 2, the manipulandum could be made to move directly to the release point, or it could be oscillated randomly prior to the release point: either in-trial strategy can yield identical performance at the goal level. Thus, in contrast with the task manifold of UCM, the GEM definition does not use the average behavior during multiple trials to define the “true” goal of an individual subject, but rather uses a relationship between the body and goal (i.e., the goal function) that can be determined objectively for any subject. By defining the task manifold in this way, we can examine the sensitivity properties that relate fluctuations observed at the body and goal levels, as we now show. This emphasis on the sensitivity properties of the GEM is unique to our approach.

3.3 Relating Body and Goal Level Variability

By definition, f(x^*) = 0 whenever x^* ∈ 𝒢. In general, however, e = f(x) is a measure of the goal-level error, that is, of the performance of the task. Any fluctuation in the body state away from the GEM will result in a fluctuation in the goal level error, e. In the ball-throwing example, the error is a scalar (e ≡ e), as illustrated in Fig. 2.

For a skilled performer, the average body state over multiple trials will be close to the GEM. Thus, in practice we can think of x^* ≈ x̄ where x̄ is the sample average, and write x = x^* + u, where u is the body-level fluctuation about the average strategy that lies on the GEM. For small fluctuations, we can expand the goal function in a Taylor series to obtain the linear approximation for the error at the target:

$$\mathbf{e}=\mathbf{f}({\mathbf{x}}^{\ast }+\mathbf{u})\approx \mathbf{f}\left({\mathbf{x}}^{\ast }\right)+\mathbf{Au}=\mathbf{Au},$$ (4)

where the body-goal variability matrix A is the matrix of partial derivatives ∂f/∂x evaluated at x^* (Cusumano & Cesari, 2006).

The matrix A describes how errors at the goal-level, e, are functionally related to small body-level fluctuations, u. By construction, A is a D_g × D_b matrix, and since D_b > D_g, it will have more columns than rows. The range of A (its column space), denoted by ℛ is assumed to have dimension D_g. This goal relevant subspace contains fluctuations that do result in error at the target. In contrast, A has a D_b − D_g dimensional null space, defined by 𝒩 = {u | Au = 0} (Golub & Van Loan, 1996). All fluctuations restricted to this goal equivalent subspace produce no error at the target. Since ℛ is orthogonal to 𝒩, the Cartesian product of 𝒩 and ℛ gives the entire body state space. It is easy to visualize 𝒩 and ℛ, since they are represented by linear subspaces that are tangent and perpendicular, respectively, to the GEM at every point. In the ball throwing example (Fig. 2B), therefore, both of these subspaces will be 1-dimensional.

To further characterize the body-goal interaction, the singular value decomposition (Golub & Van Loan, 1996) of A is computed. The D_g singular values of A quantify the degree to which the goal-relevant fluctuations at the body level are amplified to produce error at the target (Cusumano & Cesari, 2006). In the ball-throwing example, A is a 1 × 2 matrix

$$\mathbf{A}=\left[\frac{\partial f}{\partial \theta },\frac{\partial f}{\partial \omega }\right]\triangleq [A_{\theta },A_{\omega }],$$ (5)

evaluated at a point on the GEM, (θ*, ω*) ∈ 𝒢. The null space of A consists of fluctuations with the form $c{[-A_{\omega },A_{\theta }]}^{\mathrm{t}}$, where the superscript t denotes the transpose and c is any real constant. In this case, the only singular value is easily found to be $s=\sqrt{A_{\theta }^2+A_{\omega }^2}$.

Considering an ensemble of repeated trials about a given strategy x^* ∈ 𝒢, and assuming sufficiently small, independent fluctuations in each of the goal-relevant directions, it can be shown (Cusumano & Cesari, 2006) that the performance at the target, as measured by the standard deviation of the error σ_e, is given by

$${\sigma }_{\mathrm{e}}=\sqrt{\sum _{i=1}^{D_{\mathrm{q}}}{s}_i^2{\sigma }_i^2}$$ (6a)

$$\equiv \left[\frac{1}{{\sigma }_{\mathcal{R}}}\sqrt{\sum _{i=1}^{D_{\mathrm{q}}}{s}_i^2{\sigma }_i^2}\right]\left[\frac{{\sigma }_{\mathcal{R}}}{{\sigma }_{\mathrm{u}}}\right]{\sigma }_{\mathrm{u}}$$ (6b)

in which: s_i is the singular value in the direction of the i^th basis vector (i = 1, 2,…, D_g) of the goal-relevant subspace ℛ σ_i is the component of body-level variability in the same direction; and ℛ; σ_i is the component of the total body variability σ_u lying in ℛ Equation (6a) is the result in its most compact form. The expanded identity Eq. (6b) shows that the goal-level variability can be interpreted as the product of three factors, which, from left to right, are: an “gain” factor, showing how goal-relevant variability is amplified by the sensitivity properties of A; an “alignment” factor, showing the fraction of the total variability that is goal-relevant; and a body-level variability factor, which is simply σ_u. These three factors are similar in interpretation, respectively, to the tolerance, covariation, and noise costs referred to in TNC analysis. However, whereas the TNC approach uses its costs to study motor learning, Eqs. (6) explicitly connect the “steady state” or “learned” values of these quantities to goal-level performance, based only on the goal function Eq. (1).

3.4 Change of Variables

Perhaps the most fundamental issue in dynamical modeling is the need to identify appropriate state variables, and this need is particularly acute in regard to models of the human movement system (Beek et al., 1995). Furthermore, since it is usually the case that more than one set of state variables can be used, understanding the effect of coordinate transformations is of critical importance. We thus consider a new body state variable y related to the original state x by the coordinate transformation

$$\mathbf{x}=\mathbf{g}\left(\mathbf{y}\right).$$ (7)

There are two general contexts in which such a transformation might occur. The first is simply that we might want to select another minimal set of “execution variables”, generalized coordinates (Greenwood, 1988) that specify the task. For example, in the ball throwing task of Fig. 2, we have used the body state variables θ and ω, and, though these are perhaps the most natural, there are other possibilities, such as Cartesian coordinates, for specifying the position and velocity of the ball at release.

The other context is more fundamental to the problem of human movement: given a state space of execution variables, a goal function, and its related GEM, we may ask how it is that a subject actually manages to generate a given value of the state x in a given trial. That is, using a robotics analogy, we may want to use a new set of variables that describe how the “end effector” coordinate x is “actuated” during a trial. One way such new “action variables” might be obtained would be from a model of in-trial dynamics. Such a model would result in a function of the form

$$\mathbf{x}=\Phi (\tau ,{\mathbf{x}}_0;\beta ),$$ (8)

where τ is the time of the movement for the trial, x₀ is the initial condition, and β is a set of parameters that control the in-trial behavior. Assuming the same initial conditions for each trial, the in-trial “action template” of Eq. (8) can be written as x = Φ (τ; β) ≜ g(y), which gives y ≜ (τ; β) as the new action variable.

This idea has been developed at some length and will be further developed in forthcoming papers (John, 2009; John & Cusumano, 2007; John et al., 2013), however here we need only consider that a coordinate transformation Eq. (7) exists, for whatever reason. Then, the original goal function f(x) will transform to a new goal function f̃(y) by

$$\mathbf{f}\left(\mathbf{x}\right)=\mathbf{f}\left(\mathbf{g}\left(\mathbf{y}\right)\right)\triangleq \tilde{\mathbf{f}}\left(\mathbf{y}\right)=0.$$ (9)

Furthermore, the body-goal matrix A, which determines the sensitivity properties of the GEM and which is obtained by differentiation as in Eq. (5), will be related to the new matrix à by application of the chain rule:

$$\tilde{\mathbf{A}}=\frac{\partial \tilde{\mathbf{f}}}{\partial \mathbf{y}}=\frac{\partial \mathbf{f}}{\partial \mathbf{x}}\frac{\partial \mathbf{x}}{\partial \mathbf{y}}\equiv \mathbf{A}\frac{\partial \mathbf{g}}{\partial \mathbf{y}},$$ (10)

where we have substituted for A and g after the last equals sign using Eqs. (5) and (7).

The implications of these transformations are immediately apparent. First, the GEM itself will transform into the space of new variables, since by definition $\tilde{\mathcal{G}}=\{\mathbf{y}\mid \tilde{\mathbf{f}}\left(\mathbf{y}\right)=0\},$ and from Eq. (9) we see that every $\mathbf{y}\in \tilde{\mathcal{G}}$ will correspond to a unique x ∈ 𝒢. However, the transformed manifold will generally have a very different appearance. More importantly, Eq.(10) shows that the original and transformed body-goal matrices will be different, in general, and hence their singular values will also be different. This indicates that the GEM itself transforms directly, but the sensitivity properties along it are not invariant under coordinate transformations, although they do transform in a predictable way via Eq. (7).

As a simple example of how this all might work, return to the ball throwing example and consider the possibility that the manipulandum dynamics within each trial is governed by an in-trial controller that extremizes the mean-squared torque (John & Cusumano, 2007) so that

$$\delta {\int }_0^{\tau }{\left(\ddot{\theta }\right)}^{2}dt=0,$$ (11)

where τ is the time of release in the trial. This assumption, together with at-rest initial conditions, yields the following action template, which transforms the execution variables (θ,ω) into action variables (τ, β)(John & Cusumano, 2007):

$$\begin{array}{cc}\hfill & \theta =\frac{1}{6}\beta {\tau }^3\hfill \\ \hfill & \omega =\frac{1}{2}\beta {\tau }^2\hfill \end{array}$$ (12)

in which β is a parameter that controls the angular jerk of the torque-optimal action within one trial, and τ is the movement time.

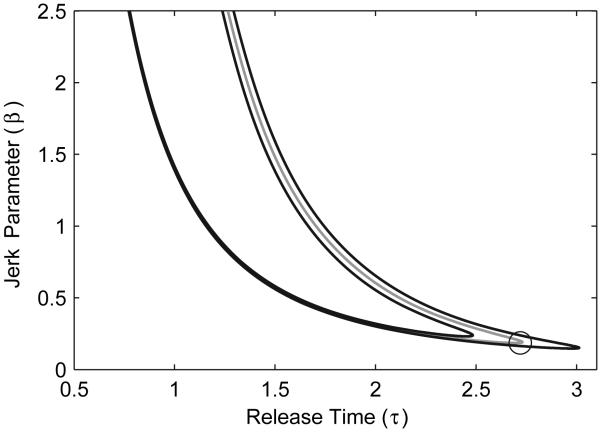
The above transformation can be directly substituted into Eq. (2) to yield the transformed goal function f̃(τ, β) which can then be used to find the transformed GEM, as shown in Fig. 3. By comparing Fig. 3 to Fig. 2B, we see that the sensitivity properties along the GEM in the two spaces, as represented by the distance between the ±10% goal-level error contours, are quite different. The best strategy in the “action space” is represented by the circle in Fig. 3: it is the point $(\tau ,\beta )\in \tilde{\mathcal{G}}$ with the lowest sensitivity to body-level errors. However, the corresponding point in the original “execution space”, also represented by a circle in Fig. 2B, does not correspond the best strategy in terms of (θ, ω) ∈ 𝒢.

Figure 3.

GEM (gray line) and ±10% error contours (black lines) for the ball throwing task (Fig. 2A) transformed to the action space, corresponding to values of (τ, β) that result in target-hitting trials. The GEM was transformed by substituting Eq. (12) into Eq. (2). The circle indicates the “best” strategy on the GEM, which has the lowest sensitivity to body-level fluctuations. Its transformed location in the execution space is identified by the same symbol in Fig. 2B.

The above discussion indicates the difficulty in making inferences on neuromotor function using only variance-based measures of movement fluctuations: the lack of coordinate invariance means that the observed variability structure can be strongly deformed merely by choosing different state variables. As we show below, this problem of coordinate dependence can be largely overcome by including a dynamical assessment of fluctuations in the GEM framework.

4 Closing the Perception-Action Loop

To this point, we have developed the GEM framework by discussing properties of the task that exist independent of any control mechanism used to regulate motor fluctuations. In this sense, the existence of a GEM, along with its sensitivity properties, can be thought of as a “passive” feature of the task. Even if one were to build a mechanism to carry out the throwing task of Fig. 2A that consisted only of inanimate bars and springs, and then applied random impulses to release the ball toward the target, such an uncontrolled, and indeed “mindless”, system would still have the GEM of Fig. 2B.

What is missing from this account, however, is any ability to examine of how a given ensemble of body-states collected over multiple trials unfolds over time, something which is of obvious importance in the study of motor regulation. We therefore add the idea of inter-trial error-correcting control to the passive properties of the GEM, which results in a class of simple explanatory models and yields a set of general hypotheses on the dynamical structure of inter-trial fluctuations observed in experiments.

4.1 Inter-Trial Error Correction

A typical experiment of this type, carried out over N trials, will result in time series of the chosen body state variable, ${\left\{{\mathbf{x}}_k\right\}}_{k=1}^N$. Our desire is to develop the simplest possible models that can contribute to a fundamental understanding of how error-correcting control and goal-equivalence interact to generate observed variability. We therefore choose to work at the level of observations, and consider the trial-to-trial task dynamics to be governed by a simple update equation of the form:

$${\mathbf{x}}_{k+1}={\mathbf{x}}_k+\mathbf{g}(\mathbf{I}+{\mathbf{N}}_k)\mathbf{c}\left({\mathbf{x}}_k\right)+{\nu }_k$$ (13)

where: c is the controller to be found, assumed to depend only on the current state; N_k is a matrix representing signal-dependent noise in the motor outputs; and v_k is an additive noise vector representing unmodeled effects from perceptual, motor, and environmental sources. For convenience, we also include a diagonal matrix of gains, G: given an optimal controller cdesigned with G = I (where I is the identity matrix), suboptimal performance can be examined by simply setting G ≠ I

The structure of Eq. (13) is motivated by the idea that, in the absence of noise, a skilled performer (for whom x_k will be near the GEM) would not need to make corrections between trials, so that the “performance” would be nearly constant (that is, x_k+1 ≈ x_k). On the other hand for zero control, c = 0, and Gaussian white noise ν_k, the fluctuations in x_k would be a Brownian motion (i.e., a random walk). Thus, heuristically speaking, we can think of the controller as “modulating” the inter-trial dynamics to lie somewhere between perfect repetition and an unconstrained random walk in state space.

Equation (13) is only intended to model the inter-trial dynamics, not the full neuro-biomechanical dynamics within trials. That is, it is a model of the process that regulates fluctuations away from perfect performance by adjusting the body state at each trial. In this sense, the chosen state variable plays the role of a control parameter for the action during individual trials. Phenomenological models of this type are consistent with the idea of an overall 532 hierarchical control with an inter-trial component (Eq. 13) that provides error correcting adjustments to an within-trial component that is approximately “ballistic” or “feed-forward” during each individual trial.

In (Burge et al., 2008; Diedrichsen et al., 2005; van Beers, 2009), error-correcting con trollers similar to Eq. (13) have been used to study motor learning. Those models, which did not consider task redundancy, had controllers that depended explicitly on the goal-level error e_k instead of the body state _xk. Here, in contrast, task redundancy is a central concern, and Eq. (4) gives e_k = A(x_k − x^*). Thus, our controller depends implicitly on the error of the previous trial. However, the error at the next trial appears explicitly in the cost function used to determine c, as discussed in the next section.

4.2 Stochastic Optimal Controller

There are multiple ways one might apply control theory to design the controller, c (Jagacinski & Flach, 2003). Motivated by a generalized interpretation of the minimum intervention principle (MIP) (Todorov, 2004; Todorov & Jordan, 2002) we here use a stochastic optimal control approach (Ogata, 1995; Stengel, 1994), and take our cost function to be the expected value $\stackrel{‒}{C}=E\left[C\right]$ where 𝒞 has the general quadratic form

$$C={\mathbf{f}}^{\mathrm{t}}\left({\mathbf{x}}_{k+1}\right){\mathrm{C}}_1\mathbf{f}\left({\mathbf{x}}_{k+1}\right)+{\mathrm{c}}^{\mathrm{t}}\left({\mathbf{x}}_k\right){\mathrm{C}}_2\mathrm{c}\left({\mathbf{x}}_k\right)+{\mathbf{u}}_k^{\mathrm{t}}{\mathrm{C}}_3{\mathbf{u}}_k,$$ (14)

in which f is the goal function, c is the controller we seek, u_k = x_k − x^* is the deviation from a “preferred operating point” (POP) on the GEM, and the positive definite matrices c_i (i = 1,2,3) are the relative weights for each component of the total cost.

The first term in Eq. (14) is the cost of error at the goal level, where here we assume direct error feedback (that is, the error is “perceived” exactly by the performer). Note that after Eq. (13) is used to replace x_k+1 in Eq. (14), the noise terms are now included in the cost function, which is why stochastic optimization is required. The second term represents the cost of the control effort, and the third term represents the cost of deviating from the POP. Thus, the system will attempt to drive the goal-level error to zero at each step, while also minimizing the control effort and the distance from the POP. By varying the weighting matrices C_i, one can study the variability generated by systems with different control structures via numerical simulations with Eq. (13).

We further restrict our attention to unbiased controllers. That is, consistent with our general assumption of a skilled performer, we assume that on average the subject’s performance is perfect so that $\stackrel{‒}{K}=E\left[\mathbf{f}\left(x_{k+1}\right)\right]=0$. We treat this as a constraint and let $\mathcal{H}=\stackrel{‒}{C}-\lambda \stackrel{‒}{\mathcal{K}}$ where λ is a Lagrange multiplier. Then, the value of x_k+1 is substituted for using the right hand side of Eq. (13), and ℋ is extremized yielding a system of D_b equations via ∂ℋ/∂c = 0, the solution of which gives the controller c. Thus, c can be categorized as a single-step, unbiased controller, obtained by solving a standard “quadratic regulator” problem (Ogata, 1995; Stengel, 1994).

Of course, it is possible to relax any number of the assumptions we have made in constructing this class of inter-trial task dynamical system. For example, we can consider a dynamical dependency on states with lags greater than 1, allow solutions to be biased, or add new terms to our cost function. However, as we show in the next section, recent experimental applications have demonstrated that these various simplifying assumptions can, indeed, yield models that provide useful insights into the structure of observed variability.

4.3 Local Stability Near the GEM

Continuing with our focus on skilled performance, as in section 3.3 we assume that the deviations ufrom the GEM are small. Adding to this the assumption of small noise inputs N_k and ν_k, we can linearize the controller Eq. (13) (John & Cusumano, 2007) about an operating point x^* on the GEM to obtain:

$${\mathbf{u}}_{k+1}={\mathrm{Bu}}_k+{\nu }_k,$$ (15)

in which the matrix B = I + GJ, where J = ∥c/∥x is the Jacobian of the controller evaluated at x^*. Thus, small fluctuations are governed by the linear map of Eq. (15), and the D_b eigenvalues and eigenvectors of B determine the dynamic stability properties of the system. In what follows, we focus on the case when B possesses real, distinct eigenvalues. We remark in passing that, as discussed in section 2.4, the linearized controller above is an autoregressive (AR) process, and hence cannot generate time series that exhibit long-range persistence.

When all eigenvalues λ_i (i = 1, 2,…,D_b) have magnitudes |λ_i| < 1 the operating point is asymptotically stable (Hirsch et al., 2004; Verhulst, 1996), meaning that in the absence of noise, fluctuations would decay to zero over multiple trials. On the other hand, if one or more eigenvalues has |λ_i| = 1 the operating point is unstable and fluctuations grow over time, something that is not to be expected in the performance of a human subject. Finally, eigenvalues with |λ_i| = 1 are transition values, representing neutrally stable directions in the state space: in the absence of noise, fluctuations neither grow nor diminish.

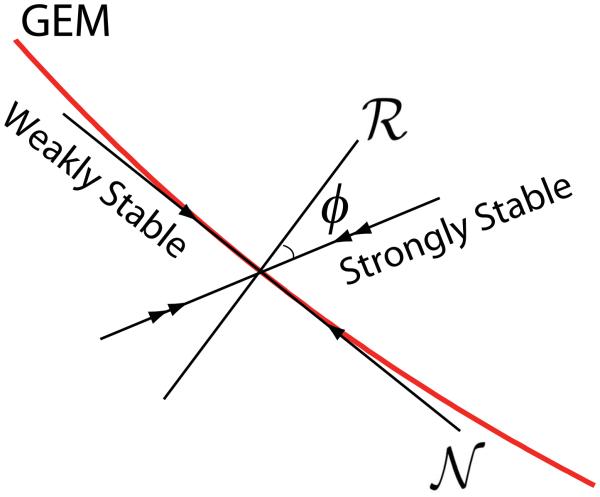
In the limit of a pure MIP controller, the POP term in Eq. (14) is absent (i.e., the matrix C₃ = 0). In this case, one can show (John, 2009; John & Cusumano, 2007) that there will be D_b − D_g eigenvectors that lie in the goal equivalent space 𝒩 which is tangent to the GEM, and the corresponding eigenvalues will be neutrally stable, having magnitudes equal to 1. The remaining D_g eigenvalues will have magnitudes between 0 and 1, and will correspond to eigenvectors that are transverse, though not necessarily perpendicular, to the GEM. For the optimal controller (G = I), these eigenvalues will be exactly equal to 0, whereas for the slightly suboptimal controller they will still be close to 0. This means that fluctuations transverse to the GEM are strongly diminished in subsequent trials, and hence we refer to these transverse eigenvalues as strongly stable. This general situation is shown schematically in Fig. (4) for the simple case when D_g = 1 and D_b = 2.

With a pure MIP controller, the GEM is similar to a UCM: by design, the GEM is “uncontrolled”, and hence fluctuations along it are not corrected. However, with a little reflection it is easy to see that in the presence of noise such uncontrolled, neutrally stable behavior will result in unbounded random walk dynamics along the GEM, something which is never observed in experiments. This is easily confirmed by simulations with models of the type discussed here (John, 2009; John & Cusumano, 2007). Thus, in general one expects to have a nonzero POP term in the cost function Eq. (14) (C₃ ≠ 0), which will localize the fluctuations around the operating point. However, consistent with our generalized interpretation of the MIP hypotheses, we expect the resulting control along the GEM to still be relatively weak (meaning that C₃ is still small), resulting in weakly stable eigenvalues tangent to the GEM, with magnitudes near to, but slightly less than, 1. For small POP perturbations to the ideal MIP controller, the weakly stable eigenvectors will still be nearly tangent to the GEM.

For the ball throwing example, an ideal MIP controller will have two eigenvalues, a neutrally stable one, λ₁ = 1, and a stable one, 0 ≤ |λ₂| < 1, with eigenvectors tangent and transverse to the GEM, respectively, as illustrated in Fig. (4). For the optimal controller, the strongly stable eigenvalue will be λ₂ = 0, and for a slightly suboptimal controller |λ₂| > 0 but still very small. Finally, by adding a weak POP component to the controller, the neutrally stable eigenvalue λ₁ will be a bit smaller than 1, that is, it will become weakly stable (again, see Fig. 4).

Figure 4.

Schematic diagram in the body state space illustrating the stability geometry for a typical MIP controller with weak POP perturbation. The dimensions of the various spaces shown are identical to those for the ball throwing example of Fig. 2B. The dimensions of ℛ and 𝒩 are D_g and D_b − D_g, respectively and typically φ ≠ 0.

Transforming the fluctuation variables by u_k = P q_k, where P is the matrix whose columns are the eigenvectors of B, allows one to study the uncoupled inter-trial dynamics in the weakly and strongly stable directions. Given the almost perfect alignment of the weakly stable subspace with the GEM, it is clear that only fluctuations in the strongly stable subspace result in appreciable error at the goal level. Though a general discussion is beyond the scope of this paper, in the case where D_g = 1 , as in the ball throwing example, it can be shown (John, 2009; John & Cusumano, 2007) that Eq. (6a) relating body and goal-level variability can be modified to include the effect of controller stability as

$${\sigma }_e=\frac{s{\sigma }_{\mathcal{R}}}{\sqrt{1-{\lambda }^2}}\approx s{\sigma }_{\mathcal{R}},$$ (16)

where: σ_e and σ_ℛ the standard deviations of the goal-level and goal-relevant fluctuations, respectively; s is the lone singular value of the body-goal matrix A; and λ ≈ 0 is the strongly stable eigenvalue governing fluctuations transverse to the GEM. The above expression shows that, for a skilled performer, strongly stable control transverse to the GEM will have little effect on the magnitude of goal-level variability. Rather, the “passive” sensitivity along the GEM, as represented by the singular value of the body-goal matrix, will control performance. Recall, however, that the scaling relationship of Eq. (16) is only expected to be valid in the limit of small fluctuations near the GEM.

4.4 General Experimental Hypotheses

The ideas presented above illustrate how the GEM framework combines a consideration of goal equivalence with error-correcting control. The result is arguably the simplest possible formal description of how goal-level fluctuations (and therefore task performance) are generated and regulated. Using these ideas, one can build a variety of models for different e discrete tasks simply by developing suitable goal functions (Eq. 2) and by adjusting the parameter matrices C_i (i = 1, 2, 3) in the cost function Eq. (14). One could also imagine more radical changes to the cost function involving the addition of new costs, for example related to ergonomic or other considerations. Thus, used as a modeling framework, the GEM approach can be used to examine the consequences of various goal function and/or controller assumptions using simulations, which in themselves can provide insight intomovement regulation.

More importantly, however, the models represent experimentally testable hypotheses on the organization of inter-trial fluctuations. Based on the mathematical features of the models, as described above, and backed by numerical simulations, we are led to a set of general hypotheses on the variability observed during repeated trials of discrete, goal-directed movement tasks. Under the assumption of skilled movements, for which fluctuations are relatively small and near the GEM, we expect to following to hold for any “GEM-aware” inter-trial controller:

• H1D_b – D_g eigenvectors of B (Eq. 15) will form a subspace that lies in, or very near, the tangent space to the GEM, N, which has the same dimension. The corresponding eigenvalues λ_i (i = 1, 2,…, (D_b – D_g)) will indicate weak stability without over-correction: that is, 0 < λ_i < 1 and λ_i ≈ 1.
• H2D_g eigenvectors of B will form a subspace that is transverse (but typically not perpendicular) to the GEM. The corresponding eigenvalues will indicate strong stability: |λ_i| ≈ 0 (i = 1, 2,…, D_g).
• H3The correlation properties of the fluctuating time series will reflect the stability properties of H1and H2, with statistical persistence tangent to the GEM, and little or no persistence transverse. In the limit as the control along the manifold is reduced to zero, the fluctuations tangent to the GEM approach a random walk.
• H4The goal-level variability σ_e will scale according to Eqs. (6). In the case when D_g = 1, this means that σ_e/σ_ℛ ≈ s, as in Eq. (16).
• H5As a natural consequence of hypotheses H1-H4, one also expects that the variability perpendicular to the GEM will be much less than variability along it: σ_ℛ/σ_𝒩 < < 1.

Hypotheses H1-H3 are related to the “active” (i.e., dynamic) properties of the controller, with H3, which is concerned with persistence (not necessarily of the long-range type), being essentially a corollary to the first two. In contrast, H4 is related to the “passive” sensitivity properties along the GEM. Note that only hypothesis H5, which is to some extent a combined effect of the other four, has been previously emphasized in other methods that have been used to explore the role of motor redundancy. However, an important weakness of H5 is that the variability ratio it describes is not invariant under coordinate transformations. For example, using principle component analysis (Mardia et al., 1979) one can easily construct a linear coordinate transformation that yields new body-level variables with arbitrary variance. While the possibility of such “artificial” coordinate transformations does not completely undermine the experimental utility of variability ratios (Sternad et al., 2010), it does suggest that variability ratios alone may be inadequate tests for hypothesized task manifolds. In contrast, H1-H4 will be true in any coordinate system (John et al., 2013), due to the coordinate invariance of the local stability properties (Hirsch et al., 2004; Verhulst, 1996).

5 Experimental Applications

We now illustrate some of the ways the ideas presented in the previous sections can be implemented by describing recent experimental studies. Our intention here is not to repeat all of the main results in each case, but rather to discuss how the hypotheses H1-H5 have been tested and, to date, verified to be true. The reader is referred to the cited papers for additional details

There are two contrasting approaches that we have so far taken in implementing the GEM-based analysis. In one, different explicit models of the form Eq. (13) are formulated and used to generate model-based “surrogate data” predicting the statistical structure of variability for the task. In the other, no such “first principles” model is constructed, but the matrix B of the linearized controller model Eq. (15) is instead estimated directly from the fluctuation data, and the eigenstructure of the estimated matrix is obtained and compared to the geometry of a hypothesized goal function and GEM.

5.1 Treadmill Walking

Walking on a motorized treadmill requires only that subjects not walk off either end of the machine (Dingwell et al., 2010). This means that subjects must, over time, walk at the same average speed as the treadmill and stay in the same average position. However, substantial fluctuations in both position and speed due to changes in stride length and/or stride time can and do occur, and can be sustained over multiple consecutive strides (Dingwell et al., 2001, 2010; Owings & Grabiner, 2004).

Considering only the sagittal plane, the treadmill walking task is specified by an inequality constraint of the form

$$\mid \sum _{n=0}^N(L_n-v{T}_n)\mid \le K,$$ (17)

where: L_n and T_n are the stride length and time, respectively, at stride n; v is the treadmill speed; K is nominally half the treadmill’s length; and N is the total number of strides. There are many possible strategies that one could use to satisfy this requirement, including a variety of “drunken” or “silly” walks. However, we chose to test the simplest possible strategy, defined by the scalar goal function f(T_n, L_n) = L_n − vT_n = 0, which makes the sum in Eq. (17) identical to zero, and is equivalent to a strategy of matching the treadmill speed at each stride (i.e., L_n/T_n = v, see Fig. 5A). Thus, the body state is x = (T_n,L_n), equivalent to a discretization of the walking task using an impact Poincaré section at heel strike, and each stride represents one “trial”. Therefore, in this case we have D_g = 1, and D_b = 2, as with the ball throwing example (Fig. 2).

Figure 5.

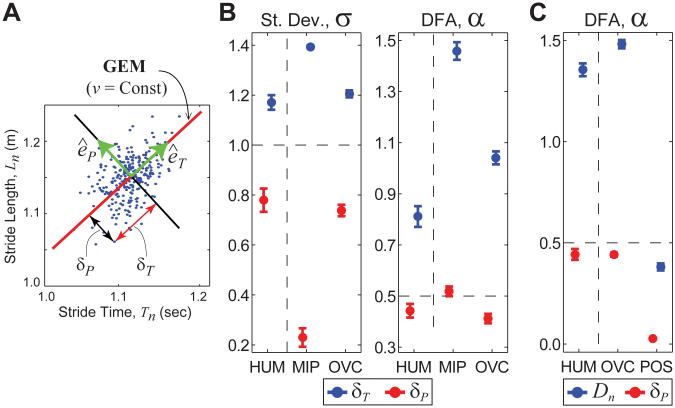
(A) GEM for walking on a treadmill at constant speed (L_n/T_n = v). (B) Experimental (HUM) results and model predictions for pure minimum intervention principle (MIP) and overcorrecting (OVC) controllers. Humans (HUM) exhibited: significantly greater δ_T variability than (δ_P) variability (p < 1 × 10⁻⁵); significantly greater statistical persistence for δ_T than for δ_P fluctuations (p < 1 × 10⁻⁵); and anti-persistence (0 < α < 1/2) for goal-relevant δ_P deviations, but persistent (1/2 < α < 1) δ_T deviations (adapted from Dingwell et al., 2010). These characteristics were matched qualitatively by the OVC model, not the MIP. (C) DFA results for absolute position D_n and δ_P deviations, from experiment (HUM) and models for OVC and absolute position control (POS). Although OVC and POS models predict the same average speed and absolute position, the OVC model qualitatively matches HUM DFA results; the POS model does not. Although both the OVC and POS models predicted the same average speed and position on the treadmill over time, the POS model clearly demonstrated very different stride-to-stride fluctuation dynamics than the OVC model and HUM subjects. All error bars indicate ±95% confidence intervals for each mean.

Stride times and lengths were recorded from healthy subjects walking at five speeds (Kang & Dingwell, 2008a,b). The specified goal function (Fig. 5A) was used to define a gait fluctuation variable u = (δ_T, δ_P), where δ_T and δ_P are deviations from the mean in directions tangent and perpendicular to the GEM, respectively. Subjects exhibited significantly lower variability for goal-relevant δ_P fluctuations than for goal-irrelevant δ_T fluctuations (Fig. 5B), consistent with H5. More importantly, DFA analysis showed antipersistent δ_P deviations (0 < α < 1/2), indicating immediate overcorrection of perturbations off of the GEM, but persistent δ_T deviations (1/2 < α < 1), consistent with indifferent control of perturbations along the GEM (Fig. 5B). Independent from any consideration of whether or not the observed persistence indicates long-range correlations (and we make no claim that it does, because that is not our focus), these results support H3, and indicate that movement regulation was organized with respect to the hypothesized GEM.

Stochastic control models of the form Eq. (13) where developed using variants of the cost function Eq. (14), each of which tried to minimize errors with respect to the hypothesized constant speed goal function. Figure 5B shows results for two such models: an ideal minimum intervention principle model (MIP), with C₃ = 0 in Eq. (14); and an overcorrecting model (OVC) with preferred operating point (C₃ ≠ 0). When compared with results from human subjects (Fig. 5B: HUM), these models demonstrated that healthy human treadmill walkers are not precisely optimal (Fig. 5B: MIP), but instead consistently slightly over-corrected small deviations in walking speed at each stride (Fig. 5B: OVC) (Dingwell et al., 2010). The OVC model predictions show a strong qualitative match with experimental findings, whereas the pure MIP model predictions do not.

To further demonstrate that the constant speed GEM of Fig. 5A was not the only one subjects could have adopted, we created an additional model (POS) that minimized errors with respect to a goal function for constant absolute position on the treadmill. On average, these two control strategies are essentially identical, but predict very different stride-to-stride fluctuation dynamics. Figure 5C compares experimental (HUM) DFA results and those predicted by OVC and POS models. The absolute position at stride n, D_n, of human subjects had highly persistent fluctuations, a feature captured by the OVC model, which is controlling speed instead of position, but not by the POS model, which controls position not speed. This further reinforces the view that nonpersistence of a quantity is associated with its control, whereas persistence indicates weak or even, if the fluctuations approach a random walk, no control.

The use of optimal control models in this context allowed us to make concrete, experimentally testable predictions about the precise nature of the stride-to-stride fluctuation dynamics. This, in turn, allowed us to draw clear conclusions about the control strategies people used when walking on treadmills. This analysis of movement fluctuations allows us to discern differences between possible control strategies, even if those strategies are not distinguishable on average. Thus, the use of computational control models via Eqs. (13) and (14) provides a degree of both explanatory and predictive capability that cannot be achieved by approaches that rely solely on analyzing variance.

5.2 Virtual Shuffleboard

Shuffleboard is one of the simplest tasks involving “throwing” at a target, making it attractive as an experimental system for studying goal-directed movement fluctuations. A virtual shuffleboard apparatus was developed (John, 2009; John et al., 2013) in which a custom built manipulandum is used to move a shuffleboard cue and puck on a virtual court. In a given trial, subjects accelerate the instrumented manipulandum from a fixed rest position along a linear bearing, and are able to track the subsequent motion of the puck as it is released from the cue and heads toward the target. The shuffleboard court, puck, cue, and target are all represented in the 3D virtual world and projected onto a screen in view of the subject.

The virtual court is modeled as a horizontal plane with Coulomb friction acting between the puck and ground. Thus, the dynamics of the puck after release is governed by the equation ẍ = −μg, where x is the position of the puck, g is the gravitational acceleration, and μ is the friction coefficient. The goal of each trial is to hit a target located a distance L from the origin of the system. The manipulandum is started from rest at x = 0 for each trial. The final rest position of the puck is a function of the position x and velocity v at the puck’s release, and so one can show (John, 2009; John et al., 2013) that the scalar goal function is

$$f(x,v)=\frac{v^2}{\mu }+x-L.$$ (18)

Any combination of the body state x = (x, v) for which f(x, v) = 0 will perfectly hit the target. Thus, for this system we again have D_g = 1 and D_b = 2.

Experiments were carried out with 4 young healthy male adults. The friction coefficient μ was selected from 8 values chosen so that perfect trials would require between 3 and 5 sec. The 8 values where split into “high” and “low” groups of 4, and each subject was given from each group. Subjects were allowed to practice until their average error over 50 trials was ≤ 10% of the target distance. Then the data collection phase began, during which subjects performed 500 trials in 10 sessions of 50 trials each over 2 days. All sessions took ≤ 7 min, and subjects had at least 5 min rest between sessions. Position and acceleration sensors on the manipulandum were used to determine the time of release of the virtual puck, by computing the moment when the contact force between puck and cue dropped to zero. At that moment, the value of (x,v) were recorded, and used to generate the subsequent motion of the puck on the screen in real time. Subjects could then observe the stopping position of the puck, and obtain error information via direct visual feedback.

In this case, rather than testing controller hypotheses using different cost functions Eq. (13), as was done with treadmill walking, we used the (x,v) fluctuation time series to estimate the matrix B in the linearized controller Eq. (15) via linear regression (John et al., 2013). The eigenvalues (i.e., the stability multipliers) and eigenvectors of B were then estimated. However, these sorts of estimates are known to be highly sensitive to matrix estimation errors, and so a simple bootstrapping method was employed to yield robust estimates with confidence limits (Akman et al., 2006; Press et al., 1992). From the initial set of 500 trials for each subject, 1000 random subsamples of 100 trials each and their subsequent were generated. Each of the 1000 subsamples was used to estimate the map B, which in turn yielded eigenvectors and eigenvalues for the fluctuation process. This procedure thus yielded empirical probability densities for all estimated quantities.

The eigenvalue results are shown in Fig. 6A: one eigenvalue, with a median value of −0.03, is very close to zero across all 8 subjects and friction conditions, indicating a strongly stable direction in which fluctuations are quickly damped out; the other, with a median value of 0.77, is much closer to unity and hence indicates a weakly stable direction. Furthermore, it was found that the eigenvector associated with the strongly stable direction had a median angle of 53.8° with the tangent to the GEM(so that ø = 36.2° in Fig. 4), whereas the eigenvector associated with the weakly stable direction had a median angle of 1.5° with the GEM. These results are entirely consistent with hypotheses H1 and H2, showing that control acts strongly to suppress deviations transverse to the GEM, but much less strongly along it.

Figure 6.

Results for the shuffleboard experiment for all subjects and friction conditions. (A) Stability multipliers (eigenvalues of B as in Eq. 15) estimated from fluctuation time series: the strongly stable eigenvalue (blue probability densities) is near zero and corresponds to an eigenvector that is transverse to the GEM, whereas the weakly stable eigenvalue (red probability densities) is close to 1 and corresponds to an eigenvector nearly tangent to the GEM. The probability densities were estimated using a bootstrapping technique. Dashed blue and red lines indicate 5 and 95 percentiles for all subjects/conditions. (B) Scaling behavior of normalized task performance, showing dominant effect of passive sensitivity: σ_e/σ_ℛ = s to high accuracy, where s is the singular value of the body-goal matrix A for the goal function (Eq. 18). Red dots indicate bootstrapping estimates from data for all 8 subjects/conditions, blue line is from regression.

Using the goal function Eq. (18), the body-goal matrix is found as A = [1, 2v*/μ], which has a single singular value $s=\sqrt{1+{(2v^{\ast }∕\mu )}^2}$ (John et al., 2013), where v* is the ensemble average velocity of release for the different subjects/conditions. The sensitivity could then be estimated for each subject/condition using this theoretical expression for s, together with the known values of μ and measured values of v*. The root mean square goal-level error, σ_e, and the component of body-level variability perpendicular to the GEM, σ_ℛ, were computed and used to obtain σ_e/σ_ℛ = s and plot it against s. The result is shown in Fig. 6B, for which the relevant quantities were again computed using a boostrapping approach. We see that ${\sigma }_e∕{\sigma }_{\mathcal{R}}=s$ to high accuracy, thus showing that the skilled performance scales with the passive sensitivity along the GEM. This result supports H4, indicating that the goal level variability of skilled performance is determined predominantly by the goal function (John, 2009), not active error correction per se, because of the strong stability found transverse to the GEM and Eq. (16). This result also validates, at least in this instance, a major assumption of our analysis, namely that for skilled movements the fluctuations are sufficiently close to the GEM to justify the use of linearized models.

5.3 Reaching

Determining if humans exploit task redundancies when the redundancy is de-coupled from the task itself is critical to determining how general such strategies are. Here, we derived a class of uni-directional reaching tasks, defined by a family of goal functions that explicitly defined the redundancy between reaching distance, D, and time, T (Smallwood et al., 2012). All (T, D) combinations satisfying any specific goal function defined a GEM. We tested how humans learned two such functions (Fig. 7A), D/T = c (for constant c), corresponding to constant speed, and DT = c, which has no direct, concrete interpretation. Thus, in both cases, the body state is given by x = (T, D), so that D_b = 2 and D_g = 1.

Figure 7.

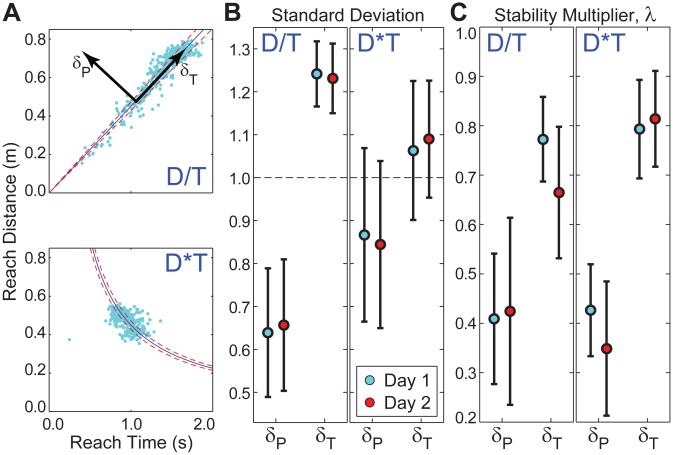
(A) GEMs for two different reaching tasks (D_n/T_n = c and D_nT_n = c), with typical data from one subject. (B) Experimental normalized standard deviations for all subjects, for each task after Day 1 and Day 2 of practice, for tangential (δ_T) and perpendicular (δ_P) deviations from each GEM. For both tasks, subjects exhibited significantly greater variance in δ_T than for δ_P. However, this effect was more pronounced for the D/T task (p < 0:0005) than for the DT task (p = 0:019). (C) Stability multipliers (λ) for all subjects estimated for each task after Day 1 and Day 2 of practice, for δ_T and δ_P deviations from each GEM. Subjects exhibited significantly higher stability (smaller λ) for goal-relevant δ_P fluctuations than for goal-equivalent λ_T fluctuations for both tasks (p < 0:0005). However, in contrast to the variability results (B), these effects were slightly more pronounced for the DT task than for the D/T task (adapted from Smallwood et al., 2012). All error bars indicate between-subject ±95% confidence intervals.

The tasks so defined, though very different, had a point of intersection that could be achieved by similar reaching movements. Ten young healthy subjects participated. The results presented here come from consecutive days, Day 1 and Day 2. Subjects made smooth, out-and-back reaching movements. They were instructed to reach as near or as far as they desired and at whatever speed they desired. After each reach, subjects were given feedback about their performance (i.e., the final T and D for that reach) and their relative % error with respect to the GEM for that task. Most importantly, however, the GEM itself was never directly displayed to the subjects. Subjects were only instructed to minimize errors.

Subjects exhibited significant learning and consolidation of learning (Brashers-Krug et al., 1996; Krakauer et al., 2006) for both tasks. Interestingly, learning the D/T task first facilitated (Brashers-Krug et al., 1996; Krakauer et al., 2006) subsequent learning of the DT task, while learning the DT task first interfered with (Brashers-Krug et al., 1996; Krakauer et al., 2006; Wulf & Shea, 2002) subsequent learning of the D/T task (Smallwood et al., 2012).

For both tasks, and consistent with hypothesis H5, subjects exhibited greater variability along each GEM than perpendicular to it (Fig. 7B), however this differences less pronounced for the DT task than for the D/T task. Additionally, consistent with hypotheses H1 and H2, for both tasks subjects actively corrected deviations perpendicular to each GEM faster than deviations along each GEM (Fig. 7C), as measured by stability multipliers λ estimated in each direction. Interestingly, the difference in stability was comparable for both tasks, though a bit more pronounced for the DT task (Fig. 7C), despite exhibiting smaller variance ratios than the D/T task (Fig. 7B). These results demonstrate that subjects’ ability to actively exploit task redundancies to minimize overall control effort, by exerting more control transverse to the GEM than along it, does indeed generalize across multiple tasks (Smallwood et al., 2012), even ones that are abstractly defined.

6 Discussion, Conclusions, and Future Directions

In this paper we have described a conceptual framework for the experimental study of movement variability that synthesizes geometrical methods, which focus on the role of motor redundancy, and dynamical methods that characterize the processes that regulate the repeated performance of skilled tasks. We have grounded the description of our approach, which is centered on the idea of the goal equivalent manifold (GEM), with a review of four of the key perspectives currently used to study movement variability. These perspectives, while each having provided many important insights, have to date eluded unification into a single, coherent description of observed fluctuations. The GEM approach provides a model-based analysis of fluctuation data that shows how dynamical measures of motor performance, such as those based on stability and correlation analyses, are related to the geometrical structure of variability resulting from goal equivalence. In so doing, our approach ensures a consistent interpretation of different variability measures that helps avoid apparent paradoxes found in the literature, particularly when using such measures to make inferences about the health of the neuromotor system.

Our approach has multiple features that distinguish it from other approaches to movement fluctuation analysis that are based on some notion of goal equivalence. First, we note that goal equivalence itself is a basic property of redundant systems, regardless of the nature of control used to regulate them. Indeed, a GEM can exist even for a completely uncontrolled, or open loop system. In this way, we make a clear distinction between the “plant” (the task definition via goal functions) and “controller” (defined via cost functions) that allows each to be tested by separate experimental hypotheses. Second, we distinguish between “passive” and “active” contributions to goal-level variability, with the sensitivity properties along the GEM representing the former, and the stability properties of fluctuation dynamics near the GEM representing the latter. Third, our approach incorporates an examination of the effect of coordinate transformations on the task manifold itself (the GEM), its sensitivity properties, and the local stability properties of error-correcting control near the GEM. Unlike approaches based purely on variability ratios, the dynamical measures central to our approach should be invariant under reasonable coordinate transformations. Finally, our description of the GEM framework culminates with a set of five general hypotheses for “GEM aware” inter-trial control, only one of which has been previously used to examine motor variability in the context of goal equivalence.

It is already generally accepted that motor control is organized around some notion of goal equivalence. Our contribution is to show that the organization of fluctuations can be studied unambiguously by analyzing only body state variables that interact directly with goal level performance variables, as defined for a specific task using goal functions. Simple optimal control models defined using these goal functions provide a model-based decomposition of the data that can be used to study specific strategies used to regulate task performance. This perspective helps to unify motor fluctuation analysis methods based on local stability, task manifolds, correlation, and feedback control. Our approach not only describes variability data, but in principle can be used to make model-based predictions about fundamental features, such as dependence of stability properties and fluctuation statistics on model parameters. One type of variability analysis with which our current approach has yet to fully reconcile is fractal dynamics (such as via DFA). This stems largely from the fact that our controller models use proportional feed back, resulting in autoregressive time-series models (as in Eq. 15) that are known to be incompatible with long-range persistence. One possible avenue to overcoming this limitation, should it be desired, would be to consider models of a completely different type, that can support true long-range memory processes (such as, for example, controllers of “bang-bang” type). Despite this limitation, however, our work has shown that a parsimonious interpretation of persistence estimates (whether or not they correspond to truly long-memory processes) is best achieved by considering the nature of error regulation near the GEM.

We have presented recent experimental applications of our approach that illustrate how the five hypotheses have, so far, been demonstrated to hold. Certainly, much more work is needed to examine the limitations of the various assumptions underlying our methods in their current form. The structure of the GEM framework, as currently implemented, depends on the tasks under consideration being either intrinsically discrete, or being amenable to discretization via, for example, Poincarée sections. This mathematical convenience yields a set of tools that are relatively simple to define and use, and can in principle be applied to a very wide range of possible movement tasks. Nevertheless, in future work one would like to see the fundamental ideas underlying the GEM approach expanded to continuous-time tasks. One avenue for pursuing this might involve developing the idea of action variables, as defined in section 3.4, and implementing them experimentally to better understand the relationship between in-trial and inter-trial control.

To date we have focused on the analysis of movement fluctuations for skilled performers, meaning that deviations from the GEM are small, so that goal-level and body-level variability scale according to Eqs. (6), and linearized controller models are adequate. There is a need to further develop these ideas for application to the movements farther from the GEM, for which nonlinear effects would be important, such as would be necessary for the study of motor learning. Our recent work on reaching tasks described in section 5.3 is a step in this direction.