A Bayesian Approach to Improved Estimation of Causal Effect Predictiveness for a Principal Surrogate Endpoint

Summary

The literature on potential outcomes has shown that traditional methods for characterizing surrogate endpoints in clinical trials based only on observed quantities can fail to capture causal relationships between treatments, surrogates, and outcomes. Building on the potential-outcomes formulation of a principal surrogate, we introduce a Bayesian method to estimate the Causal Effect Predictiveness (CEP) surface and quantify a candidate surrogate’s utility for reliably predicting clinical outcomes. In considering the full joint distribution of all potentially-observable quantities, our Bayesian approach has the following features. First, our approach illuminates implicit assumptions embedded in previously-used estimation strategies that have been shown to result in poor performance. Second, our approach provides tools for making explicit and scientifically-interpretable assumptions regarding associations about which observed data are not informative. Through simulations based on an HIV vaccine trial, we found that the Bayesian approach can produce estimates of the CEP surface with improved performance compared to previous methods. Third, our approach can extend principal-surrogate estimation beyond the previously-considered setting of a vaccine trial where the candidate surrogate is constant in one arm of the study. We illustrate this extension through an application to an AIDS therapy trial where the candidate surrogate varies in both treatment arms.

1. Introduction

The ethical and practical advantages of evaluating clinical trials on the basis of surrogate markers instead of difficult-to-obtain clinical outcomes have led to substantial research on the statistical requirements of valid surrogate endpoints. The majority of research regarding whether a surrogate predicts treatment effects on clinical outcomes builds on the criteria formulated in the seminal work of Prentice (1989). While statistical validation of candidate surrogate markers has progressed since then, most formulations rely on adjustment for an observed surrogate quantity that is measured after randomization (Weir and Walley, 2006). Dating back to ideas presented in Cochran (1957), adjustment for an observed posttreatment concomitant variable has been shown to obscure estimation of causal treatment effects.

Recognized for its relevance in settings susceptible to posttreatment selection bias, the potential-outcomes framework of principal stratification (Frangakis and Rubin, 2002) (henceforth FR) has recently motivated definition of a principal surrogate based on potential outcomes and causal effects as an alternative to standard definitions based only on observed outcomes. The goal of this approach is to determine whether knowledge of the treatment effect on the surrogate confers knowledge of the treatment effect on the primary outcome. Towards this end, principal surrogates are predicated on the definition of exactly two causal effects: the causal effect of the treatment on the candidate surrogate and the causal effect of the treatment on the primary outcome. The extent to which the former causal effect can be used to reliably predict the latter will be the basis for establishing surrogate value. Note that the principal-surrogate perspective does not involve definition of a causal effect of the surrogate on the outcome, which would require assumptions about a hypothetical intervention that acts directly on the surrogate response. This is an important distinction between establishment of a principal surrogate endpoint and the types of information delivered by related notions of direct and indirect effects (VanderWeele, 2011).

Most of the work on evaluating principal surrogates appears in the context of a vaccine trial and focuses on whether effects of the vaccine on a surrogate immune biomarker reliably predict effects of the vaccine on infection outcomes (Follmann, 2006; Gilbert, Qin, and Self, 2008; Gilbert and Hudgens, 2008; Qin, Gilbert, Follmann, and Li, 2008; Wolfson and Gilbert, 2010). Of particular importance is Gilbert and Hudgens (2008) (henceforth GH), which reframes the original definition of a principal surrogate and introduces a causal estimand for evaluating surrogate value called the causal effect predictiveness (CEP) surface. Because potential outcomes under treatments not received are unavailable, estimation of the CEP surface relies on strategies for imputing unobserved potential surrogate responses and modeling primary outcomes conditional on “complete” data. This differs from ignorable missing data problems because the data lack information on relationships among quantities that are never jointly observed. For example, surrogate responses to both treatment and control are never observed for any individual, so the data cannot reliably inform about the correlation between these responses.

Previously-proposed estimation methods for the CEP surface in vaccine trials (Follmann 2006; Qin et al. 2008; GH) have been shown in simulation studies to yield poor estimates of the CEP surface absent very specialized study designs (as in Follmann (2006)) that replace unobserved potential surrogate responses with data obtained at another point in time. One common feature of these estimation methods is that they are sequential in the sense that they rely on separate modeling stages to first estimate missing potential immune responses (the imputation stage) and then model infection outcomes conditional on complete principal strata (the risk model stage). In this paper, we propose a Bayesian method for estimation of the CEP surface that considers the full joint distribution of all potentially-observable surrogate and clinical outcomes. Unlike previously-used sequential methods, our Bayesian approach models the imputation and risk model stages simultaneously. Through detailing the Bayesian method, we illuminate that the sequential nature of previously-used strategies obscures implicit assumptions about important nonidentifiable associations in the full joint distribution of the data. We argue that these implicit assumptions result in bias. One advantage of the Bayesian method is that it facilitates natural incorporation of scientifically-interpretable prior information about key nonidentifiable associations that can avoid the more restrictive assumptions implicit in previous methods. Through simulations mimicking those of GH, we show that our Bayesian approach can yield posterior estimates of the CEP surface that improve upon estimates from previously-used sequential methods.

One key feature of HIV vaccine trials that is central to existing methods is the justification of the “constant biomarker” assumption that potential surrogate responses to control treatment take on the same value for all patients. This simplifies estimation of the CEP surface because of the reduced the number of missing potential outcomes that need to be imputed, but it is of interest to the research community to allow surrogate responses to vary in both treatment arms. For example, we explore in this article a data analysis of an HIV/AIDS clinical trial of antiretroviral therapies where the change from baseline CD4 lymphocyte count is a natural candidate surrogate that varies in both treatment arms (i.e., no constant biomarker). Through incorporation of both prior information and a sensitivity parameter to characterize nonidentifiable associations, our Bayesian approach extends estimation of the CEP surface to such a setting that does not assume a constant biomarker. To our knowledge, the only previously-described approach to principal surrogate endpoints that relaxes the constant biomarker assumption appears in Li, Taylor, and Elliott (2010) for a specific setting that assesses the surrogacy of a binary outcome for predicting the same outcome at more distant follow up. In contrast, we explore a setting with a continuous surrogate and a binary outcome, and we evaluate surrogacy from a perspective that coincides more closely with GH.

Section 2 of this paper reviews previous development of principal surrogate endpoints and the CEP surface. Section 3 discusses estimation of the CEP surface, including a transparent assessment of the assumptions implicit in previously-used methods and the development of our Bayesian approach. Section 4 evaluates the performance of our Bayesian method in a simulation study paralleling the one in GH. In Section 5, we extend estimation to settings with varying control-group response through an application to an AIDS clinical trial that does not support the constant biomarker assumption. We conclude with a discussion.

2. Principal Stratification for Evaluating Surrogate Endpoints

2.1 Notation and principal strata

Following development in FR and GH, we first define the potential-outcomes notation relevant to our setting. Let Z_i indicate assignment to treatment, for i = 1, … n patients. Denote the potential primary outcome under treatment z with the indicator Y_i(z) = 0, 1, for z = 0, 1. We assume that all surrogate responses are measured at a specified time, t, after baseline, and denote the i^th patient’s potential surrogate response under treatment z with S_i(z), for z = 0, 1. In many settings, experiencing the outcome before time t precludes definition of S_i(z). Let V_i(z) = 1 indicate that patient i would not experience the primary outcome before t and thus have a defined value of S_i(z) measured, with V_i(z) = 0 otherwise. Implicit here is the stable unit treatment value assumption (SUTVA) to clarify that there is no interference between units (Rubin, 1978). We denote pretreatment covariates by X_i and use mis and obs to denote missing and observed potential outcomes, respectively. Unless otherwise noted, we henceforth omit the i subscript to simplify notation.

Basic principal strata in this setting are defined by the vector of potential surrogate values, S(z), and potential risk-set indicators, V(z), denoted {S(0), S(1), V(0), V(1)}. A patient’s principal stratum captures information on how that patient’s surrogate response would respond to treatment, that is, the individual-level causal effect of the treatment on the surrogate. In strata with V(0) = V(1) = 1, patients with S(1) > S(0) would experience a positive causal treatment effect on the surrogate, those with S(1) < S(0) would experience a negative causal treatment effect on the surrogate, and those with S(1) = S(0) would experience no causal treatment effect on the surrogate. No analogous classifications can be made for strata with V(0) = 0 or V(1) = 0 because these strata contain at least one undefined value of S(z). Average treatment effects on primary outcomes within basic principal strata or unions of these strata constitute principal effects that permit causal interpretation as average comparisons between comparable sets of units. Estimating principal effects will guide our assessment of whether S is a useful surrogate.

2.2 Principal surrogate endpoints

As in GH, we assume ignorable treatment assignment (Rubin, 1978), which holds when treatments are randomized. We also follow GH in assuming equal individual clinical risk up to time t, stating that V(1) = 1 if and only if V(0) = 1. Equal individual clinical risk stipulates that the treatment does not affect which patients remain at risk for the primary outcome before time t, and hence precludes principal strata with V(0) ≠ V(1). For simplicity, we henceforth omit reference to V(z) and assume that probability statements involving S(z) are conditional on V(0) = V(1) = 1. This assumption is not innocuous in general, but is often made in practice when t is close to baseline (Wolfson and Gilbert, 2010).

Principal effects compare the probability of the outcome under competing treatments within principal strata. These can be denoted as comparisons between:

$$r_z(s_1,s_0)\equiv Pr(Y(z)=1\mid S(1)=s_1,S(0)=s_0),$$

for z = 0, 1. Determining whether an intermediate response qualifies as a principal surrogate involves definition of causal effects of the treatment on the outcome as being associative or dissociative with causal effects of the treatment on the surrogate. Associative effects are causal treatment effects on Y in strata with S(0) ≠ S(1) and represent causal effects of Z on Y that are associated with causal effects of Z on S. Dissociative effects are causal treatment effects on Y in strata with S(0) = S(1) and represent causal effects of Z on Y that exist in the absence of a causal effect of Z on S. A principal surrogate is one for which associative effects exist for changes in the surrogate in excess of some threshold and for which there is no dissociative effect, i.e., r₁(s₁, s₀) ≠ r₀(s₁, s₀) for all |s₁ − s₀| > C_A and r₁(s₁, s₀) = r₀(s₁, s₀) for all s₁ = s₀. Both FR and GH suggest evaluating surrogate value by quantifying associative effects relative to dissociative effects; large associative effects relative to small dissociative effects indicate that the effect of Z on Y is most pronounced in strata with an effect of Z on S, which may imply value in using the latter effect to predict the former. On the contrary, when associative effects and dissociative effects are both large (or both small), the effect of Z on S cannot reliably predict the effect of Z on Y because the treatment effect on the outcome would be similar regardless of whether there is a treatment effect on the surrogate. Note that an associative effect should not be interpreted as an indirect effect or as an effect of S on Y; associative effects capture the extent to which an effect of Z on S is associated with an effect of Z on Y. Furthermore, note that a nonzero dissociative effect implies that Z affects Y through pathways not involving S, but that absence of a dissociative effect does not necessarily preclude the existence of such pathways (VanderWeele, 2011).

2.3 The Causal Effect Predictiveness (CEP) surface

GH proposed the CEP surface to measure causal effects of Z on Y across the surface defined by all possible principal strata:

$${\mathit{CEP}}^r(s_1,s_0)\equiv h(r_1(s_1,s_0),r_0(s_1,s_0)),$$

where h(x, y) is a specified contrast function satisfying h(x, y) = 0 for x = y. CEP^r(s₁, s₀) = 0 for all s₁ = s₀ suggests no dissociative effect, and CEP^r(s₁, s₀) ≠ 0 for some s₁ ≠ s₀ represents an associative effect when Z causes a change in S from s₀ to s₁. A useful surrogate might not be a perfect principal surrogate, but should be one for which the sign and magnitude of the effect of Z on S provides information regarding the sign and magnitude of the effect of Z on Y. For example, CEP^r(s₁, s₀) increasing with s₁ − s₀ and near 0 for s₁ ≈ s₀ would indicate a useful surrogate with large associative effects relative to dissociative effects; the larger the effect of Z on S, the larger the effect of Z on Y, and little or no effect of Z on Y when there is little or no effect of Z on S.

Knowledge of the entire CEP surface would indicate the causal effect of Z on Y in any region of the surface defined by particular values of (s₀, s₁). For example, interest my lie in regions where s₀ > 0 and (s₁ − s₀) > C_A for the effect of Z on Y when S(0) is positive and the causal effect of Z on S exceeds C_A. In practice, however, researchers may be less focused on isolated regions of the surface and more interested in, say, the effect of Z on Y when the effect of Z on S is either zero, positive, or negative. To characterize such effects, GH proposed several summary quantities for the CEP surface. The expected dissociative effect (EDE) is defined as the expected value of the CEP surface in strata for which the effect of Z on S is below a certain threshold: E[CEP^r(S(1), S(0))||S(1) − S(0) | ≤ C_D], for C_A ≥ C_D ≥ 0. The constant C_D might be 0, as in GH, or some threshold below which a change in S is deemed clinically irrelevant. For areas of the surface where the effect of Z on S is positive (s₁ > s₀), we adapt definitions in GH to define the positive expected associative effect (EAE⁺) to summarize the expected value of the CEP surface among strata for which the treatment induces S to increase in excess of C_A: E[CEP^r(S(1), S(0))|(S(1) − S(0)) > C_A)]. Analogously, we define the negative expected associative effect (EAE⁻) to summarize the average effect of Z on Y in areas of the surface where the treatment causes a decrease in S: E[CEP^r(S(1), S(0))|(S(1) − S(0)) < −C_A)]. For an overall measure of associative effects, we define EAE = EAE⁺ − EAE⁻. To summarize the magnitude of associative effects relative to dissociative effects, the proportion associative effect (PAE), can be defined as $\frac{\mid \mathit{EAE}\mid }{\mid \mathit{EAE}\mid +\mid \mathit{EDE}\mid }$, where PAE ∈ (0.5, 1] indicates that associative effects are larger in magnitude than dissociative effects. Analogous definitions of PAE⁺ and PAE⁻ could be obtained by replacing EAE with its positive or negative component.

No single summary quantity can be used to completely characterize surrogate value, but used in combination, these quantities could provide evidence as to whether a treatment effect on the surrogate could be used to reliably predict a treatment effect on the outcome. For example, a small EDE, positive EAE⁺ (negative EAE⁻), and PAE ∈ (0.5, 1] would indicate, respectively, that: 1) little or no effect of Z on S is associated with little or no effect of Z on Y; 2) a positive (negative) effect of Z on S is associated with a positive (negative) effect of Z on Y; and 3) effects of Z on Y are most pronounced when Z affects S.

3. Estimation of the CEP Surface

For each patient, potential outcomes are observed for either Z = 0 or Z = 1, but never for both. As a result, neither of {Y(0), S(0)} is ever jointly observed with either of {Y(1), S(1)}, and the data lack information regarding associations between potential outcomes under competing treatments. Thus, further assumptions are required to estimate the full joint distribution of the data. As in GH, we assume Y(0) ⫫ Y(1)|S(0), S(1), X and focus on average comparisons within principal strata. The data also lack information regarding associations between:

$$\{S(0),S(1)\mid X\},\{S(0),Y(1)\mid X\},\{Y(1),X\mid S(0)\}$$ (1)

$$\{Y(0),X\mid S(1)\},\{S(1),Y(0)\mid X\}.$$ (2)

Note that specification of these pairwise components is not sufficient for characterizing the entire joint distribution, but the estimation strategies detailed below require assumptions regarding these associations. The primary difference between our proposed Bayesian approach and previously-used strategies lies in the assumptions regarding these associations. We examine the differences in the following sections.

Following GH, we parameterize the risk distributions with the following probit regressions that condition additionally on covariates, X:

$$r_z(s_1,s_0,x)=Pr(Y(z)=1\mid S(0)=s_0,S(1)=s_1,X=x)=\mathrm{\Phi }(g_z(s_1,s_0,x;{\beta }_z)),$$ (3)

where Φ is the standard normal cumulative distribution function, g_z(s₁, s₀, x; β_z) is a specified form of the relationship between S(0), S(1), X and Y(z) as a function of parameters β_z, and z = 0, 1. Furthermore, we consider settings with a single continuous pretreatment covariate, and assume that {S(0), S(1), X} ~ MV N₃(μ, Σ).

3.1 The constant biomarker special case

GH and other previous research (Follmann, 2006; Qin et al., 2008) only illustrate estimation of the CEP surface in a placebo-controlled HIV vaccine trial where an immune-response biomarker is analyzed as a candidate surrogate for infection. Because of the lack of HIV specific immune response mounted under placebo, these settings permit the constant biomarker assumption that S(0) = c (e.g., the lower limit of detection of an antibody assay) for all patients. In simplified settings with a constant biomarker, principal strata are defined by {c, S(1)}, meaning that the principal stratum is completely observed and known for all patients with Z = 1. The challenge remains to estimate the stratum membership of those with Z = 0, that is, to impute placebo recipients’ potential immune response to the vaccine. Note that a constant biomarker precludes further assumptions about the associations in (1) involving S(0), but does not obviate the need for those pertaining to the associations in (2).

3.2 Previously-used estimation strategies with a constant biomarker

Here we outline the estimated-likelihood (GH) and approximate calibrated-based EM (ACEM, Qin et al. (2008)) strategies used in previous research to estimate the CEP surface with a constant biomarker and illuminate an implicit assumption embedded in these sequential approaches. For comparison with GH, we use g_z(s₁, c, x; β_z) = β_z0 + β_z1s₁ + β_z2x for the risk distributions in (3). A constant biomarker implies that r₁(s₁, c, x) is estimable from observed data on vaccine recipients, but the unavailability of S(1) for patients with Z = 0 means that r₀(s₁, c, x) is not. Follmann (2006) and GH argue that models for r₀(s₁, c, x) are identified under the assumption that β₀₂ = β₁₂, which amounts to an assumption about the first association in (2) (i.e., Y (0), X|S(1)) and can be easily and explicitly incorporated into any estimation strategy. However, while this assumption results in identifiability of r₀(s₁, c, x), it does not suffice for identifiability of the entire joint distribution of the data, and further assumptions about the second association in (2) (i.e., S(1), Y(0)|X) are required. We argue below that the estimated-likelihood and ACEM strategies imply a conditional independence assumption that can impact estimation.

The estimated-likelihood and ACEM approaches can be loosely conceived as consisting of two separate stages: the imputation stage and the risk model stage. The imputation stage estimates a model for f(S(1)|X, Z = 1) and applies this model to estimate the missing S(1) in patients with Z = 0. This is justified because randomization ensures that f(S(1)|X, Z = 1) =^d f(S(1)|X, Z = 0), where =^d denotes equality in distribution. The risk model stage considers the risk distributions in (3) conditional on the values of S(1) estimated from the imputation stage.

Conditioning solely on X in the imputation stage implies that values of S(1) in the Z = 0 patients are estimated subject to the conditional independence assumption that S(1) ⫫ Y(0)|X, which amounts to a model assumption about the second association in (2) (i.e., S(1), Y(0)|X). Problems can arise when this conditional independence is in fact false, despite the fact that the risk-model stage does not entail this assumption when β₀₁ ≠ 0. This issue is akin to that of imputing a missing covariate without conditioning on the observed outcome, but is fraught with the additional complication that the data lack information about the association between the missing covariate, S(1), and the observed outcome, Y(0), because these quantities are never jointly observed.

This conditional independence between S(1) and Y(0) (conditional on X) when estimating missing potential outcomes has been examined in settings such as treatment noncompliance (Jo and Stuart, 2009) but appears to have been overlooked in the vaccine literature. We argue that this assumption in the imputation stage is sufficient for identifiability of models for the entire joint distribution of the data, but that estimates are subject to bias amid violations. Note that one could fully enforce this assumption in both stages (i.e., also assume that β₀₁ = 0), which Jo and Stuart (2009) refer to as assuming principal ignorability, but this assumption is not valuable for estimating the CEP surface because it assumes that the risk of infection under placebo is the same in all strata.

3.3 Bayesian estimation of the CEP Surface with or without a constant biomarker

As an alternative to previously-used sequential methods, our Bayesian approach considers the full joint distribution of the data simultaneously, which “connects” the imputation and risk model stages in the sense that the imputation stage is carried out conditional on data and parameters in the risk model stage. For example, in the constant biomarker setting, imputations for S(1) in patients with Z = 0 are carried out conditional on all model parameters and observed data, including in particular observed values of Y(0) (the sequential methods described in Section 3.2 do not condition on Y(0) in the imputation stage). A nice feature of our Bayesian approach is that the required assumptions regarding the nonidentifiable associations in (1) and (2) can be naturally incorporated via prior information to yield useful posterior estimates of the CEP surface. We explore different assumptions regarding the associations in (1) and (2) via specification of informative prior distributions on some of the parameters in r_z(s₁, s₀, x) and, in the absence of a constant biomarker, a sensitivity parameter characterizing the correlation between S(0) and S(1). A key benefit of such an approach is that placing prior information on scientifically-interpretable parameters in the risk model stage will apply to the entire joint distribution of the data, including the model for the imputation stage. Thus, in contrast to previously-used sequential methods, our Bayesian approach unifies the imputation and risk model stages and facilitates imputation of the unobserved S(1 − z) for Z = z patients conditional on both X and the observed Y(z).

Making explicit use of the i subscript, we view the random variables Z_i, S_i(0), S_i(1), Y_i(0), Y_i(1), X_i as realizations from a joint probability distribution with Z_i, X_i, S_i(Z_i), Y_i(Z_i) observed and S_i(1 − Z_i), Y_i(1 − Z_i) missing for all i. With the introduction of model assumptions, Markov chain Monte Carlo (MCMC) methods such as the Gibbs sampler (Gelfand and Smith, 1990) can simplify inference in this setting because causal estimates can be calculated conditional on “complete data” for which unobserved potential outcomes are replaced by simulated values.

We denote the full distribution of the data as

$$f(\mathbf{Z},\mathbf{S}(\mathbf{0}),\mathbf{S}(\mathbf{1}),\mathbf{Y}(\mathbf{0}),\mathbf{Y}(\mathbf{1}),\mathbf{X})=f(\mathbf{Z},\mathbf{S},\mathbf{Y},\mathbf{X})=f(\mathbf{Y},\mathbf{S},\mathbf{X}\mid \mathbf{Z})f(\mathbf{Z})=f(\mathbf{Y},\mathbf{S},\mathbf{X})f(\mathbf{Z})$$

where the last equality follows from randomization. To facilitate Bayesian inference, we express the joint distribution of all potential outcomes and covariates as the product of independently identically distributed random variables conditional on a generic parameter θ (Rubin, 1978) and write the posterior distribution of θ as

$$p(\theta \mid {\mathbf{S}}^{\mathbf{obs}},{\mathbf{Y}}^{\mathbf{obs}},\mathbf{X})\propto p(\theta )\int \int \prod f(S_i^{\mathit{obs}},S_i^{\mathit{mis}},Y_i^{\mathit{obs}},Y_i^{\mathit{mis}},X\mid \theta ){dY}_i^{\mathit{mis}}{dS}_i^{\mathit{mis}}.$$

where p(θ) is a prior distribution for θ. The integration over $S_i^{\mathit{mis}}$ is computationally difficult in general, but $Y_i^{\mathit{mis}}$ can be handled with standard strategies that average outcomes within randomized groups. We omit the $Y_i^{\mathit{mis}}$ to simplify notation. Focusing on the joint posterior

$$p(\theta ,{\mathbf{S}}^{\mathbf{mis}}\mid {\mathbf{S}}^{\mathbf{obs}},{\mathbf{Y}}^{\mathbf{obs}},\mathbf{X})\propto p(\theta )\prod f(S_i^{\mathit{obs}},S_i^{\mathit{mis}},Y_i^{\mathit{obs}},X_i\mid \theta )$$

proves more convenient because it is proportional to the standard posterior distribution of θ that would arise from complete data (Jin and Rubin, 2008). This perspective motivates a Gibbs sampler that iterates between sampling the $S_i^{\mathit{mis}}$ conditional on the current parameter values and observed data and sampling from the posterior distribution of θ conditional on complete {S_i(0), S_i(1)}.

3.4 Prior specification

We treat all parameters as a priori independent, specifying flat prior distributions for μ and proper but diffuse prior distributions for Σ. For the constant biomarker special case, we parameterize Σ with $X~N({\mu }_X,{\sigma }_X^2)$ and $S(1)~N(a_0+a_{1}X,{\sigma }_{S(1)\mid X}^2)$, with flat prior distributions for μ_X, a₀ and a₁ and proper but diffuse gamma prior distributions for $\frac{1}{{\sigma }_X^2},\frac{1}{{\sigma }_{S(1)\mid X}^2}$. For the β parameters, we specify normal prior distributions, the hyperparameters of which we describe in the applications that follow.

Table 1 reviews the modeling assumptions regarding the nonidentifiable associations in (1) and (2) implied by prior specification on the β parameters and by introduction of a sensitivity parameter, emphasizing the point that with our Bayesian strategy, assumptions about nonidentifiable relationships in the data simultaneously apply to both the imputation and risk model stages. This table compares these assumptions with those of the previously-used sequential strategies described in Section 3.2.

Table 1.

Comparisons between assumptions made regarding nonidentifiable associations in the proposed Bayesian approach and those implicit in the previously-used sequential methods. Assumptions common to both methods are: SUTVA, ignorable treatment assignment, equal individual clinical risk, and multivariate normality of {S(0), S(1), X}.

	Sequential Approach
Association	Imputation Stage	Risk Model Stage
Constant Biomarker
Y(0), Y(1)|X, S(0), S(1)	Not Applicable	Y(0) ⫫ Y(1)|X, S(0), S(1)
Y(0), X|S(1)	Not Applicable	No interaction, β02 = β12
S(1), Y(0)|X	S(1) ⫫ Y(0)|X	Possible dependence, β01 ≠ 0

	Bayesian Approach
Association	Imputation Stage	Risk Model Stage
Constant Biomarker
Y(0), Y(1)|X, S(0), S(1)	Y(0) ⫫ Y(1)|X, S(0), S(1)
Y(0), X|S(1)	Prior on β02 – β12
S(1), Y(0)|X	Prior on β01 – β11
No Constant Biomarker
Y(0), Y (1)|X, S(0), S(1)	Y (0) ⫫ Y(1)|X, S(0), S(1)
S(0), S(1)|X	Sensitivity parameter, φ
Y(1), S(0)|X	Prior on β11 – β01 and β12 – β02
Y(1), X|S(0)	Prior on β13 – β03
Y(0), S(1)|X	Prior on β01 and β02
Y(0), X|S(1)	Prior on β03

4. Simulation Study with a Constant Biomarker

Here we conduct a simulation study paralleling that in GH to compare the performance of our Bayesian approach with the sequential estimated-likelihood approach. In order to compare our simulations with the parametric simulations reported in GH, we choose C_A = C_D = 0, and set h(x, y) = Φ⁻¹(x)− Φ⁻¹(y), which yields CEP^r(s₁, c, x) = (β₁₀ − β₀₀)+(β₁₁ − β₀₁)s₁ + (β₁₂ − β₀₂)x.

We follow the simulation scheme of GH that is designed to mimic the first preventive HIV vaccine efficacy trial. The candidate surrogate in this trial was 50% neutralization titers against the HIV recombinant gp120 molecule measured at t = 1.5 months post-baseline, and the primary outcome was HIV infection at 36 months follow-up. The constant biomarker in this case is the lower limit of detection of the antibody assay, c = 0, so S(0) = 0 for all patients. We simulate data for 1,805 placebo recipients and 3,598 vaccine recipients using the case-cohort sampling scheme from GH. Infection outcomes are simulated from (3) with g_z(s₁, c, x; β_z) = β_z0 +β_z1s₁ +β_z2x. For the vaccine arm, we set (β₁₀, β₁₁, β₁₂) = (−1.21, − 0.67, − 0.1). For the placebo arm, we consider two scenarios reflecting an overall vaccine effect of 50% reduction in the number of infections: one where the surrogate has no value, corresponding to β₀₀ = −0.825, β₀₁ = −0.67, and β₀₂ = −0.1 (scenario (a)), and one where it has high value, corresponding to β₀₀ = −1.1, β₀₁ = 0.0, and β₀₂ = −0.1 (scenario (b)). In both scenarios (a) and (b), we vary the correlation between {X, S(1)} to reflect settings where the pretreatment covariate predicts immune responses to varying degrees, with ρ = 0.5, 0.7, or 0.9. Further details of the data-generating mechanism appear in Web Appendix A.

We use the Bayesian strategy described in Section 3.3 to analyze data simulated as described above, varying features of the analyses to represent different assumptions about the associations in (2). For all analyses, we anchor prior information about the β parameters to observed quantities in the treatment arm. Let (β̂₁₀, β̂₁₁, β̂₁₂) denote the maximum likelihood estimates of the parameters in r₁(s₁, c, x) obtained using observed data for patients with Z = 1. We center the prior distributions of β₀₁ and β₁₁ at β̂₁₁ and of β₀₂ and β₁₂ at β̂₁₂ to place prior weight on the absence of an associative effect and on the absence of an interaction between X and Z. For the model intercepts, we center the prior distributions of β_z0 at Φ⁻¹(p̂_z) − β̂₁₁S̄(1) − β̂₁₂X̄, where p̂_z is the observed proportion of infections in patients with Z = z, and S̄(1) and X̄ are the averages observed in the vaccine arm. Prior variances for the β_z are varied across analyses. Details of the MCMC appear in Web Appendix B.

4.1 The necessity of assumptions regarding nonidentifiable associations

To illustrate the necessity of modeling assumptions about nonidentifiable associations, we analyze five low surrogate value datasets with ρ = 0.5 under two diffuse prior specifications for β. The first completely diffuse analysis sets prior variances for each of (β₁₀, β₁₁, β₁₂, β₀₀ – β₁₀, β₀₁ – β₁₁, β₀₂ – β₁₂) to 2.0², representing substantially noninformative prior distributions on the probit scale and implying no assumptions about the associations in (2). MCMC chains failed to converge in the analysis of each of these datasets, with the potential scale-reduction statistic, R̂ (Gelman and Rubin, 1992), for some parameters as high as 17.23. The second diffuse analysis uses the same prior specification but entails the restriction that β₀₂ = β₁₂, which previous research has used to justify identifiability of r₀(s₁, c, x). This analysis also resulted in MCMC chains that did not converge, with values of R̂ as high as 29.04. Thus, imposing an identifiability assumption that pertains only to r₀(s₁, c, x) does not suffice for identifiability of models for the entire joint distribution, and further assumptions are required regarding the second association in (2) (i.e., S(1), Y(0)|X). This speaks to previous methods’ reliance on the implicit conditional independence assumption made in the imputation stage.

4.2 Performance of the Bayesian approach and comparison with previous methods

We examine in detail the Bayesian analysis that specifies prior information regarding both associations in (2). Prior variances for (β₁₀, β₁₁, β₁₂) are set to 2.0² and prior variances for (β₀₀ – β₁₀, β₀₂ – β₁₂) are set to (0.5², 0.1²). The prior variance for (β₀₁ – β₁₁) is set to (0.65², 0.9², 1.5²) in settings with ρ = (0.5, 0.7, 0.9), respectively. This prior specification represents prior belief against an interaction between Z and S(1) and stronger prior belief against an interaction between Z and X. These prior specifications correspond, respectively, to belief in the equivalence of the following pairwise associations: {S(1), Y(0)|X} = {S(1), Y(1)|X} and {X, Y(0)|S(1)} = {X, Y(1)|S(1)}, that is, they pertain to the associations in (2). We conduct the informative analysis on 200 datasets simulated under each of the scenarios described above.

Table 2 summarizes the performance of the Bayesian method under each simulated scenario. Note that in the constant biomarker special case, we define EAE⁻ = 0 since S(1) is never less than S(0) = 0, yielding EAE = EAE⁺. Bias in the posterior mean and median estimates of EDE, EAE, and PAE is small for all values of ρ in both scenarios (a) and (b), and posterior standard deviations for all summary parameters are decreasing in ρ, reflecting increased accuracy in the imputation of S^mis in the presence of a more predictive pretreatment covariate. For these summary parameters, the most pronounced bias appears in scenario (b) with ρ = 0.5, where the posterior mean and median of PAE indicate a bias of −0.05 and −0.06, respectively, which is small relative to the true value of 0.83. This likely results from the fact that β₀₁ ≠ β₁₁ in scenario (b), but the prior specification that these parameters are equivalent impacts posterior estimates when X is not particularly predictive of S(1) (i.e., when ρ = 0.5). The over coverage of the 95% posterior intervals is due to placing prior mass over the entire flat region of the likelihood around the true values of the nonidentified parameters (Gustafson and Greenland, 2009).

Table 2.

Simulation summary for Bayesian estimation of the CEP surface in the constant biomarker special case with (a) no or (b) high surrogate value and ρ = 0.5, 0.7, or 0.9. 200 datasets were simulated and analyzed for each setting. SD is the standard deviation of the posterior estimates, and PSD is the mean posterior standard deviation across datasets. Quantities under the heading “GH” represent bias and median bootstrap standard error estimates (SEE) from the parametric simulations reported in Gilbert and Hudgens (2008).

	(a) Low Surrogate Value									(b) High Surrogate Value
	True	Median		Mean		PSD	95% Coverage	GH		True	Median		Mean		PSD	95% Coverage	GH
		Bias	SD	Bias	SD			Bias	SEE		Bias	SD	Bias	SD			Bias	SEE
ρ = 0.5
EDE	−0.38	0.01	0.06	0.02	0.06	0.09	100			−0.11	−0.01	0.08	−0.01	0.08	0.11	99
EAE+	−0.38	−0.02	0.08	0	0.09	0.12	99			−0.53	0.04	0.07	0.05	0.07	0.08	93.5
PAE	0.5	0.02	0.07	0.01	0.07	0.13	99.5	−0.20	0.23	0.83	−0.05	0.07	−0.06	0.06	0.12	99	−0.25	0.23
ρ = 0.7
EDE	−0.38	0	0.05	0	0.06	0.08	99.5			−0.11	0.01	0.06	0.01	0.06	0.09	99.5
EAE+	−0.38	−0.01	0.09	0	0.09	0.09	95.5			−0.53	0.02	0.06	0.02	0.06	0.07	93.5
PAE	0.5	0	0.07	0	0.07	0.09	99.5	−0.14	0.21	0.83	−0.01	0.06	−0.01	0.05	0.09	100	−0.14	0.21
ρ = 0.9
EDE	−0.38	0	0.06	0	0.06	0.07	98.5			−0.11	0.01	0.06	0.01	0.06	0.08	98.5
EAE+	−0.38	−0.01	0.07	−0.01	0.07	0.07	94			−0.53	0.01	0.06	0.01	0.06	0.06	94
PAE	0.5	0.01	0.05	0.01	0.05	0.06	98	−0.06	0.16	0.83	0	0.05	0	0.05	0.08	99.5	−0.07	0.17

Table 2 also illustrates the improved performance of our Bayesian method over the estimated-likelihood approach in GH. Note that while simulations here are fundamentally the same as the parametric simulations in GH, there are some minor differences (e.g., GH bin X, S(1) into quartiles). For estimates of the PAE - the only CEP summary quantity reported in the parametric simulations in GH - the Bayesian approach outperforms the estimated-likelihood strategy on the basis of bias and variability of the estimates. Also note that the Bayesian approach performs well for all values of ρ, but the estimated-likelihood strategy from GH relies on a highly predictive covariate (ρ = 0.9) to yield estimates without substantial bias.

Web Appendix C examines in detail the influence of the prior distributions on posterior densities of β parameters, but we note here that the prior dominates the posterior distribution of (β₀₂ – β₁₂) reflecting prior belief in the absence of an interaction between Z and X.

5. Data Analysis Without a Constant Biomarker

Here we use our Bayesian strategy to extend estimation of the CEP surface beyond previously-considered illustrations to settings without a constant biomarker. We illustrate this extension by analyzing data from the AIDS Clinical Trials Group protocol 320 (ACTG 320). This historically important trial compared an experimental therapy of two nucleoside analog reverse transcriptase inhibitors (zidovudine and lamivudine) combined with a protease inhibitor (in-dinavir) against a control therapy consisting of only the two reverse transcriptase inhibitors, and is particularly germane to discussion of surrogate endpoints because of the trial’s early termination due to clear clinical benefit of the experimental treatment (Hammer et al., 1997). We explore whether change in log-transformed CD4 count from baseline to 4-weeks follow up (S, continuous) qualifies as a principal surrogate endpoint for progression to AIDS or death (Y, binary) at distant follow up (median follow-up time 38 weeks). We include log-transformed baseline CD4 count as a pretreatment covariate, X. Basic graphical examination of the multivariate normality assumption from Section 3 appears in Web Appendix D.

For illustrative purposes, we confine our attention to 516 treated and 490 control patients who were not censored before the end of trial follow up and who had CD4 measured at baseline and 4 weeks post-treatment. The mean (SD) 4-week change in CD4 count was 46.29 (59.62) in the treatment arm and 27.49 (49.18) in the control arm, indicating that, on average, the treatment improved CD4 counts. There was also a beneficial average treatment effect on the primary outcome, with deaths or AIDS progressions in 24 (4.6%) treatment-arm patients, compared with 46 (9.4%) control-arm patients. There is no evidence of a violation of the equal individual clinical risk assumption, with < 2% of patients in either arm progressing to AIDS or death within 4 weeks of treatment initiation.

One way to accommodate varying control-group response is to use g_z(s₁, s₀, x; β_z) = β_z0 + β_z1s₀ + β_z2(s₁ − s₀) + β_z3x for the risk distributions in (3). The adjustment for (s₁ − s₀) allows estimation of whether larger causal effects on CD4 count are predictive of clinical benefit. In contrast to the illustrations with a constant biomarker, we use $h(x,y)=\mathit{log}(\frac{x}{y})$ for ACTG 320, allowing interpretation of the CEP surface as the log relative risk (RR) of progression to AIDS or death within a principal stratum. To assess surrogate value, we use EDE, EAE⁺, and EAE⁻ to estimate the average causal effect of Z on Y when there is no, a positive, or a negative effect of Z on S. We examine PAE to quantify the relative magnitudes of associative and dissociative effects. The thresholds for summarizing the CEP surface are C_D = C_A = 0.05 to calculate dissociative effects in patients whose CD4 counts under competing treatments are estimated to be within 5% of each other, and associative effects in patients estimated to experience more pronounced causal effects on CD4.

Without a constant biomarker, model assumptions must be made regarding all of the associations in (1) and (2). For the association {S(0), S(1)|X}, we incorporate a pre-specified parameter, denoted φ, that characterizes the nonidentified correlation between S(0) and S(1). Note that the correlation between {S(0), X} observed in the Z = 0 arm is −0.29, and the correlation between {S(1), X)} observed in the Z = 1 arm is −0.59. These observable associations can rule out some values of φ that would imply an invalid covariance structure for {S(0), S(1), X}. To prevent computation of covariance structures near the positive-definiteness boundary and to reflect belief that S(0) and S(1) are nonnegatively correlated, the proposed sensitivity-analysis strategy fixes φ for each analysis and varies its value across the range [0.0, 0.8] to obtain estimates of the CEP surface.

For the other nonidentifiable associations, we anchor prior information for the β parameters in the r_z(s₁, s₀, x) to maximum likelihood estimates fit to the following model using only data available in the control arm:

$$P(Y(0)=1\mid S(0)=s_0,X=x)=\mathrm{\Phi }({\gamma }_0+{\gamma }_1{s}_0+{\gamma }_{2}x),$$ (4)

denoting these estimates with γ̂₀, γ̂₁, and γ̂₂. Note that this model differs from r₀(s₁, s₀, x) only in its omission of the quantity (s₁ − s₀). We center the prior distribution for β₀₀ at γ̂₀, for β₀₁ and β₁₁ at γ̂₁, and for β₀₃ and β₁₃ at γ̂₂. Prior means for β₀₂ and β₁₂ are centered at 0, and the prior mean for β₁₀ is centered at Φ⁻¹(p̂₁) − γ̂₁S̄(0) − γ̂₂X̄, where S̄(0), X̄ are averages observed in the Z = 0 patients. Prior variances for (β₀₀, β₀₁, β₀₂, β₀₃) are set to (0.3², 2.0², 2.0², 0.1²), and prior variances for (β₁₀ – β₀₀, β₁₁ – β₀₁, β₁₂ – β₀₂, β₁₃ – β₀₃) are set to (0.3², 2.0², 2.0², 0.01²). This prior specification places prior weight on the belief that the model in (4) is correct, that is, that after adjusting for (log-transformed) baseline CD4 count and potential response to the control treatment, the difference {S(1) − S(0)} is unrelated to the probability of progression to AIDS or death in both treatment arms, and that there are no interactions between treatment and X, S(0), or {S(1) − S(0)}. This implies prior weight on the absence of an associative effect. Note that the prior variances indicate especially strong prior belief in the relationship between X and progression to AIDS or death, but that prior belief in the other parameters is substantially more diffuse. Other prior distributions are as described in Section 3.4 and details of the MCMC appear in Web Appendix B.

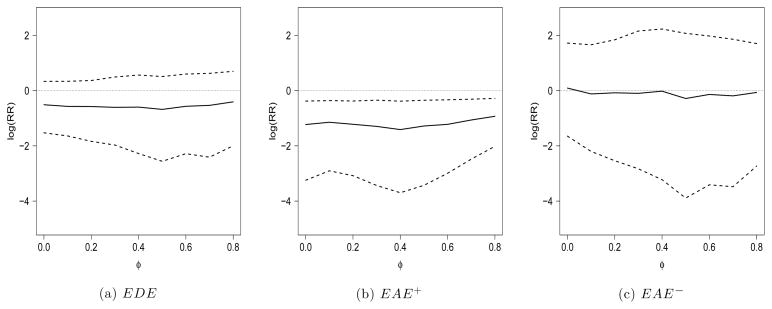
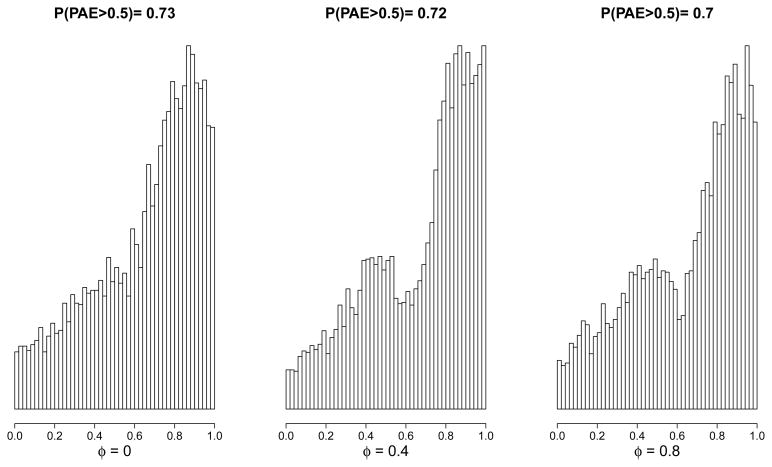
Figure 1 displays posterior estimates of the EDE, EAE⁺, and EAE⁻ across the range of values for φ. In Figure 1(a), we see that the treatment protects against progression to AIDS or death in patients who experience little or no effect on CD4 count. Figure 1(b) depicts a more pronounced protective effect in patients for whom the treatment causes an increase in CD4 count. Figure 1(c) indicates no causal effect on progression to AIDS or death when the treatment causes a decrease in CD4 count. These results are qualitatively robust to specification of φ. To measure the overall magnitude of associative effects relative to dissociative effects, Figure 2 displays histograms of posterior samples of PAE for selected values of φ to indicate that associative effects tend to be more pronounced than dissociative effects, but that values of PAE near 0.5 cannot be ruled out.

Figure 1.

Posterior means (and 95% intervals) for EDE, EAE⁺, and EAE⁻ from ACTG 320. Horizontal dotted lines are at 0.

Figure 2.

Posterior histograms of PAE for different values of sensitivity parameter φ from ACTG 320.

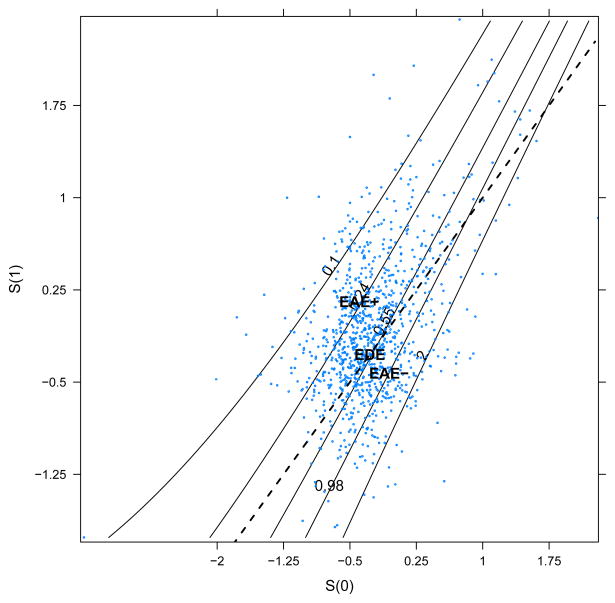
To summarize the entire CEP surface, Figure 3 depicts a contour plot, with contours corresponding to values of CEP^r(s₁, s₀, x) (labeled as relative risks), across values of S(0) and S(1). For this illustration, contours are computed using posterior mean estimates of the β parameters, and x is held fixed at X̄. The scatterplot of points on the contour plot represents values of {S(0), S(1)} simulated from one iteration of the Gibbs sampler. The results are pictured for the analysis where φ = 0.4; other assumed values of φ produced similar contours but are not pictured. We see that EDE lies on a contour with RR = 0.55, indicating that the treatment protects against progression to AIDS or death in patients who do not experience a causal effect on CD4. We see that in areas of the plot where S(1) > S(0), representing patients for whom the treatment improves CD4, the surface indicates a protective associative effect of the treatment (RR < 1) that is more pronounced as {S(1) − S(0)} increases, with EAE⁺ lying on a contour with RR = 0.24. For areas indicating that the treatment harms CD4 count {S(1) < S(0)}, we see that EAE⁻ lies on a contour with RR = 0.98, and that the risk of progression to AIDS or death is increased (RR > 1) in the small number of patients estimated to have S(1) much less than S(0).

Figure 3.

Posterior mean CEP surface calculated with X set to the sample average from ACTG 320 and φ = 0.4. Scatterplot represents values of {S(0), S(1)} from one iteration from the Gibbs sampler, and dashed line is S(0) = S(1). Contours are placed at estimated relative risk of progression to AIDS or death in treatment vs. control arm.

Detailed examination of prior vs. posterior densities for the analysis of the ACTG data appears in Web Appendix C, but we note here that prior specification dominates the posterior distributions for β₀₃ and β₁₃ − β₀₃, reflecting the the strong prior belief that the relationship between X and Y (z) estimated from (4) is correct.

In summary, our analysis indicates that the beneficial causal effect of Z = 1 on progression to AIDS or death is associated with beneficial causal effects of Z = 1 on CD4 count (EAE⁺ < 0), and that there is no evidence of an effect of Z = 1 on progression to AIDS or death for patients for whom the treatment harms CD4 count (EAE⁻ ≈ 0). However, this analysis does not suggest perfect utility for using 4-week changes in CD4 count as a surrogate endpoint because we also estimate that a beneficial causal effect on progression to AIDS or death persists even in patients for whom the treatment does not impact CD4 (EDE < 0). While our analysis does suggest some surrogate value, with associative effects that larger in magnitude than dissociative effects (PAE > 0.5), the uncertainty in these estimates cannot rule out associative and dissociative effects of similar magnitude.

6. Discussion

We have presented a Bayesian strategy for estimating the CEP surface to evaluate a principal surrogate endpoint that offers improvements over previously-used sequential methods. By considering the full joint distribution of the data simultaneously and incorporating prior information regarding nonidentifiable associations, our approach provides improved performance in the previously-considered setting of a constant biomarker, and also extends estimation to more general settings with varying control-group response.

The benefit of the Bayesian approach is most evident in comparison with existing methods that assume a constant biomarker and an implicit conditional independence assumption when imputing missing surrogate responses. Unlike existing methods in vaccine trials that rely on large values of ρ, the Bayesian method performs well in the absence of a highly predictive pretreatment covariate, in part because it makes use of additional information contained in Y(0) to impute missing S(1).

While the literature on principal stratification commonly relies on categorical S and a finite number of strata, we focus on continuous S and make use of structured models. Alternative flexible parametric assumptions or assumptions such as monotonicity could prove valuable (Jin and Rubin, 2008; Bartolucci and Grilli, 2011). For example, Web Appendix D casts some doubt on the assumption of multivariate normality for {X, S(0), S(1)}, and more flexible models could be included at the cost of significant computational complexity. Furthermore, the assumption that Y(0) ⫫ Y (1)|S(0), S(1), X could be relaxed in exchange for another sensitivity parameter analogous to φ (Jin and Rubin, 2008). Our analysis of ACTG 320 that focuses on relative risks could exhibit some sensitivity to assumptions about the association between Y(0) and Y(1).

In practice, researchers may be interested in quantities such as EDE, EAE⁺, EAE⁻, and PAE to summarize whether little/no, positive, or negative effects of Z on S correspond to little/no, positive, or negative effects of Z on Y, with PAE summarizing the relative magnitudes of associative and dissociative effects. However, it should be noted that any such summary measures could prove too coarse to uncover certain features of the entire CEP surface. For example, our definition of EDE could obscure existence of strata defined by $s_0^{\prime }=s_1^{\prime }$ and $s_0^{″}=s_1^{″}$ such that ${\mathit{CEP}}^r(s_1^{\prime },s_0^{\prime })=d$ and ${\mathit{CEP}}^r(s_1^{″},s_0^{″})=-d$, which could yield EDE = 0 in the midst of nonzero dissociative effects. Alternative summary quantities that focus on more specific regions of the CEP surface could be adopted to uncover such settings, which may require more flexible parametric models than those presented here.

Our approach to surrogate outcomes proceeds along the lines of FR and GH and defines exactly two causal effects; that of Z on both S and Y. Related causal-inference methods predicated on direct and indirect effects could provide alternative approaches (see VanderWeele (2011) and the references within). These methods imply additional assumptions that lead to definition of a third causal effect absent from our principal stratification framework, that of S on Y. For example, Chen et al. (2007) define conditions for a surrogate endpoint to ensure avoidance of the so-called “surrogate paradox” where the signs of the effects of Z on S and of S on Y cannot predict the sign of the effect of Z on Y. When interpreted correctly, principal surrogates do not suffer from this paradox because they do not use an effect of S on Y to infer anything about surrogacy. The paradox seems relevant only when interest lies in estimating causal pathways involving the following three effects: Z on S, Z on Y, and S on Y. Principal stratification only considers the first two of these effects, so to the extent that it is possible to conceive of a counterintuitive sign of the causal effect of S on Y, it does not obscure whether the effect of Z on Y coincides with the effect of Z on S.

Finally, we have considered trials with both S and Y measured in order to validate whether S qualifies as a principal surrogate in a particular setting. An important area of future research in which the Bayesian ideas presented here might prove valuable is in quantifying the predictive value of the effect of Z on S for reliably establishing the effect of Z on Y in future trials where Y may not be measured. This could contribute toward establishing a “level 2 surrogate of protection” that is predictive of efficacy across different settings or populations (Gilbert et al., 2008).