Toward genomic prediction from whole-genome sequence data: impact of sequencing design on genotype imputation and accuracy of predictions

Abstract

Genomic prediction from whole-genome sequence data is attractive, as the accuracy of genomic prediction is no longer bounded by extent of linkage disequilibrium between DNA markers and causal mutations affecting the trait, given the causal mutations are in the data set. A cost-effective strategy could be to sequence a small proportion of the population, and impute sequence data to the rest of the reference population. Here, we describe strategies for selecting individuals for sequencing, based on either pedigree relationships or haplotype diversity. Performance of these strategies (number of variants detected and accuracy of imputation) were evaluated in sequence data simulated through a real Belgian Blue cattle pedigree. A strategy (AHAP), which selected a subset of individuals for sequencing that maximized the number of unique haplotypes (from single-nucleotide polymorphism panel data) sequenced gave good performance across a range of variant minor allele frequencies. We then investigated the optimum number of individuals to sequence by fold coverage given a maximum total sequencing effort. At 600 total fold coverage (x 600), the optimum strategy was to sequence 75 individuals at eightfold coverage. Finally, we investigated the accuracy of genomic predictions that could be achieved. The advantage of using imputed sequence data compared with dense SNP array genotypes was highly dependent on the allele frequency spectrum of the causative mutations affecting the trait. When this followed a neutral distribution, the advantage of the imputed sequence data was small; however, when the causal mutations all had low minor allele frequencies, using the sequence data improved the accuracy of genomic prediction by up to 30%.

Introduction

Genomic predictions are now used routinely in selection of dairy cattle (Dalton, 2009), as well as in some crops (Heffner et al., 2011). An ongoing challenge is to improve the accuracy of these predictions, as the genetic gain that can be achieved is proportional to their accuracy. If single-nucleotide polymorphism (SNP) arrays are used, the upper bound of the accuracy of genomic prediction will be the proportion of the genetic variance captured by the array, determined by the linkage disequilibrium (LD) between the SNP and the causative mutations affecting the trait. In dairy cattle, a 50 000 SNP panel explains between 5 and 88% of the genetic variation, depending on trait (Haile-Mariam et al., 2012, Jensen et al., 2012). In some sheep breeds, the same number of SNP capture a much lower proportion of the variance (Daetwyler et al., 2012).

If full-genome sequence data were used in genomic predictions rather than SNP arrays, the accuracy that can be achieved is no longer bounded by LD between SNP and causative mutations, as the causal mutations are in the data set. Meuwissen and Goddard (2010) demonstrated in simulations that genomic predictions based on sequence data were 5–10% more accurate than predictions based even on quite dense markers, because the causal mutations were used in prediction. This increase in accuracy has not been observed in real data as yet. Ober et al. (2012) found no increase in accuracy of predictions for quantitative traits in 157 inbred lines of Drosophila melanogaster, when comparing predictions from a dense SNP panel or the full-genome sequence. However, the small size of that data set makes it difficult to draw definitive conclusions about the value of full-genome sequence data in genomic predictions—as the effect of the causative mutations on the quantitative traits may be very small, given the genetic architecture observed for many quantitative traits (for example, Kemper et al. (2011) and Stahl et al. (2012)), large numbers of individuals will still be required to estimate these effects accurately.

While the cost of genome resequencing has fallen very dramatically, it is still too expensive to consider resequencing the tens of thousands of individuals that would be required to accurately estimate the likely small effects of mutations. An alternative strategy in livestock and some crop populations would be to exploit the fact that these populations are typically derived from a small group of common ancestors just a few generations in the past. For example, in Australian Holstein Friesian dairy cattle, 50 of the elite ancestor bulls account for 51% of the genetic diversity in the current Holstein cow population (Hayes and Goddard, 2008). Provided these ancestors are sequenced, the descendant individuals need only be typed for a low-density SNP array in order to infer their genome sequence, as the low-density SNPs will be sufficient to trace the large segments of chromosome that have been inherited from the ancestors. In-silico resequencing of large numbers of individuals, selected from the population because they have high-quality phenotypes, would then enable highly accurate genomic predictions from whole-genome resequence data.

To exploit this strategy, at least two key questions must be answered given sequencing is expensive (1) what is the best method for selecting the key ancestors to sequence, and (2) how many individuals should be sequenced and at what fold coverage? In outbred species, such as cattle, fold coverage is important—calling heterozygote genotypes accurately is difficult at low fold coverage as both alleles may not be sequenced. Calling heterozygote genotypes becomes more precise as fold coverage increases.

In this paper, we propose several strategies for choosing individuals to sequence. We then used a real Belgian Blue beef cattle pedigree, with simulated sequence data gene-dropped through it, to choose with each strategy a subset of individuals to in-silico sequence. For each strategy both the percentage of real variants in the population were detected, and the accuracy of imputing sequence variants into a population with SNP panel data was evaluated. The optimum sequencing fold coverage and number of individuals to sequence when the total sequence effort was constrained was explored. Finally, we assessed the increase in accuracy of genomic predictions that can be achieved using the imputed sequence data, compared with that from the SNP panels, in the same data set, and with quantitative trait loci (QTL) allele frequency distributions from many rare alleles to neutral models.

Materials and methods

Data simulation

In order to evaluate different methods for selection of individuals for sequencing, we first required a population of individuals with full-sequence data. To ensure the structure of the population was characteristic of livestock populations, we used a real Belgian Blue beef cattle population as template to do this. The population consisted of 1142 Belgian Blue beef cattle sires, for which we had extensive pedigree data. The pedigree of these individuals included 9375 animals and traced back to the 1970s.

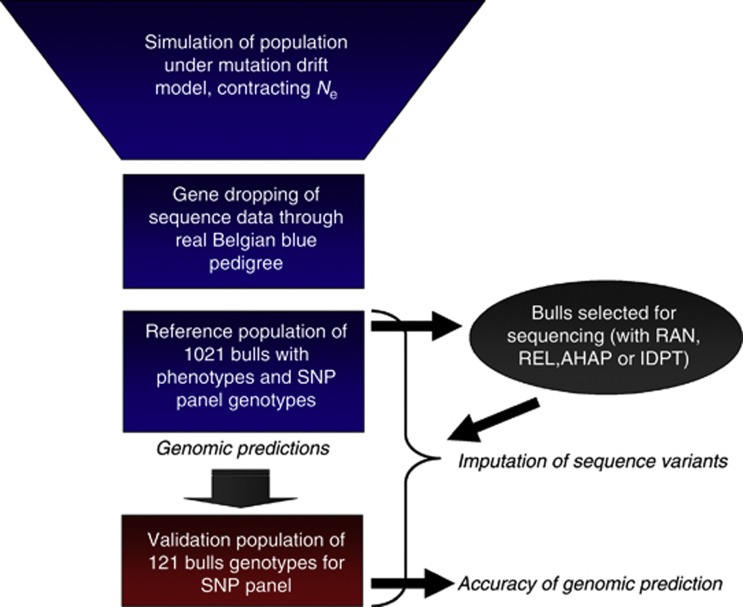
The aim was to simulate sequence data in these 1142 individuals, which would reflect realistic patterns of LD, similar to that observed among SNPs in cattle populations, as well as reflecting a typical pedigree structure. To inform the simulation of sequence data for the founders of this population, we relied on the work of Macleod et al. (2012A), which used multilocus patterns of LD in whole-genome sequence from two Holstein founder bulls (Larkin et al., 2012) to reconstruct population genetic history. Based on this population history (with variable effective population size), Macleod et al. (2012B) simulated sequence data that closely matched the multilocus LD patterns in the founder bull sequences. We observed that patterns of multilocus LD in dense SNP data from Belgian Blue cattle were very similar to Holsteins. Therefore, we used data simulated by Macleod et al. (2012B) with Fregene (Chadeau-Hyam et al., 2008) as sequence data for founders of our Belgian Blue cattle population. Figure 1 describes the overall simulation scheme.

Figure 1.

Simulation scheme. A base population was simulated according to the inferred demography of Bos Taurus cattle of Macleod et al. (2012A). The demography has a large ancient effective population size contracting to a much smaller effective size following domestication and breed formation. Fregene was used to simulate 50 MB of sequence under a mutation drift model with this demography. From this population, the founders of the real Belgian Blue cattle breed-recorded pedigree were selected at random, and the sequence data were gene-dropped through the entire pedigree with recombination. A subset of bulls was selected from the pedigree, on the basis that they had DNA samples available. These bulls were ‘genotyped' for a dense SNP panel. A much smaller subset of the bulls were selected for sequencing, with an Illumina sequencing process simulated. The sequence data was then imputed into all bulls with SNP panel genotypes. A prediction equation, based either on SNP panel genotypes or imputed sequence data, was estimated in the reference population. Finally, accuracies of genomic prediction were assessed in the validation population.

A simulated genome consisted of five chromosomes of 10 Mb. Populations of these genomes were simulated with random sampling of individuals to be parents and recombination to form gametes, through the demography described above. Then gametes were randomly assigned to the founder individuals of the pedigree (4698 founders in total). These gametes were then gene-dropped through the real pedigree of the 1142 Belgian Blue sires described above using Mendelian segregation rules and recombination probabilities (assuming 1 cM=1 Mb).

The simulated sequence data were used to generate SNP panel data and ‘in silico' next-generation sequencing data (NGS). For the SNP panel, we selected 20 SNPs per Mb (one per 50 kb window) with a minor allelic frequency (MAF) higher than 0.05 (resulting in a 1000 SNPs panel per simulated genome). For the NGS data, for each sequenced individual we simulated 100 bp reads with random starting positions in the sequence. The total number of reads generated was equal to desired cover x-fold*10 Mb per 100 bp. For SNP positions, we sampled at random one of the two alleles carried by the individual. The probability that the allele was incorrectly sequenced was set equal to ɛ=0.005 (for example, Li et al. (2011)). To call genotypes in the NGS data for each animal (that is, to derive genotype probabilities), reads at each basepair were summarized into a genotype probability based on the likelihood of a binomial distribution. Conditional on the genotype, the likelihood of observing n₁ reads with allele 1 and n₂ reads with allele 2, L(y|G), is equal to:

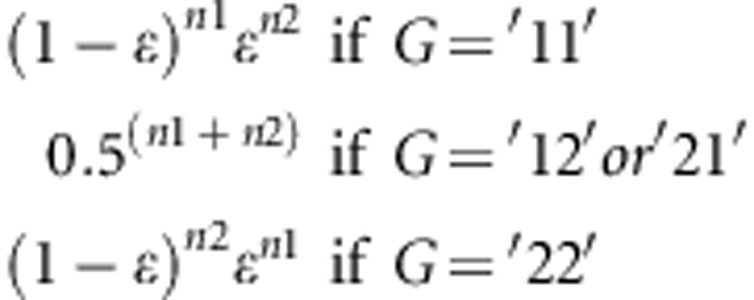Strategies for selection of sequenced individuals

Owing to the cost of sequencing and the accessibility of imputing sequence data from SNP arrays, we compared five different strategies for selecting subsets of N individuals for sequencing. All 1142 bulls were genotyped for the SNP panel but only a subset N was selected to be sequenced at cover x-fold. The five strategies are described in detail below.

(1) Maximizing the expected genetic relationship, using pedigree, between the group of sequenced bulls and the whole population (REL)

This strategy aims to maximize the proportion of the unique genomes sequenced in the population, given a predetermined number of individuals that can be sequenced, and was outlined by Hayes and Goddard (2008) but is extended here. We must select a group of bulls that maximizes the relationship with the remaining population, while accounting for relationships among the selected group of bulls. The proportion of the genome of individual i, present in the set of N sequenced individuals s={s₁, s₂, …, s_N} is:

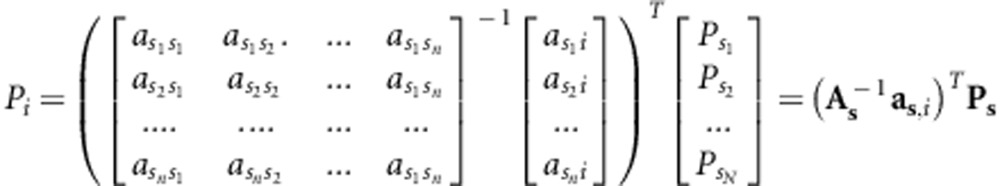Where P_i is the proportion of individual i's genome sequenced (directly through NGS or indirectly through sequenced relatives), a_ij is the additive relationship between individuals i and j, A_s is the additive relationship matrix between all sequenced individuals, a_si is the vector of additive relationships between the set of sequenced individuals s and individual i, and P_s is the vector of proportion sequenced of the set of individuals s (which is equal to 1 for sequenced individuals). The average value of P_i of all individuals of the population must be maximized:

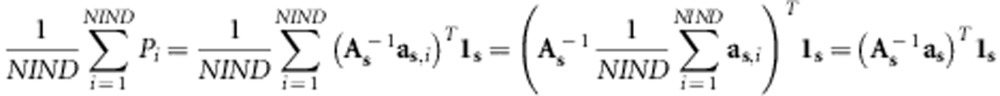Where NIND is the number of individuals in the population and 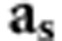is the vector of average relationships of individuals from set s and the population.

A stepwise strategy was used to select individuals in s: first, the individual with the highest average additive relationship with the population is selected and then, individuals that maximize the function when added to the group selected in previous steps are sequentially selected.

(2) Maximizing the number of independent genomes sequenced (IDPT)

The second strategy was to select a group of individuals with their expected genomes as different as possible. Therefore, we must avoid sequencing highly related individuals and, ideally, sequence N individuals with the lowest level of co-relationship (according to the pedigree). We will use a similar strategy as REL above, but this time we maximize the number of independent (according to the pedigree at least) sequenced genomes (NG) instead of the average relationship between sequenced individuals and the population. The covariance between a sequenced individual and the sum of independent genomes sequenced is equal to 1, therefore we replace 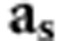by 1 (the number of genomes sequenced per individual is also 1):

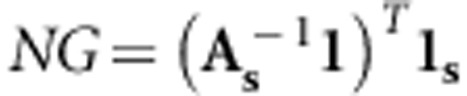We then use the same stepwise strategy as described for REL to maximize NG. Again this strategy uses only pedigree information.

(3) Maximizing haplotypes coverage from the population: phasing with DualPHASE (AHAP)

The third strategy is to use the SNP panel genotypes to estimate haplotypes present in the population, then find a subset of animals that would maximize the number of observed haplotypes sequenced. To define haplotypes, we use the 1000 SNPs from the panel within each genome (of five chromosomes 10 MB in size) to assign genome segments to ancestral haplotypes at every marker position, using DualPHASE from the PHASEBOOK package (Druet and Georges, 2010). In DualPHASE, ancestral haplotypes are based on a hidden Markov model, which assigns at each marker position a chromosome segment to an ancestral haplotype. The number of ancestral haplotypes K was set equal to 20, which is appropriate for cattle data (Druet and Georges, 2010). Then a score was computed to estimate the proportions of haplotypes in the population that were sequenced with a given subset of animals:

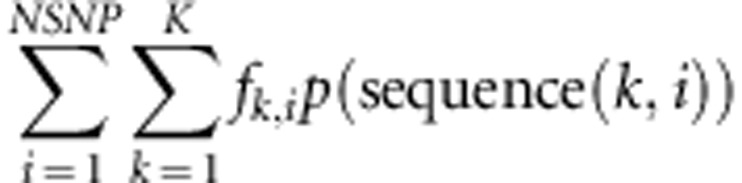where f_k,i is the frequency in the whole population of ancestral haplotype k at marker i and p(sequence(k,i)) is the probability of sequencing ancestral haplotype k at marker i, which was approximated as (1−0.5^nki) where nki is the number of ancestral haplotypes k present in the pool of sequenced individuals at marker i multiplied by the average fold coverage at which individuals are sequenced. This approximation assumes that individuals are heterozygotes and that sequencing coverage is uniform. Indeed, then 0.5^nki represents the probability that all sequenced reads of all individuals carrying ancestral haplotype k at marker i carry the complementary ancestral haplotype (and not the desired one). The formula takes into account the fact that even if an individual carrying the haplotype has been selected, the ancestral haplotype currently targeted has not necessarily been sequenced at adequate fold coverage to call genotypes (this is an issue particularly at low fold coverage). At high cover, only one individual carrying the haplotype must be sequenced, whereas at low cover, several individuals might be necessary. Finally, the weighting on haplotype frequency puts more emphasis on sequencing frequent haplotypes. The goal is to identify and sequence as large as a proportion of the population haplotypes as possible, and it relies on having SNP panel information to identify haplotypes. An alternative strategy (forth strategy) was also tested where the weights on haplotype frequency were not considered. In this case, the goal is to sequence as best as possible all unique haplotypes, without regard to their frequency (AHAP*).

(5) Selecting individuals randomly (RAN)

The RAN strategy was repeated five times (for example, individuals were chosen randomly, the variant detection was run and variant imputation was performed, five times on the sequence data from the same population) in order to obtain a s.e. for comparison with other strategies.

We tested all five strategies for the accuracy of imputing sequence variants in non-sequenced individuals that had been genotyped for the 1000 SNP panel, given that the sequencing budget was sufficient to sequence 50 individuals at cover × 12 (50@ × 12). Then, we used the AHAP strategy to investigate the effect of number of individuals sequenced by fold coverage, keeping the total sequencing effort ( × 600) constant. Either 25 individuals were sequenced at × 24 (25@ × 24), 40 individuals at × 15 (40@ × 15), 50 individuals at × 12 (50@ × 12), 60 individuals at × 10 (60@ × 10), 75 individuals at × 8 (75@ × 8), 100 individuals at × 6 (100@ × 6), 150 individuals at × 4 (150@ × 4) or 300 individuals at × 2 (300@ × 2). Finally, we investigated the increase in proportion of variants discovered and accuracy of imputation with × 1200 total sequencing effort, and × 2400 total sequencing effort, with individuals sequenced either at × 6, × 8 or × 12.

SNP calling and genotype imputation

Sequence SNPs were ‘called' if the following statistic was higher than 10 (Li et al., 2010):

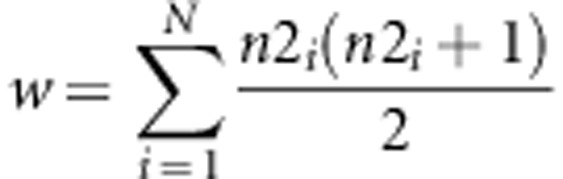Where n2_i was the number of alternative alleles observed in individual i. This means that a SNP was identified if it was observed in five reads of an individual, in three reads in two individuals or in one read for 11 individuals. Through simulation, we estimated that using a threshold of 10 would result in calling ∼1 false SNP every kb. Only true polymorphic sites were considered (we simulated sequencing errors only at true SNP locations).

Sequence SNP were imputed from the 1000 SNP panel in all genotyped individuals based on called SNP likelihoods (of sequenced individuals, as estimated above) using Beagle (Browning and Browning, 2007). Accuracy of imputation was obtained by estimating squared correlations between true allele dosage (number of copies of allele 1 at each variant) and those estimated by Beagle (only for called variants). Only those alleles in the central 5 Mb of each region were considered to avoid edge effects (that is, imputation accuracy is lower on the border of the chromosomes (for example, Druet et al. (2010) and our segments are particularly small, and therefore likely to suffer from edge effects). Results were averaged over all the 25 replications of genome simulations.

Genomic selection

We simulated breeding values for all individuals by applying QTL effects to 500 variant positions selected from the sequence data (20 QTL per Mb). For some simulations, a much lower number of QTL were chosen (five QTLs). We first chose the allele frequency range for QTL: either MAF <1%, MAF <10% or no restriction on MAF, in which case the QTL allele frequencies are as expected under a Neutral model. The QTLs were selected from the five central Mb (as for estimated accuracy of imputation described above) of five chromosome segments defining a genome. QTL effects for the ancestral allele were sampled from a double-exponential distribution (Laplace distribution) with rate equal to 1. Many of the effects were very small. Genetic values were obtained as the sum of individual QTL effects and standardized by dividing by the square root of the total genetic variance (equal to the sum over all QTLs of 2pqa²), where p is the frequency of the 1 allele, q is the frequency of the 2 allele and a is the substitution effect of the SNP (additive effect in this case as no dominance was simulated). Finally, a normally distributed random error term with variance 1.5 was added to genetic values to obtain a phenotype with a heritability of 0.40.

SNP effects and genomic breeding values were estimated with BayesR (Erbe et al., 2012), but using allele dosage obtained from Beagle (and using only called alleles), rather than discrete genotypes. Briefly, BayesR uses a mixture of four normal distributions as the prior for SNP effects, including one distribution that set SNP effects to zero. The BayesR parameters (starting values for proportion of SNP in each distribution, with the first one being the zero effect distribution, expected proportion of genetic variance explained by a SNP in each of these distributions, and Dirchelet prior pseudo counts of SNP in each distribution) were (0.55;0.40;0.049;0.001/0.00;0.0001;0.001;0.01/1;1;1;1). BayesR uses Gibbs sampling to sample from the posterior distributions of SNP effects and other parameters. Thirty thousand rounds of sampling, with the first 10 000 discarded as burn in, were used. Individuals born after 2004 (in our real Belgian Blue Cattle population) were selected as validation population (121 without phenotype) and the remaining 1021 individuals formed the reference population, where the effects of the variants were estimated using BayesR. Genomic-estimated breeding values for the 121 validation bulls were then calculated as their genotypes (dose of the second allele for each SNP) multiplied by the prediction equation from BayesR (effect of the second allele for each SNP). Reliability of genomic predictions was estimated in the validation population of 121 bulls as the squared correlation between true genetic values and the genomic-estimated breeding values. Genomic predictions were based on either the SNP panel, true genotypes in the sequence or imputed sequence data. Results are averages over 25 complete replicates.

Results

Simulations

On average, there were 28 477 SNPs per 10-Mb simulated segment, or one SNP every 351 bp. This is similar to the SNP frequency observed in cattle populations (The Bovine Hap Consortium, 2009).

The average r² statistic between SNPs (with MAF >0.10) at different distance classes is presented in Table 1. These r² values were calculated from simulated SNP genotypes in 275 of the 1142 bulls, as this allowed direct comparison with real r² values. The r² values obtained from the simulation are comparable, though slightly higher than those observed in the real Belgian Blue population, where these values were calculated from SNP on a 777 K panel in 275 genotypes sires. These sires were the same individuals in the pedigree as those used to calculate r² in the simulated data.

Table 1. Linkage disequilibrium (r ²) among SNP in real and simulated Belgian Blue cattle data.

SNP distance (in Mb)	r2 From real data	r2 From simulated data
0.00–0.05	0.368	0.374
0.05–0.10	0.180	0.223
0.10–0.25	0.115	0.166
0.25–0.50	0.086	0.127
0.50–1.00	0.073	0.114
1.00–1.50	0.065	0.094
1.50–2.00	0.059	0.081
2.00–2.50	0.055	0.073
2.50–3.00	0.052	0.067
3.00–3.50	0.048	0.061
3.50–4.00	0.046	0.057
4.00–4.50	0.044	0.054
4.50–5.00	0.042	0.050

Abbreviation: SNP, single-nucleotide polymorphism.

The real data are derived from 777 K SNP genotypes in 275 Belgian Blue sires and the simulated data are from the same 275 sires in the Pedigree. Note that r² was only calculated when MAF was >10% in both real and simulated data, as recommended by Hudson (1985).

The similarity between r² values in the real and simulated data gives some confidence that the LD structure in the real and simulated data would be broadly comparable.

Selection of sequenced individuals

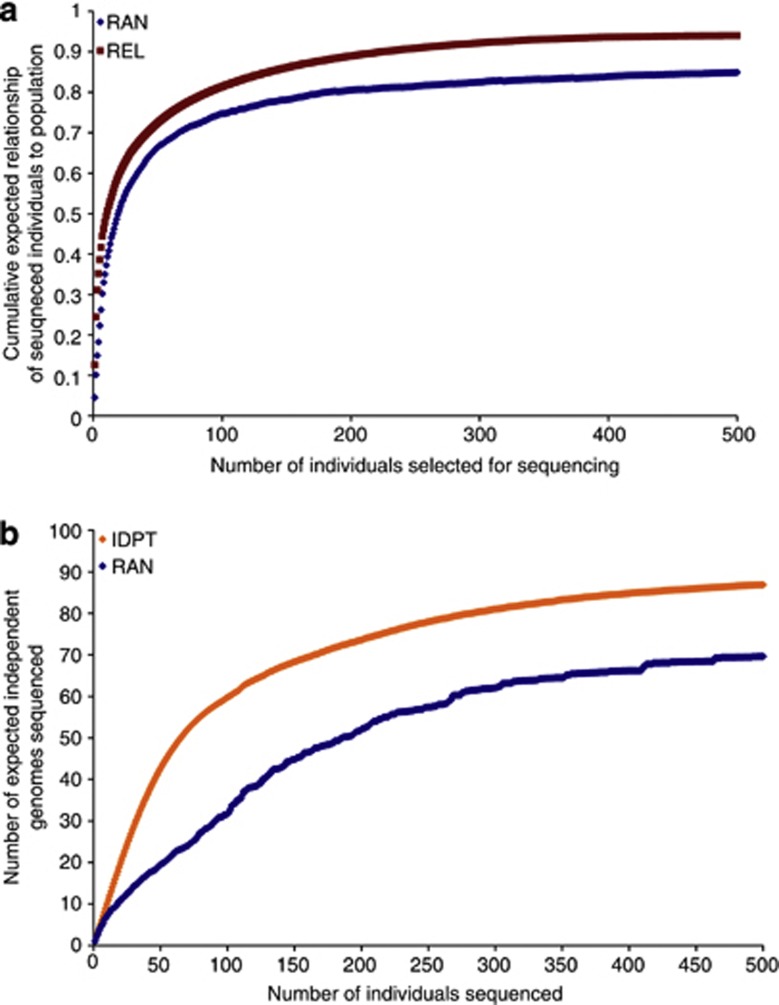
For the REL strategy (maximizing relationships between the group sequenced and the remaining population), the expected value of the average proportion of genomes of individuals of the population captured by the set of sequenced individuals rose rapidly with the number of individuals sequenced. The first animal chosen by this strategy captured 12.6% of the genomes of individuals of the population, while the 10 highest ranked individuals captured almost 50% (Figure 2). The value increased to 72% with 50 sequenced individuals and 81% with 100 sequenced individuals.

Figure 2.

The cumulative expected relationship of sequenced individuals to the 1142 bulls using either REL or RAN to select bulls for sequencing (a), or number of independent genomes sequenced, with RAN or IDPT (b), with an increasing number of individuals chosen for sequencing. The REL and IDPT algorithms are described in the text.

Using the IDPT strategy (maximizing representation of different genomes), for the 20 first sequenced individuals, it is almost possible to obtain 20 independent genomes (Figure 2). For the 1142 sires, there are only 87 independent genomes defined by the pedigree.

Similarly, for the strategies based on SNP panel haplotypes (AHAP and AHAP*), the majority of haplotypes were captured by a relatively small number of sequenced individuals, though many individuals were needed to capture all the haplotypes in the population.

Accuracy of imputation: sequencing strategies all compared for 50 bulls sequenced at × 12 cover

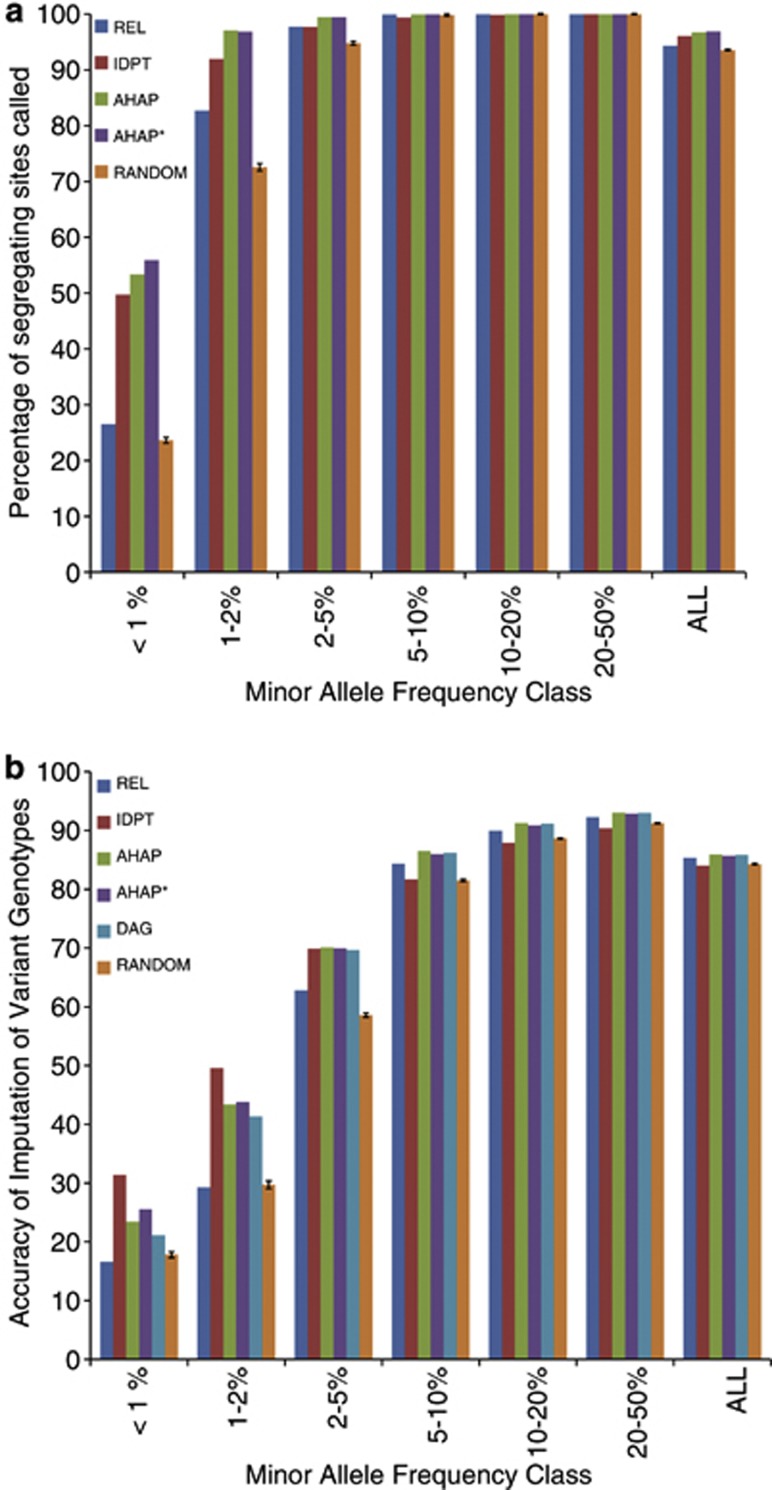
The 50 bulls selected by each strategy were ‘in-silico sequenced' as described in the methods. Variant calling was performed, followed by imputation of genotypes for bulls in the reference and validation sets at each variant. The variants called as a percentage of the real variants did not differ greatly between strategies for SNP at moderate frequencies, and all strategies found 100% or close to 100% of the variants at moderate frequencies. However, there was a dramatic difference in strategies for SNPs at low to very low frequencies (Figure 3a). This difference is much greater than the variation among the five RAN replicates, as shown by the s.e. bars in the Figure.

Figure 3.

Percentage of sequence variants detected (a), and accuracy of imputation of genotypes of sequence variants (b) when different strategies were used to select the individuals for sequencing. See methods for a description of sequencing strategies. Sequence variants were imputed into 1142 bulls with dense SNP panel genotypes. Fifty individuals were selected and sequenced at 12-fold coverage (50@ × 12).

Although no strategy detected more than 60% of very low-frequency variants (MAF <1%), AHAP* gives the greatest percentage of variants detected for this class. This is consistent with the fitness function of AHAP*, which weights rare and common haplotypes equally. When considered across all classes of variant, AHAP and AHAP* appear to be the best strategies. The fact that more than 50% of rare variants can be detected using these strategies, when only 50 individuals are sequenced, suggests that rare variants may be clustered in some individuals.

Greater differences between strategies were observed in the accuracy of imputation (Figure 3b). All strategies were better than RAN except REL for low and very low-frequency variants and IDPT for frequent variants. In fact, the performance of the strategies reranked across variant MAF classes compared with variant detection. IDPT outperformed the other strategies for low and very low variants, while AHAP performed well across the range of frequency classes (this strategy also resulted in more variants being detected). The best strategy, averaging performance across all variants, was AHAP (0.860). All haplotype strategies perform similarly, REL is quite close (0.854), and was actually the best strategy for variants with MAF >5%. Overall IDPT is the least precise (0.840).

Accuracy of imputation: comparison of constant sequencing effort, × 600, but different number of individuals sequenced at different fold coverage

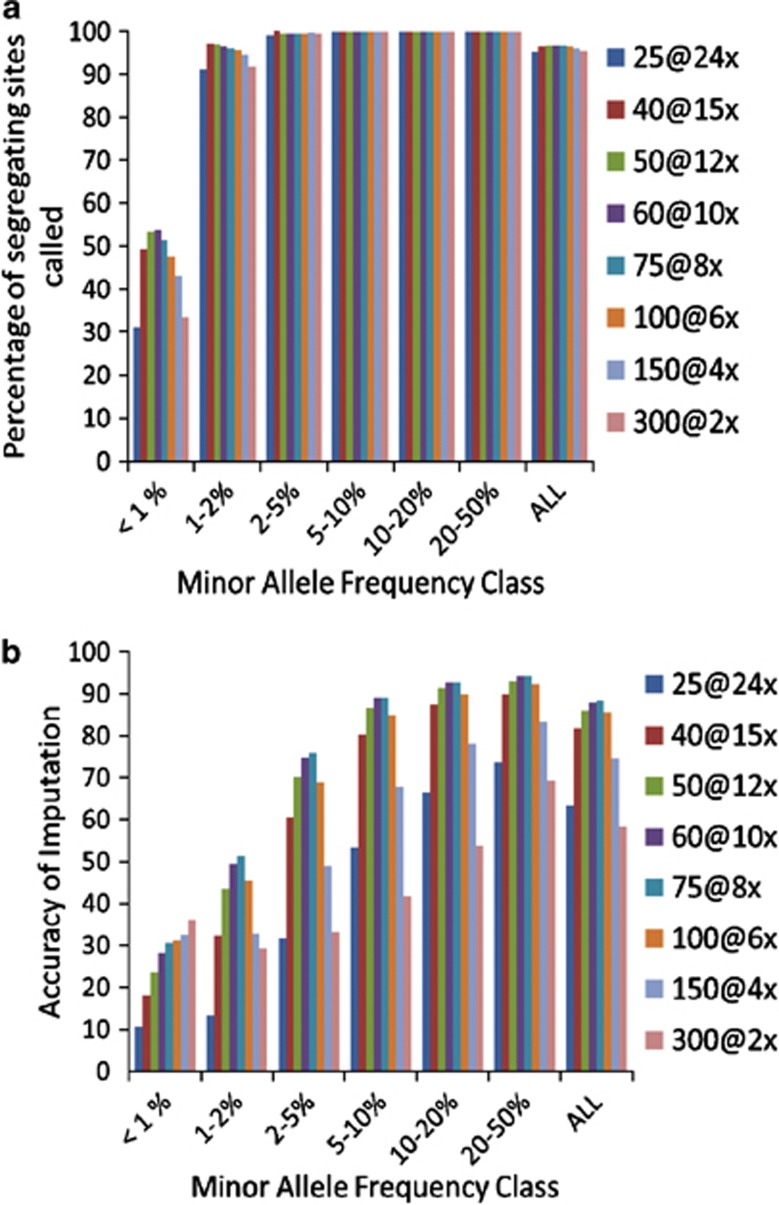
Next, we investigated the question, with a total sequencing effort available of × 600, is there an optimum number of individuals to sequence, if the aims are to detect as many variants as possible, and impute the variants accurately into a target population? For example, is it better to sequence 25 individuals at × 24 (abbreviated as 25@ × 24), or 300 individuals at × 2 (300@ × 2)? The strategy AHAP was used to select individuals for sequencing in all cases. One hundred percentage of the moderate to high-frequency variants were detected by all combinations of number individuals sequenced and fold coverage (Figure 4a). For very low-frequency variants (MAF <1%), 20% more variants were detected with 60 individuals sequenced at × 10 than with either 25@ × 24 or 300@ × 2.

Figure 4.

Percentage of sequence variants detected (a), and accuracy of imputation of genotypes of sequence variants (b) when the sequencing effort was constant ( × 600) but increasing numbers of individuals were sequenced at decreasing fold coverage. Strategy AHAP was used to select individuals for sequencing.

There was a large difference between the sequencing strategies in accuracy of imputation, even for moderate to high-frequency variants (Figure 4b). Except for very low MAF variants, 75@ × 8 was the optimum strategy. The two extreme strategies performed poorly, except 300@ × 2 for the very low-frequency variants.

Effect of increasing total sequencing effort on proportion of variants detected and accuracy of imputation

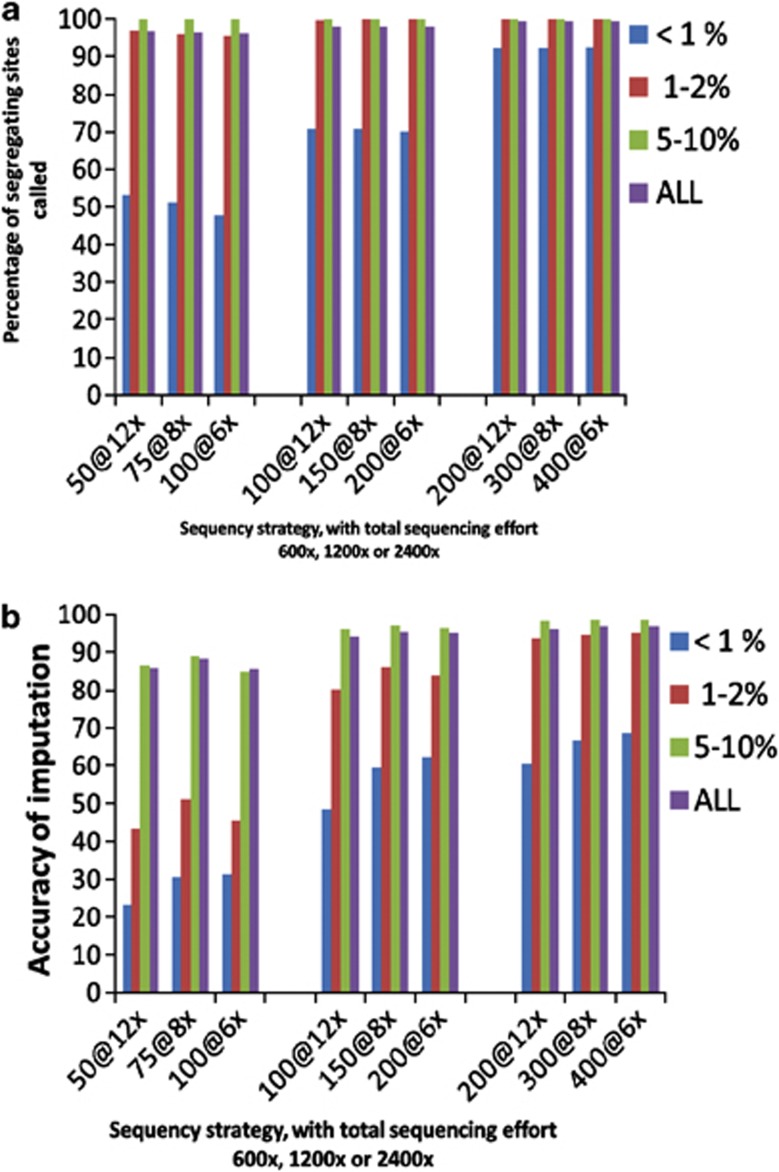
As total sequencing effort was increased, a much greater proportion of the low-frequency and very low-frequency variants were detected (Figure 5a). There was relatively little difference between sequencing strategies in overall proportion of variants detected.

Figure 5.

Percentage of sequence variants detected (a), and accuracy of imputation of genotypes of sequence variants (b) when the sequencing effort was constant at × 600, × 1200 or × 2400, but increasing numbers of individuals were sequenced at decreasing fold coverage. Strategy AHAP was used to select individuals for sequencing.

For the accuracy of imputation, however, the × 8 strategies performed well across all variants, with greatest differences in performance for the low MAF variant class. For the very low MAF class, the × 6 strategies performed the best at all three levels of sequencing effort. With larger amounts of sequencing effort, there is a trend toward lower fold coverage giving the best performance.

Additional gains in imputation accuracy for rare variants become harder and harder to achieve as the total sequencing effort increases. For example, if animals are sequenced at × 6, doubling the number sequenced from 100 to 200 gives a large increase in the accuracy of imputation for very low MAF variants from 30 to 60%. However, sequencing an additional 200 animals, to give 400@ × 6, only increases imputation accuracy of this class to 70%.

Accuracy of genomic selection from SNP panels and imputed sequence

The accuracy of genomic predictions from both the SNP panel and the sequence data (when the true sequence of all individuals in the population was used) were very dependent on the frequency of the QTL. High accuracies of genomic prediction were achieved when QTL had the same distribution as all variants (for example, QTL frequencies followed a distribution expected under a Neutral model). Much lower accuracies were achieved when the QTL all had < 1% MAF (Table 2).

Table 2. Comparison of accuracy of genomic selection for QTL with different minor allele frequency when predictions are based on SNP panel genotypes, sequence variant genotypes (all individuals sequenced) or imputed sequence variant genotypes.

	QTL frequency (MAF)
	<1%	<10%	Neutral
SNP panel	0.324	0.786	0.894
All individuals sequenced	0.448	0.817	0.907
Comparing strategies for selection of individuals (50@ × 12 for all strategies)
AHAP	0.338	0.804	0.904
REL	0.341	0.801	0.902
IDPT	0.360	0.805	0.903
Comparison of sequencing strategies
25@ × 24	0.315	0.786	0.898
50@ × 12	0.338	0.804	0.904
75@ × 8	0.339	0.806	0.904
100@ × 6	0.331	0.799	0.904
Effect of increasing sequencing effort
150@ × 8	0.381	0.812	0.905
300@ × 8	0.405	0.815	0.906

Abbreviations: MAF, minor allelic frequency; QTL, quantitative trait loci; SNP, single-nucleotide polymorphism.

Accuracies are the average of 25 replicates.

The advantage of the sequence data over the SNP panel was very small, 1.5%, for the Neutral model, but increased to 4 and 28% when the QTL had MAF <10% and MAF <1%, respectively.

When the sequence was imputed, the advantage over the SNP panel was reduced. Comparing strategies for selection of individuals, AHAP performed the best when the QTL allele frequencies followed a distribution as expected under a neutral model, while IDPT performed the best when the QTL were at very low (<1%) frequency. This reflects the fact that this strategy gave a good balance between the number of low-frequency variants detected and the accurate imputation of genotypes at these loci (Figure 3a).

The optimal sequencing strategy when the total sequencing effort was constrained to × 600 was 75@ × 8 (using AHAP to select individuals for sequencing). This is consistent with the accuracies of imputation in Figure 4. When the QTL were at low frequency, this strategy gave a 4.5% improvement over the SNP panel. Interestingly, sequencing a small number of individuals at high fold coverage (25@ × 24) and using these individuals to impute to sequence data resulted in worse predictions than from the SNP panel when QTLs are rare. This is because with this strategy for many of the rarer QTL variants, heterozygous individuals are wrongly imputed as homozygous.

Much larger improvements were observed with greater sequencing effort, with a 20% improvement over the SNP panel observed for 300@ × 8, for the scenario of QTL at <1% MAF, which is close to the 28% observed when actual sequence data on all individuals were used.

Discussion

Our results demonstrate accurate imputation of sequence data can be achieved in populations with a structure typical of most livestock species. If the variants have low minor allele frequency, the strategy used to choose individuals to sequence (as a reference for subsequent imputation) becomes important. In this situation, strategies for selecting individuals to sequence either based on pedigree (for example, IDPT) or haplotypes of SNP panel variants (for eple, AHAP) both perform well. Sequencing as many individuals as possible at × 8, for a given total sequencing effort, appears to give a good balance between detecting rare variants and having enough sequence reads to call genotypes accurately at these variants. The actual optimal value for fold coverage depends on the total sequencing effort that is available—as this increases, it becomes advantageous to sequence a larger number of animals at lower fold coverage.

Our results are generally in agreement with Le and Durbin (2011). Those authors concluded that for a given sequencing effort, more variants with low MAF would be detected by sequencing as many individuals as possible at low fold coverage. Certainly, we found many more variants using 75@ × 8 than 25@ × 24. However, with very low fold coverage at this sequencing effort ( × 600), for example, 300@ × 2, there were insufficient sequence reads covering the low-frequency allele to confidently call genotypes. One potential strategy would be to sequence animals at variable fold coverage—for example, key ancestors are sequenced at × 8, to ensure their alleles that are widespread in the population are called correctly, then a large number of individuals are sequenced at lower fold coverage, say × 4, to attempt to capture rare alleles.

The advantage of real or imputed sequence data in genomic predictions, as measured by the accuracy that can be achieved compared with SNP panels, was critically dependent on the allele frequency distribution of the QTL. If the QTL allele frequencies follow the same distribution as other variants in the sequence (Neutral), our results suggest the advantage of using sequencing data will be small. However, if the QTL alleles are at extremely low frequencies, the advantage of using sequence data over SNP panels can be a 28% increase in the accuracy of prediction if all individuals are sequenced, or 20% if the sequence variants are imputed from 300@ × 8.

The results differ both from those reported by Meuwissen and Goddard (2010), based on simulated data, and those from Ober et al. (2012), based on real data from Drosophila. Meuwissen and Goddard (2010) simulated QTL allele frequencies following that expected under a neutral model. They reported an advantage of 2.3–3.7% in the accuracy of genomic predictions of sequence data over that achieved with these densest SNP panel data they simulated. The advantage we observed (when the QTL allele frequencies followed a neutral model) was smaller at 1.4%. The difference is likely a result of the smaller recent effective population size (∼100) in our simulation, and hence greater LD, than in theirs, where a constant Ne of 1000 was used. In fact, the accuracies of genomic prediction we achieved in our simulations was high, reflecting the small effective population size, leading to extensive LD and the small size of the genome we simulated (50 MB, in five segments of 10 MB), leading to a small number of independent chromosome segment effects to be estimated (for example, Goddard, 2008) (however, considering a larger genome would not change the relative ranking of performance for the strategies for selecting animals to be sequenced). Clark et al. (2011) simulated a population with a broadly similar demography to ours. They observed larger gains in use of sequence data than those observed here (when the number of QTL was similar), perhaps a result of the larger reference population they used.

Ober et al. (2012), on the other hand, observed no advantage (over dense SNP data) of using whole-genome sequence data for genomic predictions of starvation response in D. melanogaster. In fact, it is difficult to compare our results to those of Ober et al. (2012), because the valid comparison depends on an assumption regarding the frequency of QTL alleles for starvation response. If we assume that starvation response in Drosophila has been under strong selection, and QTL alleles are at MAF <1%, then our results are not consistent with the results of Ober et al. (2012), as we did see an advantage of the sequence data in this situation. If, however, the QTL allele frequency is similar to that expected under a neutral model, our results are consistent with theirs. Another explanation for the results of Ober et al. (2012) is the small number of inbred lines used in that study (172).

So, the key question for assessing the advantage of whole-genome sequencing for genomic prediction becomes what is the allele frequency distribution for QTL affecting the target trait? Unfortunately, the allele frequency distribution of QTL for complex traits is unknown, in livestock, or in fact in any other species. In humans, for disease traits at least, both common and rare variant hypotheses, and combinations of both, have been argued for. Park et al. (2011), investigating the relationship between the effect of SNP alleles with validated associations to a range of traits, found that across all traits, an inverse relationship existed between the size of effects and allele frequencies. They reported that this trend was very pronounced for type I diabetes, a trait they suggested is likely to be influenced by selection, but the trend was less dramatic for human height and late onset diseases, suggesting QTL allele frequencies for these traits follow a distribution closer to that expected under a neutral model. Yang et al. (2010) demonstrated they could capture ∼50% of the genetic variance for human height with SNP arrays, where the SNPs on the array were at high MAF, and argued this was evidence that a reasonable proportion of the QTL were at MAF >10%. However, they concluded that the genetic variance not captured by these arrays could be explained by a proportion of the QTL with MAF <1%. Stahl et al. (2012) investigated potential alternate genetic models underlying rheumatoid arthritis, a complex disease trait, and concluded that results from genome-wide association studies that have been performed for this trait were most likely generated by hundreds of associated loci harboring common causal variants, and a smaller number of loci harboring multiple rare causal variants. However, the definition of ‘common' included SNPs with MAF >5% so overlaps with our low-frequency class (<10%).

In cattle populations, the proportion of variance captured by common SNPs is typically larger than in human populations. Haile-Mariam et al. (2012) reported that ∼50 000 SNPs were sufficient to capture 80% of the additive genetic variance for milk production traits, suggesting a high proportion of QTL affecting these traits are at moderate frequencies (otherwise LD between QTL and SNP would be limited and the genetic variance captured would be reduced). The increase in the proportion of variance captured by common SNP, compared with hman populations, likely reflects the fact that recent inbreeding in dairy catle (in fact, most livestock species) has flattened the allele frequency spectrum of QTL (for example, MacEachern et al., 2009A, 2009B). In commercial chickens, Muir et al. (2008) observed a significant absence of rare alleles, and also attributed this to recent inbreeding.

For some cattle traits, however, Haile-Mariam et al. (2012) found the proportion of variance explained by common SNP was much lower than 80%: for both fertility and longevity, only 55% of the genetic variance was captured by the 50 000 SNP panel (note that in our simulation, the SNP panel had equivalent density to a 50 000 SNP panel in cattle). In this case, a reasonable proportion of the genetic variance could be explained by many QTL with low allele frequencies, arguably because they are more likely to have been under long-term natural selection. So while for traits, such as milk production, the increase in accuracy of genomic predictions using sequence data compared with that from SNP panels will be small, the advantage for fertility and survival traits could be expected to be worthwhile. A possible counter argument to this would be that much of the genetic variation not captured by the common SNP for fertility and longevity in the study of Haile-Mariam et al. (2012) is non-additive variation. This cannot be ruled out; however, it should be pointed out that the comparison was with additive genetic variation estimated using a pedigree-based analysis.

One potential advantage of the sequence data not explored here is improving the persistence of accuracy of genomic predictions across generations, and to individuals less related to the reference set where the marker effects are estimated. In dairy cattle, at least, Habier et al. (2010) demonstrated that the accuracy of genomic-estimated breeding values decayed reasonably rapidly as the selection candidates were less and less related to the reference population. In that study, ∼50 000 SNPs were used in the genomic predictions. As the causative mutations are actually in the sequence data, the issue of decay in associations between causative mutations and SNP, which results in the decline in accuracy over time, may be overcome or at least reduced. Both Meuwissen and Goddard (2010) and Clark et al. (2011) were able to demonstrate this in simulations. Improving the persistence of accuracy is particularly important if genomic predictions are to be used for expensive and/or hard to measure traits (for example, feed conversion efficiency or methane emission levels in cattle). Otherwise, very large numbers of individuals will have to be continually phenotyped and genotyped to maintain acceptable accuracy of genomic prediction for such traits. An extreme example of the decay of accuracy of genomic predictions is when the predictions are made across breeds or distantly related lines, for example, when the reference population is one breed and the selection candidates are another breed. Using 50 000 SNP markers, Hayes et al. (2009) demonstrated that the accuracy of genomic predictions in Jersey cattle when Holstein cattle were used to derive the reference was approximately zero. If genomic predictions are made across breeds, using full-sequence data is likely to be particularly advantageous, as there is no longer the need to rely on marker—associations that may not persist across breeds (though this does assume some of the same causative mutations segregate across the breeds or lines). It should be pointed out that selection will also contribute to the decay in accuracy of genomic selection over generations, as QTL become fixed. This was demonstrated in simulations by Muir (2007). Using sequence data will not reduce decay in accuracy of genomic predictions due to selection. The relative contribution of selection, compared with breakdown in LD, to the decay of persistency, will depend, however, on the number of QTL segregating. If this is large, the contribution of selection to decay in persistency will be reduced as the changes in allele frequency at individual QTL will be small, at least for the limited number of generations we are considering here.

For fine mapping of QTL, sequence data will potentially have a large advantage over SNP panels, as the causal mutation is in the data set. However, the power of discovering the causal mutation (for example, the probability that the causal mutation will have the highest significance value in a genome-wide association study) will depend on the extent of LD (if other variants are in perfect LD with the causal variant, they will be impossible to distinguish from the true variant) and sample size.

In conclusion, in typical livestock populations, most of the advantage of using sequence data for genomic predictions (over and above SNP panels) can be captured by sequencing a relatively few individuals, and then imputing genotypes for the variants discovered in the sequence into the whole population. The accuracy of this imputation is greatly improved, particularly for low MAF variants, if animals are selected such that the haplotypes in the population, constructed from the SNP panel data, are present in the sequenced individuals (for example, strategy AHAP and AHAP*). The advantage in terms of accuracy of genomic predictions from this imputed sequence data, over and above that achieved from SNP panels, is determined both by the accuracy of imputation and, more importantly, by the allele frequency distribution of the QTL. Our results suggest that if the MAF of QTL is very low, genomic predictions from imputed sequence data can have up to 20% advantage in accuracy of genomic predictions from SNP panels. In dairy cattle, such genetic architecture is most likely for fertility, longevity and perhaps health traits. To accurately impute the rare variants that may affect such traits into reference populations for genomic selection, large numbers of individuals will need to be sequenced.

Finally, comparison of our results to those from Meuwissen and Goddard (2010) and Ober et al. (2012) suggest (1) the advantage in accuracy of genomic predictions from sequence data will be greater for populations with a larger effective population, and (2) large numbers of phenotyped and genotyped (for SNP panel) individuals will be required to take advantage of the sequence data, otherwise effects of the causative mutations, which are likely to be small, will be estimated with too much error resulting in little advantage of the sequence information.

Data archiving

There were no data to deposit.

The authors declare no conflict of interest.