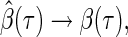Censored quantile regression with recursive partitioning-based weights

Abstract

Censored quantile regression provides a useful alternative to the Cox proportional hazards model for analyzing survival data. It directly models the conditional quantile of the survival time and hence is easy to interpret. Moreover, it relaxes the proportionality constraint on the hazard function associated with the popular Cox model and is natural for modeling heterogeneity of the data. Recently, Wang and Wang (2009. Locally weighted censored quantile regression. Journal of the American Statistical Association 103, 1117–1128) proposed a locally weighted censored quantile regression approach that allows for covariate-dependent censoring and is less restrictive than other censored quantile regression methods. However, their kernel smoothing-based weighting scheme requires all covariates to be continuous and encounters practical difficulty with even a moderate number of covariates. We propose a new weighting approach that uses recursive partitioning, e.g. survival trees, that offers greater flexibility in handling covariate-dependent censoring in moderately high dimensions and can incorporate both continuous and discrete covariates. We prove that this new weighting scheme leads to consistent estimation of the quantile regression coefficients and demonstrate its effectiveness via Monte Carlo simulations. We also illustrate the new method using a widely recognized data set from a clinical trial on primary biliary cirrhosis.

1. Introduction

Consider the survival analysis situation with right censoring. A study follows participant i until an event occurs (e.g. death or development of disease) at time 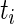which follows the continuous distribution of the random variable T. There are covariates measured at the beginning of the study that are denoted by a vector 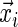. The goal is to quantify the effect 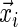has on the distribution of T. Yet, each study participant has a censoring time 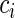(e.g. closing out of trial or lost to follow-up). The censoring time follows the distribution of the random variable C that is conditionally independent of T (i.e. T ⊥ C | 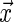, where ⊥ denotes statistical independence). Hence, a sample of right-censored survival data of size n consists of triplets 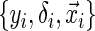, i=1,…,n, where y_i=min(t_i,c_i) and δ_i=I(t_i<c_i). There has been a large amount of focus on the relatively easy to implement, semi-parametric Cox proportional hazards model for survival analysis, which models the relationship between covariates and the log hazard function (Cox, 1972).

Censored quantile regression is a useful alternative to the Cox model that has recently gained considerable attention. Uncensored quantile regression methods have been extensively studied within the econometrics literature since the seminal work of Koenker and Bassett (1978); see Koenker (2005) for a comprehensive introduction. Quantile regression models the relationship between the event time and the covariates using the quantile function:

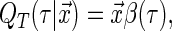(1.1)

where 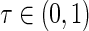is the quantile of interest and 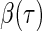is the vector of 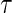th quantile effects. This enables researchers to model not only measures of central tendency, such as the median, but also other aspects of the conditional distribution such as the tails. An advantage of quantile regression is its invariance under monotonically increasing transformations, i.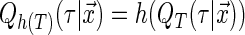e. where 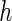is a monotonically increasing function (Koenker, 2005).

Censored quantile regression was first investigated in the econometrics literature for fixed censoring, i.e. all the censoring times are known regardless of whether the event occurs; see Powell (1986). This assumption is almost never met within applied health research. Ying and others (1995) and Yang (1999) both proposed median estimators (presumably generalizable to any quantile) that assumed unconditional independence between event and censoring times (i.e. ).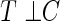

Portnoy (2003) adopted the more relaxed assumption of conditionally independent censoring (i.e. 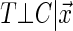). He proposed a novel method of recursively estimating a series of quantile regression functions defined on a grid along 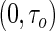, where 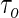is the quantile of interest. However, this recursive estimation relies on the assumption that the conditional quantile function is linear for all 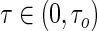. Wang and Wang (2009) refer to this assumption as the “global linearity assumption”, and observed that noticeable bias can occur when this assumption is violated.

Peng and Huang (2008) proposed an estimator, referred to hereafter as “PH”, that utilizes a martingale estimating equation which exploits the relationship between the quantiles and cumulative hazard function. Similar to Portnoy's approach, the PH estimator assumes both conditionally independent censoring and linearity in all quantiles by estimating a series of regression quantiles along a grid. Although it has not been investigated in the literature, it is anticipated that the performance of the PH estimator is likely to be influenced when the global linearity assumption is violated, as reflected in simulation results presented later in this paper.

Wang and Wang (2009) proposed a new locally weighted censored quantile regression approach that adopts the redistribution-of-mass idea of Efron (1967) and employs a local re-weighting scheme. Its validity only requires the conditional independence of the survival time and the censoring variable given the covariates, and linearity at the quantile level of interest. However, their locally weighted estimator suffers from two notable drawbacks in real data analysis. First, kernel smoothing becomes impractical, i.e. curse of dimensionality, with only a moderate number of covariates (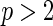). Second, kernel theory was developed for continuous covariates, so the presence of categorical variables causes the method to become ill-defined.

This paper proposes a new procedure that uses survival trees with Kaplan–Meier estimates (Kaplan and Meier, 1958) as the basis for the locally weighted estimator. By avoiding the use of a kernel, the approach is more flexible in handling moderate to high dimensions and discrete covariates while avoiding the global linearity assumption. We establish that the procedure leads to consistent estimation of the quantile regression coefficients.

The next section introduces the estimator, certain important aspects of survival trees and censored quantile regression. Section 3 shows the consistency and discusses the asymptotic normality of the estimator. Section 4 presents a series of simulations to analyze the finite sample performance of the proposed estimator, which is illustrated in Section 5 with an analysis of data on primary biliary cirrhosis (PBC). Finally, concluding remarks are discussed in Section 6.

2. Proposed estimator

We start by making important distinctions and formally defining distribution functions: capitalized letters with no subscripts indicate a random variable while lower case letters with subscripts indicate an observed variable, the conditional distribution of the event time is 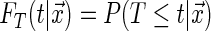, the conditional distribution of the censoring time is .

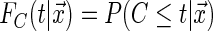2.1. Censored quantile regression

When there is no censoring (i.e. for all 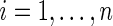), the 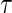th conditional quantile can be estimated by minimizing the following quantile objective function (Koenker, 2005):

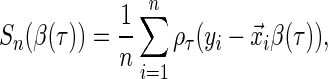(2.1)

where 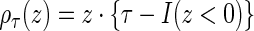is the quantile loss function and 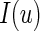is the indicator function (i.e. 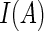is 1 if the event 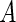is true, and 0 otherwise). When the survival time is subject to random right censoring, Wang and Wang (2009) proposed to estimate 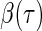by minimizing the weighted quantile objective function

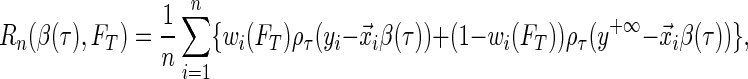(2.2)

where 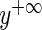represents a number large enough to be effectively infinity, and

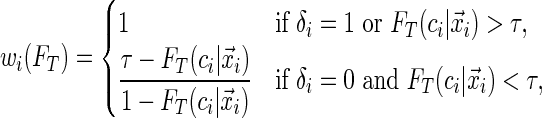with 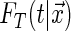being the conditional distribution function of 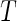given .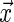

The motivation for the weighted quantile objective function in (2.2) is that the contribution of each point to the estimation of 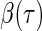depends only on the sign of the residual, where the residual is defined as 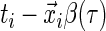. For the uncensored observations, the sign of the residual can be directly observed for a given 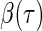. For the censored observations, there are two possibilities.

1. If 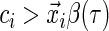, then 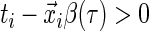. That is, if the censored time is larger than the predicted quantile of the survival time, then the sign of the residual is known since .

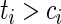2. If 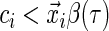, then the sign of the residual is not determined. In this case, given 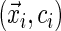, the conditional probability of obtaining a negative residual is

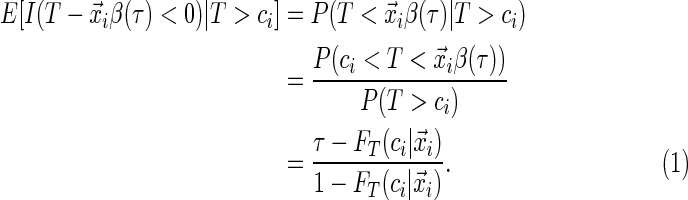
   (2.3)

In this ambiguous case, adopting the redistribution-of-mass idea of Efron (1967), we assign weight 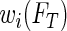to the observation at 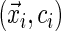and redistribute the complimentary weight 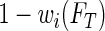to 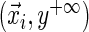without altering the quantile.

To estimate the weights, it is essential to estimate the conditional distribution of the survival time. In Section 2.2, we propose a new approach for estimating the weights that enjoy some appealing properties. It is worthwhile to note that the weighting scheme reduces to ordinary quantile regression in the presence of no censoring or when no censored observations are re-weighted (i.e. extremely late censoring relative to the quantile of interest). Also, the censoring distribution can have a direct impact beyond the marginal level of censoring. Depending on the timing, e.g. early vs. late censoring, more or less of the censored observations would be re-weighted. As an example, across a range from early to late censoring, with the same marginal level of 35% censoring, the proportion of censored observations that were re-weighted ranged from 20% to 87% using Portnoy's approach (more details are presented in Section 4). Furthermore, the subset of censored observations that are re-weighted would often differ between methods in addition to the ascribed weight (e.g. due to differences in estimates of ).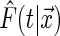

2.2. Survival trees

The proposed estimator utilizes survival trees, or recursive partitioning, as described by LeBlanc and Crowley (1993) and Butler and others (1989) to estimate the weights of censored observations described by (2.3) for the estimating equation (2.2). The goal of this article is not to fully describe recursive partitioning or survival trees in detail and so some familiarity is assumed. The interested readers are referred to Breiman and others (1984) for a comprehensive treatment of recursive partitioning and Bou-Hamad and others (2011) for a review of recent survival tree literature. Briefly, there is a need to introduce two concepts: splitting and stopping rules.

Splitting rules determine where and how to split a node. The trees used in this paper only consider splits on one variable at a time, resulting in binary trees. We use a splitting criteria that is the maximum of four 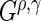statistics:

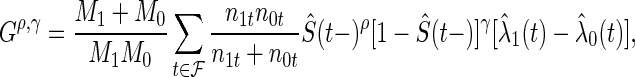(2.4)

where 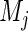is the number of subjects initially at risk in group 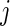, 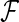is the set of unique failure times, 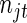is the number of subjects at risk in group 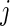at time 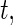and 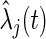is the estimated hazard of group 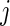at time 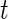(Rudser and others, 2012). The four 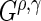statistics used are 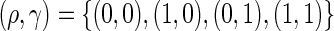. Note that (0, 0) and (1, 0) correspond to the log-rank and weighted Wilcoxon form of the log-rank test, respectively (the other two do not have common names). This cocktail of 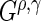statistics is used to increase the power to detect a variety of differences between survival functions (Lee, 1996). While this collection of 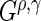statistics is designed to find several different types of differences in survival functions, one may choose fewer or only one 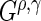statistic (e.g. only the log-rank statistic).

Stopping rules are used to indicate when to stop splitting at a particular node. These are used to prevent any particular node from not having enough information (e.g. small sample size, lack of events, etc.) to effectively estimate the probabilities of interest. This naturally leads to two “tuning parameters” that need to be specified:

1. “Minimum at Risk”: Each node is required to have a minimum number of subjects at risk for an event.

2. “Minimum Events”: Each node is required to have a minimum number of events.

For censored quantile regression, we are interested in the conditional probabilities used in the weights defined for censored observations by (2.3). By letting the minimum events depend upon the number at risk within a particular node and the quantile being estimated, we can ensure that each terminal node (i.e. a node that did not split further) has enough information to effectively estimate the probabilities of interest using a Kaplan–Meier estimator. While the Kaplan–Meier estimator is used here, it can be replaced by any cumulative distribution estimator for censored data.

Sensitivity to small changes in the data is a common criticism of trees. Breiman (1996) suggested that one effective way to alleviate this problem is to perform “bagging”. Bagging requires taking a prespecified number of bootstrapped data sets that are sampled with replacement, and then uses the average of the estimand over the bootstrapped data sets as the “bagged” estimate. In terms of trees, this means bootstrapping the data set a number of times, say 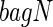, and obtaining 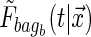for the bth bootstrapped data set. Then the final conditional distribution estimate for subject i is defined as

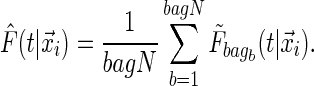(2.5)

This is expected to have a stabilizing effect on the tree-based estimate of .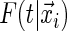

2.3. Implementation

To implement the proposed method, a researcher needs to specify three aspects of the survival trees: the splitting and stopping rules, and how many bags to use. After using (bagged) survival trees to determine the weights, re-weighted censored observations are split with weigh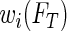t at 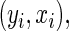and weight at 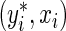, where 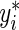is a large enough number to ensure a positive residual (e.g. 1000×(max_i{y_i}+1)). After splitting the appropriate observations between y_i and 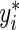, the estimating equation (2.2) can be fitted in R (R Development Core Team, 2011) using the function rq() from the “quantreg” package (Koenker, 2011) with user-defined weights.

3. Asymptotics

The proposed tree-based censored quantile regression estimator is consistent given certain regularity conditions (see supplementary material available at Biostatistics online). The following theorem summarizes this property.

Theorem 3.1 —

Assume that , , are independent and identically distributed with T independent of C conditional on , and that assumptions (A1) through (A5) in supplementary material available at Biostatistics online hold. Let be the minimizer of (2.2) with computed using a survival tree. Then

(3.1)

in probability, as .

The proof relies on the theory of Chen and others (2003) for non-smooth estimating equations with an infinite-dimensional nuisance parameter that requires the survival tree estimate to be uniformly consistent for the conditional survival function. This is shown using recursive partitioning theory developed by Gordon and Olshen (1984) and Butler and others (1989) which require the size of every terminal node to become arbitrarily small in every covariate. This suggests that the tree size, i.e. number of terminal nodes, needs to grow at a slower rate than the sample size within each terminal node with both tending to infinity or, practically, that the minimum number of events increases with the sample size.

Showing asymptotic normality is not straightforward. The sufficient conditions outlined by Chen and others (2003) for asymptotic normality require substantial additions to the recursive partitioning asymptotic literature for censored data: a more accurate limit on the rate of convergence of survival trees, and a linear representation of survival trees into mean 0 and finite variance random variables. To our knowledge, there is little to no survival tree literature on these specific topics. Most recursive partitioning asymptotic results focus on showing the consistency of estimated summary measures of conditional distribution functions while avoiding the discussion on rates of convergence and linear representations. These topics are beyond the scope of this paper.

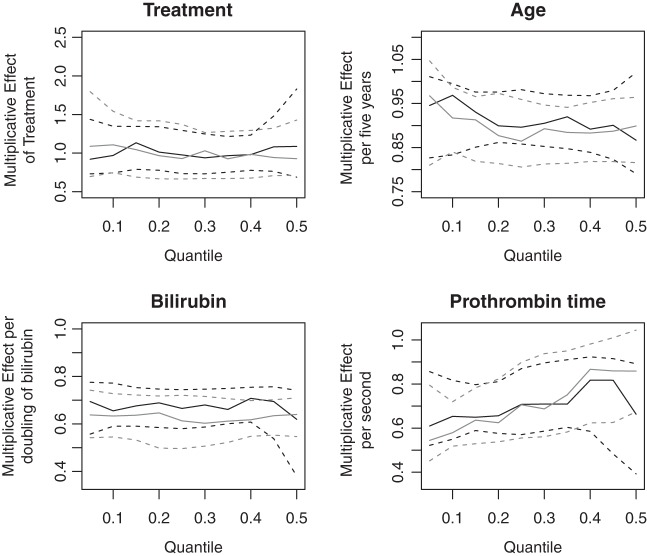
Inference is an important matter in statistics, which motivates showing the asymptotic distribution of an estimator. With any conditional quantile regression method the covariance matrix of 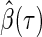depends upon an unknown conditional density (Koenker, 2005). The unknown density function makes accessible variance solutions extremely difficult to obtain. Portnoy (2003) proposed to sample the observed triplets 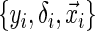with replacement (i.e. non-parametric bootstrap). After drawing a sufficient number of bootstraps, confidence intervals can be constructed based on sample quantiles or normal approximations of the bootstrap distribution. The tree-based method presented here utilizes the 2.5th and 97.5th sample quantiles of the bootstrap distribution to construct an approximate 95% confidence interval.

4. Simulations

We assess the finite sample performance of the tree-based estimator (TW) compared with the Portnoy and PH estimators through two simulation scenarios. When analyzing the effectiveness of tree-based weights, we include only bagged trees (bagN = 10). The minimum number at risk is 60 and the minimum number of events is 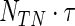, where 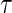is the quantile being estimated and 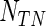is the number of observations within a node. All simulations were performed using R version 2.12.2 with the “quantreg” package used to fit the Portnoy and PH estimators. Approaches are compared based on operating characteristics of bias, mean squared error (MSE), coverage of 95% confidence intervals (Cov.), average confidence interval lengths (ECL), and power for a variety of simulation scenarios at the median 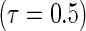and 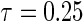quantile. The Wang and Wang estimator was left out due to the computational difficulties associated with moderate- to high-dimensional kernel estimation, but extensions are discussed in supplementary material available at Biostatistics online.

The simulation scenarios are categorized by two sets of covariate distributions (i.e. number of covariates) with varying levels of non-linearity (NL) (i.e. specification of the error distribution). The scenarios are formed from subsets of

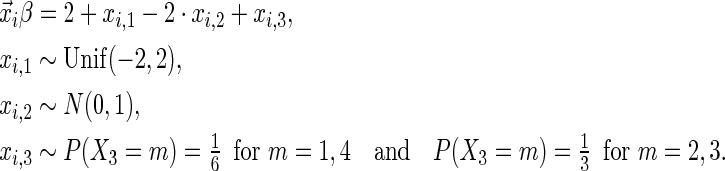The first and second simulation scenarios consist of, respectively, Ω₁={x_i,1,x_i,2} and Ω₂={x_i,1,x_i,2,x_i,3}, where Ω_k is the set of covariates for simulation k. The error structures are defined as E_l×(N(0,1)−Φ⁻¹(τ)), where E_l are the equations that induce NL, τ is the quantile of interest, and 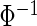is the inverse c.d.f. of the standard normal. The linear and non-linear 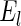's are, respectively, 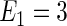and 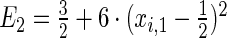. The censoring distributions are chosen depending upon the error structure with linear and NL represented by, respectively, 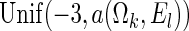and 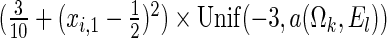, where 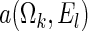is chosen to ensure 25% censoring for the median scenarios and 45% censoring for 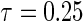scenarios. These censoring distributions lead to fairly even censoring across time and 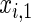. Each simulation scenario and error structure combination is evaluated over 2500 simulation iterations where each combination has a sample size of 400 with 300 bootstrap replicates for confidence intervals.

The first error structure 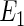possesses linearity in all quantiles for all variables. Owing to their implicit assumption of linearity in all quantiles, it is expected that the Portnoy and PH estimators will perform better than the tree-based approach. The second error structure imposes NL in all quantiles for 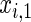except the quantile of interest. This scenario is likely to be more favorable for the tree approach compared with Portnoy and PH. Note that 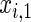is the only covariate that possesses NL in all quantiles except the quantile of interest.

The potential advantage of the proposed tree-based estimator is improved performance in multivariate scenarios with NL in some quantile. As such, we have two primary interests: whether the tree-based estimators are competitive in scenarios with linearity through all quantiles and, second, whether the tree-based estimators outperform the Portnoy and PH estimators in the presence of NL. The tree-based estimator accomplishes the former at some cost of bias for 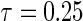, but are similar to the Portnoy and PH estimators for the median (“No NL” columns in Tables 1 and 2). For the latter question (“NL” columns), the tree-based estimator possesses less bias and MSE when estimating the median and 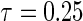. Finally, all the methods either maintained nominal coverage or were conservative (i.e. up to 97%). While the NL described above is severe, a simulation scenario with less severe NL showed advantages for the tree-based estimator albeit attenuated (see supplementary material available at Biostatistics online, Section 2.4).

Table 1.

First simulation scenario: 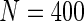, , 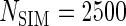censoring is 45% and 25% for 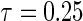and 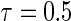, respectively, 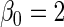, , 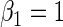, 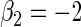300 bootstrap replicates, 95% nominal coverage with ECL representing the average CI width

			No NL					NL
Quantile	Variable	Method	Bias	MSE	Cov.	ECL	Power	Bias	MSE	Cov.	ECL	Power
0.25	Variable 1	Portnoy	0.00	0.04	0.97	0.83	1.00	0.17	0.70	0.95	3.26	0.28
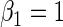		PH	0.01	0.04	0.97	0.83	1.00	−0.04	0.67	0.96	3.24	0.21
		TW	−0.06	0.04	0.96	0.81	1.00	0.01	0.59	0.96	3.09	0.25
	Variable 2	Portnoy	0.01	0.06	0.96	0.99	1.00	−0.20	0.28	0.96	2.10	1.00
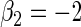		PH	−0.01	0.06	0.96	0.99	1.00	−0.26	0.31	0.95	2.13	1.00
		TW	0.10	0.06	0.95	0.97	1.00	0.06	0.21	0.97	2.02	1.00
0.5	Variable 1	Portnoy	0.01	0.03	0.96	0.71	1.00	0.10	0.52	0.95	2.85	0.34
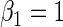		PH	0.00	0.03	0.96	0.72	1.00	−0.08	0.54	0.95	2.90	0.23
		TW	−0.01	0.03	0.97	0.71	1.00	0.04	0.52	0.96	2.90	0.31
	Variable 2	Portnoy	0.00	0.04	0.96	0.82	1.00	−0.13	0.15	0.95	1.56	1.00
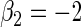		PH	0.00	0.04	0.97	0.84	1.00	−0.15	0.16	0.95	1.62	1.00
		TW	0.02	0.04	0.97	0.84	1.00	−0.03	0.13	0.97	1.60	1.00

Table 2.

Second simulation scenario: 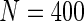, , 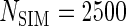censoring is 45% and 25% for 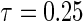and 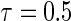, respectively, 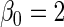, , 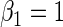, , 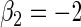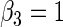300 bootstrap replicates, 95% nominal coverage with ECL representing the average CI width

			No NL					NL
Quantile	Variable	Method	Bias	MSE	Cov.	ECL	Power	Bias	MSE	Cov.	ECL	Power
0.25	Variable 1	Portnoy	−0.01	0.04	0.97	0.86	1.00	0.16	0.75	0.95	3.37	0.26
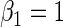		PH	0.00	0.04	0.96	0.86	1.00	−0.04	0.73	0.95	3.35	0.20
		TW	−0.06	0.04	0.97	0.86	1.00	−0.01	0.68	0.95	3.28	0.22
	Variable 2	Portnoy	−0.01	0.06	0.97	1.01	1.00	−0.19	0.29	0.97	2.27	0.99
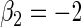		PH	−0.02	0.06	0.97	1.01	1.00	−0.24	0.33	0.96	2.29	0.99
		TW	0.06	0.06	0.97	1.02	1.00	0.02	0.25	0.97	2.21	0.98
	Variable 3	Portnoy	0.00	0.06	0.97	1.04	0.98	0.10	0.27	0.96	2.24	0.53
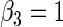		PH	0.01	0.06	0.97	1.03	0.98	0.12	0.28	0.96	2.26	0.54
		TW	−0.09	0.07	0.96	0.99	0.97	−0.11	0.21	0.97	2.01	0.44
0.5	Variable 1	Portnoy	−0.01	0.03	0.96	0.73	1.00	0.11	0.56	0.95	2.93	0.32
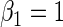		PH	−0.01	0.03	0.96	0.74	1.00	−0.07	0.56	0.95	2.96	0.23
		TW	−0.01	0.03	0.97	0.74	1.00	0.03	0.56	0.95	2.98	0.28
	Variable 2	Portnoy	−0.01	0.05	0.96	0.85	1.00	−0.12	0.17	0.95	1.66	1.00
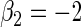		PH	−0.01	0.05	0.95	0.86	1.00	−0.15	0.19	0.95	1.72	1.00
		TW	0.00	0.05	0.96	0.86	1.00	−0.04	0.16	0.96	1.71	1.00
	Variable 3	Portnoy	0.00	0.05	0.97	0.88	0.99	0.05	0.15	0.97	1.68	0.72
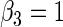		PH	0.00	0.05	0.97	0.89	1.00	0.06	0.16	0.97	1.74	0.70
		TW	0.00	0.05	0.97	0.89	1.00	0.02	0.15	0.97	1.71	0.69

The advantage of the tree-based estimator appears to depend upon the level of censoring. In particular, the tree-based estimator shows less improvement for bias when the percent of censoring increases with respect to the quantile of interest (see supplementary material available at Biostatistics online, Section 2.2). This may be due to our strict stopping rule that forces the number of events to be proportional to the quantile of interest. This stopping rule is increasingly restrictive when the marginal censoring is closer to the quantile of interest, but is necessary to guarantee coherent estimation of the weights, i.e. for the Kaplan–Meier estimate to reach the quantile of interest.

Additionally, the performance of all censored quantile regression estimators can vary wildly, depending on the location of the censored observations even, while keeping the overall marginal level of censoring constant. As an illustration, a small univariate simulation study is designed similarly to the above (see supplementary material available at Biostatistics online, Section 2.1). The bias was unaffected when the covariates were uniformly linear, but—in the presence of NL—we observed that the bias ranged from 0.17 to 0.26 for “late” to “early” censoring, respectively. Owing to the large variations in performance and percent of re-weighted observations, it is important for the literature to specify the censoring used when evaluating censored quantile regression methods, and ensure that resulting patterns of censoring are realistic. Explicitly stating the censoring distributions and the percent of observations re-weighted (Table 3) when presenting simulation results would be helpful as well.

Table 3.

Percent of total observations re-weighted by the simulation scenario (i.e. number of covariates) and the degree of NL

		Scenario 1			Scenario 2
Quantile	Method	No NL (%)	Mild NL (%)	Severe NL (%)	No NL (%)	Mild NL (%)	Severe NL (%)
0.25	Portnoy	26.8	30.1	29.1	21.3	28.9	31.1
	TW	31.2	32.8	29.5	32.3	33.3	30.8
0.5	Portnoy	18.3	20.2	16.9	17.5	20.7	19.2
	TW	19.5	21.0	17.0	21.2	21.9	19.2

The marginal censoring for all simulation scenarios was 45% and 25% for 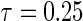and 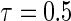, respectively.

5. Analysis of pbc data set

As an illustration, we apply the proposed method to the well-recognized PBC data set described by Fleming and Harrington (1991) from a clinical trial investigating the effect of the drug D-penicillamine conducted at the Mayo Clinic in Rochester, Minnesota. The data set is readily available in the R package “survival” as the “pbc” object (Therneau, 2012), and is widely considered a benchmark data set for survival analysis. We are interested in evaluating the association of the treatment, age, bilirubin, and prothrombin time with the log time till death or transplant. Yet bilirubin and prothrombin time appear to violate the global linearity assumption (see supplementary material available at Biostatistics online, Section 3), which is a scenario suited for the proposed tree-based estimator.

Considering only complete cases, this results in 312 patients with approximately 53.8% censoring. Portnoy's approach is compared with the proposed estimator with 10 bags. The minimum number at risk is set to 60, and the minimum number of events is 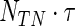, where 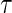is the quantile being estimated and is the number of observations within a node. Both approaches use bootstrap re-sampling for confidence intervals: the 2.5th and 97.5th quantiles were used to construct the 95% confidence intervals using 1000 bootstraps for both estimators.

Figure 1 displays the covariate effects on quantiles from 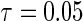to 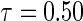. Of the four variables of interest, the treatment appears to have no effect along the estimated quantiles, while bilirubin appears to have a substantial constant effect on time till transplant or death. Longer prothrombin times appear to have a significant negative effect on survival time that attenuates for quantiles closer to the median. The estimated effects of bilirubin and age are different between the tree and Portnoy approaches. In particular, the tree-based weights have estimates closer to the null relative to Portnoy's estimator. Taking the 25th quantile as an example, the Portnoy estimator displays about 30% and 18% larger absolute effect estimates (for 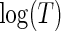) compared with the tree-based estimator for the effect of age and bilirubin, respectively. This direction and relative ordering of the two estimates are consistent with the anti-conservative bias for Portnoy's estimator in the presence of NL that was observed in the simulation results of Section 4. Additionally, the tree-based estimator generally has narrower confidence intervals around 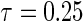compared with Portnoy, which is consistent with the simulation results. The tree-based estimator has wider confidence intervals toward the median. However, the censoring rate is above 50% for the PBC data set; hence neither method can accurately estimate the median or higher quantiles.

Fig. 1.

Estimated multiplicative effects on time to event for 0.05 to 0.5 quantiles (solid lines). 95% confidence intervals (dashed lines) are formed by taking the 2.5th and 97.5th sample quantiles of 1000 bootstrapped samples. The tree-based estimator and Portnoy's estimator are the black and gray lines, respectively.

In the analysis, we focus on the 25th quantile which corresponds to the patients with relatively short survival time. The estimated 25th conditional quantile function using the tree-based estimator is

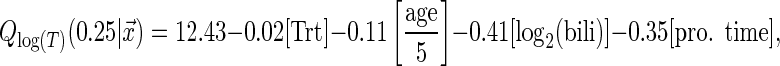(5.1)

whose coefficients are exponentiated to obtain an interpretation on the original time scale. For example, a 2-fold difference in bilirubin is associated with an average −0.41 shorter log time till transplant/death for the 25th quantile. On the original time scale, this corresponds to 33.5% shorter survival time for the 25th quantile on average while adjusting for treatment, baseline age and prothrombin time. On the other hand, a difference of 5 years of age implies, on average, 10.4% shorter survival time for the 25th quantile while adjusting for treatment, baseline bilirubin, and prothrombin time. The other covariates are interpreted in a similar fashion.

6. Discussion and future directions

Motivated in part by the practical difficulty encountered by the estimator of Wang and Wang (2009) with moderately high-dimensional data, we propose a new tree-based weighted censored quantile regression estimator. Under mild conditions, the new estimator is consistent. The simulation study demonstrated that if any variable possesses NL, then the Portnoy and PH estimators can suffer from bias and loss of precision in all covariates. Additionally, the proposed tree-based estimator can improve the bias and MSE in the presence of NL for multivariate scenarios. Interestingly, the largest improvements were for covariates that possessed linearity through all quantiles when adjusting for a covariate with NL. A limitation is that, due to strict splitting rules that enforce the quantile of interest to be defined in each node, the proposed tree-based estimator may be more sensitive to a high censoring rate relative to the quantile of interest compared with the Portnoy and PH estimators.

We found that the performance of the estimators depended heavily on the censoring distribution. In particular, in the presence of NL, the Portnoy estimator provides a biased estimate that depends on the location of the censoring distribution. As such, we recommend that future censored quantile regression articles explicitly state the censoring distribution used, and where the censoring is occurring and report the percent of observations re-weighted for approaches based on the weighted estimating equation of the form (2.2). The extent of the censoring distribution's impact is less clear for other approaches (e.g. PH). Further investigation and benchmarking of relative performance of this issue will be an interesting future research topic.

Compared with the local Kaplan–Meier estimator-based weights, i.e. Wang and Wang (2009), the tree-based weights have appealing properties that work better with moderately high-dimensional covariates while avoiding the linearity assumption of Portnoy (2003) and Peng and Huang (2008). As suggested by an anonymous referee, an alternative approach to estimating the weights is using flexible spline methods. For example, the polynomial splines developed by Kooperberg and others (1995) can flexibly estimate the conditional hazard function (the hare() function in R). This approach could be extended to estimate the conditional survival function used for censored quantile regression. This is an interesting direction to explore in our future research.

We briefly described how the sample size within terminal nodes and the overall tree size both need to approach infinity. This does not provide much guidance on how to select a good tuning parameter for the minimum number at risk. In practice, cross-validation could be used to select the most appropriate minimum number at risk, but we are currently investigating ways to combine survival trees across a range of tuning parameters to obtain better performance.

As pointed out by an anonymous referee, the bagged survival tree used to estimate the weights can be considered as a non-parametric estimator of the conditional quantile function, equation (1.1). Essentially, the bagged trees can predict quantile values for particular covariate values similar to Meinshausen (2006). While this is potentially useful for predicting survival times, this does not provide information on the relationship of the covariates with the event distribution. Rudser and others (2012) show how these predicted values could be used to form linear contrasts, while local regression extensions, e.g. splines, are straightforward (see supplementary material available at Biostatistics online).

The code to implement censored quantile regression with tree-based weights is available from the first author, or at https://sites.google.com/site/andyrswey/software.

Supplementary material

Supplementary Material is available at http://biostatistics.oxfordjournals.org.

Funding

This research reported in this publication was supported in part by the NIH grant UL1TR000114 and NSF grant DMS-1007603.