Limitations of inclusive fitness

Significance

Inclusive fitness theory is the idea that the evolutionary success of a trait can be calculated as a sum of fitness effects multiplied by relatedness coefficients. Despite recent mathematical analyses demonstrating the limitations of this approach, its adherents claim that it is as general as the theory of natural selection itself. This claim is based on using linear regression to split an individual's fitness into components due to self and others. We show that this regression method is useless for the prediction or interpretation of evolutionary processes. In particular, it fails to distinguish between correlation and causation, leading to misinterpretations of simple scenarios. The weaknesses of the regression method underscore the limitations of inclusive fitness theory in general.

Abstract

Until recently, inclusive fitness has been widely accepted as a general method to explain the evolution of social behavior. Affirming and expanding earlier criticism, we demonstrate that inclusive fitness is instead a limited concept, which exists only for a small subset of evolutionary processes. Inclusive fitness assumes that personal fitness is the sum of additive components caused by individual actions. This assumption does not hold for the majority of evolutionary processes or scenarios. To sidestep this limitation, inclusive fitness theorists have proposed a method using linear regression. On the basis of this method, it is claimed that inclusive fitness theory (i) predicts the direction of allele frequency changes, (ii) reveals the reasons for these changes, (iii) is as general as natural selection, and (iv) provides a universal design principle for evolution. In this paper we evaluate these claims, and show that all of them are unfounded. If the objective is to analyze whether mutations that modify social behavior are favored or opposed by natural selection, then no aspect of inclusive fitness theory is needed.

Inclusive fitness theory (1–10) is an approach to accounting for fitness effects in social evolution. It was introduced in 1964 by W. D. Hamilton (1), who showed that, under certain circumstances, evolution selects for organisms with the highest inclusive fitness. This result has been interpreted as a design principle: evolved organisms act as if to maximize their inclusive fitness (1, 2, 8, 9, 11, 12).

Hamilton (1) defined inclusive fitness as follows: “Inclusive fitness may be imagined as the personal fitness which an individual actually expresses in its production of adult offspring as it becomes after it has been first stripped and then augmented in a certain way. It is stripped of all components which can be considered as due to the individual’s social environment, leaving the fitness which he would express if not exposed to any of the harms or benefits of that environment. This quantity is then augmented by certain fractions of the quantities of harm and benefit which the individual himself causes to the fitnesses of his neighbours. The fractions in question are simply the coefficients of relationship appropriate to the neighbours whom he affects: unity for clonal individuals, one-half for sibs, one-quarter for half-sibs, one-eighth for cousins, … and finally zero for all neighbours whose relationship can be considered negligibly small.” (p. 8). Although modern formulations of inclusive fitness theory use different relatedness coefficients (3, 5, 13), all other aspects of Hamilton’s definition remain intact.

The crucial point here is that it is assumed that personal fitness can be subdivided into additive components caused by individual actions. The personal fitness of a focal individual is stripped of all components that are due to the “social environment.” This means we have to subtract from the personal fitness of an individual every effect due to other individuals. Subsequently we have to calculate how the focal individual affects the personal fitnesses of all other individuals in the population. In both cases we must assume that personal fitness can be expressed as a sum of components caused by individual actions. Inclusive fitness is the effect of the action on the actor plus the effects of the action on others multiplied in each case by the relatedness between the actor and the others.

It is immediately obvious that the additivity assumption, which is essential for the concept of inclusive fitness, need not hold in general. For example, the personal fitness of an individual can be a nonlinear function of the actions of others. Or the survival of an individual could require the simultaneous action of several others; for example, the reproductive success of the queen might require the coordinated action of groups of specialized workers. Experiments have found that the fitness effects of cooperative behaviors in microbes are not additive (14–16). It is clear that in general fitness effects cannot be assumed to be additive.

Two Approaches to Inclusive Fitness

Within the literature on inclusive fitness, there are two approaches for dealing with the limitation of additivity. The first approach is to restrict attention to simplified models in which additivity holds. For example, Hamilton’s original formulation of inclusive fitness theory (1) includes additivity as an assumption. Additivity also follows from assuming that mutations have only small effects on phenotypes, and that fitness varies smoothly with phenotypes (6, 7, 17, 18).

Nowak et al. (19) investigated the mathematical foundations of this first approach. They demonstrated that this approach also requires a number of restrictive assumptions beyond additivity of fitness effects, and is therefore applicable only to a limited subset of evolutionary processes. In response, more than 100 authors signed the statement that “inclusive fitness is as general as the genetical theory of natural selection itself” (20). How are we to understand this apparent contradiction?

The answer is that the above statement rests on a second, alternative approach, which deals with the additivity problem in retrospect. In this approach, the outcome of natural selection must already be known or specified at the outset, and the objective is to find additive costs and benefits that would have yielded this outcome—regardless of whether they correspond to actual biological interactions. These costs and benefits are determined using linear regression. This regression method was introduced by Hamilton (21) in a follow-up to his original work on inclusive fitness theory, and has been subsequently refined (3–5, 22) into a recipe for rewriting frequency changes in the form of Hamilton’s rule.

The regression method underpins many claims of the power and generality of inclusive fitness theory. For example, it is often claimed (5, 12, 23, 24) that the regression method allows inclusive fitness to eschew the requirement of additivity. It is also claimed that the regression method generates a prediction of the direction of natural selection (5), and leads to a quantitative understanding of any frequency change as a consequence of social interactions between related partners (3–5, 25).

Here we evaluate these claims by asking, what, if anything, the regression method reveals about a given evolutionary change. We show that claims of the method’s predictive and explanatory power are false, and the claim of its generality is not a meaningful one that could be evaluated. These findings call into question the idea that inclusive fitness provides a universal design principle for evolution—indeed, no such design principle exists.

Regression Method

To perform the regression method, one must start with quantities that describe a change in allele frequency between two time points. These quantities can be obtained either from a theoretical model or from empirical observation, or they can be arbitrarily specified. Specifically, the method requires

• • The genetic types, , of all individuals 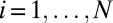present in the population at the first time point. Here 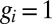(or 0) indicates that an allele of interest is present (or absent) in individual .

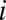• • The fitnesses , with 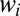defined as the fraction of individuals alive at the second time point who are descendants of individual 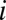from the first time point.

• • The interaction partners of each individual at the first time point.

The method also accommodates generalized versions of the above data. For instance, one can consider g values that range between 0 and 1, representing the genetic predisposition toward a trait of interest (3–5, 22). The fitnesses 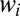can be replaced by their expected values, if these have been previously determined from a theoretical model. Also, we consider only asexual reproduction here for the sake of simplicity, but the method can accommodate sexual reproduction as well (3, 5, 22).

It is clear that, once the above quantities are specified, the change in allele frequency is known at the outset. We also observe that no information is included regarding the causes of the change, or regarding other changes that occur before, between, or after these time points.

We now describe the regression method, following refs. 3–5. The average genetic type (g value) of the partners of individual 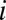is denoted 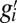. The method uses least-squares multivariate regression to fit the given values to a simplified model in which fitness effects are additive and depend linearly on g values. Specifically, one proceeds by determining values 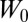, , 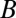and 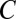such that, upon writing

the sum 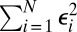is minimized. The terms 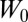, , 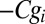and 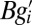, represent baseline fitness, cost to self, and benefit from others, respectively, under this simplified model. The residuals 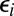quantify the deviation of this simplified model from the given data. In contrast with the usual practice of linear regression, no attention is given here as to the goodness of fit (5).

To relate Eq. 1 to the change in gene frequency, the notion of population covariance is introduced. For any quantities and 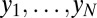describing members of a population, the population covariance of 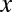and 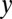is defined as

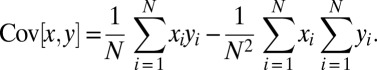We emphasize that population covariance is a descriptive, rather than inferential, statistic. The use of statistical terminology in this manner is potentially confusing (26, 27), but widespread in the literature on inclusive fitness (3–5, 21, 22, 25).

Taking the population covariance of w with g and substituting from Eq. 1 yields

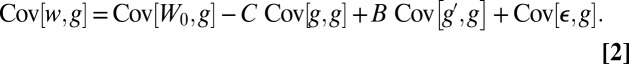The sign of the left-hand side coincides with the direction of change in allele frequency by Price’s identity (27, 28). On the right-hand side, 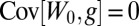because 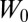is constant, and 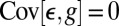as a consequence of the fact that 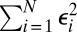is minimized. Dividing both sides of Eq. 2 by 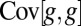, which is necessarily positive, yields that the direction of change in allele frequency coincides with the sign of

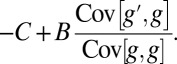Defining relatedness as 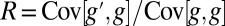, one obtains that the allele frequency increases if and only if 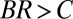(3–5).

It is claimed that the resulting values of B, C, and R give a causal explanation for the observed change in frequency (3, 4, 25). In particular, the signs of B and C are said to reveal the nature of the trait in question: costly cooperation (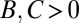), mutually beneficial cooperation (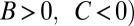, selfishness (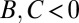), or spite (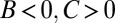) (5, 29).

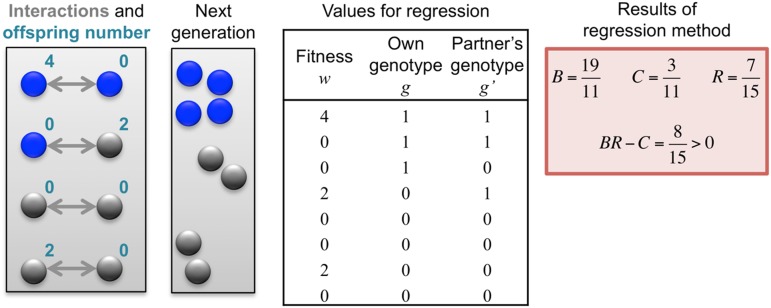
A sample application of the regression method is provided in Fig. 1. The leftmost panel shows the genetic types, offspring numbers, and interaction partners in a hypothetical population. One immediately observes that the allele of interest is increasing. Applying the regression recipe yields 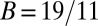, , 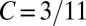and 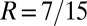. We provide a step-by-step calculation of these values in SI Appendix. Thus, according to standard interpretation (5, 29), the allele encodes costly cooperation 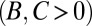, which succeeds due to high relatedness between interaction partners ().

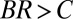Fig. 1.

Regression analysis of a hypothetical change in frequency. The starting ingredients are the genetic types (represented by colors), interaction partners (represented by arrows), and numbers of eventual offspring (represented by numbers) of each individual present at a particular time. The change in allele frequency is already known from these data. The regression recipe is applied by fitting these data to a linear model of offspring number based on each individual’s own genotype and partner’s genotype. For this process, we obtain 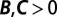and 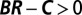, indicating that the rise in frequency of the blue type is due to costly cooperation between closely related partners. In the absence of further information, there is no statistical or scientific reason to conclude that this interpretation is correct.

Regression Method Does Not Yield Predictions

We now evaluate the various claims made regarding the regression method, starting with the claim that it predicts the direction of selection (5). This claim cannot be true, because the allele frequency change over the considered time interval is specified at the outset. The “prediction” merely recapitulates what is already known, such that the sign of 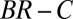agrees with the predetermined outcome.

The regression method also does not predict what will happen over different time intervals or under different conditions. With any change in the considered scenario or time interval, the starting data must be respecified and the method reapplied, yielding new and independent results.

This lack of predictive power is unsurprising. It is logically impossible to predict the outcome of a process without making prior assumptions about its behavior. In the absence of any modeling assumptions, all that can be done is to rewrite the given data in a different form.

Experimentalists (15, 30) have noticed this absence of predictive capacity. One recent study (15) applied the regression method to the cooperative production of an agent needed for antibiotic resistance in Escherichia coli. The authors conclude that “even if one has measured the values of B, C and R for a particular system of producers and nonproducers, one cannot predict what will result from changing either the structure of population or the biochemistry of the individuals” (15).

Regression Method Does Not Yield Causal Explanations

We now evaluate the explanatory power of the regression method. The current literature appears to disagree on this point. Some works claim the method yields causal explanations for frequency change (3, 4, 25), whereas others make the more limited claim that it provides a useful conceptual aid (5). Moreover, the quantities that result from the regression method are commonly described in terms of social behaviors such as altruism and spite (5, 29), imbuing these quantities with a “causal gloss” (31) even if no direct claims of causality are made.

The claim that the regression method identifies the causes of allele frequency change cannot be correct, because regression can only identify correlation, and correlation does not imply causation. For example, in the scenario of Fig. 1, we obtained 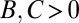, which is claimed to indicate costly cooperation (5, 29). However, without further information, there is no scientific basis to conclude that the frequency change resulted from cooperation rather than other factors or random chance.

More generally, because the regression method attempts to find additive social fitness effects that match given data, we should expect it to yield misleading results when social interactions are not additive, or when fitness variation is caused by other factors. Based on this principle, we present three hypothetical scenarios in which the regression method mischaracterizes the reasons for frequency change (Fig. 2).

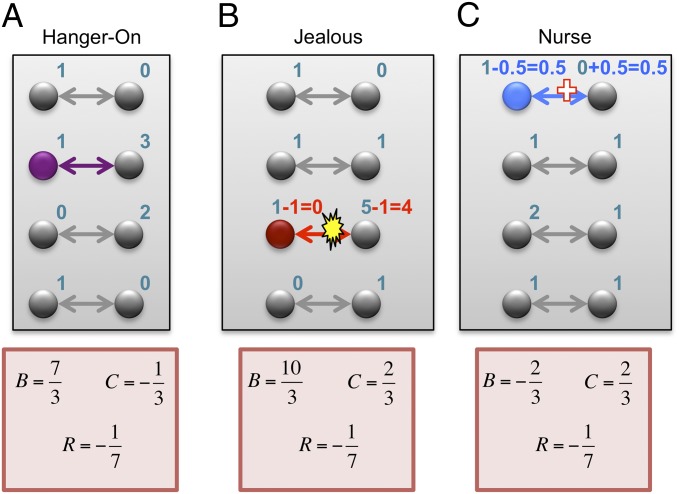
Fig. 2.

Regression does not identify the causes of frequency change. Three hypothetical examples show how the regression method leads to incorrect interpretations. (A) A hanger-on (purple) finds a high-fitness partner to interact with. The regression recipe yields 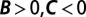, misinterpreting this behavior as mutually beneficial cooperation. (B) A jealous individual (red) attacks an individual of high fitness. This attack reduces the recipient’s fitness from 5 to 4, and the attacker’s fitness from 1 to 0. The regression recipe yields 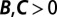, misinterpreting this attack as costly cooperation. (C) A nurse (blue) helps an individual of low fitness. This aid increases the recipient’s fitness from 0 to 0.5 (representing a 50% chance of having an offspring), and decreases the nurse’s fitness from 1 to 0.5. The regression recipe yields 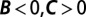, misinterpreting this aid as costly harming or spite. For all three examples, the classification of the behavior according to 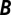and is insensitive to minor changes in the data; for example, the fitness of the hanger-on’s partner can be changed to any number greater than 1 without altering the classification as mutually beneficial cooperation.

In the first hypothetical scenario, a “hanger-on” trait leads its bearers to seek out and interact with individuals of high fitness. We suppose that these interactions do not affect fitness. However, this seeking-out behavior leads fitness to become positively correlated with having a hanger-on as a partner; thus the regression method yields 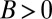. According to the proposed interpretation (5, 29), hangers-on should be understood as cooperative, bestowing high fitness on their partners. However, of course this gets causality backward—the high fitness causes the interaction, not the other way around.

Variants of this hanger-on behavior may occur in many biological systems. A bird may choose to join the nest of a high-fitness pair, with the goal of eventually inheriting the nest. Similarly, a social wasp may be more likely to stay at its parents’ nest if the parent has high fitness, also with the goal of eventual inheritance. Applying the regression method to these situations would lead one to mistake purely self-interested behaviors for cooperation.

The second example is a “jealous” trait. Jealous individuals seek out high-fitness partners and attack them with the aim of reducing their fitness. We suppose that these attacks are costly to the attacker but only mildly effective, so that the attacked individuals still have above-average fitness after the attacks. The regression method yields 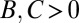, suggesting that the jealous individuals are engaged in costly cooperation. Again, this interpretation is wrong: the attacks are harmful, and the positive fitness correlation is due to the choice of interaction partners and the ineffectiveness of the attacks.

The third example is a “nurse” trait. A nurse will seek out low-fitness individuals and make costly attempts to improve their fitness. We suppose, however, that this aid is only mildly effective, so that the aided individuals still have below-average fitness. The regression method yields 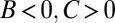, misinterpreting this remaining low fitness as due to costly sabotage on the part of the nurses.

“Assumption-Free” Approaches

Finally, we turn to the claim that inclusive fitness theory is “as general as the genetical theory of natural selection itself” (20). The argument is that, because the regression method can be applied to an arbitrary change in allele frequency (regardless of the actual causes of this change), it follows that every instance of natural selection is explained by inclusive fitness theory.

However, as we have seen, the regression method yields a “just-so story” that does not predict nor explain anything about the given scenario or any other (15). Of course, there can exist cases for which the regression method yields correct causal explanations, and there can also exist cases for which the results obtained for one scenario are approximately accurate for certain others. However, the regression method provides no criteria to identify these cases—indeed, to formulate such criteria would require additional assumptions about the underlying processes. Without such assumptions, the results of the regression method do not answer any scientific question about the situation under study. The claim of generality is therefore meaningless.

This lack of utility is not due to any technical oversight. Rather, it arises from the attempt to extend Hamilton’s rule to every instance of natural selection. This impulse is understandable, given the intuitive appeal of Hamilton’s original formulation. However, the power of a theoretical framework is derived from its assumptions, thus a theory with no assumptions cannot predict or explain anything. As Wittgenstein argued in his Tractatus Logico-Philosophicus (32), any statement that is true in all situations contains no specific information about any particular situation.

There Is No Universal Design Principle

The concept of inclusive fitness arises when one attempts to explain the evolution of social behavior at the level of the individual. For example, inclusive fitness theory seeks to explain the existence of sterile ant workers in terms of the behaviors of the workers themselves. The proposed explanation is that workers maximize their inclusive fitness by helping the queen rather than producing their own offspring (11, 29).

The claim that evolution maximizes inclusive fitness has been interpreted as a universal design principle for evolution (1, 2, 8, 9, 12). This claim is based on an argument by Hamilton (1) that evolution maximizes the mean inclusive fitness of a population (see also ref. 11), and a separate argument by Grafen (8, 9) that evolved organisms act as if to maximize their inclusive fitness. Both of these arguments depend on restrictive assumptions, including additivity of fitness effects (1, 8). Because experiments have shown that fitness effects in real biological populations are nonadditive (14–16), these results cannot be expected to hold in general. Moreover, both theory (33–36) and experiment (37, 38) have shown that frequency-dependent selection can lead to complex dynamical phenomena such as multiple and mixed equilibria, limit cycles, and chaotic attractors, ruling out the possibility of general maximands. Thus, evolution does not, in general, lead to the maximization of inclusive fitness or any other quantity.

Common-Sense Approaches to Evolutionary Theory

Fortunately, no universal maximands or design principles are needed to understand the evolution of social behavior. Rather, we may rely on a straightforward genetic approach: Consider mutations that modify behavior. Under which conditions are these mutations favored (or disfavored) by natural selection? The target of selection is not the individual, but the allele or the genomic ensemble that affects behavior.

To investigate these questions theoretically, one needs modeling assumptions. These assumptions can be highly specific, applying only to particular biological situations, or broad, applying to a wide range of scenarios. Modeling frameworks that rely on general (yet precise) assumptions have recently emerged as a powerful tool for studying the evolution of populations structured spatially (39–42), by groups (43), and physiologically (44–46); the evolution of continuous traits (47–49); and inclusive fitness theory itself (in cases where fitness effects are additive and other requirements are satisfied) (7, 19). Although these frameworks can be used to obtain general results, none of them is universal or assumption-free. Instead, they draw upon their assumptions to make well-defined, testable predictions about the systems to which they apply.

Discussion

Inclusive fitness theory attempts to find a universal design principle for evolution that applies at the level of the individual. The result is an unobservable quantity that does not exist in general (if additivity is required) or has no predictive or explanatory value (if the regression method is used). If instead we take a genetic perspective and ask whether natural selection will favor or oppose alleles that modify social behavior, there is no need for inclusive fitness.

The dominance of inclusive fitness theory has held up progress in this area for many decades. It has consistently suppressed reasonable criticism, as for example from Cavalli-Sforza and Feldman (50), Karlin and Matessi (51), and Matessi and Karlin (52), and alternative approaches. In particular, the attempt to eschew the requirement of additivity using regression methods has led to logical obfuscation and false claims of universality (5, 20, 24). Reasonable inclusive fitness calculations that assume additivity represent an alternative method to account for fitness effects in some limited situations (7, 13, 53–55), but this method is never necessary and often needlessly complicated. There is no problem in evolutionary biology that requires an analysis based on inclusive fitness.

Having realized the limitations of inclusive fitness, sociobiology now has the possibility to move forward. We encourage the development of realistic models grounded in a firm understanding of natural history. With the aid of population genetics, evolutionary game theory, and new analytic procedures to be developed, a strong and resilient sociobiological theory can emerge.