Trial-to-trial, uncertainty-based adjustment of decision boundaries in visual categorization

Significance

Categorization is an important part of perception and cognition. For example, an animal must successfully categorize a disturbing sound as being due to the wind or to a predator. Computationally, categorization amounts to applying decision boundaries to noisy stimulus measurements. Here, we examine how these decision boundaries change as the quality of the sensory evidence varies unpredictably from trial to trial. We show that both humans and monkeys adjust their decision boundaries from trial to trial, often near-optimally. We further show how a neural network can perform this computation near-optimally. Our results might lead to a better understanding of categorization.

Abstract

Categorization is a cornerstone of perception and cognition. Computationally, categorization amounts to applying decision boundaries in the space of stimulus features. We designed a visual categorization task in which optimal performance requires observers to incorporate trial-to-trial knowledge of the level of sensory uncertainty when setting their decision boundaries. We found that humans and monkeys did adjust their decision boundaries from trial to trial as the level of sensory noise varied, with some subjects performing near optimally. We constructed a neural network that implements uncertainty-based, near-optimal adjustment of decision boundaries. Divisive normalization emerges automatically as a key neural operation in this network. Our results offer an integrated computational and mechanistic framework for categorization under uncertainty.

Imagine a woman is approaching you from a distance and you are trying to determine whether or not she is the friend you are waiting for. Because of various sources of noise, your observations of her facial features, hair color, etc. will be uncertain. A sensible strategy would be to be more tolerant to deviations between your observations and your knowledge of your friend’s looks when she is far away than when she is close by and your observations are less uncertain. In this categorization problem, you are determining whether the image of the approaching woman falls into the narrow category of images of your friend or the wide category of images of all other people. Categorization can be modeled as a process of applying one or more decision boundaries to a noisy measurement in a space of stimulus features (1–7). The example suggests that adjusting such decision boundaries based on the current level of sensory uncertainty might be a better strategy than using uncertainty-independent decision boundaries.

Previous studies have not addressed whether organisms adjust their decision boundaries from trial to trial according to the level of sensory uncertainty. Perceptual studies of categorization under sensory uncertainty have typically used category distributions for which the level of uncertainty was irrelevant for optimal behavior (2, 3, 6, 8). For example, in a classic task, observers categorize the direction of motion of a set of dots coherently moving to the left or to the right, in the presence of distractor dots moving in random directions (8). Regardless of the level of sensory noise corrupting the brain’s measurement of the net motion direction, the optimal decision is simply to report whether this measurement was to the right or to the left. In other words, applying a fixed decision boundary to a scalar estimate is optimal in this task; no knowledge of uncertainty about motion direction is needed. In cognitive models of categorization, dynamic decision boundaries have been invoked to explain a broad range of phenomenona, including sequential effects (9, 10), context effects (11), and generalization (12). However, these studies limited themselves to fixed levels of sensory noise and were not able to demonstrate optimality of behavior. Thus, a dichotomy exists: perceptual models are often normative and describe behavior in tasks with variable sensory uncertainty but trivial category distributions, whereas cognitive models examine more complex forms of categorization but are typically nonnormative and ignore the role of sensory uncertainty.

Here, we attempt to connect these domains using a visual categorization task in which sensory noise is varied unpredictably from trial to trial. Our simple experimental design allows us to determine how observers should adjust their decision boundaries to achieve optimal performance; thus, our approach is normative. We found that humans and monkeys do adjust their decision boundaries from trial to trial according to sensory uncertainty. We also constructed a biologically inspired neural network model that can perform near-optimal, uncertainty-based adjustment of decision boundaries. Thus, we offer both a computational and a mechanistic account of brain function in a task in which trial-to-trial sensory uncertainty drives decision boundary dynamics.

Results

Task.

Human and monkey observers categorized the orientation of a drifting grating. The two categories (C = 1, 2) were defined by Gaussian probability distributions with the same mean (defined as 0°) and different SDs, denoted by σ₁ and σ₂ for categories 1 and 2, respectively (Fig. 1 A and B). As in related tasks (13, 14), the overlap of these distributions introduces ambiguity: a given orientation can come from either category, and therefore, categorization performance cannot be perfect even in the absence of sensory noise. Observers were trained using high-contrast stimuli and trial-to-trial feedback. During testing, contrast was varied from trial to trial to manipulate sensory uncertainty. Human observers did not receive trial-to-trial feedback during testing.

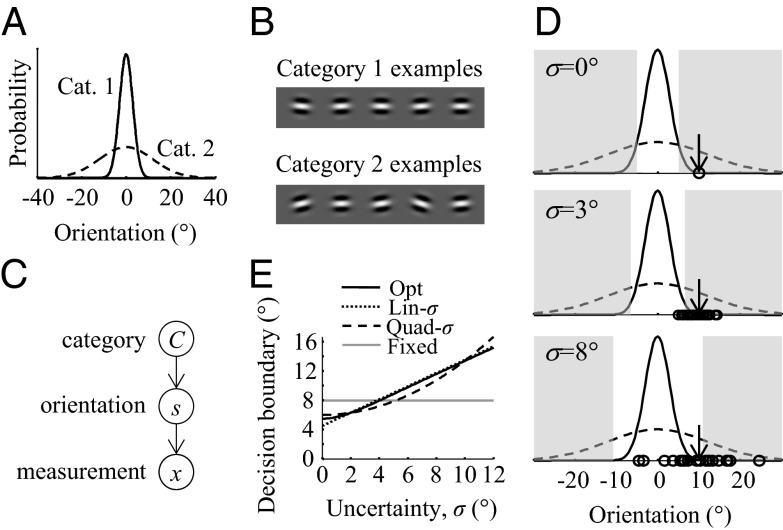
Fig. 1.

Task and models. (A) Probability distributions over orientation for Categories 1 and 2. The distributions have the same mean (0°) but different SDs (σ₁ = 3° and σ₂ = 12°; for Monkey L, σ₂ = 15°). (B) Sample stimuli drawn from each category. (C) Generative model of the task (see text). (D) A completely certain (σ = 0°) optimal observer would set the decision boundaries ±k at the intersection points of the two category distributions (black curves). The shaded areas indicate where the optimal observer would respond Category 2. When sensory noise is larger, not only will the measurements (open circles) be more variable for a given true orientation (arrow), but the optimal observer will also move the decision boundaries to larger values. In the experiment, noise levels are interleaved. (E) Decision boundary as a function of uncertainty level under four models: optimal, linear (example with k₀ = 4.5° and σ_p = 5°), quadratic (example with k₀ = 6° and σ_p = 9°), and Fixed (example with k₀ = 8°).

Theory.

The statistical structure of the task, also called the generative model, contains three variables (Fig. 1C): category C, stimulus orientation s, and measurement x. On each trial, C is drawn randomly and determines whether s is drawn from the narrow Gaussian, p(s | C = 1) with SD σ₁ or the wide Gaussian, p(s | C = 2) with SD σ₂. We assume that on each trial, the true orientation is corrupted by sensory noise to give rise to the observer’s measurement of orientation, x. We denote by p(x | s) the probability distribution over x for a given stimulus orientation s. We assume it to be Gaussian with mean s and SD σ (6). This SD is experimentally manipulated through contrast.

On a given trial, the observer uses the measurement x to infer category C. An optimal observer would do this by computing the posterior probability distribution over category, denoted p(C | x), which indicates the degree of belief that the category was C, based on x. It is convenient to express the posterior in terms of the log posterior ratio, d, which is, using Bayes’ rule, the sum of the log likelihood ratio and the log prior ratio

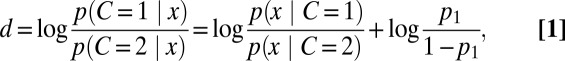where p₁ is the observer’s prior belief that C = 1. The absolute value of d is one possible measure of decision confidence. The difficulty in computing the category likelihood p(x | C) is that the stimulus s that caused x is unknown. The optimal observer deals with this by multiplying, for every possible s separately, the probability that the observed x came from this s with the probability of this s under the hypothesized category, and finally summing over all s

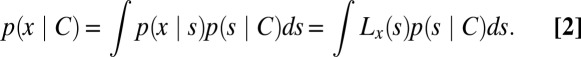Here, we use the notation L_x(s) to denote the likelihood of a stimulus value s based on a measurement x, L_x(s) = p(x|s). The width of this function, also σ, measures sensory uncertainty (Fig. 1E). Thus, Eq. 2 reflects the combination of sensory information, L_x(s), with category information, p(s | C). An integral over a hidden variable, as in Eq. 2, is known as marginalization and is a central operation in Bayesian computation (15–18). A straightforward calculation gives (SI Text)

where 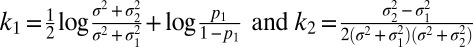. The decision strategy that maximizes accuracy is the maximum-a-posteriori (MAP) read-out, i.e., to report the value of C for which p(C | x) is larger. This rule is equivalent to reporting category 1 when d is positive, or in other words, when 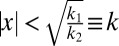. Thus, the optimal observer reports category 1 when the measurement lies within the interval from −k to k and category 2 otherwise. Critically, the optimal boundary or criterion k depends on the sensory uncertainty σ: when evidence is uncertain, the optimal observer is more willing to attribute measurements far away from zero to category 1 (Fig. 1D). This effect, which reflects the intuition of the friend recognition example, is a direct consequence of the shape of the category distributions. We consider two variants of the optimal model: one in which p₁ = 0.5, reflecting the experimental statistics (which we call the Opt model), and one in which p₁ is a free parameter (Opt-P model).

The main alternative to the optimal model is one in which the observer uses a fixed decision boundary (Fixed model). Then, the decision rule is |x|< k₀, with k₀ a constant.

Of course, the optimal model is not the only possible model in which the observer takes into account uncertainty on a trial-to-trial basis, even when we restrict ourselves to decision rules of the form |x| < function of σ. As a first step in exploring this model space, we test all linear functions of σ (we call this model Lin-σ): the observer uses the rule 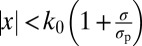. We also test a model in which the observer applies a fixed boundary not to the measurement x but to the MAP estimate of the stimulus, 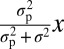, obtained under a Gaussian prior with mean 0 and SD σ_p. The decision rule is then 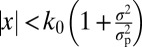. We call this the Quad-σ model (Fig. 1E). In all models except for the Fixed model, the observer takes into account the trial-to-trial level of sensory uncertainty; these models therefore describe probabilistic, but not necessarily optimal, computation (19).

In each model, we describe the relationship between noise variance σ² and contrast c (expressed as a proportion, not as a percentage) as a power law with a baseline, σ²(c) = (αc)^–β + γ, and include a lapse rate λ to account for random guesses and unintended responses (20). The Opt model has four free parameters (α, β, γ, and λ), Opt-P and Fixed each have one more (p₁ and k, respectively), and Lin-σ and Quad-σ each have two more (k and σ_p). Thus, Lin-σ and Quad-σ can be considered more flexible models than Opt and Opt-P. Models are summarized in Table S1.

Behavioral Results.

We first obtained maximum-likelihood estimates of the model parameters (Table S2). To compare models, we then computed both the marginal log likelihood (using the Laplace approximation) and the Akaike information criterion (AIC) for each model and each subject (Materials and Methods).

Our goal was to determine whether observers take into account sensory uncertainty in setting their decision boundaries. Thus, we are interested in whether or not the Fixed model accounts better for the data than all probabilistic models. It did not for any human subject or either monkey, according to either measure (Table 1 and Table S3). Moreover, the differences between the best probabilistic model and the Fixed model were large; to illustrate, Jeffreys (21) considered a marginal log likelihood difference of more than log(30) = 3.4 very strong evidence. Subjects differed in which probabilistic model described their data best, with Opt, Opt-P, Lin-σ, and Quad-σ each winning for at least one human subject, according to either method. The data of monkey A were best described by Quad-σ and those of monkey L best by Lin-σ. These results suggest that observers use different and sometimes suboptimal strategies to incorporate sensory uncertainty information on a trial-by-trial basis, but no observer ignores this information.

Table 1.

Model comparison using log marginal likelihood for main experiment

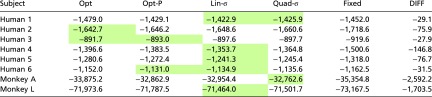Numbers are marginal log likelihoods obtained using the Laplace approximation. Shaded in green are the models whose values fall within log(30) of the value of the best model. The Fixed model is never among them. DIFF, difference between the Fixed model and the best probabilistic model.

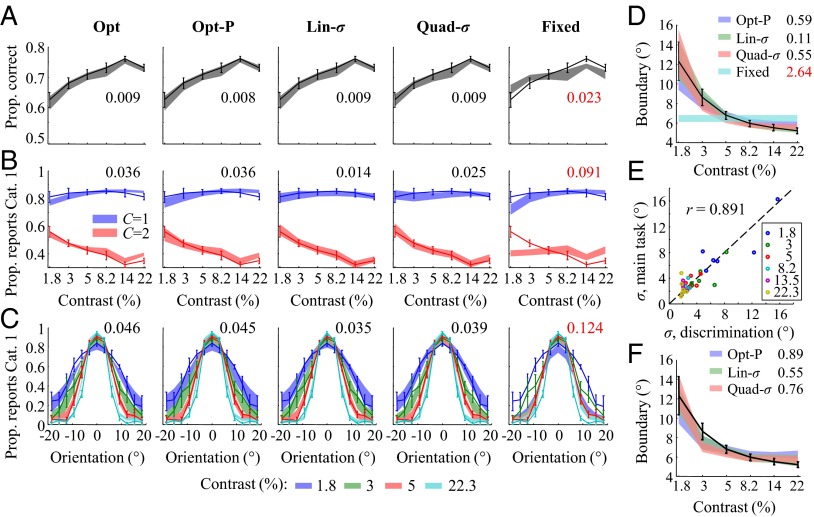
Fig. 2 shows three types of psychometric curves with corresponding model fits: proportion correct as a function of contrast (Fig. 2A), proportion of category 1 reports as a function of contrast and true category (Fig. 2B), and as a function of contrast and orientation (Fig. 2C). For each curve, the Fixed model provides a much worse fit than each of the probabilistic models (measured by RMSE), providing further indication that observers compute their decision boundaries in an uncertainty-dependent manner. In Fig. 2C, we observe that the curve widens as contrast decreases; because the Fixed model has a fixed decision boundary, it cannot account for this widening. Among the probabilistic models, the Lin-σ model fits best overall, in accordance with Table 1 and Table S3, but the differences are small. Although the Opt model provides a slightly worse fit, it should be kept in mind that in this model, the decision boundary is rigidly specified as a function of uncertainty σ: in contrast to the Lin-σ and Quad-σ models, the Opt model does not introduce any free parameters in the decision boundary function. In this light, the good fit of the Opt model is remarkable.

Fig. 2.

(A) Proportion correct versus contrast, with model fits. Model fits often do not look smooth because they were computed based on the orientations actually presented in the experiment, and those were drawn randomly (see SI Text). Here and elsewhere, error bars and shaded areas indicate 1 SEM, and numbers indicate root mean squared error between data and model means (red is worst). (B) Proportion “Category 1” responses versus contrast, separated by true category, with model fits. (C) Proportion “Category 1” responses versus orientation and contrast, with model fits. For visibility, not all contrasts are plotted. (D) Decision boundaries fitted separately at each contrast level (error bars: data; shaded areas: models). (E) Estimates of sensory uncertainty σ estimated from the categorization task against ones obtained from an independent orientation discrimination task; color labels contrast. (F) Decision boundaries predicted by three probabilistic models based on the uncertainty estimates from the discrimination task.

To agnostically estimate the uncertainty-dependent decision boundary humans use, we fitted an additional, flexible model, in which a separate boundary is fitted at each contrast level (SI Text). The decision rule is then 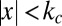, where k_c is the boundary at contrast c. The resulting estimates of k_c are plotted in Fig. 2D. We find a significant effect of contrast on k_c [repeated-measures ANOVA: F(5,25) = 12.4, P < 10⁻⁵]. The probabilistic models account for the trend in k_c much better than the Fixed model (in RMSE).

To confirm that the fitted values of sensory uncertainty σ in the probabilistic models are meaningful, we measured them in an independent experiment. The same six human observers performed a left/right orientation discrimination task (Materials and Methods) under the same contrasts and other experimental settings as in the categorization experiment. The estimates of σ obtained from the categorization task were strongly correlated with those obtained from the discrimination task (Fig. 2E; Pearson r = 0.89, P < 10⁻³). Using the estimates of σ from the discrimination task instead of those obtained from the estimates of α, β, and γ in the flexible model, although worse, still produces reasonable probabilistic model fits to the decision boundary function (Fig. 2F). Together, these results are evidence that the fitted values of σ in the main experiment are meaningful.

To ascertain that our results did not depend on the choice of vertical as the central orientation, we repeated the experiment using 45° clockwise from vertical instead. Results were consistent with the main experiment (SI Text and Fig. S1).

Monkey summary statistics are shown in Fig. 3 and Fig. S2. Again, the Fixed model did not account well for the data. For monkey L, Lin-σ provided the best fit (Fig. 3), and for monkey A, Quad-σ (Fig. S2). Taken together, our results indicate that both humans and monkeys adjust their decision boundaries from trial to trial based on sensory uncertainty, but use diverse and sometimes suboptimal strategies to do so.

Fig. 3.

As in Fig. 2, but for Monkey L.

Neural Network Results.

Our next goal is to provide a proof of concept that a biologically plausible neural network can adjust the decision boundary from trial to trial based on sensory uncertainty. We do this for the optimal model, because in this model, on each trial, the observer does not simply evaluate the decision rule, but also has a representation of the probability that the decision is correct. Although we did not explore it experimentally, knowing this probability is important for combining category information with information about the consequences of actions. For example, an animal might categorize a sound as being caused by the wind, but if the posterior probability of wind is 55% and that of predator is 45%, the best course of action would still be to run. Thus, for this animal, it is important to know whether the posterior probability of wind is 55% or 99%. In many forms of decision-making, observers must possess knowledge of posterior probability to maximize reward (3, 22–24). Although such a posterior probability is naturally given by the optimal model, it might also be possible to associate (suboptimal) posterior probabilities with the decision rules in the Lin-σ and Quad-σ models. However, this is not obvious and we leave it for future work.

To obtain a neural code, we replace the scalar observation x by the vector of spike counts in a population of orientation-tuned neurons, denoted r (Fig. 4A). We assume variability in the exponential family with linear sufficient statistics (Poisson-like variability) (25), which is consistent with the physiology of primary visual cortex (26, 27). Then, the distribution of r across trials for a given stimulus s can be described by

where g denotes the gain (mean amplitude) of the population, which is affected by contrast, and φ is an arbitrary function. Using the framework of probabilistic population coding (25), all available information about the stimulus is contained in the neural likelihood function, 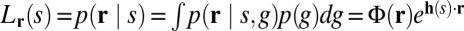(Fig. 4B), where Φ is easily expressed in terms of φ. We assume that h(s) is a quadratic function of s and thus can be written as 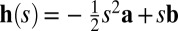, where a and b are constant vectors, so that the likelihood L_r(s) is an (unnormalized) Gaussian. The mean 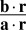and variance 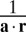of this likelihood function correspond to x and σ² in the behavioral model, respectively. In the special case of independent Poisson variability with Gaussian tuning curves, a is a vector whose entries are equal to the inverse squared widths of the neurons’ tuning curves, and 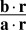is the center-of-mass decoder (28), the real-line analog of the population vector decoder (29) (SI Text). The log likelihood ratio over category can then be found from Eq. 3 by substituting the neural quantities for x and σ²

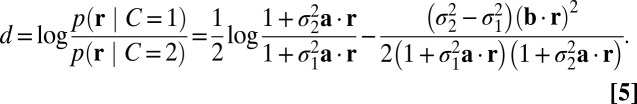Compared with Eq. 3, we have left out the log prior ratio; this is a constant shift and therefore easily implemented. A key aspect of Eq. 5 is that the log posterior ratio is a nonlinear function of r, in line with probabilistic population code implementations of other Bayesian computations that require marginalization (17, 18).

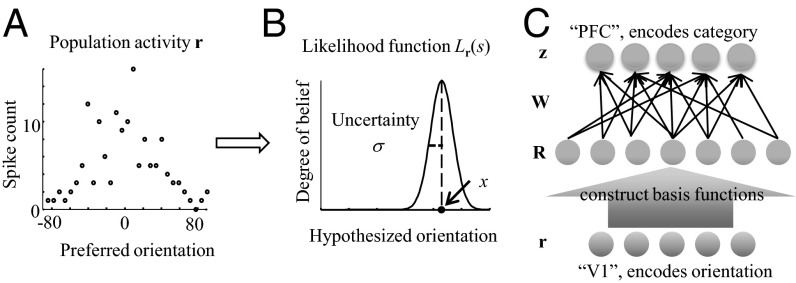
Fig. 4.

Network design for uncertainty-dependent categorization. (A) In probabilistic population coding, a population of neurons selective for orientation (single-trial activity shown on left) encodes a likelihood function over orientation on each individual trial (right). (B). The peak value of the likelihood function is the stimulus measurement (x), and its width represents sensory uncertainty (σ). The higher the gain (mean amplitude) of the population, the lower sensory uncertainty. (C) The network is feedforward and consists of three layers. The input layer represents orientation-tuned neurons. The intermediate layer computes a set of nonlinear basis functions of the activities in the first layer. The output layer computes linear combinations of these basis functions; its goal is to veridically encode the posterior over category on each trial, regardless of the level of sensory uncertainty.

We propose that categorization is performed by a feedforward neural network that is Poisson-like both in input and output (Fig. 4C). For concreteness, one could think of the input layer as primary visual cortex, encoding orientation, and of the output layer as prefrontal cortex, encoding category; however, the computation does not depend on these labels. The assumption that category is encoded by a Poisson-like output population z is supported by extant physiological findings in decision-making areas (30). The problem is then to find the mapping from r to z such that z encodes not just category, but the optimal likelihood of category. Poisson-like variability in the output can be described by a probability distribution analogous to Eq. 4, namely 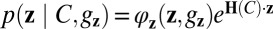. The log likelihood ratio over C encoded in z is then 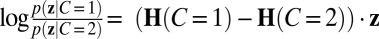, which we write shorthand as ΔH ⋅ z. To encode the optimal likelihood over category, this linear combination of output activity must equal the right side of Eq. 5.

We now approximate the optimal log likelihood ratio d by constructing a neural network consisting of a basis of nonlinear functions of input activity that are linearly combined to produce z (Fig. 4C). Our goal is to find a minimal and biologically plausible set of basis functions that can achieve near optimality. We allow operations that have been found in electrophysiology: linear, quadratic (i.e., multiplicative) (31–33), and divisive normalization (34, 35). The second term in Eq. 5 can already be constructed using these operations; we now study whether the first term can be approximated using functions of the same general form. Therefore, we consider a basis of functions that are quadratic in neural activity in the numerator and denominator: 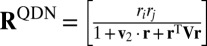, where QDN stands for “quadratic and divisive normalization.” The approximate decision variable is a linear combination of these basis functions.

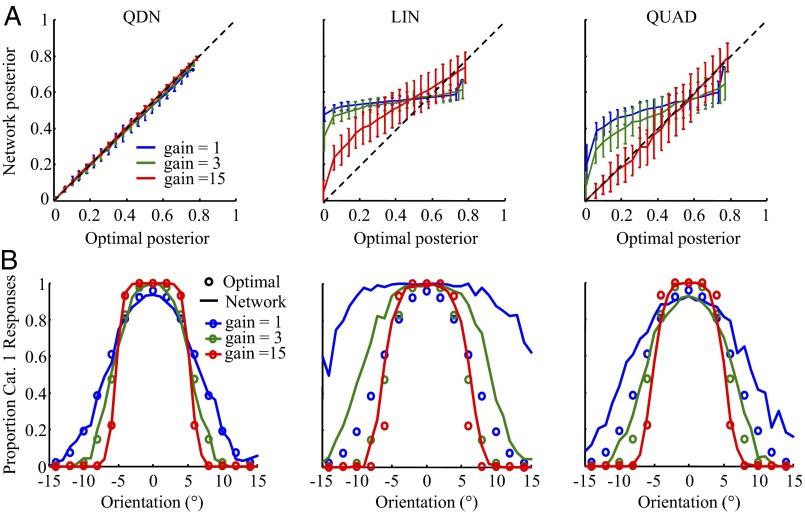
We simulated independent Poisson input with six values of gain. The network was trained using stochastic gradient descent (SI Text). After training, the network closely approximated the optimal posterior over category across a range of gains (Fig. 5A) and accurately reproduced the proportion reports of category 1 as a function of orientation of the optimal observer (Fig. 5B). Shannon information loss (Materials and Methods) was less than 0.5%. By comparison, we were unable to veridically approximate the posterior (Fig. 5A) or the psychometric curves (Fig. 5B) using a linear (LIN) network and a quadratic (QUAD) network. These networks had information losses of 42% and 21%, respectively, suggesting that the crucial operation for this categorization task is a quadratic operation combined with a divisive normalization that is itself also quadratic. We visualized the ability of the QDN network to approximate a highly nonlinear decision surface (Fig. S6).

Fig. 5.

Network results. (A) The posterior probability of Category 1 as decoded from the network versus the optimal posterior (binned), at different levels of input gain (sensory uncertainty), for a QDN network (trained for 10,000 iterations), a linear network (trained for 100,000 iterations), and a quadratic network (trained for 100,000 iterations). Error bars are SDs. Network information loss was 0.39%, 41.7%, and 21.0%, respectively; we verified that these values were close to the asymptotic ones. Note that the optimal posterior is bounded from above (see SI Text). (B) Proportion of Category 1 responses as a function of orientation for the optimal observer (dots) and the three networks (lines). The QDN network is the only of the three networks that performs well at each level of sensory uncertainty.

Discussion

We showed in a simple but nontrivial categorization task that both humans and monkeys adjust their decision boundaries according to the current level of sensory uncertainty. Despite its simplicity, the task contains both ambiguity and variable sensory uncertainty—essential elements of natural forms of categorization. Evidence that organisms possess and use trial-to-trial knowledge of sensory uncertainty is abundant in perception (18, 36, 37), but rare in tasks with nontrivial stimulus categories (38, 39). It might be worth studying the effects of sensory uncertainty on decision boundaries in more complex or more cognitive forms of categorization.

We found that some observers’ behavior is better described by simple suboptimal (but still probabilistic) decision rules than by the optimal rule. This finding raises the interesting question of whether these suboptimal rules are still associated with posterior distributions over category (and thus with a marginalization operation), but ones based on incorrect assumptions about the generative model.

We constructed a simple neural network that not only performs near-optimal categorization under varying levels of sensory noise, but also returns a good approximation of posterior probability. Divisive normalization, found in many species and brain areas, emerges automatically from our construction. This provides a normative justification for the operation (for other justifications, see ref. 35). In our framework, divisive normalization has an intuitive origin: it arises from the fact that in a Poisson-like probabilistic population code, the amplitude of the population pattern of activity encodes certainty. As a result, the stimulus estimate, x, must be computed using an amplitude-invariant operation. A representative example is the center-of-mass (or population vector) decoder, which computes the weighted sum of the neurons’ preferred orientations, with weights equal to the neurons’ spike counts; because the sum of the spike counts appears in the denominator, the center-of-mass decoder automatically contains a divisive normalization. Bayesian decision-making is performed by applying an operation to x and σ². In the present task, the decision variable is a quadratic function of x (Eq. 3), explaining why quadratic operations and quadratic divisive normalization appear in the neural implementation (Eq. 5).

Quadratic operations and divisive normalization have proven crucial for implementing a number of seemingly disparate forms of Bayesian inference (19, 20). At first sight, these frequent appearances might be surprising, because in the probabilistic population code implementation of cue combination, neither quadratic operations nor divisive normalization are needed (27). However, this is because cue combination is special in that optimal inference only involves the ratio x/σ², in which the divisive normalization is cancelled out to produce an operation linear in neural activity. However, this type of cancellation is the exception rather than the rule. In virtually every other form of Bayesian decision-making, the optimal decision variable will involve quadratic operations and divisive normalization when implemented with probabilistic population codes.

We make several predictions for physiology. First, we predict that populations of orientation-sensitive neurons in early visual cortex not only encode an estimate of orientation but also trial-to-trial information about sensory uncertainty and that this encoded sensory uncertainty correlates with the animal’s decision boundary as obtained from its behavior in the categorization task. Second, we predict that the activity of category-sensitive neurons, which might be found in prefrontal cortex (2) or lateral intraparietal cortex (LIP) (1, 5), is linearly related to the logarithm of the posterior probability ratio over category. This prediction is consistent with patterns found in LIP, where category probability can be reconstructed from a logistic mapping on neural activity (33). Third, we predict that sensory uncertainty decoded on each trial from early visual areas is propagated (along with the best estimate of orientation) to categorization neurons, so that including this decoded uncertainty as an explanatory factor should help to predict the activity of those neurons. Finally, we predict that if divisive normalization is selectively removed from a neural circuit involved in computing category, then the observer will become severely suboptimal in a way predicted by the QUAD network (Fig. 5). These predictions illustrate how a probabilistic, computationally [in the sense of Marr (40)] driven approach to categorization can guide the generation of hypotheses about neural mechanisms.

Materials and Methods

Details of all methods are provided in SI Text. Categories were defined by normal distributions with means 0° and SDs σ₁ = 3° and σ₂ = 12° (except for monkey L, for whom σ₂ = 15°). On each trial, a category was selected with equal probability. The stimulus was a drifting Gabor (50 ms for humans; 500 ms for monkeys) whose orientation s was drawn from the distribution of the selected category. Contrast was varied randomly from trial to trial. For monkeys, through training, the narrow distributon was associated with a red target and the wide distribution with a green target; the monkey reported category through a saccade to the red or the green target. Humans responded using a key press. Stimuli were delivered using Psychophysics Toolbox for Matlab (Mathworks). Models were fitted using maximum-likelihood estimation, implemented through a conjugate gradient method. Bayes’ factors were computed using the Laplace approximation. Neural networks were trained using a stochastic gradient descent on the Kullback-Leibler divergence between the true and the approximated posterior.