Infants Show Ratio-dependent Number Discrimination Regardless of Set Size

Abstract

Evidence for approximate number system (ANS) representations in infancy is robust but has typically only been found when infants are presented with arrays of four or more elements. In addition, several studies have found that infants fail to discriminate between small numbers when continuous variables such as surface area and contour length are controlled. These findings suggest that under some circumstances, infants fail to recruit either the ANS or object file representations for small sets. Here, we used a numerical change detection paradigm to assess 6-month-old infants’ ability to represent small values. In Experiment 1, infants were tested with 1 versus 3, 1 versus 2, and 2 versus 3 dots. Infants successfully discriminated 1 versus 3 and 1 versus 2, but failed with 2 versus 3. In Experiment 2, we tested whether infants could compare small and large values with a 2 versus 4 condition. Across both experiments, infants’ performance exhibited ratio dependence, the hallmark of the ANS. Our results indicate that infants can attend to the purely numerical attributes of small sets and that the numerical change detection paradigm accesses ANS representations in infancy regardless of set size.

INFANTS SHOW RATIO-DEPENDENT NUMBER DISCRIMINATION REGARDLESS OF SET SIZE

The numerical capacities of infants are frequently attributed to two core systems: an approximate number system (ANS) that represents large numbers in an imprecise fashion and an object file system that precisely tracks small numbers of objects (Dehaene, 1997; Feigenson, Dehaene & Spelke, 2004). Evidence for ANS representations in infancy comes from visual habituation and auditory head-turn behavioral studies and electrophysiological measures, in which brain and behavior measures are dependent on the ratio between the sets to be compared. For example, 6-month-old infants successfully dishabituate to large sets of visual or auditory stimuli that differ by a 1:2 ratio (e.g., 8 versus 16 dots or tones) but reliably fail to dishabituate to sets that differ by a 2:3 ratio (e.g., 8 versus 12 dots or tones; Lipton & Spelke, 2003; Xu, 2003; Xu & Spelke, 2000; Xu, Spelke & Goddard, 2005). A numerical change detection paradigm modeled after a procedure used by Oakes and colleagues to test infants’ working memory capacity (Ross-Sheehy, Oakes & Luck, 2003) confirms these findings by showing that 6-month-olds look longer to the numerically changing image stream as compared to a numerically nonchanging stream when both streams are presented simultaneously, and the numbers in the changing stream differ by at least a 1:2 ratio (Libertus & Brannon, 2010). Moreover, infants’ preference scores are graded as a function of numerical ratio providing further evidence for ratio-dependent number discrimination in infancy (Libertus & Brannon, 2010). Other evidence for ratio dependence in infant’s numerical discriminations comes from EEG studies. In one study, 7-month-old infants were habituated to a given numerosity and then presented with a novel numerical array, and spectral power in the EEG alpha band was modulated by the ratio between the habituated and novel numerosities (Libertus, Pruitt, Woldorff & Brannon, 2009). In another study, 6-month-old infants showed a mid-latency positivity (P500) that was modulated by numerical ratio for numerically large arrays (Hyde & Spelke, 2011).

Although adults (Cordes, Gelman, Gallistel & Whalen, 2001) and nonhuman animals (e.g., Brannon & Terrace, 1998) engage ANS representations for both large and small numerosities, ratio-dependent performance in infants often breaks down for small sets. For example, Feigenson and her colleagues found that 10- to 12-month-old infants reliably choose the larger of two food quantities when faced with 1 versus 2 or 2 versus 3 food items, but perform at chance when presented with 1 versus 4 or 2 versus 4 items (Feigenson, Carey & Hauser, 2002a). Likewise, 12- to 14-month-old infants succeed in a manual search task with 1 versus 2, 1 versus 3, and 2 versus 3, but fail to discriminate between 1 versus 4 and 2 versus 4 (Feigenson & Carey, 2003, 2005). These patterns of performance suggest that for small sets, infants may employ a representational system with a limited capacity that breaks down when more than three items have to be represented.

While search tasks with older infants suggest that they are able to use object file representations to precisely represent small sets of up to three items, studies with younger infants (≤7 months) suggest that they may be completely unable to discriminate between small arrays on the basis of number. Although infants at this age show precise smallnumber discrimination when number is confounded with other perceptual variables (e.g., Feigenson, Carey & Spelke, 2002b) or when numerical information is provided in multiple modalities (e.g., Jordan & Brannon, 2006; Wynn, 1996), discrimination often breaks down when infants must rely only on visually presented numerical information. Most studies that have investigated small-number discrimination in young infants have pitted number against continuous variables such as surface area in an attempt to determine which dimension is more salient to infants (e.g., Clearfield & Mix, 2001; Feigenson et al., 2002a). For example, infants have been habituated to arrays of either 1 or 2 objects (Feigenson et al., 2002b) or 2 or 3 objects (Clearfield & Mix, 2001) of a constant size and then tested with either the familiar number of objects with a novel size or a novel number of objects with the familiar size. In those studies, infants dishabituated only to changes in object size and not to changes in object number (but see Cordes & Brannon, 2009). Furthermore, when surface area was controlled during habituation, infants failed to dishabituate to the novel numerosity at test (Feigenson et al., 2002b). Similarly, with the visual habituation paradigm when continuous extent is varied throughout habituation, 6-month-old infants fail to discriminate 1 versus 2 and 2 versus 4 dots (Xu, 2003; Xu et al., 2005). Together, these studies provide little evidence that young infants can recruit either object files or ANS representations for visually presented small sets.

Physiological recordings provide some evidence that young infants process small and large numbers differently. When 6-month-old infants viewed arrays containing alternating large numbers of elements, a mid-latency positivity (P500) was modulated by the ratio between the number of elements in the arrays. In contrast, when viewing arrays containing small numbers of elements, infants displayed an earlier positivity (P400) that was modulated by the absolute value of the number of elements in the array, which is suggestive of object file representations (Hyde & Spelke, 2011). In addition, although looking time measures suggest that 7-month-olds are unable to discriminate between visual arrays containing two and three objects, differences in heart rate measures of attention suggest that infants can discriminate these values, even if they are not able to explicitly demonstrate this competence (Brez & Colombo, 2011).

Thus, it is unclear how 6-month-old infants represent small numerical values. Although behavioral data provide little evidence that young infants attend to the numerical property of small sets, physiological data suggest that they may rely on object file representations for small values and ANS representations for large values, much like older infants. Here, we tested 6-month-old infants’ small-number discrimination using the numerical change detection paradigm to determine whether the ratio-dependent performance seen with large values would also be present for small numerical sets (Libertus & Brannon, 2010).

EXPERIMENT 1

Experiment 1 investigated 6-month-old infants’ ability to discriminate small values when non-numerical continuous variables were carefully controlled. Infants were tested with 1 versus 3 dots, 1 versus 2 dots, or 2 versus 3 dots.

Method

Participants

Sixty 6-month-old infants participated (mean = 6 months 4 days, range, 5 months 13 days–6 months 19 days, 33 female), with 20 infants assigned randomly to each of three conditions. Data from 13 additional infants were excluded due to fussiness (n = 8), failing to look at both screens during a trial (n = 4), or because their preference scores were more than two standard deviations away from the group mean (n = 1). Parents gave written informed consent to a protocol approved by the local institutional review board.

Design

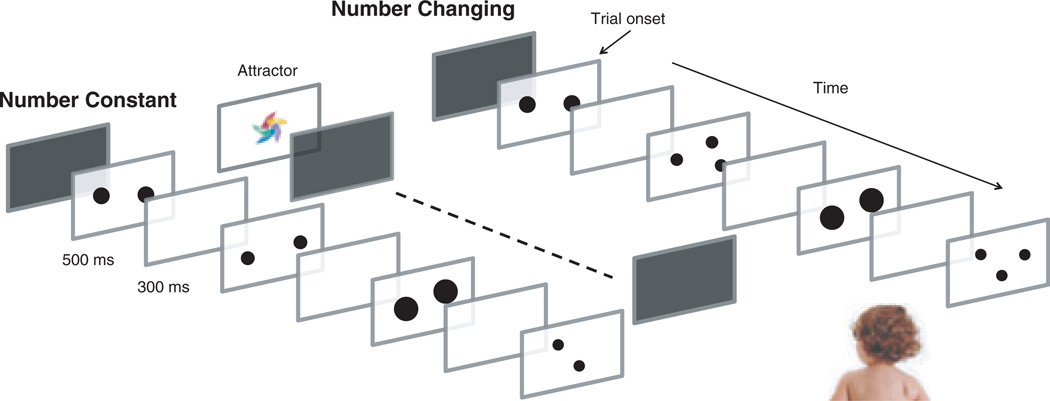
Infants were randomly assigned to one of the three conditions. In all three conditions, infants were shown two streams of images, one on each of two peripheral monitors (Figure 1). In each condition, one of the image streams contained arrays that alternated in the number of elements (changing stream), while the other image stream displayed arrays with a constant number of elements (constant stream). The conditions varied only in the number of elements presented in the changing and constant streams. In the 1 versus 3 condition, the changing stream contained 1 and 3 elements in alternation and the constant stream contained either 1 or 3 elements. In the 1 versus 2 condition, the changing stream contained 1 and 2 elements in alternation and the constant stream contained either 1 or 2 elements. In the 2 versus 3 condition, the changing stream contained 2 and 3 elements in alternation and the constant stream contained either 2 or 3 elements. Half of the infants in each condition saw the larger value in the constant stream, while the other half of the infants saw the smaller value (e.g., in the 1 versus 3 condition, half of the infants saw 1 dot in the constant stream, while the other half saw 3 dots).

Figure 1.

Schematic of the experimental design. The constant stream (left) shows images with the same number of dots each time (e.g., 2), whereas the changing stream (right) alternates between two different numerosities (e.g., 2 and 3).

Stimuli

The image streams consisted of arrays of dots presented for 500 ms followed by 300 ms of blank screen. The constant image stream always contained images with the same number of dots, while the changing image stream contained images with an alternating number of dots. Every other image across both streams was identical. One-third of the images across both streams were matched for cumulative surface area, one-third were matched for cumulative contour length, and one-third were matched for individual element size. Cumulative surface area ranged from 3.14 to 24.6 cm², cumulative contour length ranged from 6.3 to 32 cm, and individual dot diameters ranged from 1 to 5.6 cm. Orthogonally, half of the images that differed in numerosity were matched on density. These manipulations ensured that the two image streams could only be differentiated based on number and not based on other continuous variables. In all conditions, the images in both streams varied in the configurations of the elements such that even the images in the constant streams varied perceptually.

Procedure

Infants sat either in a highchair or on their parents’ lap approximately 105 cm away from three 17″ computer monitors. At the beginning of each trial, the center screen played a colorful image to orient the infant’s attention toward the screens. Once the infant was looking at the center screen, the experimenter manually started the trial. Each infant was tested with four 60-sec trials. The side of the changing image stream alternated between the trials, and trial order was counterbalanced across infants.

Infants’ looking behavior was digitally recorded and coded offline by an experienced observer. A second observer re-coded 25% of the participants, and reliability between the observers was very high (r = .99).

Data analysis

For each infant, a preference score was calculated by subtracting the proportion of time spent looking at the constant stream from the proportion of time spent looking at the changing stream. Thus, a positive preference score indicates a preference for the changing stream and a preference score of zero indicates equal time spent looking at the changing and constant streams.

Results

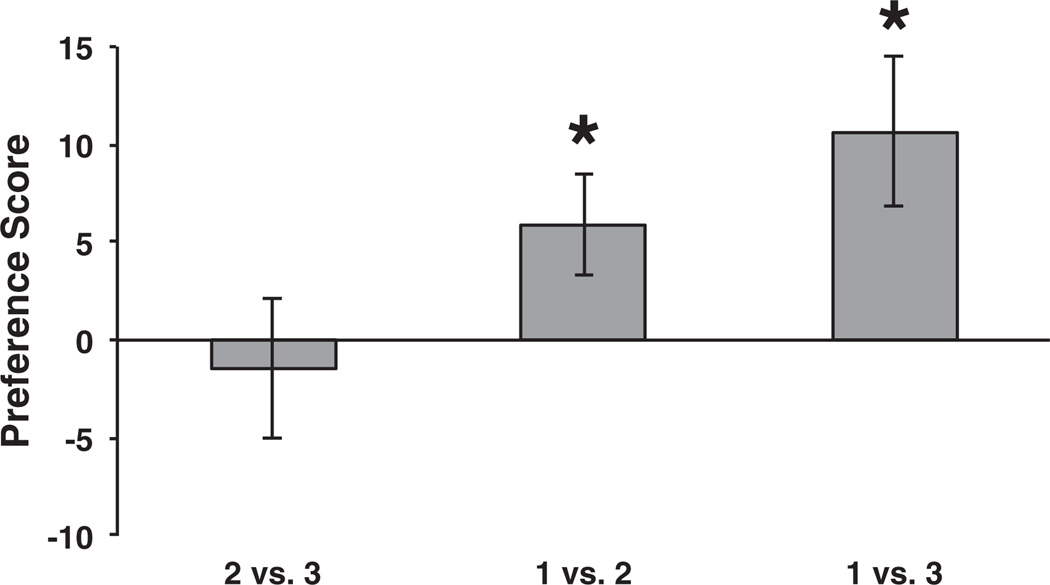
Infants successfully discriminated arrays of 1 versus 3 dots and 1 versus 2 dots, but failed to discriminate between arrays of 2 versus 3 dots (Figure 2). Infants’ mean preference scores for the changing stream were 10.7%, 5.9%, and −1.4% for the 1 versus 3, 1 versus 2, and 2 versus 3 conditions, respectively.¹

Figure 2.

Mean preference scores for each of the three conditions in Experiment 1. Infants looked significantly longer at the changing stream in the 1 versus 2 and 1 versus 3 conditions, but not in the 2 versus 3 condition. Error bars represent standard error.

One-sample t-tests were conducted to determine whether the group preference score for each condition was different from zero. In the 1 versus 3 condition, infants looked significantly longer at the changing stream compared with the constant stream [t(19) = 3.50, p < .005, r = .63]. Infants in the 1 versus 2 condition also looked significantly longer at the changing stream compared with the constant stream [t(19) = 2.27, p < .05, r = .46]. Infants in the 2 versus 3 condition, however, did not show a preference for the changing stream [t(19) = −0.39, p = .35, r = .09]. Fourteen of the 20 infants in the 1 versus 3 condition, 13 of the infants in the 1 versus 2 condition, and 9 of the infants in the 2 versus 3 condition looked longer at the changing stream.

A three-way ANOVA with condition (2:3, 1:2, 1:3), nonchanging numerosity (small or large), and side of the first changing image stream (left or right) as factors and preference score as the dependent measure revealed a main effect of condition [F(2, 48) = 4.98, p < .05, η²p = .17]. No other main effects or interactions achieved significance. Additionally, post hoc Tukey’s comparisons demonstrated that infants’ preference scores in the 1 versus 3 condition were significantly higher than the preference scores in the 2 versus 3 condition (p < .05), but preference scores in the 1 versus 2 condition were not significantly different from either of the other conditions. A linear regression performed across the three ratios indicated that preference scores increased with ratio (r = .34, p < .01).

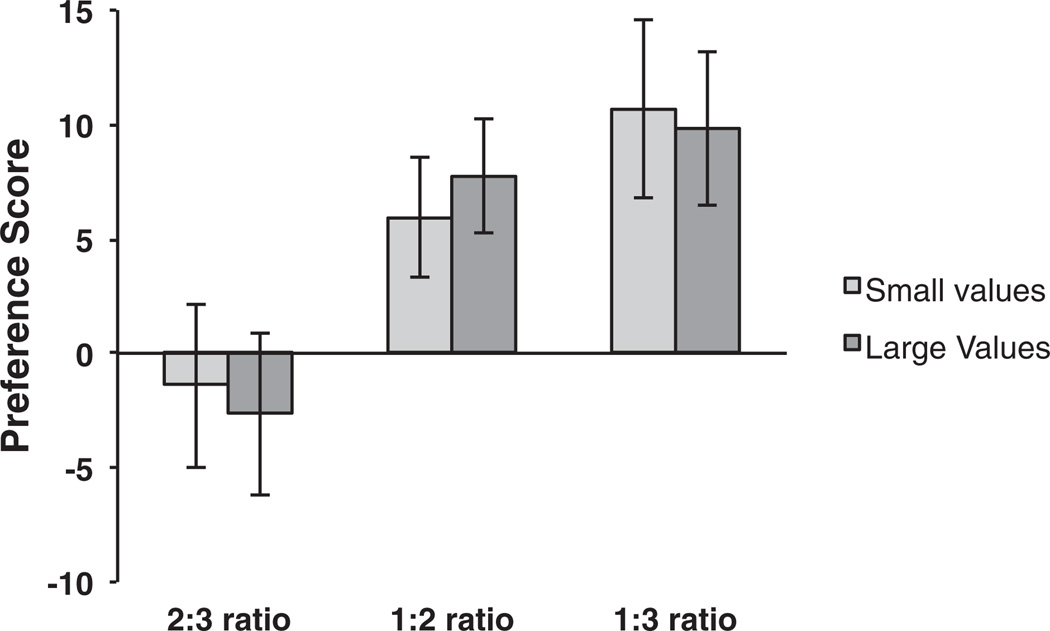
A final analysis compared data from this experiment with the large numerosity discrimination data (12 versus 18, 8 versus 16, and 6 versus 18) reported in Libertus and Brannon’s study (2010). A two-way ANOVA with ratio (2:3, 1:2, or 1:3) and set size (small or large) as factors and preference score as the dependent measure revealed a significant main effect of ratio [F(2, 102) = 7.94, p = .001, η²p = .14], no effect of set size, and no interaction between set size and ratio (Figure 3).

Figure 3.

Infants’ preference scores are modulated by ratio for both small and large values. Small-value data are taken from Experiment 1 of present study and large-value data from Libertus and Brannon (2010). Error bars represent standard error.

Discussion

The results of Experiment 1 demonstrate that 6-month-old infants are able to discriminate small arrays of elements on the basis of number. Furthermore, successful discrimination of arrays of 1 versus 2 dots and 1 versus 3 dots in conjunction with failure to discriminate 2 versus 3 dots suggests that they relied on the ANS. If infants recruited object file representations, they should have succeeded at all three comparisons including 2 versus 3 given that all of the values were below 4. In addition, comparing infants’ performance with small and large sets at the same ratios indicated that discrimination is consistently influenced by ratio and there is no effect of set size. Infants’ success with 1:3 and 1:2 ratio discriminations and failure with a 2:3 ratio are also consistent with the well-established limits of 6-month-olds’ numerical discrimination with large sets (e.g., Xu & Spelke, 2000). These results suggest that infants are able to represent both small and large numerosities using the ANS. Note that these results cannot be explained by constraints on infants’ memory capacity because at 6 months of age infants can represent only a single item in visual short-term memory (Ross-Sheehy et al., 2003). If infants were relying on short-term memory, they should be unable to discriminate 1 from 2 and 1 from 3 and should not show larger preference scores for 1 and 3 compared with 1 and 2.

An alternative interpretation of these results, however, could be that infants employed set-relational representations based on a conceptual distinction between singular and plural sets rather than the ANS. Evidence for this idea comes from the change in performance somewhere between 14 and 22 months of age in food-choice and manual search tasks. Feigenson and colleagues find that 10- to 14-month-olds perform at chance when discriminating 1 from 4, despite successful performance with 1 versus 2 or 3 in these tasks. This suggests that infants are using a system that cannot represent 4 and that they do not even represent 4 as being more than 1 (Feigenson & Carey, 2005; Feigenson et al., 2002a). However, at 22 months, infants succeed at 1 versus 4 in a manual search paradigm, suggesting that by this age, infants are able to represent 4 as a plurality (Barner, Thalwitz, Wood, Yang & Carey, 2007; Li, Ogura, Barner, Yang & Carey, 2009). Interestingly, representing the singular–plural distinction appears to come at a cost of more exact object representations, as infants in the same studies failed to differentiate between 2 and 4 objects and seemed to represent both arrays simply as pluralities. While it seems unlikely that set-relational representations could account for the results of Experiment 1 given that they have not been demonstrated in infants younger than 20–22 months of age, the data are consistent with this interpretation (Barner et al., 2007; Li et al., 2009).

Comparative research with rhesus monkeys demonstrates that task parameters, such as simultaneous versus successive item presentation, can influence whether object file or set-relational representations are engaged when discriminating between small sets of objects. Monkeys who watch food items placed sequentially into containers exhibited behavior indicative of object file representations, whereas monkeys who watched the food items placed all at once into the containers exhibited behavior consistent with set-relational representations (Barner, Wood, Hauser & Carey, 2008). A remote possibility is that the change detection paradigm, like the unified set condition in Barner et al.’s (2008) study, encourages infants to employ set-relational representations and inhibits object file or ANS representations. If this is the case, then infants may have succeeded in the 1 versus 2 and 1 versus 3 conditions because they successfully represented both 2 and 3 as plural sets larger than 1. In contrast, the 2 versus 3 condition would fail to elicit a significant preference score if both 2 and 3 were represented as plural sets (note, however, that this explanation cannot explain why infants’ discrimination showed a linear trend of increasing preference scores with ratio).

EXPERIMENT 2

In Experiment 2, we tested infants with a 2 versus 4 condition to determine whether infants’ performance in Experiment 1 resulted from ANS or set-relational representations. If infants recruit ANS representations during the change detection task with small numbers, then they should succeed at discriminating 2 versus 4 because they are capable of discriminating both small and large sets that differ by a 1:2 ratio. On the other hand, if infants recruit set-relational representations, they should fail to discriminate 2 versus 4 because both values are represented as plural sets.

Method

Participants

Twenty six-month-old infants participated (mean age = 6 months 0 days, range, 5 months 14 days–6 months 15 days, 9 females). An additional six infants were excluded due to not looking at both screens during a trial (n = 4), failure to complete the experiment (n = 1), or because their preference scores were more than two standard deviations away from the group mean (n = 1). Parents gave written informed consent to a protocol approved by the local institutional review board.

Design

The design, stimuli, and procedure were identical to Experiment 1 with the exception that the stimuli consisted of arrays of 2 and 4 dots. Cumulative surface area ranged from 6.28 to 25.12 cm², cumulative contour length ranged from 9.42 to 42.7 cm, and individual dot diameters ranged from 0.8 to 3.4 cm. A second observer re-coded 25% of the participants, and reliability between the observers was very high (r = .99).

Results and discussion

Infants’ mean preference score for the changing stream was 8.14%. Infants looked significantly longer at the changing stream compared with the constant stream [t(19) = 2.11, p < .05, r = .44; 12 of 20 infants showed this pattern].² A two-way ANOVA with nonchanging numerosity (small or large) and side of the first changing image stream (left or right) as factors and preference scores as the dependent measure revealed no significant main effects or interactions.

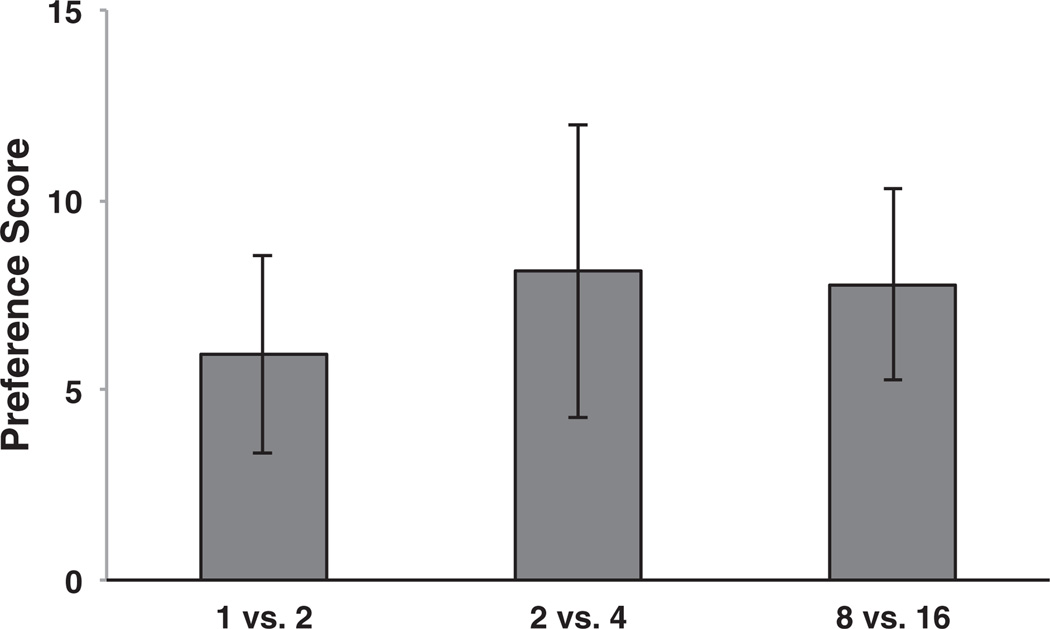
To compare infants’ performance on 2 versus 4 with their performance on exclusively small or large values at the same 1:2 ratio, we compared these data with data from the 1 versus 2 condition of Experiment 1 and the 8 versus 16 data from Libertus and Brannon’s study (2010) in a one-way ANOVA with set size (small, medium, or large) as the factor and preference score as the dependent measure. There was no effect of set size [F(2,53) = .147, p = .975, η²p = .006], indicating that infants’ discrimination of sets that differ by a ratio of 1:2 is not influenced by numerical magnitude (Figure 4).

Figure 4.

Infants can successfully discriminate arrays that differ by a ratio of 1:2 with small (Experiment 1), medium (Experiment 2), and large (Libertus & Brannon, 2010) numerical magnitudes. Error bars represent standard error.

Infants’ successful discrimination of 2 versus 4 supports the conclusion that infants recruit ANS representations throughout the range of small and large values and provides no evidence for object file or set-relational representations. The similarities in infants’ preference scores for 1 versus 2, 2 versus 4, and 8 versus 16 suggest that a single representational system, the ANS, is recruited both for small and large sets, and for sets that cross the small–large divide.

GENERAL DISCUSSION

The results of the present experiments demonstrate that 6-month-old infants are capable of making purely numerical discriminations for visually presented small sets and that discrimination is ratio dependent. Furthermore, analyses that included previously published data with the same procedure (Libertus & Brannon, 2010) revealed that preference scores increased linearly with the ratio between the two values in the changing stream regardless of the magnitude of the values. This convergent pattern of results for small and large set sizes suggests that infants can extend ANS representations to small values in the first year of life.

While the pattern observed in Experiment 1 is consistent with the ratio-dependent performance that is the hallmark of ANS representations, we reasoned that the results could also be consistent with the idea that infants used set-relational representations to distinguish singular sets from plural sets (Barner et al., 2007; Feigenson & Carey, 2005). To tease apart these possible explanations, we tested infants of the same age in a 2 versus 4 condition. Infants successfully discriminated 2 dots from 4 dots, looking longer at the changing stream regardless of the magnitude of the constant stream (2 or 4). Taken together, these results are best explained by ANS representations rather than object file or set-relational representations. If infants were recruiting object files, their performance should have been dictated by a maximum set size, allowing them to succeed at discriminating 2 from 3 but not 2 from 4. If infants were recruiting set-relational representations, they should have failed at discriminating 2 from 3 and 2 from 4 because all of those values should be represented as pluralities. However, infants failed at discriminating 2 from 3 and succeeded at discriminating 2 from 4. As predicted by ANS recruitment, infants’ performance was influenced by the ratio between the sets rather than set size or a singular–plural distinction.

Why have previous studies found young infants unable to discriminate small numbers while we found success? A critical difference between the present study and prior studies investigating infants’ small-number representations is the method used to assess numerical discrimination. We used a numerical change detection procedure that does not involve habituation or familiarization to a single numerical value but instead requires infants to detect numerical change in one visual stream. Why would this procedure be more likely to invoke the ANS than the habituation paradigm? One possibility is that there are different working memory demands in the two conditions. Hyde and Wood (2011) found that adults’ electrophysiological signatures of processing small numerical arrays were associated with both the ANS and object file representations depending on the working memory load of the task. When the working memory load was low, adults exhibited neural correlates of object file representations, whereas when the working memory load was high, they exhibited neural correlates of the ANS. The change detection paradigm, which was originally developed to assess infants’ working memory (Ross-Sheehy et al., 2003), may load infants’ memory and prohibit the recruitment of object files. Because the change detection paradigm presents infants with two rapidly changing streams of information, it is also much more dynamic than the habituation paradigm, which involves a single stream of images and longer presentation times for each image. In addition, to notice which stream is changing and which stream is constant, infants must maintain a representation of the previously displayed values in working memory and compare them with the currently displayed numbers. Hyde and Spelke (2011) similarly propose that differences in stimulus complexity may predict whether the ANS is invoked for small values or represented by object files. The ANS may only be recruited for small values when the stimuli are complex and prohibit parallel individuation. Further support for these hypotheses comes from the fact that infants can successfully discriminate between 2 and 4 moving groups of elements, whereas infants tested with static displays failed to discriminate 2 from 4 (Wynn, Bloom & Chiang, 2002; Xu, 2003). Movement of the elements in visual displays may increase the complexity of the displays and the working memory load, leading to the recruitment of the ANS.

In conclusion, the present experiments demonstrate that like adult humans and non-human animals, infants in the first year of life possess an ANS that is ratio dependent and operates over a seemingly unrestricted range of quantities. Other paradigms that involve active searching and tracking food items indicate that infants fail to recruit the ANS under some circumstances (Barner et al., 2007; Feigenson & Carey, 2003, 2005; Feigenson et al., 2002a; Li et al., 2009), and further research is needed to determine the conditions that elicit different types of numerical representations throughout development. Our results are consistent with the idea that while there may be factors that differentially inhibit the ANS in infants, small and large numbers are nevertheless represented along the same numerical continuum in infancy.