Abstract
Single-particle tracking (SPT) has been extensively used to obtain information about diffusion and directed motion in a wide range of biological applications. Recently, new methods have appeared for obtaining precise (10s of nm) spatial information in three dimensions (3D) with high temporal resolution (measurements obtained every 4ms), which promise to more accurately sense the true dynamical behavior in the natural 3D cellular environment. Despite the quantitative 3D tracking information, the range of mathematical methods for extracting information about the underlying system has been limited mostly to mean-squared displacement analysis and other techniques not accounting for complex 3D kinetic interactions. There is a great need for new analysis tools aiming to more fully extract the biological information content from in vivo SPT measurements. High-resolution SPT experimental data has enormous potential to objectively scrutinize various proposed mechanistic schemes arising from theoretical biophysics and cell biology. At the same time, methods for rigorously checking the statistical consistency of both model assumptions and estimated parameters against observed experimental data (i.e. goodness-of-fit tests) have not received great attention. We demonstrate methods enabling (1) estimation of the parameters of 3D stochastic differential equation (SDE) models of the underlying dynamics given only one trajectory; and (2) construction of hypothesis tests checking the consistency of the fitted model with the observed trajectory so that extracted parameters are not over-interpreted (the tools are applicable to linear or nonlinear SDEs calibrated from non-stationary time series data). The approach is demonstrated on high-resolution 3D trajectories of single ARG3 mRNA particles in yeast cells in order to show the power of the methods in detecting signatures of transient directed transport. The methods presented are generally relevant to a wide variety of 2D and 3D SPT tracking applications.
Keywords: single particle tracking, stochastic differential equations, diffusion, goodness-of-fit testing, 3D microscopy
Introduction
Optical microscopy can now provide high resolution 2D and 3D measurements of individual biomolecule motion in living cells. The ability to track biomolecules at single-molecule resolution in their native environment permits researchers to address open questions in various fields, e.g.1–12. Time-ordered 3D measurements can assist in providing unambiguous physical interpretations regarding how tagged particles dynamically interact with structures in living cells1,3,10,13. Analyzing transient 3D kinetic phenomena in live cell measurements poses new and exciting statistical modeling challenges.
Many early single particle tracking (SPT) analysis methods aimed to quantify single-molecule kinetics by assuming relatively simple stochastic motion models which leveraged either mean square displacement (MSD) methods14–18 or autocorrelation-based (AC) techniques19 to extract model parameters summarizing the experimental data. AC methods (time or Fourier domain) often require signals to be stationary; this stationarity assumption can be problematic in several single-molecule situations where the dynamics changes in real time20–22. Classic MSD methods lose valuable temporal information due to the aggregation of lag information from different time points and also require researchers to select heuristic tuning parameters16.
Improvement in experimental resolution and problems with the aforementioned analysis approaches have motivated new SPT analysis techniques. For example, Ref.23 presents a new scheme for systematically selecting the “time-lag” parameter required for extracting both the diffusion coefficient and localization precision (or measurement noise) from an MSD curve. In addition, more statistically motivated methods have been proposed which aim to make better use of time ordered observations. These include maximum likelihood24 and Bayesian estimation strategies25,26. For example, Ref.25 demonstrated Bayesian techniques accounting for 2D force interactions in membrane diffusion simulations. These prior efforts, though insightful, did not rigorously account for the statistical effects of a priori unknown measurement noise. The measurement noise estimation issue has been discussed recently20,27; likelihood-based procedures for extracting parameter estimates treating measurement noise in simple SPT diffusion-only models (e.g., models neglecting 2D/3D force) have been recently introduced28.
Moreover, existing SPT analysis methods still encounter three serious technical problems: (i) Methods often require researchers to subjectively specify the types of motion followed by the experimental data. (ii) Many existing methods do not utilize statistically justified methods for checking the consistency of assumed motion models against experimental single-molecule SPT data. (iii) Even if modeling assumptions are consistent, estimation techniques typically assume that the parameters of the motion model are not slowly changing over time in a single trajectory.
With respect to (i), qualitative motion types like “directed”, “corralled (or confined)”, and “diffusive” are often assumed. SPT researchers typically classify the motion type describing the experimental data and then extract parameters estimates depending on the assumed motion type (various heuristic criteria are used to guide motion classification, e.g.10,29). It would be advantageous to consider an estimation scheme which nests all popular SPT models as special cases (i.e., the experimental data “speaks for itself”) while also permitting more flexibility in accounting for different types of 2D or 3D forces. Regarding (ii), a parameter estimate and model can be extracted from any data set, but this does not imply that the estimate and model reflect the actual experimental situation. Before one worries about extracting optimal parameter estimates, the consistency of modeling assumptions compared to data should be checked; the value of a parameter estimate predicated on an inapplicable model is not high. This article demonstrates how goodness-of-fit hypothesis testing (i.e., statistical methods for directly determining if an observed time series is consistent with a given model) can assist in analyzing SPT data. Regarding (iii), it is well known that the local micro-environment and/or properties of the underlying biomolecule can cause the diffusion coefficient to change over time16,30,31. A wide variety of anomalous diffusion approaches have been proposed to handle SPT trajectories experiencing changing effective diffusion coefficients, e.g.32,33, but such approaches still induce temporal averaging of increments which can hide important transient single-molecule kinetic phenomena (quantitative examples are provided in the Results and SI). Likelihood ratio24 and Bayes factor-based techniques34 for identifying abrupt state changes have been proposed for special case situations where the dynamic models fall into one or several discrete states, but these methods assume that one possesses a priori reliable statistical information describing the system’s stochastic motion and that the states can be discretely classified. In the next section, we discuss other approaches aiming to extract kinetic information from single-molecule trajectories20,21,25–28,32,34–38 and contrast these approaches to our methods which offer solutions to items (i–iii).
To motivate our work, consider the following example. Suppose one is interested in tracking a complex molecular aggregation process, e.g., ribonucleoprotein complex formation39, where the aggregate’s radius changes in a non-trivial fashion over the course of an experimental trajectory. If the effective hydrodynamic radius of the aggregate containing one or more fluorescently tagged particles has a “state change” that is effectively continuous (i.e., the radius length changes by small amounts between adjacent frames but the radius changes appreciably over multiple frames), then many existing SPT approaches would encounter serious technical difficulties in both parameter estimation and detecting state changes. Worse yet, the estimated parameters of traditional SPT models would be of questionable quality since the assumptions behind the models are inconsistent with the molecular motion underlying the experimental data.
In order to demonstrate how our proposed approach can provide both estimation and goodness-of-fit hypothesis testing in scenarios where the system dynamics are inconsistent with traditional SPT models and/or parameters are time varying, we analyze 3D ARG3 mRNA trajectories measured in live Saccharomyces cerevisiae 10. This system was selected because only one or two copies of the mRNA are present in the cytoplasm at any given time10,40,41, thus associating a fluorescent signal between different image frames measured by the microscope with a single molecule is straightforward. Simulations and experiments demonstrate what types of 3D dynamical interaction effects can be extracted from individual trajectories. We also discuss how ideas ported from other disciplines42–47 can help to identify signatures of subtle molecular interactions in biophysical measurements that are not explicitly accounted for in models commonly used in analyzing SPT data.
Theoretical Methods
Qualitative SPT modeling background
In single-molecule studies, the emphasis is on avoiding ensemble averaging since each experimental trajectory is associated with different unresolved latent features (e.g., different conformational molecular degrees of freedom or varying local micro-environments). The unresolved latent features often induce substantial “heterogeneity” in the dynamics7,10,16,48,49. No pair of trajectories are exactly alike, but researchers in biophysics and cell biology are interested in accurately quantifying / understanding this heterogeneity7,10. Therefore, it is important to consider methods that cannot only estimate models on a trajectory-wise basis36,50, but it is also critical to check the consistency of a estimated model against the single-molecule trajectory used to obtain the parameter estimates36,51. Goodness-of-fit testing is crucial since inferring model parameters that have a biophysical interpretation requires researchers to both (1) make testable assumptions about the effective dynamical models and (2) develop schemes for estimating the parameters respecting the complex nature of effective thermal and measurement noise associated with the experimental data. The methods employed in this study permit trajectory-wise goodness-of-tit testing and also check all distributional dependence assumptions43 implied by an assumed model against observed experimental data directly. The methods utilized are general43,52 and are not constrained to linear or Gaussian dynamics; advantages of the goodness-of-fit approach are discussed in the Methods, SI, and elsewhere51.
The techniques presented not only handle trajectory to trajectory heterogeneity, but can also identify transient dynamical phenomena occurring in a single trajectory (e.g., an unobserved conformational degree of freedom may be changing in an appreciable fashion over the course of a single trajectory measurement). The trajectory-wise goodness-of-fit testing employed is crucial for identifying these phenomena. Problems other popular methods (e.g., MSD-based analyses) encounter when the dynamical parameters of the system slowly change over time in a single trajectory are discussed and demonstrated using simulation and experimental data in the main text and SI.
Since checking the consistency of fitted stochastic models against experimental SPT data is of paramount importance to any quantitative scientific SPT study, it may be surprising that such methods are not widely utilized in SPT data analysis. A major reason underlying why the goodness-of-fit testing issue has not been thoroughly studied in SPT works is that the time series coming from these experiments pose technical challenges (e.g., non-stationary signals with potential non-linear dynamics on top of measurement noise corrupting state observations). Recent research emerging from time series analysis and econometrics are able to address some long-standing technical challenges that previously complicated goodness-of-fit testing associated with complex, transient (i.e., non-stationary) 2D or 3D signals in the past43–47. The SI provides simulation examples showing how standard time series diagnostics not checking all distributional assumptions can fail in situations relevant to our SPT study.
Other related works
The methods presented here overlap in goals with some other recent efforts aiming to analyze the time series of single-molecule experimental data. In this subsection, we briefly summarize some related efforts. The research closest in spirit to the 3D SPT work presented here can be found in Refs.20,21,36 where 1D linear and nonlinear stochastic differential equations (SDEs) are estimated and trajectory-wise goodness-of-fit tests checking all model assumptions43 are applied to experimental single-molecule trajectories subjected to external force manipulation. Bayesian estimation techniques aiming to achieve efficient parameter estimation in situations where an accurate 2D SDE model is assumed known a priori have recently been developed and demonstrated on simulated SPT trajectories25. Methods falling under the category of “p–variation” methods have been proposed for estimating and testing 1D SPT data in situations where experimental measurement noise is small compared to inherent thermal fluctuations32. Refs.27,28 demonstrate various approaches for estimating simple 1D SDE models in the presence of measurement noise; these works also provide discussions outlining the advantages of applying likelihood-based methods to estimate SDE parameters. Ref.26 applied hidden Markov models to characterize complex diffusion patterns in situations where accurate SDE models describing experimental data were assumed known a priori; the technique showed promise for quantifying complex protein diffusion patterns in live bacterial cell lines.
In this work, 3D SDE models are estimated from experimental data, measurement noise is inferred using MLE methods, the methods allow one to resolve effectively continuous changes in SDE parameters over time, we employ a flexible modeling framework imposing relatively few a priori assumptions about the particle’s dynamics (popular SPT models, such as directed and confined diffusion, are covered within a single parametric framework10,29), and the consistency of the assumed/fitted model is checked directly against individual experimental trajectories in a trajectory-wise fashion (i.e., goodness-of-fit hypothesis tests checking the consistency of all model assumptions can be carried out using only one experimental trajectory). No other published SPT work provides a framework allowing for all of these features (the 2D/3D goodness-of-fit testing accounting for measurement noise is not provided in any SPT work to our knowledge). Accounting for (and detecting) time changing parameters characterizing 2D and/or 3D SDE models, e.g., effective measurement noise that is changing significantly over time for a single trajectory, is another contribution of this work (other numerical approaches for quantifying effective continuous parameter changes in single-molecule trajectories are discussed in Ref.53).
In terms of other potential SPT modeling approaches, nonlinear filters (such as particle filters35 and interacting multiple model filters37) are tools that show promise when both measurement noise and particle dynamics are accurately known a priori, but these nonlinear filtering techniques do not address goodness-of-fit or parameter estimation issues directly. For situations expanding the utility of interacting multiple model filters to scenarios where model parameters and/or priors are not known a priori, “non-parametric” Bayesian methods show some promise38. However, one still must make some assumptions regarding the statistical nature of the dynamics and measurement noise; furthermore the approach used in Ref.38 does not address the goodness-of-fit question. More broadly, Bayesian methods (like those in Refs.25,26,34,38) by themselves cannot determine if the assumed dynamical models are statistically consistent with experimental data. For example, it is possible that the Bayesian modeler assumes a collection of models all having Gaussian measurement noise with some fixed variance, but the true data generated by the actual experimental situations is Poisson distributed with a time varying intensity (or worse yet, draws may come from a time-varying unknown distribution); Bayesian model selection54 approaches would attempt to find the best model in the assumed model class (e.g., parametric models assuming a Gaussian measurement noise process). Once the best model is in-hand, uncertainty estimates can be extracted from the computed posterior distribution; this uncertainty depends not only on the “best” model, but also on the real data and the assumed prior distribution which may also be inconsistent with real experimental data. One can extract a single parameter estimate from the posterior and then apply frequentist goodness-of-fit testing51, but the assumed prior may substantially affect the results.
The methods used here aim to detect any inconsistency of the data with modeling assumptions whereas a pure Bayesian method cannot detect that the observed data exhibits features outside of the class of dynamical models considered51. We should explicitly point out two limitations of the goodness-of-fit methods advocated herein: (i) rejection of a fitted model does not specifically point out what is incorrect about the model and (ii) some modeling assumptions may be incorrect (e.g., the diffusion coefficient is state or position dependent20) but there is not enough evidence in the data (i.e., the sample size is too small) to reject the null hypothesis. The power of the testing procedure depends on the true data, the assumed model, and the data sampling frequency43. Despite these limitations, the formal goodness-of-fit hypothesis testing machinery shows great promise in quantitatively and more objectively studying experimental single-molecule data.
At a high-level, our method processes individual experimental trajectories by 1) selecting parametric SDE model(s); 2) dividing the trajectory into disjoint time windows; 3) within each window extract the MLE vector summarizing the forces, diffusion, localization precision in that local time window for each model under consideration; 4) checking all of the statistical assumptions implicit in the assumed model against data via goodness-of-fit tests; and 5) if the goodness-fit-test are not rejected and multiple models are under consideration, select a parametric model via model selection criteria (if rejection occurs, consider a new model class and repeating procedure).
General Stochastic Differential Equation (SDE) model considered
We consider estimation and statistical inference problems associated with an SDE of the form:
| (1) |
| (2) |
where the three dimensional position of the particle at time t is denoted by the vector rt ≡ (xt, yt, zt)T (the superscript denotes a matrix transpose). The subscript t is used to index time in the stochastic process. Bt represents a standard 3D Brownian motion process. The notation dBt is used as shorthand for an Ito55 stochastic integral (similarly for drt). The remaining terms (and their physical interpretation) in Eqn. 1 will be described in greater detail after additional notation is established. Stochastic effects inherent to SPT experiments, such as photon count uncertainty, prevent us from directly observing rt. The only quantity we can directly measure in the lab is denoted by ψ. This process is also indexed by time, e.g. ψti, but measurements are only available at discrete time points. The random variable εti represents one 3D measurement noise realization at time ti.
We use the notation εti ~
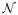 (0, R) to convey that εti is assumed to be distributed according to a mean zero multivariate Gaussian with covariance R. Using an R inconsistent with the value associated with an experimental trajectory (or assuming an incorrect measurement error distribution) may bias parameter estimates of physically interesting quantities. Motivated by these considerations, we estimate the inferred measurement noise from the observed data using likelihood methods. In SPT applications, R is often unknown a priori because the number of photons available for detection decreases during data collection. Furthermore, complex background fluorescence and other experimental artifacts make effective measurement noise difficult to predict and/or relate in a simple fashion to nominally detected photons27,56.
(0, R) to convey that εti is assumed to be distributed according to a mean zero multivariate Gaussian with covariance R. Using an R inconsistent with the value associated with an experimental trajectory (or assuming an incorrect measurement error distribution) may bias parameter estimates of physically interesting quantities. Motivated by these considerations, we estimate the inferred measurement noise from the observed data using likelihood methods. In SPT applications, R is often unknown a priori because the number of photons available for detection decreases during data collection. Furthermore, complex background fluorescence and other experimental artifacts make effective measurement noise difficult to predict and/or relate in a simple fashion to nominally detected photons27,56.
Linear SDE model considered
The specific model we consider is a linear SDE parameterized by a finite dimensional vector denoted by θ. The parameters contained in θ and the remaining terms in Eqns. 1 and 2 are defined by the following equations:
| (3) |
| (4) |
| (5) |
| (6) |
The collection of parameters to be estimated by the data will be denoted by θ ≡ (A, B, C, R). A is a 3D vector (i.e., A ∈ ℝ3). B, C, and R are 3 × 3 real matrices.
Physical interpretation of the SDE model parameters
The equations above were inspired by models in statistical physics49,53. For example, kBT represents Boltzmann’s constant multiplied by the system temperature. The fitted SDE is used to infer physical information about dynamical processes acting on the tagged particle, e.g., F(rt) denotes the effective force acting on the particle implied by the observations. A quantity like F(rt) contains information about how the local cellular environment is affecting the tagged particle. The parameter C = σ determines the local diffusion53 matrix defined by the relation D ≡ σσT (i.e., σ is the Cholesky factor of D). Inertia of the particle is ignored through a fluctuation dissipation relationship stated in Eqn. 5, i.e., the tagged particle is in the “overdamped” regime53; Φ is a matrix quantifying effective friction (inducing the “overdamping”). The instantaneous velocity of the overdamped particle is quantified by ΦF(rt). B can be interpreted as an elasticity parameter. We later check the modeling assumptions (e.g., overdamped regime and Brownian noise) against experimental data43.
Time window-based parameter estimation and testing
Parameters approximating the dynamics or measurement statistics of the tagged particle change in an effective continuous fashion with time in many SPT applications. In all cases analyzed, the tagged particle measurement noise changed smoothly over the course of one trajectory. If a fixed constant measurement noise for single a SPT trajectory was assumed, this would be enough to cause model rejection by the goodness-of-fit hypothesis tests employed (see Figs. S8 & S9, Table S1, and associated SI discussion). Motivated by the fact that parameters characterizing the dynamics and measurement noise change over time, we subdivide each trajectory into K blocks of contiguous time windows. In each window, we fit the parameters of an SDE to each of the following time series: . The inferred information from a single trajectory is summarized in K parameter vectors: θ(1), θ(2), … θ(K).
We force the value of the differences W ≡ (ni+1 − ni) + 1 representing the number of observations in a given local time window to be a constant value. The term “micro-time” is used to refer to the times within local windows. For example, in local time window 2, we have the observations indexed by the micro-times tn1, tn1+1, …, tn2; the time-ordered sequence is subsequently used to infer the SDE parameter vector θ(2). The local time window is independent of the volume traversed by the particle. This was done in order to keep the time series sample sizes the same and hence facilitate comparing goodness-of-fit test statistics coming from each window (i.e., the number of experimental observations used to scrutinize model predictions is the same in each local window).
In this article, we restrict our attention to the 3D linear SDE model described earlier because this model can be fit via maximum likelihood methods using quantities associated with the Kalman filter57. The Kalman filter is well-established58 and has been used in SPT analyses35,59–62. Details outlining how MLE and the likelihood can be extracted from the linear model are contained in the SI.
Even though the likelihood of the measurement sequence can be computed exactly under the Kalman filter, goodness-of-fit tests simultaneously checking all distributional assumptions were difficult to rigorously address before the advent of recent advances in time series analysis43–45,47. The aforementioned approaches have been utilized extensively in scalar time series, but statistical inference in the multivariate non-stationary case is currently an open problem45,47. A brief description of the tests used here43 are provided in the next subsection; a more detailed discussion is contained in the SI Theory and Methods section where we discuss how the technical difficulties associated with the multivariate version of Hong and Li’s test43 are addressed (advantages over traditional Kalman filter techniques are also provided in the SI, e.g. see Fig. S9 and associated discussion).
Throughout, we also restrict attention to the case where C and R are diagonal (uncorrelated thermal and measurement noise) and F(r) comes from the gradient of a scalar potential (hence B is symmetric). It should be noted that one can also consider non-gradient forces and/or nonlinear multivariate SDEs in both estimation53,63 and inference43,45; we focus on the linear case described above to simplify exposition. In the cases rejected in this article, using nonlinear polynomial SDE models did not improve the model fit (quantified in next section).
Experimental Methods
Sample preparation and microscopy
A time ordered image stack where consecutive images were measured every 4ms was used to generate each SPT trajectory. Sixty ARG3 mRNA trajectories in budding yeast visualized by EGFP fusions to proteins binding MS2 loop repeats were analyzed in total at this sampling frequency. 3D measurements were obtained by analyzing a double-helix point spread function (DH-PSF)8,10,64 response in each image. The experimental setup and data processing method used are described in Thompson et al.10. The mRNA trajectory extracted from the image stack was divided into contiguous windows each containing W = 400 noisy 3D observations (the number of contiguous observations was determined to provide a balance between variance and bias). The results reported were not found to depend on the window size or the temporal sampling rate (see SI). Using W = 400 resulted in a total of 473 windows of 3D data. Individual single particle trajectories were associated with K= 4–12 blocks of local window data. The length of data associated with one trajectory depended stochastically on photobleaching effects.
Signal processing
Initially, we assumed that the three position coordinates evolved statistically independently of one another when estimating the SDE parameters in the 473 windows of 3D data. The assumption of statistical independence of the position coordinates effectively increased the number of 1D SDE parameter vectors estimated to 1419 = 3 × 473. In the 3D cases considered, the total number of parameters to estimate for each trajectory is 15 in the 3D SDE models considered.
Local MLE of 3D trajectories
Estimation of the parameters in local window j was achieved by recording the measurements at W micro-times and using them to obtain the maximum likelihood estimate (MLE) defined by:
| (7) |
where the parameter vector θ̂(j) ≡ (Â, B̂, Ĉ, R̂) is the MLE assuming the initial measurement is precisely known57. Finding the MLE requires one to evaluate the transition density, p(ψti | ψti−1; θ(j)). In the Kalman filter case considered, the transition density is a multivariate Gaussian density. The SI contains the equations connecting the continuous time SDE to the discrete Kalman filter57, as well as details of initial parameter guesses and goodness-of-fit statistics. Throughout, we focus on W = 400, but other values are explored in the SI.
Hypothesis testing procedure
After fitting models to observed experimental data, we used the MLE to form the “null hypothesis”43 and computed two test statistics: 1) the omnibus “Q-test” introduced by Hong and Li43; this test statistic simultaneously checks the distributional shape and the statistical dependence in the probability integral transform (PIT) and 2) the “M-test”43. The latter focuses only on statistical dependence in the computed PIT sequence. More specifically, the name “M-test” is used to refer to M(1,1)43 with a lag truncation parameter of 20; in this study, results obtained using M(i, j) were similar for i, j ∈ {1, 2} and lag parameters of 10 and 30. We used the sampling parameters j = 1 and p = 2043 to construct the Q test statistic, but our findings supported those reported in Hong and Li43. That is, the M and Q test results are effectively independent of sampling parameters.
For the Kalman filter model, the PIT sequence (required for the tests mentioned above) was computed using the normalized innovation sequence (i.e., the innovation vector multiplied by the inverse matrix square root of the innovation covariance) using the observed data and the fitted θ̂(j). Note that this approach uses a linear combination of 3D elements and aims at removing empirical correlation between observations; this partially mitigates issues associated computing the PIT of a multivariate time series43.
Computing Error Bars
Finite time series sample sizes in introduce inherent parameter uncertainty into the estimates. If an SDE is fitted, and the goodness-of-fit test suggests that there is no evidence of inconsistency between the model and data, then we turn to Monte Carlo Simulations for extracting error bars. The point MLE is used to generated multiple synthetic trajectories (each having the same number of observations as the experimental data); subsequently, the MLE of each synthetic path is extracted. From this collection of estimated parameters, the standard error, SE, of each element of θ̂(j) is extracted and the range of plausible parameters is approximated by θ̂(j) ± SE.
Results and Discussion
Control simulations
To begin, we start with a situation where a 3D SDE simulation is used to generate data (i.e., measurement noise with precisely known statistics was added to the synthetic observations). The parameters were forced to be fixed for the duration of the simulation and the interest is in quantifying how accurately parameters describing x, y, z force interactions can be characterized under a correctly and incorrectly specified model with simulation parameters selected to mock experimental conditions. Table 1 reports the mean and standard deviation of these parameters (see caption for additional Monte Carlo simulation details). The last column of Tab. 1 provides the parameter of the underlying true data generating model; the 1st and 3rd columns present parameter estimation results using the 3D SDE model proposed (the columns differ in the number of temporal observations used for each MLE estimate); the 2nd and 4th columns present results obtained by a “classic 1D SPT” model where interaction terms (e.g., Bxy) are set to zero. Note that parameter estimates for the classic 1D SPT induce appreciable bias in both the “elasticity” parameters (components of B) and the diffusion coefficient. These results indicate that using a time series size of W = 400 has power to detect 3D force interaction terms in the sample sizes and observation frequencies studied. Table S4 provides additional evidence that the method has adequate power to detect kinetic phenomena of interest in the experimental mRNA trajectories.
Table 1.
Parameter Estimates for 3D Simulation Data. In each case, a time series consisting of 1 × 105 observations uniformly spaced by 4ms was simulated to create draws from the stationary distribution of a 3D model. Parameters were estimated by dividing the long stationary signal into windows using various schemes. Case 1: Computed average and standard deviation (reported in parenthesis) of 3D model estimated with 400 observations per window; Case 2: Results with 1D model estimated with 400 observations (interaction terms Bxy, Bxz, Byz are set to zero); Case 3 and 4: Correspond to Case 1 and 2 except using a window of size 1600 (resulting in a larger sample size for each parameter estimate).
| Case | 1 | 2 | 3 | 4 | Truth |
|---|---|---|---|---|---|
| Ax | −0.003 (0.008) | −0.000 (0.006) | 0.000 (0.003) | 0.001 (0.002) | 0 |
| Ay | 0.003 (0.015) | −0.000 (0.007) | 0.000 (0.009) | −0.000 (0.001) | 0 |
| Az | 0.003 (0.031) | −0.001 (0.004) | 0.009 (0.014) | −0.001 (0.004) | 0 |
| Bxx | −10.735 (3.236) | −3.896 (0.889) | −9.790 (1.138) | −3.586 (0.556) | −10 |
| Bxy | 10.542 (3.267) | - | 9.825 (1.442) | - | 10 |
| Bxz | −0.597 (3.080) | - | −0.140 (1.941) | - | 0 |
| Byy | −16.319 (4.071) | −5.879 (1.245) | −15.190 (2.005) | −5.397 (0.519) | −15 |
| Byz | 1.049 (2.959) | - | 0.351 (1.807) | - | 0 |
| Bzz | −45.543 (14.190) | −42.906 (11.842) | −43.790 (4.924) | −42.353 (4.107) | −40 |
| Cx | 0.209 (0.050) | 0.159 (0.025) | 0.209 (0.012) | 0.157 (0.007) | 0.2 |
| Cy | 0.148 (0.028) | 0.121 (0.016) | 0.143 (0.016) | 0.119 (0.009) | 0.15 |
| Cz | 0.103 (0.033) | 0.106 (0.042) | 0.095 (0.015) | 0.098 (0.015) | 0.10 |
| Rx | 0.020 (0.002) | 0.021 (0.001) | 0.020 (0.001) | 0.021 (0.001) | .020 |
| Ry | 0.015 (0.001) | 0.016 (0.001) | 0.015 (0.001) | 0.016 (0.001) | 0.015 |
| Rz | 0.010 (0.002) | 0.010 (0.002) | 0.010 (0.001) | 0.010 (0.001) | 0.010 |
Estimation of SPT models with time varying parameters
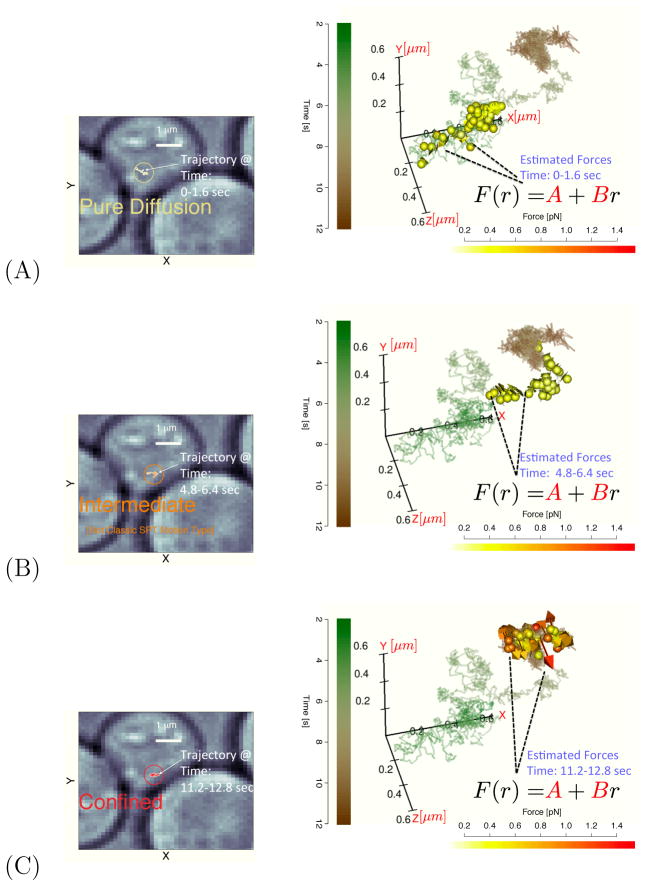
Here we first consider an actual experimental case of motion of a single mRNA particle in a cell where the assumption of statistical independence between the coordinates was not rejected by the goodness-of-fit tests employed. Figure 1 presents three panels where the entire noisily measured trajectory (containing both thermal and measurement noise) is plotted and the behavior during time windows one, four, and eight are highlighted. Superimposed, the inferred forces at different micro-times are plotted as colored arrows in the three panels; in case (A) the force vectors are so short that only the yellow tails of the force vectors are visible.
Figure 1.
The left column panels display 2D segments of a single mRNA trajectory for three different time windows. The right panels repeatedly plot the full 3D trajectory as a solid line (time color coded); in each panel, the inferred force vectors corresponding to the time segments shown the 2D panel to the left are plotted (force magnitude color code shown in scale bar). These forces were obtained by first estimating the SDE parameters in the window and then using the measurements to evaluate the force at several “micro-times” in the local time window. Panel (A) corresponds to the force estimated in window 1 (this panel also shows the time legend used for all plots as well as the white light cell image). This panel would be typically labeled as a “pure diffusion” as the force vectors estimated are very small; Panel (B) corresponds to time window 4 where there is a transient regime that would not fall into any classical single particle tracking motion type. Panel (C) plots time window 8 data which would be considered as “confined”. The inferred force vectors can be estimated from the observed time series without using an external force probe; the magnitude and direction of the forces arrows help identify the inward facing forces experienced by the confined particle. All 3D images were produced using the RGL package65.
It is possible that a single tagged particle tracked for a long enough time can exhibit a dynamical regime change29,66. For example, the particle can change from exhibiting “pure” diffusion to one consistent with another mode of motion such as “directed motion” or “corralled/confined” diffusion16,29,66. We clearly observe regime changes in this single trajectory; for example window one (Fig 1A) would be considered a “pure diffusion” regime whereas window eight (Fig. 1C) would likely be classified as “corralled diffusion”29. However, window three (Fig. 1B) would not cleanly fit into any classic SPT motion model (it is intermediate between diffusive and corralled). The change between the two regimes is relatively smooth and slow relative to the temporal sampling frequency. The inferred vectors quantify the magnitude and direction of the forces acting on the particle in the corralled/confined region. A discussion comparing and contrasting the type of corralled/confined diffusion model considered here to other classical confinement models15,17 is presented in Ref.67.
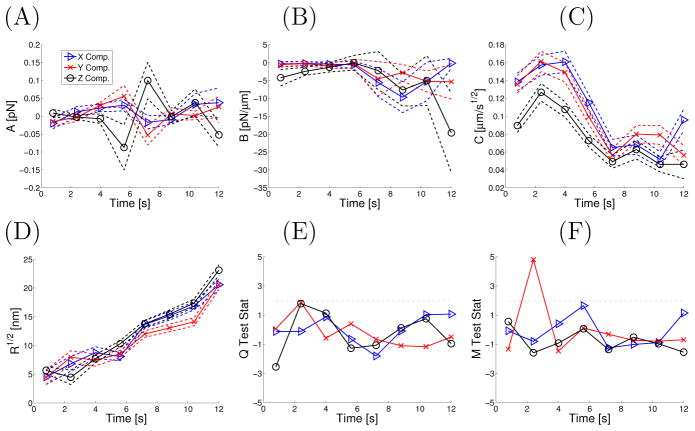
Figure 2 presents more quantitative results illustrating that the particle shown in Figure 1 is experiencing smooth changes in the SDE parameters. In Fig. 2A, we plot the estimated  (see Methods) vs. time. The dashed lines corresponds to parameter uncertainty in the estimate. The confidence bands were obtained via Monte Carlo simulation techniques outlined in the Methods. Panels B-D are similar except they correspond to the parameters B̂, Ĉ and R̂, respectively. Regarding potential physical interpretation, the time varying Ĉ can correspond to the mRNA-protein (mRNP) complex changing its effective hydrodynamic radius in a non-trivial fashion as it traverses the cell; the increase in magnitude of B̂ can be explained by a tagged mRNP aggregate slowly binding to a larger physical object in the cytoplasm. However, both of these explanations require additional studies (e.g. multi-color SPT experiments) to verify the posited interpretations since the effective diffusion coefficient and elasticity can change for other reasons, such as changes in local viscosity or other factors53. The time dependence of R̂ showing increasing measurement noise (increasing uncertainty in position) is far less ambiguous since multiple GFPs are attached to the mRNA10; the decay in intensity is caused mainly by different dyes photobleaching at different random times and this reduces the experimenter’s ability to extract precise positions.
Figure 2.
The parameters of the local SDEs estimated from experimental data in each time for the data shown in Figure 1 are plotted as symbols in panels A–D. The solid lines connect the parameters estimated in the different windows and the dashed lines correspond to the standard deviation (parameter uncertainty) associated with a simulated SDE possessing the same parameters as those observed for the experimental data. Panels E–F plot two test statistics used in assessing the fit of the assumed SDE model given the observational data. The results shown are for a case where traditional SPT models were not rejected (hence the off-diagonal terms in B are set to zero).
Figure 2 also demonstrates that the change in dynamical responses is not instantaneous on timescales now resolvable in single-molecule experiments (a pure diffusion continuously morphs into a corralled diffusion). Figure S6 demonstrates that parameter estimates obtained by analyzing the experimental mRNA SPT data are insensitive to the sampling parameter W and the time between successive observations. Panels E–F in Fig. 2 plot the Q and M goodness-of-fit statistics associated with the observed data and the estimated θ(j). The dashed lines in panels E–F denote the asymptotic critical values of the Q and M test statistics; test statistic values above this threshold indicate a fitted model inconsistent with the observed data with an asymptotic one-sided significance level (without multiple testing correction) of 2.5%.
SDEs with smoothly evolving parameters was a common feature in this mRNA SPT data. For example, in all observed trajectories, the effective measurement noise was observed to smoothly vary over the course of data collection and the change within individual trajectories was statistically significant (see Fig. S4). Parameters characterizing particle motion smoothly changing over time has important implications in regards to explaining causes of anomalous diffusion14,22,31,68,69 and for tracking groups of particles in the cytoplasm where dynamical models (with fixed parameters) are often utilized35,59–62.
The SI (Fig. S5 and Tables S1–S3) displays some problems that can occur if one does not account for time-varying parameters in classic SPT analysis methods. Traditional models estimated by MLE assume fixed parameters or impose heuristics for truncating trajectories, e.g.10,16; if the underlying data changes appreciably then significant biases can be introduced. Worse yet, large transient forces of physical interest may go unnoticed (e.g., as shown in the next subsections). Tables S1 and S3 show that the testing procedure employed can quantitatively determine if there is adequate evidence in the data to detect time changing parameters in one trajectory. Figure S5 provides results analogous to Fig. 2 where a windowing approach is used in conjunction with the MSD estimator utilized in Ref.10. It can be observed that bias and variance of a commonly used MSD method is substantial even if local time windows are used with the MSD estimator. Figure S5 also shows that for this trajectory (with time changing SDE parameters), the bias is most substantial in the estimated effective measurement noise (this parameter is also known as the effective localization precision).
In the Experimental Methods, we discussed how an initial screening of 1419 1D models was carried out. In this data set, 136/1419 1D SDE models were rejected by the Q-test and 290/1419 were rejected by the M-test43 using a one-sided Type I error rate threshold of 97.5%. The initial screening was done in order to reduce the computational load associated with fitting a large batch of 3D SDE models. After further inspection of the rejected cases, it was found that several trajectories where 1D SDE models assuming independently evolving coordinates were rejected exhibited rich dynamics (some examples are presented in the sections that follow; other examples can be found in the Figs. S2-S4). Of the trajectories rejected, inclusion of a 3D force permitting coupling between the x,y,z, forces in the SDE improved the fit in terms of the AIC and BIC model selection criteria and/or goodness-of-fit. Note that increasing the polynomial order of the SDE, producing a 3D analog of the nonlinear SDE model utilized in21, did not improve the fit; the M-test only rejected 266/1419 whereas the linear Kalman filter performed similarly (265/1419).
Note that the models considered do not explicitly account for a single-ended hard boundary (e.g., a cell wall). If the wall is static and the particle continually strikes a single-ended boundary, this modeling imperfection will likely be detected by the goodness-of-fit tests. The reason for rejection would not be provided, but additional diagnostic analyses would likely show that a region of occluded phase space is visited less frequently than the assumed model predicts it should. In general, if the particle has an affinity for a singled-ended boundary and it hits this boundary often on the experimental time scale, another model should be considered. In systems we have encountered, 2–4 “hard” reflections in a time series of size 200–400 hitting a (nominally) known physical barrier have not adversely affected estimation or goodness-of-fit testing. Effects of two-ended boundaries (with hard or soft repulsions) have been recently analyzed by the first author67; in this work, the focus was on studying short SPT trajectories (100–400 observations) containing thermal and measurement noise. The work in Ref.67 complements the study provided in Ref.18 where long (> 4000) trajectories were analyzed.
Discoveries enabled via goodness-of-fit tests
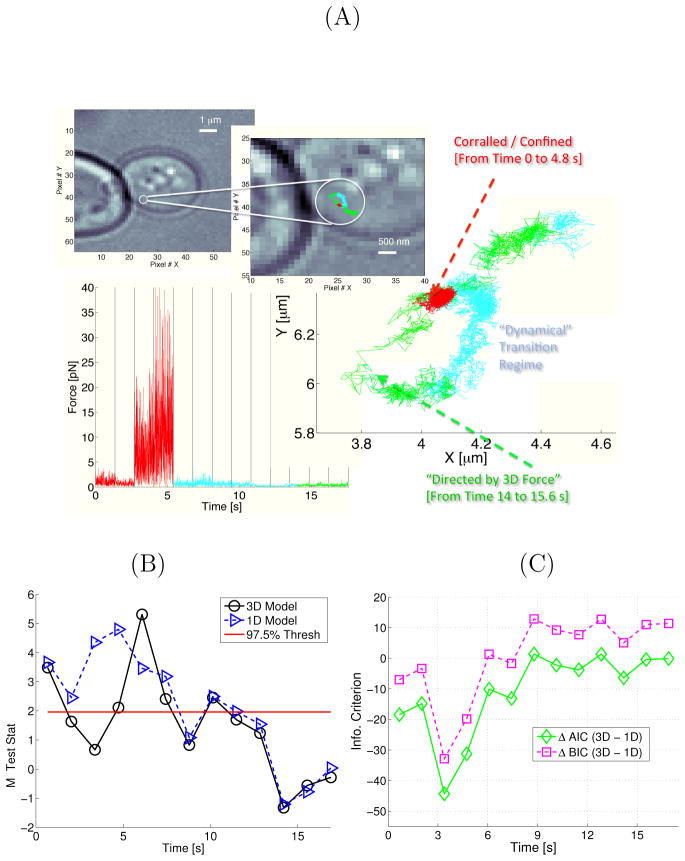
Next, we demonstrate another case where a dynamical regime change was observed along a single 3D trajectory. Importantly, this trajectory was flagged by the goodness-of-fit test as not being consistent with three independent traditional 1D SPT models. The white light image of the cell containing the tagged particle is shown in Fig. 3A. The 2D projection of the measured 3D DH-PSF trajectory is shown in the white light image magnification displayed in Fig. 3A. The 2D projection is color-coded by a loose qualitative regime labeling we applied to the data after analysis of the implied force magnitudes (these regimes are discussed more in subsequent sections). The 3D force magnitude was inferred from K = 13 windows. The window boundaries are indicated by vertical lines in the bottom left plot of Panel A. The red color label denotes the confined regime where the particle was observed to exhibit large bursts of force ranging from 1–30pN. Fig. S7 demonstrates that the force bursts were not overly dependent on the sampling parameter W. Note that the elasticity inferred during the force burst (e.g., in z) is much larger than standard RNA elasticities reported in the literature70,71 and the size of the force magnitude is consistent with those forces studied via in vitro ribosome/mRNA studies72,73. Figure 3B presents the M test statistic which indicates superior performance from a 3D model during the confinement period. Figure 3C demonstrate quantitatively that the 3D SDE model also improves performance in terms of the AIC and BIC54 model selection criteria (a value less than zero in Fig. 3C suggests a 3D model is preferred by the model selection criteria). The green region shown in Fig. 3A is a “directed by 3D force regime”. By this we mean that an SDE model allowing for statistically correlated 3D forces was used, i.e., the elasticity matrix had statistically significant terms in the off-diagonal entries (as determined by AIC and the inferred force arrows).
Figure 3.
A case where the particle interacts with an object in the cytoplasm. Panel A shows the location in the cell where the image was taken. The microscope images is magnified and the x–y coordinates of the experimentally measured trajectory is shown in color. The red region shows where the particle was confined by large constraint forces. The inferred forces reached magnitudes as high as 30pN for long time bursts (Fig. S7 illustrates that this force burst was insensitive to W); the cyan region is a dynamical regime encountered before the particle experiences a “3D directed force” (a regime denoted by green and discussed in the text). Panel B plots the goodness-of-fit test statistic and Panel C plots the AIC and BIC comparing a genuine 3D model to a 1D model (lower values indicate better fits for both goodness-of-fit and model selection statistics). The trajectory strongly suggests constraint forces and the AIC and BIC model selection criteria verified that adding correlation between the effective forces governing the particle dynamics improves the fit. The experimental trajectory and effective forces imply the existence of a manifold on which the particle evolves. The SDE quantifies the strength of the “tether” to this manifold.
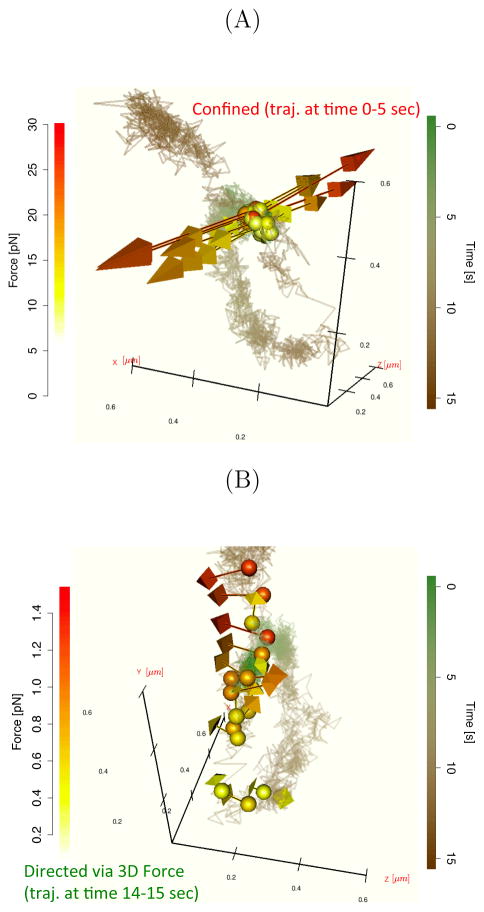
Figure 4 plots the raw 3D trajectory (i.e., the full information afforded by the DH-PSF measurements) as well as the inferred forces in the two different regimes (these regimes were highlighted in Fig. 3A). Fig. 4A displays a confined regime where the tagged particle experiences equal and opposite forces pointing in spatial directions indicated by the force vectors. Fig. 4B shows, after an intermediate transition time occurring between seconds 5 – 14, that the type of dynamics the tagged particle experiences changes during time 14–15s. The tagged particle experiences statistically significant constraint forces during time 14 – 15s. In this regime, the SDE model selection analysis (see Fig. 3C) suggests that the sequence of measurements is best explained by forces whose components are statistically dependent.
Figure 4.
Inferred force vectors for the trajectory in Figure 3. The solid lines show the 3D measurements and the colored spheres and arrows denote the inferred 3D force vector. Panel A plots representative forces associated with the confined motion regime and Panel B shows those associated with the directed regime.
Some possible physical interpretations of the dynamical transitions described above are posited in the text below. In the confined regime (Fig. 4A), the mRNA particle appears to be tightly bound to another molecule. After this binding, the dynamics experienced by the particle slowly change into forces suggesting that the mRNA complex engages in active transport (Fig. 4B). In the active transport regime (Fig. 4B), the mRNP complex appears to be tethered to a cytoskeletal track (e.g. a microtubule or actin cable) and subsequently shuttled (i.e., directed) by 3D forces plotted in Fig. 4B. The estimated 3D forces are described in greater detail in the next subsection. Another, albeit more ambitious, interpretation of this data is that the observed phenomenon is a dynamical signature associated with the translation of mRNA by a ribosome72,74,75. The force magnitudes inferred by the SDE are in the 1–30 pN range for bursts; this range can possibly be explained by ribosomal forces72, however our experiments are different in spirit (namely, the fluorescently tagged molecule is being “passively” observed in vivo) so directly comparing force magnitudes is not straightforward. However, further research is needed to determine what would cause the constrained motion observed (e.g., techniques able to resolve both mRNA and a binding ribosome with high spatial and temporal resolution are needed, such as two color imaging). The ribosome interpretation is admittedly ambitious, but the highly directed inferred force vectors are nonetheless useful in determining that the particle is interacting strongly with another object in the cytoplasm. This discovery was enabled by goodness-of-fit tests identifying inconsistencies of the SPT data with traditional SPT models.
New kinetic signatures of in vivo transport
Typically, a mean square displacement analysis coupled with a large measured velocity characterizes directed motion. However, both the velocity magnitude and duration of directed motion on cytoskeletal structures in cells are dificult to reliably quantify at the single-molecule level10,29. The use of inferred SDE forces evaluated for each SPT measurement in-hand can help in providing another dynamical fingerprint of directed transport along a cytoskeletal track.
Regarding the experimental system under study, molecular motors are believed to shuttle mRNP complexes in yeast cells29. When a mRNP complex is moved by a motor along a track, a force must act tangential along the track in order for “directed transport” to occur, but other forces must also be involved. For example, a motor stalk must tether the cargo near the track. The force vectors observed in Fig. 4B are suggestive of both a classic directed force (the force arrows point in a common direction) and a tethering force constraining the mRNP near a cytoskeletal track (this induces forces “orthogonal” to the direction of motion). The implied SDE forces just described thus display a 3D pattern as opposed to a 1D pattern typically used to characterize directed motion in SPT studies. The velocity of the directed transport observed in this trajectory reached an average value of 490nm/s in the directed regime. This magnitude is not excessively large but coupled with the force vector magnitude and directionality (suggesting a tethering force), the possibility of the tagged mRNP being shuttled across the cytoskeletal highway seems more plausible.
To classify the motion of all trajectory segments studied in the spirit of traditional SPT literature, four 1D model types were estimated via MLE. In other sections we did not need to select a category for the dynamics (SDE parameters were simply estimated; then the statistical significance and physical interpretation of model parameters can be determined a posteriori), but to assign categories to all trajectories and compare to other published literature classifications, we selected the model type using the simplest model not rejected by the Q test. For example, a trajectory would be labeled “static” if the goodness-of-fit test failed to reject a model whose only nonzero MLE parameters were contained in R̂. Using this approach, the fraction of trajectory segments identified to be undergoing 1D directed motion (≈ 6.7%) and “static motion” (≈ 28.1%) is comparable to previously published literature values29. In Fusco et al.29 another “housekeeping” mRNA was studied in yeast; the fractions of trajectories reported to experience directed motion was ≈ 3.0% and those considered static was ≈ 31.0%. We compared these two motion types because unambiguously distinguishing between other motion types can be even more subjective10,29.
Conclusions
We have demonstrated how likelihood-based statistical inference can lead to new quantitative insights about complex biological processes in live cells. Our methods were able to quantify the 3D forces associated with tagged mRNA interacting with cellular structures in yeast. The goodness-of-fit tools coupled with the multidimensional SDE estimation methods provided strong evidence of the tagged particle interacting with other components in the cytoplasm. Accurately quantifying the time evolving measurement and thermal noise was crucial in the success of this endeavor. The statistical diagnostics tested if the various assumptions implicit in our model (e.g., local linear overdamped forces and Gaussian measurement noise) were justified given the data. It is known that distinguishing between pure diffusion, corralled/confined diffusion, and a “static” particle is a difficult and mildly subjective task16,29; fortunately our models can be applied without assuming a subjective label. The only subjective information assumed was the parametric model form, but we used the goodness-of-fit tests to check our assumptions (with single-molecule precision) against experimental data.
Many interesting 3D forces were only uncovered because of the statistical rejection of classic SPT diffusion models by the goodness-of-fit tests employed43. Without the use of new goodness-of-fit tests capable of simultaneously testing all distributional assumptions (properly accounting for inherent thermal and measurement noise and also able to measure inconsistencies in assumed velocity or force) along a single trajectory, these interesting scientific results would have been missed due to the volume of trajectory data produced. The unusual number of statistical rejections along a subset of trajectories flagged some dynamically unusual trajectories and inspired additional investigation. New kinetic signatures of directed motion and binding were suggested when classic SPT models were rejected. Kinetic signatures not depending on (relatively) long-lived large constant velocity can assist in identifying both “traditional directed transport” and “tug-of-war” type forces acting on a tagged particle76,77. Utilizing and expanding on recent advances in rigorous time series analysis43–47 shows promise in SPT applications where dynamical models required by linear or nonlinear tracking tools need to be systematically checked. It should be stressed that the goodness-of-fit testing approach used here43 is readily applicable to local nonlinear SDEs and other more complex stochastic models20,36,53. Examples of other trajectories exhibiting directed transport and forces discovered by the goodness-of-fit screening can be found in Figs. S1–S3.
Supplementary Material
Acknowledgments
The authors would like to thank Prof. Patrick Brown for useful discussions related to this work and Dr. Bryon Donohoe for providing comments on a draft of the manuscript. C.P.C. and R.C.P. were funded by internal R&D funds provided by Numerica Corporation; W.E.M. was supported by a grant from the National Institute of General Medical Sciences (R01GM085437).
Footnotes
Supporting Information Available: A PDF containing extra simulation and experimental results (with table of contents). This material is available free of charge via the Internet at http://pubs.acs.org.
Contributor Information
Christopher P. Calderon, Numerica Corporation, Loveland, CO.
Michael A. Thompson, Dept. of Chemistry, Stanford University, Stanford, CA.
Jason M. Casolari, Dept. of Biochemistry, Stanford University, Stanford, CA.
Randy C. Paffenroth, Dept. of Biochemistry, Numerica Corporation, Loveland, CO
W. E. Moerner, Dept. of Chemistry, Stanford University, Stanford, CA.
References
- 1.Arhel N, Genovesio A, Kim K, Miko S, Perret E, Olivo-Marin J, Shorte S, Charneau P. Quantitative Four-Dimensional Tracking of Cytoplasmic and Nuclear HIV-1 Complexes. Nature Methods. 2006;3:817–824. doi: 10.1038/nmeth928. [DOI] [PubMed] [Google Scholar]
- 2.Brandenburg B, Zhuang X. Virus Trafficking - Learning from Single-Virus Tracking. Nature Reviews Microbiology. 2007;5:197–208. doi: 10.1038/nrmicro1615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lessard GA, Goodwin PM, Werner JH. Three-Dimensional Tracking of Individual Quantum Dots. Applied Physics Letters. 2007;91:224106. [Google Scholar]
- 4.Nägerl UV, Willig KI, Hein B, Hell SW, Bonhoeffer T. Live-Cell Imaging of Dendritic Spines by STED Microscopy. Proceedings of the National Academy of Sciences of the United States of America. 2008;105:18982–7. doi: 10.1073/pnas.0810028105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Huang B, Wang W, Bates M, Zhuang X. Three-Dimensional Super-Resolution Imaging by Stochastic Optical Reconstruction Microscopy. Science. 2008;319:810– 813. doi: 10.1126/science.1153529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Rohatgi R, Milenkovic L, Scott MP. Patched1 Regulates Hedgehog Signaling at the Primary Cilium. Science (New York, NY) 2007;317:372–6. doi: 10.1126/science.1139740. [DOI] [PubMed] [Google Scholar]
- 7.Manley S, Gillette J, Patterson G, Shroff H, Hess H, Betzig E, Lippincott-Schwartz J. High-Density Mapping of Single-Molecule Trajectories with Photoactivated Localization Microscopy. Nature Methods. 2008;5:155–157. doi: 10.1038/nmeth.1176. [DOI] [PubMed] [Google Scholar]
- 8.Pavani SRP, Thompson MA, Biteen JS, Lord SJ, Liu N, Twieg RJ, Piestun R, Moerner WE. Three-Dimensional, Single-Molecule Fluorescence Imaging Beyond the Diffraction Limit by Using a Double-Helix Point Spread Function. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:2995–9. doi: 10.1073/pnas.0900245106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rohatgi R, Milenkovic L, Corcoran RB, Scott MP. Hedgehog Signal Transduction by Smoothened: Pharmacologic Evidence for a 2-step Activation Process. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:3196–201. doi: 10.1073/pnas.0813373106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Thompson MA, Casolari JM, Badieirostami M, Brown PO, Moerner WE. Three-Dimensional Tracking of Single mRNA Particles in Saccharomyces Cerevisiae Using a Double-Helix Point Spread Function. Proceedings of the National Academy of Sciences of the United States of America. 2010;107:17864–71. doi: 10.1073/pnas.1012868107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sahl SJ, Leutenegger M, Hilbert M, Hell SW, Eggeling C. Fast Molecular Tracking Maps Nanoscale Dynamics of Plasma Membrane Lipids. Proceedings of the National Academy of Sciences of the United States of America. 2010;107:6829–34. doi: 10.1073/pnas.0912894107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Grünwald D, Singer RH. In Vivo Imaging of Labelled Endogenous β-actin mRNA During Nucleocytoplasmic Transport. Nature. 2010;467:604–609. doi: 10.1038/nature09438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lange S, Katayama Y, Schmid M, Burkacky O, Bräuchle C, Lamb DC, Jansen RP. Simultaneous transport of different localized mRNA species revealed by live-cell imaging. Traffic (Copenhagen, Denmark) 2008;9:1256–67. doi: 10.1111/j.1600-0854.2008.00763.x. [DOI] [PubMed] [Google Scholar]
- 14.Qian H, Sheetz MP, Elson EL. Single Particle Tracking. Analysis of Diffusion and Flow in Two-Dimensional Systems. Biophysical Journal. 1991;60:910–21. doi: 10.1016/S0006-3495(91)82125-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kusumi A, Sako Y, Yamamoto M. Confined Lateral Diffusion of Membrane Receptors as Studied by Single Particle Tracking (Nanovid Microscopy). Effects of Calcium-Induced Differentiation in Cultured Epithelial Cells. Biophysical Journal. 1993;65:2021–40. doi: 10.1016/S0006-3495(93)81253-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Saxton MJ, Jacobson K. Single-Particle Tracking: Applications to Membrane Dynamics. Annual Review of Biophysics and Biomolecular Structure. 1997;26:373– 99. doi: 10.1146/annurev.biophys.26.1.373. [DOI] [PubMed] [Google Scholar]
- 17.Kusumi A, Nakada C, Ritchie K, Murase K, Suzuki K, Murakoshi H, Kasai RS, Kondo J, Fujiwara T. Paradigm Shift of the Plasma Membrane Concept from the Two-Dimensional Continuum Fluid to the Partitioned Fluid: High-Speed Single-Molecule Tracking of Membrane Molecules. Annual review of biophysics and biomolecular structure. 2005;34:351–78. doi: 10.1146/annurev.biophys.34.040204.144637. [DOI] [PubMed] [Google Scholar]
- 18.Jin S, Haggie PM, Verkman aS. Single-Particle Tracking of Membrane Protein Diffusion in a Potential: Simulation, Detection, and Application to Confined Diffusion of CFTR Cl- Channels. Biophysical Journal. 2007;93:1079–88. doi: 10.1529/biophysj.106.102244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Savin T, Doyle PS. Static and Dynamic Errors in Particle Tracking Microrheology. Biophysical Journal. 2005;88:623–38. doi: 10.1529/biophysj.104.042457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Calderon CP, Chen W, Harris N, Lin K, Kiang C. Quantifying DNA Melting Transitions Using Single-Molecule Force Spectroscopy. J Phys : Condens Matter. 2009;21:034114. doi: 10.1088/0953-8984/21/3/034114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Calderon CP, Harris N, Kiang C, Cox D. Analyzing Single-Molecule Manipulation Experiments. J Mol Recognit. 2009;22:356. doi: 10.1002/jmr.959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Calderon CP. A Data-Driven Approach to Decomposing Complex Enzyme Kinetics. Phys Rev E. 2009;80:061118. doi: 10.1103/PhysRevE.80.061118. [DOI] [PubMed] [Google Scholar]
- 23.Michalet X. Mean Square Displacement Analysis of Single-Particle Trajectories with Localization Error: Brownian Motion in an Isotropic Medium. Physical Review E. 2010;82:041914. doi: 10.1103/PhysRevE.82.041914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Montiel D, Cang H, Yang H. Quantitative Characterization of Changes in Dynamical Behavior for Single-Particle Tracking Studies. Journal of Physical Chemistry B. 2006;110:19763–70. doi: 10.1021/jp062024j. [DOI] [PubMed] [Google Scholar]
- 25.Voisinne G, Alexandrou A, Masson JB. Quantifying Biomolecule Diffusivity Using an Optimal Bayesian Method. Biophysical Journal. 2010;98:596–605. doi: 10.1016/j.bpj.2009.10.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Persson F, Lindén M, Unoson C, Elf J. Extracting Intracellular Diffusive States and Transition Rates from Single-Molecule Tracking Data. Nature methods. 2013;10 doi: 10.1038/nmeth.2367. [DOI] [PubMed] [Google Scholar]
- 27.Berglund AJ. Statistics of Camera-Based Single-Particle Tracking. Physical Review E. 2010;82:011917. doi: 10.1103/PhysRevE.82.011917. [DOI] [PubMed] [Google Scholar]
- 28.Michalet X, Berglund A. Optimal Diffusion Coefficient Estimation in Single-Particle Tracking. Physical Review E. 2012;85:061916. doi: 10.1103/PhysRevE.85.061916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Fusco D, Accornero N, Lavoie B, Shenoy SM, Blanchard JM, Singer RH, Bertrand E. Single mRNA Molecules Demonstrate Probabilistic Movement in Living Mammalian Cells. Curr Biol. 2003;13:161–167. doi: 10.1016/s0960-9822(02)01436-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Feder T, Brust-Mascher I, Slattery J, Baird B, Webb WW. Constrained Diffusion or Immobile Fraction on Cell Surfaces: A New Interpretation. Biophysical J. 1996;70:2767–2773. doi: 10.1016/S0006-3495(96)79846-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Saxton MJ. Single-Particle Tracking: the Distribution of Diffusion Coefficients. Biophysical Journal. 1997;72:1744–53. doi: 10.1016/S0006-3495(97)78820-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Magdziarz M, Klafter J. Detecting Origins of Subdiffusion: P-variation test For Confined Systems. Physical Review E. 2010;82:011129. doi: 10.1103/PhysRevE.82.011129. [DOI] [PubMed] [Google Scholar]
- 33.Burov S, Jeon JH, Metzler R, Barkai E. Single Particle Tracking in Systems Showing Anomalous Diffusion: The Role of Weak Ergodicity Breaking. Physical chemistry chemical physics : PCCP. 2011;13:1800–12. doi: 10.1039/c0cp01879a. [DOI] [PubMed] [Google Scholar]
- 34.Ensign DL, Pande VS. Bayesian Detection of Intensity Changes in Single Molecule and Molecular Dynamics Trajectories. Journal of Physical Chemistry B. 2010;114:280–92. doi: 10.1021/jp906786b. [DOI] [PubMed] [Google Scholar]
- 35.Godinez WJ, Lampe M, Wörz S, Müller B, Eils R, Rohr K. Deterministic and Probabilistic Approaches for Tracking Virus Particles in Time-Lapse Fluorescence Microscopy Image Sequences. Medical Image Analysis. 2009;13:325–42. doi: 10.1016/j.media.2008.12.004. [DOI] [PubMed] [Google Scholar]
- 36.Calderon CP, Harris N, Kiang C, Cox D. Quantifying Multiscale Noise Sources in Single-Molecule Time Series. J Phys Chem B. 2009;113:138. doi: 10.1021/jp807908c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Chenouard N, Dufour A, Olivo-Marin JC. Tracking Algorithms Chase Down Pathogens. Biotechnology journal. 2009;4:838–45. doi: 10.1002/biot.200900030. [DOI] [PubMed] [Google Scholar]
- 38.Fox E, Sudderth EB, Jordan MI, Willsky AS. Bayesian Nonparametric Inference of Switching Dynamic Linear Models. IEEE Transactions on Signal Processing. 2011;59:1569–1585. [Google Scholar]
- 39.Meister G, Fischer U. Assisted RNP Assembly: SMN and PRMT5 Complexes Cooperate in the Formation of Spliceosomal UsnRNPs. The EMBO J. 2002;21:5853–63. doi: 10.1093/emboj/cdf585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Holstege FC, Jennings EG, Wyrick JJ, Lee TI, Hengartner CJ, Green MR, Golub TR, Lander ES, Young Ra. Dissecting the Regulatory Circuitry of a Eukaryotic Genome. Cell. 1998;95:717–28. doi: 10.1016/s0092-8674(00)81641-4. [DOI] [PubMed] [Google Scholar]
- 41.Zenklusen D, Larson DR, Singer RH. Single-RNA Counting Reveals Alternative Modes of Gene Expression in Yeast. Nature structural & molecular biology. 2008;15:1263–71. doi: 10.1038/nsmb.1514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Zhang L, Mykland P, Ait-Sahalia Y. A Tale of Two Time Scales: Determining Integrated Volatility With Noisy High-Frequency Data. Journal of the American Statistical Association. 2005;100:1394–1411. [Google Scholar]
- 43.Hong Y, Li H. Nonparametric Specification Testing for Continuous-Time Models with Applications to Term Structure of Interest Rates. Rev Fin Studies. 2005;18:37–84. [Google Scholar]
- 44.Cho JS, White H. Generalized Runs Tests for the IID Hypothesis. Journal of Econometrics. 2011;162:326–344. [Google Scholar]
- 45.Chen B, Hong Y. Characteristic FunctionBased Testing for Multifactor Continuous-Time Markov Models Via Nonparametric Regression. Econometric Theory. 2010;26:1115–1179. [Google Scholar]
- 46.Aït-Sahalia Y, Fan J, Jiang J. Nonparametric Tests of the Markov Hypothesis In Continuous-Time Models. Annals of Statistics. 2010;38:3129–3163. [Google Scholar]
- 47.Remillard B, Papageorgiou NA, Soustra F. Copula-Based Semiparametric Models for Multivariate Time Series. Journal of Multivariate Analysis. 2012;110:30–42. [Google Scholar]
- 48.Calderon CP, Arora K. Extracting Kinetic and Stationary Distribution Information from Short MD Trajectories via a Collection of Surrogate Diffusion Models. J Chem Theory Comput. 2009;5:47. doi: 10.1021/ct800282a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Calderon CP. On the use of Local Diffusion for Path Ensemble Averaging in Potential of Mean Force Computations. J Chem Phys. 2007;126:084106. doi: 10.1063/1.2567098. [DOI] [PubMed] [Google Scholar]
- 50.Calderon CP, Janosi L, Kosztin I. Using Stochastic Models Calibrated from Nanosecond Nonequilibrium Simulations to Approximate Mesoscale Information. J Chem Phys. 2009;130:144908. doi: 10.1063/1.3106225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Calderon CP. Detection of Subtle Dynamical Changes Induced by Unresolved Conformational Coordinates in Single-Molecule Trajectories via Goodness-of-Fit Tests. J Phys Chem B. 2010;114:3242–3253. doi: 10.1021/jp911124z. [DOI] [PubMed] [Google Scholar]
- 52.Hong Y, Li H, Zhao F. Can the Random Walk Model be Beaten in Out-of-Sample Density Forecasts? Evidence from Intraday Foreign Exchange Rates. Journal of Econometrics. 2007;141:736–776. [Google Scholar]
- 53.Calderon CP, Martinez J, Carroll R, Sorensen D. P-splines Using Derivative Information. Multiscale Model Simul. 2010;8:1562–1580. doi: 10.1137/090768102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Claeskens G, Hjort N. Model Selection and Model Averaging. Cambridge University Press; Cambridge, UK: 2008. [Google Scholar]
- 55.Kloeden P, Platen E. Numerical Solution of Stochastic Differential Equations. Springer-Verlag; Berlin: 1992. [Google Scholar]
- 56.Thompson RE, Larson DR, Webb WW. Precise Nanometer Localization Analysis for Individual Fluorescent Probes. Biophysical Journal. 2002;82:2775–83. doi: 10.1016/S0006-3495(02)75618-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Hamilton J. Time Series Analysis. Princeton University Press; Princeton, NJ: 1994. [Google Scholar]
- 58.Stengel R. Optimal Control and Estimation. Dover Publications; Toronto, Ontario: 1994. [Google Scholar]
- 59.Genovesio A, Liedl T, Emiliani V, Parak WJ, Coppey-Moisan M, Olivo-Marin JC. Multiple Particle Tracking in 3-D+t Microscopy: Method and Application to the Tracking of Endocytosed Quantum Dots. IEEE Transactions on Image Processing. 2006;15:1062–70. doi: 10.1109/tip.2006.872323. [DOI] [PubMed] [Google Scholar]
- 60.Bertaux N, Marguet D. Dynamic Multiple-Target Tracing to Probe Spatiotemporal Cartography of Cell Membranes. Nature Methods. 2008;5:687–694. doi: 10.1038/nmeth.1233. [DOI] [PubMed] [Google Scholar]
- 61.Jaqaman K, Loerke D, Mettlen M, Kuwata H, Grinstein S, Schmid SL, Danuser G. Robust single-particle tracking in live-cell time-lapse sequences. Nature Methods. 2008;5:695–702. doi: 10.1038/nmeth.1237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Sergé A, Bertaux N, Rigneault H, Marguet D. Dynamic Multiple-Target Tracing to Probe Spatiotemporal Cartography of Cell Membranes. Nature Methods. 2008;5:687–94. doi: 10.1038/nmeth.1233. [DOI] [PubMed] [Google Scholar]
- 63.Jimenez J, Ozaki T. An Approximate Innovation Method for the Estimation of Diffusion Processes from Discrete Data. J Time Series Analysis. 2006;27:77–97. [Google Scholar]
- 64.Pavani SR, Piestun R. High-efficiency rotating point spread functions. Opt Express. 2008;16:3484–3489. doi: 10.1364/oe.16.003484. [DOI] [PubMed] [Google Scholar]
- 65.Adler D, Murdoch D. RGL: 3D Visualization Device System (OpenGL) 2011. R package version 0.92.798. [Google Scholar]
- 66.Saxton MJ. Single-Particle Tracking: Connecting the Dots. Nature Methods. 2008;5:671–2. doi: 10.1038/nmeth0808-671. [DOI] [PubMed] [Google Scholar]
- 67.Calderon CP. Correcting for Bias of Molecular Confinement Parameters Induced by Small-Time-Series Sample Sizes in Single-Molecule Trajectories Containing Measurement Noise. Phys Rev E. 2013;88:012707. doi: 10.1103/PhysRevE.88.012707. [DOI] [PubMed] [Google Scholar]
- 68.Granger C, Joyeux R. An Introduction to Long-Memory Time Series Models and Fractional Differencing. J Time Series Analysis. 1980;1:15–30. [Google Scholar]
- 69.Lubelski A, Sokolov IM, Klafter J. Nonergodicity Mimics Inhomogeneity in Single Particle Tracking. Physical Review Letters. 2008;100:250602. doi: 10.1103/PhysRevLett.100.250602. [DOI] [PubMed] [Google Scholar]
- 70.Liphardt J, Onoa B, Smith SB, Tinoco I, Bustamante C. Reversible Unfolding of Single RNA Molecules by Mechanical Force. Science. 2001;292:733–7. doi: 10.1126/science.1058498. [DOI] [PubMed] [Google Scholar]
- 71.Gerland U, Bundschuh R, Hwa T. Mechanically Probing the Folding Pathway of Single RNA Molecules. Biophysical Journal. 2003;84:2831–40. doi: 10.1016/S0006-3495(03)70012-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Wen JD, Lancaster L, Hodges C, Zeri AC, Yoshimura SH, Noller HF, Bustamante C, Tinoco I. Following Translation by Single Ribosomes One Codon at a Time. Nature. 2008;452:598–603. doi: 10.1038/nature06716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Qu X, Wen JD, Lancaster L, Noller HF, Bustamante C, Tinoco I. The Ribosome Uses Two Active Mechanisms to Unwind Messenger RNA During Translation. Nature. 2011;475:118–21. doi: 10.1038/nature10126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Zhang W, Dunkle J, Cate J. Structures of the Ribosome in Intermediate States of Ratcheting. Science. 2009;325:1014. doi: 10.1126/science.1175275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Ben-Shem A, Jenner L, Yusupova G, Yusupov M. Crystal Structure of the Eukaryotic Ribosome. Science. 2010;330:1203–9. doi: 10.1126/science.1194294. [DOI] [PubMed] [Google Scholar]
- 76.Müller MJI, Klumpp S, Lipowsky R. Tug-of-War as a Cooperative mechanism for Bidirectional Cargo Transport by Molecular Motors. Proceedings of the National Academy of Sciences of the United States of America. 2008;105:4609–14. doi: 10.1073/pnas.0706825105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Welte MA. Bidirectional Transport: Matchmaking for Motors. Current Biology. 2010;20:R410–3. doi: 10.1016/j.cub.2010.03.018. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.