Abstract
Multicellular organisms depend on developmental programs to coordinate growth and differentiation from single cells, but the origins of development are unclear. A possible starting point is stochastic phenotypic variation generated by molecular noise. Given appropriate environmental conditions, noise-driven differentiation could conceivably evolve so as to come under regulatory control; however, abiotic conditions are likely to be restrictive. Drawing from an experimental system, we present a model in which environmental fluctuations are coupled to population growth. We show that this coupling generates stable selection for a single optimal strategy that is largely insensitive to environmental conditions, including the number of competitors, carrying capacity of the environment, difference in growth rates among phenotypic variants, and population density. We argue that this optimal strategy establishes stabilizing conditions likely to improve the quality and reliability of information experienced by evolving organisms, thus increasing opportunity for the evolutionary emergence of developmental programs.
Introduction
The emergence of multicellular organisms from single cells marks a major transition in evolution [1]. Of prime importance is the evolution of mechanisms that integrate and align the activities of single cells with those of the collective [2]–[6]. In extant multicellular organisms such integration is brought about by developmental programs which regulate cellular activities across space and time – including those necessary for the formation of a multicellular body from a single cell propagule [2], [5], [7]–[9]. By virtue of such developmental programs multicellular organisms effect their own reproduction. Indeed, the earliest multicellular developmental programs were likely those that determined the reproduction of groups, thereby ensuring that newly emergent groups became units of selection [4]. Although developmental programs are pervasive in the multicellular world, their evolutionary origins are unclear [2], [5], [9]–[11].
The most primitive developmental programs are likely to have been rudimentary and based on little other than noise [8]–[10], [12]. For example, a mutation, or an abrupt shift in environmental conditions, might cause a cell of one specific genotype to stochastically switch between two or more phenotypes [13]. If cells of different phenotypes are selectively favored, then the capacity to switch is likely to become established within a population [14]–[20]. Subsequent modification might even lead to the evolution of regulatory mechanisms that tune the production of cell types to specific environmental cues [8], [10], [13], [14], [21].
Molecular details by which stochastic mechanisms of phenotype switching might come under regulatory control are unknown [13]. Specific genetic events are clearly required. However, their fixation requires appropriate opportunity. Such opportunity is likely to depend on environmental factors that maintain stochastic switches for sufficient lengths of time to allow for eventual accommodation within regulatory networks.
Fluctuating environments are known for their ability to select for – and maintain – stochastic mechanisms of gene expression [15], [16], [18]–[20]. While in principle such environments are sufficient to provide opportunity for stabilization of stochastic switches, fluctuating conditions wrought by external factors are unlikely to oscillate in a constant manner. Without regular oscillations, the rate of switching is likely to be subject to change. However, if there is feedback between organism and environment, then stabilization may be possible. In this regard, ecological circumstances that couple environmental change to population growth may have been central to the emergence of primitive developmental programs.
By coupling environmental change to population growth, organisms exert some control over the selective pressures they face [22]–[25]. For example, organisms that reproduce quickly can, as a consequence of exponential growth, reach large population sizes rapidly. If there is coupling between population growth and environmental change, then this will provoke environmental change on a similar time scale. Such rapid environmental change is likely to increase the selective pressure on populations to switch phenotype. Organisms that reproduce slowly, however, are likely to reduce the rate of environmental change and thus relieve selection for rapid switching. At the same time, organisms that reproduce slowly risk being outcompeted by mutants with the capacity for rapid reproduction. Because the activity of an organism influences the selective pressures it experiences, organismal success is determined by both individual reproduction and switch rates, as well as by the reproduction and switch rates of competitors. As populations evolve, so too does the frequency of environmental oscillations. This adds complexity because optimal switching rates may need to be tuned to particular population compositions and sizes.
Here, we consider a biological model for this coupling based on experimental populations of the bacterium Pseudomonas fluorescens [11], [26]–[30]. When grown in a simple laboratory microcosm P. fluorescens establishes a cycle of environmental states and phenotypes [26], [30] (Figure 1a) that produces a primitive life cycle by which groups of cells leave group-level offspring via a propagule stage [11]. In this way, P. fluorescens also serves as a model for studying the evolutionary origins of multicellularity. Using a combination of mathematical models and simulations we show that the coupling of environmental change to population growth selects for cells that switch between stages of the life cycle at high frequency. The high rate of switching favors types that switch via an epigenetic mechanism over those relying on mutation. Our models also show that there is an optimal switching strategy which is largely independent of environmental carrying capacity, the number of competitors, the switching strategies of competitors, and the relative differences in growth rates of different types. Switching types that adopt this optimal strategy can dominate a variety of environmental conditions. Importantly, this optimal strategy – arising from the coupling of phenotypic and environmental states – stands to generate stabilizing conditions likely to improve the quality and reliability of information experienced by the evolving organism, thus increasing opportunity for the evolution of developmental programs.
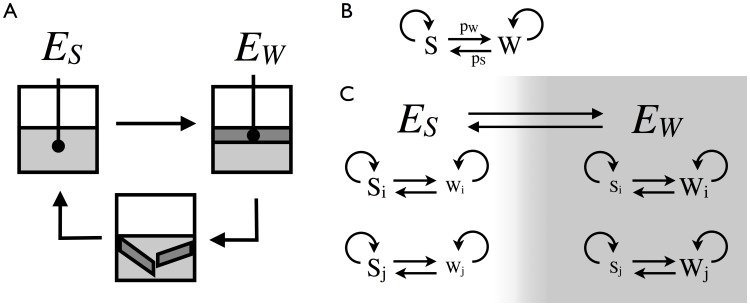
Figure 1. Model schematics.
(A) The upper left ( ) represents initial growth in an oxygen rich broth that favors the smooth
) represents initial growth in an oxygen rich broth that favors the smooth 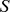 phenotype. As organisms grow and divide, they consume oxygen and eventually the air-liquid interface is the only place with available oxygen. This environment (
phenotype. As organisms grow and divide, they consume oxygen and eventually the air-liquid interface is the only place with available oxygen. This environment (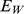 ) selects for the wrinkly
) selects for the wrinkly 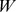 phenotype because it forms a mat at the air-liquid interface through production of a cell-to-cell glue. The mat grows and ultimately collapses under its weight, causing oxygen to flood back into the broth. This, in a sense, returns the system to its starting point. (B)
phenotype because it forms a mat at the air-liquid interface through production of a cell-to-cell glue. The mat grows and ultimately collapses under its weight, causing oxygen to flood back into the broth. This, in a sense, returns the system to its starting point. (B)  organisms are modeled as stochastic switchers whose one genotype is capable of giving rise to either an
organisms are modeled as stochastic switchers whose one genotype is capable of giving rise to either an 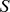 type or a
type or a 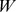 type at division. The
type at division. The 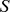 type produces a
type produces a 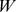 type with probability
type with probability 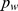 and the
and the 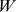 type produces an
type produces an 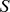 type with probability
type with probability 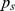 . (C) Two organisms
. (C) Two organisms 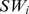 and
and 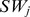 compete in environments
compete in environments 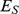 and
and 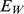 . Each organism stochastically switches between
. Each organism stochastically switches between 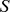 and
and 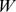 phenotypes which are suited to environments
phenotypes which are suited to environments 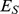 and
and 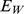 , respectively. The environments switch when the total population reaches a fixed value, the carrying capacity
, respectively. The environments switch when the total population reaches a fixed value, the carrying capacity 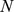 , analogous to the amount of oxygen in the broth or maximum weight supported by a mat.
, analogous to the amount of oxygen in the broth or maximum weight supported by a mat.
Models
We consider an environment that switches between two states: 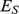 and
and 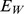 . Switching is not stochastic, but rather, is driven by organisms in the environment. The environment is populated by
. Switching is not stochastic, but rather, is driven by organisms in the environment. The environment is populated by 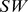 organisms, that is, organisms with the capacity to stochastically switch between one of two phenotypes:
organisms, that is, organisms with the capacity to stochastically switch between one of two phenotypes: 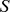 or
or 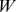 . Organisms expressing the
. Organisms expressing the 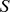 phenotype thrive in
phenotype thrive in 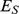 but not in
but not in 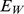 , conversely those with the
, conversely those with the 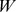 phenotype grow well in
phenotype grow well in 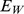 but not in
but not in 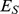 . The population expansion of each
. The population expansion of each 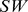 organism in a given environment is governed by four parameters: growth rate of the
organism in a given environment is governed by four parameters: growth rate of the 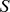 types (“growth” is used in the sense of population growth, i.e. reproduction), growth rate of the
types (“growth” is used in the sense of population growth, i.e. reproduction), growth rate of the 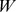 types, probability that an
types, probability that an 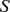 type produces a
type produces a 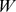 type on division, and the probability that a
type on division, and the probability that a 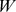 type produces an
type produces an 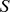 type on division (Figure 1b).
type on division (Figure 1b).
The environment switches states when the total population of 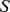 and
and 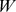 types reaches a fixed value
types reaches a fixed value 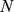 .
. 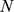 might represent the carrying capacity or the total number of cell divisions permitted by the nutrient content of an environmental state. By this measure, environmental transitions depend on the absolute populations of the
might represent the carrying capacity or the total number of cell divisions permitted by the nutrient content of an environmental state. By this measure, environmental transitions depend on the absolute populations of the 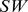 organisms and not the relative abundances of types. It is not necessary that the
organisms and not the relative abundances of types. It is not necessary that the 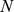 value for the
value for the 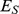 to
to  transition be the same as the
transition be the same as the 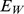 to
to 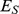 transition.
transition.
We represent the expected population of a particular 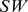 genotype growing in an environmental state, say
genotype growing in an environmental state, say 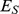 , by a set of finite difference equations (Eqn Set 2) that specify the abundance of each phenotype (
, by a set of finite difference equations (Eqn Set 2) that specify the abundance of each phenotype (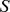 and
and 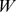 ). These are similar to equations of stochastic switchers and life cycles elsewhere [31], [32]. The step size
). These are similar to equations of stochastic switchers and life cycles elsewhere [31], [32]. The step size  is defined in terms of cell divisions of the faster growing phenotype:
is defined in terms of cell divisions of the faster growing phenotype: 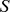 types when in
types when in 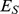 and
and 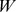 types when in
types when in 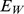 . By defining the step size in terms of cell divisions, the number of parameters is reduced by one. The transitions between types are governed by
. By defining the step size in terms of cell divisions, the number of parameters is reduced by one. The transitions between types are governed by 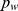 , the probability an
, the probability an 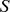 type gives rise at division to a
type gives rise at division to a 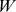 type, and
type, and 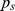 , the probability a
, the probability a 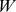 type produces an
type produces an 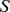 type. Since
type. Since 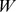 types do not reproduce as quickly as
types do not reproduce as quickly as 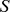 types in
types in 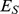 , we scale their growth rate by
, we scale their growth rate by 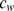 (
(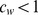 ) which is the average fraction of
) which is the average fraction of 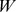 types that grow per cell division of
types that grow per cell division of 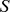 types, that is, the population’s geometric mean per step.
types, that is, the population’s geometric mean per step.
| (1) |
For population growth in 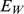 , the equations take a similar form. Here, the transition probabilities
, the equations take a similar form. Here, the transition probabilities 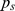 and
and 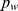 become
become 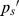 and
and 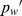 to indicate that the probability of one phenotype producing another may be environmentally dependent. The
to indicate that the probability of one phenotype producing another may be environmentally dependent. The 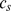 term is the analog of
term is the analog of 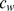 and corresponds to the slower reproduction of
and corresponds to the slower reproduction of 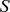 types in
types in 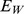 .
.
| (2) |
We simulate competition within an environmental state by iterating these equations and computing the population size of each type (see File S1 for computer code). The finite difference equations enable rapid calculations using matrix multiplication in the numerical software MATLAB(version 7.12.0.635 Natick, Massachusetts: The MathWorks Inc., 2011). Often populations reached 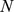 between two rounds of discrete division, say
between two rounds of discrete division, say  and
and 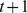 . We determine the number of new types to add to the populations at time
. We determine the number of new types to add to the populations at time  by proportionally scaling the number generated between
by proportionally scaling the number generated between  and
and 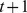 which is the finite approximation to growth limitations imposed by a carrying capacity in Verhulst differential equations.
which is the finite approximation to growth limitations imposed by a carrying capacity in Verhulst differential equations.
Results
Drawing inspiration from experimental populations of Pseudomonas fluorescens, we couple environmental oscillations to populations of 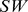 organisms which stochastically switch between two phenotypes
organisms which stochastically switch between two phenotypes 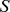 and
and 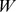 (See Models and Figure 1c). This coupling ties the success of an organism to the dynamics and composition of the population. In actual biological systems there may be hundreds of
(See Models and Figure 1c). This coupling ties the success of an organism to the dynamics and composition of the population. In actual biological systems there may be hundreds of 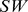 genotypes with different phenotypic characteristics competing simultaneously. Since the dynamics of each genotype in our model is governed by 6 parameters (See Models and Figure 1b & c), the system can become intractable. As a consequence, we use a bottom-up approach in which we analyze a reduced system and then add successive layers of complexity to determine how they contribute to the full model.
genotypes with different phenotypic characteristics competing simultaneously. Since the dynamics of each genotype in our model is governed by 6 parameters (See Models and Figure 1b & c), the system can become intractable. As a consequence, we use a bottom-up approach in which we analyze a reduced system and then add successive layers of complexity to determine how they contribute to the full model.
Reduced System
We begin by considering competition between two 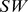 organisms in environment
organisms in environment 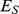 . Populations of both organisms are founded by a single
. Populations of both organisms are founded by a single 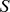 type with growth continuing until the total population reaches
type with growth continuing until the total population reaches 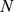 , at which point the environment switches to
, at which point the environment switches to 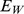 . Since
. Since 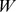 types are more suited to
types are more suited to 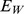 , the organism with the most
, the organism with the most 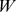 types at the time the environment transitions from
types at the time the environment transitions from 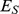 to
to 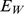 has an advantage. For the moment, we do not consider growth in the
has an advantage. For the moment, we do not consider growth in the 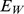 environmental state and are, therefore, interested in strategies that will best prepare an organism for the next environmental state. We further assume that
environmental state and are, therefore, interested in strategies that will best prepare an organism for the next environmental state. We further assume that 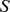 types of each
types of each 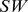 organism are equally fit and the
organism are equally fit and the 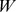 types do not grow at all. Both of these assumptions will be lifted later but in this limited case, the only difference between competitors is the probability (
types do not grow at all. Both of these assumptions will be lifted later but in this limited case, the only difference between competitors is the probability (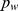 ) an
) an 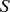 type produces a
type produces a 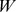 type.
type.
To determine which strategy for 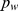 leaves the greatest number of types adapted to the next environmental state, we systematically compete pairs of
leaves the greatest number of types adapted to the next environmental state, we systematically compete pairs of 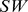 organisms with different, fixed values of
organisms with different, fixed values of 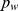 (ranging from
(ranging from 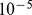 to 1). For each competition, we compute the number of
to 1). For each competition, we compute the number of 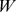 types produced by each organism during growth in
types produced by each organism during growth in 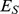 before the environmental state changes to
before the environmental state changes to 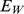 , that is, the point at which the total population reaches a fixed number
, that is, the point at which the total population reaches a fixed number 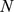 (
(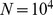 in Figure 2a). For values of
in Figure 2a). For values of 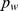 below
below 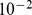 , the organism with the higher transition probability (
, the organism with the higher transition probability (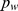 ) leaves more
) leaves more 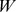 , i.e. it “wins” because it sets up a numerical advantage in the next environmental state. At high
, i.e. it “wins” because it sets up a numerical advantage in the next environmental state. At high 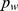 values (
values (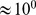 ), the opposite is true, such that the organism with the lower
), the opposite is true, such that the organism with the lower 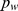 wins. This occurs because organisms with lower
wins. This occurs because organisms with lower 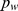 initially invest more in the fast-growing
initially invest more in the fast-growing 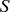 type and, thereby, defer the expected production of
type and, thereby, defer the expected production of 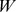 types until they have amassed a large population of
types until they have amassed a large population of 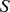 (they thus contribute many more
(they thus contribute many more 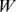 types). The result is a single optimal strategy.
types). The result is a single optimal strategy.
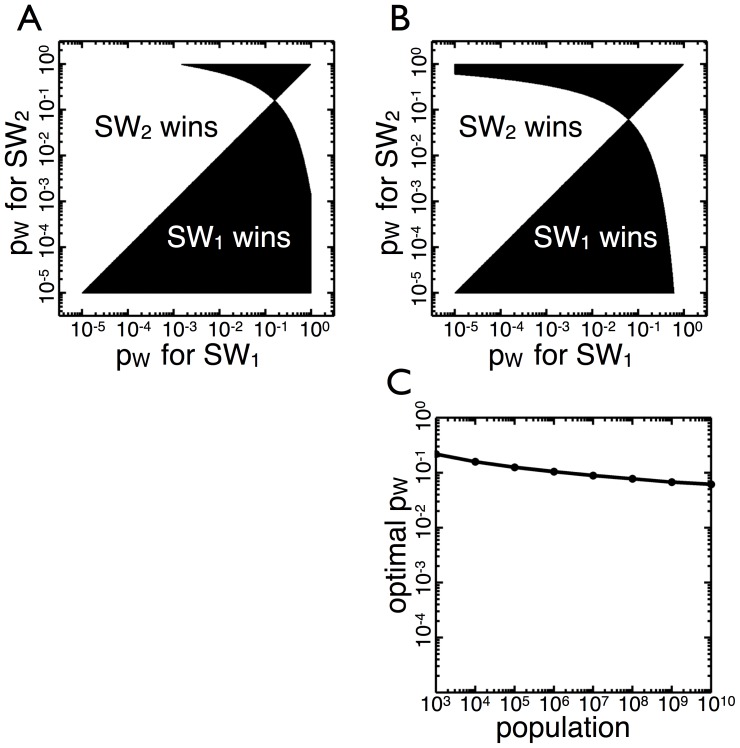
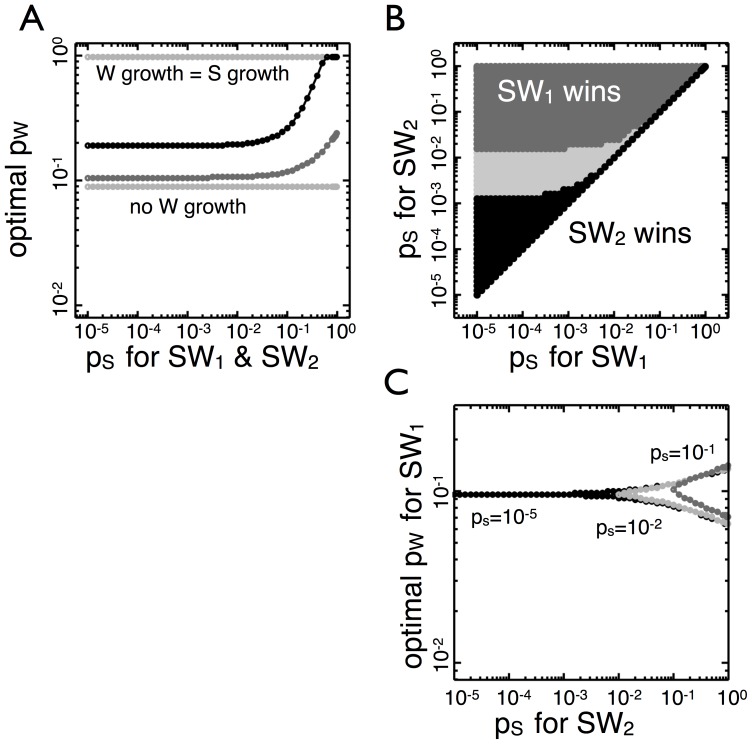
Figure 2. Competition between 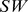 genotypes with different transition probabilities,
genotypes with different transition probabilities, 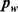 .
.
(A) The black area corresponds to specific combination of 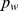 values for two
values for two 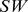 genotypes in which
genotypes in which 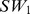 leaves more
leaves more 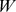 types than
types than 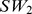 when the environmental state changes to
when the environmental state changes to 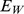 at
at 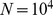 . The white area represents the converse. There is an optimal
. The white area represents the converse. There is an optimal 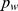 (
(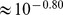 ) which results in more
) which results in more 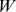 types compared to any other
types compared to any other 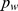 . (B) The same as A but with
. (B) The same as A but with 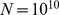 . The optimal
. The optimal 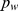 has decreased to
has decreased to 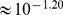 . (C) The optimal
. (C) The optimal 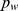 is calculated for
is calculated for 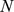 values between
values between 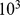 and
and 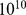 . As
. As 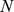 increases over seven orders of magnitude,
increases over seven orders of magnitude, 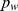 remains relatively constant, decreasing less than an order of magnitude.
remains relatively constant, decreasing less than an order of magnitude.
Qualitative outcomes of the competition remain unchanged even when the population size necessary to effect an environment switch is as large as 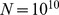 (Figure 2b). There remains a single optimal strategy which can beat higher and lower transition probabilities. The higher carrying capacity (
(Figure 2b). There remains a single optimal strategy which can beat higher and lower transition probabilities. The higher carrying capacity (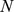 ) enlarges the range (top shaded region) in which organisms with high transition probabilities can be defeated by those with low transition probabilities. Because higher
) enlarges the range (top shaded region) in which organisms with high transition probabilities can be defeated by those with low transition probabilities. Because higher 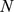 means populations go through more rounds of cell division, the production of
means populations go through more rounds of cell division, the production of 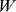 types can be deferred until later rounds of division. Consequently, higher population sizes
types can be deferred until later rounds of division. Consequently, higher population sizes 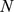 lead to a slight reduction in the optimal transition probability from
lead to a slight reduction in the optimal transition probability from 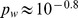 in
in 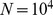 to
to 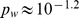 in
in 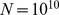 .
.
To see how the value of 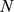 affects the optimal
affects the optimal 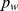 , we vary
, we vary 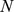 from
from 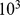 to
to 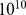 and calculate the optimal
and calculate the optimal 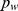 (Figure 2c). As
(Figure 2c). As 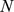 increases the optimal
increases the optimal 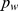 decreases monotonically approximately half an order of magnitude, but this change is small in comparison to the seven order of magnitude difference in
decreases monotonically approximately half an order of magnitude, but this change is small in comparison to the seven order of magnitude difference in 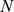 . Thus, the optimal transition probability remains close to
. Thus, the optimal transition probability remains close to 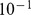 for a wide range of population sizes and is, therefore, insensitive to environmental carrying capacity.
for a wide range of population sizes and is, therefore, insensitive to environmental carrying capacity.
Unfair Competitions
Thus far, the competition between the two 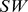 organisms has been fair with each starting at the same initial number and with the same growth rate. In actual biological systems, new competitors can invade or emerge via mutation. This is likely to result in an unfair competition in which one competitor faces an initial numerical or growth rate disadvantage. Disadvantages can also occur when an organism trades reduced growth rate in one environment against heightened performance in a second. Such an organism has a growth disadvantage in one environmental state and an initial numerical disadvantage in the second. It is likely that by changing transition probabilities organisms may compensate for any such disadvantage: a slower reproducing organism may do better if it has a higher transition probability. If compensation occurs then organisms evolving in such ecological conditions will face different selective pressures depending on their frequencies in the population.
organisms has been fair with each starting at the same initial number and with the same growth rate. In actual biological systems, new competitors can invade or emerge via mutation. This is likely to result in an unfair competition in which one competitor faces an initial numerical or growth rate disadvantage. Disadvantages can also occur when an organism trades reduced growth rate in one environment against heightened performance in a second. Such an organism has a growth disadvantage in one environmental state and an initial numerical disadvantage in the second. It is likely that by changing transition probabilities organisms may compensate for any such disadvantage: a slower reproducing organism may do better if it has a higher transition probability. If compensation occurs then organisms evolving in such ecological conditions will face different selective pressures depending on their frequencies in the population.
To see how an initial numerical advantage affects the competition, we allot one organism, 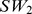 , a three fold advantage (150: 50) over the other,
, a three fold advantage (150: 50) over the other, 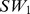 , and allow the total population to increase until the environmental state changes at
, and allow the total population to increase until the environmental state changes at 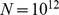 (population expansion from 2 to
(population expansion from 2 to 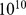 is the same fold as growing from 200 to
is the same fold as growing from 200 to 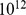 ). The initial numerical advantage allows
). The initial numerical advantage allows 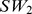 to maintain an advantage for a range of transition probabilities (Figure 3a), including the transition probability that is optimal in a fair competition. Still,
to maintain an advantage for a range of transition probabilities (Figure 3a), including the transition probability that is optimal in a fair competition. Still, 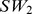 can be overtaken if its transition probability is below
can be overtaken if its transition probability is below 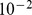 or if it is too high. For larger numerical advantages the range of unbeatable transition probabilities increases (Figure 3b). With a 100 fold advantage, an organism can maintain a numerical advantage for transition probabilities spanning three orders of magnitude. The value of
or if it is too high. For larger numerical advantages the range of unbeatable transition probabilities increases (Figure 3b). With a 100 fold advantage, an organism can maintain a numerical advantage for transition probabilities spanning three orders of magnitude. The value of 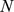 shifts the range of unbeatable transition probabilities such that lower
shifts the range of unbeatable transition probabilities such that lower 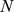 ’s require higher transition probabilities to maintain the advantage while higher
’s require higher transition probabilities to maintain the advantage while higher 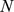 ’s permit lower transition probabilities.
’s permit lower transition probabilities.
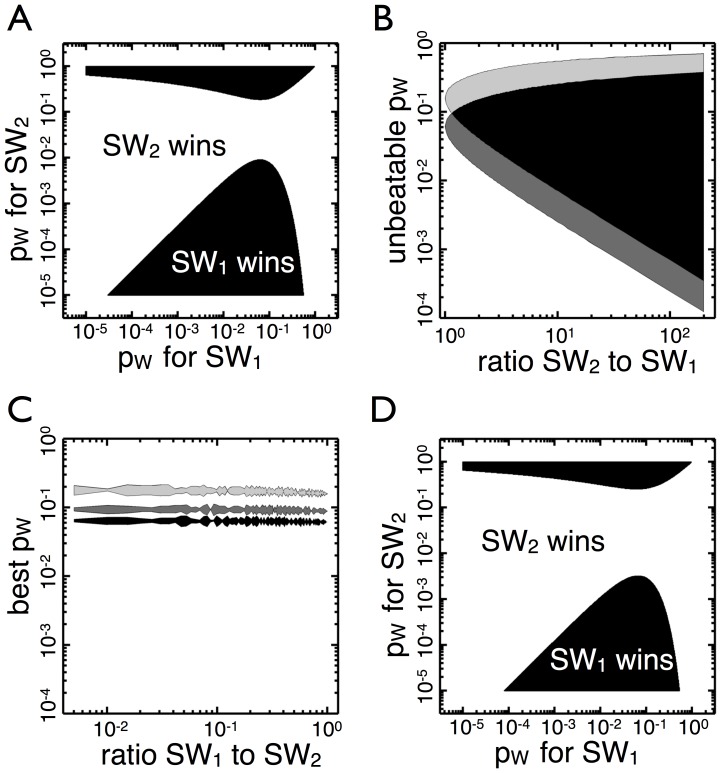
Figure 3. Competitions in which one organism has a numerical or growth advantage.
(A) 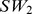 begins growth in
begins growth in 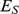 with a 3: 1 advantage to
with a 3: 1 advantage to 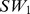 (150: 50, growing to N =
(150: 50, growing to N = 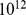 ). The black area corresponds to combinations of
). The black area corresponds to combinations of 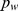 in which
in which 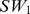 leaves more
leaves more 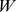 types than
types than 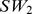 (white is the converse). The gap between the two areas corresponds to a range of transition probabilities in which
(white is the converse). The gap between the two areas corresponds to a range of transition probabilities in which 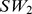 maintains an advantage independent of the transition probability of
maintains an advantage independent of the transition probability of 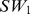 . (B) The range of transition probabilities for which
. (B) The range of transition probabilities for which 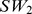 maintains an advantage is shown as a function of the initial numbers advantage. The light gray area corresponds to
maintains an advantage is shown as a function of the initial numbers advantage. The light gray area corresponds to 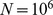 , the dark gray is
, the dark gray is 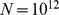 , and black is the overlap. Increased carrying capacity (N) shifts the range of transition probabilities down but does not greatly alter the total area. (C) The transition probability
, and black is the overlap. Increased carrying capacity (N) shifts the range of transition probabilities down but does not greatly alter the total area. (C) The transition probability 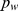 that minimizes the losses for
that minimizes the losses for 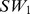 is shown as a function of its numerical disadvantage. The light gray is
is shown as a function of its numerical disadvantage. The light gray is 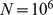 , the dark gray is
, the dark gray is 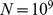 , and the black is
, and the black is 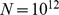 . There is a slight increase in the optimal transition probability as the disadvantage increases (left of the graph) but it is less than a tenth of an order of magnitude away from the optimal transition probability when the competition is fair. (D)
. There is a slight increase in the optimal transition probability as the disadvantage increases (left of the graph) but it is less than a tenth of an order of magnitude away from the optimal transition probability when the competition is fair. (D) 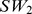 has a growth advantage compared to
has a growth advantage compared to 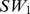 , dividing 10% faster. The two begin with one organism and divide until
, dividing 10% faster. The two begin with one organism and divide until 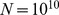 . Again
. Again 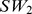 has a range of unbeatable transition probabilities, and the graph resembles A.
has a range of unbeatable transition probabilities, and the graph resembles A.
If an organism with an initial numerical disadvantage has the transition probability that is optimal in a fair competition then it minimize its chances of remaining outnumbered in the next environment (Figure 3c), regardless of the size of its disadvantage. Thus, the optimal transition probability in fair competitions is also the best in unfair competitions– whether an organism has an initial numerical advantage or disadvantage.
An initial numerical advantage is qualitatively similar to a growth advantage. The rate at which a homogeneous 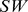 population grows depends not only on the doubling times of both phenotypes, but also the corresponding transition probabilities. For example, an
population grows depends not only on the doubling times of both phenotypes, but also the corresponding transition probabilities. For example, an 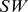 population growing in
population growing in 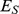 that never produces the slow-growing
that never produces the slow-growing 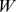 types will reach higher numbers than one that frequently produces
types will reach higher numbers than one that frequently produces 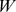 types. Instead of comparing absolute population growth rates of
types. Instead of comparing absolute population growth rates of 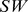 genotypes, we compare the growth rates of only the
genotypes, we compare the growth rates of only the 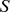 types in the
types in the 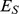 environment. As in the case where one genotype has an initial numerical advantage, a genotype with a faster growth rate (10% increase) is afforded a range of unbeatable transition probabilities (Figure 3d).
environment. As in the case where one genotype has an initial numerical advantage, a genotype with a faster growth rate (10% increase) is afforded a range of unbeatable transition probabilities (Figure 3d).
Growth Disparity between Phenotypes
A disparity in growth rates between 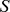 and
and 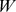 phenotypes creates a cost to producing the slower dividing, maladapted type (
phenotypes creates a cost to producing the slower dividing, maladapted type (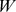 in
in  or
or 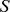 in
in 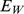 ). For each maladapted type that is produced there is less investment in the faster growing phenotype, and consequently the average growth rate for the
). For each maladapted type that is produced there is less investment in the faster growing phenotype, and consequently the average growth rate for the 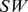 genotype decreases. Thus far, we have considered the case in which the maladapted types impose a maximum cost because they never divide. At the opposite extreme is the minimum cost in which
genotype decreases. Thus far, we have considered the case in which the maladapted types impose a maximum cost because they never divide. At the opposite extreme is the minimum cost in which 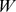 types grow at an identical rate to
types grow at an identical rate to 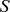 types in
types in 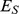 (Figure 4a). Since the goal is to leave the most
(Figure 4a). Since the goal is to leave the most 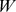 for the next environmental state (
for the next environmental state (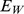 ) and there is no growth disadvantage to the
) and there is no growth disadvantage to the 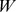 types, the optimal transition probability is 1,
types, the optimal transition probability is 1, 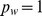 .
.
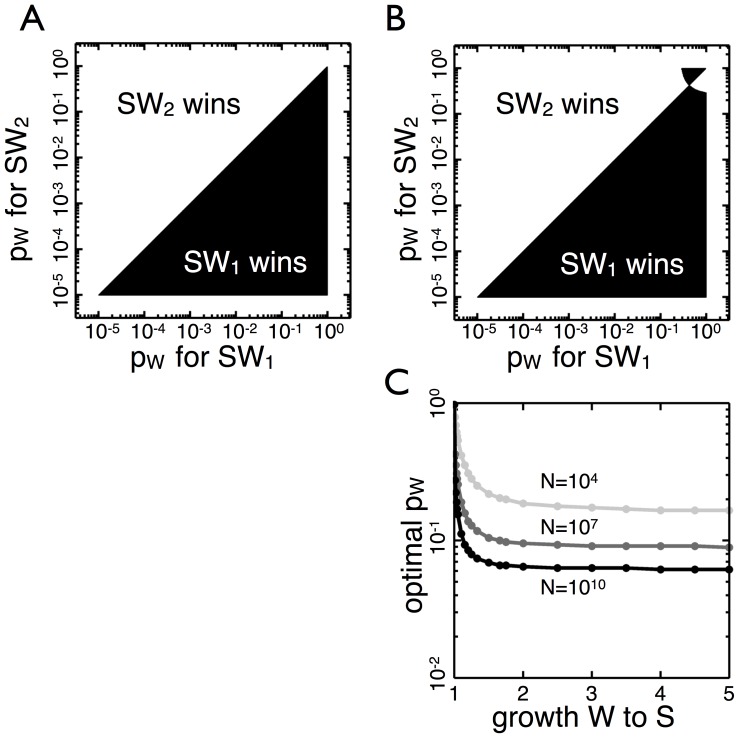
Figure 4. The effect of the maladapted type’s growth on the optimal transition probability.
(A) Two 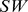 organisms compete (
organisms compete (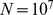 ) with different transition probabilities,
) with different transition probabilities, 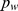 , when
, when 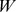 types grow at the same rate as
types grow at the same rate as 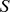 types– when the cost of maladapted type (
types– when the cost of maladapted type (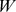 ) is minimal. Without a penalty for producing
) is minimal. Without a penalty for producing 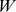 types the organism with the higher
types the organism with the higher 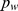 always wins. (B)
always wins. (B) 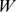 types grow 1% slower than S types (
types grow 1% slower than S types (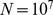 ). The optimal transition probability decreases and the top black area of the transition probability competition graph increases. (C) The optimal
). The optimal transition probability decreases and the top black area of the transition probability competition graph increases. (C) The optimal 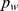 is shown as a function of the growth discrepancy between S and W types for three different values of N. The optimal transition probability when W types grow by a factor of 1.5 times slower than S types is approximately the same as when the W types do not reproduce at all.
is shown as a function of the growth discrepancy between S and W types for three different values of N. The optimal transition probability when W types grow by a factor of 1.5 times slower than S types is approximately the same as when the W types do not reproduce at all.
If a small cost is imposed so that the growth rate of W is reduced by 1–5% then the optimal transition probability drops super linearly (Figure 4b). Further increases in the cost show that the optimal transition probability quickly drops close to 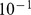 (Figure 4c). As the growth rate of the W types approaches half that of the S types, the optimal transition probability is the same as when the W types do not grow at all. The insensitivity of the optimal transition probability to the growth rate of the maladapted type is independent of N, the population size at which the environment transitions. Thus, as long as there is a growth disparity between the two phenotypes, there is selective pressure to stably produce both types at high frequency.
(Figure 4c). As the growth rate of the W types approaches half that of the S types, the optimal transition probability is the same as when the W types do not grow at all. The insensitivity of the optimal transition probability to the growth rate of the maladapted type is independent of N, the population size at which the environment transitions. Thus, as long as there is a growth disparity between the two phenotypes, there is selective pressure to stably produce both types at high frequency.
Closing the Life Cycle
Since we have only been considering one environmental transition 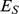 to
to 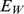 , we have focused attention on the probability of producing W types from S types. Indeed, this determines the preparedness of an organism to succeed when the environment switches to the
, we have focused attention on the probability of producing W types from S types. Indeed, this determines the preparedness of an organism to succeed when the environment switches to the 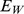 state. To survive multiple environmental oscillations, however, organisms must be able to switch back and forth between types. The probability that a W type produces an S type upon division (
state. To survive multiple environmental oscillations, however, organisms must be able to switch back and forth between types. The probability that a W type produces an S type upon division (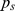 ) is therefore essential to surviving the transition from
) is therefore essential to surviving the transition from 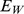 back to
back to 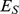 . While essential during growth in
. While essential during growth in 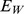 ,
, 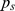 counteracts the effect of
counteracts the effect of 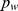 during growth in
during growth in 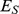 . Since the success of SW organisms depends on both transition probabilities,
. Since the success of SW organisms depends on both transition probabilities, 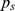 and
and 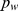 , we investigate their interactions and the effects on the optimal strategy.
, we investigate their interactions and the effects on the optimal strategy.
To uncover how 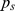 and
and 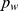 interact, we first fix
interact, we first fix 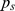 for both SW organisms to ensure that their W types have the same probability of producing S upon cell division. For different combinations of
for both SW organisms to ensure that their W types have the same probability of producing S upon cell division. For different combinations of 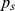 and growth rates of W, we calculate the optimal transition probability
and growth rates of W, we calculate the optimal transition probability 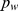 (Figure 5a). The upper and lower bounds of
(Figure 5a). The upper and lower bounds of 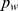 are set by the maximal and minimal cost of the maladapted phenotype, that is, the upper bound is at the point where W never divides and the lower bound is defined by the point at which W divides at the same rate as S. The optimal
are set by the maximal and minimal cost of the maladapted phenotype, that is, the upper bound is at the point where W never divides and the lower bound is defined by the point at which W divides at the same rate as S. The optimal 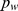 in either case does not depend on the value of
in either case does not depend on the value of 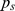 . When W never divides,
. When W never divides, 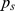 has no effect on the optimal
has no effect on the optimal 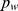 because W never has the opportunity to produce S. When W divides at the same rate as S, the optimal strategy is to produce W types as often as possible regardless of how often W types give rise to S types. For intermediate growth rates, when W grows at 66% or 90% the rate of S, the optimal value of
because W never has the opportunity to produce S. When W divides at the same rate as S, the optimal strategy is to produce W types as often as possible regardless of how often W types give rise to S types. For intermediate growth rates, when W grows at 66% or 90% the rate of S, the optimal value of 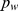 is unaffected by
is unaffected by 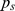 as long as
as long as 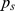 is low (
is low (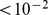 ). Once
). Once 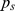 increases above
increases above 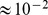 the optimal
the optimal 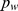 also increases. Since the effect of
also increases. Since the effect of 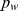 is to produce W types, high values of
is to produce W types, high values of 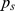 counteract this effect and thereby act as a leak. In order for an organism to leave enough W types at the end of growth in an environmental state, it must increase
counteract this effect and thereby act as a leak. In order for an organism to leave enough W types at the end of growth in an environmental state, it must increase 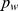 to offset the loss of potential W types due to
to offset the loss of potential W types due to 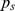 .
.
Figure 5. The effect of the probability 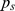 on the optimal transition probability.
on the optimal transition probability.
(A) The optimal value of 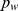 is shown as a function of a fixed
is shown as a function of a fixed 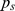 for both organisms. The light gray horizontal lines represent the trivial cases when W types never divide (bottom) or grow at the same rate as S types (top). When W grows 90% of the rate of S (black) or 66% of the rate of S (dark gray) the optimal
for both organisms. The light gray horizontal lines represent the trivial cases when W types never divide (bottom) or grow at the same rate as S types (top). When W grows 90% of the rate of S (black) or 66% of the rate of S (dark gray) the optimal 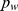 does not change until
does not change until 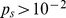 , at which point it increases to counteract
, at which point it increases to counteract 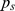 . (B) For competitions between SW organisms with different values of
. (B) For competitions between SW organisms with different values of 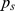 (
(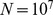 ), the organism with the lower
), the organism with the lower 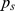 has an advantage and has a range of transition probabilities for which it does not lose in frequency. The shading color corresponds to the size of this range:
has an advantage and has a range of transition probabilities for which it does not lose in frequency. The shading color corresponds to the size of this range: 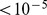 (black),
(black), 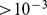 (light gray), and
(light gray), and 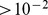 (dark gray). For larger differences in
(dark gray). For larger differences in 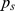 , there exist more transition probabilities
, there exist more transition probabilities 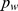 that an organism can adopt to maintain or gain in frequency. (C) The optimal
that an organism can adopt to maintain or gain in frequency. (C) The optimal 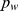 is shown as a function of the advantage in
is shown as a function of the advantage in 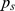 for competitions from B. The
for competitions from B. The 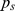 for
for 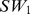 is fixed at either
is fixed at either 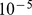 (black),
(black), 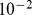 (light gray), or
(light gray), or 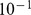 (dark gray). The range of the optimal
(dark gray). The range of the optimal 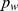 (area between curves of the same color) is narrow until the
(area between curves of the same color) is narrow until the 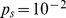 for
for 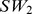 . Thus, the range depends on the magnitude of the advantage only when
. Thus, the range depends on the magnitude of the advantage only when 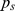 is sufficiently high.
is sufficiently high.
When the condition that competing SW organisms have identical values of 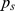 is relaxed, the organism with the lower
is relaxed, the organism with the lower 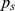 is more successful (Figure 5b). If there is a large discrepancy in
is more successful (Figure 5b). If there is a large discrepancy in 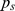 , the organism with the lower
, the organism with the lower 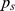 has a range of unbeatable
has a range of unbeatable 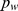 transition probabilities similar to what was observed in the case of unfair competitions (Figure 3). High values of
transition probabilities similar to what was observed in the case of unfair competitions (Figure 3). High values of 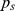 are detrimental because they impede accumulation of W types. During growth in
are detrimental because they impede accumulation of W types. During growth in 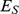 , the best strategy is to balance the faster division of S types with the production of W types that are essential to future success. Each time a W type gives rise to an S type it results in one W and one S. This same result could be obtained more quickly if an S type divides to give rise to a W. The delay due to waiting for a W type to divide as opposed to an S type, effectively reduces the growth rate of the SW genotype and allows those with lower values of
, the best strategy is to balance the faster division of S types with the production of W types that are essential to future success. Each time a W type gives rise to an S type it results in one W and one S. This same result could be obtained more quickly if an S type divides to give rise to a W. The delay due to waiting for a W type to divide as opposed to an S type, effectively reduces the growth rate of the SW genotype and allows those with lower values of 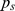 to dominate.
to dominate.
Although the organism with the lower 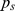 has an advantage it is unclear how this affects the optimal transition probability
has an advantage it is unclear how this affects the optimal transition probability 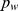 . We assign organism
. We assign organism 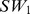 a lower back probability,
a lower back probability, 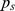 , than its competitor
, than its competitor 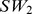 and calculate the range of unbeatable transition probabilities
and calculate the range of unbeatable transition probabilities 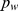 for
for 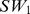 (Figure 5c). If
(Figure 5c). If 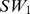 has
has 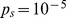 there is a narrow range of optimal transition probabilities
there is a narrow range of optimal transition probabilities 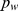 in which winning is possible even when
in which winning is possible even when 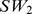 has a
has a 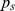 value two orders of magnitude higher. By contrast if
value two orders of magnitude higher. By contrast if 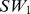 has a
has a 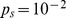 and competes against an
and competes against an 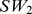 whose
whose 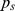 is only slightly higher then there is a wide range of unbeatable transition probabilities – as wide as if the
is only slightly higher then there is a wide range of unbeatable transition probabilities – as wide as if the 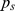 for
for 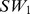 had been
had been 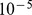 . This reflects the fact that
. This reflects the fact that 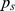 does not affect the optimal strategy unless it is sufficiently frequent. Furthermore the transition probability
does not affect the optimal strategy unless it is sufficiently frequent. Furthermore the transition probability 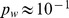 remains unbeatable regardless of the advantage in
remains unbeatable regardless of the advantage in 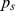 .
.
The Number of Competitors
As organisms grow and colonize environments, it is likely there will be more than just two competing genotypes. With more competitors, there is more opportunity for complex interactions between diverse strategies. It is possible that the previous optimal transition probabilities do not fare well against combinations of strategies. Furthermore, the competition may no longer produce a single unbeatable strategy. To explore these possibilities, we consider an expanded competition between hundreds of genotypes.
Increasing the number of competitors, however, means that it is no longer feasible to systematically search parameter combinations as was done before. Instead, we establish a tournament to find the best strategy in the space of transition probabilities. First, we randomly generate competing genotypes by sampling transition probabilities from a uniform distribution in log space (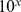 , where
, where  is sampled from a uniform distribution between
is sampled from a uniform distribution between 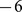 and 0). Each genotype is defined by its four transition probabilities:
and 0). Each genotype is defined by its four transition probabilities: 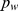 in
in 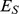 ,
, 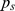 in
in 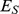 ,
, 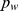 in
in 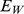 , and
, and 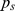 in
in 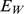 . We then simulate the population dynamics of competing genotypes through a full environmental cycle: beginning in
. We then simulate the population dynamics of competing genotypes through a full environmental cycle: beginning in 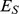 , moving to
, moving to 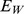 , and returning back to
, and returning back to 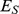 . In each environmental state the population grows by a factor of
. In each environmental state the population grows by a factor of 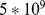 , which is equivalent to two organisms growing to a population of
, which is equivalent to two organisms growing to a population of 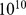 . Maladapted types (W in
. Maladapted types (W in 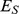 and S in
and S in 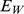 ) require twice the time to reproduce as the adapted types (S in
) require twice the time to reproduce as the adapted types (S in 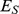 and W in
and W in 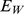 ). As the environment switches states only the previously maladapted type can pass through, e.g. when
). As the environment switches states only the previously maladapted type can pass through, e.g. when 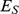 changes to
changes to 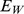 only W types can pass through. After one complete cycle the most abundant genotype is the winner and allowed to continue to the next round. The remaining competitors are replaced with new competitors whose transition probabilities are identical to that of the winner, except that one is randomly changed. This process allows tuning of the winning strategy as each new winner represents the adjustment of one parameter. If all transition probabilities were changed simultaneously it would take longer to find the optimal strategy because optimal parameters would be linked with potentially poor parameters.
only W types can pass through. After one complete cycle the most abundant genotype is the winner and allowed to continue to the next round. The remaining competitors are replaced with new competitors whose transition probabilities are identical to that of the winner, except that one is randomly changed. This process allows tuning of the winning strategy as each new winner represents the adjustment of one parameter. If all transition probabilities were changed simultaneously it would take longer to find the optimal strategy because optimal parameters would be linked with potentially poor parameters.
Due to the symmetry of the system, 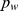 in
in 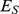 should act similarly to
should act similarly to 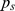 in
in 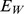 because both of these probabilities correspond to production of the type better suited to the next environment. From our analysis of the reduced model, we predict a successful organism will have these probabilities tuned close to
because both of these probabilities correspond to production of the type better suited to the next environment. From our analysis of the reduced model, we predict a successful organism will have these probabilities tuned close to 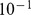 . Likewise, the other two transition probabilities (
. Likewise, the other two transition probabilities (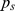 in
in 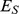 and
and 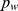 in
in 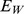 ) share a similar role in opposing the direction of environmental change. Tuning of these probabilities should result in as low a value as possible (
) share a similar role in opposing the direction of environmental change. Tuning of these probabilities should result in as low a value as possible (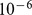 in this expanded model).
in this expanded model).
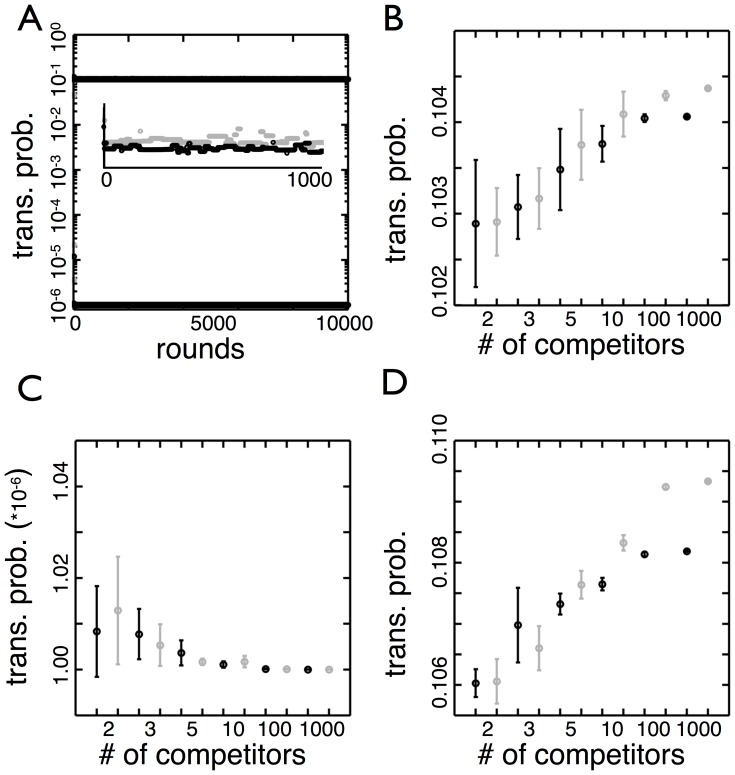
For numbers of competitors ranging from 2 to 1000, we conduct the tournament for 10,000 rounds 10 independent times (see File S1 for sample computer code). An example simulation using 1,000 competitors (Figure 6a) shows that though there are frequent replacements, the winning transition probabilities are close to the predicted values. The optimal values for 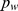 in
in 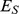 and
and 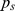 in
in 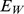 (black and gray in Figure 6b) are between
(black and gray in Figure 6b) are between 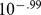 and
and 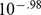 for all competitions between 2 to 1000 competitors. While the optimal transition probabilities for tournaments with 1,000 competitors are higher (significance tested with t-test,
for all competitions between 2 to 1000 competitors. While the optimal transition probabilities for tournaments with 1,000 competitors are higher (significance tested with t-test, 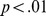 ) than those with 2 competitors, the relative difference is less than 2%. The optimal values for
) than those with 2 competitors, the relative difference is less than 2%. The optimal values for 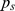 in
in 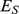 and
and 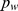 in
in 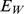 (black and gray in Figure 6c) also match with predictions and are close to
(black and gray in Figure 6c) also match with predictions and are close to 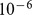 .
.
Figure 6. Competition between more than two genotypes.
(A) The transition probabilities of the winning genotype are shown over 10,000 environmental cycles (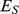 to
to 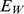 to
to 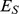 ). Each cycle begins with 1,000 genotypes in equal number and at the end of a full cycle the most abundant genotype (the winner) advances to the next round to compete against new, randomly generated genotypes. The transition probabilities of the winner are grouped by environmental state: black is
). Each cycle begins with 1,000 genotypes in equal number and at the end of a full cycle the most abundant genotype (the winner) advances to the next round to compete against new, randomly generated genotypes. The transition probabilities of the winner are grouped by environmental state: black is 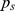 and
and 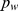 in
in 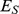 and gray is
and gray is 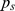 and
and 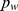 in
in 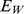 . The inset is a magnification that shows the winner changes frequently but in the long run the winner appears as unbroken lines. (B) The transition probabilities (
. The inset is a magnification that shows the winner changes frequently but in the long run the winner appears as unbroken lines. (B) The transition probabilities (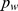 in
in 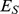 is black and
is black and 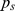 in
in 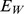 is gray) of the winning genotypes are shown as a function of the numbers of competitors. Each point is the average of 10 runs of tournaments (as shown in A) sampled every 100 rounds after 2500 rounds (“burn-in phase”). The error bars are the standard deviation of the 10 runs. The values remain close to
is gray) of the winning genotypes are shown as a function of the numbers of competitors. Each point is the average of 10 runs of tournaments (as shown in A) sampled every 100 rounds after 2500 rounds (“burn-in phase”). The error bars are the standard deviation of the 10 runs. The values remain close to 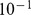 for different numbers of competitors. (C) The same as B but this shows the other two transition probabilities (
for different numbers of competitors. (C) The same as B but this shows the other two transition probabilities (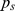 in
in 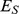 is black and
is black and 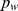 in
in 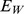 is gray) for winning genotypes. The values are all close to the lower bound of transition probabilities considered (
is gray) for winning genotypes. The values are all close to the lower bound of transition probabilities considered (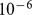 ), so the number of competitors has no effect. (D) The transition probabilities of the winning genotype are shown when the probabilities do not depend on the environmental state. Due to the symmetry of the system the optimal
), so the number of competitors has no effect. (D) The transition probabilities of the winning genotype are shown when the probabilities do not depend on the environmental state. Due to the symmetry of the system the optimal 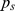 (gray) and
(gray) and 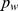 (black) are identical. There is a statistically significant increase in the transition probabilities for the competition of 1000 competitors versus 2, but the magnitude of difference is small.
(black) are identical. There is a statistically significant increase in the transition probabilities for the competition of 1000 competitors versus 2, but the magnitude of difference is small.
So far, the transition probabilities between phenotypes have varied with environmental state but this may not always be the case. If, instead, the probabilities are independent of the environment, then only two parameters define a genotype in this tournament. Moreover, this means while 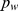 is beneficial in
is beneficial in 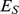 it is a hinderance in
it is a hinderance in 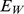 . To see how this affects the optimal strategy, we repeat the tournaments with transition probabilities that do not depend on the environment (Figure 6d) and find that both transition probabilities are close to
. To see how this affects the optimal strategy, we repeat the tournaments with transition probabilities that do not depend on the environment (Figure 6d) and find that both transition probabilities are close to 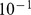 regardless of the number of competitors. This indicates that the benefit for a high
regardless of the number of competitors. This indicates that the benefit for a high 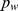 in
in 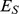 outweighs its cost in
outweighs its cost in 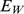 . As found previously, the transition probabilities increase as the number of competitors increases (significance tested with t-test
. As found previously, the transition probabilities increase as the number of competitors increases (significance tested with t-test 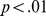 ) but the difference is small in comparison with the change due to the number of competitors.
) but the difference is small in comparison with the change due to the number of competitors.
Exclusions during Environmental Transitions
As environmental states alternate in the Pseudomonas fluorescens experimental system, phenotypes are excluded so that only one type can advance to the next state. As oxygen in the broth becomes exhausted by growth of S types, opportunity is created for mat-forming W types that colonize the air-liquid interface. Once a mat collapses and oxygen penetrates into the broth phase, only the unentangled S types are free to grow. This exclusion, as incorporated into our model, is perfect in that none of the other type is able to pass through to the next environmental state. In other biological systems, it is possible that fractions of both types might survive changes in environmental states, i.e. the environmental transitions do not perfectly filter phenotypes. Such imperfect filtering may reduce the pressure to switch at high frequencies and, thereby, reduce the effectiveness of the switching strategy that was optimal under perfect filtering.
Imperfect filtering is implemented by allowing a fraction of the type better adapted to the current environment to survive as the environment transitions, for example, some S survive as 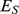 switches to
switches to 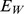 . This introduces three new parameters to the model: the fraction of each type that survives along with the total number of types permitted to advance to the next environment (the size of the bottleneck). A full investigation of the effects of these parameters is beyond the scope of this paper. However, we simulate a competition between two organisms through repeated environmental cycles to discover what qualitative dynamics are possible. As the environment transitions from
. This introduces three new parameters to the model: the fraction of each type that survives along with the total number of types permitted to advance to the next environment (the size of the bottleneck). A full investigation of the effects of these parameters is beyond the scope of this paper. However, we simulate a competition between two organisms through repeated environmental cycles to discover what qualitative dynamics are possible. As the environment transitions from 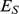 to
to 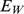 we allow 1% of the S types to survive, and likewise for the converse. From a bottleneck size of 105 the populations grow an additional 1010 cells, i.e. the carrying capacity is
we allow 1% of the S types to survive, and likewise for the converse. From a bottleneck size of 105 the populations grow an additional 1010 cells, i.e. the carrying capacity is 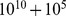 . The competing genotypes (
. The competing genotypes ( and
and 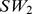 ) have identical growth rates for W and S types with maladapted types (W in
) have identical growth rates for W and S types with maladapted types (W in 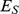 and S in
and S in 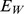 ) reproducing half as fast as adapted types. The only difference between genotypes is the set of transition probabilities between states. The environments cycle until the populations reach a stable state. The results of the simulations show qualitatively different dynamics depending on the combinations of transition probabilities (Figure 7).
) reproducing half as fast as adapted types. The only difference between genotypes is the set of transition probabilities between states. The environments cycle until the populations reach a stable state. The results of the simulations show qualitatively different dynamics depending on the combinations of transition probabilities (Figure 7).
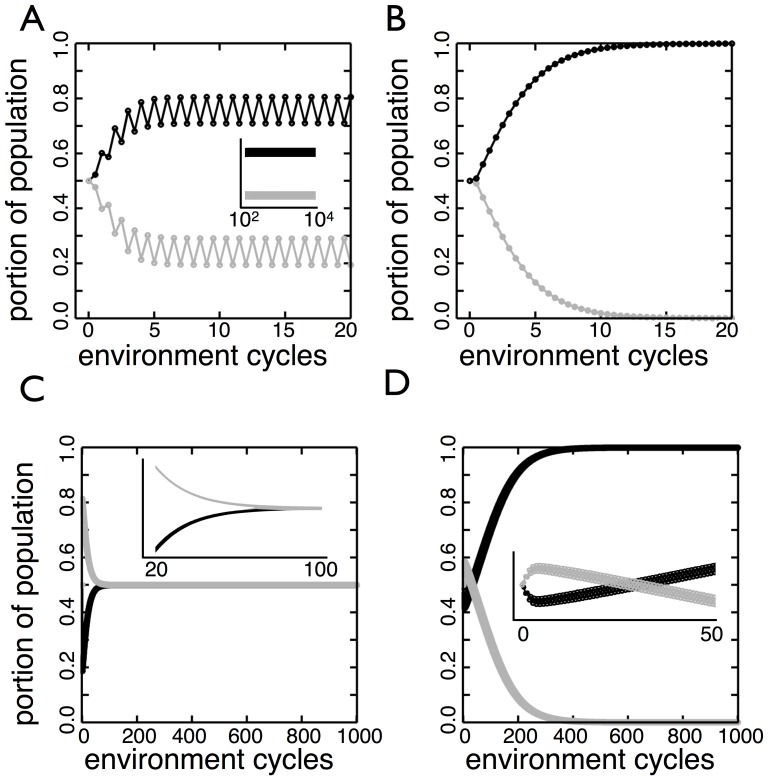
Figure 7. Different behaviors with an imperfect filter between environments.
(A) The populations of 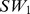 (black) and
(black) and 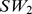 (gray) form a stable oscillation as the environments cycle between
(gray) form a stable oscillation as the environments cycle between 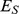 and
and 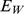 . The transition probabilities are presented
. The transition probabilities are presented 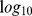 in the order of
in the order of 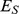
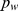 ,
, 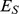
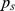 ,
, 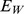
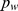 , and
, and 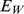
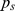 . For
. For 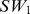 the transition probabilities are
the transition probabilities are 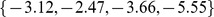 and for
and for 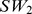 they are
they are 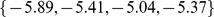 . (B)
. (B)  (black) drives
(black) drives 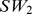 (gray) extinct. For
(gray) extinct. For 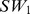 the transition probabilities are the optimal set using perfect filters
the transition probabilities are the optimal set using perfect filters 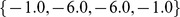 and for
and for 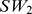 they are
they are 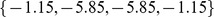 . (C)
. (C) 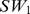 (black) and
(black) and 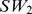 (gray) monotonically approach the same frequency in the population. For
(gray) monotonically approach the same frequency in the population. For 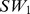 the transition probabilities are
the transition probabilities are 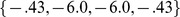 and for
and for 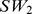 they are the optimal set when perfect filters are used
they are the optimal set when perfect filters are used 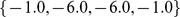 . (D)
. (D) 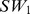 (black) decreases in frequency for five rounds before changing direction and driving
(black) decreases in frequency for five rounds before changing direction and driving 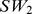 (gray) extinct. The transition probabilities for
(gray) extinct. The transition probabilities for 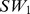 are
are 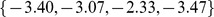 and for
and for 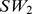 they are
they are 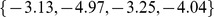 .
.
The two types of system dynamics most common to imperfect filters are those involving stable oscillations or extinctions. In a stable oscillation the SW organisms cycle between two different frequencies corresponding to growth in the different environments (Figure 7a). Each organism is more adapted to one environmental state and alternates between high and low abundance. In those instances where extinction is the norm (Figure 7b) models show that the approach to extinction can be monotonic or oscillatory depending on whether an organism repeatedly gains in frequency in one or both environmental states.
While stable oscillations and extinctions are common, imperfect filters do permit behavior that was not observed when perfect filters were applied. For example, the switching strategy that was optimal in earlier sections (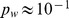 ,
, 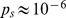 in
in 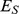 and the converse in
and the converse in 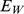 ) is no longer dominant in the face of an imperfect filter. Figure 7c shows a monotonic approach to a polymorphism in which one organism steadily increases at the expense of the other organism. The decreasing organism has the switching strategy that was previously optimal under perfect exclusion. Although, the steady state frequency could be any value between 0 and 1, we show the case in which both organisms represent exactly half of the population despite their different transition probabilities. Another instance of behavior that is only possible with imperfect filters is the “come from behind win”. In Figure 7d, the gray organism initially increases in frequency over the first five complete environmental cycles and then begins a steady decline to extinction. This example demonstrates that the absolute abundance of an organism is not indicative of how it is performing. The gray organism appears as though it will drive the other organism extinct. With each environmental cycle, however, the organism in black shifts its allocation of types so that at the start of growth in a future environmental state it has the numerical advantage in the fast-growing type. These two examples demonstrate that although coupling environmental transitions to organismal growth stably selects for a switching strategy when perfect exclusion is in operation, it is less straightforward when the environment imperfectly filters types.
) is no longer dominant in the face of an imperfect filter. Figure 7c shows a monotonic approach to a polymorphism in which one organism steadily increases at the expense of the other organism. The decreasing organism has the switching strategy that was previously optimal under perfect exclusion. Although, the steady state frequency could be any value between 0 and 1, we show the case in which both organisms represent exactly half of the population despite their different transition probabilities. Another instance of behavior that is only possible with imperfect filters is the “come from behind win”. In Figure 7d, the gray organism initially increases in frequency over the first five complete environmental cycles and then begins a steady decline to extinction. This example demonstrates that the absolute abundance of an organism is not indicative of how it is performing. The gray organism appears as though it will drive the other organism extinct. With each environmental cycle, however, the organism in black shifts its allocation of types so that at the start of growth in a future environmental state it has the numerical advantage in the fast-growing type. These two examples demonstrate that although coupling environmental transitions to organismal growth stably selects for a switching strategy when perfect exclusion is in operation, it is less straightforward when the environment imperfectly filters types.
Discussion
Multicellular organisms depend on developmental programs to coordinate their growth and differentiation from single-celled propagules so as to effect a life cycle [3], [5], [7], [9]. Yet, the evolutionary origins of such developmental programs are unknown [2], [5], [9]–[11]. It is likely that early developmental programs began as little more than phenotypic noise in the form of genotypes that probabilistically produce different phenotypes [8]–[10], [12]. Possibly, such phenotypic switching might itself have been the product of evolution in fluctuating or unpredictable environments [14]–[20]. Noisy expression of phenotypes could conceivably come under regulatory control if evolving organisms experience environmental conditions that provide reliable information of appropriate quality [13], [33]. Our models show that if there is coupled feedback between phenotypic and environmental states then this can lead to stabilizing selection for a single optimal switch probability. Circumstances that maintain switches of this kind are likely to define conditions central to the ecology of development.
The findings from our model expand the evolutionary role of phenotypic noise as embodied by stochastic switchers. Typically, phenotypic noise is understood to be an evolved response to uncertain, fluctuating environments: genotypes capable of stochastically switching phenotypes can hedge their evolutionary bets to maximize long-term geometric fitness [34]. Moreover, organisms whose switch rates are better tuned to the frequency of environmental oscillations are fitter. To predict how switching rates evolve requires knowledge of the frequency of environmental fluctuations. Without some force driving regular environmental oscillations, prolonged periods in one environmental state is likely to result in loss of the capacity to switch. In contrast, when environmental oscillations are coupled to organismal growth there is a steady drive to maintain switching. Coupling establishes conditions that select for a single optimal switch rate (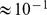 for the type suited to the next environmental state), so organisms can maximize their fitness by adopting this rate regardless of the rates of competing organisms. Furthermore, the fact that this optimal switch rate is high increases selection for organisms to find a non-mutational route to phenotypic innovation. Thus, coupling environmental oscillations to organismal growth produces conditions that favor organisms that tune phenotypic noise towards the optimal switch rate.
for the type suited to the next environmental state), so organisms can maximize their fitness by adopting this rate regardless of the rates of competing organisms. Furthermore, the fact that this optimal switch rate is high increases selection for organisms to find a non-mutational route to phenotypic innovation. Thus, coupling environmental oscillations to organismal growth produces conditions that favor organisms that tune phenotypic noise towards the optimal switch rate.
While coupling yields a single optimal strategy, it would not be much use if the strategy relied on very specific environmental conditions. For example, if the optimal strategy depended on a particular carrying capacity then small fluctuations to nutrient availability would jeopardize its long-term success. Additionally, if the optimal strategy changed with the composition of the population then there would be frequent pressure to adjust the switching rate. Such sensitivities, however, do not appear in our model. The optimal switching strategy is robust to changes in the carrying capacity of the environment as well as the number, growth rates, and switching strategies of competing organisms. This robustness means that organisms who adopt the optimal strategy can remain dominant despite environmental perturbations. Moreover, there is more opportunity to spread and successfully colonize other environments as long as coupling between phenotypic state and environment is maintained. This extended success affords organisms who adopt the optimal strategy more time to realize a chance mutation that moves phenotypic switching away from noisy mechanisms and towards developmental regulation.
One key assumption of our model is that the probability of producing phenotypes, the switching rates, can evolve. Although stochastic switchers have been engineered to switch at different rates [35], there has not yet been experimental characterization of the capacity of switches to evolve. The degree to which a switch can be tuned through evolutionary processes likely depends on the mechanism of the switch and the underlying regulatory networks [21], [33], [36]. For example, if the switch frequency depends on the binding of a protein to some molecule then the switch might be tuned through modification of the protein’s amino acid composition or its regulation. If, however, the switch were a product of a whole pathway then the number of evolutionary targets would likely increase as would the potential for pleiotropic effects. In either case, it is not clear what switch rates can be obtained or what type of resolution there is in switch rate tuning. Moreover, it is possible that the recurring 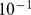 optimal transition probability may be too high for some systems to achieve. In these cases, our model predicts that the highest obtainable transition probability would then be optimal.
optimal transition probability may be too high for some systems to achieve. In these cases, our model predicts that the highest obtainable transition probability would then be optimal.
Despite the coupling between environmental change and organismal growth in our model, there does not need to be any regularity to the frequency of environmental oscillations– even if the entire population has the same switching rate. This potential disconnect between switch rates and environmental oscillations stems from the way our model implements environmental change. We assume that environmental states do not change until the population of organisms has reached the carrying capacity (N). Once the population equals the carrying capacity, the environmental state can change immediately or any time afterwards as long as the population composition does not change before the environmental state changes. As a consequence, the population may evolve to an optimal switching rate without necessarily creating a regular frequency of environmental oscillations. If, however, the environment does change a fixed time after the population reaches N then an optimal set of transition probabilities implies the environment will oscillate at a specific frequency.
Although our model captures the basic cyclic ecological conditions present in the Pseudomonas fluorescens experimental system, it is unclear how prevalent these conditions are in other biological systems. Certainly there are many instances in which organisms modify the environment to favor another phenotype that they, themselves, produce [22], [25]. This is a particular issue in the evolution of cooperation as cooperative phenotypes modify the environment to favor cheater types who arise via mutations [26], [37]–[39]. Indeed, the Pseudomonas fluorescens experimental system has been used to study the evolution of cooperation with the mat formers (W) representing cooperators and the smooth types (S) representing cheats [11]. The key aspect of the experimental system– and our model– is the closed cycle, i.e. how the cheats change the environment to favor the cooperators. The likelihood of this event should determine the prevalence of the ecological conditions. If the cycle can be closed, our model shows that there is a strong pressure to switch rapidly between types.
Finally, the extent to which environmental transitions filter phenotypes turns out to be critical. This makes sense given that the amount of filtering depends in part on the differences between environmental states, i.e., similar environmental states are less likely to filter phenotypes. As environmental states become more alike it is expected that generalist strategies emerge. Conversely, with greater differentiation between environmental states greater phenotypic exclusion is expected, and, therefore, selection for switching at high frequency [28], [29] While it is easier to imagine imperfect filters as being more prevalent in biological systems, perfect filters exist in multicellular organisms in the form of the germ-soma distinction. By denying soma the ability to reproduce without the germ line and vice versa, multicellular organisms use perfect filters to assure the continued reliable production of a life cycle.
Supporting Information
Sample computer code for simulations.
(PDF)
Acknowledgments
The authors thank Maria Abou Chakra and Yuriy Pichugin for useful feedback and commentary.
Funding Statement
This research was supported in part by grant RFP-12-20 from the Foundational Questions in Evolutionary Biology Fund as well as the Marsden Research Council. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Smith JM, Szathmáry E (1997) The Major Transitions in Evolution. Oxford University Press, USA.
- 2. Wolpert L (1990) The evolution of development. Biol J Linn Soc 39: 109–124. [Google Scholar]
- 3.Wolpert L (1994) The evolutionary origin of development: cycles, patterning, privilege and continuity. Dev Suppl: 79–84. [PubMed]
- 4.Okasha S (2009) Evolution and the Levels of Selection. Oxford University Press, USA.
- 5.Buss LW (1987) The evolution of individuality. Princeton University Press, USA.
- 6. Wolpert L, Szathmáry E (2002) Multicellularity: evolution and the egg. Nature 420: 745. [DOI] [PubMed] [Google Scholar]
- 7. Arthur W (2002) The emerging conceptual framework of evolutionary developmental biology. Nature 415: 757–764. [DOI] [PubMed] [Google Scholar]
- 8.West-Eberhard MJ (2003) Developmental Plasticity and Evolution. Oxford University Press, USA.
- 9. Schlichting CD (2003) Origins of differentiation via phenotypic plasticity. Evol Dev 5: 98–105. [DOI] [PubMed] [Google Scholar]
- 10. Minelli A, Fusco G (2010) Developmental plasticity and the evolution of animal complex life cycles. Philos Trans R Soc Lond B Biol Sci 365: 631–640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Rainey PB, Kerr B (2010) Cheats as first propagules: a new hypothesis for the evolution of individuality during the transition from single cells to multicellularity. BioEssays 32: 872–880. [DOI] [PubMed] [Google Scholar]
- 12. Ancel LW (2000) Undermining the Baldwin expediting effect: does phenotypic plasticity accelerate evolution? Theor Popul Biol 58: 307–319. [DOI] [PubMed] [Google Scholar]
- 13. Moczek A, Sultan S, Foster S, Ledón-Rettig C, Dworkin I, et al. (2011) The role of developmental plasticity in evolutionary innovation. Proc R Soc B 278: 2705–2713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Moran NA (1992) The evolutionary maintenance of alternative phenotypes. Am Nat 139(5): 971–989. [Google Scholar]
- 15. Levins R (1962) Theory of fitness in a heterogeneous environment. I. The fitness set and the adaptive function. Am Nat 96: 361–373. [Google Scholar]
- 16. Bull JJ (1987) Evolution of phenotypic variance. Evolution 41: 303–315. [DOI] [PubMed] [Google Scholar]
- 17. Via S, Lande R (1985) Genotype-environment interaction and the evolution of phenotypic plasticity. Evolution 39: 505–522. [DOI] [PubMed] [Google Scholar]
- 18. Donaldson-Matasci MC, Lachmann M, Bergstrom CT (2008) Phenotypic diversity as an adaptation to environmental uncertainty. Evol Ecol Res 10: 493–515. [Google Scholar]
- 19. Kussell E, Leibler S (2005) Phenotypic diversity, population growth, and information in fluctuating environments. Science 309: 2075–2078. [DOI] [PubMed] [Google Scholar]
- 20. Thattai M, van Oudenaarden A (2004) Stochastic gene expression in fluctuating environments. Genetics 167: 523–530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Newman SA, Müller GB (2000) Epigenetic mechanisms of character origination. J Exp Zool 288: 304–317. [DOI] [PubMed] [Google Scholar]
- 22. Laland KN, Odling-Smee FJ, Feldman MW (1999) Evolutionary consequences of niche construction and their implications for ecology. PNAS 96(18): 10242–10247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Schoener TW (2011) The Newest Synthesis: Understanding the interplay of evolutionary and ecological dynamics. Science 331(6016): 426–429. [DOI] [PubMed] [Google Scholar]
- 24. Fussmann GF, Loreau M, Abrams PA (2007) Eco-evolutionary dynamics of communities and ecosystems. Funct Ecol 21(3): 465–477. [Google Scholar]
- 25. Donohue K (2005) Niche construction through phenological plasticity: life history dynamics and ecological consequences. New Phytol 166(1): 83–92. [DOI] [PubMed] [Google Scholar]
- 26. Rainey PB, Rainey K (2003) Evolution of cooperation and conflict in experimental bacterial populations. Nature 425(4): 72–74. [DOI] [PubMed] [Google Scholar]
- 27. Beaumont HJE, Gallie J, Kost C, Ferguson GC, Rainey PB (2009) Experimental evolution of bet hedging. Nature 462: 90–93. [DOI] [PubMed] [Google Scholar]
- 28. Libby E, Rainey PB (2011) Exclusion rules, bottlenecks and the evolution of stochastic phenotype switching. Proc Biol Sci 278(1724): 3574–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Rainey PB, Beaumont HJE, Ferguson GC, Gallie J, Kost C, et al. (2011) The evolutionary emergence of stochastic phenotype switching in bacteria. Microb Cell Fact 10 Suppl: 1–14 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Rainey PB, Travisano M (1998) Adaptive radiation in a heterogeneous environment. Nature 394: 69–72. [DOI] [PubMed] [Google Scholar]
- 31. Loreau M, Ebenhöh W (1994) Competitive exclusion and coexistence of species with complex life cycles. Theor Popul Biol 46: 58–77. [DOI] [PubMed] [Google Scholar]
- 32. Balaban NQ, Merrin J, Chait R, Kowalik L, Leibler S (2004) Bacterial persistence as a phenotypic switch. Science 305: 1622–1625. [DOI] [PubMed] [Google Scholar]
- 33. Nijhout HF (2003) Development and evolution of adaptive polyphenisms. Evol Dev 5(1): 9–18. [DOI] [PubMed] [Google Scholar]
- 34. Lewontin RC, Cohen D (1969) On population growth in a randomly varying environment. PNAS 62(4): 1056–1060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Acar M, Mettetal JT, van Oudenaarden A (2008) Stochastic switching as a survival strategy in fluctuating environments. Nat Genet 40: 471–475. [DOI] [PubMed] [Google Scholar]
- 36. Snell-Rood EC, Van Dyken JD, Cruickshank T, Wade MJ, Moczek AP (2010) Toward a population genetic framework of developmental evolution: the costs, limits, and consequences of phenotypic plasticity. BioEssays 32(1): 71–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Axelrod R, Hamilton WD (1981) The evolution of cooperation. Science 211: 1390–1396. [DOI] [PubMed] [Google Scholar]
- 38. Michod RE (1997) Cooperation and Conflict in the Evolution of Individuality. I.Multilevel Selection of the Organism. Am Nat 149(4): 607–645. [Google Scholar]
- 39. Michod RE (1996) Cooperation and Conflict in the Evolution of Individuality. II. Conflict Mediation. Proc R Soc B 263: 813–822. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Sample computer code for simulations.
(PDF)