Biological-Effect Modeling of Radioimmunotherapy for Non-Hodgkins Lymphoma: Determination of Model Parameters

Abstract

Treatment with Tositumomab and ¹³¹I tositumomab anti-CD20 radioimmunotherapy (Bexxar) yields a nonradioactive antibody antitumor response (the so-called cold effect) and a radiation response. Numerical parameter determination by least-squares (LS) fitting was implemented for more accurate parameter estimates in equivalent biological-effect calculations. Methods: One hundred thirty-two tumors in 37 patients were followed using five or six SPECT/CT studies per patient, three each (typical) post-tracer (0.2 GBq) and post-therapy (∼3 GBq) injections. The SPECT/CT data were used to calculate position- and time-dependent dose rates and antibody concentrations for each tumor. CT-defined tumor volumes were used to track tumor volume changes. Combined biological-effect and cell-clearance models were fit to tumor volume changes. Optimized parameter values determined using LS fitting were compared to previous fitted values that were determined by matching calculated to measured tumor volume changes using visual assessment. Absorbed dose sensitivity (α) and cold-effect sensitivity (λ_p) parameters were the primary fitted parameters, yielding equivalent biological-effect (E) values. Results: Individual parameter uncertainties were approximately 10% and 30% for α and λ_p, respectively. LS versus previously fit parameter values were highly correlated, although the averaged α value decreased and the averaged λ_p value increased for the LS fits compared to the previous fits. Correlation of E with 2-month tumor shrinkage data was similar for the two fitting techniques. The LS fitting yielded improved fit quality and likely improved parameter estimation.

Introduction

Biological-effect (E)¹ modeling, where the major functions affecting therapeutic response are used to calculate total therapeutic effect, may increase understanding of therapy effects by quantifying parameters that can be correlated with patient outcome. In the case of B-cell non-Hodgkins lymphoma (NHL) treated with tositumomab and ¹³¹I- tositumomab (Bexxar), a significant correlation with absorbed dose has not been found.^2–4 There is evidence of therapeutic effects from other factors, such as tumor shrinkage due to nonradioactive antibody (the so-called cold effect). In our calculation of E, in addition to absorbed dose, we have included the absorbed dose rate nonuniformity, the radiation sensitivity, the sensitivity of the tumor response to the cold effect, and cell proliferation.

Previously, a wide range of radiation and cold-effect sensitivities were found, implying the possibility of categorizing patients for outcome prediction.⁵ Parameters were determined for each tumor imaged using SPECT/CT at six time points, three each over the tracer interval (∼8 days) and the therapy interval (∼8 days). Equivalent uniform dose (EUD) calculations based on the equivalent biological-effect model were performed and demonstrated improved correlation of EUD with outcome compared with absorbed dose with outcome.⁴ In the present work, the biological-effect model output was changed to E rather than EUD. EUD is equal to E/α, where α is the linear radiosensitivity coefficient. This removes an unnecessary influence of the varying patient-specific radiosensitivity from the biological-effect model output.

The equivalent biological-effect model was combined with a cell-clearance model to fit relative tumor volume change data. The equivalent biological-effect model used three parameters, radiosensitivity (α), cold-effect sensitivity (λ_p), and cell proliferation rate (λ_t). The cell-clearance model used two parameters, a cell-clearance rate and a cell-clearance delay for the therapy interval only. The radiosensitivity parameter and the cell-clearance parameter were significantly correlated because both can directly affect the slope of the change in tumor volume with time. Since tumor growth for NHL is typically very slow, cell proliferation has minimal effect over the ∼16 days initially used for fitting. Therefore, the cell doubling rate was held constant in the initial fitting. This implied that the deviation of the cell proliferation rate from the chosen value biased the fit parameters, seen mostly in the effect on the α parameter.

With many freely varying parameters, unrealistic local minima are frequently found. Model assumptions, random data error, and unusual patient data presentation can significantly affect the model interpretation. A stepwise approach with fitted parameter constraints was used to help avoid local minima and maintain a strong correlation of model parameter interpretation with data.

In the present work, optimized parameter fitting using least squares (LS) is compared to previously reported fitting,⁵ where the calculated and measured tumor volume changes were matched by visual assessment by focusing on the relationship of the radiation and cold-effect sensitivities to the slope of the tumor volume change (slope-matched or SM fitting). In SM fitting, an attempt was made to keep all other model parameters constant. However, it was not possible to keep the cell-clearance parameters constant and fit the tumor volume data, thus requiring a change in the cell-clearance parameters in a minority of fits. LS fitting was performed with a five-parameter fit (all fitted parameters varied except proliferation rate) with generous parameter variation intervals, allowing a more accurate fit and potentially more accurate estimates of the fitted parameters. Comparison of E calculated by the model to relative tumor volume change at 2 months post-therapy was used to determine relative success of the fitting techniques.

Materials and Methods

Data collection

One hundred thirty-two tumors in 37 patients were followed using five or six SPECT/CT studies, three each (typical) post-tracer (0.2 GBq) and therapy (∼3 GBq) injections. The imaging protocol was approved by the University of Michigan Internal Review Board. Each patient provided written informed consent for the additional imaging required. Both tracer and therapy injections used identical antibody mass, 450 mg antibody plus 35 mg of ¹³¹I-labeled antibody. Patients were imaged on a Siemens Symbia TruePoint SPECT/CT scanner (Hoffman Estates, IL) with a six-slice CT capability. The high-energy parallel-hole collimation was used, with 180^o and 30 stops per head, 40 seconds per stop, body contouring, 20% photopeak at 364 keV, two adjacent 6% scatter correction windows, and a 128×128 matrix with a pixel size of 4.8 mm. The CT used full rotation, 130 kVp, and 35 mAs. The CT dataset yielded a 1×1×2 mm (typical) voxel size. University of Michigan software was used for SPECT/CT reconstruction and quantification. Projection data were reconstructed with ordered subsets expectation maximization (OSEM) using 35 iterations and six subsets and included three-dimensional (3D) depth-dependent detector response compensation, attenuation correction, and scatter correction. Partial volume recovery coefficients⁶ ranged from 99% to 58% for 100 to 4 mL volumes, respectively. Registered SPECT/CT data were used to determine voxelized descriptions of tissue densities and activity concentrations, as described by Dewaraja et al.⁴ SPECT-determined activity distributions and Monte Carlo-calculated 3D dose rate distributions⁷ were combined with tumor and rest-of-the-body time-activity curves to yield a position and time-dependent dose rate distribution and antibody concentration distribution for each tumor. Tumor volume contours defined on CT were used to derive the time dependence of tumor volumes for tracer and therapy time points. Shown in Figure 1 are example CT images with tumor contour (Fig. 1A) and SPECT overlay (Fig. 1B). Tumor time-activity data were fit using a biexponential function with the two components representing the uptake and clearance of antibody, respectively. Rest-of-the-body (whole body minus tumor) time-activity data were fit using a monoexponential function representing antibody clearance.⁸

FIG. 1.

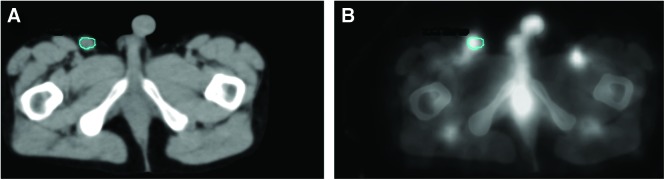
Fused SPECT and CT Images for a Representative Patient. Shown are central slice tumor images for the first therapy scan for the inguinal region (A) CT with contour, (B) SPECT overlay on CT. Color images available online at www.liebertpub.com/cbr

Equivalent biological-effect model

The equivalent biological effect, E, is defined at the minimum (time of minimum, t_min in hours) of the voxelized cell survival fraction S(v,t), averaged over voxels,

Viable cell loss or gain is a function of the biological-effective therapy, BET, containing three terms representing radiation effect, proliferation, and cold effect with coefficients α, λ_t and λ_p, respectively.

where N(v,t) is the number of viable cancer cells in the tumor in voxel v at time t and

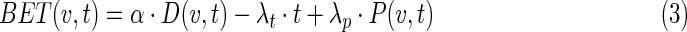The radiation effect and proliferation terms are defined in the standard terminology.⁹ D(v,t) is the cumulative dose to voxel v at time t postinjection. Dose rate effects (from the quadratic dose response term) represented approximately 1% at study dose rates and were ignored.⁵ The proliferation constant can be expressed as an effective doubling time, T_p in days,

The cold-effect term is proportional to the antibody concentration residence time (in grams of antibody protein times hour per gram of tumor),

where P_inj and A_inj are the quantity of antibody mass and activity at time of injection, ρV is the tumor mass in g, 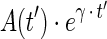is the decay-corrected activity as a function of time (time-activity curve), and f(v,t) is the voxelized activity distribution at time t, which averages over voxels to unity.

Cell-clearance model

If Z(v,t) is the volume of viable tumor cells in voxel v at time t, then the time dependence of the total tumor volume is given by,

Z(v,t) has two components, the number of inactivated (but not yet cleared) cells, U(v,t) and the number of viable cells, N(v,t)

where C_z is the volume occupied by a cancer cell, and is assumed to be constant and equivalent for both viable and inactive cells. We also assume that at t=0 the tumor is composed of only viable cells, Z(v,0)=C_z N(v,0). The position and time dependence of the tumor volume is

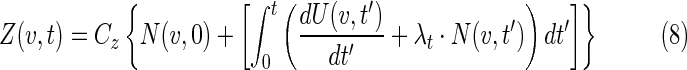where the first term is the number of initial cells and the terms in the bracket represent viable cell loss due to therapy and cell gain due to proliferation. The proliferation term is proportional to the number of viable cells. Cell loss has two components, loss due to the radiation effect and loss due to the cold effect,

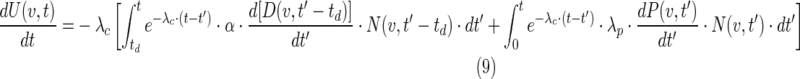where the cell-clearance parameter, λ_c can be expressed as a clearance half-time, T_c in days,

and t_d is the clearance delay imposed for the observed delay in cell clearance for the radiation effect, and can be expressed in days as T_d. The terms in the integrand in equation 8 can be expressed in N(v,t)/N(v,0), which was explicitly calculated from equations 2 and 3.

Parameter descriptions are given in Table 1. Additional detail has been previously published.^5,10

Table 1.

Parameter Descriptions for the Equivalent Biological Effect and Cell-Clearance Models

Parameter (units)	Description
E	Equivalent biological effect
S(v,t)	Fractional cell survival at voxel v and time t
N(v,t)	Number of viable tumor cells at voxel v and time t
tmin, hr	Time of cell survival minimum
BET	Biological-effective therapy
α, Gy−1	Linear dose–response coefficient
D(v,t), Gy	Dose at voxel v and time t
λt, h−1 and Tp, d	Proliferation rate and effective cell doubling time
λp, gT/gp/ha	Cold-effect response coefficient
P(v,t), gp-h/gT	Antibody concentration residence time at voxel v and time t
A(t), Bq	Tumor activity time t
γ, h−1	Radioactive decay constant
f(v,t)	Relative activity distribution at voxel v and time t
Z(t), mL	Tumor volume at time t
Cz, mL	Volume per cell
U(v,t)	Number of inactive (nonviable) tumor cells at voxel v and time t
λc, h−1 and Tc, d	Cell-clearance constant and cell clearance half-life
td, h and Td, d	Cell-clearance delay time

^aGram of tumor per gram of antibody protein per hour.

Voxelized tumor volume

Tumor volumes were defined on CT and registered over time with deformable registration using center of mass alignment and radial deformation. Voxels from the initial scan were tracked in subsequent scans by fixing the number and relative positions of voxels for all time points. The tumor time-activity curves at the voxel level followed the curve for the tumor as a whole. Local discontinuities in the voxel curves were allowed at times midway between scans. Dose rates followed the position and time dependence of the activity distribution. The time history of the voxelized tumor dose rates were calculated with a self-absorption term due to tumor activity and a rest-of-the-body term due to the rest-of-the-body activity. The self-absorption term was calculated using the SPECT-derived source term, which was multiplied by a recovery coefficient, and the tumor time–activity curve. The rest-of-body tumor dose rates were calculated from the rest-of-body source term and the rest-of-body time–activity curve.

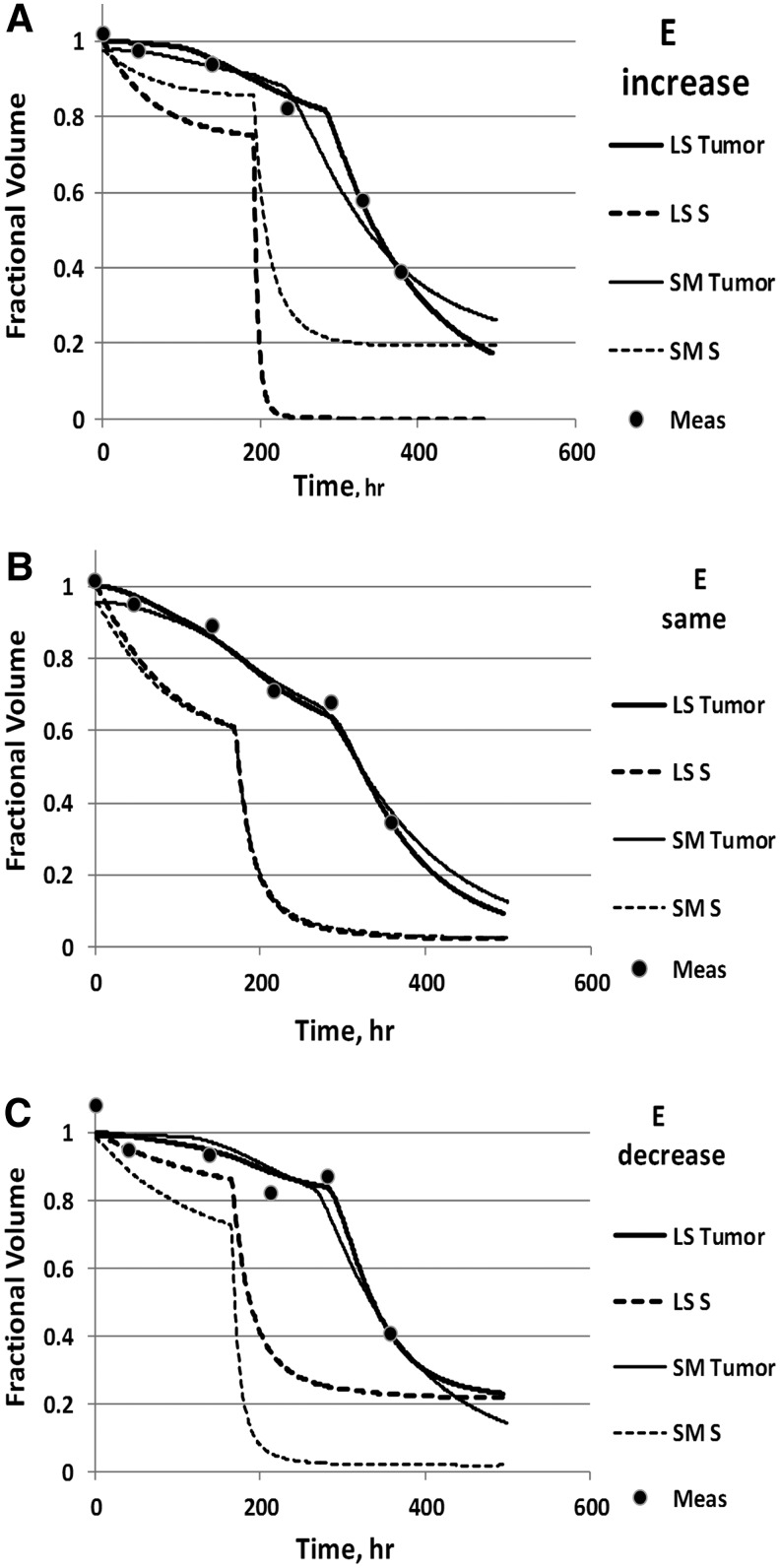
The calculated time dependence of the tumor volume (equation 6) was compared to the six measured CT-defined volumes. Model parameters were radiosensitivity (α), cold-effect sensitivity (λ_p), proliferation rate (λ_t) from Equation 3, effective cell-clearance rate (λ_c) from Equation 9 and 10, cell-clearance delay for cell inactivation by the radiation effect (t_d) from Equation 9, and tumor volume normalization. Model input data were dose rate and activity distributions. Model output was the equivalent biological effect (E) from Equation 1. Tumor volume normalization was a parameter that multiplied the tumor volume data. It was used as a fitted parameter because of the observed increased variability of the day 0 tumor volumes compared with days 2 and 5 volumes. By allowing the tumor volume normalization to vary, tumor volume errors at all times were treated equally. Example graphs of fitted time-dependent tumor volumes are presented in Figure 2.

FIG. 2.

Tumor Volume Data and Example Fits. Shown are measured volumes (dots), tumor–volume fitted curves (solid) and fractional cell survival (S, dashed) for least-squares (LS) and slope-matched (SM) fitting. Data and curves are normalized to the tumor volume at time zero for the LS fit. Plots are shown for an (A) increase in E (Patient 5, Tumor 4); (B) no change in E (Patient 39, Tumor 3); (C) decrease in E (Patient 36, Tumor 3) for the LS fit relative to the SM fit, respectively.

Slope-matched fitting

Slope-matched (SM) fitting was performed by adjusting the α and λ_p parameters for optimum agreement between the slopes of the calculated tumor-volume curve (equation 6) and the tumor-volume data for the tracer and therapy time intervals.⁵ The fitting procedure attempted to hold other parameters constant, but allowed variations of the cell-clearance parameters when required to achieve a fit. Variations of the clearance parameters were used in a minority of tumor fits and were chosen based on tumor volume data characteristics. Emphasis was placed on determining the radiation and nonradioactive antibody sensitivities based on slopes of the tumor volume change data (i.e., tumor shrinkage) with the least influence of confounding effects. Tumor volume data in the tracer time interval was primarily sensitive to the cold-effect parameter, while data post-therapy injection was primarily sensitive to the radiosensitivity parameter. Tumor volume data normalization depended on the volume variations observed for the tracer time interval. Tumor data showing little or no cold effect used the average of all three tracer volumes (in 115 of 132 fits). Tumor data with a large cold effect were normalized to the initial volume only (9 of 132 fits). For tumor data with large decreases between the initial volume and following two volumes (ranging from 16% to 48% in 8 of 132 tumor fits), it was not reasonable to assume the change in tumor volume was due to tumor cell clearance alone, which appeared to violate model assumptions. For these, the second and third data points only were used for normalization, while the first point was ignored during the fitting. The cell clearance half-time was 3 days (T_c, equation 10), unless this assumption was inconsistent with the tumor volume data. Alternative values used were 1, 1.5, or 2 days (1, 2, and 9 of 132, respectively). The clearance delay parameter (t_d, equation 9) was set based on the time of the sharp drop in tumor size, assumed to be due to cell clearance secondary to radiation damage. Clearance delays were 0, 1.5, or 4 days (17, 112 and 3 of 132, respectively). Proliferation was held constant at a half-time of T_p=150 days (equation 4) to represent the median time to progression for low-grade NHL.¹¹ While observing the tumor–volume curve match to data points, parameters λ_p and α were varied until the slopes of the tumor–volume curves approximately matched the data points for the tracer and therapy intervals, respectively. Fit conditions are summarized in Table 2.

Table 2.

Parameter Ranges for Slope-Matched Fitting

Parameter		Condition	Value (frequency)
Tumor volume normalization		Typical	First 3 points (115)
		Large cold effect	First point (9)
		Large decrease from points 1 to 2 and 3	Points 2 and 3 (8)
Radiosensitivity	α, Gy−1	Match slope (therapy)	Fitted
Cold sensitivity	λp, gT/gp/h	Match slope (tracer)	Fitted
Clearance half-life	Tc, d	Typical	3 (120)
		Alternative values	1 (1)
			1.5 (2)
			2 (9)
Clearance delay	Td, d	No delay	0 (17)
		Typical	1.5 (112)
		Long delay	4 (3)
Effective cell doubling time	Tp, d (constant)	Mean time to progression	150

Discrete values were chosen to provide adequate fits to tumor volume data, while only the radiosensitivity and cold-effect sensitivity parameters were continuously varied.

LS fitting

LS fitting allowed more freedom of parameter variation. Parameters were limited to finite ranges to avoid nonphysical local minima. Parameter limits were generous (given in Table 3). T_p was held constant at 500 days, a value consistent with the progression observed at 2 months for the majority of tumors in this study. In a first step, fitting was performed using tumor–volume normalization and λ_p, keeping other parameters at nominal values. In a second step, fitting was performed keeping tumor–volume normalization and λ_p fixed and optimizing α, λ_c, and t_d within the chosen intervals. Fitting was performed at least twice per tumor, iteratively for the first and second steps, using the previous best fit parameters as initial values. To avoid local minima, multiple overlapping intervals for t_d were chosen based on the observed time of rapid tumor volume decrease following the therapeutic injection. Some tumors required a refitting with an alternative t_d interval with the best final fit chosen. A small overlap between t_d intervals helped determine the best fit values without danger of a local minimum trap. The numbers of tumor fits were 3, 33, 74, and 22 in 4 t_d intervals listed in Table 3, respectively.

Table 3.

Parameter Ranges for Least-Squares Fitting

Parameter		Low limit	High limit
Radiosensitivity	α, Gy−1	0.05	2.0
Cold Sensitivity	λp, gT/gp/hr	0.7	700
Clearance half-life	Tc, d	1	4
Clearance delay	Td, d (intervals)	0.15	2.0
		1.2	3.8
		3.5	4.8
		>4.8
Effective doubling time	Tp, d (constant)	500

E value correlations with 2-month shrinkage data were used to determine relative quality of the fitting procedures for both SM and LS techniques. The log of the ratio of the 2-month tumor volume to the initial tumor volume was plotted against E. Complete response at 2 months (i.e., tumor volume not observed on CT) was plotted using a minimum volume of 0.25 mL.

To illustrate potential errors in fitting with only the first ∼16 days of data, example tumor fits were refit using LS with λ_t varying (least squares including time term, or LST, fit) and using the 2-month data. Tumor fits farthest from the LS shrinkage-versus-E best fit line were chosen for LST fitting. Tumor size normalization was held constant at the previous LS fit value, leaving five fit parameters (α, λ_p, λ_c, t_d, and λ_t). A larger λ_c interval was allowed to enable the 2-month data to be reliably fit while maintaining a similar fit quality compared to the LS fit with λ_t constant described above.

Results

LS fitting provided an estimate of parameter uncertainty per fit based on the variability of the data. The one standard deviation uncertainty was approximately 10% and 30% for α and λ_p, respectively. For some tumors, the LS fit resulted in a significant departure from previous fitting for the alpha parameter due to the added freedom of the clearance parameters. Figure 2A–C show example fits where the resulting E value increased, stayed approximately the same, or decreased, respectively, for the LS fit relative to the SM fit.

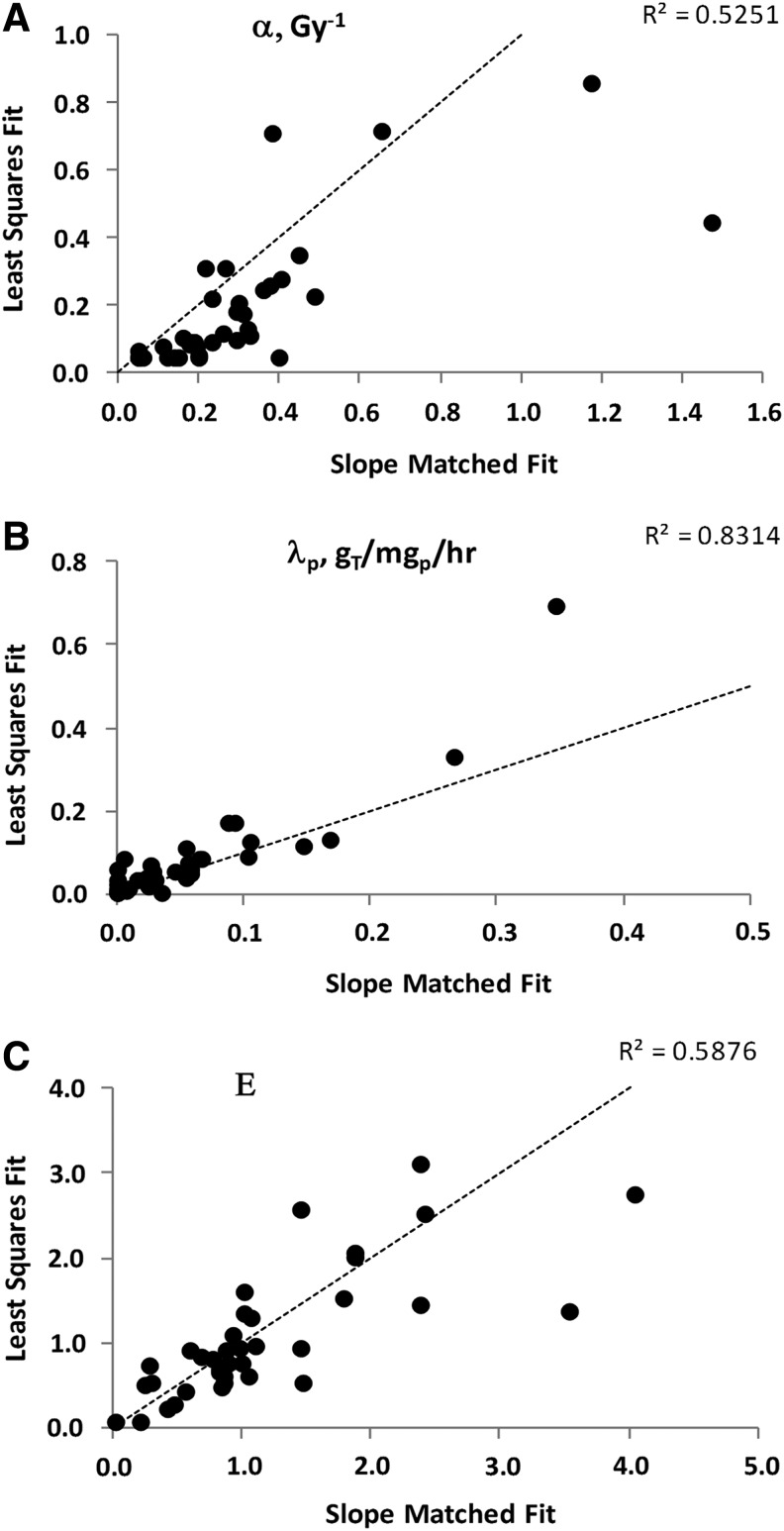
LS versus SM parameter results were correlated for individual tumor data fits, as illustrated by the square of the correlation coefficient, R²=0.40 for α (p<10⁻³, data not shown) and R²=0.66 for λ_p (p<10⁻³, data not shown). Using results averaged over tumors for each case, R²=0.53 for α (p<10⁻³, Fig. 3A) and R²=0.83 for λ_p (p<10⁻³, Fig. 3B). On average, the LS α values decreased while the λ_p values increased compared with the comparable SM fit values. The shift in the averaged α value was attributed to the greater variation allowed for the clearance parameters. A shift in α driven by data in the therapy interval typically caused a shift in λ_p in the opposite direction. The E values, averaged over tumors for each case, were significantly correlated between fitting techniques (R²=0.59, p<10⁻³, Fig. 3C).

FIG. 3.

SM versus LS Fit Comparison for (A) Radiosensitivity, (B) Cold-Effect Sensitivity, and (C) E. Also shown are the line of equal value and the square of the correlation coefficient. Parameter values are averaged over tumors for each patient.

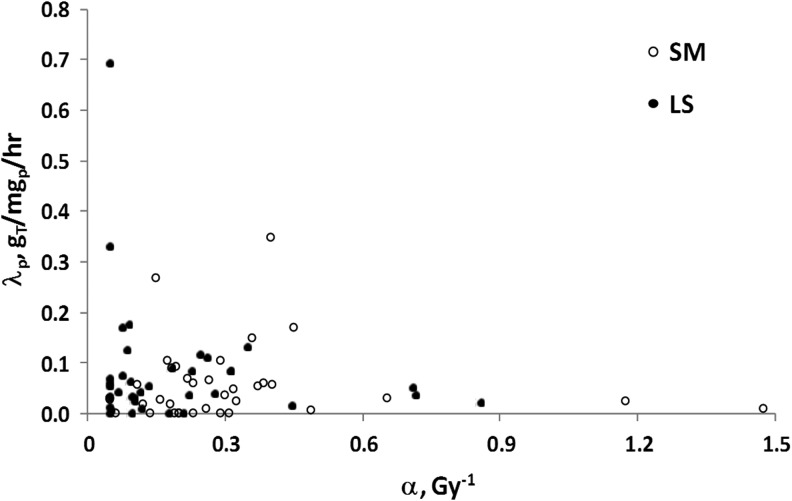
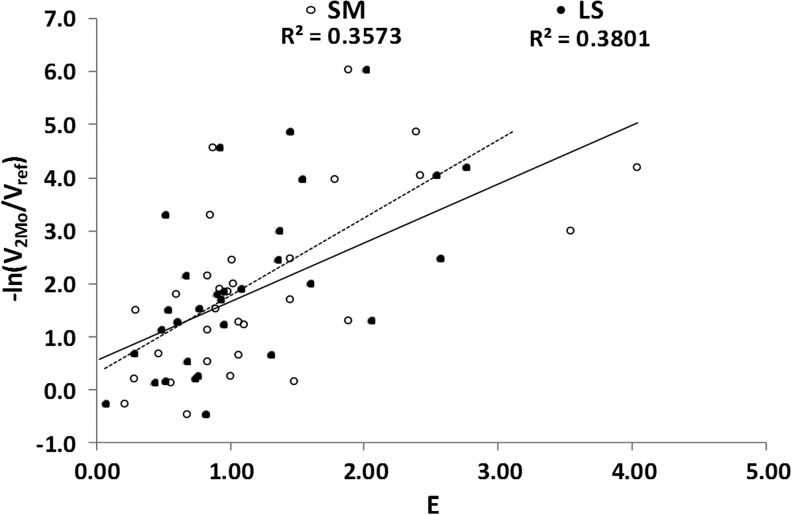
Figure 4 presents the relationship between radiosensitivity and cold-effect sensitivity. The LS results appear to have increased the level of case clustering in cell sensitivity to therapy. Examples of high radiosensitivity and low cold-effect sensitivity or high cold-effect sensitivity and low radiosensitivity are more apparent. The LS compared to SM fit results showed a comparable correlation with 2-month shrinkage data (Fig. 5). The R² increased from 0.36 (p=0.023) for SM fitting to 0.38 (p=0.014) for LS fitting.

FIG. 4.

Fitted Sensitivity Parameters Averaged Over Tumors for Each Patient for SM and LS Methods.

FIG. 5.

Correlation of E with 2-Month Tumor Shrinkage for SM Fitting (solid line, R²=0.36, p=0.023) and LS Fitting (dashed line, R²=0.38, p=0.014).

A concern is that the observed correlations are mainly related to high E values due to patients with higher radiosensitivity or cold-effect sensitivity. However, when patients with radiosensitivity greater than 0.5 Gy⁻¹ or with cold-effect sensitivity greater than 150 g_T/g_p/h (gram tumor per gram protein per hour) were removed, the correlation between E and 2-month tumor shrinkage was still apparent, but with reduced R² values of 0.23 and 0.34 for SM and LS fitting, respectively.

Two patients each with large positive and large negative differences between the location on the plot of LS E versus 2-month shrinkage and the line of correlation (see Fig. 5) were chosen for repeat LS fitting with the 2-month data included and with λ_p varying (LST fit). The patients plotted above the line of correlation represent a larger therapeutic effect than was predicted from a linear fit to the LS results. The LST compared with the LS fit resulted in much larger radiosensitivities and longer cell-clearance times (Table 4, columns 2–5). The patients plotted below the line of correlation represent a smaller therapeutic effect than predicted. The LST fit had increased cell proliferation (decreased cell doubling time, Table 4, columns 6–7) or decreased cold-effect sensitivity and reduced cell-clearance time (Table 4, columns 8–9).

Table 4.

Least-Squares Fit Parameter Comparison Without (LS) and With (LST) λ_τ Varying and 2-Month Tumor Size Data for the Four Plotted Points in Figure 5 in Most Disagreement With the E Versus 2-Month Shrinkage Best Fit Line

	Plot point (0.92,4.6)		Plot point (1.45,4.9)		Plot point (0.82,−0.5)		Plot point (2.05,1.3)
Parameter	LS	LST	LS	LST	LS	LST	LS	LST
α, Gy−1	0.222	1.60	0.718	1.62	0.05	0.05	0.05	0.05
λp, gT/gp/h	35.0	0.70	35.7	49.3	12.5	19.7	329	192
Tc, d	2.5	8.0	1.0	3.3	2.7	1.0	4.0	1.4
Td, d	2.8	2.8	2.3	2.3	2.0	2.0	3.8	3.8
Tp, d	500	549	500	513	500	188	500	500
E	0.92	5.71	1.45	3.27	0.82	0.42	2.05	1.03

Point coordinates refer to [E,log tumor shrinkage] values plotted in Figure 5.

Discussion

The equivalent biological effect and cell-clearance models, as used here, contain parameters representative of the major therapeutic and cell-clearance effects. All of the parameters should be considered “effective” parameters as representing a group of biological response functions. For example, it is likely that cells inactivated by radiation versus inactivated by the cold effect have different clearance mechanisms and therefore different cell-clearance times, as partially represented by the differing time delay to clearance (t_d). Yet, for convenience, both processes are represented by the same cell-clearance (λ_c) parameter. There is evidence that a synergistic relationship exists between cell response to tositumomab and subsequent radiation.¹² While this effect is not explicitly included in the model, it may be partially represented in the wide variation of radiosensitivity required to fit the data.

Using a multiparameter model to fit data should be done cautiously. SM fitting was done to get a visual relationship between the slope of the tumor shrinkage curve and the tumor volume data, focusing on estimates of the primary model parameters (radiosensitivity and cold-effect sensitivity). Historical use of dose response is equivalent to holding all model parameters constant, so variation of only two parameters was a small departure. Cell-clearance parameters were kept constant if doing so resulted in a fit to data. They were changed only when required to achieve a fit. Allowing the clearance parameters to vary continuously was explored as a means of improving the fit quality. Comparison to the 2-month shrinkage data was used as a test of the need to vary these parameters and the adequacy of the model to represent the data.

The proliferation (λ_t) and cold-effect (λ_p) parameters played a relatively minor role in the differences due to fitting technique. The effective doubling time was changed from 150 days for the SM fitting to 500 days for the LS fitting. While the approximate mean doubling time (estimated from average time to progression) was used for the initial SM fitting, most cases were consistent with the much longer time used for the LS fitting. This change is equivalent to using the mode rather than the mean of the distribution. The change in T_p did not cause a substantial shift in the cold-effect parameter, which was determined by tumor volumes from the first 5 days post-tracer injection. The volume normalization and λ_p were determined together so that the initial tumor volumes could be used to determine an unbiased normalization while accounting for the (mostly) modest tumor response to the antibody alone. All following LST fits kept the volume normalization fixed to reduce the number of fit variables.

The strategy of shifting to LS fitting generated some concern that the correlation of the radiosensitivity and cell-clearance (α and λ_c) parameters would adversely affect the estimate of α. A relatively small interval for the clearance parameter was allowed for this reason. However, the added flexibility for LS fitting allowed higher quality fits. Improved performance of the LS fitting was consistently apparent for both the tumor-specific and patient-specific results. Patient-specific results showed a higher correlation than tumor-specific fits, probably because some averaging over multiple tumors per patient reduced the effects of random fluctuations in the data. For patients with multiple tumors, variations between tumor shrinkage data was much less intra-patient compared to inter-patient. Some testing with larger intervals of λ_c for LS fitting was performed, but it was concluded that any further gains in model performance would be modest at best. The upper limit placed on T_c was reached in 36 of 132 (27%) of LS fits. The lower limit of T_c was close to a practical minimum value and was not explored. LST fits that included 2-month data and varying proliferation parameter required an increased range for the clearance parameter to provide an adequate representation of the data, with reduced concern for a correlation between α and λ_c because of the additional constraint provided by the 2-month data point. The improved fit quality of LS fitting compared to the previous SM fitting was a validation that the effective cell-clearance time varied between tumors and between patients.

The LST fits were performed to explore the further parameter variations resulting from adding additional time data, which allowed inclusion of λ_t as a fit parameter. Since using λ_t and the 2-month data in fitting would yield almost perfect agreement between E and the 2-month data, only the points in furthest disagreement needed to be tested. As indicated by comparing changes for LST versus LS fits, there are fits that yielded much larger or smaller cell-clearance times to reproduce the tumor shrinkage data. A larger cell-clearance time can mask a high radiosensitivity if the analysis uses data for the first several weeks only. Likewise, ignoring variations in tumor cell proliferation can yield incorrect estimates of therapeutic effect in some cases. LST fits are expected to yield more accurate estimates of the sensitivity parameters.

Because proliferation for NHL is typically low, the minimum of the cell survival curve (used to derive E) is similar to the cell survival at 2 months. Thus, it is reasonable that E should predict shrinkage at 2 months if the model correctly represents the observed cell survival during the tracer and therapy intervals. This relationship holds even when high responders are removed from the dataset. Variability of cell sensitivity to therapy is a consistent feature of tumor response at both high and low tumor sensitivities. Following the removal of high-sensitivity cases, the remaining case with high E value (>2) was distinguished from other cases by significantly higher absorbed dose.

Full parameter variation of the model is not limited by the quality of the fit to tumor shrinkage data, but by the accuracy of those data. Validation of the full fit is hampered by the increased difficulty of obtaining high quality outcome data at times longer than 2 months, since many patients with recurrent disease go on to other therapies. While a correlation of the model parameters with tumor size was expected, a correlation was not found for the LS fit results. At a minimum, LST fit results would be required to test for a correlation of proliferation rate with tumor size.

The usefulness of the model may be judged by correlating model parameters with pretherapy biomarkers. Optimum parameter values are obtained with the full fit including the 2-month shrinkage data and a fitted proliferation parameter. A prediction of the radiosensitivity, cold-effect sensitivity, and proliferative potential based on biomarkers would allow an estimate of therapy effect. A prospective study of the predictability of outcome using biomarkers would be required. Example biomarkers under study include disease diagnosis (e.g., follicular lymphoma), p53 for apoptosis or cell repair potential and Ki67 for proliferative potential. Prediction of outcome could influence patient enrollment in dose escalation or radiosensitizer studies or encourage the use of alternative therapeutic options for some patients.

Conclusion

LS fitting allowed more variation of model parameters and yielded more accurate fits to the tumor shrinkage data in the tracer and therapy intervals. Comparisons of LS fitting to previous SM fitting increased confidence in fitting techniques and allowed the inclusion of proliferation rate as a fitted parameter. Three of 37 cases were classified as more radiosensitive (α>0.5 Gy⁻¹) and 4 of 37 cases as more cold-effect antibody sensitive (λ_p>150 g_T/g_p/h). E was significantly correlated with the 2-month tumor shrinkage data, with likely improvement in parameter estimation from fitting that included proliferation. Equivalent biological-effect calculations promise to improve understanding of the disparity of therapy results from this patient population by segmenting populations into low or high effective radiosensitivity, cold-effect sensitivity, and/or proliferative potential categories, each category potentially benefitting from a different therapeutic strategy. Biomarker correlation with effective radiosensitivity, effective cold-effect sensitivity, and/or proliferative potential may yield pretherapy predictions of therapy outcome, and thus potentially influence the therapeutic management of B-cell NHL patients.

Acknowledgment

The authors acknowledge the help of Ryan Thorwarth for automating and testing the LS analysis. This work was supported by NIH 2R01 EB001994 awarded by the National Institutes of Health, United States Department of Health and Human Services.

Disclosure Statement

No financial conflict of interests exist.