Parameter Sensitivity Analysis of Stochastic Models Provides Insights into Cardiac Calcium Sparks

Abstract

We present a parameter sensitivity analysis method that is appropriate for stochastic models, and we demonstrate how this analysis generates experimentally testable predictions about the factors that influence local Ca²⁺ release in heart cells. The method involves randomly varying all parameters, running a single simulation with each set of parameters, running simulations with hundreds of model variants, then statistically relating the parameters to the simulation results using regression methods. We tested this method on a stochastic model, containing 18 parameters, of the cardiac Ca²⁺ spark. Results show that multivariable linear regression can successfully relate parameters to continuous model outputs such as Ca²⁺ spark amplitude and duration, and multivariable logistic regression can provide insight into how parameters affect Ca²⁺ spark triggering (a probabilistic process that is all-or-none in a single simulation). Benchmark studies demonstrate that this method is less computationally intensive than standard methods by a factor of 16. Importantly, predictions were tested experimentally by measuring Ca²⁺ sparks in mice with knockout of the sarcoplasmic reticulum protein triadin. These mice exhibit multiple changes in Ca²⁺ release unit structures, and the regression model both accurately predicts changes in Ca²⁺ spark amplitude (30% decrease in model, 29% decrease in experiments) and provides an intuitive and quantitative understanding of how much each alteration contributes to the result. This approach is therefore an effective, efficient, and predictive method for analyzing stochastic mathematical models to gain biological insight.

Introduction

Parameter sensitivity analysis is an important method for evaluating mathematical models of biological processes. A thorough parameter sensitivity analysis generates a comprehensive set of predictions that indicate quantitatively how changes in any model parameter affect biologically relevant model outputs. This procedure can:

• 1.Identify model predictions that are either consistent with or inconsistent with existing experimental data;
• 2.Suggest novel experiments to either validate or falsify the model; and
• 3.Determine which biological pathways make the most effective targets for efforts to perturb the physiology, either experimentally or therapeutically.

Traditionally, parameter sensitivity analysis is performed by altering model parameters in sequence to determine how each change modifies model behavior (1,2). In recent studies, we have developed methods that involve generating a population of candidate models by modifying all model parameters simultaneously (3–5). Population behavior is then analyzed statistically using multivariable regression to compute parameter sensitivities. This method has provided insight into deterministic mathematical models of the ventricular myocyte.

With stochastic mathematical models, however, parameter sensitivities can be challenging to evaluate because each simulation generates a different result. Thus, if a parameter is altered and a change in behavior is observed, one does not know whether this resulted from the parameter modification or simply from the model’s inherent randomness. Repeated simulations are therefore usually computed for each parameter change, but this process quickly becomes tedious and computationally demanding. One goal of this study was to determine whether our technique of modifying all parameters simultaneously could help to overcome these challenges in analyzing stochastic models.

The cardiac Ca²⁺ spark, an elementary unit of Ca²⁺ release from the sarcoplasmic reticulum (SR), is an intensively studied stochastic biological phenomenon (6). Ca²⁺ sparks occur spontaneously in quiescent myocytes at a low rate of ∼100/cell/s, and thousands of Ca²⁺ sparks are triggered probabilistically during each action potential. Because a Ca²⁺ spark reflects release from a cluster of 10–100 ryanodine receptors (RyRs) in the SR membrane, these events exhibit variability in measures such as amplitude and duration (7,8). Numerous modeling studies have used Monte Carlo methods to simulate these stochastic events (9–17). In most cases, however, a limited number of parameters have been investigated, according to the specific biological questions being addressed. Simulations with the so-called sticky cluster model, for instance, have provided predictions regarding Ca²⁺ spark termination (11) and the recovery of Ca²⁺ sparks from refractoriness (18,19). To understand such a model at a more global scale, however, requires a more thorough and systematic exploration of the parameter space.

Here we extend our recently developed methods for model parameter sensitivity analysis through parameter randomization followed by multivariable regression (3,4), and we apply this method to analyze a stochastic mathematical model of the cardiac Ca²⁺ spark (11,18). We demonstrate that this procedure can provide accurate and biologically meaningful predictions, even when simulation results are variable due to randomness in the model. We also show that this procedure can be more computationally efficient, by roughly an order of magnitude, than standard methods for evaluating parameter sensitivities. Most important, we experimentally validate predictions of the analysis by measuring Ca²⁺ sparks in cells isolated from genetically modified mice (20). This study therefore:

• 1.Provides insight into the variables that determine the characteristics of Ca²⁺ sparks in cardiac myocytes; and
• 2.Presents a general strategy that can be used to efficiently generate experimentally testable predictions in stochastic mathematical models.

Materials and Methods

Simulation with the stochastic sticky cluster model of Ca²⁺ sparks

Ca²⁺ sparks, considered the elementary units of excitation-contraction coupling in heart cells (6), are stochastic due to the small number of RyRs that contribute to each event. We simulated Ca²⁺ sparks using an established model known as the sticky cluster (11,18). This model, schematically illustrated in Fig. 1, A and B, simulates the following processes:

• 1.Stochastic gating of 28 RyRs that are assumed to be clustered and physically connected;
• 2.Changes of [Ca²⁺] in a local cytosolic subspace based on the balance between Ca²⁺ release through RyRs and diffusion of Ca²⁺ into the cytosol; and
• 3.Ca²⁺ depletion and refilling in the junctional sarcoplasmic reticulum (JSR).

Figure 1.

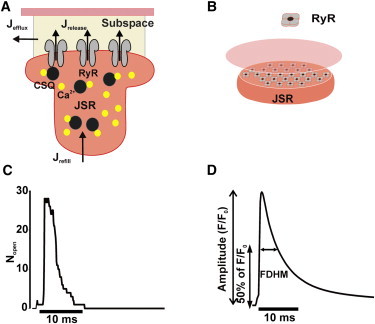
Schematic of sticky cluster Ca²⁺ spark model and representative results. (A) Sticky cluster model of local Ca²⁺ release. (B) Arrayed RyR channels in a junctional SR. (C) Number of open RyRs (N_open) versus time of Ca²⁺ spark simulation with 28 RyRs. (D) Simulated Ca²⁺ spark, computed as fluorescence versus time.

Each RyR was assumed to have two states: open and closed. Transition rates between the two states depend on the dyadic subspace [Ca²⁺], junctional SR [Ca²⁺], and a factor that accounts for physical coupling between channels. Simulations of RyR gating and changes in local [Ca²⁺] were performed using Monte Carlo methods, as in our previous studies (11,18).

Two important outputs of the sticky cluster model are the number of open RyRs versus time (Fig. 1 C) and the cluster release flux versus time. The latter was used as the input to a model that simulates Ca²⁺ diffusion, Ca²⁺ binding to fluo-3 and stationary buffers, and blurring by the confocal microscope (21). The output of this model was fluorescence as a function of location and time. From Ca²⁺ spark time courses (Fig. 1 D), we computed spark amplitudes and durations for the parameter sensitivity analyses. Amplitudes were computed as maximal normalized change in fluorescence (ΔF/F₀) at the center of each spark. To compute ΔF/F₀, each fluorescence time course was normalized by F₀, the fluorescence preceding the spark at diastolic [Ca²⁺] (100 nM), then 1 was subtracted from the maximum value to obtain ΔF/F₀. Durations were calculated as full duration at half-maximal amplitude.

All simulations were performed in MATLAB (The MathWorks, Natick, MA). Complete model equations and parameters are provided in the Supporting Material.

Multivariable regression method

We computed parameter sensitivities using a newly developed approach (3–5) that involves varying all parameters at random, running a single simulation with each set of parameters, then using statistical methods to relate the changes in parameters to changes in model outputs. In these simulations we randomly varied 18 model parameters, listed in Table 1.

Table 1.

Model parameters used for the sensitivity analysis

Parameter	Definition	Default Value
[Ca2+]Myo	Bulk myoplasmic Ca2+ concentration	0.1 μmol/L
[Ca2+]NSR	NSR Ca2+ concentration	1000 μmol/L
τefflux	Subspace efflux time constant	1.78 × 10−3 ms
τrefill	JSR refilling time constant	6.5 ms
DRYR	RyR Permeability constant	2.2 × 10−9μL s−1
NRyR	Number of RyR channels in a cluster	28
Kmax	Sensitivity of opening to subspace [Ca2+]	19.87 μmol/L
α	RyR luminal dependence factor	1.0 × 10−3 (unitless)
Hill	Exponent for RyR activation by Ca2+	4
Buffercyto1	Cytosolic buffer concentration	24 μmol/L
Buffercyto2	Cytosolic buffer concentration	47 μmol/L
Buffercyto3	Cytosolic buffer concentration	900 μmol/L
[CSQ]total	Total calsequestrin concentration	30 mmol/L
EJ	RyR-RyR coupling energy	0.1
Vds	Subspace volume	1.0 × 10−12μL
VJSR	Junctional SR volume	1.6 × 10−12μL
K+max	Maximum RyR opening rate	3 × 104 s−1
K−max	Maximum RyR closing rate	480 s−1

To randomly vary the parameters for each trial, we multiplied the baseline value of each parameter by a log-normally distributed random scale factor. The scale factors had a median value of 1, and the log-transformed scale factors had a standard deviation of 0.3. This procedure was repeated for 2000 trials. With each simulation of the stochastic system, we opened a single RyR in the cluster at time t = 0, then simulated the resulting RyR cluster behavior over 50 ms. We first determined whether a spark occurred with each trial. This was recorded for each set of parameters as either a 0 (no spark) or a 1 (spark). When a stochastic trial resulted in a spark (976 trials out of 2000), we computed two outputs:

• 1.Ca²⁺ spark amplitude (in units of ΔF/F₀); and
• 2.Spark duration, computed as full duration at half-maximal amplitude (see Fig. 1 D).

To perform the regression analysis, randomly varied parameters were log-transformed and converted into z-scores by subtracting the mean across all trials and dividing by the standard deviation. These values were then placed in an input matrix X with dimensions 976 (trials) × 18 (parameters). Outputs were log-transformed and converted to z-scores, then placed in an output matrix Y with dimensions 976 × 2. With parameters and outputs in matrices X and Y, respectively, we calculated a regression matrix B of dimension 18 × 2 such that X^∗B = Ŷ $\approx$ Y. Elements in each column of B indicate how much a change in a parameter affects a particular model output. The Supporting Material describes how these parameter sensitivities can be understood quantitatively; Fig. S2 in the Supporting Material illustrates the procedure, and Fig. S3 demonstrates the convergence of parameter sensitivities with increasing number of trials.

Logistic regression method

Multivariable logistic regression was used to analyze the binary output of whether or not a particular trial produced a spark. The randomly varied parameters from a separate set of 1000 simulations were placed in the input matrix X, and the output matrix Y consisted of ones and zeros corresponding to whether or not each trial produced a spark.

The MATLAB routine MNRFIT was used to derive a multivariable logistic model that can predict Ca²⁺ spark probability as a function of changes in parameters. The MATLAB routine generates an intercept term b₀ and a set of regression coefficients, b₁, b₂, … b₁₈, corresponding to the 18 model parameters. If each log-transformed parameter x₁, x₂, … x₁₈ is expressed as a z-score, then the predicted spark probability P for any combination of parameters can be calculated from the following equation:

$$\text{log}\left(\frac{P}{1-P}\right)=b_0+b_1{x}_1+\dots +b_{18}{x}_{18}.$$ (1)

This equation can be expressed equivalently as

$$P\left(z\right)=\frac{1}{1+\text{exp}\left(-z\right)},$$ (2)

where z = b₀ + b₁x₁ + b₂x₂ + … + b₁₈x₁₈. The Supporting Material provides an example of how we can predict the change in spark probability resulting from a change in a single parameter.

To evaluate the performance of the logistic regression model, we performed eightfold cross-validation and generated a receiver operator characteristic (ROC) curve. This analysis assesses the quality of a classifier by plotting the true positive rate versus the false positive rate. Details of the cross-validation and ROC curve generation are provided in the Supporting Material.

Support Vector Machine analysis

We also analyzed the simulation results using Support Vector Machine (SVM), a popular algorithm for classification problems when data fall into two categories (22). As with the logistic regression model, eightfold cross-validation was performed. An SVM was built from each set of 700 trials (using the MATLAB function SVMTRAIN), and the outcomes of the remaining 100 trails were predicted (using SVMCLASSIFY). A ROC curve was generated as described in the Supporting Material. Fig. 4 B plots the weights that were generated during the model-building phase.

Figure 4.

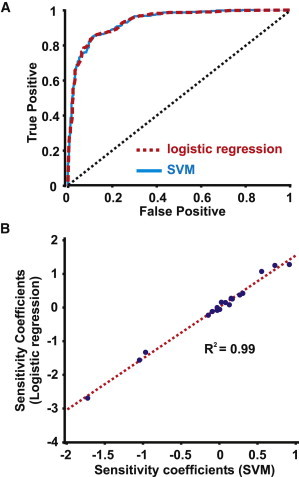
(A) Accuracy of logistic regression (dashed line) and Support Vector Machine (SVM) predictions (solid line) assessed using receiver operator characteristic (ROC) analysis. Each method had strong predictive power, exemplified by curves that deviated significantly from the line of identity, and quantified as the area under the curve (AUC). AUC, logistic regression = 0.9344. AUC, SVM = 0.9329. (B) Parameter sensitivities calculated from logistic regression were strongly correlated with weights calculated in building the SVM.

Experimental measurements of Ca²⁺ sparks

All experimental protocols were approved by the Institutional Animal Care and Use Committee of Vanderbilt University School of Medicine and complied with the Guide for the Care and Use of Laboratory Animals published by the US National Institutes of Health (Bethesda, MD). Mice with deletion of the TRDN gene (Trdn^−/− mice) were generated using Cre-Lox recombination methods previously reported in Shen et al. (23). For measurements of Ca²⁺ sparks, cells from Trdn^−/− (KO) mice were compared with wild-type (WT) littermates (Trdn^+/+). Ventricular myocytes from 3- to 4-month-old Trdn^−/− or Trdn^+/+ mice were prepared by enzymatic digestion, as previously described in Chopra et al. (20) and Hwang et al. (24). Myocytes were incubated with 6.6 μM fluo-4AM and 0.16% Pluronic F127 in Tyrode’s solution for 20 min. Tyrode’s solution contained (in mM) NaCl 134, KCl 5.4, CaCl₂ 1, MgCl₂ 1, glucose 10, HEPES 10, pH adjusted to 7.4 with NaOH. Ca²⁺ sparks were detected in line-scan mode using a confocal microscope (LSM 510, Carl Zeiss, Peabody, MA), with the scan line (1.9 ms/line) positioned along the longitudinal axis of each cell. Cells were illuminated at 488 nm, and emitted fluorescence was measured at >515 nm. Confocal images were analyzed with the ImageJ plug-in SparkMaster (25).

Results

Cardiac Ca²⁺ sparks (6) are stochastic events that are important for both normal physiology and pathophysiology, and many studies have used stochastic models to understand and generate predictions about these events (9–17). Ca²⁺ spark models therefore provide a useful test case for evaluating parameter sensitivities in an inherently stochastic system. To determine whether parameter randomization followed by multivariable regression (3) could successfully evaluate stochastic models, we applied this technique to an established mathematical model of the cardiac Ca²⁺ spark (11,18).

Sensitivity analysis identifies parameters that affect Ca²⁺ spark amplitude and duration

We ran 2000 trials with randomized model parameters. Using results from the 976 trials in which a spark was triggered, we employed multivariable regression to relate changes in the parameters to changes in Ca²⁺ spark amplitude and duration (see Materials and Methods for details). Despite the stochasticity in the model even without parameter variation, Fig. 2 A indicates a strong correlation between the true values of Ca²⁺ spark amplitude and duration, computed in the simulations, and the values predicted by the multivariable regression model.

Figure 2.

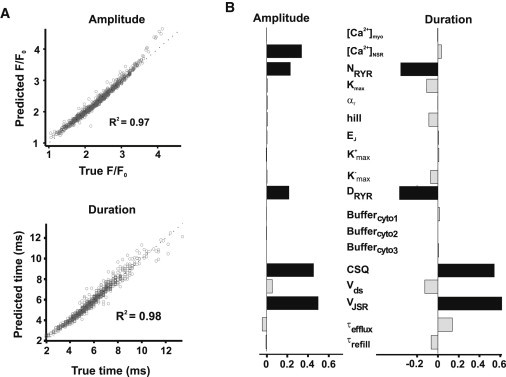
(A) Predictions of regression analysis on Ca²⁺ spark amplitude and duration. Data (circles) are displayed from 2000 trials. (B) Parameter sensitivities by regression analysis on Ca²⁺ spark amplitude and duration, which are columns of B matrix. Each number corresponding to each parameter denotes how changes in the parameter influence model outputs.

The parameter sensitivities contained in the regression matrix B (Fig. 2 B) indicate how each model parameter affects amplitude (left) or duration (right). Each parameter sensitivity therefore represents a quantitative model prediction, and a comparison of values illustrates the relative effects of different parameters. For instance, spark amplitude is predicted to be most strongly influenced by the following five parameters (see Table 1 for explanation): V_JSR, CSQ, Ca_NSR, N_RYR, and D_RYR. Ca²⁺ spark duration is influenced by these same parameters with the exception of Ca_NSR. Interestingly, the number of RyRs per cluster (N_RyR) and the permeability of each channel (D_RyR) have opposite effects on amplitude and duration. This is because greater Ca²⁺ flux through the RyR cluster will increase Ca²⁺ spark amplitude but will also cause faster depletion of JSR [Ca²⁺], thereby abbreviating the Ca²⁺ spark. Similar effects were demonstrated in the original article describing this model (11)—this analysis summarizes the effect in more precise terms and allows for a direct comparison with other parameter changes.

Logistic regression is an effective method to predict spark probability

To determine how model parameters influenced the probability that a single RyR opening would induce a Ca²⁺ spark, we analyzed a different set of 1000 simulations. Standard multivariable regression, however, seemed inappropriate to analyze spark probability, because each stochastic simulation either produced or failed to produce a Ca²⁺ spark. We therefore analyzed the results with multivariable logistic regression, using the model parameters as the independent variables and whether or not a spark occurred as the dependent variable (see Materials and Methods).

Parameter sensitivities calculated using logistic regression are shown in Fig. 3 A. Positive values mean that augmenting the parameter will increase the probability of triggering a spark, and vice versa. Thus larger than normal values of Ca_NSR, D_RyR, and τ_efflux will increase spark probability. Any of these changes will lead to higher local [Ca²⁺] in the subspace, making it more likely that an individual RyR opening will induce the opening of neighboring channels. Conversely, increases in V_ds, the Hill coefficient, or K_max decrease Ca²⁺ spark probability. It is notable that these parameters are essentially independent of those previously shown to affect spark amplitude and duration. In this particular model, therefore, spark amplitude and spark probability are controlled by different sets of parameters.

Figure 3.

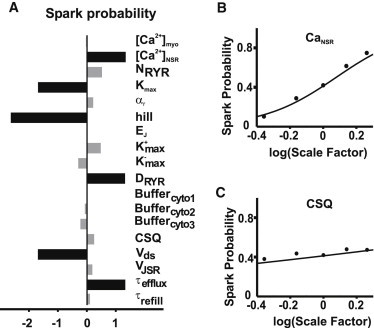
(A) Parameter sensitivity on Ca²⁺ spark probability performed by logistic regression analysis. (B) Spark probabilities by stochastic simulation results (dots) are compared to prediction curves of logistic regression (solid line) with changes in (B) Ca_NSR and (C) CSQ.

We next tested the accuracy of the logistic regression model that was computed through the analysis of the simulation results. Equation 2 defines a smooth curve of spark probability as a function of any model parameter. Fig. 3 B shows these curves for two model parameters: Ca_NSR, which has a large effect on spark probability, and CSQ, which has a smaller effect. To determine whether these predictions were accurate, we ran stochastic simulations (1000 trials each) in which either Ca_NSR or CSQ was altered from the control level. These are shown as the dots in Fig. 3 B. The two approaches yield nearly identical results, indicating that the logistic regression model generates accurate predictions (see Fig. S4 for additional validations).

To further test the accuracy of the logistic regression model, we performed eightfold cross-validation and generated a receiver operator characteristic (ROC) curve. This involves systematically varying the prediction threshold and plotting the true positive rate versus the false positive rate (see the Supporting Material for details). The ROC curve shown in Fig. 4 A (dashed line) demonstrates the strong predictive power of the logistic regression model. We also analyzed the simulation results using Support Vector Machine (SVM), a popular method for classifying data that can be grouped into binary Yes or No categories (22). The ROC curve generated from the SVM (Fig. 4 A, solid line) essentially overlaps the logistic regression ROC curve, indicating that the two methods are equally predictive. Indeed, the logistic regression parameter sensitivities were strongly correlated with the weights computed in deriving the SVM (Fig. 4 B).

Logistic regression is computationally more efficient than stochastic simulations

Next we compared the computational costs of the logistic regression and one-at-a-time parameter sensitivity methods. Any attempt to express spark probability as a function of a parameter will contain some noise because of the model’s inherent randomness. For instance, if logistic regression is performed on multiple sets of N = 540 simulations, each regression will generate slightly different predictions (see Fig. S5 A). Similarly, if a single parameter is varied, each set of stochastic simulations will compute a slightly different Ca²⁺ spark probability (see Fig. S5 B). To compare the computational efficiency of these two approaches, we plotted the standard deviation of spark probability (computed from 50 sets of simulations) versus the number of trials in each set. Fig. 5 shows that for either method, the standard deviation decreases as the number of trials per set increases, as expected.

Figure 5.

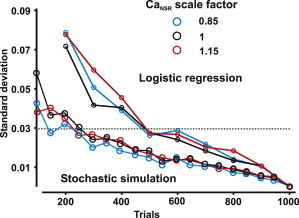
Relation between variability in Ca²⁺ spark probability calculation and number of simulations. Three scale factors (0.85, 1, 1.15) in Ca_NSR were used for both logistic regression analysis and stochastic simulation with varying trial number. At each trial number, the standard deviation was calculated for both methods. The standard deviation of the predictions decreases with an increase in the number of simulations.

To compare the two methods directly, we observed that a standard deviation of 0.03 was seen with either N = 240 trials per set for stochastic simulations or with N = 540 trials per set for logistic regression. These two estimates of Ca²⁺ spark probability are therefore equally accurate, seemingly implying that stochastic simulation is more efficient than logistic regression. It is important to note, however, that our stochastic simulations vary only one parameter whereas the logistic regression model simultaneously predicts the effects of changes in all 18 model parameters. To generate the same predictive power with stochastic simulations, one would need to increase and decrease each of the 18 parameters, for a total of 240 × 18 × 2 = 8640 simulations. The logistic regression method is therefore more efficient than one-at-a-time parameter sensitivity analysis by a factor of 8640/540 = 16.

Regression models generate experimentally testable model predictions

The parameter sensitivity analysis method generates quantitative predictions that can, in theory, be tested experimentally. Many of the important parameters, however, such as the number of RyRs and the JSR volume, cannot be altered in acute (i.e., pharmacological) experiments. Several of these parameters, however, may be altered in genetic experiments. For instance, Chopra et al. (20) developed mice with cardiac-specific knockout of triadin. This SR protein normally forms a complex with the RyR and the SR Ca²⁺ buffer calsequestrin (26), and loss of function mutations in triadin have recently been shown to cause ventricular arrhythmias in humans (27). Compared with wild-type littermates, myocytes isolated from Trdn^−/− mice exhibited both altered SR load and Ca²⁺ release units with modified morphology (20). We sought to determine whether the multivariable regression model would successfully predict changes in Ca²⁺ spark amplitude in myocytes from these mice.

Fig. 6 A illustrates the changes to Ca²⁺ release unit morphology reported by Chopra et al. (20): a decrease in the number of RyRs (N_RyR in the model; 38% of WT), a decrease in junctional SR volume (parameter V_JSR; 64% of WT), and an increase in SR Ca²⁺ load (parameter Ca_NSR; 128% of WT). In isolation, either of the first two changes reduces Ca²⁺ spark amplitude, whereas the latter causes a small increase (Fig. 6 B). The matrix formulation of the regression model, moreover, allows us to compute the overall change in amplitude as the dot product of the vector describing the three parameter changes and the vector of parameter sensitivities (Fig. 6 C). This calculation predicts that the three effects of triadin knockout will together cause a 30% decrease in Ca²⁺ spark amplitude (Fig. 6 D).

Figure 6.

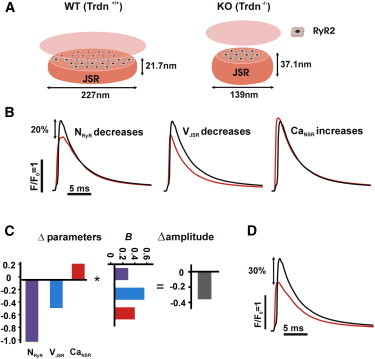
Prediction by regression analysis of Ca²⁺ spark amplitude in triadin KO mouse heart. (A) Schematic of morphological changes in Ca²⁺ release unit of triadin KO compared with WT. (B) Effects on Ca²⁺ spark amplitude of individual parameter changes. According to the measurements previously presented by Chopra et al. (20), triadin KO caused a reduction in the number of RyRs per cluster (38% of WT), a decrease in the junctional SR volume (64% of control), and an increase in SR Ca²⁺ content (129% of control). (C) Matrix formulation of the regression model. Spark amplitude is calculated as the dot product of the vector describing the three parameter changes and the vector of parameter sensitivities. (D) Comparison of Ca²⁺ spark amplitudes between WT (larger) and KO (smaller). Model predicts a 30% decrease in Ca²⁺ spark amplitude due to triadin KO.

To test this model prediction, we measured Ca²⁺ sparks in cells isolated from Trdn^−/− mice. Line-scan images (Fig. 7 A) show that Ca²⁺ sparks from Trdn^−/− cells appear less bright than those from Trdn^+/+ littermates. Fluorescence time courses produced by spatial averaging confirm that Ca²⁺ sparks from Trdn^−/− cells are generally smaller than those from Trdn^+/+ littermates (Fig. 7 B). Summary data (Fig. 7 C) show that Ca²⁺ sparks are, on average, 29% smaller in Trdn^−/− cells compared with Trdn^+/+ cells, consistent with the model prediction (Fig. 6 D). This successful prediction provides indirect evidence in support of the model’s assumptions, and, more important, illustrates that the overall effects of a complex perturbation can be understood quantitatively through the multivariable regression model.

Figure 7.

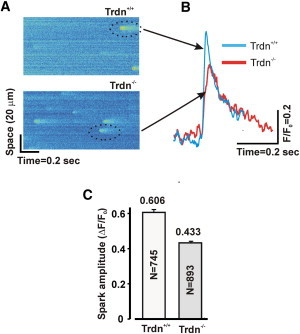
Experimental results of Ca²⁺ spark amplitudes. (A) Line-scan images (x-t) of Ca²⁺ sparks in WT (Trdn^+/+) and KO (Trdn^−/−). (B) Normalized fluorescent images of Ca²⁺ sparks along a line in WT and KO. (C) Ca²⁺ spark amplitudes in WT and KO.

Discussion

The results presented in this study have demonstrated the following:

• 1.Parameter randomization followed by multivariable regression can calculate parameter sensitivities not only in deterministic models as previously demonstrated (3,4), but also in stochastic models (Fig. 2);
• 2.Multivariable linear regression is appropriate for assessing effects on continuous model outputs, whereas multivariable logistic regression is appropriate for evaluating categorical outputs such as whether a stimulus induces a Ca²⁺ spark (Fig. 3);
• 3.The procedure we have outlined is more computationally efficient than standard techniques by roughly an order of magnitude (Fig. 5); and
• 4.Perhaps most important, the procedure generates quantitative, experimentally testable predictions (Figs. 6 and 7).

When we evaluate how changes in parameters affect continuous model outputs, we usually log-transform both inputs and outputs before performing the regression. This ensures that changes to both parameters and outputs can be interpreted as percentage changes, which is more intuitive than considering absolute changes (3). For instance, a parameter sensitivity of 0.45 (Fig. 2) means that a 50% increase in CSQ causes a 20% increase in Ca²⁺ spark amplitude (see the Supporting Material). This procedure of linear multivariable regression on log-transformed inputs and outputs had strong predictive power for the continuous model outputs of Ca²⁺ spark amplitude and duration. This method was not appropriate, however, for analyzing the discrete model output of whether a particular simulation generated a spark. These results were instead analyzed with multivariable logistic regression. It seems remarkable that analyzing 1000 trials with different parameters, each generating only a yes-or-no result, could nonetheless produce a reliable continuous model describing how all model parameters influence Ca²⁺ spark probability. Nonetheless, additional validations (Fig. 3 and Fig. S3) demonstrated the accuracy of the logistic regression model. These results, along with the ROC curves shown in Fig. 4 A, demonstrate the utility of logistic regression for analyzing categorical outputs in stochastic models.

The success of logistic regression in this study suggests another possible application of this technique. Many deterministic models exhibit bifurcations such that altering a parameter leads to qualitatively different model behavior. In cardiac models, for instance, rapid pacing will eventually lead to beat-to-beat alternation in both Ca²⁺ transient amplitude and action potential duration (28,29), and decreases in excitability or cell-to-cell coupling will eventually lead to propagation failure (30). The conditions that lead to such qualitative changes could conceivably depend on all model parameters, but in most studies only a few variables are examined. To obtain a more comprehensive view, we suggest that in these situations model output, such as whether or not conduction failure occurred, can be treated as a categorical variable. Logistic regression can then be used to evaluate how model parameters affect the probability that a qualitative change occurs. In this way the locations of bifurcations can be assessed more globally.

The method we have described for analyzing stochastic models has two advantages, both practical and conceptual. First, as shown in Fig. 5 and Fig. S4, the logistic regression model requires more samples than one-at-a-time stochastic simulations to produce similar precision in the estimate of spark probability. The logistic regression, however, evaluates all parameters simultaneously rather than just one at a time. Thus, for a comprehensive analysis the procedure outlined here would be more computationally efficient by more than an order of magnitude.

Second, the matrix framework provides a convenient way to consider the overall effects when several parameters are altered simultaneously (4,5). Triadin knockout leads to three changes that correspond to identifiable model parameters. The overall effect of these changes on Ca²⁺ spark amplitude can be computed through a simple matrix multiplication that sums the effects of the individual changes (Fig. 6 C). Finally, because we randomly vary all parameters at once, our method implicitly considers a population of models, each with slightly different properties. Model parameters—in this case, variables describing Ca²⁺ release unit structure and RyR gating—are clearly quite variable, not only between individuals, but even within a single cell (31,32). Our strategy offers a method to consider not just a single model, considered typical or representative, but a population of models that reflects biological variability (5,33).

In addition to demonstrating the potential usefulness of a novel procedure, we have shown how this method can provide biological insight. For instance, the parameter sensitivities in Fig. 2 show that Ca²⁺ spark amplitude and duration are primarily determined by physical and structural parameters such as fixed [Ca²⁺] concentrations and compartment volumes. Some of these predictions have previously been tested experimentally. For instance, Terentyev et al. (34) have shown that acute manipulation of CSQ levels, using adenoviral overexpression or knockdown, causes changes in Ca²⁺ spark amplitude and duration as predicted by the sticky-cluster model. In contrast to spark amplitude and duration, Ca²⁺ spark probability depends on both these structural parameters and parameters controlling RyR gating (Fig. 3). This differential dependence on parameters suggests a potential advantage of these types of modeling strategies when designing therapeutics. If parameter sensitivity analyses are comprehensive, they can identify targets that affect certain physiological behaviors while avoiding undesirable effects on other behaviors. Of course, if a modeling study wished to systematically explore strategies for influencing myocardial Ca²⁺ signaling, such an analysis should be performed in a more complete myocyte model that includes Ca²⁺ flux balance between different cellular compartments (16,17,35,36).

To perform an independent test of the model predictions and obtain additional biological insight, we recorded Ca²⁺ sparks in cells isolated from Trdn^−/− mice. It is important to note that triadin is not explicitly represented in the mathematical model—rather, we simulated triadin knockout by changing V_JSR, N_RyR, and Ca_NSR according to the quantitative changes previously documented by Chopra et al. (20). We observed a remarkable correspondence between the model predictions (Fig. 6) and the experimental measurements (Fig. 7)—both showed a roughly 30% decrease in Ca²⁺ spark amplitude due to the combined effects of the three changes. Additional experimental tests are required to determine whether this accuracy validates the model or is merely a coincidence. More broadly, however, the example demonstrates how predictions generated using sensitivity analysis can be tested experimentally. This strategy will likely prove especially useful for differentiating between competing models when multiple representations of the same biological process have been constructed with different assumptions (3).

Some limitations of the approach should be noted:

The first limitation concerns the assumption of a linear relationship between parameters and model outputs. Although this linear approximation has proven adequate for predicting Ca²⁺ spark amplitude and duration (Fig. 2 A), more complex representations may be required for alternative outputs or for different models. In such cases the regression model can be expanded by including additional terms that represent interactions between parameters.

The second limitation is that our approach relating parameters to outputs is purely empirical, which means that the sensitivities cannot be related directly to the underlying equations of the system. Existing sensitivity analysis methods for stochastic systems (37,38) are based on the chemical master equation and the calculation of probability density functions of the model states. These semianalytical methods have the advantage of a close relationship between model equations and parameter sensitivities. These approaches would most likely prove less useful, however, for complex model outputs such as spark amplitude that depend on processes such as JSR depletion, Ca²⁺ diffusion, and buffering. Our empirical method therefore offers the advantage of flexibility.

Conclusion

We have demonstrated that parameter randomization followed by multivariable regression (3–5) can be used to analyze parameter sensitivities of stochastic mathematical models. Using a model of the cardiac Ca²⁺ spark as a test case, we showed that this method is more computationally efficient than standard techniques by more than an order of magnitude. More important, we experimentally tested predictions of how changes in parameters influence Ca²⁺ spark amplitude. Our approach can be extended to gain additional insight into myocardial Ca²⁺ signaling and other biological processes in which stochasticity plays an important role.