Biomolecular cryocrystallography: Structural changes during flash-cooling

Abstract

To minimize radiation damage, crystal structures of biological macromolecules are usually determined after rapid cooling to cryogenic temperatures, some 150–200 K below the normal physiological range. The biological relevance of such structures relies on the assumption that flash-cooling is sufficiently fast to kinetically trap the macromolecule and associated solvent in a room-temperature equilibrium state. To test this assumption, we use a two-state model to calculate the structural changes expected during rapid cooling of a typical protein crystal. The analysis indicates that many degrees of freedom in a flash-cooled protein crystal are quenched at temperatures near 200 K, where local conformational and association equilibria may be strongly shifted toward low-enthalpy states. Such cryoartifacts should be most important for strongly solvent-coupled processes, such as hydration of nonpolar cavities and surface regions, conformational switching of solvent-exposed side chains, and weak ligand binding. The dynamic quenching that emerges from the model considered here can also rationalize the glass transition associated with the atomic fluctuations in the protein.

Within a mere decade, biomolecular structure determination by x-ray diffraction has moved from ambient to cryogenic temperature (1–3). Today, ≈90% of all protein crystal structures are determined from diffraction data recorded at temperatures of 90–120 K (3). Cryocrystallography evolved primarily as a means to combat radiation damage to crystals from intense synchrotron x-ray beams, based on the idea that radiation-induced free radicals do not damage the biomolecule once they are trapped in the vitrified bulk solvent within the crystal (2). Much effort has been spent on optimizing flash-cooling protocols to avoid ice formation, usually with the aid of cryoprotectants, such as glycerol or polyethylene glycol, and to minimize thermally induced inhomogeneities that limit the resolution (1–3). In contrast, remarkably little concern has been expressed about the fact that cryocrystallography examines biomolecules some 200 K below their normal physiological temperature range.

The native 3D structures of proteins and nucleic acids result from a delicate balance of interactions, where the solvent-mediated hydrophobic effect plays a major role (4). Accordingly, biomolecules are expected to unfold, not only at high temperature, but also at low temperature (5). In general, it is assumed that such cold denaturation is too slow to intervene during flash-cooling, and this assumption is corroborated by the finding that cryostructures usually differ little from the corresponding room-temperature structures (6–9). Indeed, in a comparison of 15 protein structures determined both at cryogenic and room temperature, the rms deviation of nonhydrogen backbone atoms in the optimally superimposed structures was only 0.2–0.8 Å (9).

Biomolecules are complex systems with many coupled degrees of freedom. Even if the global backbone fold is virtually unaffected by flash-cooling, the local structure may be altered in regions that are critical for biological function. In one of the few studies focusing on thermal artifacts in cryocrystallography, Juers and Matthews (9) showed that the area involved in protein–protein crystal contacts typically increases by 50% on cooling to cryogenic temperature. Furthermore, they proposed that protein–protein interactions are enhanced at low temperature largely because of the reduced entropic cost of locking flexible, polar side chains into energetically favorable conformations at protein–protein interfaces. Whatever the cause, these findings raise concerns about the validity of cryostructures of biomolecular complexes (9). Significant conformational differences between cryogenic and room-temperature protein structures have been reported also for solvent-exposed side chains (not located at crystal contacts) and associated water molecules (10–12), sometimes in the catalytic site of enzymes.

The effect of cooling on the structure of proteins and other biological macromolecules can be conceptualized in terms of the conformational energy landscape. In the limit of infinitely fast cooling, the system would be quenched into an amorphous solid (glass) state, where thermal atomic motions (as reflected in crystallographic B factors) would be reduced in amplitude, whereas the mean atomic positions would not change significantly and then only as a result of the anharmonic character of the local potential wells. However, this limit is not attained with practical flash-cooling protocols, which, for protein crystals in the typical size range, yield characteristic cooling times on the order of 0.1–1 s (13). Flash-cooling of a protein crystal should therefore be viewed as a continuous temperature-jump relaxation experiment, where different degrees of freedom participate to different extents.

Bulk water can be vitrified by cooling from >273 K to a temperature below the glass transition temperature of 136 K at a cooling rate of ≈10⁶ Ks^–1 (14, 15). Such high cooling rates can be achieved for micrometer-sized water droplets, but not for the millionfold larger volume of a typical protein crystal. Because of protein–water interactions, a cooling rate of ≈100 K s^–1 is usually sufficient to vitrify the solvent in a protein crystal; penetrating cryoprotectants, such as glycerol, reduce the critical cooling rate even further (2, 13). Water occupying wide (>50 Å) channels in protein crystals behaves like bulk water, transforming into ice on heating from cryogenic temperature, whereas water in direct contact with the protein does not crystallize and exhibits a broad glass transition in the range 160–220 K (16, 17). Similar results have been reported for hydrated protein powders (18, 19). During flash-cooling of a protein crystal, solvent, ligands, and side chains should thus exhibit liquid-like mobility down to ≈200 K. Once the protein crystal has reached the cryogenic temperature of ≈100 K, it is in a glassy state (with a 10¹⁵-fold or so higher viscosity than room-temperature water) where all motions are effectively arrested, except for localized vibrational modes. During storage, transport, and data acquisition, the structure of the protein crystal should thus not change further as long as the cryogenic temperature is maintained. The question is: What happens with the structure during cooling from room temperature to the temperature of kinetic arrest?

Methods

Heat Conduction. In a spherically symmetric solid material, characterized by an isotropic and spatially uniform thermal diffusivity tensor, the temperature T(r, t) at radial position r and time t is governed by the radial heat conduction equation (20):

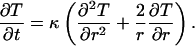[1]

The thermal diffusivity, κ (m² s^–1), is related to the thermal conductivity, K (W K^–1 m^–1), the specific heat, c_P, and the mass density, ρ, through κ = K/(c_Pρ). We consider a spherical solid of radius a, which initially has a uniform temperature, T₀. At time t = 0, the surface temperature is reduced to T_S and thereafter held constant. The space–time evolution of the temperature within the sphere is obtained by solving Eq. 1 subject to the initial condition T(r, 0) = T₀ and the boundary conditions T(a, t) = T_S and T(0, t) = finite. The result is (20):

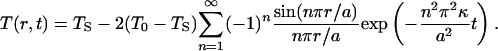[2]

The spatial average of T(r, t) over the innermost one-third (by volume) of the sphere is

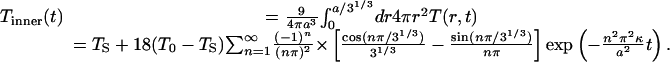[3]

Similar expressions are obtained for the average temperature in the middle and outer one-third of the sphere.

Nonequilibrium Populations During a Continuous Temperature Change. We consider a two-state equilibrium,

[4]

Let x_A and x_B = 1 – x_A be the fractional populations in the two states. When the system is in equilibrium at temperature T, the A state population is

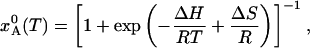[5]

where the ΔH = H_B – H_A and ΔS = S_B – S_A are the changes in enthalpy and entropy per mole of state A (or B).

If the temperature is suddenly changed from T₁ to T₂, the A state population, x_A(t), evolves exponentially toward the new equilibrium value :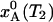

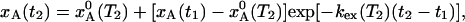[6]

where 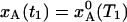if the system was in equilibrium before the temperature jump. Making use of the detailed balance condition, we can express the exchange rate constant, k_ex = k_A→B + k_B→A, in terms of the mean lifetime of state A, τ_A, and the equilibrium population:

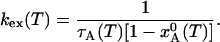[7]

To calculate the time-dependent nonequilibrium population, x_A(t), when the temperature is varied continuously, we must solve a rate equation with a time-dependent rate constant, k_ex[T(t)]. Numerically, this solution can be obtained by dividing the time axis in sufficiently small intervals and by applying Eq. 6 to each step, with the initial population x_A(t₁) given by the nonequilibrium population at the end of the previous interval.

Results

Thermal Evolution During Flash-Cooling. The physics of flash-cooling has recently been examined by Kriminski et al. (13). Here, we are interested specifically in how the temperature of the crystal changes with time. We consider a spherical crystal of radius a that is instantaneously transferred from ambient conditions, with a uniform crystal temperature T₀ = 293 K, to a cryogenic bath that maintains the crystal surface at a temperature T_S = 77 K. In this idealized plunge-cooling scenario, we assume that heat transport occurs exclusively by conduction through the protein crystal. The temperature, T(r, t), at radial position r in the crystal then evolves in time according to Eq. 2. In the alternative gas-cooling method, the rate-limiting convection in the boundary layer results in considerably lower cooling rate (13). The case considered here thus corresponds to the maximum, theoretically possible, cooling rate for given crystal geometry and cryogen temperature. With current flash-cooling protocols, nitrogen evaporation at the crystal surface and/or convective heat transfer through the boundary layer result in cooling rates that are lower than the theoretical maximum by at least one order of magnitude (13).

To use Eq. 2, we need to specify the thermal diffusivity, κ, of the crystal. Protein crystals typically contain 30–60 vol% water (21) and the effective κ is a volume-weighted average of the thermal diffusivities of protein and solvent. Normal-mode calculations on myoglobin (in the absence of water) yield κ = 1.38 × 10^–7 m² s^–1 at 300 K (22), close to the value 1.46 × 10^–7 m² s^–1 for water at this temperature (23). For our purposes, the κ value below the glass transition is of little consequence. On going from 300 to 200 K, κ increases by 20% for myoglobin (22) and decreases by 35% for water [based on a linear extrapolation of data from >273 K (23)]. To a first approximation, we ignore the resulting weak (partly compensated) temperature dependence in the effective κ and use a constant value of 1.2 × 10^–7 m² s^–1 for the protein crystal.

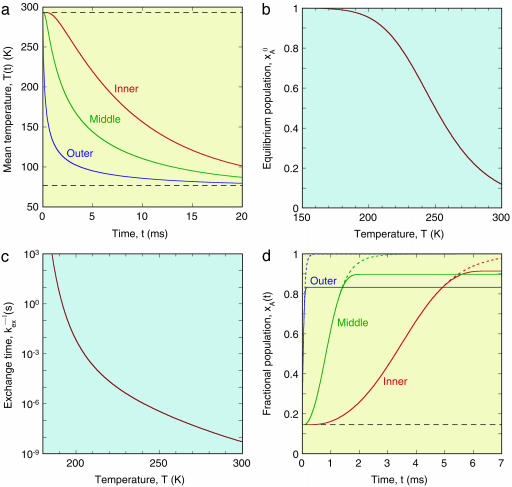
A characteristic time, τ_cool, for crystal cooling can be defined as the time required for the temperature at the center of the crystal (r = 0) to drop halfway from T₀ to T_S. It follows from Eq. 2 that τ_cool = 0.14 a²/κ. With the adopted κ value, this yields τ_cool = 12 ms for a = 0.1 mm. This crystal radius was used in the calculations reported here. However, to illustrate the effect of crystal size, we include some results obtained with a larger crystal radius, a = 0.5 mm, for which τ_cool = 290 ms. Whereas the smaller crystal radius is more representative of the crystals typically used with synchrotron x-ray beams, the larger radius yields, in our heat conduction calculation, a cooling rate that is closer to what is commonly achieved in practice (13). Fig. 1a shows the time evolution of the mean temperature averaged over the inner, middle, or outer third of the volume of a 0.1-mm spherical crystal (see Eq. 3).

Fig. 1.

(a) Evolution of crystal temperature during flash-cooling from 293 to 77 K for a spherical crystal with radius a = 0.1 mm and thermal diffusivity κ = 1.2 × 10^–7 m² s^–1. The three curves refer to the spatially averaged temperature in the inner, middle, and outer thirds of the crystal volume. (b) Temperature dependence of the equilibrium population, 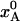, of the low-enthalpy state A in a two-state equilibrium with ΔH = 25 kJ mol^–1 and ΔS = 100 J K^–1 mol^–1. (c) Temperature dependence of the exchange time, 1/k_ex, as predicted by Eqs. 7 and 8 with τ₀ = 10 ns, ΔH^# = 40 kJ mol^–1, D(T) from the Vogel–Tamman–Fulcher fit for water, and 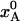as in b. (d) Evolution of A state population x_A(t) during flash-cooling, computed numerically with the aid of Eq. 6, and based on the temperature profiles in a, the equilibrium population in b, and the exchange time in c. The dashed curves correspond to the equilibrium Boltzmann population, 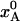, at the time-dependent temperature.

The results of our analysis are not sensitive to the shape of the crystal. Our choice of a spherical shape is dictated mainly by mathematical convenience. Real protein crystals are often anisometric, but, for a given smallest dimension, a spherical crystal yields the highest conductive cooling rate. For example, a plate-like crystal of thickness 2a has a 2.7-fold slower cooling rate (τ_cool = 0.38 a²/κ if end effects are ignored) than a sphere of diameter 2a.

Structural Changes During Flash-Cooling. To illustrate the structural changes that take place during flash-cooling of a biomolecular crystal, we consider the equilibrium between an enthalpically stabilized low-temperature state A and an entropically stabilized high-temperature state B. When the system is in thermal equilibrium at a temperature T, the fractional population, 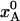, in state A is given by Eq. 5. In the calculations, we set ΔH = 25 kJ mol^–1 and ΔS = 100 J K^–1 mol^–1, independent of temperature. [Note that the purely “thermal” contributions to ΔH and ΔS cancel out identically in the Gibbs energy and, hence, do not contribute to the temperature dependence of 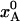(24, 25).] For this choice of parameter values, 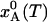goes from 1.000 at 77 K to 0.146 at 293 K (see Fig. 1b).

During flash-cooling, the temperature in the crystal decreases continuously. To obtain the time-dependent nonequilibrium population, x_A(t), we must solve a rate equation with a time-dependent exchange rate constant, k_ex[T(t)]. Alternatively, we can discretize the time variable and treat the cooling process as a series of finite temperature jumps. After each jump, the population relaxes toward the new equilibrium population according to Eq. 6. As the time steps are made smaller, the solution to this multistep-relaxation problem converges toward the solution of the continuous-cooling problem.

To complete the model, we must specify the temperature dependence of the mean lifetime, τ_A, in state A, which determines the exchange rate constant, k_ex, through Eq. 7. The processes of interest here can be reasonably modeled in terms of diffusion over a potential barrier of height ΔH^#, in which case (26),

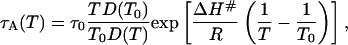[8]

where τ₀ = τ_A(T₀) is the A state lifetime at a reference temperature, T₀, which we choose as the initial temperature (293 K). The processes that we have in mind either involve water displacement directly or are strongly coupled to solvent dynamics. We therefore identify D with the translational diffusion coefficient of water. The temperature dependence is taken from the Vogel–Tamman–Fulcher representation (27) of experimental diffusion data (28) in the range 238–298 K: D(T) = D₀ exp[–B/(T – T_C)], with B = 371 K and T_C = 169.7 K (the constant D₀ cancels out in Eq. 8). This empirical extrapolation formula obviously fails near (and below) the “critical” temperature, T_C, where a solid-like defect-controlled diffusion mechanism is believed to take over (29). However, the Vogel–Tamman–Fulcher formula should be adequate down to the glass transition temperature of ≈200 K. Below this temperature, the dynamics are too slow to have an appreciable effect on the evolution of the population x_A during flash-cooling. In fact, the results reported here are virtually identical with those obtained by enforcing complete quenching (k_ex = 0) of A ↔ B transitions at <200 K. Fig. 1c shows the inverse of the exchange rate constant in the relevant temperature range, computed from Eq. 8 with τ₀ = 10 ns and ΔH^# = 40 kJ mol^–1.

By combining the results shown in Fig. 1 a–c, we can now compute the time evolution of the nonequilibrium population, x_A(t), during the flash-cooling process. As seen from Fig. 1d, this evolution exhibits two distinct phases. In the first phase, A ↔ B interconversion is sufficiently fast to maintain the equilibrium Boltzmann population as the temperature drops (dashed curves). Consequently, 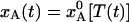throughout this phase. In the second phase, A ↔ B interconversion is too slow to maintain equilibrium as the temperature drops further. The system is dynamically quenched and the population remains constant, 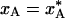, as cooling proceeds to the final cryogenic temperature, T_S. The transition between these two evolution phases occurs when the cooling rate matches the A ↔ B interconversion rate. Because of the very strong temperature dependence of the interconversion rate constant k_ex near 200 K (see Fig. 1c), the transition is abrupt (see Fig. 1d).

The intersection of the equilibrium curve, 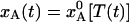, and the quenching level, 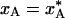, in Fig. 1d defines a quenching time, t*, which depends on the radial position in the crystal. In Table 1 we give t* and 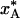for the three regions of spherical crystals of radius 0.1 mm (as in Fig. 1) or 0.5 mm. The table also lists the quenching temperature, T* = T(t*), obtained from the cooling curves in Fig. 1a (after scaling the time axis by a factor 25 for the larger crystal). At the quenching temperature, the exchange time, 1/k_ex, matches the characteristic cooling time, τ_cool, defined (see above) as the time for the mean temperature in the region to reach a value halfway between T₀ and T_S (185 K in our example). In other words, T* is determined by the condition k_ex(T*) τ_cool ≈ 1.

Table 1. Quenching times, temperatures, and populations for a two-state process during flash-cooling of a protein crystal.

	a = 0.1 mm			a = 0.5 mm
	Inner	Middle	Outer	Inner	Middle	Outer
t*, ms	5.7	1.6	0.1	155	47	3.5
T*, K	209	212	221	200	202	208
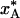	0.92	0.90	0.83	0.95	0.94	0.92

The results are for conductive cooling from 293 to 77 K of a spherical crystal of radius, a. For each radius, the three columns refer to the inner, middle, and outer thirds of the crystal volume. The parameter values describing the A ↔ B interconversion process are as in Fig. 1.

For the example considered in Fig. 1, flash-cooling quenches the examined degree of freedom at a temperature of ≈210 K throughout most of the 0.1-mm crystal. A subsequent x-ray diffraction experiment, carried out at cryogenic temperature, will thus yield a structure that reflects the A ↔ B equilibrium at the quenching temperature, T* ≈ 210 K. 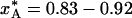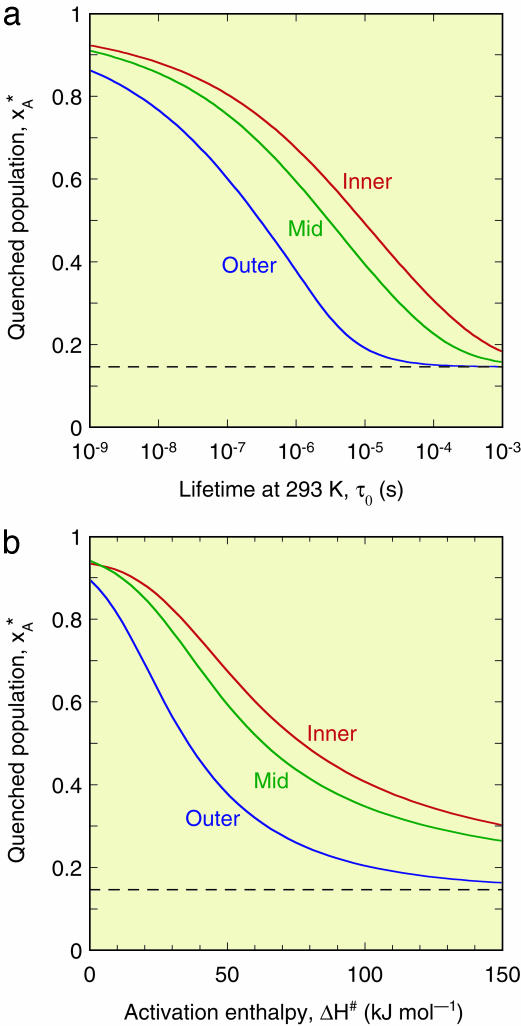At this temperature, the A state predominates ( for the three regions), whereas the B state is most populated at the ambient initial temperature, 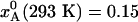. The cryogenic temperature has thus not only reduced the amplitude of local thermal motions (B factors), but has essentially converted the structure from one state to another. The extent of such cryoartifacts depends on the interconversion rate k_ex. However, for a temperature-dependent equilibrium of the type shown in Fig. 1b, substantial cryoinduced shifts of substate populations can be expected even for ambient-temperature substate lifetimes in the microsecond range and longer and for activation enthalpies exceeding 100 kJ mol^–1 (see Fig. 2). For the 0–150 kJ mol^–1 range examined in Fig. 2b, the quenching temperature T* varies from 190 to 257 K (middle region). The ranges of τ₀ and ΔH^# examined in Fig. 2 should encompass most conformational and association processes occurring at or near the biomolecule–solvent interface.

Fig. 2.

Dependence of the quenched A state population, 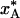, on the A ↔ B interconversion rate for (a) ΔH^# = 50 kJ mol^–1 and variable A state lifetime, τ₀, at 293 K, and (b) τ₀ = 1 μs and variable activation enthalpy ΔH^#. The population 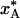was computed for the cooling curves in Fig. 1a and the two-state equilibrium in Fig. 1b.

A 5-fold increase in radius increases the crystal volume by two orders of magnitude but has little effect on the quenching behavior. The cooling curves are identical with those shown in Fig. 1a, apart from a 25-fold lengthening of the timescale. However, the quenching temperature, T*, and population, 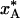, are much the same as for the smaller crystal (see Table 1).

Discussion

Implications for Structural Biology. Structural models derived from diffraction data recorded at cryogenic temperatures do not portray biological macromolecules at thermodynamic equilibrium. This fact is probably widely appreciated within the crystallography community, although rarely stated explicitly. With a few notable exceptions (6–12), it is usually taken for granted that the cryostructure is quenched at ambient temperature (T* = T₀ in our notation) and, therefore, that the only structural effect of the low temperature is to sharpen the atomic displacement distributions without significantly displacing the mean atomic positions [apart from a more-or-less uniform contraction of the protein (6–9)]. In contrast to this conventional wisdom, the present analysis indicates that many degrees of freedom are quenched at temperatures near 200 K, where local conformational and association equilibria may be strongly shifted toward low-enthalpy states. In general, a cryostructure does not represent the equilibrium state of the macromolecule at T₀ or T_S or any other single temperature. For example, a protein structure determined at 100 K may have the same global backbone fold as at room temperature, whereas exposed side chains and solvent components sample a 200 K equilibrium distribution of substates. Flash-cooling thus induces an artificial thermal heterogeneity, where different degrees of freedom correspond to different temperatures. On the other hand, our calculations do not indicate that flash-cooling produces any substantial spatial heterogeneity. Although different parts of the crystal are cooled at widely different rates (see Fig. 1a), the quenching temperature, T*, and the quenched population, 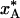, differ little between the three regions (see Table 1). This point is important, because a thermally induced macroscopic gradient in protein structure could not easily be distinguished from intrinsic conformational heterogeneity, for example, a side chain with an intrinsically bimodal conformational distribution.

The view advocated here, with different degrees of freedom being quenched at different temperatures, calls for caution in the interpretation of cryostructures. The functionally most interesting parts of biomolecules, such as sites for recognition, binding, or catalysis, usually involve the interfacial region, where delayed quenching and consequent cryoartifacts are expected to be most pronounced. Detailed comparisons with ambient-temperature diffraction data are therefore required to validate cryocrystallographic studies of, for example, hydration phenomena, weak ligand binding, salt bridges, and conformations of exposed side chains.

In ultrahigh-resolution protein crystal structures obtained at cryogenic temperature, extensive hydrogen-bond networks of fused five-, six-, and seven-membered rings of water molecules are commonly observed (30–32). If such cooperative hydration structures were present at ambient temperature, water motions in the hydration layer would be strongly retarded as compared with bulk water. However, ²H and ¹⁷O magnetic relaxation dispersion studies indicate a mere 2-fold dynamic retardation for the vast majority of water molecules in the hydration layer of proteins (33). For the small protein crambin, where ultrahigh-resolution structures have been reported at several temperatures from 100 to 293 K, the six- and seven-membered rings disappear at >200 K (30), indicating that they are, in fact, cryoartifacts.

The possibility that monovalent cations can replace ordered water molecules at the floor of the narrowed minor groove in AT tracts of B form duplex DNA has generated considerable interest and controversy (34, 35). The crystallographic evidence in favor of this proposition is based entirely on cryogenic diffraction data (36–38). ²³Na and ⁸⁷Rb magnetic relaxation dispersion studies (39, 40) of DNA in solution at ambient temperatures indicate that ion binding is weak (partial occupancy) and relatively short-lived (submicrosecond at 277 K), so the thermodynamic and kinetic parameters should fall in the range of values examined here. The crystal structures are therefore likely to reflect the ion-binding equilibrium at a quenching temperature near 200 K. With a negative binding enthalpy, as indicated by the magnetic relaxation dispersion results (40), ion binding will be artificially enhanced in cryostructures, as compared with ambient temperature.

The hydration of nonpolar cavities and channels in proteins may also be susceptible to cryoartifacts. This process is probably entropy-driven (41), with the low-temperature A state corresponding to an empty cavity. For example, water molecules in the central channel of bacteriorhodopsin are thought to play an active role in the proton translocation mechanism (42). The high-resolution cryostructure of bacteriorhodopsin shows a network of water molecules on the highly polar, extracellular side of the retinal molecule, but a corresponding network that could transport the proton through the mainly nonpolar, cytoplasmic half of the channel is not evident (43). ²H and ¹⁷O magnetic relaxation dispersion measurements (44) are consistent with more water molecules in the channel than seen in the crystal structure and show that the internal water molecules exchange with bulk water on a microsecond timescale (at 277 K). With a probable quenching temperature near 200 K, some of the channel waters may thus have been expelled during flash-cooling.

Crystallographic studies of cryotrapped photocycle intermediates of bacteriorhodopsin have revealed displacements of key water molecules within the proton translocation channel (45–47). Mechanistic interpretations of such findings must rely on the assumption that the hydration structure is quenched at ambient temperature, rather than at 200 K (as seems more likely). Caution would also seem to be warranted in crystallographic studies of enzyme mechanisms based on cryotrapped catalytic intermediates (48). Side-chain conformations, hydration structures, ligand association, and proton dissociation equilibria may all be affected by flash-cooling.

Relation to the Protein Glass Transition. X-ray diffraction (6, 49), dynamic neutron scattering (50), and other investigations (18, 51) of protein crystals and hydrated protein powders indicate that the thermal fluctuations of protein atoms undergo a qualitative change at a temperature that, depending on conditions, usually falls in the range 180–220 K. This dynamical transition is thought to involve a low-temperature glassy state, where only harmonic vibrations are possible, and a high-temperature fluid state, where also diffusive motions take place on the experimental timescale.

The simple two-state model used here to illustrate the structural implications of flash-cooling can also be used to rationalize the protein glass transition. Given that many protein conformational degrees of freedom are strongly coupled to thermal fluctuations in the solvent (52–57), the A ↔ B interconversion rate constant k_ex given by Eqs. 7 and 8 can also describe the diffusive dynamics of such conformational degrees of freedom. In this simple model, the protein glass transition is a consequence of the very strong temperature dependence of k_ex near 200 K (see Fig. 1c). This, in turn, is a result of a cooperative restructuring of the hydrogen-bond network in liquid water toward perfect tetrahedral coordination (58) and at the expense of the more highly coordinated configurations (with bifurcated hydrogen bonds) that are responsible for the high fluidity of water (29).

In cryocrystallography, the cooling rate plays a dual role. First, it must be higher than the rate of ice nucleation in wide solvent channels within the crystal (17, 59) and in any external solvent in contact with the crystal (2). In protein crystals without wide channels (17) and in protein powders at low hydration levels (18, 19), ice is not the thermodynamically stable phase of low-temperature water. The glassy state is then formed even when the sample is cooled slowly. The second role of the cooling rate, and the one we are concerned with here, is to determine the interval available for structural rearrangements. This interval is the time required to cool the sample to the quenching temperature, T*, which is ≈200 K for the two-state process considered in Fig. 1c. Because k_ex(T*) τ_cool ≈ 1, it follows from Eqs. 7 and 8 that T* depends only logarithmically on the cooling rate. The quenching temperature defined here should therefore not differ much from the glass transition temperature determined under slow-cooling conditions.