SUMMARY
Neuronal computation involves the integration of synaptic inputs that are often distributed over expansive dendritic trees, suggesting the need for compensatory mechanisms that enable spatially disparate synapses to influence neuronal output. In hippocampal CA1 pyramidal neurons, such mechanisms have indeed been reported, which normalize either the ability of distributed synapses to drive action potential initiation in the axon or their ability to drive dendritic spiking locally. Here we report that these mechanisms can coexist, through an elegant combination of distance-dependent regulation of synapse number and synaptic expression of AMPA and NMDA receptors. Together, these complementary gradients allow individual dendrites in both the apical and basal dendritic trees of hippocampal neurons to operate as facile computational subunits capable of supporting both global integration in the soma/axon and local integration in the dendrite.
INTRODUCTION
Excitatory inputs onto a single neuron are distributed over its often expansive dendritic arbor, which can span hundreds of microns (Häusser et al., 2000; Magee, 2000; Williams and Stuart, 2003; Spruston, 2008). Synaptic signals must therefore travel over a wide range of distances before reaching the soma and axon. Cable theory (Rall, 1977) and experiments (Rall, 1959; Iansek and Redman, 1973; Stuart and Spruston, 1998; Magee and Cook, 2000; Williams and Stuart, 2003; Golding et al., 2005; Branco and Häusser, 2010) have established that signal propagation through dendrites is subject to distance-dependent filtering and attenuation, potentially reducing the influence of distal synapses on somatic voltage. Importantly, however, mechanisms to counteract this situation have been proposed and substantiated, such as increasing synaptic strength with distance from the soma to offset distance-dependent voltage attenuation (Magee and Cook, 2000; Nicholson et al., 2006).
Neither dendrites nor synapses are uniform, however. For example, the diameter of dendrites near their terminal ends tapers, resulting in distance-dependent increases in local input impedance. Moreover, dendrites are “sealed” at their terminal ends, resulting in even higher input impedance and, consequently, large local synaptic potentials (Rall and Rinzel, 1973; Rinzel and Rall, 1974). Synapses on dendritic spines are also diverse (Bourne and Harris, 2008; Nicholson and Geinisman, 2009), being comprised of two major synaptic subtypes—perforated and nonperforated—that differ in size, number, and ligand-gated receptor expression. Therefore, mechanisms that offset dendritic filtering in some dendritic segments may not be effective in other parts of the dendrites and, further, the role of perforated and nonperforated synapses in such mechanisms may differ.
In agreement with such diversity among dendrites and synapses, studies of hippocampal CA1 pyramidal neurons have shown that their apical dendrites implement multiple compensatory mechanisms that, together, counteract the influence of dendritic cable properties on distal synaptic signals. First, along the somatodendritic axis, the expression of AMPA-type glutamate receptors (AMPARs) increases, on average, with distance from the soma, largely due to an increased number of strong synapses at distal locations (Magee and Cook, 2000; Nicholson et al., 2006; Nicholson and Geinisman, 2009). This local increase in average synapse strength reduces the location dependence of unitary somatic excitatory postsynaptic potentials (EPSPs) (Magee and Cook, 2000; Smith et al., 2003; Nicholson et al., 2006). Second, along individual oblique dendrites, which radiate from the main apical dendrite, synapse number decreases. This within-dendrite numerical scaling normalizes the contribution of individual synapses to dendritic spike generation, reducing the location dependence of dendritic spike-triggering synapses (Katz et al., 2009). Together, these studies show that synaptic strength increases along the somatodendritic axis but that synapse number decreases along individual apical dendritic branches, thereby balancing the competing objectives of minimizing EPSP attenuation and maximizing the number of synapses that contribute to dendritic spikes and axonal action potentials.
Much less is known about such compensatory mechanisms in the basal dendrites of CA1 pyramidal neurons. Morphologically, the basal dendrites of CA1 pyramidal neurons are different from the apical dendrites, despite sharing common afferents (i.e., inputs from CA3). Basal dendrites in stratum oriens (SO) are shorter and are distributed in a radially uniform manner, lacking the distinction among the trunk, oblique branches, and the tuft present in the apical tree. In addition, several main parent basal dendrites connect directly to the soma, whereas the apical dendritic arbor connects to the soma via a single main apical dendrite (Amaral and Lavenex, 2006). Despite these differences in dendrite structure, synaptic signals in both basal and apical oblique dendrites are subjected to similar dendritic cable properties. First, because synapses on apical and basal dendrites are distributed throughout relatively long dendrites, EPSPs from the most distal synapses in both regions undergo the most distance-dependent filtering as they propagate toward the soma. Second, both apical and basal dendrites have a branch point on one end and a tapering “sealed” end on the other, creating a low-input impedance at the former and a high-input impedance at the latter. One prediction from such similarities is that synapses on both basal and apical oblique dendrites could utilize similar mechanisms to compensate for the consonant effects of dendritic filtering on their local and somatic EPSPs.
To address this issue, we first determined whether any of the mechanisms identified as influencing synaptic integration in apical dendrites are present in basal dendrites. Next, we analyzed synaptic receptor expression on the axospinous synapses of both basal and apical oblique dendrites, segregated on the basis of their parent dendrites’ diameters, with the presumption that synapses on the thinnest dendrites are closest to the dendrites’ terminal ends.
Finally, we performed simulations using computational models to analyze the impact of the observed gradients of synapse number and receptor expression for events both above and below the threshold for triggering local dendritic spikes. Our analyses suggest that synapses in both regions use the same combination of mechanisms to regulate their contribution to somatic and dendritic depolarization, as well as Ca2+ influx through NMDARs. Moreover, the present study provides strong evidence that single-dendrite gradients in synapse number and receptor expression confer to individual hippocampal dendrites the dual capabilities of integrating activity locally in the dendrite and participating in global integration at the soma with remarkable location independence.
RESULTS
Synapse Number Decreases with Distance along Individual Dendrites
Like apical oblique dendrites (Golding and Spruston, 1998; Losonczy and Magee, 2006), synapses on basal dendrites can influence somatic voltage cooperatively via local dendritic Na+ spikes (Remy et al., 2009; see also Nevian et al., 2007). To determine whether basal dendrites show evidence for single-dendrite scaling of synapse number, which was shown in apical oblique dendrites to maximize dendritic impact on somatic voltage and normalize the location of dendritic spike-triggering synapses (Katz et al., 2009), we reconstructed individual basal dendrites from CA1 pyramidal neurons using serial section electron microscopy (see also Figure S1 available online).
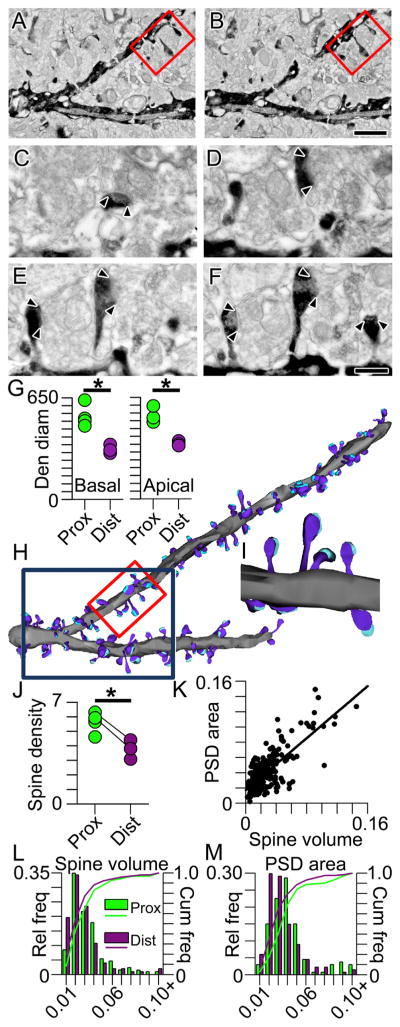
Three-dimensional reconstructions of biotinylated dextranamine-labeled dendritic segments from serial electron micrograph mosaics allowed us to measure the density and volume of spines and to determine the size of many of their postsynaptic densities (PSDs; Figures 1A–1M). As is also apparent from the three-dimensional array tomographic renderings (Figure S1), dendritic diameter in the electron microscopic reconstructions tapers as individual dendrites course to their terminal ends, regardless of whether they are basals or apical obliques (Figure 1G; basal: F(1,5) = 24.8, p < 0.01; apical oblique: F(1,4) = 27.8, p < 0.01). Additionally, as found in apical oblique dendrites, spine density is ~33% lower in distal basal dendritic segments within SO, as compared to proximal segments (Figure 1J; t(5) = 3.30, p < 0.05). To assess whether synapse size also decreases along the length of an individual dendrite as seen in apical oblique dendrites, we measured 266 PSDs from proximal and distal branch segments. As might be predicted from the correlation between spine volume and PSD area (r = 0.75, p < 0.001; Figure 1K), both are significantly smaller (by 18% and 28%, respectively) in the distal basal dendrites (spine volumes: mean ± SEM proximal = 0.029 ± 0.002 μm3; distal = 0.024 ± 0.001 μm3; p < 0.05; PSD areas: proximal = 0.046 ± 0.002 μm2; distal = 0.033 ± 0.001 μm2; p < 0.0001; Figures 1L and 1M).
Figure 1. Intradendritic Scaling of Spines and Synapses Using Reconstructive Electron Microscopy.
(A and B) Serial electron micrograph mosaics through a BDA-labeled proximal branch segment with spines and synapses. Red boxed region denotes the higher magnification images depicted in (C)–(F). Scale bar represents 1 μm, also applies to (H).
(C–F) Higher-magnification series through red boxed region in (A) and (B). Arrowheads indicate boundaries of each postsynaptic density (PSD). Scale bar represents 0.25 μm, also applies to (I).
(G) Dendritic diameters measured on electron microscopically reconstructed dendritic segments from proximal (green) and distal (purple) portions of basal (left) and apical (right) dendrites. Asterisk indicates that proximal dendrites have significantly larger diameters than distal dendrites. In all figures, group data are represented as means ± SEM.
(H) Lower-magnification three-dimensional reconstructions of the two dendritic branch segments shown at higher magnification in (C)–(F). The red boxed segment is the same portion of the dendrite shown in serial sections in (C)–(F) and reconstructed in (I); the dark blue box denotes the dendritic segment shown in (A) and (B).
(I) Three-dimensional reconstructions of spines (dark blue), their synapses (cyan), and their parent dendrite (gray) from micrographs shown in (C)–(F).
(J) Scatter plot showing spine densities on basal branch segments proximal (green) and distal (purple) to the soma. Connected circles represent segments from the same branch. Asterisk indicates that proximal segments have a significantly higher spine density than distal segments.
(K) Scatter plot showing the linear relationship between spine volume (on the abscissa) and PSD area (on the ordinate).
(L) Histograms showing the relative (bars) and cumulative (lines) frequencies of spine volumes in basal dendritic segments proximal (green) and distal (purple) to the soma.
(M) Same as (L) but for PSD area.
Taken together, reconstructions of individual dendrites show that spines on both basal and apical oblique dendrites are progressively sparser toward each dendrite’s terminal end. These single-dendrite gradients are very similar for the basal dendrites in the SO and the apical dendrites in the stratum radiatum (SR), suggesting that any compensatory function of such distance-dependent regulation is similar in both regions (e.g., Katz et al., 2009). We next used unbiased quantitative serial section electron microscopy to determine whether basal dendritic synapses show scaling along the somatodendritic axis resembling that described for apical dendrites (Nicholson et al., 2006).
Selective Decrease of Nonperforated Synapses Results in Fewer Synapses in Distal Dendrites
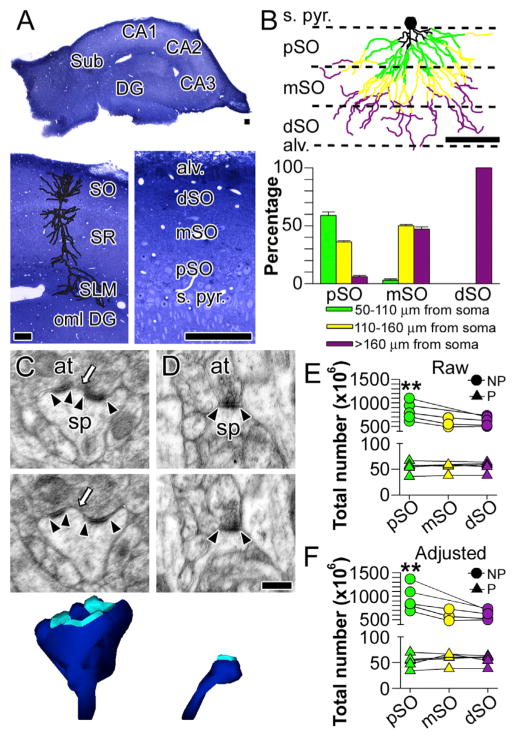
The two major axospinous synaptic subtypes in the hippocampus are distinguished by the configuration of their PSDs into perforated and nonperforated synapses (Bourne and Harris, 2008; Nicholson and Geinisman, 2009). Perforated synapses have significantly higher expression levels of AMPARs and NMDARs compared to their nonperforated counterparts (Nicholson and Geinisman, 2009), which implies that they generate significantly larger synaptic currents than the latter. Thus, the number of perforated and nonperforated synapses in different regions of the dendritic arbor can be used to infer information about the role, or relative importance, of basal dendritic synapses at different distances from the soma. To determine whether their numbers change with distance from the soma as seen in the apical dendrites, we used unbiased quantitative electron microscopy to determine the total number of perforated and nonperforated synapses in proximal, middle, and distal stratum oriens in the CA1 region of hippocampus (pSO, mSO, and dSO, respectively).
Because of the radial distribution of basal dendrites, a small proportion of middle and distal branch segments are interspersed with proximal segments in pSO and, similarly, a few proximal and distal segments are present in mSO (Figures 2A and 2B). To correct for this, we divided the neuropil lying between the pyramidal cell layer and the alveus into thirds (Figure 2B). This approach allowed us to determine the contribution of proximal, middle, and distal branch segments to each region in a set of seven reconstructed neurons (Figure 2B; see also Supplemental Experimental Procedures). Axospinous synapses were categorized as perforated when their PSD profile in serial sections displayed at least one discontinuity (Figure 2C) or nonperforated, which by definition have PSDs that lack such discontinuities (Figure 2D).
Figure 2. Distance-Dependent Distribution of Perforated and Non-perforated Synapses in CA1 Stratum Oriens.
(A) Division of CA1 stratum oriens (SO) into proximal (pSO), middle (mSO), and distal (dSO) regions. Other regions identified include dentate gyrus (DG), CA2, CA3, subiculum (Sub), stratum radiatum (SR), stratum pyramidale (s. pyr.), alveus (alv.), stratum lacunosum moleculare (SLM), and the outer molecular layer of the dentate gyrus (oml). Scale bars represent 100 μm.
(B) Top: schematic showing the distribution of proximal segments (50–110 μm from the soma), middle segments (110–160 μm from the soma), and distal segments (>160 μm from the soma) in the proximal (pSO), middle (mSO), and distal (dSO) regions of stratum oriens. Scale bar represents 100 μm. Bottom: the proportion of each segment type in each region. Error bars represent SEM.
(C) Two serial electron micrographs through a perforated synapse between a dendritic spine (sp) and an axon terminal (at). Arrowheads indicate the boundaries of the postsynaptic density (PSD); the arrow identifies the discontinuity in the perforated PSD. Bottom: three-dimensional reconstruction of the entire dendritic spine (dark blue) and its PSD (cyan).
(D) Two serial electron micrographs through a nonperforated synapse between a dendritic spine (sp) and an axon terminal (at). Arrowheads denote the boundaries of the PSD. Bottom: three-dimensional reconstruction of the entire dendritic spine (dark blue) and its PSD (cyan). Scale bar represents 0.25 μm and applies to (C) and (D).
(E) Plot showing the total raw, unadjusted number of perforated (P) and non-perforated (NP) synapses in proximal (pSO), middle (mSO), and distal (dSO) segments. Lines connect estimates from the same animals. Asterisks indicate that pSO has significantly more NP synapses than dSO.
(F) Plot showing the total adjusted number of perforated (P) and nonperforated (NP) synapses in pSO, mSO, and dSO segments. Lines connect estimates from the same animals. Asterisks indicate that pSO has significantly more NP synapses than dSO.
We found that there are no differences in the total number of perforated synapses in the basal dendrites as a function of distance from the soma (Figures 2E and 2F), but the number of non-perforated synapses, the most numerous axospinous synaptic subtype, is significantly lower in distal basal dendrites (dSO) as compared to proximal ones (Figures 2E and 2F; F(2,20) = 9.95, p > 0.01). Such a distance-dependent shift among the synaptic subtypes is consistent with the single-dendrite analyses, which indicate that distal segments have a lower overall density of synapses/spines (Figure 1), and identifies the selective downregulation of nonperforated synapses as the substrate for lower synapse numbers in distal branches.
AMPARs Increase, NMDARs Decrease with Distance from the Soma among Perforated Synapses
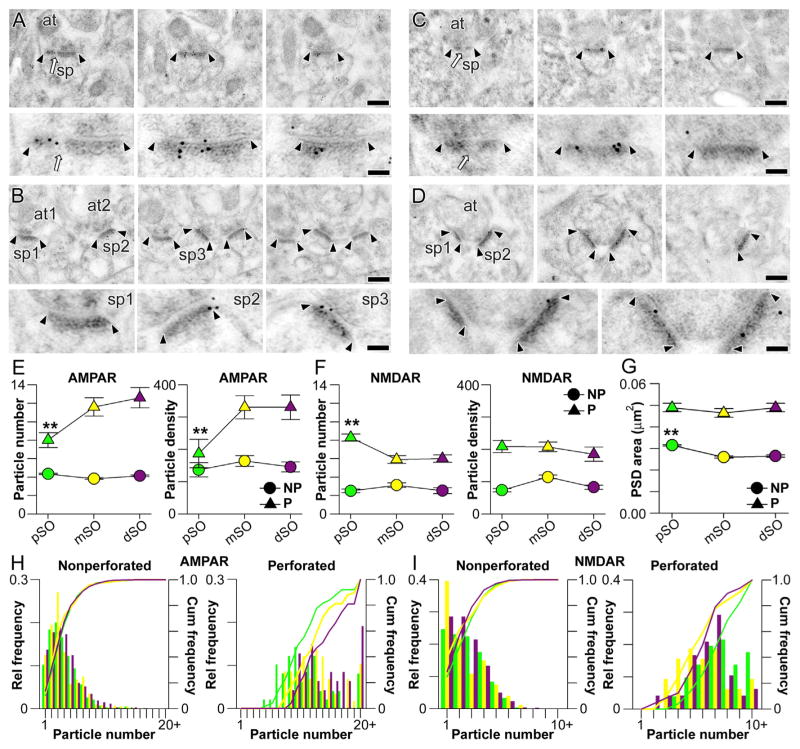
We next compared the expression of ligand-gated ion channels at synapses in pSO, mSO, and dSO by localizing and quantifying postsynaptic AMPAR and NMDAR expression with serial section, postembedding immunogold electron microscopy. The number of immunogold particles projected onto the PSD of each synapse in serial sections was used to estimate synaptic receptor expression in terms of particle number and density (Figures 3A–3D). As in the apical dendrites (Nicholson and Geinisman, 2009), we found that for both AMPARs and NMDARs in SO, immunogold particle number (per synapse) is greater for perforated synapses than for nonperforated synapses (Figures 3E and 3F; multivariate analysis of covariance, AMPAR, F(2,2422) = 21.12, p < 0.0001; NMDAR F(2,1335) = 10.13, p < 0.0001). Additionally, and also consistent with apical dendrites, receptor expression levels for nonperforated synapses throughout all of SO are similar (Figures 3E and 3F), whereas perforated synapses show distance-dependent differences (Figures 3E and 3F). Interestingly though, AMPARs and NMDARs in perforated synapses are regulated in opposite directions: AMPAR expression increases with distance from the soma in SO (Figure 3E), whereas NMDAR expression decreases (Figure 3F). The only distance-dependent change among non-perforated synapses is that distal nonperforated PSDs are ~10% smaller on average than proximal ones (Figure 3G; non-perforated: F(2,3483) = 14.58, p < 0.0001; mean ± SEM: proximal = 0.031 ± 0.001 μm2; distal = 0.028 ± 0.001 μm2; perforated: F(2,282) = 2.02, p > 0.05; proximal = 0.050 ± 0.001 μm2; distal = 0.049 ± 0.001 μm2). Plotting the distributions of the number of particles per synapse supports these observations because nonperforated synapses show no differences, whereas the distributions for perforated synapses show that a larger proportion have a high number of AMPAR particles in mSO and dSO as compared to pSO (Figure 3H). The opposite is true for NMDAR particles: perforated synapses in pSO tend to have higher numbers of immunogold particles (Figure 3I).
Figure 3. Synapse-Specific Converse Regulation of AMPAR and NMDAR Expression with Distance from the Soma in Stratum Oriens.
(A) Serial section immunogold electron micrographs through a perforated synapse immunolabeled for AMPARs. Arrowheads mark the boundaries of the postsynaptic density (PSD), and the perforation is indicated by an arrow. Spines (sp) and axon terminals (at) are also indicated. Bottom: the PSD at higher magnification, with clearly visible immunogold particles. Scale bars for (A)–(D) represent 0.5 and 0.1 μm.
(B) Same as (A) but with three nonperforated synapses, which have no discontinuities in their PSDs.
(C) Same as (A) but with immunogold particles marking labeled NMDARs.
(D) Same as (C) but with two nonperforated synapses.
(E) Plot showing the number of AMPAR immunogold particles per synapse (left) and particle density (right) for perforated (P; triangles) and nonperforated (NP; circles) synapses in proximal, middle, and distal stratum oriens (pSO, mSO, and dSO, respectively). Error bars indicate SEM. The asterisks indicate that P synapses in pSO have fewer immunogold particles for AMPARs (left) and lower particle densities (right) than those in mSO and dSO.
(F) Same as (E) but for immunogold particles for NMDARs. Asterisks denote that P synapses in pSO have a higher number of immunogold particles for NMDARs than those in either mSO or dSO.
(G) Plot showing the average PSD area for perforated (P) and nonperforated (NP) synapses in pSO, mSO, and dSO. Asterisks mark that NP synapses in pSO are larger than their counterparts in mSO and dSO.
(H) Histogram showing the relative (bars) and cumulative (lines) frequencies of immunogold particle numbers for AMPARs in nonperforated (left) and perforated (right) synapses on proximal (green), middle (yellow), and distal (purple) segments.
(I) Same as (H) but for immunogold particles for NMDARs.
In summary, our experimental results indicate that the number of nonperforated synapses decreases with distance from the soma but that their relative strength remains constant. In contrast, the number of perforated synapses remains constant throughout SO, but their AMPAR and NMDAR expression levels are regulated in opposite directions. To provide a functional context for these results, and a computational comparison of the impact of such scaling in the apical dendrites (Nicholson et al., 2006; Katz et al., 2009), we conducted simulations examining their impact on somatic and dendritic voltage, as described below.
Normalization of Somatic EPSPs and Local NMDAR-Mediated Current in Perforated Synapses
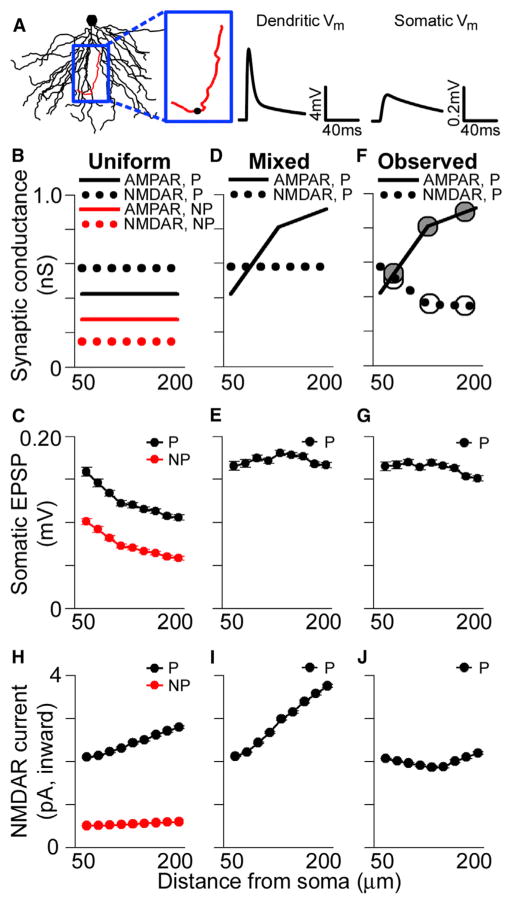
To explore the effects of the observed distribution of synapses and their ion channels on synaptic integration in the basal dendrites, we used the NEURON simulation environment to run multicompartmental simulations with a reconstructed CA1 pyramidal neuron model (Figure 4A). The passive properties of the model were fit using previous experimental data (Golding et al., 2005), and all synapses were placed on simulated spines with neck resistances of ~500 MΩ (see Harnett et al., 2012). Synaptic AMPAR conductances were set such that individual proximal perforated synapses generated an ~0.2 mV somatic EPSP on average (Figure 4B). This conductance was then divided by the average number of immunogold particles for AMPARs among perforated synapses in pSO, yielding the conductance associated with a single immunogold particle (gparticle). AMPAR-mediated synaptic conductance, gsyn, was then determined using linear interpolation of the experimentally observed particle numbers (Figure 3) as a function of dendritic location. The gparticle for NMDAR immunogold particles was scaled such that NMDAR conductances matched experimentally observed ratios between unitary AMPAR- and NMDAR-mediated currents. In agreement with experimental data (Bloodgood et al., 2009), simulated NMDAR-mediated conductances have a significant impact on EPSPs, even when the local depolarization is less than 2 mV. Consistent with this observation, in our simulations, some NMDAR-mediated current flows at synapses even in the absence of activation of their AMPARs (see also Harnett et al., 2012). Simulations were conducted with the parsimonious, though unverified, presumption that conductances scale linearly with receptor number.
Figure 4. Location-Independent Contribution of Individual Perforated Synapses to Subthreshold Somatic Voltage.
(A) Basal dendritic tree of a reconstructed CA1 pyramidal neuron. Voltage traces are the local EPSP (left) and the somatic EPSP (right) in response to an activated synaptic conductance located on the red dendrite (depicted as a black circle).
(B) AMPAR- and NMDAR-mediated conductance values used in the uniform case for simulated nonperforated (NP) and perforated (P) synapses at varying distances from the soma.
(C) Average amplitudes of simulated unitary somatic EPSPs in response to activated perforated (black) and nonperforated (red) synaptic conductances at various distances from the soma using uniform parameters. All group data are represented as means ± SEM.
(D) AMPAR- and NMDAR-mediated conductance values using in the “mixed” case for simulated perforated synapses.
(E) Average amplitudes of simulated unitary somatic EPSPs in response to activated perforated synaptic conductances at various distances from the soma using the “mixed” conductance values.
(F) Experimentally observed AMPAR- and NMDAR-mediated synaptic conductances for perforated synapses. Superimposed circles show the conductances for pSO, mSO, and dSO obtained directly from the particle number data for AMPARs (gray circles) and NMDARs (white circles).
(G) Average amplitudes of simulated unitary somatic EPSPs in response to activated perforated synaptic conductances scaled according to experimentally observed AMPAR and NMDAR expression patterns.
(H–J) Peak local NMDAR-mediated current for the different conditions shown in (B), (D), and (F).
For nonperforated synapses, which show no distance-dependent variation in either AMPAR- or NMDAR-mediated conductance, simulations indicate that proximal synapses generate measurably larger somatic voltage changes than distal ones (Figure 4C). This is also the case for perforated synapses lacking distance-dependent variation in AMPAR- and NMDAR-mediated conductance (Figure 4C). These simulations suggest that uniform synaptic conductances, within either perforated or nonperforated synapses, lead to underrepresentation of middle and distal synaptic input.
Our previous work has shown that AMPAR-mediated conductance among perforated synapses scales with distance from the soma in the apical dendrites, whereas NMDAR-mediated conductance remains constant (Nicholson et al., 2006). We simulated such a scenario (referred to as the “mixed conductance” case) in the basal dendrites (Figure 4D), which notably results in somatic EPSP amplitudes that are location independent (Figure 4E). Given that perforated synapses do not have uniform AMPAR- and NMDAR-mediated conductances throughout the basal dendritic tree (based on Figures 3E and 3F), we ran simulations where they matched the experimentally observed distributions (Figure 4F). This conductance distribution also leads to somatic EPSP amplitudes that are largely independent of the activated synapse’s location (Figure 4G). Therefore, in both the “mixed” and the experimentally observed conductance simulations, the distance-dependent increase in AMPAR-mediated conductance among perforated synapses allows their unitary somatic EPSPs to be independent of the location of the activated synapse.
The observation that the AMPAR-mediated conductance gradient alone accounts for normalization of somatic EPSPs among perforated synapses raises the question of why the observed distribution of their NMDARs exhibits a decrease in the distal dendrites. One possibility is that the experimentally observed distance-dependent decrease in NMDAR expression helps to regulate the local influx of current through NMDARs, thereby normalizing Ca2+ entry at the synapse. The high input impedance and large AMPAR-mediated currents at distal synapses are expected to cause large local depolarizations and thus more effective relief of Mg2+ block at distal synaptic NMDARs, provided spine neck resistances are within physiologically reasonable limits (0.1–1.5 GΩ; Figure S2). Consistent with this notion, peak local NMDAR-mediated currents are location dependent when simulating either the uniform AMPAR- and NMDAR-mediated conductances or the “mixed” conductance situation (Figures 4H and 4I). Current flowing through NMDARs is location independent among perforated synapses only when using the experimentally observed values for both AMPAR-and NMDAR-mediated conductances (Figure 4J). Importantly, these results are also observed in simulations with spines that contain active Na+ and A-type K+ conductances (Figure S3).
Together, the single-synapse activation simulations show that AMPAR-mediated conductance scaling among perforated synapses normalizes their somatic EPSPs but that the tapering, sealed end of the dendrite causes their local EPSPs to be very large distally. Distal synapses appear to compensate for this effect of conductance scaling by reducing their NMDAR expression, which normalizes local NMDAR-mediated currents, possibly producing location-independent local Ca2+ influx in response to activation of single synapses.
Numerical Scaling of Nonperforated Synapses Confers Location-Independence to Spike-Triggering Synapses
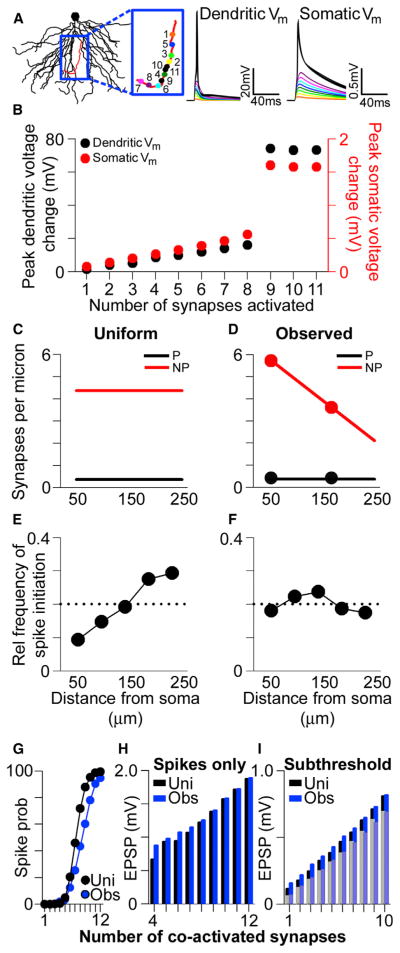
Another possible consequence of conductance scaling in single dendrites is that the large local unitary EPSPs in the high input impedance distal dendrites usurp influence from more proximal ones with regard to triggering local nonlinear events like dendritic Na+ spikes. Such appropriation of control over dendritic output would involve both perforated and nonperforated synapses in distal dendrites but would be exacerbated in the former due to their scaled conductances. To examine this possibility, we conducted multicompartmental simulations of multiple synapses on single branches to assess their ability to trigger local dendritic Na+ spikes (Golding and Spruston, 1998; Gasparini et al., 2004; Remy et al., 2009). Using the same model described above, we activated synaptic conductances on spines located randomly along the length of a single dendrite (n = 5 dendrites). For the first run, only a single synapse was activated; then, a second randomly placed synapse was added to the simulation and both synapses were activated simultaneously. Synapses were added incrementally until a dendritic Na+ spike was generated, as defined by a nonlinear jump in the local dendritic voltage (Figures 5A and 5B). Though inputs were activated simultaneously, the location of the last added synapse—the “spike-generating synapse”—was noted, providing a statistical estimate of the relative influence of a given synaptic location on dendritic spike initiation. All simulations included both perforated and nonperforated synapses, with the ratio between the two fixed at the middle value for the uniform case (Figure 5C), or varying linearly with distance for the experimentally observed case (Figure 5D). Each trial was repeated ~200 times and the spike-triggering conductance location data were aggregated.
Figure 5. Location-Independent Contribution of Synapses to Dendritic Spike Initiation and Maximized Dendritic Impact at the Soma.
(A) The basal dendrites of a reconstructed CA1 pyramidal neuron. Voltage traces show the simulated local (left) and somatic (right) membrane potential (Vm) in response to iterative simultaneous activation of synaptic conductances, whose locations are shown in the blue box. Color-coded voltage traces derive from the iterative activation protocol; i.e., the voltage trace in response to conductance activation at “1” is depicted in orange, the voltage trace in response to simultaneous conductance activation at both “1” and “2” is depicted in yellow, etc.
(B) Peak dendritic- (black) and somatic- (red) simulated voltage change in response to simultaneous activation of progressively higher numbers of synaptic conductances. Note the nonlinear nature of the voltage change as the number of activated conductances increases.
(C) Synapse density per unit length of dendrite in the uniform case for simulated perforated (black) and nonperforated (red) synapses.
(D) Synapse density scaled according to experimentally observed values. Superimposed circles represent the density obtained from experimental values in pSO and dSO, by multiplying the spine density data in Figure 1 by the proportion of nonperforated and perforated synapses from Figure 2.
(E) Plot showing the relative probability that a dendritic spike is generated by a synapse placed at a given location along the length of an individual dendrite, using the uniform conductance values shown in Figure 4B and uniform synapse densities shown in (C). Data are aggregated from 900 simulations containing both perforated and nonperforated synapses. The dashed line represents the uniform, or completely distance independent, probability.
(F) Same as (E) but with experimentally observed synaptic conductance values (Figure 4F) and synapse densities (D).
(G) The probability of triggering a dendritic spike as a function of the number of coactivated synapses in the simulations using uniform values (black) or experimentally observed values (blue).
(H) The average somatic EPSP on simulation trials where the local EPSP exceeded the threshold for triggering a dendritic spike for simulations using uniform (black) or experimentally observed (blue) values.
(I) Same as (H) but for trials on which the local EPSP failed to trigger a dendritic spike. Bars in the background derive from trials in which a perforated synapse was activated; superimposed, lightened bars are from trials in which only nonperforated synapses were activated.
To verify the impact of the sealed end in our simulations, we first randomly activated synapses of uniform strength either within the most proximal third or the most distal third of the same individual dendrites (n = 200 simulations for each condition). As anticipated, the number of synapses required to trigger a dendritic Na+ spike is much lower when their locations are confined to the distal third (5.3 ± 0.07 synapses) as compared to the proximal third (12.9 ± 0.09 synapses) of individual dendrites. Even in simulations of entire dendrites with synapses of uniform strength and uniform spatial distribution (Figures 4B and 5C), the locations of the spike-generating synapse are more likely to be near the terminal end of the dendrite in dSO (Figure 5E). In both cases, this tendency results from the fact that distal synaptic conductances generate larger local EPSPs than their proximal counterparts, which is a combined effect of the high input impedance of the tapering dendrite and its sealed terminal end. Interestingly, in simulations with synapses whose distribution and strengths mirror our experimental results (Figures 4F and 5D), this pattern disappears and is replaced by one in which the spike-generating synapse is located at proximal and distal dendritic locations with approximately equal probability (Figure 5F). As with the single synapse simulations, this pattern remains even when spines contain active Na+ and A-type K+ conductances (Figure S4). These simulations therefore demonstrate that the lower number of nonperforated synapses in dSO has a functional consequence on nonlinear integration: it reduces the overall probability of distal synaptic activation, which offsets the influence of the scaled distal perforated synapses on dendritic spike initiation, thus balancing the influence of proximal and distal synapses on dendritic spike initiation.
In the simulations as in experiments (Remy et al., 2009), clustered synaptic activation influences somatic voltage cooperatively as either dendritic spikes or subthreshold local, multisynaptic EPSPs. As found in the apical dendrites (Katz et al., 2009), the observed distribution of synaptic weights and numbers shifts the relationship between the number of coactivated synapses and the probability of triggering a dendritic Na+ spike to the right (Figure 5G). Importantly, however, the observed distribution maximizes the representation of the dendrite at the soma regardless of whether their clustered activation results in a dendritic spike (Figure 5H) or a multisynaptic, local EPSP (Figure 5I), as also observed in simulations of apical oblique dendrites (Katz et al., 2009).
Taken together, the experimentally observed synapse numbers and receptor levels create a basal dendritic tree that resembles the apical tree in its remarkable resistance to the effects of synapse location. At the single synapse level, AMPAR-mediated conductance scaling among perforated synapses normalizes their somatic EPSP (Figures 4C–4G), whereas complementary scaling of NMDAR-mediated conductances protects against excessive NMDAR activation in the distal dendrites (Figures 4H–4J). At the single dendrite level, the reduced number of synapses in the distal dendrites (Figure 5D) lowers the probability of their activation, which counteracts their large local impact and normalizes the influence of single synapses on dendritic spike initiation (Figure 5F). Moreover, the reduced number of synapses near the terminal ends maximizes dendritic representation at the soma by shifting the center of mass of the local voltage closer to the soma.
Synthesizing Synapse and Ion Channel Gradients in SO and SR
To this point, we have revealed numerous similarities between synapses on basal dendrites and those on apical ones of hippocampal CA1 pyramidal neurons. Yet, unlike in the present study, we did not detect any distance-dependent changes in NMDAR expression among perforated synapses in the apical dendrites, nor did we find that synapses near the terminal ends of dendrites in dSO are weaker than those near the branch points (Katz et al., 2009).
One possibility is that the patterns revealed here are indeed present in both basal and apical dendrites but that our ability to detect them in the basal dendrites is facilitated by their structural organization, as the most distal dendritic region is comprised exclusively of dendritic segments near the dendrites’ terminal ends. In contrast, synapses from different single-dendrite locations bestrew the entirety of SR, making the detection of single-dendrite synapse and ion channel gradients much more difficult in the apical dendrites. To test this hypothesis, we reanalyzed the immunogold data from the present study, as well as from our previous study on apical dendrites (Nicholson et al., 2006), taking into account the diameter of each axospinous synapse’s parent dendrite.
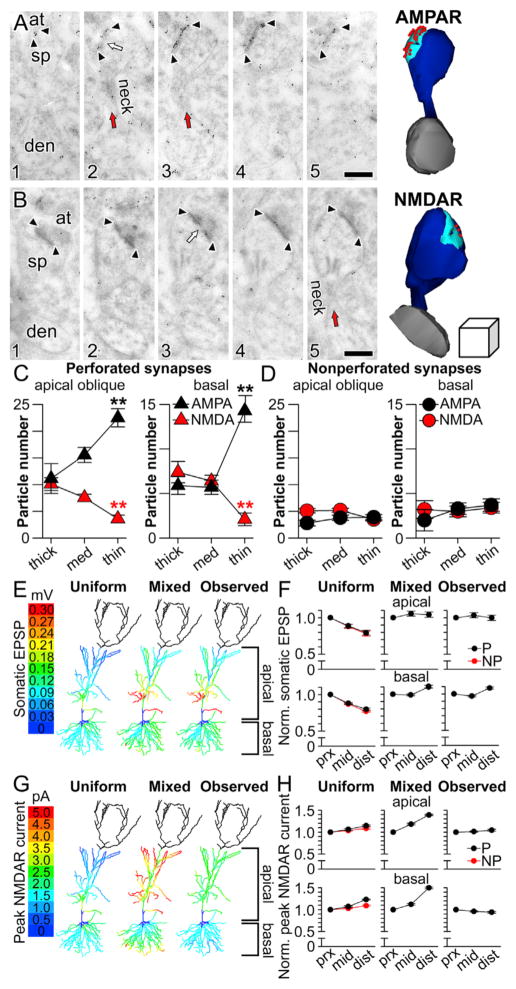
Both basal and apical oblique dendrites taper as they course to their terminal ends (Figures 1G), yielding dendritic segments that can be categorized on the basis of their diameter as thick, medium, and thin. A reasonable assumption based on this observation is that the thinnest dendritic segments are nearest the dendrites’ terminal ends, and thicker dendritic segments are closer to the soma (for basal dendrites) or the branch point off of the main apical dendrite (for apical oblique dendrites). Using these assumptions as a proxy for single-dendrite synapse location, we identified 760 axospinous synapses whose spine↔dendrite connections were captured electron microscopically (Figures 6A and 6B) and we grouped them according to the diameter of their parent dendrites into those on thick-(>700 nm diameter), medium- (400–700 nm diameter), or thin-caliber (<400 nm diameter) dendrites.
Figure 6. Ion Channel Gradients in the Dendrites of Hippocampal CA1 Pyramidal Neurons.
(A) Serial section immunogold electron micrographs of a perforated synapse immunolabeled for AMPARs. Arrowheads mark the boundaries of the post-synaptic density (PSD), and the perforation is indicated by a white arrow. Spine (sp), axon terminal (at), parent dendrite (den), and spine neck (neck; red arrow) are also indicated. Right: three-dimensional reconstruction of the synapse (cyan), its parent spine (dark blue) and dendrite (gray), and the immunogold particles projected onto the PSD (red spheres). Scale bar represents 0.2 μm.
(B) Same as in (A) but with immunogold particles marking labeled NMDARs. The cube on the right of the three-dimensional reconstruction represents 0.2 μm3.
(C) Plot showing the number of AMPAR (black) and NMDAR (red) immunogold particles per perforated axospinous synapse in apical oblique dendrites of stratum radiatum (left) and basal dendrites of stratum oriens (right). Asterisks indicate that axospinous synapses on the thinnest dendrites have the highest number of immunogold particles for AMPARs (black asterisks) and the lowest number of immunogold particles for NMDARs (red asterisks). All group data are represented as means ± SEM.
(D) Same as in (C) but for nonperforated synapses.
(E) Color-coded plots projected onto a morphologically realistic model hippocampal CA1 pyramidal neuron, showing the somatic EPSP generated in response to activated synaptic conductances at perforated synapses with three different patterns of AMPAR- and NMDAR-mediated conductances. In the uniform case (left), conductances were the same as depicted in Figure 4B. In the mixed case, AMPAR-mediated conductances were scaled according to dendritic diameter as shown in (C). In the observed case, both AMPAR-mediated and NMDAR-mediated conductances were scaled according to diameter as shown in (C). The dendrites of the apical tuft were not simulated and are therefore darkened.
(F) Average normalized amplitudes (normalized to the proximal third of each individual dendrite) of simulated unitary somatic EPSPs in response to activated perforated (black) and nonperforated (red) synaptic conductances at various distances from the soma using uniform (left), mixed (middle), or observed (right) parameters for apical oblique dendrites (top row) or basal dendrites (bottom row).
(G) Color-coded plots projected onto a morphologically realistic model hippocampal CA1 pyramidal neuron, showing the peak NMDAR-mediated current (inward) to activated synaptic conductances at perforated synapses with three different patterns of AMPAR- and NMDAR-mediated conductances. In the uniform case (left), conductances were the same as depicted in Figure 4B. In the mixed case, AMPAR-mediated conductances were scaled according to dendritic diameter as shown in (C). In the observed case, both AMPAR-mediated and NMDAR-mediated conductances were scaled according to diameter as shown in (C). The dendrites of the apical tuft were not simulated and so are darkened.
(H) Average normalized peak NMDAR-mediated currents (normalized to the proximal third of each individual dendrite) in response to activated perforated (black) and nonperforated (red) synaptic conductances at various distances from the soma using uniform (left), mixed (middle), or observed (right) parameters for apical oblique dendrites (top row) or basal dendrites (bottom row).
Remarkably, we found that the synaptic subtype-specific, complementary expression patterns of AMPARs and NMDARs first detected along the somatodendritic axis in basal dendrites (Figure 3) are also present in apical oblique dendrites (Figure 6C, left). Importantly, the expression patterns found using the population-level approach in basal dendrites (Figure 3) are preserved when considered in the context of the diameter of each synapse’s parent dendrite (Figure 6C, right). Moreover, in both regions, these gradients are synaptic subtype specific, because expression among nonperforated synapses is not related to parent dendrite diameter (Figure 6D). Thus, perforated axospinous synapses on thin dendrites have more AMPARs and fewer NMDARs than those on thicker dendrites regardless of whether they are within the basal or apical arbor, an observation that was verified statistically with a significant receptor × synaptic subtype × dendritic caliber interaction (F(2,552) = 12.9, p < 0.00001). In other words, the same single-dendrite synapse and glutamate receptor gradients that confer to basal dendrites the dual capabilities of participating in global integration of EPSPs at the soma (Figure 4) and local integration of unitary EPSPs into sub- or suprathreshold dendritic output (Figure 5) are also present in the apical oblique dendrites.
To address this idea directly, we ran single-synapse activation simulations throughout SO and SR, scaling the AMPAR- and NMDAR-mediated conductances of perforated synapses to match those shown in Figure 6C, using linear interpolation of the observed data. When simulated according to uniform, “mixed,” or experimentally observed conductance patterns, only the latter conferred location independence to both somatic EPSPs (Figures 6E and 6F) and peak NMDAR-mediated current flow in the spine head (Figures 6G and 6H) throughout SO and SR.
DISCUSSION
Determining how neurons optimize the strength of their inputs at different dendritic locations is essential to understanding synaptic integration and neuronal input-output properties. Our experimental and computational results provide evidence that synapses in both the basal and apical oblique dendrites resolve these issues through a hybrid solution that balances distance-dependent conductance scaling with the high input impedance of the distal dendrites’ sealed ends. Moreover, there are distinct regulation patterns for perforated and nonperforated synapses, which countervail dendritic cable properties for subthreshold somatic EPSPs and dendritic spike initiation, respectively.
Using reconstructive electron microscopy, we show that synapse number decreases toward the terminal ends of both basal and apical oblique dendrites. Our quantitative electron microscopy studies show that this decrease is attributable to a selective reduction of nonperforated synapses in the distal basal dendrites. This is consistent with our previous results from apical oblique branches, showing that synapse density is lower in distal dendritic segments as compared to proximal ones (Katz et al., 2009). Together, these results suggest that the density of nonperforated synapses is lower in the distal parts of dendritic branches of both basal and apical oblique dendrites.
By contrast, we find no evidence for a decreased number of perforated synapses along basal dendritic branches. Rather, the density of these synapses is constant along the somatodendritic axis (Figures 2E and 2F). Although their nonuniform orientation precluded direct quantitative estimates of perforated synapse number along apical oblique branches, the lower synapse density in distal portions of single apical oblique dendrites (Katz et al., 2009) is most likely explained by a reduction in nonperforated synapses, as seen in the basal dendrites. Thus, it is likely that perforated synapses are distributed approximately evenly along the proximal-distal extent of both basal and apical oblique branches.
While conventional electron microscopy revealed a change exclusive to nonperforated synapses, our immunogold electron microscopy experiments revealed distance-dependent differences in AMPAR and NMDAR expression exclusive to perforated synapses. Specifically, AMPAR expression in perforated synapses increases with distance from the soma along dendrites, whereas NMDAR expression decreases. No such gradients in receptor expression were detected among nonperforated synapses.
Notably, in both basal and apical dendrites, nonperforated synapses are over 5-fold more abundant than perforated synapses, whereas the latter are more than 5-fold stronger (Figures 2, 3, and 6; Nicholson and Geinisman, 2009). Such reciprocation suggests that these two synaptic subtypes may be approximately equally represented in terms of total excitatory synaptic weight in the dendrites of hippocampal CA1 pyramidal neurons. Thus, it is important to consider the compensatory mechanisms and integrative implications for both types of synapses.
When single synapses are activated in either the basal or apical oblique dendrites, the somatic impact of a single synapse is location dependent for nonperforated synapses, where distal synapses produce smaller EPSPs, as observed experimentally for synapses in the basal dendrites of layer 5 pyramidal neurons (Nevian et al., 2007). For perforated synapses, however, the higher number of AMPARs at more distal synapses compensates for cable filtering, resulting in location-independent somatic EPSPs, as observed experimentally for synapses in the apical dendrites of CA1 neurons (Magee and Cook, 2000). These electrophysiological observations were likely heavily influenced by activation of perforated synapses, because of their relatively strong synaptic weight. By contrast, many of the smallest dendritic EPSPs, a large of proportion of which our experiments suggest were generated by nonperforated synapses, were undetectable at the soma (Magee and Cook, 2000). Thus, our electron microscopic analysis is consistent with the interpretation that the earlier identification of normalized somatic EPSP amplitude (Magee and Cook, 2000) can be explained by distance-dependent compensation of AMPAR expression exclusively at perforated synapses (see also Nicholson et al., 2006).
That perforated synapses are stronger than nonperforated ones suggests that their activation will result in more relief of magnesium block at NMDARs. Our simulations show that this effect is expected to be particularly large for perforated synapses on distal branches, owing to interactions between their increased AMPAR expression and the higher input impedance at these dendritic locations. Our data suggest, however, that this consequence of AMPAR scaling is minimized by reducing NMDAR expression at distal perforated synapses, resulting in distance-independent current through synaptically activated NMDARs (Figures 5 and 6).
By activating groups of synapses, consisting of randomly selected perforated and nonperforated subtypes, we found that distal synapses are more likely to trigger dendritic spikes if synapse density is assumed to be constant along the proximal-distal extent of single dendrites. This effect is caused by the higher input impedance of distal dendrites, resulting in larger local EPSPs (and therefore more dendritic sodium channel activation) when distal synapses are activated. However, when synapse density was modeled as observed in our experiments, with fewer nonperforated synapses at more distal locations, we found that the “spike-triggering” synapse is equally likely to be located anywhere along the dendritic branch. In other words, the observed distribution of nonperforated synapse density compensates for the electrotonic structure of the dendrite and eliminates an otherwise inherent bias for distal synapses to contribute disproportionately to the initiation of dendritic spikes, a consequence of the high input impedance of the dendrites near their terminal, sealed ends (Rall and Rinzel, 1973; Rinzel and Rall, 1974). An intriguing aspect of our findings is that perforated and nonperforated synapses employ distinct mechanisms to compensate for their distance from the soma. Why do CA1 pyramidal neurons adjust nonperforated synapse number along the proximal-distal extent of each dendrite but modify AMPAR and NMDAR expression among perforated synapses? A likely explanation is that these two populations of synapses use different compensatory mechanisms because they perform very different functions in the dendritic tree.
Nonperforated synapses are expected to have minimal influence on somatic membrane potential when activated individually. When activated in groups, however, they can influence somatic voltage significantly. Adjusting the distribution of these synapses so there are fewer in the distal portions of dendritic branches shifts their collective weight closer to the soma (Figure 5; see also Katz et al., 2009), thus increasing their overall impact on somatic depolarization. If enough synapses are activated throughout the dendrites, this could result in an axonal action potential—a process that we have called “global integration” (Katz et al., 2009), because of the likely requirement for the cooperative action of many synapses at different locations throughout the dendritic tree.
Additionally, groups of activated synapses also drive axonal action potential firing by first triggering spikes locally in dendritic branches. Although these spikes do not propagate to the soma reliably (Golding and Spruston, 1998; Losonczy and Magee, 2006), they can influence axonal spiking through a process we have called “two-stage integration” (Katz et al., 2009; see also Poirazi et al., 2003; Polsky et al., 2004), because it involves local spike initiation in multiple, single dendrites, followed by collective integration in the axon to drive axonal action potentials. The observed distribution of nonperforated synapses (with fewer at distal locations of each branch) reduces the inherent bias for dendritic spikes to be initiated by groups of synapses on the distal portions of dendritic branches (Figure 5; see also Katz et al., 2009). Overall, then, our results show that it is computationally advantageous to decrease distal nonperforated synapse density within single dendrites.
Another consequence of local dendritic spikes is potentiation of nearby synapses, which results in part from activation of synaptic NMDARs (Golding et al., 2002; Remy and Spruston, 2007). If activity-dependent plasticity is involved in converting nonperforated synapses into perforated ones (Greenough and Bailey, 1988; Geinisman, 2000; Bourne and Harris, 2007), then the numerical gradients among the former may also explain the presence of the latter throughout the dendritic tree. As a consequence of the gradient of nonperforated synapses, dendritic spikes can be triggered with equal probability by groups of activated synapses anywhere on a dendrite (Figure 5; see also Katz et al., 2009). We posit that groups of nonperforated synapses trigger dendritic spikes, causing Ca2+ influx throughout the dendrite and promoting the conversion of nonperforated (weak) synapses into perforated (strong) ones in a location-independent manner in dendrites. Such a mechanism could explain the presence of perforated synapses at all locations of the dendritic tree.
Moreover, our observations suggest that the strength of these distributed perforated synapses is calibrated such that, individually, they have a significant and approximately equal impact on somatic voltage. Numerical gradients among such synapses cannot be used as a compensatory mechanism for individually strong synapses. Rather, distance-dependent gradients in AMPAR expression of individual synapses accomplish this, with concordant NMDAR expression gradients that offset the effects of large local EPSPs on Ca2+ influx in the spine head. Therefore, synaptic strength among perforated synapses may be coordinated to produce a population of synapses that influences somatic membrane potential in small numbers, regardless of their dendritic location, even in the absence of a dendritic spike. Indeed, their comparatively small numbers are consistent with this idea. We suggest, therefore, that a different mechanism has evolved to normalize the contribution of perforated synapses independent of their dendritic position: the distance-dependent scaling of AMPAR and NMDAR expression.
Taken together, the results described here show that the basal and apical dendrites that connect hippocampal CA1 pyramidal neurons with their counterparts in hippocampal region CA3 utilize cognate compensatory mechanisms, namely single-dendrite gradients in synapse number and glutamate receptor expression. The implications of our observations are of necessity speculative and will therefore require further experimental validation. Importantly, we do not assume that these observations or functional implications apply to all neurons (or even all pyramidal neurons) or even to CA1 synapses with other sources, such as inputs from the entorhinal cortex, which innervate the most distal region of the CA1 dendrites. Indeed, synapses in the apical tuft have properties that differ from those described here, including different proportions of perforated and nonperforated synapses, different AMPAR expression levels, and excitatory synapses on both the dendritic shaft and spines (Desmond et al., 1994; Megías et al., 2001; Nicholson et al., 2006). Thus, the mechanisms that neurons implement to compensate for a synapse’s location within the dendritic tree are likely to vary among different neurons, and even within a single neuron, thereby producing sophisticated and diverse solutions supporting synaptic integration and plasticity that match the multiplicity of neuron structure throughout the brain.
EXPERIMENTAL PROCEDURES
Institutional Approval
All experiments were conducted using protocols approved by the Northwestern University and Rush University Institutional Animal Care and Use Committees.
Electron Microscopy with BDA Labeling
Two young adult (6-month-old) male F1 hybrid Fischer344 × Brown Norway rats (Harlan) were anesthetized with an injection of ketamine and xylazine. Biotinylated dextran amine (BDA-3000, Invitrogen; 10% dissolved in 0.12 M PBS) was pressure injected into the subiculum (0.05 ml/min for 5 min) and visualized as previously described (Katz et al., 2009; see Supplemental Experimental Procedures).
Unbiased Quantitative Electron Microscopy
Five young adult (6-month-old) male F1 hybrid Fisher344 × Brown Norway rats were intracardially perfused with a mixture of paraformaldehyde and glutaraldehyde, and tissue slices were prepared for conventional electron microscopy as previously described (Nicholson et al., 2006; see Supplemental Experimental Procedures).
Quantification of AMPAR and NMDAR Immunoreactivity
Postembedding immunogold electron microscopy was used to assess the expression of postsynaptic AMPARs and NMDARs in three young adult hybrid Fisher344 × Brown Norway rats, as specified previously (Nicholson and Geinisman, 2009; see Supplemental Experimental Procedures).
Data Adjustment
See Supplemental Experimental Procedures for full details.
Computational Modeling
The CA1 pyramidal neuron model used in all simulations was reconstructed from a stained neuron in a hippocampal slice as described previously (Golding et al., 2005). To maximize comparability to other work, we used dendritic diameters obtained from optical reconstructions. Importantly, however, similar results are obtained when diameters are based on the electron microscopically measured values (Figure S5). All simulations were carried out using the NEURON simulation environment (Hines and Carnevale, 1997). See Supplemental Experimental Procedures for full details. All models will be made available on the authors’ website (http://dendrites.esam.northwestern.edu).
Supplementary Material
Acknowledgments
The authors thank Stephen Smith’s laboratory and John Morrison’s laboratory for help with array tomography and fluorescent dye loading, respectively, and members of the Nicholson and Spruston laboratories for helpful discussions. This work was supported by R01 AG017139, R00 AG031574, and the Charles and M.R. Shapiro Foundation (D.A.N.); T32 AG000269 (T.F.M); and R01 NS046064 (W.L.K. and N.S.), R01 NS077601 (W.L.K. and N.S.), R01 NS035180 (N.S.), and the Howard Hughes Medical Institute (N.S.).
Footnotes
Supplemental Information includes Supplemental Experimental Procedures, five figures, and two movies and can be found with this article online at http://dx.doi.org/10.1016/j.neuron.2013.09.027.
References
- Amaral DG, Lavenex P. Hippocampal neuroanatomy. In: Andersen P, Morris R, Amaral D, Bliss T, O’Keefe J, editors. The Hippocampus Book. Oxford: Oxford University Press; 2006. pp. 37–114. [Google Scholar]
- Bloodgood BL, Giessel AJ, Sabatini BL. Biphasic synaptic Ca influx arising from compartmentalized electrical signals in dendritic spines. PLoS Biol. 2009;7:e1000190. doi: 10.1371/journal.pbio.1000190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bourne J, Harris KM. Do thin spines learn to be mushroom spines that remember? Curr Opin Neurobiol. 2007;17:381–386. doi: 10.1016/j.conb.2007.04.009. [DOI] [PubMed] [Google Scholar]
- Bourne JN, Harris KM. Balancing structure and function at hippocampal dendritic spines. Annu Rev Neurosci. 2008;31:47–67. doi: 10.1146/annurev.neuro.31.060407.125646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Branco T, Häusser M. The single dendritic branch as a fundamental functional unit in the nervous system. Curr Opin Neurobiol. 2010;20:494–502. doi: 10.1016/j.conb.2010.07.009. [DOI] [PubMed] [Google Scholar]
- Desmond NL, Scott CA, Jane JA, Jr, Levy WB. Ultrastructural identification of entorhinal cortical synapses in CA1 stratum lacunosum-moleculare of the rat. Hippocampus. 1994;4:594–600. doi: 10.1002/hipo.450040509. [DOI] [PubMed] [Google Scholar]
- Gasparini S, Migliore M, Magee JC. On the initiation and propagation of dendritic spikes in CA1 pyramidal neurons. J Neurosci. 2004;24:11046–11056. doi: 10.1523/JNEUROSCI.2520-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geinisman Y. Structural synaptic modifications associated with hippocampal LTP and behavioral learning. Cereb Cortex. 2000;10:952–962. doi: 10.1093/cercor/10.10.952. [DOI] [PubMed] [Google Scholar]
- Golding NL, Spruston N. Dendritic sodium spikes are variable triggers of axonal action potentials in hippocampal CA1 pyramidal neurons. Neuron. 1998;21:1189–1200. doi: 10.1016/s0896-6273(00)80635-2. [DOI] [PubMed] [Google Scholar]
- Golding NL, Staff NP, Spruston N. Dendritic spikes as a mechanism for cooperative long-term potentiation. Nature. 2002;418:326–331. doi: 10.1038/nature00854. [DOI] [PubMed] [Google Scholar]
- Golding NL, Mickus TJ, Katz Y, Kath WL, Spruston N. Factors mediating powerful voltage attenuation along CA1 pyramidal neuron dendrites. J Physiol. 2005;568:69–82. doi: 10.1113/jphysiol.2005.086793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenough WT, Bailey CH. Anatomy of memory: convergence of results across a diversity of tests. Trends Neurosci. 1988;11:142–147. [Google Scholar]
- Harnett MT, Makara JK, Spruston N, Kath WL, Magee JC. Synaptic amplification by dendritic spines enhances input cooperativity. Nature. 2012;491:599–602. doi: 10.1038/nature11554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Häusser M, Spruston N, Stuart GJ. Diversity and dynamics of dendritic signaling. Science. 2000;290:739–744. doi: 10.1126/science.290.5492.739. [DOI] [PubMed] [Google Scholar]
- Hines ML, Carnevale NT. The NEURON simulation environment. Neural Comput. 1997;9:1179–1209. doi: 10.1162/neco.1997.9.6.1179. [DOI] [PubMed] [Google Scholar]
- Iansek R, Redman SJ. The amplitude, time course and charge of unitary excitatory post-synaptic potentials evoked in spinal motoneurone dendrites. J Physiol. 1973;234:665–688. doi: 10.1113/jphysiol.1973.sp010366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katz Y, Menon V, Nicholson DA, Geinisman Y, Kath WL, Spruston N. Synapse distribution suggests a two-stage model of dendritic integration in CA1 pyramidal neurons. Neuron. 2009;63:171–177. doi: 10.1016/j.neuron.2009.06.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Losonczy A, Magee JC. Integrative properties of radial oblique dendrites in hippocampal CA1 pyramidal neurons. Neuron. 2006;50:291–307. doi: 10.1016/j.neuron.2006.03.016. [DOI] [PubMed] [Google Scholar]
- Magee JC. Dendritic integration of excitatory synaptic input. Nat Rev Neurosci. 2000;1:181–190. doi: 10.1038/35044552. [DOI] [PubMed] [Google Scholar]
- Magee JC, Cook EP. Somatic EPSP amplitude is independent of synapse location in hippocampal pyramidal neurons. Nat Neurosci. 2000;3:895–903. doi: 10.1038/78800. [DOI] [PubMed] [Google Scholar]
- Megías M, Emri Z, Freund TF, Gulyás AI. Total number and distribution of inhibitory and excitatory synapses on hippocampal CA1 pyramidal cells. Neuroscience. 2001;102:527–540. doi: 10.1016/s0306-4522(00)00496-6. [DOI] [PubMed] [Google Scholar]
- Nevian T, Larkum ME, Polsky A, Schiller J. Properties of basal dendrites of layer 5 pyramidal neurons: a direct patch-clamp recording study. Nat Neurosci. 2007;10:206–214. doi: 10.1038/nn1826. [DOI] [PubMed] [Google Scholar]
- Nicholson DA, Geinisman Y. Axospinous synaptic subtype-specific differences in structure, size, ionotropic receptor expression, and connectivity in apical dendritic regions of rat hippocampal CA1 pyramidal neurons. J Comp Neurol. 2009;512:399–418. doi: 10.1002/cne.21896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicholson DA, Trana RE, Katz Y, Kath WL, Spruston N, Geinisman Y. Distance-dependent differences in synapse number and AMPA receptor expression in hippocampal CA1 pyramidal neurons. Neuron. 2006;50:431–442. doi: 10.1016/j.neuron.2006.03.022. [DOI] [PubMed] [Google Scholar]
- Poirazi P, Brannon T, Mel BW. Pyramidal neuron as two-layer neural network. Neuron. 2003;37:989–999. doi: 10.1016/s0896-6273(03)00149-1. [DOI] [PubMed] [Google Scholar]
- Polsky A, Mel BW, Schiller J. Computational subunits in thin dendrites of pyramidal cells. Nat Neurosci. 2004;7:621–627. doi: 10.1038/nn1253. [DOI] [PubMed] [Google Scholar]
- Rall W. Branching dendritic trees and motoneuron membrane resistivity. Exp Neurol. 1959;1:491–527. doi: 10.1016/0014-4886(59)90046-9. [DOI] [PubMed] [Google Scholar]
- Rall W. Core conductor theory and cable properties of neurons. In: Kandel ER, Brookhart JM, Mountcastle VB, editors. Handbook of Physiology. The Nervous System. Cellular Biology of Neurons. Bethesda: American Physiological Society; 1977. pp. 39–97. [Google Scholar]
- Rall W, Rinzel J. Branch input resistance and steady attenuation for input to one branch of a dendritic neuron model. Biophys J. 1973;13:648–687. doi: 10.1016/S0006-3495(73)86014-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Remy S, Spruston N. Dendritic spikes induce single-burst long-term potentiation. Proc Natl Acad Sci USA. 2007;104:17192–17197. doi: 10.1073/pnas.0707919104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Remy S, Csicsvari J, Beck H. Activity-dependent control of neuronal output by local and global dendritic spike attenuation. Neuron. 2009;61:906–916. doi: 10.1016/j.neuron.2009.01.032. [DOI] [PubMed] [Google Scholar]
- Rinzel J, Rall W. Transient response in a dendritic neuron model for current injected at one branch. Biophys J. 1974;14:759–790. doi: 10.1016/S0006-3495(74)85948-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith MA, Ellis-Davies GCR, Magee JC. Mechanism of the distance-dependent scaling of Schaffer collateral synapses in rat CA1 pyramidal neurons. J Physiol. 2003;548:245–258. doi: 10.1113/jphysiol.2002.036376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spruston N. Pyramidal neurons: dendritic structure and synaptic integration. Nat Rev Neurosci. 2008;9:206–221. doi: 10.1038/nrn2286. [DOI] [PubMed] [Google Scholar]
- Stuart G, Spruston N. Determinants of voltage attenuation in neocortical pyramidal neuron dendrites. J Neurosci. 1998;18:3501–3510. doi: 10.1523/JNEUROSCI.18-10-03501.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams SR, Stuart GJ. Role of dendritic synapse location in the control of action potential output. Trends Neurosci. 2003;26:147–154. doi: 10.1016/S0166-2236(03)00035-3. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.