Exponential synchronization rate of Kuramoto oscillators in the presence of a pacemaker

Abstract

The exponential synchronization rate is addressed for Kuramoto oscillators in the presence of a pacemaker. When natural frequencies are identical, we prove that synchronization can be ensured even when the phases are not constrained in an open half-circle, which improves the existing results in the literature. We derive a lower bound on the exponential synchronization rate, which is proven to be an increasing function of pacemaker strength, but may be an increasing or decreasing function of local coupling strength. A similar conclusion is obtained for phase locking when the natural frequencies are non-identical. An approach to trapping phase differences in an arbitrary interval is also given, which ensures synchronization in the sense that synchronization error can be reduced to an arbitrary level.

I. Introduction

The Kuramoto model was first proposed in 1975 to model the synchronization of chemical oscillators sinusoidally coupled in an all-to-all architecture [1]. Although it is elegantly simple, the Kuramoto model is sufficiently flexible to be adapted to many different contexts, hence it is widely used and is regarded as one the most representative models of coupled phase oscillators [2]. Recently, the Kuramoto model has received increased attention. For example, the authors in [3], [4], [5] discussed synchronization conditions for the Kuramoto model. The work in [6] gave a synchronization condition for delayed Kuramoto oscillators. Results are also obtained for Kuramoto oscillators with coupling topologies different from the original all-to-all structure. For example, the authors in [7] and [8] considered the phase locking of Kuramoto oscillators coupled in a ring and a chain, respectively. Using graph theory, the authors in [9], [10], [11] discussed the synchronization of Kuramoto oscillators with arbitrary coupling topologies. The authors in [12] proved that exponential synchronization can be achieved for Kuramoto oscillators when phases lie in an open half-circle.

Studying the influence of the pacemaker (also called the leader, or the pinner [13]) on Kuramoto oscillators is not only of theoretical interest, but also of practical importance [14], [15]. For example, in circadian systems, thousands of clock cells in the brain are entrained to the light-dark cycle [16]. In the clock synchronization of wireless networks, time references in individual nodes are synchronized by means of intercellular interplay and external coordination from a time base such as GPS [17]. Hence, Kuramoto oscillators with a pacemaker are attracting increased attention. The authors in [14] and [18] studied the bifurcation diagram and the steady macroscopic rotation of Kuramoto oscillators forced by a pacemaker that acts on every node. Based on numerical methods, the authors in [19] showed that the network depth (defined as the mean distance of nodes from the pacemaker, a term closely related to pinning-controllability in pinning control [20]) affects the entrainment of randomly coupled Kuramoto oscillators to a pacemaker. Using numerical methods, the authors in [21] discovered that there may be situations in which the population field potential is entrained to the pacemaker while individual oscillators are phase desynchronized. But compared with the rich results on pacemaker-free Kuramoto oscillators, analytical results are relative sparse for Kuromoto oscillators forced by a pacemaker. And to our knowledge, there are no existing results on the synchronization rate of arbitrarily coupled Kuramoto oscillators in the presence of a pacemaker.

The synchronization rate is crucial in many synchronized processes. For example, in the main olfactory system, stimulus-specific ensembles of neurons synchronize their firing to facilitate odor discrimination, and the synchronization time determines the speed of olfactory discrimination [22]. In the clock synchronization of wireless sensor networks, the synchronization rate is a determinant of energy consumption, which is vital for cheap sensors [23], [24].

We consider the exponential synchronization rate of Kuramoto oscillators with an arbitrary topology in the presence of a pacemaker. In the identical natural frequency case, we prove that synchronization (oscillations with identical phases) can be ensured, even when phases are not constrained in an open half-circle. In the non-identical natural frequency case where perfect synchronization has been shown cannot be achieved [2],[25], we prove that phase locking (oscillations with identical oscillating frequencies) can be ensured and synchronization can be achieved in the sense that phase differences can be reduced to an arbitrary level. In both cases, the influences of the pacemaker and local coupling strength on the synchronization rate are analyzed.

II. Problem formulation and Model transformation

Consider a network of N oscillators, which will henceforth be referred to as ‘nodes’. All N nodes (or a subset) receive alignment information from a pacemaker (also called the leader, or the pinner [13]). Denoting the phases of the pacemaker and node i as ϕ₀ and ϕ_i, respectively, the dynamics of the Kuramoto oscillator network can be written as

$$\{\begin{array}{l}{\stackrel{.}{\varphi }}_0=w_0\hfill \\ {\stackrel{.}{\varphi }}_i=w_i+\sum _{j=1,j\ne i}^N{a}_{i,j}sin({\varphi }_j-{\varphi }_i)+g_{i}sin({\varphi }_0-{\varphi }_i)\hfill \end{array}$$ (1)

for 1 ≤ i ≤ N, where w₀ and w_i are the natural frequencies of the pacemaker and the ith oscillator, respectively, a_i,j sin (ϕ_j − ϕ_i) is the interplay between node i and node j with a_i,j ≥ 0 denoting the strength, g_i sin(ϕ₀ − ϕ_i) denotes the force of the pacemaker with g_i ≥ 0 denoting its strength. If a_i,j = 0 (or g_i = 0), then oscillator i is not influenced by oscillator j (or the pacemaker).

Assumption 1

We assume symmetric coupling between pairs of oscillators, i.e., a_i,j = a_j,i.

Next, we study the influences of the pacemaker, g_i, and local coupling, a_i,j, on the rate of exponential synchronization.

Solving the first equation in (1) gives the dynamics of the pacemaker ϕ₀ = w₀t + φ₀, where the constant φ₀ denotes the initial phase. To study if oscillator i is synchronized to the pacemaker, it is convenient to study the phase deviation of oscillator i from the pacemaker. So we introduce the following change of variables:

$${\varphi }_i={\varphi }_0+{\xi }_i=w_{0}t+{\phi }_0+{\xi }_i$$ (2)

ξ_i ∈ [−2π, 2π] denotes the phase deviation of the ith oscillator from the pacemaker. Due to the 2π-periodicity of the sine-function, we can restrict our attention to ξ_i ∈ [−π, π]. Substituting (2) into (1) yields the dynamics of ξ_i:

$${\stackrel{.}{\xi }}_i=w_i-w_0+\sum _{j=1,j\ne i}^N{a}_{i,j}sin({\xi }_j-{\xi }_i)-g_{i}sin({\xi }_i)$$ (3)

Since ξ_i is the relative phase of the ith oscillator with respect to the phase of the pacemaker, it will be referred to as relative phase in the remainder of the paper.

By studying the properties of (3), we can obtain:

• Condition for synchronization: If all ξ_i converge to 0, then we have ϕ₁ = ϕ₂ = …= ϕ_N = ϕ₀ when t → ∞, meaning that all nodes are synchronized to the pacemaker.

• Exponential synchronization rate: The rate of synchronization is determined by the rate at which ξ_i decays to 0, namely, it can be measured by the maximal α satisfying

  $$\Vert \xi (t)\Vert \le {Ce}^{-\alpha t}\Vert \xi (0)\Vert ,\xi -{[{\xi }_1,{\xi }_2,\dots ,{\xi }_N]}^T$$ (4)

  for some constant C, where ||•|| is the Euclidean norm. α measures the exponential synchronization rate of (3): a larger α leads to a faster synchronization rate.

Remark 1

When w_i and w₀ are non-identical, synchronization (ξ_i = 0) cannot be achieved in general. But we will prove in Sec. IV-C that the synchronization error can be made arbitrarily small by tuning the strength of the pacemaker g_i.

Assigning arbitrary orientation to each interaction, we can get the N × M incidence matrix B (M is the number of interaction edges, i.e., non-zero a_i,j (1 ≤ i ≤ N, j < i)) of the interaction graph [26]: B_i,j = 1 if edge j enters node i, B_i,j = −1 if edge j leaves node i, and B_i,j = 0 otherwise. Then using graph theory, (3) can be recast in a matrix form:

$$\stackrel{.}{\xi }=\mathrm{\Omega }-Gsin\xi -BWsin(B^T\xi )$$ (5)

where Ω = [w₁ − w₀, w₂ − w₀, …, w_N − w₀]^T, G = diag(g₁, g₂, …, g_N), and W = diag(ν₁, ν₂, …, ν_M). Here ν_i (1 ≤ i ≤ M) are a permutation of non-zero a_i,j (1 ≤ i ≤ N, j < i) and diag(•) denotes a diagonal matrix.

III. The identical natural frequency case

When w₁ = w₂ = … = w_N = w₀, (5) reduces to:

$$\stackrel{.}{\xi }=-Gsin\xi -BWsin(B^T\xi )$$ (6)

To study the exponential synchronization rate, we first give a synchronization condition:

Theorem 1

For the network in (6), denote $\epsilon \triangleq \underset{1\le i\le N}{max}\mid {\xi }_i\mid$ and sinc(x) ≜ sin(x)/x, then

1. when $\epsilon <\frac{\pi }{2}$, the network synchronizes if at least one g_i is positive and the coupling a_i,j is connected, i.e., there is a multi-hop link from each node to every other node;

2. when $\frac{\pi }{2}\le \epsilon <\pi$, the network synchronizes if the following inequality is satisfied:

   $$g_{min}>max\left\{\frac{\text{sinc}(2{\epsilon }_0){\lambda }_{max}(BW{B}^T)}{-\text{sinc}(\epsilon )},\underset{i}{max}\{\sum _{j=1,j\ne 1}^N\frac{a_{i,j}}{sin(\epsilon )}\}\right\}$$ (7)
   where λ_max(•) denotes the maximal eigenvalue, g_min and ${\epsilon }_0\in (\frac{\pi }{2},\pi )$ are determined by

   $$g_{min}=min\{g_1,\dots ,g_N\},2{\epsilon }_{0}cos(2{\epsilon }_0)=sin(2{\epsilon }_0)$$ (8)

Proof

We first prove that when ξ ∈ [−ε, ε] × … × [−ε, ε] = [−ε, ε]^N where × denotes Cartesian product, they will remain in the interval under conditions in Theorem 1, i.e, the n-tuple set [−ε, ε]^N is positively invariant for (6).

To prove the positive invariance of [−ε, ε]^N, we only need to check the direction of vector field on the boundaries. When $\epsilon <\frac{\pi }{2}$, if ξ_i = ε, we have −π < −2ε ≤ ξ_j − ξ_i ≤ 0 for 1 ≤ j ≤ N. So in (3), sin(ξ_j − ξ_i) ≤ 0 and sin(ξ_i) > 0 hold, and hence ξ̇_i < 0 holds (Note that w_i − w₀ = 0). Hence the vector field is pointing inward in the set, and no trajectory can escape to values larger than ε. Similarly, we can prove that when ξ_i = −ε, ξ̇_i > 0 holds. Thus no trajectory can escape to values smaller than −ε. Therefore [−ε, ε]^N is positively invariant when $\epsilon <\frac{\pi }{2}$. When $\frac{\pi }{2}\le \epsilon <\pi$, if ξ_i = ε, we have sin ξ_i = sin ε > 0 and sin(ξ_j − ξ_i) ≤ 1 for 1 ≤ j ≤ N. So when w_i = w₀, if (7) is satisfied, the right hand side of (3) is negative, i.e., ξ̇_i < 0 holds. Therefore the vector field is pointing inward in the set and no trajectory can escape to values larger than ε. Similarly, we can prove that if ξ_i = −ε, ξ̇_i > 0 holds under condition (7). Thus no trajectory can escape to values smaller than −ε. Therefore [−ε, ε]^N is also positively invariant for $\frac{\pi }{2}\le \epsilon <\pi$ if (7) is satisfied.

Next we proceed to prove synchronization. Define a Lyapunov function as $V=\frac{1}{2}{\xi }^T\xi$. V ≥ 0 is zero iff all ξ_i are zero, meaning the synchronization of all nodes to the pacemaker.

Differentiating V along the trajectories of (6) yields

$$\begin{array}{l}\stackrel{.}{V}={\xi }^T\stackrel{.}{\xi }=-{\xi }^T\left(Gsin\xi +BWsin(B^T\xi )\right)\\ =-{\xi }^T{GS}_1\xi -{\xi }^{T}BW{S}_2{B}^T\xi \end{array}$$ (9)

where S₁ ∈ 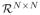and S₂ ∈ 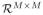are given by

$$\begin{array}{l}{S}_1=\text{diag}\{\text{sinc}({\xi }_1),\dots ,\text{sinc}({\xi }_N)\},\\ S_2=\text{diag}\{\text{sinc}{(B^T\xi )}_1,\dots ,\text{sinc}{(B^T\xi )}_M\}\end{array}$$ (10)

with (B^Tξ)_i denoting the ith element of the M ×1 dimensional vector B^Tξ.

From dynamic systems theory, if GS₁ +BWS₂B^T in (9) is positive definite when ξ ≠ 0, then V̇ is negative when ξ ≠ 0 and V will decay to zero, meaning that ξ will decay to zero and all nodes are synchronized to the pacemaker.

1. When all ξ_i are within [−ε, ε] with $0\le \epsilon <\frac{\pi }{2}$, (B^Tξ)_i is in the form of ξ_m − ξ_n (1 ≤ m, n ≤ N), and hence is restricted to (−π, π). Given that in (−π, π), sinc(x) > 0 holds, it follows that S₁ and S₂ satisfy the following inequalities:

   $$\begin{array}{l}{S}_1\ge {\sigma }_{1}I,{\sigma }_1\triangleq \underset{-\epsilon \le x\le \epsilon }{min}\text{sinc}(x)=\text{sinc}(\epsilon ),\\ S_2\ge {\sigma }_{2}I,{\sigma }_2\triangleq \underset{-2\epsilon \le x\le 2\epsilon }{min}\text{sinc}(x)=\text{sinc}(2\epsilon )\end{array}$$ (11)
   So we have GS₁ + BWS₂B^T ≥ σ₁G + σ₂BWB^T, which in combination with (9) produces

   $$\stackrel{.}{V}\le -{\xi }^T({\sigma }_{1}G+{\sigma }_{2}BW{B}^T)\xi$$ (12)
   It can be verified that σ₁G + σ₂BWB^T is of form:

   $${\sigma }_{1}G+{\sigma }_{2}BW{B}^T={\sigma }_1\text{diag}\{g_1,g_2,\dots ,g_N\}+{\sigma }_{2}L$$ (13)

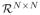   with L ∈ given as follows: for i ≠ j, its (i, j)th element is −a_i,j, for i = j, its (i, j)th element is ${\sum }_{m=1,m\ne i}^N{a}_{i,m}$. Since σ₁ and σ₂ are positive, g_i and a_i,j are non-negative, it follows from the Gershgorin Circle Theorem that σ₁G + σ₂BWB^T only has non-negative eigenvalues [27]. Next we prove its positive definiteness by excluding 0 as an eigenvalue.

   Since the topology of a_i,j is connected, σ₁G + σ₂BWB^T is irreducible from graph theory [27]. This in combination with the assumption of at least one g_i > 0 guarantees that σ₁G + σ₂BWB^T is irreducibly diagonally dominant. So from Corollary 6.2.27 of [27], we know its determinant is non-zero, and hence 0 is not its eigenvalue. Therefore σ₁G + σ₂BWB^T is positive definite, and hence V will converge to 0, meaning that the nodes will synchronize to the pacemaker.

2. When ξ_i ∈ [−ε, ε] (1 ≤ i ≤ N) with $\frac{\pi }{2}\le \epsilon <\pi$, S₁ is positive definite but S₂ is not since (B^Tξ)_i is in [−2ε, 2ε], and thus sinc(B^Tξ)_i may be negative. It can be proven that sinc(x) is monotonically decreasing on [0, 2ε₀] and monotonically increasing on [2ε₀, 2π] (using the first derivative test), where ${\epsilon }_0\in (\frac{\pi }{2},\pi )$ is determined by (8). Hence we have S₁ ≥ sinc(ε)I and S₂ ≥ sinc(2ε₀)I where sinc(2ε₀) < 0. Therefore (9) reduces to

   $$\begin{array}{l}\stackrel{.}{V}\le -\text{sinc}(\epsilon ){\xi }^{T}G\xi -\text{sinc}(2{\epsilon }_0){\xi }^{T}BW{B}^T\xi \\ \le -{\xi }^T\left(\text{sinc}(\epsilon )G+\text{sinc}(2{\epsilon }_0)BW{B}^T\right)\xi \end{array}$$ (14)

   Thus ξ → 0 if g_minsinc(ε) + sinc(2ε₀)λ_max(BWB^T) > 0 holds.

Remark 2

It is already known that for general Kuramoto oscillators without a pacemaker, synchronization can only be ensured when $\underset{i}{max}{\varphi }_i-\underset{i}{min}{\varphi }_i$ is less than π, i.e., the initial phases lie in an open half-circle [9], [10], [11], [12], [28], [29] (although when phases are lying outside a half-circle, almost global synchronization is possible by replacing the sinusoidal interaction function with elaborately designed periodic functions [30], [31], it may introduce numerous unstable equilibria [31]). Here, synchronization is ensured even when ξ_i is outside ( $-\frac{\pi }{2},\frac{\pi }{2}$), i.e., when phase difference ϕ_i − ϕ_j = ξ_i − ξ_j is larger than π, meaning that the phases can lie outside a half-circle. This shows the advantages of introducing a pacemaker.

Remark 3

Theorem 1 indicates that when ξ_i is outside ( $-\frac{\pi }{2},\frac{\pi }{2}$), i.e., when phases cannot be constrained in one open half-circle, all nodes have to be connected to the pacemaker to ensure synchronization. In fact, when some oscillators are not connected to the pacemaker, the relative phases may not converge to 0. For example, consider two connected oscillators, 1 and 2, with coupling strength a_1,2 = a_2,1 = κ. If the pacemaker only acts on oscillator 1 with strength g₁ = κ and the phases of the pacemaker, oscillator 1 and 2 are π, 0.4π, and 1.6π, respectively, though ξ₁ = −0.6π and ξ₂ = 0.6π are all within [−0.6π, 0.6π], numerical simulation shows that ξ₂ will not converge to 0 no matter how large κ is.

Remark 4

Since the eigenvalues of BWB^T are nonnegative [26], λ_max(BWB^T) > 0.

Based on a similar derivation, we can get a bound on the exponential synchronization rate:

Theorem 2

For the network in (6), denote $\epsilon \triangleq \underset{1\le i\le N}{max}\mid {\xi }_i\mid$

. If the conditions in Theorem 1 are satisfied, then the exponential synchronization rate can be bounded as follows:

1. when $0\le \epsilon <\frac{\pi }{2}$ holds, the exponential synchronization rate is no worse than

   $$\begin{array}{l}{\alpha }_1=\underset{\xi }{min}\{{\xi }^T\left({\sigma }_{1}G+{\sigma }_{2}BW{B}^T\right)\xi /({\xi }^T\xi )\}\\ ={\lambda }_{min}\left({\sigma }_{1}G+{\sigma }_{2}BW{B}^T\right)\end{array}$$ (15)

   with σ₁G + σ₂BWB^T given in (13);

2. when $\frac{\pi }{2}\le \epsilon <\pi$ holds, the exponential synchronization rate is no worse than

   $${\alpha }_2=g_{min}\text{sinc}(\epsilon )+\text{sinc}(2{\epsilon }_0){\lambda }_{max}(BW{B}^T)$$ (16)

Proof

From the proof in Theorem 1, when $0\le \epsilon <\frac{\pi }{2}$, we have V̇ ≤ −2α₁V, which means V (t) ≤ C²e^−2α₁tV(0) ⇒ ||ξ(t)|| ≤ Ce^−α₁t||ξ(0)|| for some positive constant C. Thus the synchronization rate is no less than α₁.

Similarly, when $\frac{\pi }{2}\le \epsilon <\pi$ holds, we have V̇ ≤ −2α₂V. Hence the exponential synchronization rate is no less than α₂, which completes the proof.

Remark 5

When $0\le \epsilon <\frac{\pi }{2}$ holds and there is no pacemaker, i.e., G = 0, using the average phase $\overline{\varphi }={\sum }_{i=1}^N\frac{{\varphi }_i}{N}$ as reference, we can define the relative phase as ξ_i = ϕ_i − ϕ̄. Since ξ^T1 = 0 with 1 = [1,1, …, 1]^T, the constraint ξ^T1 = 0 is added to the optimization $\underset{\xi }{min}\{{\xi }^T({\sigma }_{1}G+{\sigma }_{2}BW{B}^T)\xi /({\xi }^T\xi )\}$ in (15). Given that G = 0 and BWB^T is the Laplacian matrix of interaction graph and hence has eigenvector 1 with associated eigenvalue 0 [27], λ_min in (15) reduces to the second smallest eigenvalue, which is the same as the convergence rate in section IV of [32] obtained using contraction analysis.

Eqn. (16) shows that when $\underset{i}{max}\mid {\xi }_i\mid =\epsilon \ge \frac{\pi }{2}$, a stronger pacemaker, i.e., a larger g_min leads to a larger α₂, but the relation between α₁ and g_i when $\underset{i}{max}\mid {\xi }_i\mid =\epsilon <\frac{\pi }{2}$ is not clear. (In this case, g_min may be zero.) We can prove that in this case α₁ also increases with g_i for any i = 1, 2, …, N:

Theorem 3

Both α₁ in (15) and α₂ in (16) increase with an increase in pacemaker strength.

Proof

As analyzed in the paragraph above Theorem 3, we only need to prove Theorem 3 when $\epsilon <\frac{\pi }{2}$ holds, i.e., α₁ is an increasing function of g_i. Recall from (13) that σ₁G + σ₂BWB^T is an irreducible matrix with non-positive off-diagonal elements, so there exists a positive μ such that μI − (σ₁G + σ₂BWB^T) is an irreducible non-negative matrix. Therefore, λ_max (μI − (σ₁G + σ₂BWB^T)) is the Perron-Frobenius eigenvalue of μI − (σ₁G + σ₂BWB^T) and is positive [27]. Given that for any 1 ≤ i ≤ N, μ − λ_i(σ₁G + σ₂BWB^T) is an eigenvalue of μI − (σ₁G + σ₂BWB^T) where λ_i denotes the ith eigenvalue, we have μ − λ_min(σ₁G + σ₂BWB^T) = λ_max (μI − (σ₁G + σ₂BWB^T)), i.e., α₁ = λ_min(σ₁G + σ₂BWB^T) = μ − λ_max (μI − (σ₁G + σ₂BWB^T)).

Since the Perron-Frobenius eigenvalue of μI − (σ₁G + σ₂BWB^T) is an increasing function of its diagonal elements [27], which are decreasing functions of all g_i, it follows that λ_max (μI − (σ₁G + σ₂BWB^T)) is a decreasing function of g_i, meaning that α₁ is an increasing function of all g_i.

Remark 6

When all ξ_i are in ( $-\frac{\pi }{2},\frac{\pi }{2}$), since S₂ in (10) is positive definite, which leads to −ξ^T BWS₂B^T ξ < 0, the local coupling will increase α₁ in (15). But when $\underset{i}{max}\mid {\xi }_i\mid$ is larger than $\frac{\pi }{2}$, S₂ can be indefinite, hence −ξ^T BWS₂B^T ξ can be positive, negative or zero, thus the local coupling may increase, decrease or have no influence on the synchronization rate. This conclusion is confirmed by simulations in Sec. V.

IV. The non-identical natural frequency case

When natural frequencies are non-identical, Kuramoto oscillators cannot be fully synchronized [2], [25]. Next, we will prove that synchronization can be achieved in the sense that the synchronization error (defined as the maximal relative phase) can be made arbitrarily small. This is done in two steps: first we show that under some conditions, the oscillators can be phase-locked, then we prove that the relative phases can be trapped in [−δ, δ] for an arbitrary δ > 0 if the pacemaker is strong enough. The role played by the phase trapping approach is twofold: on the one hand, it makes the conditions required in phase locking achievable, and on the other hand, in combination with the phase locking, it can reduce the phase synchronization error to an arbitrary level.

A. Conditions for phase locking

When the natural frequencies are non-identical, the dynamics of the oscillator network are given in (5). As in previous studies, we assume that the natural frequencies are constant with respect to time. The results are summarized below:

Theorem 4

Denote $\epsilon \triangleq \underset{i}{max}\mid {\xi }_i\mid$, then the network in (5) can achieve phase locking if

1. $0\le \epsilon <\frac{\pi }{4}$ holds, at least one g_i is positive, and the coupling a_i,j is connected;

2. $\frac{\pi }{4}\le \epsilon <\frac{\pi }{2}$ and $g_{min}>\left\{\frac{-cos(2{\epsilon }_0){\lambda }_{max}(BW{B}^T)}{cos\epsilon },\underset{i}{max}\{{\displaystyle \sum _{j=1,j\ne 1}^N}-\frac{a_{i,j}cos(2\epsilon )}{cos(\epsilon )}\}\right\}$ hold.

Proof

To prove phase locking, i.e., all oscillators oscillate at the same frequency, we need to prove that the oscillating frequencies ϕ̇_i are identical. From (2), we have ϕ̇_i = w₀ + ξ̇_i, so if ζ ≜ ξ̇ converges to zero, then phase locking is achieved.

Differentiating (5) yields

$$\stackrel{.}{\zeta }=-{GS}_3\zeta -BW{S}_4{B}^T\zeta$$ (17)

where

$$\begin{array}{l}{S}_3=\text{diag}(cos{\xi }_1,cos{\xi }_2,\dots ,cos{\xi }_N),\\ S_4=\text{diag}(cos{(B^T\xi )}_1,cos{(B^T\xi )}_2,\dots ,cos{(B^T\xi )}_M)\end{array}$$ (18)

Following the line of reasoning of the proof of Theorem 1, we can prove that ζ is positively invariant under conditions in Theorem 4. Next we proceed to prove the convergence of ζ.

Define a Lyapunov function as $V=\frac{1}{2}{\zeta }^T\zeta$. Differentiating V along the trajectory of (17) yields

$$\stackrel{.}{V}={\zeta }^T\stackrel{.}{\zeta }=-{\zeta }^T{GS}_3\zeta -{\zeta }^{T}BW{S}_4{B}^T\zeta$$ (19)

Following the line of reasoning of Theorem 1, when ζ ≠ 0, we can obtain V̇ < 0 under the conditions in Theorem 4. So V, and hence ζ will converge to 0. Thus oscillating frequencies become identical and phase locking is achieved.

Remark 7

In the absence of a pacemaker, the authors in [3] proved that if the phase difference between any two oscillators, i.e., ϕ_i − ϕ_j, ∀i, j, is within [ $-\frac{\pi }{2},\frac{\pi }{2}$], then phase locking can be achieved. Given ϕ_i−ϕ_j = ξ_i−ξ_j, ∀i, j, the condition in [3] only applies to $-\frac{\pi }{4}\le {\epsilon }_i\le \frac{\pi }{4}$ in our formulation framework.

B. A bound on the exponential rate of phase locking

Theorem 5

For the network in (5), denote $\epsilon =\underset{i}{max}\mid {\xi }_i\mid$. If the conditions in Theorem 4 are satisfied, then

1. when $0\le \epsilon <\frac{\pi }{4}$ holds, the exponential phase-locking rate is no worse than

   $${\alpha }_3{\lambda }_{min}({\sigma }_{3}G+{\sigma }_{4}BW{B}^T)$$ (20)

   with σ₃ ≜ cosε and σ₄ ≜ cos 2ε;

2. when $\frac{\pi }{4}\le \epsilon <\frac{\pi }{2}$ holds, the exponential phase-locking rate is no worse than

   $${\alpha }_4=g_{min}cos(\epsilon )+cos(2\epsilon ){\lambda }_{max}(BW{B}^T)$$ (21)

Proof

Theorem 5 can be derived following the line of reasoning of Theorem 2 and thus is omitted.

Remark 8

Following Theorem 3, we can prove that a stronger pacemaker always increases α₃ (and α₄). But a stronger local coupling can have different impacts: when $0\le \epsilon <\frac{\pi }{4}$, S₄ in (18) is positive definite, −ζ^TBWS₄B^T ζ is negative, so the local coupling will increase α₃. However, when $\frac{\pi }{4}\le \epsilon <\frac{\pi }{2}$, since S₄ in (18) can be indefinite, −ζ^TBWS₄B^T ζ can be positive or negative. Thus the local coupling may increase or decrease the rate of phase locking. The conclusion will be confirmed by simulations in Sec. V.

C. Method for trapping relative phases

In this section, we will give a method such that the relative phases are trapped in any interval [−δ, δ] with an arbitrary 0 < δ < π.

Theorem 6

For (5) with frequency differences Ω, denote $\epsilon =\underset{i}{max}\mid {\xi }_i\mid$ and $\Vert \mathrm{\Omega }\Vert =\sqrt{{\mathrm{\Omega }}^T\mathrm{\Omega }}$, then the relative phases can be trapped in a compact set [−δ, δ] for an arbitrary 0 < δ < π

1. if $0\le \epsilon <\frac{\pi }{2}$ and the following condition is satisfied:

   $$g_{min}>\Vert \mathrm{\Omega }\Vert /(\delta \text{sinc}(\epsilon ))$$ (22)
2. if $\frac{\pi }{2}\le \epsilon <\pi$ and the following condition is satisfied:

   $$g_{min}>\Vert \mathrm{\Omega }\Vert /(\delta \text{sinc}(\epsilon ))-\frac{\text{sinc}(2{\epsilon }_0){\lambda }_{max}(BW{B}^T)}{\text{sinc}(\epsilon )}$$ (23)

   where ε₀ is defined in (8).

Proof

Differentiating Lyapunov function $V=\frac{1}{2}{\xi }^T\xi$ along the trajectory of (5) yields

$$\begin{array}{l}\stackrel{.}{V}={\xi }^T\stackrel{.}{\xi }={\xi }^T\mathrm{\Omega }-{\xi }^{T}Gsin\xi -{\xi }^{T}BWsin(B^T\xi )\\ ={\xi }^T\mathrm{\Omega }-{\xi }^T{GS}_1\xi -{\xi }^{T}BW{S}_2{B}^T\xi \end{array}$$ (24)

with S₁ and S₂ defined in (10).

1. When $0\le \epsilon <\frac{\pi }{4}$ holds, we have S₁ ≥ sinc(ε)I > 0 and S₂ ≥ 0 from previous analysis. Using (24), (10), and the fact λ_min(G) = g_min, we have

   $$\stackrel{.}{V}\le \Vert \xi \Vert \Vert \mathrm{\Omega }\Vert -g_{min}\text{sinc}(\epsilon ){\Vert \xi \Vert }^2$$ (25)

   If ξ_i is outside [−δ, δ] for some i, we have $\Vert \xi \Vert =\sqrt{{\sum }_{i=1}^N{\xi }_i^2}>\delta$, which in combination with (22) leads to V̇ < 0. Therefore all ξ_i will converge to [−δ, δ].

2. When $\frac{\pi }{2}\le \epsilon <\pi$ holds, from the analysis in Theorem 1, we have S₁ ≥ sinc(ε)I > 0 and S₂ ≥ sinc(2ε₀)I. Then using (24) and the fact λ_min(G) = g_min, we have

   $$\stackrel{.}{V}\le \Vert \xi \Vert \Vert \mathrm{\Omega }\Vert -g_{min}\text{sinc}(\epsilon ){\Vert \xi \Vert }^2-\text{sinc}(2{\epsilon }_0){\lambda }_{max}(BW{B}^T){\Vert \xi \Vert }^2$$ (26)

   If ξ_i is outside [−δ, δ] for some i, we have ||ξ|| > δ, which in combination with (23) leads to V̇ < 0. Thus all ξ_i will converge to the interval [−δ, δ].

Remark 9

Theorem 6 used the important fact that if $\Vert \xi \Vert =\sqrt{{\sum }_{i=1}^N{\xi }_i^2}$ is restricted to the interval [0, δ], then all ξ_i are restricted to the interval [−δ, δ].

Remark 10

When ||ξ|| < π, [3] gives a condition under which ξ_i can be trapped in an arbitrary compact set. Since for a large number of oscillators N, $\Vert \xi \Vert =\sqrt{{\sum }_{i=1}^N{\xi }_i^2}\le \pi$ is difficult to satisfy, our result is more general.

V. Simulation results

We consider a network composed of N = 9 oscillators. The coupling strengths a_i,j are randomly chosen from the interval [0, 0.1]. They were found to form a connected interaction graph. As in previous studies, we use the modulus of the order parameter $r=\left|\frac{1}{N}{\sum }_{i=0}^N{e}^{j{\varphi }_i}\right|$ to measure the degree of synchrony [25]. The value of r (r ∈ [0, 1]) will approach 1 as the network is perfectly synchronized, and 0 if the phases are randomly distributed [25]. According to [25], we have r ≈ 1 when the oscillators are synchronized. So we define synchronization to be achieved when r exceeds 0.99.

When the natural frequencies are identical, we set the phase of the pacemaker ϕ₀ to ϕ₀ = w₀t with w₀ = 1 and simulated the network using initial phases ϕ_i = ϕ₀ + ξ_i with ${\xi }_i\in (-\frac{\pi }{2},\frac{\pi }{2})$ and initial phases ϕ_i = ϕ₀ + ξ_i with ξ_i ∈ (−π, π), respectively. In the former case, we connected the first oscillator to the pacemaker and set g₁ = g, g₂ = g₃ = … = g₉ = 0. In the latter case, we connected all oscillators to the pacemaker and set g₁ = g₂ = … = g₉ = g. In both cases, we set g = 1. To show the influences of the pacemaker on the synchronization rate, we fixed a_i,j and simulated the network under different pacemaker strengths m × g, where m = 1, 2, …, 10. To show the influences of local coupling on the synchronization rate, we fixed the strength of the pacemaker to 3g and simulated the network under different local coupling strengths m × a_i,j for all a_i,j, where m = 1, 2, …, 10. All the synchronization times are averaged over 100 runs with initial ξ_i in each run randomly chosen from a uniform distribution on ( $-\frac{\pi }{2},\frac{\pi }{2}$) (in the former case) or on (−π, π) (in the latter case). The results are given in Fig. 1. It is clear that a stronger pacemaker always increases the synchronization rate, whereas the local coupling increases the synchronization rate when all ξ_i are within ( $-\frac{\pi }{2},\frac{\pi }{2}$), and it may increase or decrease the synchronization rate when the maximal/minimal ξ_i is outside ( $-\frac{\pi }{2},\frac{\pi }{2}$).

Fig. 1.

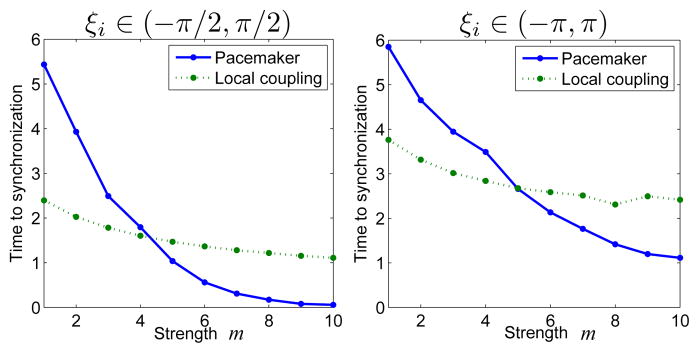
Times to synchronization under different strengths of pacemaker/local coupling (with all oscillators having identical natural frequencies).

When the natural frequencies are non-identical, we simulated the network using initial phases ϕ_i = ϕ₀ + ξ_i with ${\xi }_i\in (-\frac{\pi }{4},\frac{\pi }{4})$ and initial phases ϕ_i = ϕ₀ + ξ_i with ${\xi }_i\in (-\frac{\pi }{2},\frac{\pi }{2})$ , respectively. In the former case, we connected the first oscillator to the pacemaker and set g₁ = g. In the latter case, we connected all the oscillators to the pacemaker and set g₁ = g₂ = … = g₉ = g. The natural frequencies were randomly chosen from (0, 1). Tuning the strengths in the same way as in the identical natural frequency case, we simulated the network under different strengths of the pacemaker and local coupling. All of the times to phase locking are averaged over 100 runs with initial ξ_i randomly chosen from a uniform distribution on ( $-\frac{\pi }{4},\frac{\pi }{4}$) (in the former case) or on ( $-\frac{\pi }{2},\frac{\pi }{2}$) (in the latter case). The results are given in Fig. 2. It is clear that a stronger pacemaker always increases the rate to phase locking, whereas the local coupling increases the rate to phase locking when all ξ_i are within ( $-\frac{\pi }{4},\frac{\pi }{4}$), and it may increase or decrease the rate to phase locking when the maximal/minimal ξ_i is outside ( $-\frac{\pi }{4},\frac{\pi }{4}$).

Fig. 2.

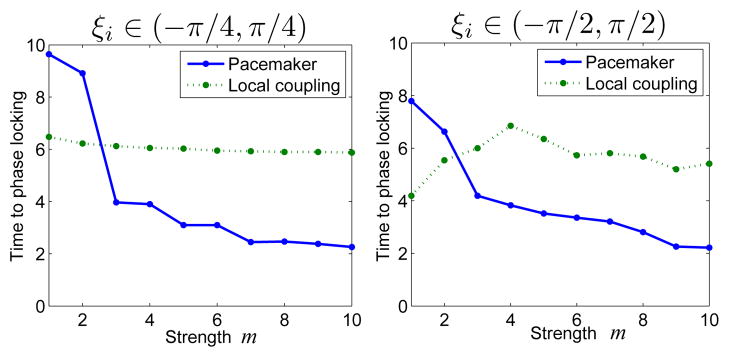
Times to phase locking under different strengths of pacemaker/local coupling (with oscillators having non-identical natural frequencies).

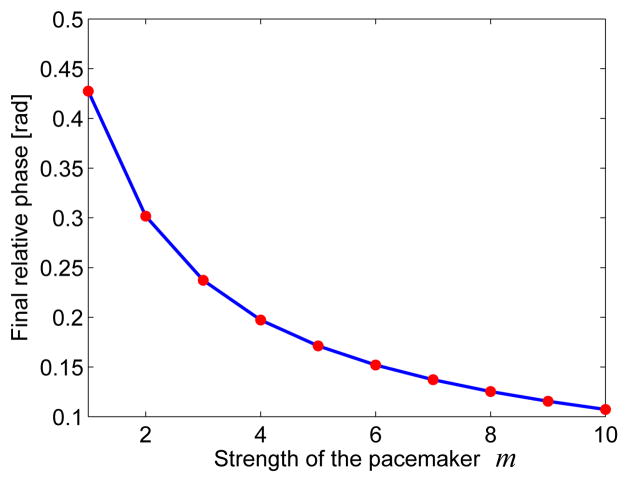
To confirm the prediction that ξ_i can be made smaller by making the pacemaker strength stronger, we set g₁ = … = g₉ = g and simulated the network under initial phases ϕ_i = ϕ₀ + ξ_i with ξ_i ∈ (−π, π). Using the same ξ_i, the maximal final relative phase when the strength of the pacemaker g is made m (m = 1, 2, …, 10) times greater is recorded and given in Fig. 3. It can be seen that the maximal final relative phase (i.e., synchronization error) decreases with the strength of the pacemaker, confirming the prediction in Theorem 6.

Fig. 3.

The maximal final relative phase (phase synchronization error) under different strengths of the pacemaker when oscillators have non-identical natural frequencies (which are randomly chosen from the interval (0, 1)).

VI. Conclusions

The exponential synchronization rate of Kuramoto oscillators is analyzed in the presence of a pacemaker. In the identical natural frequency case, we prove that synchronization to the pacemaker can be ensured even when the initial phases are not constrained in an open half-circle, which improves the existing results in the literature. Then we derive a lower bound on the exponential synchronization rate, which is proven an increasing function of the pacemaker strength, but may be an increasing or decreasing function of the local coupling strength. In the non-identical natural frequency case, a similar conclusion is obtained on phase locking. In this case, we also prove that relative phases (synchronization error) can be made arbitrarily small by making the pacemaker strength strong enough. The results are independent of oscillator numbers in the network and are confirmed by numerical simulations.