3D super-resolution imaging with blinking quantum dots

Abstract

Quantum dots are promising candidates for single molecule imaging due to their exceptional photophysical properties, including their intense brightness and resistance to photobleaching. They are also notorious for their blinking. Here we report a novel way to take advantage of quantum dot blinking to develop an imaging technique in three-dimensions with nanometric resolution. We first applied this method to simulated images of quantum dots, and then to quantum dots immobilized on microspheres. We achieved imaging resolutions (FWHM) of 8–17 nm in the x-y plane and 58 nm (on coverslip) or 81 nm (deep in solution) in the z-direction, approximately 3–7 times better than what has been achieved previously with quantum dots. This approach was applied to resolve the 3D distribution of epidermal growth factor receptor (EGFR) molecules at, and inside of, the plasma membrane of resting basal breast cancer cells.

The breakthrough of single molecule imaging has revolutionized biology. However, the great potential of single molecule measurements is often restricted by two phenomena: photobleaching and blinking. Photobleaching of organic fluorophores limits the duration of measurements. In contrast, quantum dots (QDs) are very resistant to photobleaching and can last for hours¹. Furthermore, QDs have other exceptional photophysical properties, such as intense brightness, broad excitation spectra, and narrow symmetric and controllable emission spectra. Therefore QDs are promising candidates for single molecule imaging and have been broadly used in single particle tracking².

However, quantum dots are notorious for (and featured for) their blinking: sudden jumps between the fluorescent “on” state and non-fluorescent “off” state^3–5. It was found that the probabilities of the on- and off-times (t) follow a power law: P(t) ∝ t^−α, where the exponent α is usually 1 < α < 2, and typically close to ~ 3/2. In addition, the blinking of quantum dots is weakly non-ergodic: ensemble averages are not equal to time averages.

The blinking of quantum dots limits their applications in certain biophysical areas, such as in single particle tracking where an abrupt dark off-state terminates the tracking of a QD². As a result, various attempts to suppress or eliminate quantum dots blinking have been made^6–16. On the other hand, the blinking of quantum dots can facilitate achieving super-resolution. For example, the blinking statistics of quantum dots were analyzed by an independent component analysis (ICA) to resolve groups of closely spaced quantum dots¹⁷. In a technique termed super-resolution optical fluctuation imaging (SOFI)¹⁸, the authors got 55 nm resolution (FWHM) in x-y plane with the 25^th order SOFI and (we calculate) ~ 400 nm resolution (FWHM) in z with the 16^th order SOFI¹⁸. The blinking was purposefully enhanced by Watanabe et al. to improve the temporal resolution for SOFI¹⁹. More recently Chien et al. used the blinking in the intensity traces to determine the number (~ three) of quantum dots in a group, which was then used to localize them with high resolution²⁰.

In this letter, we report another way to take advantage of quantum-dots blinking, in this case, getting three-dimensional super-resolution imaging with 8–17 nm in the x-y plane and 58 nm (on coverslip) or 81 nm (deep in solution) in the z-direction. This exceeds the resolution found in SIM and STED techniques^21–24. Similar resolution is achieved with 3D-STORM (and related techniques, such as PALM, dSTORM etc.)^25–29 although these techniques rely on activating a subset of organic-dye fluorophores or pairs of fluorophores to achieve super-resolution. In addition, inadvertent photobleaching before imaging might be a problem in certain situations. Also, in some situations, difficulty of placing two fluorophores in close proximity, or the use of two different lasers^25–28,30, or external chemicals which need to be added to encourage fluorophore-activation^30,31, create problems. In contrast, quantum dots do not need to be photoactivated, have tremendous resistance to photobleaching, and require a single laser for excitation.

We call our technique QDB3, Quantum Dot Blinking with 3 dimensional imaging. To demonstrate our technique, we first used simulated images of quantum dots whose exact positions are known beforehand. Next we used QDB3 to look at quantum dots immobilized on microspheres where the distribution of the quantum dots is spherical, although the exact positions of the quantum dots are not known. Finally, we resolved the 3D distribution of epidermal growth factor receptor (EGFR) molecules at, and inside of, the plasma membrane of resting basal breast cancer cells.

Principles of QDB3

QDB3 works in a very different but more intuitive way than SOFI and other existing techniques that make use of blinking of quantum dots. For example, SOFI calculates the (cumulant) correlation functions (or variance) of various orders and the intensities of pixels in the resultant SOFI images are assigned with the values from the correlation functions^18,19. In another technique, Lidke et al’s work uses Independent Component Analysis were also used to identify single quantum dots in a group¹⁷. In these techniques, the actual emission from a single quantum dot is never extracted and resolved. In contrast, QDB3 resolves individual quantum dots and utilizes the actual emission of a single quantum dot to determine its position accurately.

The idea of QDB3 originates from two 2D super-resolution imaging of organic fluorophores which were recently developed independently by our lab and others^32,33. (They are known as gSHRImP and BaLM.) Briefly, a movie of quantum dots is taken, from which two intermediate movies are created by subtracting adjacent frames in both backward and forward directions (i.e. I_n − I_n−1 and I_n − I_n+1) (SI Fig. 1b and 1c). If a single quantum dot undergoes a transition between on and off states (on → off, or off → on) due to blinking (or occasionally photobleaching and photoactivating), it appears in the intermediate movies as a single spot, whose intensity and point spread function (PSF) are exactly the contribution from this specific quantum dot to the original movie. Therefore the PSF in the intermediate movies can be utilized to localize the quantum dot. Due to the stochastic nature of quantum dot blinking, it is not likely that multiple quantum dots in a diffraction-limited spot blink simultaneously. As a result, quantum dots can be localized sequentially by this method. We emphasize that the current method is conceptually different from SOFI¹⁸ or other methods such as 3B analysis³⁴ or faster STORM using compressed sensing³⁵, where individual fluorophores/quantum dots are not isolated and localized.

Because the complete PSF of the quantum dot is obtained, it is possible to localize not only the x-y positions of the quantum dot but also its z position by astigmatism (i.e. ellipticity). The z position is achieved by insertion of a cylindrical lens (f = 1m) in the emission path of an epi-fluorescence microscope^27,36–38 (100X oil immersion objective, NA=1.4, and IX71 inverted microscope, Olympus America; excitation: 532nm laser, CrystaLaser, NV; filter set: T550LPXR together with HQ615/30, Chroma technology corp., VT; camera: EMCCD iXon^EM+, Model: DU-897E-CS0-#BV, Andor technology, CT). This allows QDB3 to be faster than 3D SOFI where z localization requires scanning in the z direction with a stepper¹⁸. The spots appearing in the intermediate movies are detected and fitted with 2D Gaussian functions. Those spots, which are too dim (SI Fig. 1f), too strong (SI Fig. 1g), too wide, or too elliptical (e.g. beyond the sensitive z range, see Fig. 1), are rejected. For the spots surviving the rejection criteria, the center of the elliptical Gaussian gives the x-y localization of the quantum dot and the ellipticity gives the z-localization (SI Fig 1d and 1e). The actual z-position of the quantum dot from the ellipticity of the fitted elliptical Gaussian function is given by comparing with a calibration curve, with corrections from mismatch of refractive index, if necessary^27,39,40.

Figure 1.

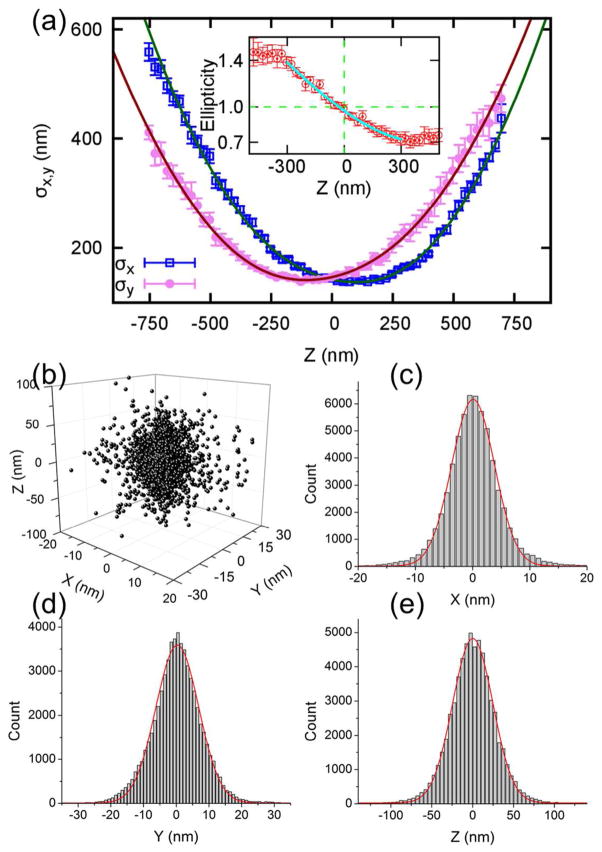
Calibration and resolution of QDB3. (a) The widths of the point spread functions (represented as the standard deviations of the fitted elliptical Gaussian, σ_x and σ_y) are plotted as a function of z, obtained from single quantum dots in aqueous solution. Each data point represents the average value obtained from seven quantum dots. Inset: ellipticity (σ_x/σ_y, red circles) as a function of z. The fitting curve (cyan line) is used for the determination of z-positions of quantum dots in experiments. The sensitive range of the ellipticity lies between −300 to +300 nm. (b–e) Three-dimensional localization distribution of single quantum dots. Each quantum dot gives a cluster of localizations due to blinking for multiple times. Then localizations from 588 clusters (i.e. 588 quantum dots) were aligned by their center of mass to generate the overall 3D presentation of the localization distribution. Histograms of the distribution in x, y, and z were fit to a Gaussian function, yielding standard deviations of σ_x = 3.7 ± 0.0 nm in x, σ_y = 6.6 ± 0.0 nm in y, and σ_z = 24.6 ± 0.4 nm in z.

It is noted here that, apart from the extension from 2D to 3D, another advantage of QDB3 over gSHRImP and BaLM is the temporal resolution of QDB3. This originates from the characteristic statistics of quantum dot blinking: a power law, which results in scale invariance, i.e. the probabilities (P) of on/off times (t) follow the same power law regardless of time scale, P(c × t) ∝ P(t) ∝ t^−α where c is any arbitrary constant. In other words, they blink at all time-scales and thus, in principle, it is possible to use arbitrary camera frame rates. This feature, combined with the resistance of quantum dots to photobleaching (thus quantum dots can be excited at very high excitation power), allows use of various frame rates. In our experiments, the frame rates ranged from 10 fps (100 ms) to 333.3 fps (3 ms) without obvious loss of localization accuracy.

Calibration and resolution of QDB3

In order to get the z-position, one needs to generate a calibration curve. To do this, we imaged quantum dots (Qdot® 605 streptavidin conjugate, catalog number: Q10101MP, Life technologies corporation, CA; 100 pM in PBS) by immobilizing them on a glass surface (covered with biotinylated polyethylene glycol) and stepping z via a mechanical stage. 10 mM DTT was added into the solution to suppress the blinking of quantum dots^11,12. From seven individual quantum dots, which lasted for the whole movie without blinking, the widths of the PSF’s, represented as the standard deviations of the fitted elliptical Gaussian function (σ_x and σ_y) and the ellipticity of the PSF (ε = σ_x/σ_y) were measured as a function of z (Fig. 1a). The widths are fitted with ${\sigma }_{x,y}(z)={\sigma }_{0(x,y)}\times \sqrt{1+{\left(\frac{z-c}{d}\right)}^2+A{\left(\frac{z-c}{d}\right)}^3+B{\left(\frac{z-c}{d}\right)}^4}$ and the ellipticity ε is fitted with a cubic polynomial²⁷. Note that the specific functional form for the fitting curve is not important²⁷. The fitted curve of ε vs. z is then used as the calibration curve in our experiments. We observed that the ellipticity is sensitive from −300 nm to 300 nm in z (inset of Fig. 1a). Therefore, we limited the detection of quantum dots in this range. Note that the actual sensitive region is slightly greater than this range. However, to guarantee detection accuracy, we have chosen this moderate range. Another point is that the sensitive region is limited by the cylindrical lens (600 nm), which is smaller than the depth of field (DOF) of the objective (100X oil immersion, NA=1.4, Olympus America Inc, PA) in the current setup. However, it is possible to use different cylindrical lenses to match the sensitive region with the DOF.

To quantify the resolution that QDB3 can achieve, we looked at individual quantum dots immobilized on a coverslip. Each quantum dot blinks for multiple times, allowing localization for multiple times, resulting in a cluster of localizations (for each localization event, we achieved ~ 1 nm precision; see SI for details). Then, similar to Ref²⁷, the localizations from many clusters (588 quantum dots) were aligned by their center of mass to generate the overall 3D presentation of the localization distribution (Fig. 1b). Histograms of the distribution in x, y, and z were fit to Gaussian functions, yielding standard deviations of σ_x = 3.7 ± 0.0 nm in x, σ_y = 6.6 ± 0.0 nm in y, and σ_z = 24.6 ± 0.4 nm in z (Fig. 1c – 1e), corresponding to resolutions (FWHM = 2.35 σ) in the three directions of 8.7, 15.5 and 57.8 nm. Compared to the 25^th-order SOFI imaging, which also used quantum dots and achieved FWHM of 55 nm in x-y plane¹⁸, the resolution of QDB3 is ~ 4–7 folds higher. Similarly, z-resolution of QDB3 is ~ 7 times better than that from the 16^th order SOFI¹⁸. We note that intermediate movies generated in this method can be viewed as the raw data obtained in STORM/PALM microscopy. On each frame, only a small subset of quantum dots (i.e., the ones undergo stochastic transitions) is “activated”. Bearing this in mind, it is reasonable that we achieved resolutions similar to the values from STORM²⁷, but a few times better than SOFI.

In addition, we examined the resolutions for localizing quantum dots deep in solution. This is done by looking at individual quantum dots on surfaces of 1260 nm beads (see SI for details). We achieved ~ 1nm precision for each localization event. For the localization distribution, we achieved σ_x = 3.3 ± 0.1 nm in x, σ_y = 7.2 ± 0.5 nm in y, and σ_z 34.6 ± 1.3 nm in z (corrected for refractive index mismatch), corresponding to resolutions (FWHM = 2.35 σ) in the three directions of 7.8, 16.9 and 81.3 nm. Therefore, the resolution in x-y plane does not change much, but the resolution in z is slightly higher, compared to the z-resolution for quantum dots on a coverslip surface. Nonetheless, compared to the 25^th order SOFI imaging, the x-y resolution of QDB3 is 3–7 folds better and z- resolution of QDB3 is ~ 5 times better than that from the 16^th order SOFI ¹⁸.

QDB3 applied to simulated movies

To demonstrate this new technique, we first applied it to simulated movies of quantum dots. The advantage of simulated movies is that the exact positions of the quantum dots are known beforehand, making it possible to quantify how well the QDB3 algorithm works.

Two types of movies were generated for this purpose. In one type, the positions of quantum dots are designed to show specific patterns, for example, a 3D spiral coil (Fig. 2a), a 3D letter Y (SI Fig. 3) and a 3D letter W (SI Fig. 3). In the second type, the positions of quantum dots were random but their distribution was known, i.e., a random spherical distribution on a 400 nm sphere (SI Fig. 3). The advantage of the first type is that the positions of quantum dots are pre-defined and therefore they are perfect for verification of the QDB3 technique. However, they are not feasible in practice. In contrast, the second type can be achieved in experiments, as described in the next section, “QDB3 applied to quantum dots with spherical distribution”.

Figure 2.

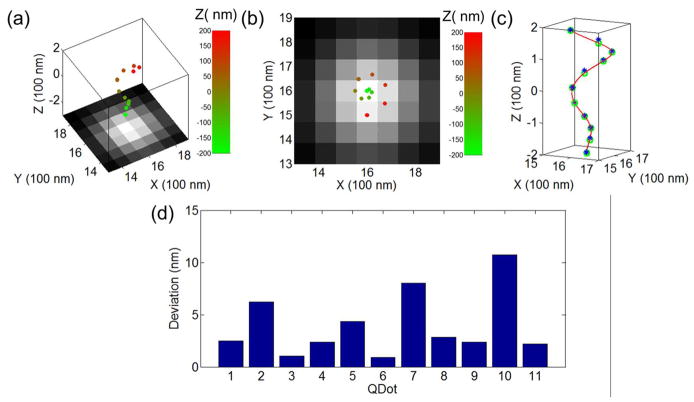
Three-dimensional images of simulated movie of quantum dots with a pattern of a 3D spiral coil using QDB3, in the absence of photon noise. (a) (b) The 3D positions of the quantum dots (with z positions highlighted by color), obtained by QDB3, are shown on top of the corresponding epi-fluorescence images. (c) Comparison between the 3D super-resolution images of quantum dots (blue stars) with their actual positions (green circles) shows that they overlap very well. (d) Deviations of the detected locations of quantum dots from their actual positions, δ = |r_d − r_a|, are small (≤ 10 nm). The average deviation for this specific example is ~ 4.0 nm. Note that, although photon noises are not present, the deviation is not zero presumably due to fitting errors.

The simulated movies have lengths of 1000 frames and contain 9 to 11 quantum dots. Both the on and off states of quantum dots obeys the power law, P(t) ∝ t^−α, where α_on = 1.5 for the on state and α_off = 1.5 for the off state (see SI Fig. 2). Note that the exact parameters (α_on and α_off) or the distribution of on-time and off-time are not important: QDB3 works as long as the quantum dots switch states (on → off, or off → on); however, in our simulations, the values α_on and α_off were taken from experiments in the literature^1,3,4. Each frame of the simulated movies is a superposition of light intensities from all quantum dots. The light intensity, or PSF, from each quantum dot is represented by an elliptical Gaussian function, $I(x,y,z)=I_{0}exp\left(-\frac{{(x-x_c)}^2}{2{\sigma }_x{(z)}^2}-\frac{{(y-y_c)}^2}{2{\sigma }_y{(z)}^2}\right)$, where the standard deviations, σ_x(z) and σ_y (z), are functions of the z position of the quantum dot and are from the experimental data (Fig. 1a).

We applied the QDB3 algorithm to the simulated movies and obtained super-resolution images, as shown in Fig. 2 and SI Fig. 3. With the simulated movies, we are able to compare the detected quantum dots (blue asterisks in Fig. 2c) to their actual positions (green circles in Fig. 2c). The detected quantum dots overlaps with their actual positions very well. To quantify the goodness of imaging with QDB3, we calculated the deviation of the detected locations of quantum dots from their actual positions, δ = |r_d − r_a|, shown in Fig. 2d. It turns out that the deviations are usually ≤ 10 nm, although not zero, presumably due to fitting errors, in the absence of photon noises. For the 3D spiral coil (Fig. 2), the average deviation is ~ 4.0 nm.

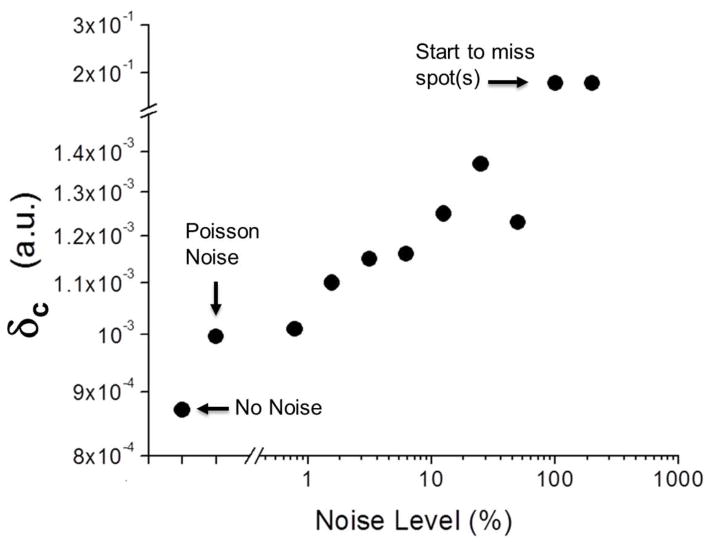
The new technique QDB3 is also robust in the presence of photon noises. We show this by adding various noises to the simulated movies. Poisson noise is a basic form of uncertainty associated with the measurement of light, inherent to the quantized nature of light and the independence of photon detections^41–44. Consequently, we first tried adding Poisson noises such that the resultant intensities of pixels follow Poisson distributions with a center at N and a standard deviation $\sqrt{N}$ where N is the original intensities of pixels^41–44. It turns out that QDB3 was able to detect the quantum dots correctly and accurately (Fig. 3 and SI Fig. 4), although the deviation is slightly higher (4.5 nm) than that in the absence of noise (4.0 nm). Furthermore, to examine the detection limit of QDB3, we tested QDB3 with the addition of Gaussian noises at different noise levels. The Gaussian noises were chosen here to respect the nature of photon noise (i.e. Poisson noise) because Poisson noises can be often modeled using a Gaussian distribution, with mean and variance equal to the photon count N. We varied the noise level (defined by the ratio of N to the photon number from a single quantum dot) and observed that QDB3 can faithfully localize all the quantum dots correctly, up to noise level of ~ 100%. When the noise level is above ~ 100%, QDB3 started to fail detection of some quantum dots (≤ 2 out of 10 quantum dots at noise level 200%). To take into account the missing quantum dots, we re-define a new deviation to quantify the error of QDB3 in a way similar to Canberra distance⁴⁵: ${\delta }_c({\mathit{r}}_d,{\mathit{r}}_a)=\frac{\mid {\mathit{r}}_d-{\mathit{r}}_a\mid }{\mid {\mathit{r}}_d\mid +\mid {\mathit{r}}_a\mid }$, where r_d and r_a are the detected and actual locations of a quantum dot and r_d = ∞ for a missing quantum dot. Note that δ_c = 0 for an exactly-accurately-detected quantum dot and δ_c = 1 for a missing one. As shown in Fig. 4, although it slightly increases when the noise level increases, the error of QDB3 keeps being low until ~ 100% noise level, after which QDB3 starts to miss quantum dots. This shows the robustness of QDB3.

Figure 3.

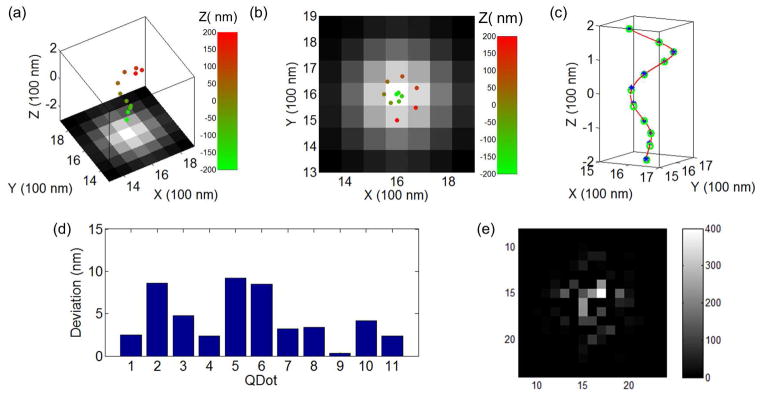
Three-dimensional images of simulated movie of quantum dots with a pattern of a 3D spiral coil using QDB3, in the presence of Poisson noise. (a) (b) The 3D positions of the quantum dots (with z positions highlighted by color), obtained by QDB3, are shown on top of the corresponding epi-fluorescence images. (c) Comparison between the 3D super-resolution images of quantum dots (blue stars) with their actual positions (green circles) shows that they overlap very well in the presence of Poisson noise. (d) Deviations of the detected locations of quantum dots from their actual positions are still small (on average ~ 4.5 nm) although slightly higher than those without photon noises. (e) An image of typical Poisson noises added to the simulated images.

Figure 4.

Deviation of detected locations of quantum dots from their actual positions in the presence of Gaussian noises at various levels (defined by the ratio of N to the photon number from a single quantum dot). The deviation is defined as ${\delta }_C({\mathit{r}}_d,{\mathit{r}}_a)=\frac{\mid {\mathit{r}}_d-{\mathit{r}}_a\mid }{\mid {\mathit{r}}_d\mid +\mid {\mathit{r}}_a\mid }$, where r_d and r_a are the detected and actual locations of a quantum dot and r_d = ∞ for a missing quantum dot. Gaussian noises were chosen to respect the nature of photon noise (i.e. Poisson noise) because it can be often modeled using a Gaussian distribution, 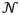(μ = N, σ² = N), whose variance depends on the expected photon count (N). QDB3 can faithfully localize all the quantum dots correctly, up to noise level of ~ 100%. When the noise level is above ~ 100%, QDB3 started to fail detection of some quantum dots (≤ 2 out of ~ 10 quantum dots at noise level 200%).

QDB3 applied to quantum dots with spherical distribution

The QDB3 technique is next applied to image quantum dots (biotin-labeled Qdot® 605 nanocrystals, catalog number: Q10301MP, Life technologies corporation, CA) on microspheres. The exact positions of the quantum dots are not known but the distribution of the quantum dots, by design, is spherical.

Two different sizes of polystyrene beads were used in our experiments. The smaller ones were 400 – 690 nm in diameter (SVP-05-10, Spherotech Inc, IL, average size 440 nm determined by the manufacturer), while the larger ones were 1000 – 1400 nm (SVP-10-5, Spherotech Inc, IL, with average size 1260 nm determined by the manufacturer). The sizes were chosen based on the sensitive z-range of the imaging technique (600 nm, Fig. S3); we could then image either the whole microsphere or part of it.

The size of the smaller beads falls into the sensitive z-range (600 nm) of the QDB3 technique in our setup, and therefore, we could image the whole bead. In our experiments, the focus of the objective was placed at the center of individual polystyrene beads. The movie was then taken for 180 sec at a speed of 33.33 frames per second (fps), and processed with the QDB3 algorithm. Mismatch of refractive index was taken into account by rescaling z localizations by a factor of 0.79^27,40. Figure 5 shows an example of quantum dots immobilized on a microsphere of 400 – 690 nm. The epi-fluorescence image is shown in black-and-white, on top of which are drawn the positions of the detected quantum dots as dots with colors indicating their z positions. Both the top view and the side view (Fig. 5a and 5b) show that the quantum dots are distributed circularly. To quantify the distribution of the quantum dots, we fitted the positions of the quantum dots with a three-dimensional sphere that is shown as a gray surface in Fig. 5c; the detected quantum dots are drawn as red dots. The fitting gives that the diameter of the bead is 480 nm, consistent with the expectation (400 – 690 nm). This indicates that the QDB3 algorithm works well. Furthermore, we quantified the deviation of the positions of spots from the fitted sphere by relative residuals (residual / diameter * 100%) in the radial direction and found that the fitting residuals were generally small (averagely 3.9%), with the highest deviation <10%, as shown in Fig. 5d.

Figure 5.

QDB3 applied on quantum dots immobilized on a microsphere of diameter 400 – 690 nm. (a–b) 3D super-resolution images of the quantum dots overlapped on normal images from microscope in different views. The relative z positions of the quantum dots are indicated with color from red (high z) to green (low z). (c) The positions of the quantum dots are fitted to a sphere, resulting in a fitted diameter of 480 nm. The fitted sphere is shown as a gray and the detected quantum dots are drawn as red dots. (d) Relative residuals in the radial direction of the spherical fitting show that the fitting errors are small, < 10%.

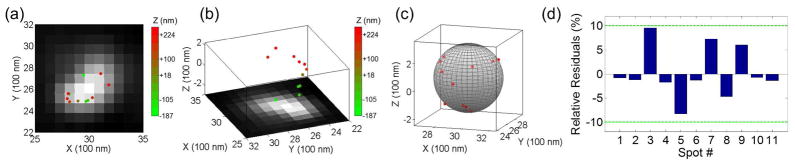
We also imaged larger polystyrene beads with diameters of 1000 – 1400 nm (with an average of 1260 nm) using the QDB3 technique. As the size of the beads exceeds the sensitive range of optical astigmatism (600 nm, Fig. 1a), the beads are expected to show different shapes (Fig. 6). For example, if the objective is focused at the top (or bottom), the bead is expected to be a bowl (Fig. 6a). On the other hand, if focused at the middle it will be like a cylinder (Fig. 6a). This is exactly what we observed using the QDB3 technique on larger beads. Figure 6b shows the 3D images of quantum dots on two larger beads when focusing at two different z-positions. The color indicates their relative z-positions (z decreases from yellow to red). This furthermore, validates the QDB3 technique.

Figure 6.

(a) Predicted distributions of quantum dots immobilized on a 1260 nm microsphere when focusing at different z positions of the microsphere, given that the sensitive range of optical astigmatism in our setup is ± 300 nm. (b) Measured distributions of quantum dots immobilized on microspheres of 1000 – 1400 nm.

QDB3 applied to EGFR on breast cancer cell

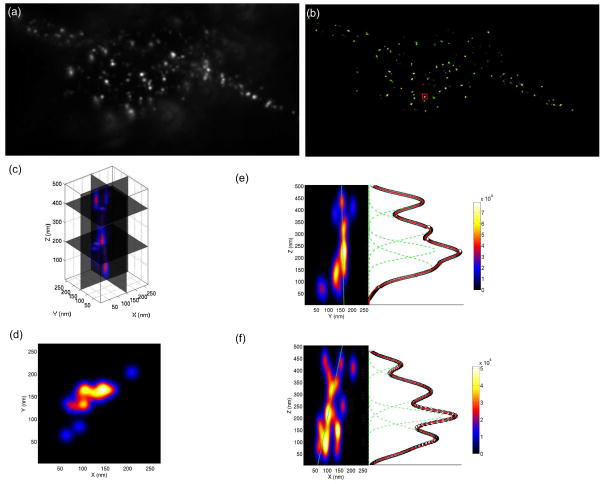
We then applied the QDB3 technique to image epidermal growth factor receptor (EGFR) at the plasma membrane on, and inside, resting basal breast cancer cells (HCC1143). EGFR is involved in breast cancer⁴⁶ and the class of basal-like breast cancer cells are major players⁴⁷. EGFR, which primarily resides on the cell membrane, tends to oligomerize and be internalized upon activation through its ligand (such as EGF). EGFR overexpression is frequent in human cancers and EGFR is a major drug target for the treatment of various types of breast cancers^48,49. Here, the QDs are attached to the epidermal growth factor (EGF) via biotin-streptavidin coupling. Pre-formed complexes were then used to treat the breast cancer cells at 37°C for 10 minutes and the complexes thereby linked the qdot via EGF to its receptor, EGFR. Although unlikely due to the stoichiometry used in our experiments, it is still possible that a very small fraction of QDs is labeled with multiple EGFs, which might induce additional agglomeration of EGFRs. However, this will not affect the analysis and results presented here. The samples were mounted in Mowiol 4-88 (Polysciences Inc., Warrington, PA, U.S.), which was partially intended to match the refractive index of immersion oil. An example of breast cancer cells is shown in Fig. 7 (frame rate = 33.3 Hz for data acquisition, total acquisition time = 3 min). The epi-fluorescence image (Fig. 7a) shows that some spots are much brighter than others, indicating the presence of aggregates of EGFR. We applied the QDB3 algorithm to the movie and produced a 3D super-resolution image, whose top view is shown in Fig. 7b.

Figure 7.

QDB3 applied to image epidermal growth factor receptor (EGFR), labeled with quantum dots, at the plasma membrane of resting basal breast cancer cell. (a) Image from a normal fluorescent microscopy. (b) Three-dimensional super-resolution image reconstructed with 3D-gSHRImP algorithm. (c) 3D intensity profile of an aggregate of quantum dots the rectangular area in (b). (d) Top view of the aggregate. (e–f) Side views of the aggregate. The intensity profiles along specific lines are also plotted at the sides of the contour plots. Also the intensity profiles were fitted with multiple Gaussians (4 peaks), showing the capability of QDB3 of resolving different quantum dots separated by ~ 100 – 150 nm in the z direction in this specific aggregate.

To faithfully demonstrate the capability of the QDB3 technique of resolving 3D-distributions of quantum dots, the localization resolution of the imaging method (Fig. 1) must be considered. To do this, we represent each quantum dot as a three dimensional Gaussian function, whose standard deviations are the measured values from experiments (σ_x,y = 10 nm, σ_z = 30 nm). In this way an aggregate is a superposition of multiple 3D Gaussians. We note that the intensity contours do not mean collected photons. Instead, they are proportional to the localization probability. The aggregate (red rectangle in Fig. 7b) in this representation is shown in Fig. 7c. The top view (Fig. 7d) shows the distribution of quantum dots inside an aggregate in the x-y plane: we resolve the z-distribution as well. In Fig. 7e and 7f, we plotted the light intensity in x-z and y-z planes. To be quantitative, we investigated the intensity profiles along specific lines (green lines on the left parts in Fig. 7e and 7f) and plotted these as functions of z (black thick lines in Fig. 7e and 7f), showing the capability of QDB3 of resolving quantum dots in the z direction. We were able to resolve different quantum dots separated by ~ 100 – 150 nm in the z direction, for this specific aggregate. Note that certain peaks might contain multiple quantum dots and thus give different widths.

Discussion

In summary, we developed a simple three-dimensional nano-scale imaging technique (QDB3) based on the blinking of quantum dots. We were able to extract the PSF of individual quantum dots, even if the quantum dot was in a group of other quantum dots within a diffraction-limited spot. This allowed us to perform super-resolution imaging, achieving 3–9 fold resolution improvement compared to other methods, such as SOFI. We first showed the technique with simulated movies of quantum dots. It was then successfully applied to quantum dots immobilized on microspheres. Finally, we applied the new technique to resolve the three-dimensional distribution of EGFR at the plasma membrane of breast cancer cells. In the latter case, it was particularly important to use quantum dots. This experiment is part of a plan to watch the temporal evolution of the endocytosis of EGFR; it is important not to have photobleaching, which can be problematic with organic fluorophores.

Due to advantages of quantum dots over organic fluorophores, the new technique QDB3 could be a better choice in certain situations than other three dimensional super-resolution imaging techniques^{21–29,50,51}. Generally speaking, for example, higher precision of localization can be achieved because quantum dots are intensely bright, compared to most organic fluorophores (roughly localization precision $\propto 1/\sqrt{N}$ where N is the collected photon number)^52,53. In addition, QDB3 would be very useful in experiments where longer time is needed between sample-labeling and super-resolution imaging: quantum dots are very resistant to photobleaching but many organic fluorophores are photobleached during the same time period. Furthermore, quantum dots blink at all time-scales, from microseconds to hours^1,3,4. In addition, quantum dots can be excited at high power without photobleaching them. As a result, in principle, arbitrary camera frame rate could be used. This feature would be useful for fast super-resolution imaging, facilitating dynamic studies in live cells at super-resolution. Due to the non-photobleaching nature of quantum dots, the current method is also capable of making time-course-imaging, i.e., the entire imaging sequence can be repeated every minute, every hour, etc. In addition, the QDB3 technique does not require complicated optics as in SIM and STED^21–24 and it is generally more convenient than PALM/STORM in the sense of simplicity of optics (one laser here, compared to two-lasers in the original PALM/STORM setup) and choice of fluorophores (multiple fluorophores placed together in close proximity for STORM, or photoactivatable fluorophore proteins for PALM)^28,29, except certain variants such as SPRAIPAINT⁵⁴. In contrast, commercial quantum dots with various emission spectra are readily available.

Another advantage of the QDB3 technique is the insignificance of background. In 3D imaging, a typical concern is the background, contributed from out-of-focus planes. Therefore special care was usually required, including, for example, confining the activation/illumination to a small region⁵⁵, or carefully adjusting the angle of illumination²⁷. However, because QDB3 uses the subtraction between adjacent frames, the (common) background in adjacent frames is subtracted off. As a result, the background issue is not as significant in QDB3 as in other 3D techniques.

On the other hand, QDB3 has certain limitations, similar to gSHRImP and BALM. For example, the density of quantum dots can be too high, preventing resolution between quantum dots; the number of quantum dots in the diffraction-limited region is limited by the dynamic range of the camera in order to guarantee certain localization accuracy; the simultaneous blinking of closely-spaced quantum dots can possibly produce “fake” particles (i.e., the sum of two or more closely spaced quantum dots), or cause throwing out of data; the reversible blinking of quantum dots makes it more difficult to count copy numbers exactly (although this is a general difficulty of super-resolution imaging-based stochasticity, such as STORM and PALM); quantum dots are generally large, usually 10–20 nm, much bigger than organic fluorophores. Finally, we also note that frame-subtraction is required for this technique and thus it requires that no motion from frame to frame exists.

To conclude, we report a novel way to make use of quantum dots blinking to develop a three- dimensional super-resolution imaging technique. This has a 3–9 fold resolution improvement over alternative state of the art techniques.