Abstract
Regularized logistic regression is a standard classification method used in statistics and machine learning. Unlike regularized least squares problems such as ridge regression, the parameter estimates cannot be computed in closed-form and instead must be estimated using an iterative technique. This paper addresses the computational problem of regularized logistic regression that is commonly encountered in model selection and classifier statistical significance testing, in which a large number of related logistic regression problems must be solved for. Our proposed approach solves the problems simultaneously through an iterative technique, which also garners computational efficiencies by leveraging the redundancies across the related problems. We demonstrate analytically that our method provides a substantial complexity reduction, which is further validated by our results on real-world datasets.
1 Introduction
Regularized logistic regression is a standard classification technique for predicting a binary label from a set of features. It has been used successfully across a wide array of applications. Since it is capable of not only predicting the class from the data, but also the posterior class probabilities, it has particularly become popular in the medical and life sciences fields (Hosmer and Lemeshow 2000, and references therein).
While the parameter estimates in regularized least squares regression, such as ridge regression, can be computed in closed-form, logistic regression necessitates an iterative solver. The most popular technique is a variant of Newton’s method, iteratively re-weighted least squares (IRLS), which iteratively minimizes a quadratic approximation to the likelihood. This approach may be slow because it requires computing the inverse of a Hessian matrix. This step scales poorly with problem size unless the Hessian has special structure, such as being sparse or banded.
Many papers have addressed this computational problem. For example, cyclic coordinate descent (Zhang and Oles 2001, Genkin et al. 2007) avoids inverting the Hessian matrix by updating the estimates one coordinate at a time. The technique of Komarek and Moore (2003,2005) also avoids computing the inverse of the Hessian by solving each Newton step by a conjugate gradient method. Bound optimization techniques (Böhning and Lindsay 1988, Krishnapuram et al. 2005) complete a sequence of Newton steps with only a single Hessian matrix inversion.
Although these approaches have been very successful at improving the efficiency of logistic regression, real-world applications rarely consist of solving only a single problem. Instead, an entire machine learning application involves solving hundreds or even thousands of regression problems over the course of model selection and significance testing. For example, model selection strategies based on cross-validation estimate prediction accuracy by re-training the classifier on different splits of the data. Additionally, assessing the statistical significance of a chosen model involves running a nonparametric test that trains the classifier on different permutations of the data. These model fits are computed sequentially in a loop, or in parallel if a computing cluster is available.
For large problems, cross-validation and significance testing can be very expensive endeavors, even with efficient logistic regression solvers. In the context of cross-validation, this has sometimes been addressed by deriving upper bounds on generalization error that are fast to compute from the training data (Zhang 2003, Cawley and Talbot 2004). These bounds, however, can be loose and may greatly overestimate prediction error. For regularized least squares (ridge regression), it is well known that leave-one-out error can be computed exactly from one model fit to the training data (Rifkin and Lippert 2007). This special case, unfortunately, does not extend to logistic regression.
With these considerations in mind, this paper addresses the computational problems of logistic regression from a different perspective. Instead of learning each classifier’s parameters tabula rasa, we solve the multitude of problems simultaneously, and leverage the shared structure to improve computational performance. Our method is simple to implement and is based on the well-established theory of stationary iterative methods for solving linear systems of equations. It can be applied to a large number of applications, including K-fold cross-validation and classifier significance testing through permutation tests.
In Section 2 we introduce the necessary preliminaries and outline the details of our approach, along with a complexity analysis that highlights its merits. We then offer a summary of applications of our method in Section 3. Finally, we validate our approach on real-world datasets in Section 4 and conclude with potentials for future work in Section 5.
2 Methods
2.1 Preliminaries
Let a classification dataset be given by , with features xi ∈ ℝD and binary labels yi ∈ {0, +1}. Logistic regression attempts to find a separating hyperplane in feature space, parameterized by normal vector w = (w1, …, wD) ∈ ℝD, that separates the two classes. The posterior label probability is modeled as:
| (1) |
We assume for simplicity that the bias is estimated by incorporating a constant regressor into the feature space so that wD is the bias term. We will denote by μ(xT w) = p(y = 1|x, w). Also, let X = [x1, x2, …, xN] be the data matrix.
For logistic regression, the negative log-likelihood is:
| (2) |
In many cases, the maximum-likelihood estimator may overfit to the training data. To reduce overfitting, penalized likelihood methods based on l2-regularization seek to minimize a version of:
| (3) |
The matrix L can be any symmetric positive semi-definite (PSD) matrix, in which case J(w) is a convex function. For example, L could be a graph Laplacian matrix (Belkin et al. 2004), or the identity matrix.
Newton-type methods optimize for w by iteratively minimizing a quadratic approximation to J(w). The log-likelihood is approximated locally around a current estimate w(t) by a quadratic function
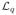 (w, w(t)) given by (ignoring terms independent of w):
(w, w(t)) given by (ignoring terms independent of w):
| (4) |
where H and ∇
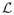 (w(t)) are the Hessian matrix and gradient of
(w(t)) are the Hessian matrix and gradient of
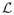 (w) evaluated at w = w(t):
(w) evaluated at w = w(t):
| (5) |
| (6) |
Here, we have overloaded the notation μ(XT w(t)) to denote a column vector whose ith entry is given by . Also, the Hessian changes on each iteration based on the diagonal matrix R, whose diagonal entries contain the current variances of the model fits:
| (7) |
Substituting
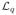 (w, w(t)) into (3) gives us our objective to minimize at each iteration:
(w, w(t)) into (3) gives us our objective to minimize at each iteration:
| (8) |
Equating the gradient of Jq(w) to zero, we obtain:
| (9) |
This procedure repeats until convergence.
2.2 Simultaneous Logistic Regression
The update equation in (9) amounts to solving a linear system of equations. In many situations, including cross-validation and permutation testing, this computation is performed repeatedly for a set of P different problems. Despite this, there is frequently a large amount of shared structure across the P problems that is otherwise ignored. We propose an efficient method to compute the update in (9) simultaneously across a set of P related problems. Specifically, our approach simultaneously solves P linear systems of the form:
| (10) |
where the matrix Ap is of the form:
| (11) |
and Rp is a diagonal matrix with nonnegative entries as in (7). Note that (9) can be put into the form of (10) and (11) by taking C = 2λL and . Here, we use the subscript p on a variable to emphasize that it depends on the problem p ∈ {1, …, P}. Without the subscript, the variable is assumed to be shared across the P problems.
There are many ways to effectively solve related systems of linear equations such as (10). For example, given a Cholesky factorization for A1, which enables the linear system to be solved via back substitution, techniques exist to update the factorization for other Ap, p > 1 (Golub and Van Loan 1996). However, these methods are geared for situations in which the matrices are related by very low rank perturbations, such as rank-one changes of the form for some column vector up. The difficulty with (10) is that since the model fits are in general different across the P problems, the weights in the diagonal entries of Rp are not shared across the problems. As a result, the variability in Ap across the P problems cannot be modeled simply as a low-rank perturbation.
Instead, we focus on stationary iterative methods for solving a linear system Ax = b because of their simplicity to implement, and efficiency when designed appropriately. Throughout, we assume that A is invertible. In this case, stationary methods define a sequence of iterates of the form (Young 1971):
| (12) |
where G is typically called the iteration matrix.
Two important issues involving these methods are: (a) does the sequence in (12) converge; and (b) consistency – when the sequence does converge, does it converge to the unique solution A−1b? Fortunately, these questions can be easily answered when the iteration matrix G takes a special form. Specifically, given an additive splitting A = M − N, the sequence (12) is consistent provided the iterates take the form:
| (13) |
Moreover, the sequence will converge from any initialization x(0) iff the spectral radius of G = M−1N is less than one, ρ(G) < 1 (Young 1971). The rate of convergence also depends heavily on the spectral radius. In particular, an estimate, K̃, of the number of iterations K required to reduce the norm of the error by a factor ζ is given by (Hageman and Young 1981):
| (14) |
Stationary iterative methods are most often used to solve a single linear system efficiently. In these cases, M is taken to have a special structure so that Mx = y can be solved very efficiently. For example, the Jacobi iteration takes M to be the diagonal portion of A, while the Gauss-Seidel iteration takes M to be the lower-triangular portion of A.
Our approach, however, is focused on solving many related problems efficiently, rather than one individual problem. As a result, we are willing to spend some time towards solving Mx = y, as long as this solution can then be applied to all of the P problems to be solved. Thus, we produce an additive splitting in which the M matrix is shared across the P problems. Given a template matrix M = XRXT + C, for some diagonal matrix R, we define our splittings as:
| (15) |
| (16) |
and the iterations are defined as:
| (17) |
Since the iterations in (17) are based on an additive splitting, we are assured of consistency. For convergence, however, we must consider the spectral radius of Gp = M−1Np for each p = 1, …, P. In this regard, we have the freedom to design the diagonal matrix R to ensure convergence for all p.
Since M and Np are both symmetric matrices, we know that the eigenvalues of M−1Np are all real. Moreover, the eigenvalues of M−1Np are equal to the generalized eigenvalues λMx = Npx. Thus, ρ(Gp) = maxx |xT Npx|/|xT Mx|. In the following, we assume that C is positive definite, with γmin > 0 its minimum eigenvalue. Also, let σmax > 0 be the maximum singular value of X. Then we can bound ρ(Gp) as follows:
| (18) |
| (19) |
| (20) |
| (21) |
To ensure that ρ(Gp) < 1, it is sufficient to design the template weighting matrix R so that, for each p,
| (22) |
for all unit vectors w. This can be satisfied by taking
| (23) |
the element-wise maximum. In this case, both R and R – Rp are PSD for all p, and (22) reduces to:
| (24) |
which is true since Rp is a PSD matrix, and the right-hand-side of (24) is strictly negative.
2.3 Connection to Bound Optimization Methods
Bound optimization methods are EM-style algorithms that utilize an upper bound on the Hessian (Böhning and Lindsay 1988), (Krishnapuram et al., 2005). For logistic regression, the bound arises from the fact that the diagonal entries of R in (7) are limited to the range [0, , and so upper bounds the Hessian in (6) in the sense that H̃ – H is PSD (denoted H̃ ≽ H). From this, a sequence of quasi-Newton steps are taken, with H replaced by H̃.
Thus, applying this technique simultaneously to P problems amounts to solving a set of P linear systems of equations of the form Awp = Xmp, where A = H̃ + C. Since A is constant through the iterations, the entire sequence of quasi-Newton steps may be taken with only a single inversion computation.
A connection to our approach may be made by the fact that the template matrix computed at each iteration also serves as an upper bound to the Hessian, since taking R as in (23) ensures that XRXT ≽ XRpXT for each p. Thus, our approach may be interpreted as initializing each Newton step from the approximate solution given by the bound optimization, followed by a sequence of iterates in (17) that refines the estimates to the true Newton step solution.
The refinement stage can have a significant improvement in convergence properties: while our system implements the true Newton step, which has quadratic convergence properties in general, the bound optimization method can only guarantee linear convergence (Böhning and Lindsay 1988). Moreover, we show in the next section that the refinement iterates may be computed efficiently.
2.4 Complexity Analysis
In this section, we analyze the computational complexity of each Newton step for our proposed approach and compare it with the brute-force inversion method, which we refer to as the direct method. The key variables in this analysis are the number of features, D, the number of training examples, N, the number of problems to be solved, P, and for our approach, the number of iterations required for (17) to converge, K.
The direct approach requires computing XRpXT, for each p = 1, …, P, which is O(DN + D2N). Subsequently, the inversion step of solving Apwp = Xmp is O(D3 +2D2). This results in an overall complexity for the direct method of:
| (25) |
Before detailing the complexity of our approach, we first show that the updates in (17) can be computed in one matrix multiplication across all P problems. Let the D × N matrix Y be the solution to MY = X, where M is the template matrix and X is the data matrix. Also, let W (k) be the D × P matrix whose pth column is equal to the regression weight estimates for problem p at iteration k, . Finally, denote R̂ as the N × P matrix whose pth column is the diagonal entries of R – Rp, and B the matrix whose pth column is equal to Y mp. Then W (k+1) can be expressed as:
| (26) |
where ∘ denotes the elementwise Hadamard product.
We are now equipped to compute the complexity of our approach. Solving for Y from MY = X requires O(D3 + 2D2N) operations, and computing B is O(DNP). The update in (26) requires O(2P DN + P N), and is computed K times. Thus, the overall complexity of our proposed approach is given by:
| (27) |
As is clear from (14), the number of iterations K for the linear system solver is a balance between the spectral radius of the iteration matrices M−1Np, and the initial error. K does not, however, tend to grow with D or N. Thus, in comparing (25) and (27), we see that while the direct method has two cubic terms D2N and D3 that grow with P, our proposed approach scales much better with problem size, having only at most second order terms that grow with P.
Pseudo-code for the algorithm is provided in Algorithm 1. In the following two sections, we discuss two modifications that further improve upon the complexity in (27). The first is based on continuation methods and has the effect of decreasing the number of inner loop iterations K. This is followed by a result in Section 2.6, which is applicable in high-dimensional feature spaces and exploits the discrepancy between the number of features D and the rank of the data matrix. This has the effect of replacing D in (27) with s = rank(X).
Algorithm 1.
Simultaneous Newton Steps
| Given data matrix X and regularization matrix C | |
| Given Rp, mp for each problem p = 1, …, P | |
| Initialize and assemble as columns into W (0) | |
| Assemble diagonals of Rp as columns into R̂ | |
| Compute R as row-wise maximum of R̂ | |
| Compute template matrix M = XRXT + C | |
| Solve MY = X for Y | |
| Compute B, whose pth column is equal to Y mp | |
| for k = 1, … do | |
| Compute update correction: | |
|
| |
| if maxj ||(W (k+1) – W(k))T ej||2 < tol then | |
| K = k | |
| break | |
| end if | |
| end for | |
| The pth column of W (K) contains the solution to Apwp = Xmp, where Ap = XRpXT + C |
2.5 Continuation Methods
The regularization matrix C in (11) generally incorporates a parameter λ that trades-off the likelihood fit with the regularization. For example, the ridge penalty takes C = 2λI. Since this parameter is not know a-priori, it is often selected by a cross-validation technique that fits the model for a range of λ values.
Similar to (Friedman et al. 2010), requiring fits for multiple λ values can be used to our advantage by a warm-starting procedure, in which results from larger λ values are used to initialize fits for successively smaller λ values. The intuition is that the higher regularization further constrains the problem, making it easier to solve. The solution can then be used to better initialize the more challenging (smaller λ) problems.
In general, the larger λ problems are easier to solve in that they require fewer Newton steps. In the context of the proposed algorithm though, there is a secondary advantage in that for larger λ values, each Newton step is more efficient because the iterative solver (17) tends to require fewer iterations to converge. The reasoning is twofold. First, the spectral radius of the iteration matrix decreases for higher regularization. To see this, let C(1), C(2), …, C(M) denote the regularization matrices in (11) for a decreasing sequence of regularization parameters λ1 > λ2 > … > λM = 0. Note that since C(k) = λkC, for some base PSD matrix C, we know that the eigenvalues of C(k) grow proportionally with λ. From this, it is easy to see that the spectral radius of the iteration matrix G(k) = (XRXT + C(k))−1Np tends to decrease as k increases. The second reason fis that higher regularization acts to shrink the estimates, so that there is decreased variability in the model fits. As a result, there tends to be less variability in the entries of the Rp matrices, in which case the template matrix M serves as a better model for the Hessian of all P problems. These intuitions are confirmed in the results.
Additionally, we see from (14) that the number of iterations K also depends on the accuracy of our initialization. Thus, warm-starting can significantly improve convergence for smaller λ values by decreasing the initial approximation error even though the spectral radius of the iteration matrix is larger.
2.6 Exploiting low-rank data matrices
Further computational improvements can be made if there is a large disparity between the number of features in the dataset, D, and the rank of the data matrix, s = rank(X), (e.g., when N < D). In effect, (10) can be transformed from systems of D equations into systems of s equations. For this, we require a low-rank factorization of the data matrix, X = QZ, with Q ∈ ℝD×s having orthonormal columns and Z ∈ ℝs×N. The result follows from the next 2 lemmas, whose proofs are given in supplementary material.
Lemma 1
The solution wp to Apwp = Xmp satisfies wp ∈ range(C−1Q).
Lemma 2
Let be a matrix with orthonormal columns that is a basis for range([Q, C−1Q]). Note that W has at most s columns. Then the solution wp to Apwp = Xmp can be computed by first solving a linear system of s equations:
| (28) |
where
| (29) |
| (30) |
| (31) |
Then wp can be obtained from w̃p by:
| (32) |
Since (28) takes the same form as (10), we may implement our proposed algorithm to solve (28). This yields significant computational savings when s < D. Specifically, in the complexity equation of our approach in (27), all occurrences of D are replaced with s.
3 Applications
3.1 Permutation Testing
Permutation tests are a popular nonparametric technique for estimating classifier significance (Ojala and Garriga 2010). Here, a hypothesis test is formulated to see whether or not a meaningful relationship between the features and the class labels has been identified by the classifier. A distribution of classifier accuracy under the null hypothesis that no relationship exists is computed by re-training the classifier on new datasets in which the labels have been permuted across instances. This allows the derived classifier accuracy to be assigned a p-value of statistical significance.
Permutation tests fit naturally into our method. Since only the binary labels y change in each permutation problem p = 1, …, P, the data matrix X is shared across the P problems. As a result, each permutation p can be written in the form (10) for some Rp and mp.
3.2 Cross-validation
For K-fold cross-validation, the logistic regression model is trained on K different subsets of the training data. At first glance, it appears that the data matrix is not shared across problems, because even though there will be a large amount of overlap in training data across folds, each fold still contains a different subset.
This technicality is overcome by a small modification. For a particular fold p of the data, let hp index the training instances that are excluded from the training data. Expressing this fold’s Newton step in the form of (10) simply involves zeroing out the hp diagonals of Rp, as well as the hp indices of mp. With this modification, the full data matrix X can be shared across all K folds.
Thus, K-fold cross-validation fits into our approach given the slight modification mentioned above, with the problem size P equal to the number of cross-validation folds. For leave-one-out cross-validation with P = N, our approach yields significant savings when there are a large number of trials. However, the true value of our approach is not really apparent if the number of folds is small, as in 10-fold cross-validation. As noted in Kohavi (1995), the cross-validation error depends on the random split of the data and may be highly biased for small K. To minimize this bias, it is best to average cross-validation error over multiple random K-fold splits of the data. In this case, our approach is again valuable, even if K is small.
4 Results
We applied our algorithm to a number of real-world datasets and benchmarked its speed against the direct method of inverting the Hessian matrix independently for each problem p. To enable a fair comparison, the convergence tolerance used in our algorithm was set very conservatively at tol = 1 × 10−11. In all analyses, the regularization matrix was taken to be a scaled identity matrix, with the last diagonal entry set to zero. Zeroing out the last entry prevents shrinkage of the bias term. The amount of regularization is controlled by the parameter λ.
The MNIST handwritten digits database (LeCun et al. 1998), is a well established machine learning dataset. The data consist of 6, 000 grey-level 28 × 28 images for each digit 0 through 9. Two binary classification datasets were derived from this database – discriminating digit 0 from digit 1, and the more challenging case of distinguishing digits 4 and 9. Features corresponded to pixel intensities, with D = 282 + 1 = 785.
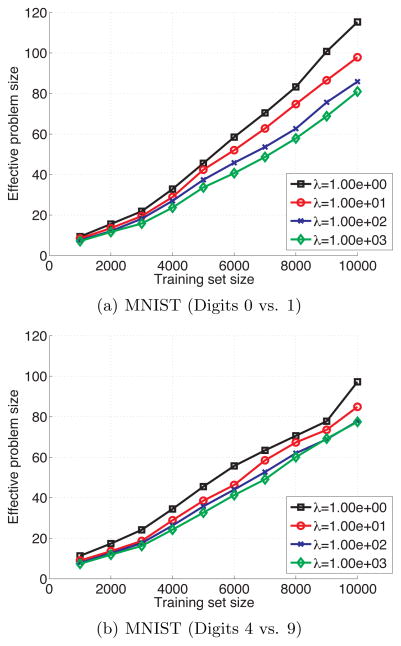
Leave-one-out classification was performed on subsampled datasets of size 1, 000 up to 10, 000, in increments of 1, 000. For each training set size, we compared the computation times of our approach and the direct method by computing the number of leave-one-out runs that could be computed by the direct method in the same amount of time that was required by our method to complete the full leave-one-out cross-validation set. We call this quantity the effective problem size of our method, and the ratio of P (training set size) to effective problem size gives the overall speedup factor. Plots of effective problem size are given in Figure 1. It is clear that the computational speedup is consistently around 100× for both MNIST datasets and values of the regularization parameter λ.
Figure 1.
Leave-one-out cross-validation (P = training set size) using the proposed method compared against the direct IRLS method for the MNIST datasets and various training set sizes. The effiective problem size represents the number of problems that can be solved by the direct method in the same amount of time as the entire LOO set for the proposed method. For example, LOO cross-validation by our proposed approach on a training set size of P = 2000 may be computed in the same time as approximately P = 20 folds by the direct method, resulting in a speedup of 100×.
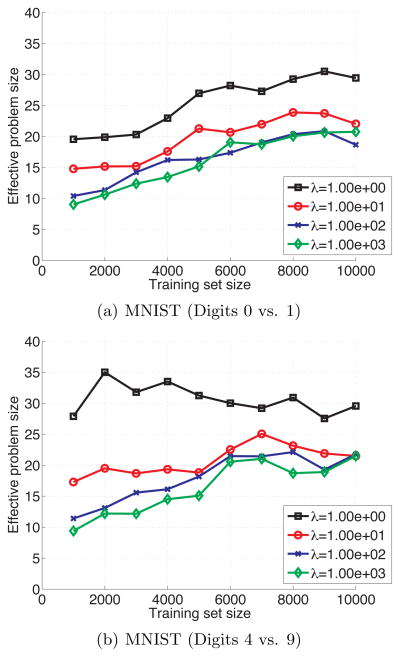
We also benchmarked our algorithm on the MNIST data for the case of 10-fold cross-validation repeated over 100 random splits, so that P = 1000 total problems. Similar to the leave-one-out analysis, we again plot effective problem size against the training set size for various values of the regularization parameter. In this case, P is constant over training set size, so the speedup factor is the ratio of 1000 to effective problem size. Plots are given in Figure 2. In this case, speedup ranges from 30× to 100×. A contributing factor for the reduced speedup, as compared to the leave-one-out analysis, is due to the fact that there is more variability in the model fits for 10-fold cross-validation than leave-one-out cross-validation.
Figure 2.
10-fold cross-validation using the proposed method for the MNIST datasets and various training set sizes. Each cross-validation run was repeated over 100 random splits, resulting in P = 1000 total problems. The effective problem size represents the number of problems that can be solved by the direct method in the same amount of time as the P problems for the proposed method. Here, the ratio of 1000 to the effective problem size gives the computational speedup, which varies between 30× to 100×.
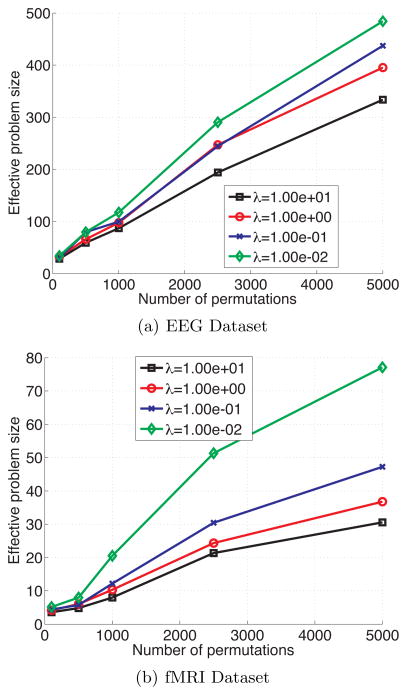
We also applied our technique to classifier significance testing problems on electroencephalography (EEG) and functional MRI (fMRI) datasets collected during an auditory oddball detection task (Goldman et al. 2009). Permutation tests were used to evaluate performance of oddball vs. standard prediction performance of classifiers derived separately from the EEG and fMRI data. There were a total of N = 374 examples, with the EEG feature space corresponding to the measured voltages from 43 bipolar electrodes averaged over a 50ms window (D = 44), while for the fMRI classifier the feature space was the BOLD response of 300 voxels in auditory cortex (D = 301).
Figure 3 plots the effective problem size against the number of permutation tests P for both the EEG classifier and the fMRI classifier and various regularization values λ. For the EEG classifier, the computational improvement is ~ 10×, while for the fMRI classifier, the improvement is ~ 100×. The more dramatic improvement for the fMRI case is due to the higher feature space dimension (D = 301 vs. D = 44).
Figure 3.
Permutation testing using the proposed method compared against the direct IRLS method for the EEG and fMRI datasets and various numbers of permutations P. The effective problem size represents the number of permutations that can be solved by the direct method in the same time as the entire set of P permutations by our proposed approach. Here, the ratio of number of permutations P to the effective problem size gives the computational speedup.
Finally, we ran an additional analysis on the MNIST dataset to test the effectiveness of applying a continuation method to our approach, as detailed in Section 2.5. Here we compared the overall time required to perform leave-one-out cross-validation for regularization values λ ∈ {1, 10, …, 1e10} between initializing each regularization from w = 0, and warm starting from the results of the next highest regularization value. This comparison was performed across a variety of training set sizes. The continuation method provided an additional improvement of ~ 1.5×, and this was consistent across training set sizes.
5 Conclusion and Future Work
This paper addresses the computational problem of l2-regularized logistic regression that is commonly encountered in model selection and assessment, where the solution to a large number of related problems must be computed. We derive a principled iterative algorithm that is simple to implement and efficiently solves all of the problems simultaneously. We show that this results in a significant improvement in complexity over the direct approach, and we demonstrate this empirically on real-world datasets.
There are a number of avenues of future research related to this algorithm. The first involves extending this algorithm to fitting other regression problems. Logistic regression is one example of a generalized linear model (GLM), which allows for very flexible modeling assumptions. Since all GLM’s can be fit almost completely analogously to the IRLS procedure of logistic regression, generalizing the algorithm to all GLM’s and testing its validity is a natural next step.
Finally, the current version of the algorithm is limited to l2-regularized problems, which excludes the sparsity-inducing LASSO regularizers. Extending this algorithm to l1 and mixed l1-l2 regularizers, such as the elastic net, is another important open question.
Supplementary Material
Acknowledgments
The authors acknowledge Jennifer Walz for providing the EEG and fMRI datasets used in the results. This work was supported by National Institutes of Health grant R01-MH085092.
Footnotes
Appearing in Proceedings of the 15th International Conference on Artificial Intelligence and Statistics (AISTATS) 2012, La Palma, Canary Islands.
Contributor Information
Bryan Conroy, Email: bc2468@columbia.edu, Columbia University New York, NY.
Paul Sajda, Email: psajda@columbia.edu, Columbia University New York, NY.
References
- Belkin M, Matveeva I, Niyogi P. Regularization and Semi-supervised Learning on Large Graphs. In: Shawe-Taylor J, Singer Y, editors. Learning Theory, 17th Annual Conference on Learning Theory. COLT; Banff, Canada: 2004. [Google Scholar]
- Böhning D, Lindsay BG. Monotonicity of Quadratic Approximation Algorithms. Annals Institute of Statistical Mathematics. 1988;40(4):641–663. [Google Scholar]
- Cawley GC, Talbot NLC. Efficient model selection for kernel logistic regression. Proceedings of the 17th International Conference on Pattern Recognition (ICPR); Cambridge, UK. 2004. [Google Scholar]
- Friedman J, Hastie T, Tibshirani R. Regularization Paths for Generalized Linear Models via Coordinate Descent. Journal of Statistical Software. 2010;33(1):1–22. [PMC free article] [PubMed] [Google Scholar]
- Genkin A, Lewis DD, Madigan D. Large-Scale Bayesian Logistic Regression for Text Categorization. Technometrics. 2007;49(3):291–304. [Google Scholar]
- Goldman RI, Wei CY, Philiastides MG, Gerson AD, Friedman D, Brown TR, Sajda P. Single-trial discrimination for integrating simultaneous EEG and fMRI: Identifying cortical areas contributing to trial-to-trial variability in the auditory oddball task. NeuroImage. 2009;47(1):136–147. doi: 10.1016/j.neuroimage.2009.03.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golub GH, Van Loan CF. Matrix Computations. Baltimore, MD: Johns Hopkins University Press; 1996. [Google Scholar]
- Hageman LA, Young DM. Applied Iterative Methods. Mineola, NY: Dover Publications; 1981. [Google Scholar]
- Horn RA, Johnson CR. Matrix Analysis. New York, NY: Cambridge University Press; 1990. [Google Scholar]
- Hosmer DW, Lemeshow S. Applied Logistic Regression. USA: John Wiley & Sons, Inc; 2000. [Google Scholar]
- Komarek PR, Moore AW. In: Bishop CM, Frey BJ, editors. Fast Robust Logistic Regression for Large Sparse Datasets with Binary Outputs; Proceedings of the 9th International Workshop on Artificial Intelligence and Statistics (AISTATS); Key West, Florida. 2003. [Google Scholar]
- Komarek P, Moore A. CMU Tech Report CMU-RI-TR-05-27. Robotics Institute, Carnegie Mellon University; 2005. Making Logistic Regression A Core Data Mining Tool: A Practical Investigation of Accuracy, Speed, and Simplicity. [Google Scholar]
- Kohavi R. A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection. Proceedings of the 14th International Joint Conference on Artificial Intelligence; Montreal, Quebec. 1995. [Google Scholar]
- Krishnapuram B, Carin L, Figueiredo MAT, Hartemink AJ. Sparse Multinomial Logistic Regression: Fast Algorithms and Generalization Bounds. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2005;27(6):957–968. doi: 10.1109/TPAMI.2005.127. [DOI] [PubMed] [Google Scholar]
- LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proceedings of the IEEE. 1998;86(11):2278–2324. [Google Scholar]
- Ojala M, Garriga GC. Permutation Tests for Studying Classifier Performance. Journal of Machine Learning Research. 2010;11:1833–1863. [Google Scholar]
- Rifkin RM, Lippert RA. Notes on Regularized Least Squares. MIT Computer Science and Artificial Intelligence Laboratory (CSAIL) Technical Report 2007 [Google Scholar]
- Young DM. Iterative solution of large linear systems. Mineola, NY: Dover Publications; 1971. [Google Scholar]
- Zhang T, Oles F. Text Categorization Based on Regularized Linear Classifiers. Information Retrieval. 2001;4:5–31. [Google Scholar]
- Zhang T. Leave-One-Out Bounds for Kernel Methods. Neural Computation. 2003;15(6):1397–1437. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.