Electrophoretic Measurements of Lipid Charges in Supported Bilayers

Abstract

While electrophoresis in lipid bilayers has been performed since the 1970’s, the technique has until now been unable to accurately measure the charge on lipids and proteins within the membrane based on drift velocity measurements. Part of the problem is caused by the use of the Einstein-Smoluchowski equation to estimate the electrophoretic mobility of such species. The source of the error arises from the fact that a lipid head group is typically smaller than the Debye length of the adjacent aqueous solution in most electrophoresis experiments. Instead, the Henry equation can more accurately predict the electrophoretic mobility at sufficient ionic strength. This was done for three dye-labeled lipids with different sized head groups and a charge on each lipid of −1. Also, the charge was measured as a function of pH for two titratable lipids that were fluorescently labeled. Finally, it was shown that the Henry equation also has difficulties measuring the correct lipid charge at salt concentrations below 5 mM, where electroosmotic forces are more significant.

Introduction

The lipid bilayer is the gateway to the cell. Indeed, a variety of proteins, small molecules and ions that interact with cells need to pass through this interface. Developing tools that can reveal molecular-level information about such interactions is crucial to understanding membrane biophysics. Supported lipid bilayer (SLB) electrophoresis can be useful for this purpose. Bilayer electrophoresis was first used to manipulate concanavalin A on the surface of muscle cells in the 1970s.¹ Over the last two decades, SLB electrophoresis has been employed to separate and focus numerous lipids and membrane-bound proteins, as well as polymers and lipid vesicles attached to SLBs.^2–13 It has also been used to determine the charge on streptavidin molecules bound to biotinylated lipids within the membrane.⁵ Curiously, however, this method has usually underestimated the magnitude of the charge on non-neutral lipids and proteins.

In SLBs, charged species undergo a random two-dimensional walk when the membrane is in the liquid crystalline phase. When placed in an electric field, these components will also migrate electrophoretically. The drift velocity (V_D) for such species is proportional to the sum of the electroosmotic (F_{Electrosmosis}) and electrophoretic (F_{Electrophoresis}) forces acting upon them and can be described by Eq. 1.^5,7

$$V_D\propto F_{\mathit{Total}}=F_{\mathit{Electrosmosis}}+F_{\mathit{Electrophoresis}}$$ (1)

If the electroosmotic force on a charged lipid is zero, its drift velocity will be entirely the result of the electrophoretic force. In this case, the drift velocity is the product of the electrophoretic mobility, μ, and the magnitude of the applied electric field, E: ²

$$V_D=\mathrm{\mu }E$$ (2)

Drift velocity measurements of charged objects in electric fields can be used to determine the number of charges, q, on the object. In order to determine this number, the electrophoretic mobility of the object must be known. Its value for a spherical object is often calculated using the Einstein-Smoluchowski relationship (Eq. 3):^2,3,5,14

$${\mathrm{\mu }}_{ES}=\frac{\mathit{Dqe}}{kT}$$ (3)

where D is the self-diffusion coefficient (referred below simply as the diffusion coefficient) of the object, k is the Boltzmann constant, T is the temperature, and e is the fundamental unit of charge. If the diffusion coefficient of a lipid is known, Eq. 3 and Eq. 2 can be used to calculate its charge in a supported lipid bilayer. The diffusion coefficient can be measured using a variety of techniques, including fluorescence recovery after photobleaching (FRAP) or NMR.^15,16

The Einstein-Smoluchowski relationship and diffusion coefficient measurements obtained by FRAP have been employed to calculate the electrophoretic mobility of several dye labeled lipids. For example, Stelze et. al. used electrophoresis in a supported bilayer in the early 1990s to measure the drift velocity of a dye-labeled anionic lipid, NBD-DPPE, and a cationic probe, D291.² From their measurements, the authors computed μ_ES and found that the calculated value for NBD-DPPE and D291 was 70% and 80%, respectively, of the expected value. In another set of experiments, Han et al. used the shape of the concentration gradient from fluorescently labeled lipids that were electrophoretically forced against a barrier to determine the electrophoretic mobility of Texas Red DHPE.⁵ They found that the measured electrophoretic mobility was 60% of the value predicted by the Einstein-Smoluchowski relationship. The zeta potential of streptavidin bound to biotinylated lipids was also determined in these steady state measurements. The protein’s measured zeta potential was 70% of the expected value. By contrast, Zhang and Hill showed that the electrophoretic mobility of NBD-DOPE in SLBs containing lipopolymers is actually about 20% higher than expected based on the Einstein-Smoluchowski equation.¹² In this unique case, it was suggested by the authors that the enhanced electrophoretic mobility of NBD-DOPE could be explained by a chemical association between the dye-labeled lipid and the co-migrating charged lipopolymers. It may also be possible that a reduction of the dielectric constant in the polymer layer was responsible for the enhanced mobility.

In the work of Stelze and Han, electroosmotic forces acting on the charged lipids were invoked to explain the attenuation in the measured mobility compared with the expected values for NBD-DPPE and Texas Red DHPE. Sometimes, a correction factor, α, is introduced.¹⁷ The electrophoretic mobility is multiplied by this factor in order to maintain consistency with the expected charge value.¹⁷ As we will demonstrate, it is possible to determine the charge on lipids in SLBs from their electrophoretic mobilities under some circumstances without invoking an electroosmotic contribution, if the electrophoretic mobility is calculated using the Henry equation. In fact, the Einstein-Smoluchowski relation should only hold for objects whose radius is much smaller than the Debye length.¹⁸ Otherwise, the Henry equation more accurately computes these values.^18,19 Indeed, the electrophoretic mobility of a lipid is predicted to change as the size of its lipid head group is modulated according to the Henry equation.

Herein, we show the validity of the Henry equation by experimentally demonstrating that the electrophoretic mobilities of lipids vary with head group size. We also vary the ionic strength of the buffer solutions employed in these measurements to directly show the influence of electroosmotic forces present on the charged lipids. Finally, we determine the charge as a function of pH for two titratable and charged fluorescently-tagged lipids, ortho- and para-Texas Red DHPE. These final experiments demonstrate that the pK_A of the sulfonamide moiety on the dye is far lower in the case of ortho-Texas Red compared with the para- isomer.

Methods

Materials

Fibrinogen was purchased from Sigma (St. Louis, MO). 1-Palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) and 1-oleoyl-2-12-[(7-nitro-2-1,3-benzoxadiazol-4-yl)amino]dodecanoyl-sn-glycero-3-phosphoserine, (ammonium salt) (NBD-PS) were purchased from Avanti Polar Lipids (Alabaster, AL). Texas Red 1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine, triethylammonium salt (Texas Red DHPE) was purchased from Life Technologies (Grand Island, NY). Poly(dimethylsiloxane) (PDMS) was obtained from Dow Corning (Sylgard, silicone elastomer-184).

Vesicle Formation

Small unilamellar vesicles of various chemical compositions were prepared using a combination of the vesicle extrusion and freeze-thaw methods.^20,21 First, lipids were mixed in chloroform in the appropriate molar ratio. The chloroform was then evaporated under a stream of nitrogen. To remove any residual chloroform, the lipids were placed in a vacuum dessicator for at least two hours. They were then rehydrated in a phosphate buffered saline (PBS) solution containing 10 mM sodium phosphate and 100 mM NaCl. The pH of the solutions was adjusted to 7.5 by the addition of a small amount of HCl. The lipids were diluted with buffer solution to a concentration of 1 mg/ml. The sample was then put through a total of 10 freeze-thaw cycles and extruded through a polycarbonate filter (Whatman) with 100 nm pores. Dynamic light scattering measurements demonstrated that the mean vesicle size was ~110 nm ± 10 nm (90Plus Particle Size Analyzer, Brookhaven Instrument Corp., Holtsville, NY).

Separation of ortho and para-Texas Red DHPE

Ortho and para-Texas Red DHPE were separated from each other using thin layer chromatography (TLC). To accomplish this, Texas Red DHPE in chloroform was spotted onto a TLC plate using a glass capillary tube. The spotted plate was then placed into a development jar and eluted with ethanol. Texas Red labeled phospholipids were recovered from the TLC plate by carefully scraping the separated bands with a razor blade and re-suspending the material in ethanol to extract the lipids from the silica surfaces. The mixture was centrifuged at 13,500 RPM (5415, Eppendorf) for 5 minutes and the supernatant was collected. This procedure was repeated five times or until no Texas Red phospholipids could be visually observed in the pellet. Mass spectroscopy confirmed that the two bands were indeed the Texas Red DHPE isomers.

Cleaning Glass Substrates

Supported lipid bilayers were formed on clean and annealed glass substrates (Fisher Scientific Co., Pittsburgh, PA). To prepare the cover slips, they were heated in a near boiling 1:7 by volume mixture of 7X^™ cleaning solution and purified water. The water was obtained from an Ultrapure Water System (Thermo Scientific Barnstead Nanopure Life Science, Marietta, OH). After 2 hours, the cover slips were removed and rinsed with copious amounts of purified water and dried under flowing nitrogen gas. The cleaned glass was then annealed at 530 °C for five hours.

Fibrinogen Patterning and SLB Formation

Fibrinogen was patterned on individual glass cover slips using a PDMS stamping method developed previously.²² The purpose of the fibrinogen patterns was to create barriers between supported lipid bilayer patches that were fused to the adjacent bare glass portions of the substrate (Figure 1). The first step in the process was to mix the PDMS monomer and cross-linker (Sylgard 184, Dow Corning Corporation, Midland MI) in a 9:1 mass ratio. This mixture was degassed under vacuum for 1.5 hours and then poured onto a glass master that was patterned with ten 900 μm wide parallel lines that were each 1 cm long and separated from one another by 600 μm spacers. The master was prepared using standard HF etching techniques.²³ Upon removal from the glass master, the nascently produced PDMS stamp was washed with ethanol and water. Next, the stamp was immersed in a 1 mg/ml solution of fibrinogen in purified water. This led to the formation of an adsorbed protein layer on the surface of the polymer (Fig. 1A).²² After ~20 minutes, the stamp was removed from the solution and washed thoroughly with purified water. Excess water was removed by blowing nitrogen over the surface. The PDMS mold was then stamped onto a glass cover slip, taking care to ensure good contact between the glass and PDMS stamp (Fig. 1B). After 5 minutes, the stamp was removed, leaving a striped pattern of protein molecules behind on the surface (Fig. 1C). A 1.0 mg/ml vesicle solution was then introduced above the protein-patterned glass substrate and allowed to incubate for 20 minutes (Fig. 1D). This formed a supported lipid bilayer via the vesicle fusion method.²⁴ Finally, excess vesicles were washed away with copious amounts of purified water (Fig. 1E). A top-down view of the patterned bilayer is shown in Fig. 1F.

Fig. 1.

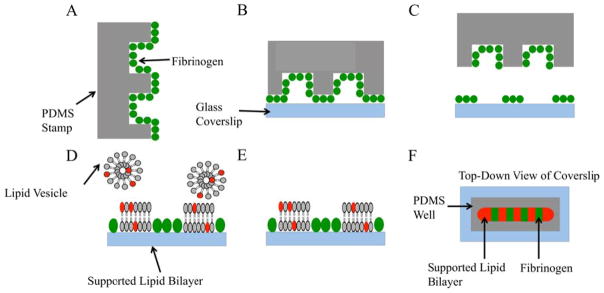
A series of schematic diagrams are shown that depicts the method used to pattern SLBs on glass coverslips. (A) A patterned PDMS mold is first soaked in a fibrinogen solution and then blown dry with nitrogen gas. (B) The mold is stamped onto a glass cover slip. (C) After waiting five minutes, the stamp is peeled away, leaving behind a layer of fibrinogen adsorbed to the glass surface. (D) A lipid vesicle solution is incubated over the fibrinogen patterned substrate. (E) Excess vesicles are removed by copiously rinsing with purified water. (F) A top-down view of the bilayer and protein patterned cover slip.

Fluorescence Recovery after Photobleaching (FRAP) and Fluorescence Imaging

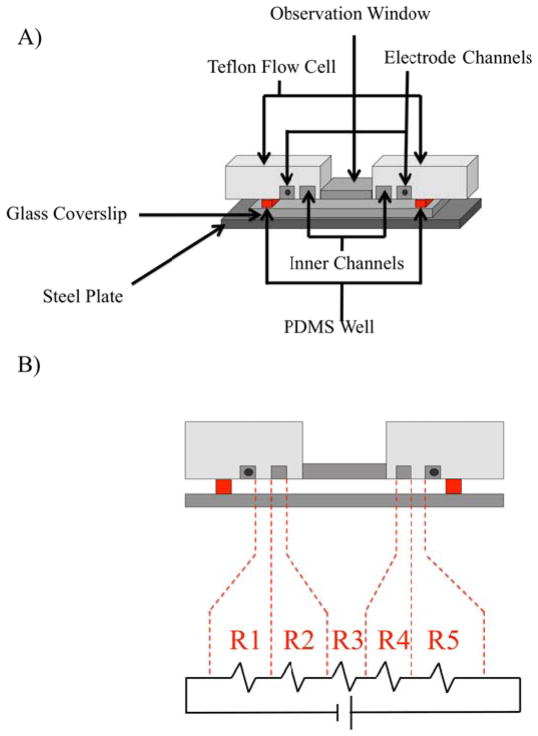
FRAP studies were performed using an inverted epifluorescence Nikon Eclipse TE2000-U microscope equipped with a 10× objective.¹⁵ The purpose of these experiments was to measure the diffusion coefficient of Texas Red DHPE and NBD-PS molecules in POPC SLBs. To do this, 568 nm light from a 2.5 W mixed gas Ar+/Kr+ laser (Stabilite 2018, Spectra Physics) was employed to bleach the dye molecules. Images of the sample were initially obtained every 3 seconds with a MicroMax 1024b CCD camera (Princeton Instruments). The same fluorescence microscopy setup was also used to image the bilayer during electrophoresis inside an assembled Teflon flow cell (Fig. 2A). In this case, the bilayer was imaged within the flow cell by placing it on an inverted microscope stage and using a 10× objective. The diffusion coefficient values obtained by FRAP were averages of six experiments on three separate bilayers. The error values reported represent the standard deviation amongst the diffusion coefficient values obtained for the six measurements. A detailed explanation for determining the self-diffusion coefficient using FRAP measurements can be found in the supporting information section.

Fig. 2.

(A) The homemade flow cell used in the electrophoresis experiments. To assemble the apparatus, a patterned SLB on a glass cover slip is seated between a steel plate and an observation window. SLB fluorescence is observed from below through the observation window by epifluorescence microscopy. (B) 5 distinct regions of resistance inside the flow cell that correspond to the cross sectional area above each location.

Electrophoresis Flow Cell

Drift velocity measurements were carried out in the home-made flow cell (Fig. 2A). The parameters and performance of the cell have been described previously.⁶ In order to obtain accurate charge values, the electric field strength (E) inside of the cell must be known to high precision. There are varying regions of resistance across this device that correspond to the cross sectional area above the surface at each position (Figure 2B).⁶ Specifically, the device can be thought of as a circuit of five resistors connected in series to a DC power supply (R1 through R5). The resistance over the bilayer, R3, accounted for 84.6% of the overall resistance. Therefore, the voltage drop in this region could be determined by dividing the voltage applied between the cathode and anode by the distance between the two inner channels and multiplying by 0.846. For the experiments described herein, the voltage drop across this region was 86.7 V/cm.

Drift Velocity Measurements

Electrophoresis measurements were carried out for time periods varying from 4 to 10 min. with membranes containing 0.1 mole % ortho-Texas Red DHPE, 0.1 mol% para-Texas Red DHPE or 1 mole % NBD-PS. The running buffer for pH 2 to pH 5 was 5 mM NaCl and 1 mM NaH₂PO₄. Near neutral pH (pH 5–9), a 1 mM Na₂HPO₄ buffer was employed. Finally, under basic conditions (10–11), 1 mM Na₃PO₄ was used.

Determining the distance traveled by ortho-Texas Red DHPE in its non-fluorescent state at high pH was accomplished by exchanging the buffer in the flow cell with a pH 5 buffer after the electric field was turned off. Exchanging the buffer in the electrophoresis device took approximately 2 minutes, which was a sufficiently short time period to prevent lipids from diffusing a significant distance in the absence of the electric field. Drift velocity measurements reported herein are averages of measurements taken from four separate lipid bilayers. The error values reported represent the standard deviations of these measurements.

The Electrophoretic Mobility of Lipids in a Lipid Bilayer

The Stokes equation (Eq. 4) relates the diffusion coefficient (D) of a spherical object of radius, a, in a medium with a known viscosity, η, to the thermal energy, kT, where k is the Boltzmann constant and T is the temperature.²⁵

$$D=\frac{kT}{6\pi \eta a}$$ (4)

Substituting Eq. 4 for D in Eq. 3 yields Eq. 5:

$${\mu }_{ES}=\frac{qe}{6\pi \eta a}$$ (5)

Eq. 5 allows us to compute the electrophoretic mobility of an object of known size in a medium of known viscosity.

The electrophoretic mobility of a spherical particle can also be defined in terms of its zeta potential (ξ) by the Helmholtz-Smoluchowski equation (Eq. 6):¹⁸

$${\mu }_{HS}=\frac{{\epsilon }_0{\epsilon }_r}{\eta }\xi$$ (6)

where ε₀ is the permittivity of free space and ε_r is the relative permittivity. The zeta potential of a spherical particle is expressed by the following equation:¹⁸

$$\xi =\frac{q{\kappa }^{-1}}{4\pi {\epsilon }_0{\epsilon }_{r}a({\kappa }^{-1}+a)}$$ (7)

where κ⁻¹ is the Debye length which is given by Eq. 8.¹⁸

$${\kappa }^{-1}={\left(\frac{{\epsilon }_0{\epsilon }_r\text{kT}}{{\mathrm{\sum }}_j{n}_j{\mathrm{q}}_{\mathrm{j}}^2}\right)}^{1/2}$$ (8)

In Eq. 8, n is the concentration of the j^th ion component and q is the charge on that ion. If the lipid head group can be modeled as a charged ball tethered to the viscous bilayer by two neutral hydrocarbon chains (Fig. 3), then Eq. 7 should be a reasonable approximation of its zeta potential.

Fig. 3.

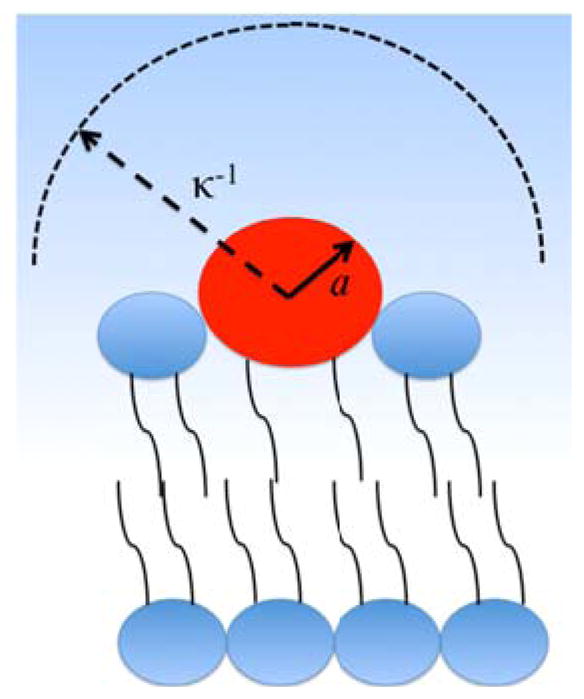
Schematic diagram of a charged lipid head group (red ball) in a lipid bilayer. The radius of the head group, a, and the Debye length, κ⁻¹, of the surrounding aqueous solution are shown for the case where aκ<1.

Eq. 6 is only valid under conditions such that the radius of the object moving electrophoretically is significantly larger than the Debye length, expressed mathematically as the product aκ ≫1.¹⁹ In this case, κ is the reciprocal of the Debye length. The radius of a lipid head group is on the order of 0.4 to 1.0 nm^26–28 and the Debye length in aqueous solutions typically employed in electrophoresis experiments vary from 3 to 10 nm. This unfortunately leads to the case where aκ< 1 or aκ ≈ 1. Fig. 3 schematically depicts the Debye length in comparison to the size of a lipid head group under this scenario. Fortunately, the Henry equation, Eq. 9, should be valid for objects at any value of aκ:¹⁹

$${\mu }_H=\frac{2}{3}\frac{{\epsilon }_0{\epsilon }_r}{\eta }\xi f(a\kappa )$$ (9)

It should be noted that f(aκ) in Eq. 9 is a smoothly varying function that has a value which approaches 1 as aκ approaches zero and a value of 3/2 at infinitely large aκ (eq. 10):²⁹

$$f(a\kappa )=1+\frac{1}{2}{\left[1+\left(\frac{25}{a\kappa [1+2e^{-a\kappa }]}\right)\right]}^{-3}$$ (10)

The Einstein-Smoluchowski relationship (Eq. 5) for a spherical particle in solution is essentially the limiting case of the Henry equation where aκ ≪1. This can be demonstrated as follows. If the particle’s radius is significantly smaller than the Debye length, the zeta potential from Eq. 7 simplifies to Eq. 11:

$$\xi =\frac{q}{4\pi {\epsilon }_0{\epsilon }_{r}a}$$ (11)

Moreover the value of Eq. 10, f(aκ), approaches 1. Therefore, plugging Eq. 11 into Eq. 9 yields the familiar Einstein-Smoluchowski relationship, Eq. 5. However, the size of a lipid head group is not usually significantly smaller than the Debye length. Under these conditions, the electrophoretic mobility calculated by the Einstein Smoluchowski relationship overestimates the electrophoretic mobility of lipids in an SLB. As such, the Henry equation should be a better way to express the electrophoretic mobility.

As noted above, the Einstein-Smoluchowski equation has been exploited to directly estimate the value of the electrophoretic mobility from the diffusion coefficient. Invoking the Henry equation, the diffusion coefficient can be employed in an analogous fashion by plugging Eq. 7 into Eq. 9 and substituting Eq. 4 to include D, giving Eq. 12:

$${\mu }_H=\frac{{\kappa }^{-1}}{({\kappa }^{-1}+a)}f(a\kappa )\frac{Dq}{\kappa T}$$ (12)

This allows us to use the Henry equation to relate the electrophoretic mobility of a lipid with the diffusion coefficient, charge and radius of a lipid head group.

Results

Exploring the Validity of the Henry’s Equation

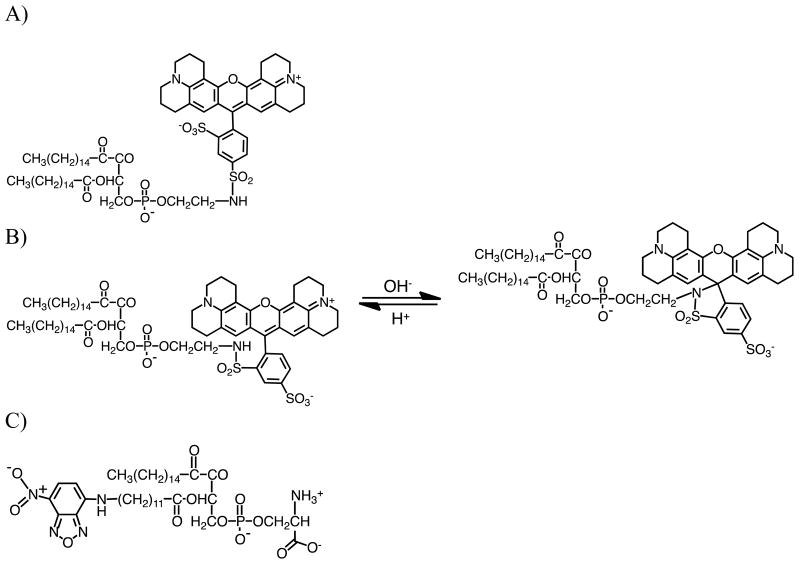
The ability of the Henry equation (Eq. 12) to predict the electrophoretic mobility of lipids was tested using tail-labeled NBD-PS and head group-labeled ortho and para-Texas Red DHPE. The structures of these lipids are depicted schematically in Fig. 4. It should be noted that Fig. 4B shows the two structures of ortho-Texas Red under low and high pH conditions, respectively. Drift velocity measurements were made in SLBs composed of 99.9% POPC and 0.1% ortho or para-Texas Red DHPE as well as 99.0% POPC and 1 % NBD-PS. The head group radii of both Texas Red DHPE isomers are considerably larger than tail-labeled NBD-PS (Table I),^27,28,30 which according to Eq. 12 should affect the relative electrophoretic mobilities of these dyes.

Fig. 4.

Molecular structures for three fluorescently labeled lipids: (A) para-Texas Red DHPE, (B) ortho-Texas Red DHPE at low and high pH values and (C) NBD-PS.

Table I.

Measured Drift Velocities and μ_H Values Lipid Probes at pH 4.9

Property	K	Measured or Calculated	NBD-PS	ortho- TR DHPE	Para- TR DHPE
Lipid Headgroup Radius27,28,30			0.5 nm	1.0 nm	1.0 nm
VD*	3.4 nm		11 ± 1 ×10−3	7.6 ± 0.2 × 10−3	7.0 ± 0.4 × 10−3
	10 nm		4.1 ± 1.3 × 10−3	6.0 ± .5 × 10−3	7.0 ± .3 × 10−3
μH#	3.4 nm	Measured	0.88 ± 0.8	0.76 ± 0.2	0.70 ± 0.2
		Calculated	0.87	0.77	0.77
	10 nm	Measured	0.33± 0.1	0.60± 0.05	0.71± .03
		Calculated	0.95	0.91	0.91

^*The drift velocity, V_D, values are in units of (μm/s)•(V/m)⁻¹.

^#The electrophoretic mobility, μ_H, values are in units of (μm/s) •(V/m)⁻¹ •C⁻¹, where C is the charge in Coulombs.

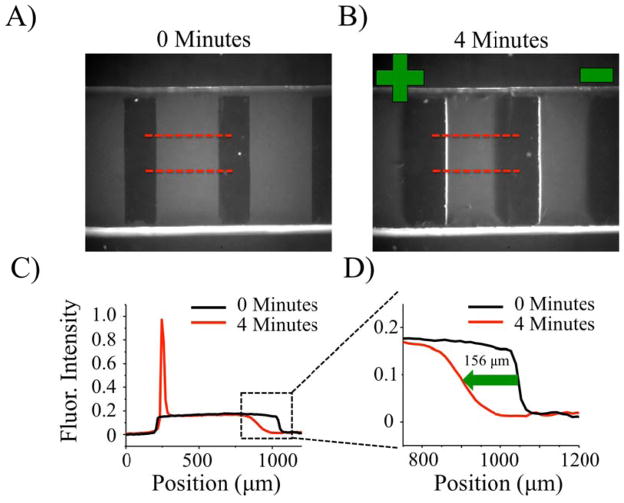
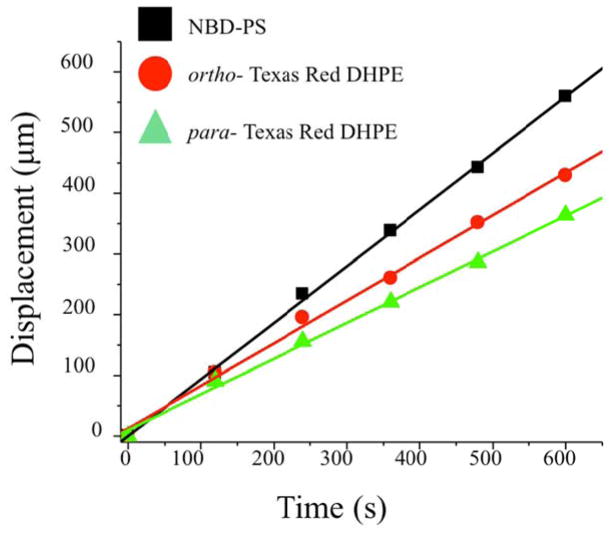
To test the Henry equation, each of the three dye-labeled probes was patterned into 900 μm wide strips separated by 600 μm wide fibrinogen barriers (Fig. 1). As an example, Fig. 5A and B shows the patterned lipid bilayer before and after 4 minutes of electrophoresis with ortho-Texas Red DHPE. The electrophoretic mobility of the dye-labeled lipids was measured at pH 4.9 in 1 mM phosphate buffer with 5 mM NaCl (corresponding to a Debye length, κ⁻¹, of 3.4 nm) at 23 °C. Under these rather acidic conditions, the charges on the labeled lipids are expected to be −1.0 and the ortho-Texas Red isomer should be protonated (Fig. 4B, left structure). Upon application of an 86.7 V/cm electric field, these fluorescently labeled lipids migrated towards the positive electrode as expected. This caused a build-up of ortho-Texas Red DHPE adjacent to the fibrinogen barrier on the side of the membrane patches nearer to the positive electrode. Line profiles of the fluorescence intensity across the bilayer patches in Fig. 5 A & B are shown in Fig. 5C. A region of depleted fluorescence was observed on the opposite side of the membrane patches. Most significantly, a region where the fluorescence intensity varied sigmoidally can be found. Fig. 5D shows this area in greater detail. The fluorescence profile in this region could be fit with a sigmoidal curve shape to find the midpoint. The position of the midpoint moved 156 μm over 4 min. as denoted by the green arrow in Fig. 5D. Moreover, this displacement was almost perfectly linear as a function of time (Fig. 6). It should be noted that the sigmoidal region broadened over time due to diffusion. The midpoint, however, migrated at the drift velocity¹⁴ until it encountered the barrier on the left-hand-side of the bilayer. Thus, the slope of the lines from the three different fluorophores can be used to determine their individual drift velocities, V_D. These values are provided in the row for which κ⁻¹ = 3.4 nm in Table I.

Fig. 5.

Fluorescent micrographs of a patterned POPC bilayer containing 0.1% ortho- Texas Red DHPE (A) before and (B) after a four-minutes of electrophoresis with an 86.7 V/cm field at pH 4.9. The positions of the positive and negative electrodes relative to the SLB are shown in green in (B). (C) The corresponding line profiles averaged over the area between the dotted red lines. The initial line profile is in black and the one after electrophoresis is in red. (D) A blow-up of the region within the black dashed-line region in (C).

Fig. 6.

The displacement of NBD-PS (black squares), ortho-Texas Red DHPE (red circles) and para- Texas Red DHPE (green triangles) over time in 5 mM NaCl and 1 mM NaH₂PO₄ at pH 4.9. The solid lines represent the bes st fits to the data.

As can be seen, NBD-PS migrated about 50% faster than both ortho- and para-Texas Red DHPE. This difference in drift velocity should be related to differences in the electrophoretic mobility of the lipids. The electrophoretic mobility could be calculated independently of the experimentally measured mobility. This is done using Eq. 12 in conjunction with the lipid head group sizes provided in the second row of Table I, the known Debye length, κ, and the measured diffusion coefficients obtained by FRAP. FRAP values for ortho- and para-Texas Red DHPE were found to be 3.0 ± 0.6 μm²/s, while NBD-PS was 3.7 ±0.8 μm²/s. Additionally, the charge on each lipid was assumed to be −1 under acidic conditions (see Fig. 4 for structures). The measured electrophoretic mobility, μ_H, obtained by plugging the slopes from Fig. 6 into eqn. 2, as well as the calculated value for each lipid are provided in Table I at κ⁻¹ = 3.4 nm. As can be seen from the table, the measured and calculated values compare quite well, although the measured value for para-Texas Red DHPE is about 10% too low. If instead of assuming the charge on each lipid is −1, one could alternatively use the calculated mobility to obtain the charges. In that case, the measured charges on ortho-Texas Red DHPE and NBD-PS remain −1, but the charge on para-Texas Red would be measured as −0.9.

The difference in measured and calculated electrophoretic mobility for para-Texas Red may correspond to different positions of the dye in the lipid bilayer. The calculated electrophoretic mobility values found in Table I were obtained by using the relative permittivity of water, 78.5. This is fine for ortho-Texas Red DHPE and NBD-PS, which presumably indicates that they reside near or even slightly above the water/bilayer interface. However, a permittivity value of ~38 is needed to obtain the correct mobility (or charge) for the para-Texas Red lipid isomer. As such, the para isomer should be more buried. This is consistent with a computational study that has found para-Texas Red DHPE to reside rather deeply within the head group region.²⁸ By contrast, NBD-PS is known to reside closer to the water/lipid plane from NMR studies.³¹ It should be noted that the head group region of a lipid bilayer has been found to have a dielectric constant of 30 by AFM measurements.³²

Although in the example provided above, we employed the Henry equation to predict electrophoretic mobilities, future studies may use this equation to measure self-diffusion coefficient values instead, as long as the charge and size of the lipid head groups are known to reasonable accuracy. This may provide an advantage relative to FRAP, which is currently employed to make self-diffusion constant measurements. Indeed, FRAP has relatively large error bars (±20% is common), while drift velocity measurements can be made with an accuracy of ±10% or even better. By the same token, it should also be possible to use drift velocity measurements to more accurately determine the position of lipid probes inside of the membrane based upon the corresponding calculated dielectric constant.

It should be noted that the Henry equation is expected to break down at higher zeta potentials due to the polarization of the double layer.³³ The zeta potentials of all lipids in these experiments, however, were below 2 kT/e (52 mV) (specific values given in the Supporting Information). As such, a reduction of the electrophoretic mobility due to polarization of the Debye layer should not occur.³³ Lipids on different leaflets of the bilayer may also respond differently to the electric field. Under the low ionic strength conditions of these experiments, the concentration of negatively charged lipids should be highly enriched in the leaflet of the bilayer facing away from the glass support.^34,35 The experiments here suggest that only one lipid population exists. This is consistent with the notion that these dye-labeled lipids are highly enriched in the upper leaflet.

Electroosmotic Effects

The measurements described in the section above suggest that the charge (or electrophoretic mobility) on each dye-labeled lipid can be determined without taking electroosomis into account. Indeed, one might suspect that lipids are not subject to a large electroosmotic force at relatively high salt concentration since they do not protrude significantly above the plane of the bilayer. This idea can be tested, since the drift velocity of a lipid in an electric field is proportional to the difference between the zeta potential of the lipid and the zeta potential of the surface, which includes the charge on the lipids in the bilayer as well as the charge on the glass support (Eq. 13):^7,36

$$V_D\propto {\xi }_{\mathit{lipid}}-{\xi }_{\mathit{surface}}$$ (13)

At the low percentages of charged lipids used in these experiments (1% NBD-PS and 0.1% Texas Red DHPE) the surface charge should be dominated by the glass support, rather than the lipid bilayer itself.^24,37 At low zeta potentials, the zeta potential of a surface is proportional to the Debye length (Eq.14):⁷

$${\xi }_{\mathit{surface}}=\frac{{\kappa }^{-1}\sigma }{{\epsilon }_0{\epsilon }_r}$$ (14)

Changing the Debye length is accomplished by modulating the ionic strength of the solution. In fact, lowering the concentration of salt from 5 mM NaCl and 1 mM phosphate to 0.5 mM phosphate and no NaCl increases κ⁻¹ from 3.4 nm to ~10 nm as calculated using Eq. 8. This change in the Debye length should have a large effect on the drift velocity of lipids in SLBs, if they are subject to significant electroosmotic forces. Additionally, changing the Debye length will change the electrophoretic mobility of the lipids as calculated by Eq. 12. The measured and calculated V_D and μ_H values for the larger Debye length conditions (κ⁻¹ = 10 nm) are provided in Table I.

As can be seen from Table I, the measured electrophoretic mobility of para- Texas Red DHPE is approximately 78% of the calculated value under these low salt conditions, whereas the measured electrophoretic mobility of ortho-Texas Red DHPE is 66% of the calculated value. Significantly, the drift velocity of tail labeled NBD-PS decreased to 35% of its calculated value at low ionic strength. This again suggests that the NBD on the tail of the PS lipid resides near the water/lipid interface of the bilayer where electroosmotic forces are present. By contrast, the Texas Red isomers seem to be somewhat shielded from electroosmotic forces under low ionic strength conditions, suggesting that they lie closer to the hydrophobic interior of the membrane. These conclusions are consistent with the calculated relative permeability measurements discussed above. Thus, the electroosmotic forces are different for different lipids depending upon their position in the membrane. However, it appears that the electroosmotic force for NBD-PS is negligible at sufficiently high ionic strength where the measured and calculated values of μ_H were nearly identical.

The dependence of the electrophoretic mobility on the Debye length may also help explain why Stelze’s original work, using the Einstein-Smoluchowski equation, calculated the electrophoretic mobility of the cationic probe D291 reasonably accurately (80% of the expected value).² The head group of the D291 probe should lie near the water/bilayer interface. Stelze’s experiments were conducted in 2.5 mM HEPES buffer, making the Debye length approximately 10 nm.² In fact, D291 has a very small, but charged headgroup and, therefore, &aκ <1 for these experiments. As such, the electrophoretic mobility predicted by the Einstein-Smoluchowski and Henry equations will be very similar.

Charge Measurements of ortho and para-Texas Red DHPE with pH

In a final set of experiments, the charges on ortho- and para-Texas Red DHPE were determined at different pH values. It is known that the fluorescence of ortho-Texas Red DHPE is turned off at high pH due to the deprotonation of the sulfonamide and the formation of a 5-membered ring (Fig. 4B).^38,39 This reversibly disrupts the conjugation of the xanthene ring system. Additionally, the deprotonation of ortho-Texas Red DHPE should cause this dye-labeled lipid to undergo a change in charge from −1.0 to −2.0. According to Eq. 12, the change should double the electrophoretic mobility of the molecule and thus double its drift velocity in an electric field of constant magnitude.

The measured drift velocity for ortho-and para-Texas Red DHPE at different pH values is plotted in Fig. 7A (black and red curves, respectively). The concentration of Texas Red DHPE in these experiments is 0.1 mole %. At pH 5.1, ortho-Texas Red DHPE has a drift velocity of 7.6 × 10⁻³ ± 0.2 ×10⁻³ (μm·sec⁻¹)/(V·cm⁻¹). As the fluorescence of ortho-Texas Red DHPE is greatly diminished at high pH, the drift velocity cannot be measured in situ above pH 9.0. As outlined in the Methods section, however, the drift velocity was measured after electrophoresis by reverting to pH 4.9. By doing this, it was found that the drift velocity was 1.4 × 10⁻² ± 0.1 × 10⁻² (μm·sec⁻¹)/(V·cm⁻¹) at pH 10.9, which is just slightly less than double the initial value. The drift velocity as a function of pH was fitted to a sigmoidal curve and used to determine the mid-point, pH = 8.7. This agrees well with the pK_A value determined by the corresponding fluorescence assay.³⁸ Using Eq. 12 and a self-diffusion coefficient value of 3.0 ± 0.6 μm²/sec to solve for the charge on ortho-Texas Red DHPE yields a value of −1.0 ± 0.2 at pH 5.1 and −2.0 ± 0.2 at pH 10.9, which is in excellent agreement with expectations (Fig. 7B, black curve).

Fig. 7.

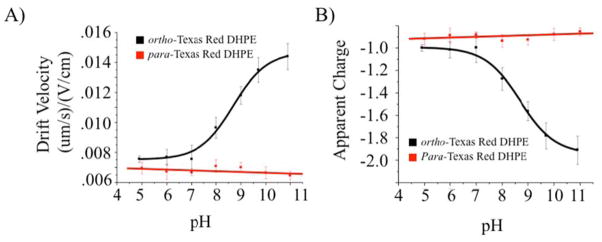
(A) Drift velocity measurements of ortho-Texas Red DHPE (red curve) and para-Texas Red DHPE (black curve) in 1 mM phosphate buffer with 5 mM NaCl at different pH values. (B) Shows the calculated charge values for both ortho- and para-Texas DHPE using the measurements in (A), the diffusion values from FRAP data and Eq. 12.

By contrast with the ortho-isomer, the fluorescence intensity from para-Texas Red DHPE should not be pH sensitive.³⁸ However, it should still be possible for the sulfonamide of para-Texas Red DHPE to be deprotonated, even though a 5-membered ring structure cannot be formed. In order to test this, the drift velocity of this dye-labeled lipid was measured under the same conditions as the ortho-isomer (Figure 7A, red curve). As can be seen, the drift velocity remained unchanged within experimental error between pH 5.0 and 11.0. Using a diffusion coefficient value of 3.0 μm²/sec and Eq. 12 yielded a charge of −0.9 ± 0.2 over the entire pH range (Fig. 7B, red curve). Exposure of SLBs containing 0.1% Texas Red DHPE to solutions more basic than pH 11 caused them to delaminate from the glass surface²⁴ and thus couldn’t be explored. Nevertheless, it appears that the deprotonation of the para isomer does not even begin by pH 11. Therefore, the pK_A of the sulfonamide on para-Texas Red DHPE must be a minimum of 3 pH units higher than that of the ortho isomer. The inability of the sulfonamide on para-Texas Red DHPE to be deprotonated might be somewhat unexpected based upon the pKa of other benzene sulfonamides, which have been measured to be approximately 10.⁴⁰ However, the proximity of para-Texas Red DHPE to the negatively charged phosphate on the same lipid, as well as the negative charges from other lipids and the glass surface may significantly increase the energetic cost of deprotonation.

Discussion

Finding an appropriate model to understand the electrophoretic mobility of lipids in bilayers has proved to be challenging over the years. Lipids at the bilayer/aqueous interface are surrounded by water, ions and other dipolar lipid head groups. Modeling the double layer as diffuse, which is assumed by the Henry equation, can be a good starting point as demonstrated by the experiments described above. Nevertheless, it is certainly a simplification of these complex systems. On the other hand, modeling lipids moving electrophoretically through a viscous fluid as point charges without any double layer as in the Einstein Smoluchowski equation represents an even more dramatic oversimplification. Further steps will now needed to be taken to find the limits of employing the Henry equation and trying to improve upon them.

Next, we would note that ortho- and para-Texas Red DHPE have been shown to separate from one another in SLBs by electrophoresis.⁴¹ The current results provided in herein suggest that such separation occurs on the basis of the charge difference between these isomers at pH values equal to or greater than 7.0. The present work may point the way for the separation of more complicated lipid membrane mixtures. One goal of SLB electrophoresis is to separate membrane proteins in their native membranes on a planar substrate.^17,41,42 A more complete understanding of the electrokinetic and electroosmotic forces at play in these situations should be critical to understanding the electrophoretic mobility for such systems and thus maximize the potential of SLB electrophoresis as a separation technique.

Beyond separations, a variety of chemical changes could potentially be elucidated by SLB electrophoresis. For example, the binding of divalent cations such as Ca²⁺ and Mg²⁺ with lipids in a supported lipid bilayers should change the charge on the target lipid.⁴³ By tailoring the composition of a supported lipid bilayer, drift velocity measurements could be made at a variety of ion concentrations in order to abstract binding constants for these ions. It may also be possible to study the binding of species to SLBs without changing the formal charge on the lipids. For example, the binding of uncharged peptides should attenuate the diffusion coefficient of the lipids and result in a slowing of their drift velocity. Additionally, lipid-lipid interactions that result in a change in charge or diffusion coefficient could also be observed.

Conclusion

We have demonstrated that the electrophoretic mobility of a lipid can be accurately described by the Henry equation. This equation can be used to calculate the charge on dye-labeled lipids by measuring their drift velocity in supported lipid bilayers undergoing electrophoresis. This work has also demonstrated that different lipids are subject to different electroosmotic forces, which is likely correlated to the position of the head group with respect to the bilayer plane. Lastly, changes in electrophoretic drift velocity have been exploited to monitor the protonation of ortho-Texas Red DHPE. The model and techniques presented in this paper should extend the ability of SLB electrophoresis to explore lipid-ion, lipid-protein and lipid-lipid interactions as well as generate a deeper understanding of separations carried out in SLBs.