Differentiation between genomic and non-genomic feedback controls yields an HPA axis model featuring Hypercortisolism as an irreversible bistable switch

Abstract

Background

The hypothalamic-pituitary-adrenal axis (HPA axis) is a major part of the neuroendocrine system responsible for the regulation of the response to physical or mental stress and for the control of the synthesis of the stress hormone cortisol. Dysfunctions of the HPA axis characterized by either low (hypocortisolism) or increased (hypercortisolism) cortisol levels are implicated in various pathological conditions. Their understanding and therapeutic correction may be supported by mathematical modeling and simulation of the HPA axis.

Methods

Mass action and Michaelis Menten enzyme kinetics were used to provide a mechanistic description of the feedback mechanisms within the pituitary gland cells by which cortisol inhibits its own production. A separation of the nucleus from the cytoplasm by compartments enabled a differentiation between slow genomic and fast non-genomic processes. The model in parts was trained against time resolved ACTH stress response data from an in vitro cell culture of murine AtT-20 pituitary tumor cells and analyzed by bifurcation discovery tools.

Results

A recently found pituitary gland cell membrane receptor that mediates rapid non-genomic actions of glucocorticoids has been incorporated into our model of the HPA axis. As a consequence of the distinction between genomic and non-genomic feedback processes our model possesses an extended dynamic repertoire in comparison to existing HPA models. In particular, our model exhibits limit cycle oscillations and bistable behavior associated to hypocortisolism but also features a (second) bistable switch which captures irreversible transitions in hypercortisolism to elevated cortisol levels.

Conclusions

Model predictive control and inverse bifurcation analysis have been previously applied in the simulation-based design of therapeutic strategies for the correction of hypocortisolism. Given the HPA model extension presented in this paper, these techniques may also be used in the study of hypercortisolism. As an example, we show how sparsity enforcing penalization may suggest network interventions that allow the return from elevated cortisol levels back to nominal ones.

Background

The HPA axis is a major part of the neuroendocrine system in mammals and particularly in humans. A main task of this hormonal network is the regulation of the response to physical or mental stress that threatens to disrupt the homeostatic balance of the organism. If a stressor is sensed by the nervous system the hypothalamus is stimulated to produce and secret the corticotropin-releasing hormone (CRH). The secretion of CRH causes the anterior pituitary to synthesize adrenocorticotropin (ACTH). ACTH then stimulates the adrenal glands to release cortisol, which down regulates the blood concentration of CRH and ACTH via different negative feedback mechanisms [1-4].

The HPA axis is subject of intensive research in endocrinology as HPA malfunctions are implicated in various pathological conditions. These are often characterized by either elevated or insufficient blood cortisol levels compared to the average healthy human. For instance, hypocortisolism (insufficient cortisol level) is reported in patients suffering from the chronic fatigue syndrome and post traumatic stress disorders (cf. [5-9]), whereas hypercortisolism (elevated cortisol level) is observed in depression, dementia or postoperative delirium (cf. [10-15]). Especially in the context of personalized medicine the use of modeling and simulation of biological systems for the rational design of treatments and drug intervention strategies is more and more recognized [16-20]. For such endeavors the integration of biological information of different type into computational, hence predictive, models is a prerequisite. The emphasis of earlier HPA modeling approaches with ordinary and delay differential equations has been put on self regulatory ultradian and circadian oscillatory behavior in [21-27], oscillations in response to an independent external pacemaker from the suprachiazmatic nucleus have been described in [28,29]. In comparison, the article [30] stands out as it incorporates intracellular glucocorticoid receptor kinetics which mediate bistable behavior of the HPA axis. Despite its parsimonious character the four state ODE model of [30] offers an explanation for hypocortisolism as an irreversible biological switch and served in [31] as a basis for the design of a therapeutic corrections of the HPA dysfunction. In [19] it is shown that the model of [30] also exhibits stable limit cycle oscillations, in [32] the four state rate equations of [30] were modified in order to fit oscillatory data of patients suffering from post traumatic stress disorder.

A parsimonious HPA model featuring hypocortisolism

The HPA axis model of [30] captures the basic feedback mechanisms and includes an intracellular glucocorticoid receptor GR in the anterior pituitary gland as one of the four state variables, see Figure 1. The dynamics of the model are described by the ODE system

Figure 1.

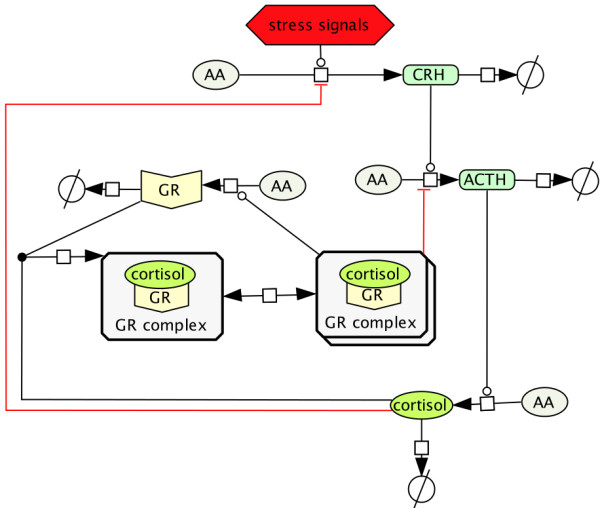
The HPA axis feedback network. Diagram of the biochemical feedback network of the HPA axis as modeled in [30]. Physical or mental stress triggers the secretion of corticotropin releasing hormone CRH in the hypothalamus. CRH is transported to the anterior pituitary gland and stimulates the release of the adrenocorticotropic hormone ACTH. ACTH signals to the adrenal gland to secrete cortisol COR. After binding to the glucocorticoid receptor GR in the pituitary, cortisol negatively regulates the production of CRH and ACTH. The homo dimerization introduces a positive feedback loop giving rise to bistable behavior in accordance with hypocortisolism.

$$\begin{array}{l}\frac{\mathrm{d}[\mathit{\text{CRH}}]}{\mathrm{d}t}=\frac{k_c+\text{stress}}{1+\frac{[\mathit{\text{COR}}]}{k_{i1}}}-k_{\mathit{\text{cd}}}[\mathit{\text{CRH}}],\end{array}$$ (1)

$$\begin{array}{l}\frac{\mathrm{d}[\mathit{\text{ACTH}}]}{\mathrm{d}t}=\frac{k_a[\mathit{\text{CRH}}]}{1+\frac{[\mathit{\text{COR}}-\mathit{\text{GR}}]}{k_{i2}}}-k_{\mathit{\text{ad}}}[\mathit{\text{ACTH}}],\end{array}$$ (2)

$$\begin{array}{l}\frac{\mathrm{d}[\mathit{\text{GR}}]}{\mathrm{d}t}=\frac{k_r{[\mathit{\text{COR}}-\mathit{\text{GR}}]}^2}{k+{[\mathit{\text{COR}}-\mathit{\text{GR}}]}^2}+k_{\mathit{\text{cr}}}-k_{\mathit{\text{rd}}}[\mathit{\text{GR}}],\end{array}$$ (3)

$$\begin{array}{l}\frac{\mathrm{d}[\mathit{\text{COR}}]}{\mathrm{d}t}=k_o[\mathit{\text{ACTH}}]-k_{\mathit{\text{od}}}[\mathit{\text{COR}}],\end{array}$$ (4)

where the ODE variables [CRH], [ACTH], [GR] and [COR] denote the concentrations of CRH, ACTH, GR and cortisol. If GR is bound to cortisol, the resulting complex is denoted by [COR-GR]. As this binding is very fast compared to the other dynamics it is assumed to be in equilibrium, i.e. [COR-GR] = [COR] · [GR]. The GR dimerization may generate an irreversible bistable switch in the model by which the dysfunctional abidance of the system at an alternative stable steady state characterized by low cortisol level can be explained. The therapeutic strategy of [31] for the correction of hypocortisolism based on (1)-(4) is to force the HPA axis by a further suppression of cortisol to a point where the only stable condition in proximity is the original healthy state. An alternative for supporting the search for pharmaceutical therapies is the manipulation of the feedback network by means of inverse bifurcation techniques in order to transform the irreversible switch into a reversible one, see [19,33]. Though the model of [30] sheds new light on possible causes for hypocortisolism, its dynamic repertoire could not be shown to feature the opposite scenario of hypercortisolism. Furthermore, while the model takes the intracellular glucocorticoid receptor GR into account, it does not consider feedback mechanisms known to act on faster time scales.

Motivation of model extensions

The above mentioned GR mediated negative feedback on the production of ACTH acts at the genomic level. Specifically, cortisol COR binds to the glucocorticoid receptor GR and forms a homodimer (cf. [34,35]). This homodimer is known to work as a transcription factor, enhances the expression of the GR gene and down regulates the expression of the ACTH related gene. A consequence of the transcriptional regulation is that the GR feedback control works rather slowly compared to other cellular processes such as a vesicle transport, cell signaling or extracellular events such as changes in the CRH blood concentration. For mammalian cells one can expect at least a delay of the down regulation in the range of 15 minutes up to 2 hours (c.f. [1]). However, it has been frequently reported that cortisol induced inhibitory effects on anterior pituitary gland cells can already occur after a few seconds (c.f. [36,37]), a phenomenon that cannot be explained by means of the genomic feedback mechanism.

The common hypothesis for this observation is that besides the GR receptor a second receptor in the membrane may directly inhibit the release of ACTH when bound to cortisol (cf. [38-42]). In [43] the authors were able to provide evidence of a glucocorticoid receptor (GPCR) in the anterior pituitary cell membrane, possibly enabling the fast response related to cortisol induced inhibition. In the following we incorporate this fast and non-genomic feedback mechanism and for this purpose integrate a detailed pituitary gland cell model into the HPA network of [30]. As a consequence, the extended dynamic repertoire of the resulting HPA axis feedback network also features bistable behavior compatible with the dysfunctional state of hypercortisolism and the ability to simulate time resolved ACTH stress response data from in vitro AtT-20 pituitary tumor cells.

Results

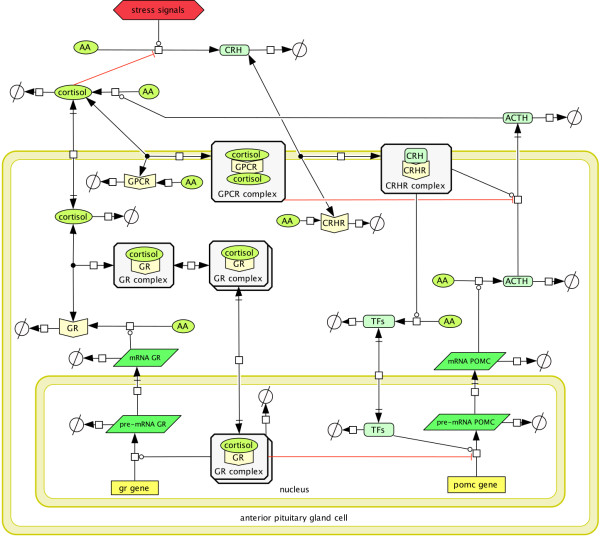
Using mass action and Michaelis Menten enzyme kinetics we developed a mechanistic ODE system model of the glucocorticoid feedback mechanisms within the anterior pituitary gland cell. In particular, we incorporated the glucocorticoid membrane receptor GPCR found in [43] and distinguished between slow genomic and fast non-genomic processes by using different compartments for the nucleus and the cytoplasm. Figure 2 displays the reaction network graph of the resulting HPA axis model while the details are discussed in the Methods section.

Figure 2.

Integration of an anterior pituitary gland cell model into the HPA network. Diagram of the biochemical feedback network of the HPA axis after incorporation of the cortisol mediated feedback mechanisms in the anterior pituitary gland cells. The recently found membrane glucocorticoid receptor GPCR [43] and the intracellular receptor GR introduced in [30] act on different time scales. The modeling of the corresponding feedback mechanisms requires a distinction between slow genomic processes within the nucleus and fast non-genomic processes within the cytoplasm. In particular, the dimerized cortisol-glucocorticoid receptor complex (GR complex) and the transcription factors TF associated to the CRH receptor CRHR are explicitly considered. See Figure 3 for further details.

Model comparison with experimental data

The experimentally observed fast inhibitory effect of cortisol on the anterior pituitary gland cell motivated the model incorporation of the GPCR receptor in order to allow for non-genomic, hence fast, signal processing. In order to test the capability of our model to capture these fast effects against actual data, we conducted experiments in cultures of the murine AtT-20 pituitary cell line (cf. [44]). After administering doses of CRH and cortisol samples were taken from the medium and analyzed with respect to the total ACTH concentration in the cell medium, see Figure 4A for the data obtained for two different experimental setups. In the first setup (indicated by the triangle markers in Figure 4A) we considered the situation of a single stress stimulus by 10nM CRH at time point zero in the absence of cortisol. We observed an immediate increase of the ACTH secretion, followed by a slight stagnation and then a constantly increasing total ACTH concentration. In the second experiment (indicated by the dot markers in Figure 4A) 10nM CRH and in addition 100nM cortisol were administered. As depicted, this immediately activated the fast non-genomic pathway inhibiting the release of ACTH. This led to an increased amount of ACTH stored in the vesicles within the cell and thus to a delayed but strong release of ACTH after approximately 15 minutes. However, after 30 to 60 minutes the genomic feedback mechanisms become effective resulting in an overall reduced ACTH concentration in the medium.

Figure 4.

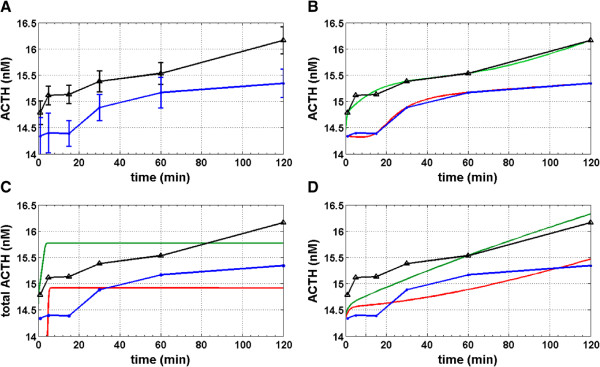
Experimental and simulated ACTH concentration profiles. The figure shows experimental ACTH profiles (black and blue lines) from murine AtT-20 pituitary cell lines described in [44] and simulations (green and red lines) after data fitting with different HPA network models. A) The black line corresponds to an experiment in which the system was exposed to 10 nM of CRH at time zero, the blue line corresponds to an experiment in which - in addition to 10 nM - 100 nM of cortisol was administered at time zero. The error bars show the 95% confidence intervals for the measurements at the different time points. B) Fit of experimental data with the HPA network model of Figure 2. C) Fit of experimental data with the HPA network model of Figure 2 after knockout of the membrane glucocorticoid receptor GPCR pathway. D) Fit of experimental data with the HPA network model of Figure 1. The results underpin the need for including the membrane glucocorticoid receptor GPCR in models of the pituitary gland cells.

For training the model against the experimental data by adaptation of the model parameters we followed a variational regularization approach (cf. [33,45]), see Methods for details. Sparsity enforcing penalization was used to eliminate model components less relevant for reproducing the observed kinetics. Figure 4B shows that the experimental data can be fitted by the HPA model of Figure 2 even if the autocatalytic loop for the GR gene regulation would be neglected and if the production of the TF (transcription factors for CRH) receptors would be considered to be independent of CRH.

In order to assess the relevance of the featured GPCR receptor for the model we knocked out the corresponding pathway by elimination of the respective ODE equations from our model and addressed the data fitting task with the reduced model. The result in the data space is shown in Figure 4C and indicates that the consideration of the GPCR feedback pathway in the model is in fact vital for reproducing the experimentally observed dynamics. For comparison we finally run the data fitting procedure with the parsimonious model (1) - (4) from [30]. The model lacks a GPCR mediated feedback pathway for fast response and fails to reproduce the corresponding experimental observation, see Figure 4D.

Exploration of the dynamic repertoire of the model

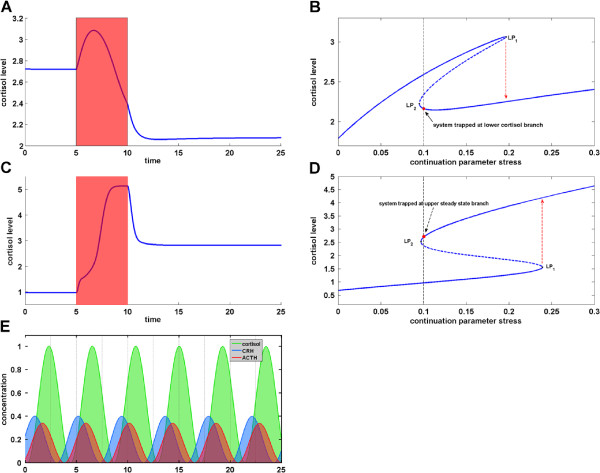
One important aspect of [30] is the inclusion of the glucocorticoid receptor GR which generates bistability for a model based explanation of hypocortisolism as an irreversible biological switch. As the GR mediated feedback pathway is also a constituent of the extended HPA network model of Figure 2, the capability of our model to reflect the bistable behavior of (1)-(4) is an imperative requirement. Tools [46,47] for studying the dynamic repertoire of ODE systems with respect to bistability or oscillations solve optimization problems that involve the eigenvalues of the Jacobian matrix f _x (x,q) (with f denoting the right hand side of an ODE model) and search for regions in the parameter space that give rise to limit-point or Hopf bifurcations. Figure 5B displays a resulting bifurcation diagram for the extended HPA model from Figure 2 with the stress level of Equation (8) as the bifurcation parameter. It gives an explanation of the dysfunctional alteration from a steady state of normal cortisol level (upper branch of the equilibrium curve) to a second steady state with low cortisol level (lower branch of the equilibrium curve) in response to a temporary stressor. If the abscissa of the limit point LP₂ lies below the basal stress level, say for instance 0.1, the return to the upper branch is hampered and the HPA axis is trapped at low cortisol as observed in hypocortisolism. Figure 4A shows a corresponding cortisol concentration profile obtained by simulation of the model from Figure 2.

Figure 5.

Dynamic Repertoire of the HPA network model. The figure displays different types of qualitative dynamic behavior featured by the HPA axis model from Figure 2 which is larger than for other HPA network models reported earlier in the literature. The corresponding model parameter settings have been found using inverse problems and bifurcation discovery tools. The bifurcation diagrams (B) and (D) show the steady state concentration of cortisol in dependence on the stress level. For a certain stress region the system exhibits two stable steady states (indicated by solid lines) and one unstable steady state (dashed line). A) Simulation of a dysfunctional stress response of cortisol in hypocortisolism. Though the stress is only temporary (red period), the system is driven to and eventually caught in an alternative stable steady state characterized by an insufficient cortisol level. B) Irreversible bistable switch explaining the behavior shown in (A). Once the system is driven from the upper steady state branch it is trapped at the lower branch due to a limit point LP₂ abscissa smaller than the basal stress level 0.1. C) Simulation of a dysfunctional stress response of cortisol in hypercortisolism. Though the stress is only temporary (red period), the system is driven to and eventually caught in an alternative stable steady state characterized by an excessive cortisol level. D) Irreversible bistable switch explaining the behavior shown in (C). Note the inverted alignment of cortisol steady state branches and alternative location of limit points in comparison to (B). E) Simulation of limit cycle oscillations in the hormone concentrations of CRH, ACTH and cortisol (relative to the maximum cortisol level).

Further explorations of the dynamic repertoire of the extended HPA model revealed a region in the parameter space which allows for an alternative bistable behavior that can be linked to the pathological condition of hypercortisolism. Figure 5D provides an example of a corresponding bifurcation diagram in which the qualitative scenario of Figure 5B is inverted. If a stressor drives the HPA axis from the lower cortisol branch to the upper one, it abides at elevated cortisol levels even after removal of the stressor if the abscissa of the limit point LP₂ lies below the basal stress level, again say for instance 0.1. Figure 5C shows a corresponding cortisol concentration profile obtained by simulation of the model depicted in Figure 2. While the positive feedback mediated by the glucocorticoid receptor GR dimerization has been already suggested in [30] as the cause for the bistable behavior associated to hypocortisolism, our in-silico pathway knock out tests on the extended HPA model indicate that the positive feedback on the genomic level mediated by the CRH hormone is vital for the bistability associated to hypercortisolism. Without this component, we could not find a parameter region giving rise to a bifurcation diagram as displayed in Figure 5D. Similarly, the results of our numerical analysis suggest that the dynamic repertoire of the parsimonious model of [30] excludes the bifurcation behavior of Figure 5D, possibly due to its simplistic description of the CRH pathway.

Finally, we explored the parameter space of the extended HPA network model with objective functions for the detection of Hopf bifurcations and found parameter regions allowing for stable limit cycle oscillations, see Figure 5E. The displayed temporal sequence in which the core species CRH, ACTH and cortisol reach their maximum value is in accordance with the established cascade in release of the HPA hormones. While oscillatory behavior for the parsimonious model was obtained in [30] in response to repeated stress pulses, limit cycle oscillation for (1)-(4) were found in [19] and for a modified version also in [32]. However, to our knowledge the HPA model shown in Figure 2 is the first one able to capture two distinct types of bistability (as reflected in Figures 5B and 5D) as well as autonomous oscillatory behavior.

Model based correction of Hypercortisolism

Based on the parsimonious model of Figure 1 from [30] a therapeutic strategy for the correction of hypocortisolism has been suggested in [31]. This therapy aims at perturbing the HPA axis trapped at the low cortisol branch by a further suppression of cortisol in order to enable the return to a healthy cortisol level. An alternative idea for the treatment of hypocortisolism has been presented in [33] which aims at an intervention with the reaction network in order to turn the dysfunctional irreversible switch into a reversible one by shifting the critical limit point in the bifurcation diagram. As the extended HPA model of Figure 2 also captures a switching scenario associated to hypercortisolism, the inverse bifurcation approach of [33,48,48,49] can also be applied to study which parts of the HPA network need to be targeted in order to allow the return from the abnormal hypercortisol steady state back to a healthy cortisol level.

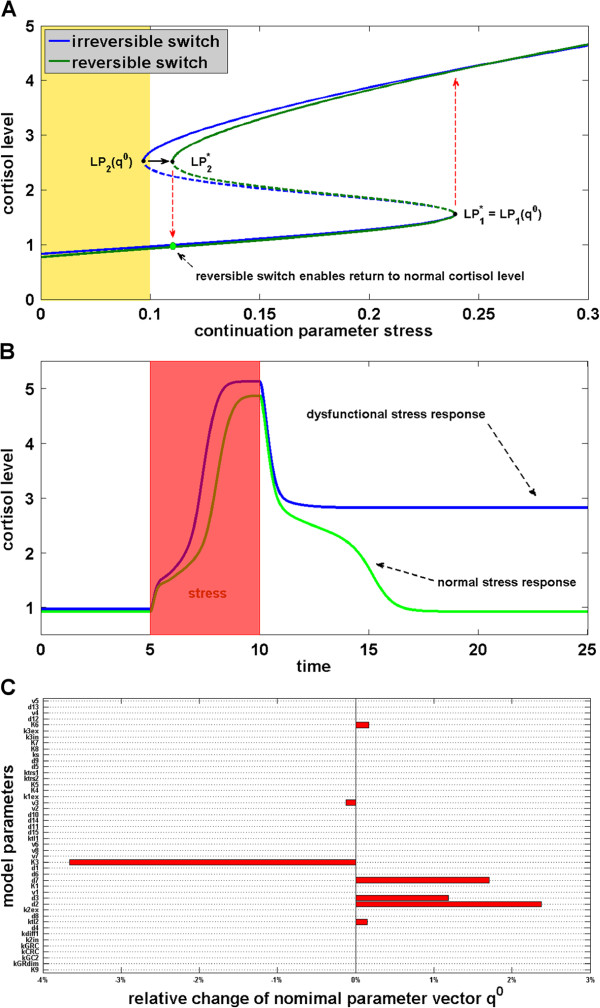
For the purpose of illustration we suppose that a representative q⁰ out of the parameter region compatible with the switching behavior of Figure 5D has been chosen (for instance by fitting of corresponding patient data) in which the abscissa S₂(q⁰) of the limit point LP₂(q⁰) lies below the basal stress level S = 0.1 (on a fictive scale). Then, a short but strong stress signal may drive the system from a normal cortisol level to an abnormal elevated one where it abides even if the stress drops back to basal level, see Figure 5C. A therapeutic qualitative change from an irreversible to a reversible steady state transition can be achieved by interfering with the HPA model such that the abscissa of the limit point LP₂(q⁰) is shifted to a value $S_2^{\ast }$ with $S_2^{\ast }>0.1$ while, e.g., maintaining the abscissa value of the second limit point LP₁(q⁰), see Figure 5A.

A corresponding interference strategy can be derived by solving the nonlinear inverse problem

$$F(x)=\left(\begin{array}{c}{S}_1(q^0)\\ S_2^{\ast }\end{array}\right),$$ (5)

where F maps the correction x onto the abscissas S₁(q⁰ + x) and S₂(q⁰ + x) of the limit points LP₁(q⁰ + x) and LP₂(q⁰ + x) defined by the HPA model with altered parameter vector q⁰ + x. In order to keep the number of necessary interventions with the HPA network as low as possible a sparse solution of (5) is sought for by solving the optimization problem

$$\underset{q}{\text{min}}\parallel \left(\begin{array}{c}{S}_1(q^0)\\ S_2^{\ast }\end{array}\right)-F(q){\parallel }_2^2+\alpha \phi (x)$$ (6)

with φ as in (35) and the sparsity promoting choice p < 1.

Figure 6C displays the solution of (6) (in relation to q⁰) giving rise to the re-engineered bifurcation diagram of Figure 6A (green curve) and allowing the return to normal cortisol levels, see Figure 6B. The parameters K₆, v₃ and d₇ to be altered concern the feedback controls related to the hormone CRH. A decrease of v₃ and an increase of d₇ correspond to a reduction of the sensitivity of the cells with respect to extracellular CRH. Moreover, an increase of the dissociation/Michaelis-Menten constant K₆ reduces the sensitivity of the TFs transcription factor regulation by the CRH-CRHR related pathways. Furthermore, the increase of k_tl2 calls for an increase of the translation rate of GR mRNA in order to further diminish the effect of extracellular CRH due to higher availability of GR. The intervention strategy shown in Figure 6C also suggests to alter the parameters K₃, d₃ and d₂ in order to reduce the production of CRH and to increase the sensitivity with respect to the feedback via cortisol. As these parameters concern processes outside of the anterior pituitary gland cells, an extension of HPA model by a mechanistic description of the hypothalamus is necessary in order to enable a more detailed interpretation of those parameter changes.

Figure 6.

Targeting the irreversible switch of the HPA axis model for hypercortisolism. A) The blue equilibrium curve corresponds to the irreversible switch of hypercortisolism depicted also in Figure 4B. A shift of the limit point LP₂(q⁰) to the region right to the basal stress level turns the irreversible switch into a reversible one (green equilibrium curve). This design goal can be formulated and solved using inverse problems techniques. B) Comparison of the dysfunctional stress response with the normal stress response after network manipulation allowing the return to normal cortisol levels following a short stress period (red area). C) Display of the necessary model parameter corrections x (relative to the nominal values of q⁰) in order to achieve the transition from an irreversible to a reversible switch as shown in Figure 5A. Due to the use of a sparsity promiting penalty function only a few parameters need to be altered.

Conclusions

Motivated by the experimental detection of a glucocorticoid membrane receptor GPCR we have built a mathematical model of the anterior pituitary cell that differentiates between genomic and GPCR mediated non-genomic signaling pathways. After the integration of our model into a literature framework of the hypothalamus pituitary adrenal axis and the training against stress induced ACTH concentration profiles of murine AtT-20 pituitary tumor cells we obtained a dynamic repertoire capturing two types of bistable switches as well as stable limit cycle oscillations. While the first bistable switch has been previously associated to the diseased state of hypocortisolism and utilized in the development of therapeutic strategies, to our knowledge the second bistable switch is novel in the context of HPA axis modelling. Along similar lines it can be linked to another dysfunctionality of the HPA axis referred to as hypercortisolism in which a continued abidance of the axis at elevated cortisol levels is observed even after complete removal of the stressing factor. Our in-silico knockout studies in particular indicate that the positive feedback on the genomic level mediated by the CRH hormone is responsible for the generation of the hypercortisolism switch. Using inverse bifurcation analysis with sparsity enforcing penalization we finally detected key model parameters that need to be altered in order to turn the irreversible switch into a reversible one then featuring a healthy stress response characterized by a return to normal cortisol levels.

While systems biology strongly advertises the use of modeling and simulation in the design of future drugs and therapies, one current challenge is to appropriately picture the complexity of the biological system at hand in the defining mathematical equations and their parameters. Though with respect to HPA axis modeling we reached a certain level of detail by introducing both genomic and non-genomic signaling pathways in the pituitary cell, we only adopted the parsimonious description of the link between the pituitary and the hypothalamus as well as the adrenal from the literature. Furthermore, the information content of the available ACTH concentration did not allow to sufficiently constrain the model parameters such that we so far have to content ourselves with parameter space regions corresponding to different qualitative model behaviour. Nevertheless, even at its current stage our model offers to endocronologists a different view on hypercortisolism as an irreversible bistable switch while the outlined mathematical methodologies will also apply to more realistic models and improved data sets. Finally, the model may also serve as a tool for the design of a model predictive control based treatment of hypercortisolism in which the HPA axis is driven by a - though at first glance counter-intuitive - additional administration of cortisol to a point where the only stable condition in proximity is the original healthy state, compare with [31].

Methods

Model development

In order to distinguish between slow genomic and fast non-genomic processes we use the modeling concept of compartments and separate the nucleus from the cytoplasm of the pituitary gland cell. Moreover, we base our model on the principles of Michaelis-Menten enzyme kinetics ( [50-52]) in order to deal with physical meaningful parameters.

We refrain from a detailed description of gene regulation, RNA processing or cleaving and rather concentrate on the rate limiting processes such as transport/diffusion in and out of the nucleus. We apply this modeling strategy not only to the glucocorticoid mediated feedbacks but also to the stimulating pathways involving the hypothalamic hormone CRH. CRH does not enter the pituitary gland cells but interacts with a specific membrane receptor (CRHR) only. Still, also the binding of CRH induces both a genomic and a non-genomic feedback (cf. [53-55]). As this positive feedback via CRH counteracts the negative feedback via cortisol on the genomic as well as on the non-genomic level, also the catalyzing mechanisms related to CRH have to be modeled in more detail than in [30] for the purpose of differentiating between genomic and non-genomic effects in the anterior pituitary gland cells. Concerning the molecular mechanisms of the anterior pituitary cells, our model involves three different pathways which are associated with the three main receptors, namely the intracellular glucocorticoid receptor GR and the two membrane receptors (GPCR and CRHR) with respect to cortisol and CRH, see Figure 2 and Figure 3.

Figure 3.

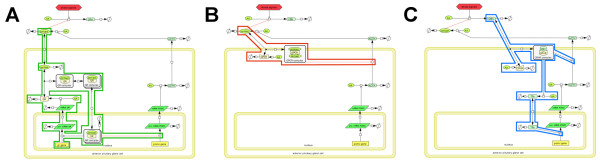
The three core feedback pathways of the (anterior) pituitary gland cell model. Illustration of the intracellular pathways of the extended HPA model of Figure 2 showing the three main feedback mechanisms (with respect to the involved receptors) in the anterior pituitary gland cells. A) Genomic pathway of the GR mediated feedback: Outline of the modeled species involved in the inhibition of POMC (Proopiomelanocortin) transcription which corresponds to the inhibition of ACTH production. ACTH is obtained via post-translational cleavaging of the POMC protein. The central transcription factor is the GR-cortisol complex which down regulates the POMC transcription and enhances the production of the GR receptor. B) Non-genomic pathway of the GPCR mediated feedback: The non-genomic negative feedback mechanism via the glucocorticoid membrane receptor GPCR, inhibiting the release of ACTH. C) CRHR mediated feedback: The positive feedback mechanisms associated with the CRH membrane receptor (CRHR), which causes an increased release of ACTH from vesicles and an increased expression of the POMC gene.

Extracellular species and the controls related to the adrenals and the hypothalamus

Regarding the feedback controls related to the adrenals and the hypothalamus we follow the approach of [30] in order to insure consistency and comparability as far as possible. In particular, we consider the following ODE describing the extracellular concentration of cortisol, with an additional term reflecting the diffusion (diffusion constant k_diff1) of cortisol into the anterior pituitary cells:

$$\frac{\mathrm{d}[{\text{COR}}_{\text{ex}}]}{\mathrm{d}t}=\frac{V_{\text{in}}}{V_{\text{ex}}}{k}_{\text{diff1}}([{\text{COR}}_{\text{in}}]-[{\text{COR}}_{\text{ex}}])+\frac{v_1[{\text{ACTH}}_{\text{ex}}]}{K_1+[{\text{ACTH}}_{\text{ex}}]}-d_1[{\text{COR}}_{\text{ex}}].$$ (7)

Here V_ex and V_in are the volumes of the extracellular compartment and the intracellular compartment. Analogously to [30] we model the temporal development of the CRH concentration by

$$\frac{\mathrm{d}[\text{CRH}]}{\mathrm{d}t}=\frac{k_s\left(k_{\text{sb}}+\text{stress}\right)}{1+[{\text{COR}}_{\text{ex}}]/K_3}-d_2[\text{CRH}].$$ (8)

The GR mediated feedback control

One significant extension over [30] in our modeling approach concerns the regulatory pathway related to the intracellular glucocorticoid receptor GR and in particular to the transcription factor, being the homodimer of the GR-COR complex, see Figure 3A. The following equation describes the intracellular concentration of cortisol

$$\begin{array}{ll}\frac{\mathrm{d}[{\text{COR}}_{\text{in}}]}{\mathrm{d}t}& =k_{\text{diff1}}([{\text{COR}}_{\text{ex}}]-[{\text{COR}}_{\text{in}}])-d_4[{\text{COR}}_{\text{in}}]\\ & +F\left([{(\text{GR-COR})}_{\text{2,nu}}],[{\text{COR}}_{\text{in}}],[\text{GR}]\right).\end{array}$$ (9)

The change in the amount of cortisol in the cytoplasm (COR_in) is subject to the transport of the dimerized GR-COR complex into the nucleus. This is described by

$$\begin{array}{ll}F\left(,[{(\text{GR-COR})}_{\text{2,nu}}],[{\text{COR}}_{\text{in}}],[\text{GR}],\right)& :=\overline{k}\left(\frac{k_{2\text{ex}}{k}_{\text{GRC}}^2{k}_{\text{GRdim}}[{(\text{GR-COR})}_{\text{2,nu}}]}{{[{\text{COR}}_{\text{in}}]}^2·[\text{GR}]+[{\text{COR}}_{\text{in}}]·{[\text{GR}]}^2}\right)\\ & -\left(\frac{k_{2\text{in}}[{\text{COR}}_{\text{in}}]·[\text{GR}]}{([{\text{COR}}_{\text{in}}]+[\text{GR}])}\right),\end{array}$$ (10)

which follows from the assumption of the fast binding of cortisol and GR and the quick formation of the homodimer. A detailed derivation is provided in the Additional file 1.

The dimerized GR-COR complex is transported to the nucleus, where it acts as a transcription factor and binds to the respective DNA sites. In particular it binds in the promoter region of the GR gene and enhances the transcription of the GR RNA sequences

$$\frac{\mathrm{d}[\text{pmGR}]}{\mathrm{d}t}=-k_{\text{trs2}}[\text{pmGR}]+v_7+\frac{v_8[{(\text{GR-COR})}_{\text{2,nu}}]}{K_9+[{(\text{GR-COR})}_{\text{2,nu}}]}-d_{15}[\text{pmGR}],$$ (11)

which then are transported to the cytoplasm and translated to the GR protein.

The second gene regulated by the GR-COR complex is the Proopiomelanocortin gene POMC, which yields the ACTH peptide after post-translational cleavage. While the POMC gene is up-regulated by certain transcription factors (TFs) related to the CRH stimulus, it is down-regulated by the GR-COR complex. It has been observed that these two transcription factors counteract via competitive inhibition (cf. [53,56]), i.e. the binding of the GR-COR complex prevents the catalyzation of the POMC expression and thus down regulates the transcription. This can be described by the following equation for the transcribed RNA

$$\begin{array}{ll}\frac{\mathrm{d}[\text{pmPOMC}]}{\mathrm{d}t}& =v_5+\frac{v_6[{\text{TFs}}_{\text{nu}}]}{K_7\left(1+[{(\text{GR-COR})}_{\text{2,nu}}]/K_8\right)+[{\text{TFs}}_{\text{nu}}]}\\ & -k_{\text{trs1}}[\text{pmPOMC}]-d_{14}[\text{pmPOMC}].\end{array}$$ (12)

The GPCR mediated feedback control

The second pathway we consider in our model is the negative feedback on the release of ACTH via the glucocorticoid membrane receptor (GPCR), see Figure 3B. Concerning the production of the GPCR receptor we assume no regulation by means of other compounds and hence disregard the processes on the genomic level. With respect to the complex formation (COR-GPCR) we suppose a (quasi) equilibrium as it has been experimentally observed that two ligands bind to the receptor and exhibit positive cooperativity (cf. [43]).

The GPCR mediated feedback control only regulates the release of ACTH from intracellular vesicles. Again this mechanism counteracts the positive stimulus by CRH which is also detected via a membrane bound receptor (CRHR). It is well known that the anterior pituitary gland cells show a fast response to exposure with cortisol and CRH and that this is achieved by signaling cascades, directly relating the stimuli to the fusing of the vesicles (c.f. [36,37]). Consequently, we assume that the release of ACTH directly depends on the amount of formed receptor ligand complexes, where the catalysis of the CRH-receptor complex and the inhibitory effect of the cortisol-receptor complex are modeled as competitive inhibition. The following ODE describes the extracellular ACTH concentration

$$\begin{array}{l}\frac{\mathrm{d}[{\text{ACTH}}_{\text{ex}}]}{\mathrm{d}t}=\frac{V_{\text{in}}}{V_{\text{ex}}}\frac{k_{1\text{ex}}[\text{CRHR-CRH}]·[{\text{ACTH}}_{\text{in}}]}{K_4\left(1+[\text{GPCR-}{\text{(COR)}}_2]/K_5\right)+\text{CRHR-CRH}]}-d_3[{\text{ACTH}}_{\text{ex}}].\end{array}$$ (13)

The CRHR mediated feedback control

The last pathway we consider concerns the feedback mechanism related to CRH and the respective membrane receptor CRHR, see Figure 3C. The main effects are the stimulated release of ACTH and the enhanced expression of the POMC gene. The genomic effects of the CRH mediated feedback involve several transcription factors (the Nur factors, Tpit/Tbx19, Pitx1, cf. [53]), which catalyze the expression of the POMC gene. However, for keeping the complexity moderate we only incorporate a single CRH related transcription pathway into our model and denote the representative factor by TFs, see Equation (12). The alternative would be to model each of the transcription pathways separately at the cost of additional equations and parameters to be identified, for details on transcription modeling at different levels see, e.g., [57]. Consequently, we also model the catalyzed production of TFs only in a coarse manner, where we account for the fast signaling of the binding of CRH onto the production of TFs by a hill factor, leading to

$$\frac{\mathrm{d}[{\text{TFs}}_{\text{in}}]}{\mathrm{d}t}=\frac{V_{\text{nu}}}{V_{\text{in}}}{k}_{3\text{ex}}[{\text{TFs}}_{\text{nu}}]-k_{3\text{in}}[{\text{TFs}}_{\text{in}}]+\frac{v_4{[\text{CRHR-CRH}]}^h}{K_6^h+{[\text{CRHR-CRH}]}^h}-d_{12}[{\text{TFs}}_{\text{in}}].$$ (14)

Concerning the fast response to CRH stimulation it is the common hypothesis that the release of ACTH is regulated via a signaling cascade which is induced by the binding of CRH to the CRHR receptor in the cell membrane. Signaling cascades are very fast compared to other cellular processes. In fact the response to cortisol or CRH has been observed already after a few micro seconds (cf. [40,54,58,59]). Thus we assume an immediate effect of the membrane receptor complex formation on the release of ACTH, as modeled in the ODE (13).

Figure 2 gives a graphical outline of the complete model which is mathematically described by means of the following non-linear ODE system with 46 modeling parameters in 15 equations

$$\begin{array}{l}\frac{\mathrm{d}[{\text{COR}}_{\text{ex}}]}{\mathrm{d}t}=\frac{V_{\text{in}}}{V_{\text{ex}}}{k}_{\text{diff1}}([{\text{COR}}_{\text{in}}]-[{\text{COR}}_{\text{ex}}])+\frac{v_1[{\text{ACTH}}_{\text{ex}}]}{K_1+[{\text{ACTH}}_{\text{ex}}]}-d_1[{\text{COR}}_{\text{ex}}]\end{array}$$ (15)

$$\begin{array}{l}\frac{\mathrm{d}[\text{CRH}]}{\mathrm{d}t}=\frac{k_s\left(k_{\text{sb}}+\text{stress}\right)}{1+[{\text{COR}}_{\text{ex}}]/K_3}-d_2[\text{CRH}]\end{array}$$ (16)

$$\begin{array}{ll}\frac{\mathrm{d}[{\text{ACTH}}_{\text{ex}}]}{\mathrm{d}t}& =\frac{V_{\text{in}}}{V_{\text{ex}}}\frac{k_{1\text{ex}}[\text{CRHR-CRH}]·[{\text{ACTH}}_{\text{in}}]}{K_4\left(1+[\text{GPCR-}{\text{(COR)}}_2]/K_5\right)+[\text{CRHR-CRH}]}\\ & -d_3[{\text{ACTH}}_{\text{ex}}]\end{array}$$ (17)

$$\begin{array}{ll}\frac{\mathrm{d}[{\text{COR}}_{\text{in}}]}{\mathrm{d}t}& =k_{\text{diff1}}([{\text{COR}}_{\text{ex}}]-[{\text{COR}}_{\text{in}}])-d_4[{\text{COR}}_{\text{in}}]\\ & +F\left([{(\text{GR-COR})}_{\text{2,nu}}],[{\text{COR}}_{\text{in}}],[\text{GR}]\right)\end{array}$$ (18)

$$\begin{array}{ll}\frac{\mathrm{d}[{\text{ACTH}}_{\text{in}}]}{\mathrm{d}t}& =k_{\text{tl1}}[\text{mPOMC}]-d_5[{\text{ACTH}}_{\text{in}}]\\ & -\frac{k_{1\text{ex}}[\text{CRHR-CRH}]·[{\text{ACTH}}_{\text{in}}]}{K_4\left(1+[\text{GPCR-}{\text{(COR)}}_2]/K_5\right)+[\text{CRHR-CRH}]}\end{array}$$ (19)

$$\begin{array}{l}\frac{\mathrm{d}[\text{GPCR}]}{\mathrm{d}t}=v_2-d_6[\text{GPCR}]\end{array}$$ (20)

$$\begin{array}{l}\frac{\mathrm{d}[\text{CRHR}]}{\mathrm{d}t}=v_3-d_7[\text{CRHR}]\end{array}$$ (21)

$$\begin{array}{l}\frac{\mathrm{d}[\text{GR}]}{\mathrm{d}t}=k_{\text{tl2}}[\text{mGR}]+F\left([{(\text{GR-COR})}_{\text{2,nu}}],[{\text{COR}}_{\text{in}}],[\text{GR}]\right)-d_8[\text{GR}]\end{array}$$ (22)

$$\begin{array}{l}\frac{\mathrm{d}[{(\text{GR-COR})}_{\text{2,nu}}]}{\mathrm{d}t}=k_{2\text{in}}[{(\text{GR-COR})}_{\text{2,in}}]-k_{2\text{ex}}[{(\text{GR-COR})}_{\text{2,nu}}]-d_9[{(\text{GR-COR})}_{\text{2,nu}}]\end{array}$$ (23)

$$\begin{array}{l}\frac{\mathrm{d}[\text{mPOMC}]}{\mathrm{d}t}=\frac{V_{\text{nu}}}{V_{\text{in}}}{k}_{\text{trs1}}[\text{pmPOMC}]-d_{10}[\text{mPOMC}]\end{array}$$ (24)

$$\begin{array}{l}\frac{\mathrm{d}[\text{mGR}]}{\mathrm{d}t}=\frac{V_{\text{nu}}}{V_{\text{in}}}{k}_{\text{trs2}}[\text{pmGR}]-d_{11}[\text{mGR}]\end{array}$$ (25)

$$\begin{array}{ll}\frac{\mathrm{d}[{\text{TFs}}_{\text{in}}]}{\mathrm{d}t}& =\frac{V_{\text{nu}}}{V_{\text{in}}}{k}_{3\text{ex}}[{\text{TFs}}_{\text{nu}}]-k_{3\text{in}}[{\text{TFs}}_{\text{in}}]-d_{12}[{\text{TFs}}_{\text{in}}]\\ & +\frac{v_4{[\text{CRHR-CRH}]}^h}{K_6^h+{[\text{CRHR-CRH}]}^h}\end{array}$$ (26)

$$\begin{array}{l}\frac{\mathrm{d}[{\text{TFs}}_{\text{nu}}]}{\mathrm{d}t}=k_{3\text{in}}[{\text{TFs}}_{\text{in}}]-k_{3\text{ex}}[{\text{TFs}}_{\text{nu}}]-d_{13}[{\text{TFs}}_{\text{nu}}]\end{array}$$ (27)

$$\begin{array}{ll}\frac{\mathrm{d}[\text{pmPOMC}]}{\mathrm{d}t}& =-k_{\text{trs1}}[\text{pmPOMC}]+v_5-d_{14}[\text{pmPOMC}]\\ & +\frac{v_6[{\text{TFs}}_{\text{nu}}]}{K_7\left(1+[{(\text{GR-COR})}_{\text{2,nu}}]/K_8\right)+[{\text{TFs}}_{\text{nu}}]}\end{array}$$ (28)

$$\begin{array}{l}\frac{\mathrm{d}[\text{pmGR}]}{\mathrm{d}t}=-k_{\text{trs2}}[\text{pmGR}]+v_7+\frac{v_8[{(\text{GR-COR})}_{\text{2,nu}}]}{K_9+[{(\text{GR-COR})}_{\text{2,nu}}]}-d_{15}[\text{pmGR}],\end{array}$$ (29)

where

$$\begin{array}{ll}F\left([{(\text{GR-COR})}_{\text{2,nu}}],[{\text{COR}}_{\text{in}}],[\text{GR}]\right)& :=\overline{k}\left(\frac{k_{2\text{ex}}{k}_{\text{GRC}}^2{k}_{\text{GRdim}}[{(\text{GR-COR})}_{\text{2,nu}}]}{{[{\text{COR}}_{\text{in}}]}^2·[\text{GR}]+[{\text{COR}}_{\text{in}}]·{[\text{GR}]}^2}\right)\\ & -\left(\frac{k_{2\text{in}}[{\text{COR}}_{\text{in}}]·[\text{GR}]}{([{\text{COR}}_{\text{in}}]+[\text{GR}])}\right)\end{array}$$ (30)

with $\overline{k}=\frac{V_{\text{nu}}}{2V_{\text{in}}}$.

Model parameters

We now comment on the role of the parameters in our ODE model. We have three subsidiary parameters describing the average volumes of the three compartments V_in, V_ex and V_nu. These parameters are phenomenological and are fixed in the subsequent analysis.

Another class of parameters are the constants related to diffusion and transport of the compounds. In our model k_diff1, k_1ex, k_2in, k_2ex, k_3ex and k_3in comprise the list of these parameters. We do not explicitly model active transport, as this would involve additional regulatory species and mechanisms and consequently would lead to an even more complex model. Subsequently, we assume that the rate of diffusion/transport is constant on average.

The largest portion of model parameters is related to degradation processes whose rates are assumed to be proportional to the concentration of the respective species. The associated rate constants are denoted by d₁, d₂, …, d₁₄ and d₁₅.

As a consequence of the considered enzymatic reactions and ligand-receptor complexes the model includes several dissociation constants. Moreover, we have some constants arising due to the Michaelis-Menten approximations, i.e. the maximum reaction rates and the Michaelis-Menten constants. They are closely related to the dissociation constant of the respective complex and approximate them if the rate of the product formation dominates the degradation of the enzyme-substrate complex. k_GRdim, k_GC2, k_CRC and k_GRC denote the dissociation constants of the considered ligand-receptor complexes. K₁, K₃, …, K₉ denote the Michaelis-Menten constants of the respective enzyme-substrate complexes. v₁, k_s, k_sk_sb and v₄ denote the corresponding limiting rates of the Michaelis-Menten approximations.

Our description of the genomic mechanisms involves rates for transcription (v₅, v₆, v₇ and v₈), translation (k_tl1 and k_tl2) and transport (k_trs1 and k_trs2) of mRNA. We neglect the post-processing of mRNA as our focus is on the respective timescales and as the time delay is mainly due to the translocation. The constants v₂ and v₃ denote the production rate of the two membrane receptors. As we have not considered their regulatory mechanism we lumped the transcription and translation rate together.

Model training against data

The central idea of variational regularization is to augment the least-squares term that measures the mismatch between the data and the model with a penalizing term φ that guarantees the continuous dependence of the parameter solution on the data

$$\begin{array}{ll}& {∥x(q,{\rho }_1)-y_1^{\delta }∥}_2^2+{∥x(q,{\rho }_2)-y_2^{\delta }∥}_2^2+\alpha \phi (q)\to \underset{(q,{\rho }_1,{\rho }_2)}{\text{min}}\end{array}$$ (31)

$$\begin{array}{l}\text{subject to:}\dot{x}(q,{\rho }_k)=f(x,q)\end{array}$$ (32)

$$\begin{array}{l}x(q,{\rho }_k)={\rho }_{k}k\in \{1,2\}\end{array}$$ (33)

$$\begin{array}{l}c({\rho }_k)\le 0k\in \{1,2\}\end{array}$$ (34)

The ODE system (32) represents the HPA axis model of Figure 2 along with its parameter vector q of length 46. ρ₁ and ρ₂ in (33) denote the initial conditions corresponding to the two different experimental settings as described above and the two resulting data sets $y_1^{\delta }$ and $y_2^{\delta }$ displayed in Figure 5A. While the initial concentration of some species are known from the experimental setup and can be taken into account by the constraints (34), the remaining components of ρ₁, ρ₂ have to be estimated from the data as well. As the available amount of data is not sufficient to uniquely determine the model parameters, we have chosen a two step approach for finding the model components most relevant for reproducing the data. First, we applied classical Tikhonov regularization [45] and solved (31) with p = 2 in the penalty term

$$\phi (q)=\sum _i|q_i{|}^p$$ (35)

using a combination of global and local optimization routines. The resulting parameter vector q ^tik then served as an initial guess for solving (31) with a p-value less than one. Sparsity enforcing ℓ _p functionals with the choice 0 < p ≤ 1 aim at solutions whose less important components are driven to zero [60-62] and have been used in the context of parameter identification in [63,64]. For nonlinear inverse problems, the regularization properties of (35) with 0 < p ≤ 1 have been analyzed in [65,66]. Figure 7 displays the parameter vector q^∗ obtained for p = 0.9 in relation to q ^tik . The near zero components of q^∗ correspond to reactions and pathways that can rather be neglected in fitting the experimental data, see Figure 5B. In particular, the autocatalytic loop for the GR gene regulation, represented by the parameters k_trs, v₇, v₈, v₉, d₁₅, d₁₁, seems negligible with respect to the fast dynamics. Furthermore, the near zero value of K₆ indicates that the production of the TFs receptors is independent of CRH, i.e. the genomic part of the CRH related feedback.

Figure 7.

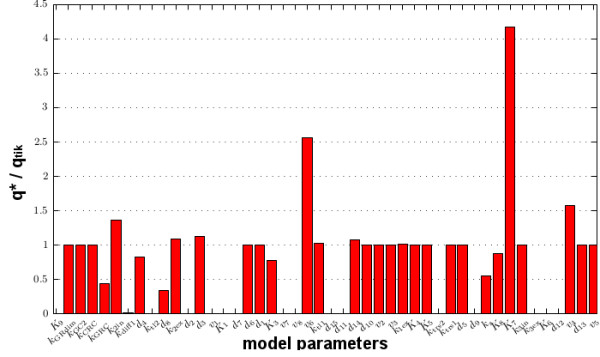
Comparison of parameter solutions for data fitting. Plot of q^∗/q^tik (in componentwise sense) with the parameter vectors q^∗ and q^tik as inferred from the experimental data of Figure 4A in a two step approach. The result shows that certain pathways of the model are of minor relevance for the reproduction of the experimentally observed dynamics as given in Figure 4B.

Origin of experimental data

Murine anterior pituitary AtT-20 cells (passage 12-24) were seeded and maintained as previously described [44]. After 92 hours of cell growth AtT-20 cells were exposed to doses of 10nM CRH and in addition 100nM cortisol. The supernatant was carefully removed from the cell layer after 1 minute to 1 hour of administration and centrifuged for 10 minutes with 800xg at 37°C. The concentration of ACTH-molecules in the cell-free supernatant was detected using Fluorescence Correlation Spectroscopy Immunoassay [44].

The AtT-20 cells (ATCC no. CCL-89) were purchased from the American Type Culture Collection (ATCC, Manassas, USA). Cell culture media and reagents were from Sigma (Sigma-Aldrich Inc., St. Louis, MI).

Competing interests

The authors declare that they have no competing interests.

Authors’ contributions

PK and CZ wrote the manuscript, discussed and simulated the HPA model, CZ developed the HPA model, MP conducted the lab experiments, MP and GK designed the lab experiments. All authors read and approved the final manuscript.

Supplementary Material

Additional file 1

Detailed derivation of the mathematical model.

Acknowledgements

Financial support by the Viennese Science and Technology Funds WWTF, project grant MA07–30, is kindly acknowledged.