Multi-resolution Shape Analysis via Non-Euclidean Wavelets: Applications to Mesh Segmentation and Surface Alignment Problems

Abstract

The analysis of 3-D shape meshes is a fundamental problem in computer vision, graphics, and medical imaging. Frequently, the needs of the application require that our analysis take a multi-resolution view of the shape’s local and global topology, and that the solution is consistent across multiple scales. Unfortunately, the preferred mathematical construct which offers this behavior in classical image/signal processing, Wavelets, is no longer applicable in this general setting (data with non-uniform topology). In particular, the traditional definition does not allow writing out an expansion for graphs that do not correspond to the uniformly sampled lattice (e.g., images). In this paper, we adapt recent results in harmonic analysis, to derive Non-Euclidean Wavelets based algorithms for a range of shape analysis problems in vision and medical imaging. We show how descriptors derived from the dual domain representation offer native multi-resolution behavior for characterizing local/global topology around vertices. With only minor modifications, the framework yields a method for extracting interest/key points from shapes, a surprisingly simple algorithm for 3-D shape segmentation (competitive with state of the art), and a method for surface alignment (without landmarks). We give an extensive set of comparison results on a large shape segmentation benchmark and derive a uniqueness theorem for the surface alignment problem.

1. Introduction

The representation of an image signal at different resolutions as a means to obtain invariance to scale is among the most fundamental concepts in computer vision. Its applications span interest point detection, denoising/filtering, and compression, and is often studied in vision as Scale space theory via its most common application (i.e., convolving a 2-D signal with a Gaussian kernel). A strong analog to this concept from the Signal processing domain, with similar utility but a different formalization, is Wavelets. Interestingly, even before the core ideas were formalized under this name, wavelet type methods were already being adopted to extract multi resolution image information by early pioneers of computer vision, see Koenderink [12], Marr [15], Witkin [22], and Rosenfeld [16]. Wavelets continue to be used today in low-level image processing tasks such as image enhancement and texture discrimination, and drives the design of feature extraction filters central to many computer vision methods.

The considerable success notwithstanding, the reader will notice that in the last decade of vision research, there are only few instances of wavelets and scale-space theory adopted in problems outside of the classical applications identified above. In general, it is difficult to find scenarios where wavelets/scale-space approaches were exploited in non-traditional ways within solutions to ‘new’ problems (i.e., distinct from filtering, denoising). In fact, even in applications where a multi-resolution perspective intuitively makes sense such as 3-D shape analysis and surface registration, the existing suite of solutions have been developed almost independently of wavelets/scale-space, and make little explicit use of multi-resolution theory. Part of the reason may be that the standard definition of a wavelet expansion is in Euclidean space: which means that for images, wavelets are defined on a uniformly sampled lattice. When restricted to this regime, the ‘natural’ applications that fall out are precisely those where these ideas are already deployed today.

The main goal of this work is to develop multi-resolution methods for shape analysis with an eye on two specific problems of interest: shape segmentation and surface alignment. The first problem of 3-D mesh segmentation deals with parsing the shape into perceptually meaningful regions and serves a key role in computer animation, texture mapping, morphing, and shape retrieval. Ideally, the algorithm should ignore local noise and instead focus on topological features that are globally meaningful. But the importance of a feature (or artifact) is invariably modulated by both its local and global context. By itself, this line of reasoning provides a strong motivation for a multi-resolution algorithm.

The second problem of 3-D surface alignment seeks the alignment of a pair of highly convoluted surfaces (e.g., brain cortical surface). A reasonable approach here will evaluate the relevance of each topological feature in approximating the underlying surface, and attempt to align these features in some order of their importance. Again, this reasoning suggests that a multi-resolution method will be a good fit. The natural mathematical construct, one which is natively multi-resolutional, is Wavelets. Unfortunately, writing a wavelet representation for the input datum for these problems is problematic, since traditionally wavelets are limited to the Euclidean setting. Notice that the meshes we operate on above are arbitrary, not uniformly sampled, and depend entirely on the objects they represent. Readers familiar with wavelets will instantly recognize that the bottleneck here is to come up with analogs of dilation and translation on the graph. Successfully defining all wavelet properties on the graph will enable a truly multi-resolutional analysis, and open the doors for extending wavelet theory to a range of 3-D shape analysis problems.

In this paper, we adapt an interesting set of recent results from harmonic analysis [8, 5] to derive efficient multi-resolution algorithms for shape analysis problems in computer vision. Briefly, instead of analyzing the structure in the original shape mesh, we approach these problems using spectral graph theory (i.e., via eigenvalues of the graph Laplacian). The spectral graph domain serves as an analog of the frequency domain in the Fourier transform. When combined with a few additional steps, the formalization allows obtaining the Wavelet transform of the shape of interest, and analyzing its characteristics at different bandwidths. Wavelet based signatures fall out nicely from this framework, which we call Wavelet Kernel Descriptor (WKD) and Maximum Wavelet Kernel Density (MWKD) field. These are the essential objects which allow obtaining perceptually based 3-D mesh segmentation and landmark-less registration of brain surfaces. The contributions of this work are:

1. Wavelet-based algorithms for multi-resolution shape analysis;

2. Mechanisms for obtaining perceptually meaningful segmentation of 3-D shape meshes with experiments on a large community benchmark;

3. An algorithm and uniqueness/optimality theorem for mesh alignment and its application to brain surfaces.

2. Definition and Key Properties of Wavelets

Wavelets are similar to the Fourier representation in that it uses a set of bases to decompose and construct a signal. However, while the Fourier transform is localized in frequency only, wavelets can be localized in both time and frequency [14]. The classic construction of wavelets is defined by a mother wavelet function ψ and a scaling function φ. Here, the mother wavelet ψ on x is a function of two parameters, the scale s and translation a:

$${\psi }_{s,a}(x)=\frac{1}{a}\psi (\frac{x-a}{s}).$$ (1)

The mother wavelet ψ_s,a(x), serves as a local support in the original domain [18] in the form of a localized oscillating function with finite duration. Various scales form bases that can be used to approximate a signal using wavelet expansion, and it is occasionally convenient to think of ψ as a band-pass filter. Using ψ, the wavelet transform of a signal f(x) is defined as the inner product of the wavelet and signal and can be represented as

$$W_f(s,a)=\langle f,\psi \rangle =\frac{1}{s}\int f(x){\psi }^{\ast }(\frac{x-a}{s})\mathrm{d}x,$$ (2)

where W_f(s, a) is the wavelet coefficient at scale s and at location a, and the function ψ* represents the complex conjugate of ψ. Such a transform is invertible, that is

$$f(x)=\frac{1}{C_{\psi }}\int \int W_f(s,a){\psi }_{s,a}(x)\mathrm{d}a\mathrm{d}s$$ (3)

where $C_{\psi }=\int \frac{{\mid \mathrm{\Psi }(j\omega )\mid }^2}{\mid \omega \mid }\mathrm{d}\omega <\infty$ is called the admissibility condition constant, Ψ is the Fourier transform of the wavelet [18], and ω denotes the frequency domain.

The scale (or resolution) parameter s controls the dilation of the basis and can be used to produce both short and long basis functions. While short basis functions correspond to high frequency components and are useful to isolate signal discontinuities, longer basis functions correspond to lower frequencies. In fact, wavelets transforms have an infinite set of possible basis functions unlike the single set of basis functions (sine and cosine) in the Fourier transform. Note that the results above are not directly applicable to non-uniform graph topologies such as those encountered in shape meshes and surfaces. One of our goals in later sections will be to utilize analogs of these properties.

3. Non-Euclidean Wavelets

Recent work in harmonic analysis [8, 5, 9] provides Wavelet bases on structured data which expresses in a wide spectrum of frequencies. The solution in [8] relies on the graph Fourier transform to derive a spectral graph wavelet transform (SGWT). This formalization is shown to preserve the localization properties at fine scales as well as other wavelets specific properties [11]. But beyond constructing the transform, we discuss how the operator-valued functions of the Laplacian are very useful to derive a powerful multi-resolution descriptor localized at different frequencies.

3.1. Deriving Multi Resolution Descriptors

In deriving Wavelet expansions of arbitrary graphs, the first problem is to formalize scaling. For a function f(n) defined on a vertex n of a graph, writing down f(sn) for a scaling parameter s is not meaningful due to the irregularity of the domain. This problem can be avoided by defining an operator $T_g^s=g(sL)$ in the dual domain using the graph Fourier transformation briefly introduced later. Here, the spectrum of the graph Laplacian is analogous to the frequency domain, where scales can be easily defined. This directly provides the key module in obtaining a multi-resolutional view of the signal localized at n. Indeed, for graphs, this gives a mechanism to simultaneously analyze various local topologically-based contexts around each vertex, at various resolutions. And for a specific scale s, we can now construct a kernel function g which act as band-pass filter in the frequency domain. When transformed back to the original domain, we directly obtain a representation of the signal for that resolution. Repeating this process for multiple scale/resolutions, the set of coefficients obtained for S scales gives a multi-resolutional descriptor for that vertex.

Given a mesh with N vertices, the graph Laplacian is computed as L = D − A, where A and D are the graph adjacency matrix and degree matrix. Then we obtain the orthonormal basis χ_l and eigenvalues λ_l, l ∈ {0, 1,…, N − 1} for the graph Laplacian. Using these bases, the forward and inverse graph Fourier transformation are defined using eigenvalues/eigenvectors of L simply as,

$$\widehat{f}(l)=\langle {\chi }_l,f\rangle =\sum _{n=1}^N{\chi }_l^{\ast }(n)f(n)$$ (4)

$$f(n)=\sum _{l=0}^{N-1}\widehat{f}(l){\chi }_l(n)$$ (5)

Using these transforms, we construct spectral graph wavelets by applying band-pass filters at multiple scales and localizing it with an impulse function. This is important: since the transformed impulse function in the frequency domain is equivalent to a unit function, the wavelet ψ localized by a delta function at vertex n can now be defined as,

$${\psi }_{s,n}(m)=T_g^s{\delta }_n=\sum _{l=0}^{N-1}g(s{\lambda }_l){\chi }_l^{\ast }(n){\chi }_l(m)$$ (6)

where m is a vertex index on the graph. With this in hand, the wavelet coefficients of a given function f(n) is given by the inner product of wavelets and the given function as well as the wavelet transform operator,

$$W_f(s,n)=(T_g^{s}f)(n)=\sum _{l=0}^{N-1}g(s{\lambda }_l)\widehat{f}(l){\chi }_l(n)$$ (7)

The coefficients obtained from the transformation yield a set of wavelet coefficients at each vertex n for each scale s. We further define Wavelet Kernel Descriptor (WKD) on vertex n as the self-effect of the wavelet localized on itself, and normalized at each resolution in the following manner.

$${\text{WKD}}_s(n)=\frac{{\psi }_{s,n}(n)-{min}_m{\psi }_{s,m}(m)}{{max}_m{\psi }_{s,m}(m)-{min}_m{\psi }_{s,m}(m)}$$ (8)

This descriptor is highly suitable for structured data where the underlying graph is weighted but no signal is defined on the vertices – for instance, a structured shape mesh where the edge weights are a function of the distance between a pair of mesh vertices. Intuitively, WKD represents the process of hitting the vertex with a ‘hammer’ (an impulse function) and computing the impact on the vertex as a function of its topology viewed at multiple resolutions. It may seem that obtaining eivenvectors of a large graph can be burdensome, but the contributions of the eigenvalues exponentially decay, and so computing them all is not necessary.

Final Remarks

Representation schemes for characterizing the shape-based contexts around key points has a rich history in computer vision. Most of this analysis is not natively multi-resolution and restricted to the Euclidean setting. The discussion above shows how the ideas can be expanded to the non-Euclidean space in a fully multi-resolution manner. Using these descriptors, we can derive new strategies for segmentation and alignment problems.

4. Interest Point detection on Shapes

WKD is a smooth function over the surface and encodes the behavior of the signal at various bandwidths via the resolution/scale parameter. Perceptually, those regions of a surface that ‘stand out’ are interpreted as key (or interest) points. So it seems natural to evaluate WKD peaks, and define the extremas of the WKD as the interest points. But it is not obvious that at which resolution the extremas of the function will yield interest points. Instead, we evaluate all resolutions concurrently and define an interest point field,

$$\text{MWKD}(n)=\underset{s}{max}({\text{WKD}}_s(n))$$ (9)

and then search for spatial extremas on the resultant MWKD field (which has the multi-resolution information in-built). We define the Wavelet Range (WR) as a set of vertices that are inside the influence of a wavelet centered at a certain vertex (i.e., absolute value is over a threshold η),

$${\text{WR}}_s(n)=\{m\in \mathcal{M}\mid \mid {\psi }_{s,n}(m)\mid \ge \eta \}$$ (10)

Observe that WR gives a range on the input graph which serves as a window, which generally is non-trivial to define in a non-Euclidean space. Varying the scale s controls the width of WR by changing the dilation of the wavelet localized at a vertex n. By defining MWKD field on the domain/manifold and range WR, we now obtain a 1-D density field. This is the input we search over to identify interest points on the mesh. The extrema finding algorithm is simple. It starts from a random seed center and finds the index of the maximum MWKD within the range of a wavelet effect defined on that point, and sets it as a new WR center. It iteratively searches for the maximas within the WR until it converges to a certain critical point. Starting from a moderately large r random seed points, it finds an arbitrary number of extremas – these extremas are the interest points. The number of interest points correspond directly to the clusters our segmentation method will use later. The choice of scale s and η enables the algorithm to find different number of interest points, thus can be adjusted (if desired) according to the size of the manifold and the spatial density of interest points desired. Regions where the WKD remains low across varying resolutions are unlikely to give key points.

Results

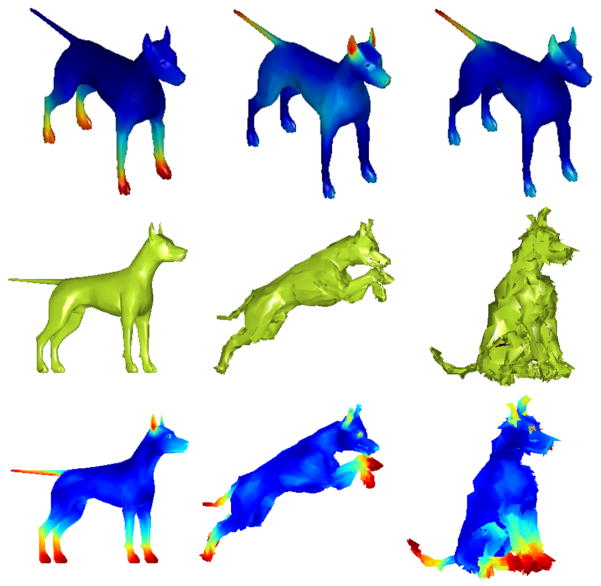
Representative examples of WKD and MWKD field are shown for a dog mesh in Fig. 2. The results highlight two aspects: a) the interest points correspond to regions found interesting at varying resolutions, and b) for a fixed resolution, the consistency of interest points detected under varying levels of noise and pose variation. In Fig. 2 first row, we see heat regions of interest points at scales 2, 10, and 34 (out of 50 in all). We see that for each distinct resolution, key points correspond to different regions of the mesh — lower parts of the leg, ears, and tip of the tail. In the second row, we introduce noise in mesh for the various deformations. Keeping the resolution fixed, even in the noisy setting, the key points detected are consistent across the three meshes highlighting the robustness and consistency of the method. Note that due to lack of standard benchmarks, we do not quantitatively evaluate the key point detection separately. Instead, it serves as a first step in our shape segmentation, evaluations of which will be presented shortly.

Figure 2.

Top row: WKD field in different resolutions. Middle row: Dog shape mesh with deformation and noise Bottom row: MWKD field on the dog mesh. The MWKD field seems consistent across shape/form variation and noise.

5. 3-D Shape Mesh Segmentation

It is well known that 3-D shape segmentation based only on information extracted from local topology may not yield results that are consistent with perceptual shape parsing and also suffer from high variablity in the presence of noise (since the underlying features may change abruptly as a function of noise). A powerful solution to these limitations has come from the design of algorithms based on diffusion. Methods such as Global Point Signature (GPS), Heat Kernels and Heat Mean Signature (HMS) [17, 21, 6] have been shown to be effective for the segmentation problem. Interestingly, a wavelet based algorithm inherits all diffusion specific properties (e.g., [5] articulates how wavelets directly tie to diffusion via a random walk based argument), and further provides native multi-resolution behavior via the key-points. Below, we describe a surprisingly simple and easy to implement method with the above properties, that yields results that are competitive to the state of the art.

The multi-resolution topology information is already encoded within the interest points which serve as the given segment ‘centers’. Therefore, what remains is to choose the coordinate representation of the points, an appropriate distance and a suitable off-the-shelf clustering method. First, we construct the coordinate of each vertex v̂(n) as,

$${\widehat{v}}_s(n)={(g(s{\lambda }_1){\chi }_1(n),\cdots ,g(s{\lambda }_k){\chi }_k(n))}^T,k\le l$$

where g(·) is the bandwidth kernel introduced in Section 3, and χ_j gives the j-th eigenvector of the Laplacian. To keep the clustering scheme as rudimentary as possible, we use Euclidean distance and apply a simple Nearest Neighbor clustering (with given centers).

Our actual cluster assignment procedure can be summarized in two steps: 1) Compute distance between the points to each of the key points (i.e., cluster centers), and 2) Assign each point to its closest key point. Of course, one can adopt more sophisticated schemes, but our purpose here is to underscore how even a scheme like this performs well if it has access to an informative representation. In our implementation, we used Mexican hat wavelet for kernel g, and k was chosen to be the number of IPs. Other types of wavelets can also be applied in the same manner and provide similar results, as long as they behave as a band-pass filter in the frequency domain.

Results

Our algorithm was applied to and evaluated on various existing 3D shape mesh datasets: non-rigid world [1], benchmark [3], deformation transfer for triangle meshes data [20], LIRIS/EPFL general purpose data [13], and SHREC [2]. We first present a qualitative/quantitative walk-through of various results and the algorithm’s behavior before summarizing benchmark comparisons.

A) Coarse to Fine behavior

First, in Fig. 3, we show the performance of the algorithm as a function of the resolution parameter s keeping the shape mesh fixed (by varying s for WR, we indirectly adjust the number of keypoints). In this example result, by adjusting this parameter, we can incrementally obtain a more detailed segmentation of the head, feet, and leg regions. The result in the third column looks to be the most meaningful segmentation, but the first two segmentations nonetheless correspond to perceptually meaningful components of the shape, albeit at a coarser scale.

Figure 3.

Giraffe shape mesh segmentation with different parameters. A finer scale s detects segments at smaller scales: (left to right) s = 5, s = 38, and s = 48 find 8, 10, and 14 segments respectively.

B) Robustness to deformations

Fig. 4 provides a representative example showing that keeping the resolution fixed, the segmentations obtained by the algorithm are highly robust to rather significant shape deformations and articulation of the mesh. For all six shapes, the segmentations are useful in that they correspond to the same body regions.

Figure 4.

Segmentation results of a centaur shape mesh undergoing deformations. Notice that the segments obtained by our algorithm are mostly consistent across the sequence.

C) Qualitative Results

To illustrate the perceptual relevance of the segments obtained by our algorithm on a variety of shapes, we provide a few representative examples in Fig. 5 (an extensive set of additional results is provided in the supplement). In the twelve examples shown here, if we consider each distinct object ‘part’ (hands, head, tail) as a segment, our method seems to provide good segmentations on a diverse set of real and man-made objects. An interesting case is the chess board shape mesh. Here, we observed that a coarse segmentation gives regions corresponding to the board and chess pieces. As we move to finer segmentations, the model captures topological regions for perceptually meaningful sub-parts of each chess piece. For these experiments, s was set to a value in the range of 1 to 30.

Figure 5.

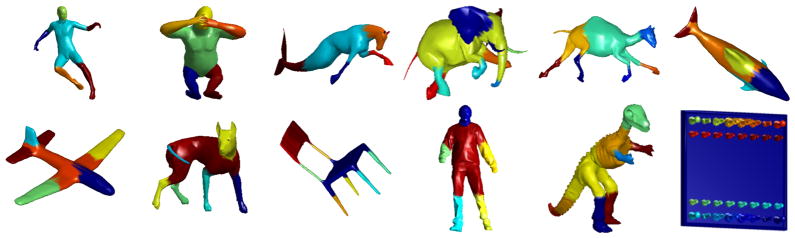
Segmentation results on meshes from various datasets

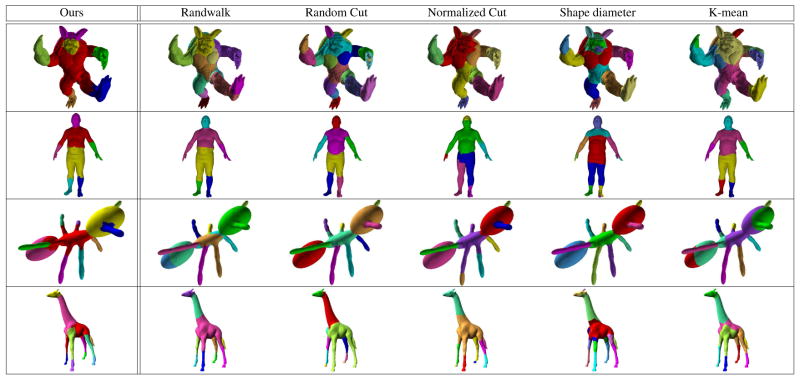
D) Comparisons on Shape Segmentation benchmark

We performed evaluations on a 3D mesh benchmark from [3] on 10 different classes (includes fourleg, human, glasses, airplane, ant, octopus, hand, plier, armadillo, and fish meshes). A few of the classes in the dataset were discarded because the sub-components were nearly flat/rectillinear where all methods work well. Ground truth is provided in this dataset. We performed comparisons with a set of state of the art shape segmentation methods used in this benchmark analysis [3]. These are denoted as Shape Random Walks (SRW), Shape Random cuts (SRC), Shape Normalized cut (SNC), Shape K-means (SKM), and Shape Diameter (SD). When needed by an algorithm, the number of segments was manually specified. The first ten surfaces from each category were used to evaluate the result. We fixed parameters for our method for each category. Our results evaluate two different measures, cut discrepancy (CD) and random index (RI), both used in [3]. The first measures variation between the segmented and ground truth boundaries whereas the second measures the likelihood that a pair of faces are either in the same segment in different segmentations, see [3] for details. Table 2 presents the summaries of these comparisons. We see that while our error summaries are not the best overall, the quality of segmentations given by our algorithm is highly competitive (among the best three) with the top shape segmentation methods available today. This behavior underscore the utility of a wavelet based model since the segmentation is driven by the multi-resolution encoding rather than a powerful clustering scheme.

Table 2.

User study summary on shapes from eight classes.

Category	Ant	Chair	Horse	Hand	Armadillo	Human	Fish	Airplane
Ours	3.07	3.33	2.8	2.93	2.47	3	3.2	3.2
SKM	1.33	2.93	2.6	1.2	1.8	2.67	2.2	1.5
RW	1.87	2.13	2.4	2.8	2.8	2.73	2	2.5
RC	3.73	1.6	2.2	3.07	2.93	1.6	2.6	2.8

E) User study

A majority of shape mesh datasets used here (except the benchmark above) did not provide ground truth segmentations. To quantitatively evaluate the performance of our model relative to other methods on these meshes, we setup a user study using a population of 15 subjects (11 Male, 4 Female, mean age 27.8). Each rater was asked to assess segmentation of four different methods (ours versus SRW, SRC, SNC, SKM, SD) on a set of 8 shape meshes (chosen so that diverse shape types are well represented). Users were blind to the method’s names and ranked the results from best (4) to worst (1). Then, the mean score for each class was computed, shown in Table 2. Our proposed method was best ranked in six out of eight categories, which suggests that the results were perceptually meaningful.

6. Wavelets based Alignment of 3-D Surfaces

Finally, we evaluate the effectiveness of multi-resolution wavelet based methods for deriving novel algorithms for alignment of a pair of 3-D surfaces. This is an important problem in brain imaging, where scientists are interested in identifying disease specific effects on measures such as cortical thickness (which can be thought of a function defined on the surface). The most popular method available today are based on expansions in terms of a global Fourier basis. For example, weighted Spherical Harmonics can be used to represent the convoluted brain surface and the function defined on it, see [19, 7, 4]. Since applying SPHARM involves first transforming/projecting the data on to a sphere, it invariably introduces some distortion. Nonetheless, once the projection on the sphere is obtained, alignment/registration is a simpler problem. Our goal here is to evaluate whether the framework developed in this paper can yield algorithms that avoid the sphere mapping step altogether, and perform direct alignment of the given surfaces accurately.

We will define the wavelet basis on a surface manifold (i.e., an arbitrary mesh graph). Each vertex v is represented in Cartesian coordinate as v = (v₁, v₂, v₃). These coordinates v_i across all the vertices in are modeled as,

$$v_i(n)=h_i(n)+{\epsilon }_i(n),$$ (11)

where ε_i is a zero mean random noises, and n is the vertex index. Traditionally, the unknown smooth function h_i(·) is estimated via harmonic representation using Fourier basis in the Euclidean space. But if we know that our domain of analysis is a discrete manifold , which is a subset of the Euclidean space, we can obtain more efficient methods. Coordinates h_i are conventionally estimated by minimizing the integral of weighted L₂-norm of difference as

$${\widehat{h}}_i(n)=arg\underset{h\in \mathcal{M}}{min}{\int }_{\mathcal{M}}{\mid v_i(m)-h(m)\mid }^{2}d\mu (m)$$ (12)

Interestingly, the minimization of (12) can be obtained via the graph Fourier transform as

$${\widehat{h}}_i(n)=\sum _{l=0}^{N-1}\langle v_i,{\chi }_l\rangle {\chi }_l(n),$$ (13)

where N is the total number of vertices in 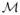. Recall that a disadvantage of the Fourier transform is that it is only localized in frequency: sudden changes in a function cannot be fully reconstructed using Fourier bases which leads to ringing artifacts. But wavelets are localized in both space and frequency, and wavelets with local support gives a solution to problems caused by the infinite support of Fourier bases. Next, we derive a result which translates this advantage to (12) for registration.

Define a subspace H_k spanned by up to the k-th degree graph Fourier bases, ${\mathcal{H}}_k=\{{\sum }_{l=0}^k{\beta }_l{\chi }_l(m)\mid x{\beta }_l\in ℝ\}$ The discrete convolution of a function f with the wavelet on a manifold is defined as

$${\psi }_s★f(n)=\sum _{l=0}^{N-1}g(s{\lambda }_l)\widehat{f}(l){\chi }_l(n)$$ (14)

Observe that convolution is the same as the spectral graph wavelet transformation described before. The following result proves that the solution to (12) can be obtained using these wavelet bases.

Theorem 1

$$\sum _{l=0}^{N-1}g(s{\lambda }_l)\langle v_i,{\chi }_l\rangle {\chi }_l=arg\underset{h\in {\mathcal{H}}_k}{min}{\int }_{\mathcal{M}}{\int }_{\mathcal{M}}{\psi }_{s,n}(m){\mid v_i(m)-h(n)\mid }^2\mathrm{d}n\mathrm{d}m,$$

where n and m are indices on manifold .

Proof

Let $h(n)={\sum }_{l=0}^{N-1}{\beta }_l{\chi }_l(n)$ where β_l is the l-th degree coefficient (unknown). The inner integral I can be rewritten as

$$I={\int }_{\mathcal{M}}{\psi }_{s,n}(m){\left|v_i(m)-\sum _{l=0}^{N-1}{\beta }_l{\chi }_l(n)\right|}^2\mathrm{d}n.$$

This can be further written as

$$I=\sum _{l=0}^{N-1}\sum _{\overline{l}=0}^{N-1}{\chi }_l(m){\chi }_{\overline{l}}(m){\beta }_l{\beta }_{\overline{l}}-2{\psi }_s\ast v_i(m)\sum _{l=0}^{N-1}{\beta }_l\chi (m)+{\psi }_s\ast v_i^2(m).$$

The outer integral is a quadratic function of β_l given by

$${\int }_{\mathcal{M}}I\mathrm{d}m=\sum _{l=0}^{N-1}{\beta }_l^2-2\sum _{l=0}^{N-1}g(s{\lambda }_l)\langle v_i,{\chi }_l\rangle {\beta }_l+\sum _{l=0}^{N-1}g(s{\lambda }_l)\langle v_i^2,{\chi }_l\rangle .$$

The minimum of the above expression is achieved when the partial derivatives of I repect to β_l are all set to zero:

$${\int }_{\mathcal{M}}\frac{\partial I}{\partial {\beta }_l}\mathrm{d}m=2{\beta }_l-2_g(s{\lambda }_l)\langle v_i,{\chi }_l\rangle =0$$

Therefore, β_l = g(sλ_l)〈v_i, χ_l〉 and ${\sum }_{l=0}^{N-1}g(s{\lambda }_l)\langle v_i,{\chi }_l\rangle {\chi }_l$ is the unique minimizer.

The theorem shows that the objective function is minimized when the coefficient β_l is the wavelet coefficient of v_i. Further, we can force one manifold to have the same topological structure as another by resampling the wavelet coefficients from the second manifold and reconstructing it. Finally, vertex-wise matching can be obtained simply by solving for the minimum of the difference of a set of wavelet coefficients, which is exactly WD defined in Section 3. Once corresponding landmarks are found by this scheme, a simplified version of an inexact diffeomorphic registration routine from [10] can be used. Note that finding putative matches is the major bottleneck in most of diffeomorphic registration methods, and Thm.1 suggests a workaround. We next show our results for vertex matching and surface alignment which ensures that the two surfaces have identical mesh topology.

Results

In order to evaluate the ideas above, we obtained a set of brain surface data that were affinely normalized. We applied registration as follows. The first surface is the template surface and the second surface is a floating brain surface. When applied to a population of subjects, one may choose one individual’s brain surface as the template (or atlas) and deform all other surfaces to it.

Fig. 7 presents a representative registration result. Here, each surface consists of 6146 and 6555 vertices respectively and corresponds to a distinct cortical shape. Finding the vertices on the subject surface with minimum ℓ₂ norm of vertex-wise wavelet coefficient difference from a vertex on the template surface, we can identify the correspondence from one vertex to another. To visualize this surface registration, the 5th eigenfunction of the template surface is mapped to the subject surface using the correspondence information, and Fig. 7 (a) shows the correspondence result. If the vertex correspondence were not properly done, the eigenfunction of the template would be mapped to a different positions on the other surface. Note that each surface has different mesh topologies, therefore pre-registration surfaces have different eigenfunctions — Fig. 7 (b) shows visually that the 5th eigenfunctions are originally different on each surface. After finding correspondences, we transform the floating surface to have the same topology as the template. The wavelet coefficients on each vertex in a subject/floating surface are sampled (using the correspondences) and the surface is reconstructed using the wavelet bases of the template surface. The result of this transform is shown in Fig. 7 (c). The 20th eigenfunction of the template and transform surface are shown together (similar colors in similarly placed regions).

Figure 7.

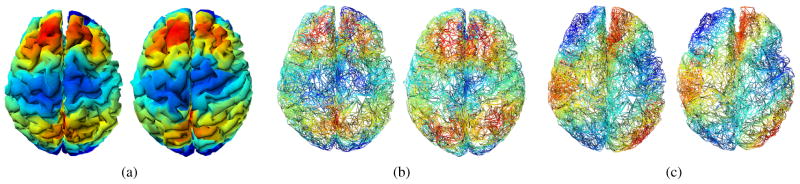
a) The 5th eigenfunction of the template surface is mapped by the wavelet registration. b) Mesh representation of two different brain surfaces and their 5th eigenfunctions. Each has different mesh topology with different eigenfunctions. c) Transformed surfaces into the template surface and its 20th eigenfunction. The surfaces are aligned in the same topology.

Group Analysis

Finally, we applied the alignment method for statistical group analysis on 16 autism subjects and 11 healthy controls. The cortical surfaces had a cortical thickness signal defined on the surface, and the question is whether this measure statistically varies between the two groups (such analysis can only be performed post-registration). Each surface had 10241 vertices but different mesh topology, so cannot be compared directly. Setting one surface in the dataset as a template surface and the others as floating surfaces, our algorithm was used find the alignment. Applying a two-sample t-test on the two groups on the cortical thickness signal, we identified 319 vertices statistically significant p-values (uncorrected p < 0.05), which is 3.1% of the total vertices. This provides a proof-of-principle evaluation that the registration preserved the underlying signal differences, and is meaningful.

7. Conclusions

This paper demonstrates how non-Euclidean wavelet theory provides multi-resolutional capabilities for a range of 3-D shape analysis problems in Computer Vision. We give algorithms for interest point detection, perceptually meaningful shape mesh segmentation, and surface alignmen. The segmentation results are comtetitive with other state-of-art methods, and registration result shows promising fields of applications as well. The implementation will be available at http://pages.cs.wisc.edu/~wonhwa/.

Figure 1.

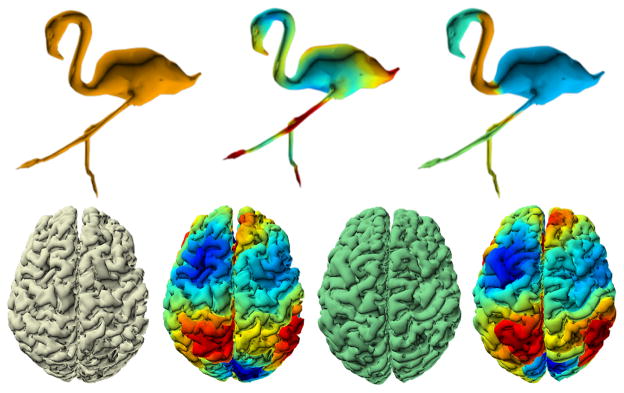
(Top) Segmentations at different resolutions provide coarse-to-fine partitioning of a flamingo shape mesh. (Bottom) Surface alignment of two different brain surfaces, color coding refers to a wavelet kernel field: similar colors in the two surfaces are potentially similar regions.

Figure 6.

Comparison of the results with other method from shape segmentation benchmark.

Table 1.

Error evaluation of using 3-D mesh benchmark.

Category	Ours	SRC	SNC	SRW	SKM	SD
CD	0.285	0.222	0.335	0.276	0.355	0.277
RI	0.173	0.219	0.210	0.170	0.212	0.182