The Distribution of Word Matches Between Markovian Sequences with Periodic Boundary Conditions

Abstract

Word match counts have traditionally been proposed as an alignment-free measure of similarity for biological sequences. The D₂ statistic, which simply counts the number of exact word matches between two sequences, is a useful test bed for developing rigorous mathematical results, which can then be extended to more biologically useful measures. The distributional properties of the D₂ statistic under the null hypothesis of identically and independently distributed letters have been studied extensively, but no comprehensive study of the D₂ distribution for biologically more realistic higher-order Markovian sequences exists. Here we derive exact formulas for the mean and variance of the D₂ statistic for Markovian sequences of any order, and demonstrate through Monte Carlo simulations that the entire distribution is accurately characterized by a Pólya-Aeppli distribution for sequence lengths of biological interest. The approach is novel in that Markovian dependency is defined for sequences with periodic boundary conditions, and this enables exact analytic formulas for the mean and variance to be derived. We also carry out a preliminary comparison between the approximate D₂ distribution computed with the theoretical mean and variance under a Markovian hypothesis and an empirical D₂ distribution from the human genome.

1. Introduction

The D₂ statistic is defined as the number of short word matches of a given pre-specified length k between two sequences of letters from a finite alphabet . This statistic was first analyzed in the precise form studied below by Lippert et al. (2002). It was motivated by more general statistics based on word counts proposed by Blaisdell (1986), and by a statistic defined as a sum over word lengths of weighted inner products of word counts, known as d² (Torney et al., 1990; Hide et al., 1994). Such statistics have been proposed as a measure of similarity between biological sequences in cases where the more commonly used alignment methods may not be appropriate. A review of word-based alignment-free sequence comparison measures in existence at or about the time of the Lippert et al. article [including angle metrics (Stuart et al., 2002a, b), which bear considerable similarity to D₂] can be found in Vinga and Almeida (2003).

In subsequent developments, a number of variants of the D₂ statistic have been studied and analyzed. A shortcoming of the D₂ statistic, first noted by Lippert et al. (2002), is that the signal of biological sequence similarity one is trying to detect, namely, simultaneous over-representation of certain words in both sequences, is masked by the natural variability of word counts in each of the two sequences. This is most likely to be a problem for longer sequences, although perhaps not for sequences of short to moderate length (Burden et al., 2012a). To address this problem, Reinert et al. (2009) introduced centered and standardized statistics, which were demonstrated to have higher power to detect sequence similarity (Wan et al., 2010). Other variations on the D₂ statistic include allowing word matches up to a certain number of mismatches (Burden et al., 2008) for detecting regulatory modules (Forêt et al., 2006, 2009a; Göke et al., 2012), and the introduction of weighting factors to acknowledge chemically similar amino acids when studying protein sequences (Jing et al., 2011; Burden et al., 2012b).

The distributional properties of the D₂ statistic under the null hypothesis of sequences composed of independently and identically distributed (i.i.d.) letters have been studied extensively. Rigorous results for limiting asymptotic distributions have been derived for D₂ by Lippert et al. (2002) and Kantorovitz et al. (2006) and for D₂ with mismatches by Burden et al. (2008). Exact analytic formulas exist for the mean (Waterman, 1995) and variance (Kantorovitz et al., 2006; Forêt et al., 2009b) of D₂, and of the weighted (Jing et al., 2011) and centered (Burden et al., 2012a) versions of D₂. Accurate approximations to distribution of D₂ and its variants in terms of gamma and Pólya-Aeppli (or compound Poisson) distributions have been demonstrated via Monte Carlo simulations by Forêt et al. (2009a,b), Jing et al. (2011), and Burden et al. (2012a), allowing for fast and practical calculations of approximate p values under the i.i.d. null hypothesis.

However, analysis of the k-mer spectra of the genomes of several species by Chor et al. (2009a) provides strong evidence that genomic sequences are more appropriately modeled as having a Markovian dependence, possibly up to fifth order. In the current work, we extend previous exact analytic results for the mean, variance, and an empirical distribution of D₂ for i.i.d. sequences to the case of Markovian sequences. A previous study of this problem, with some approximations, has been carried out by Kantorovitz et al. (2007) in the process of developing a method for detecting regulatory modules in genomic sequences.

The current study differs in that we consider sequences with periodic boundary conditions (PBCs), for which we introduce a new definition of Markovian sequences. For i.i.d. sequences, Forêt et al. (2009b) have found imposition of PBCs to be an approximation that works well for biologically realistic sequences. In practice, PBCs are imposed on the D₂ calculation for finite-length biological sequences simply by sewing the ends together and including in the word count words that overlap the join. The motivation for the restriction to periodic sequences is that it simplifies calculations of the mean and variance, enabling exact analytic formulas that are readily computable on a laptop computer to double precision accuracy for arbitrary sequence lengths. They also enable accurate practical approximations to the D₂ distribution under the null hypothesis of Markovian sequences for biologically realistic parameter values. The approximation does not model boundary effects, but it does capture accurately the more important effect of nonindependence of overlapping words (see terms V₁ to V₄ in the variance formula, Section 3.3).

The layout of the article is as follows: In Section 2, we define Markovian sequences of arbitrary order with PBCs in terms of an algorithm for generating such sequences. In Section 3, we define the D₂ statistic and derive exact analytic formulas for its mean and variance for Markovian sequences. In Section 4, the accuracy of the mean and variance formulas is checked numerically, and hypothesized asymptotic distributions are demonstrated to provide accurate representations of the complete D₂ distribution. These distributions are compared with empirical distributions of D₂ from the human genome. Conclusions are drawn in Section 5. Technical details of the derivation of Var (D₂) are given in the Appendix, and computer codes for evaluating the mean and variance are given in the Supplementary Material (Supplementary Material is available online at www.liebertonline.com/cmb).

2. Definitions

Consider a sequence of letters from an alphabet 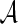of size d. We say that x has periodic boundary conditions (PBCs) and is of length m if x_i+m = x_i for all .

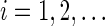A sequence 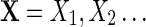of random letters has a θ-th order Markovian dependence if

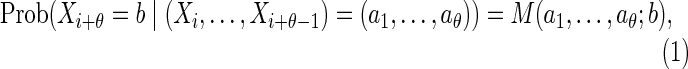for a specified d^θ × d matrix M satisfying

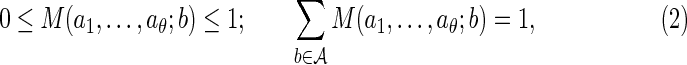for all 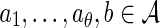. As a shorthand notation, we will write a string of length θ with an arrow above:

and write any substring of X of length θ in a similar fashion, labeled by the index of the first element:

Thus, Equation (1) is written more compactly as

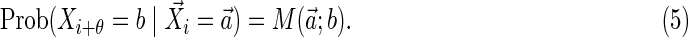Following the notation of Reinert et al. (2005), define a d^θ × d^θ square matrix 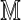as

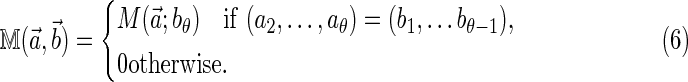Then the Markovian dependency can be written as a first-order Markovian dependency as

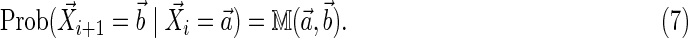2.1. Markovian sequences with PBCs

Given an order θ transition matrix M, we first attempt to define a periodic random sequence 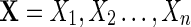of length n via the following algorithm:

Step 0: Choose a probability distribution on the set of strings of length 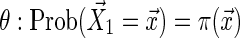, where 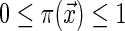and .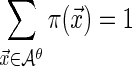

Step 1: Generate 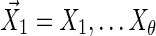from this distribution.

Step 2: Generate 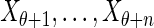using Equation (5).

Step 3: If 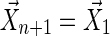, accept the sequence 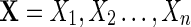, otherwise repeat from Step 1 until an accepted sequence is obtained.

Clearly this algorithm entails that

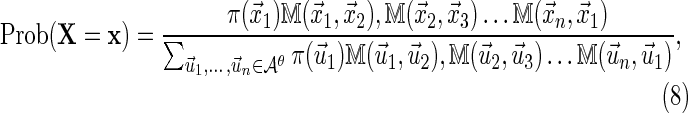where 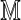is the transition matrix of the equivalent-first order Markov chain defined by Equation (6). The idea behind PBCs is that there should be no privileged position along the sequence from which to begin numbering. Thus, we further impose a condition that the sequence should have no privileged starting point, that is, for each ,

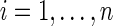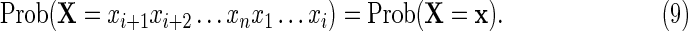Equations (8) and (9) imply that 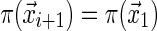for each i and for every sequence 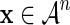, which can only happen if

This leads to the following definition:

Definition Given a transition matrix M of order θ, a random Markovian sequence with PBCs of length n is one generated by the algorithm of Section 2.1 with the initial distribution π in Step 0 equal to the uniform distribution Equation (10).

It follows from Equation (8) that for a random Markovian sequence X of length n, the probability of the configuration 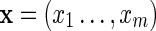occurring is

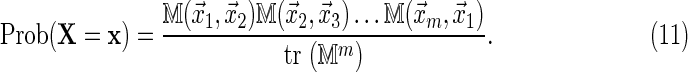The distribution Equation (11) has also been proposed by Percus and Percus (2006), who made an extensive study of the probability distribution of words on periodic sequences, which they refer to as rings. Our approach is novel in that it gives an algorithm that can be implemented in practice to generate an ensemble of such sequences.

3. The D₂ Statistic

3.1. Definition of D₂

Definition Given two random sequences X and Y with PBCs of length m and n, respectively, the D₂ statistic is defined as the number of k-word matches, including overlaps, between X and Y:

where

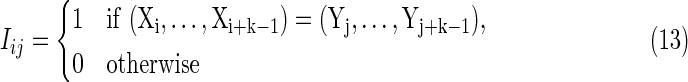is the word match indicator random variable for words length k positioned at site i in sequence X and site j in sequence Y.

Two Markovian sequences X and Y of order θ generated by the d^θ × d matrix M define a random variable D₂(k, M). By Equation (7), an equivalent specification of this situation is a pair of first-order Markovian sequences 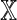and 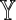consisting of letters of an alphabet of size d^θ generated by the square matrix 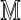defined by Equation (6). The sparse structure of 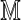ensures that the set of possible sequence pairs 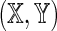is in one-to-one correspondence with the set of possible sequence pairs (X, Y), and furthermore, for k ≥ θ, a word match of length k between X and Y is equivalent to a word match of length k − θ + 1 between 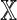and 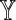. It follows that the distributional properties of D₂ for Markovian sequences can be determined in terms of the properties of D₂ for an equivalent first-order system:

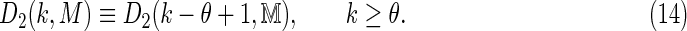3.2. D₂ mean for arbitrary θ

Below we derive an exact formula for E(D₂) for arbitrary-order Markovian sequences. In principle, the mean for any k ≥ θ case can be derived in terms of an equivalent θ = 1 case. However, here we give an ab initio proof for any θ, noting that, for k ≥ θ, the result is consistent with Equation (14).

Define the Hadamard product 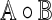of two matrices 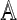and 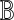as the matrix whose (α, β)-th element is

The mean of D₂ is

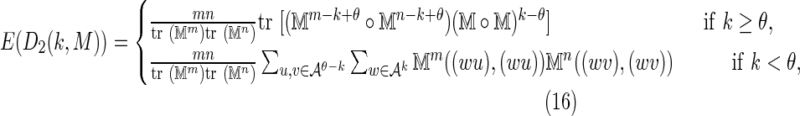where 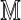is defined by Equation (6), (wu) means the θ-tuple 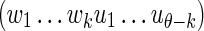, and similarly for (wv).

Proof: We have that

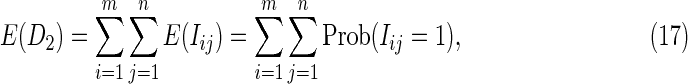where

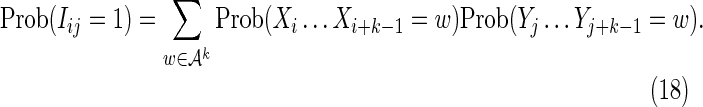To calculate 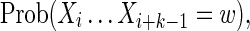we must consider separately the cases k ≥ θ and k < θ.

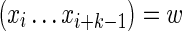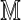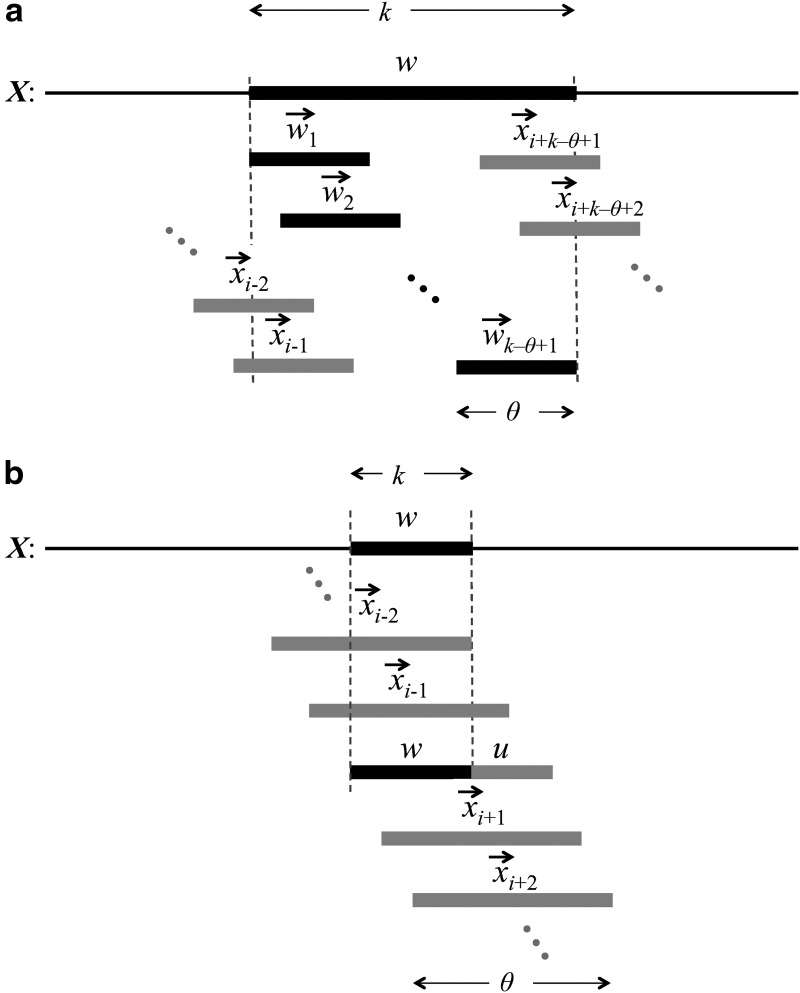
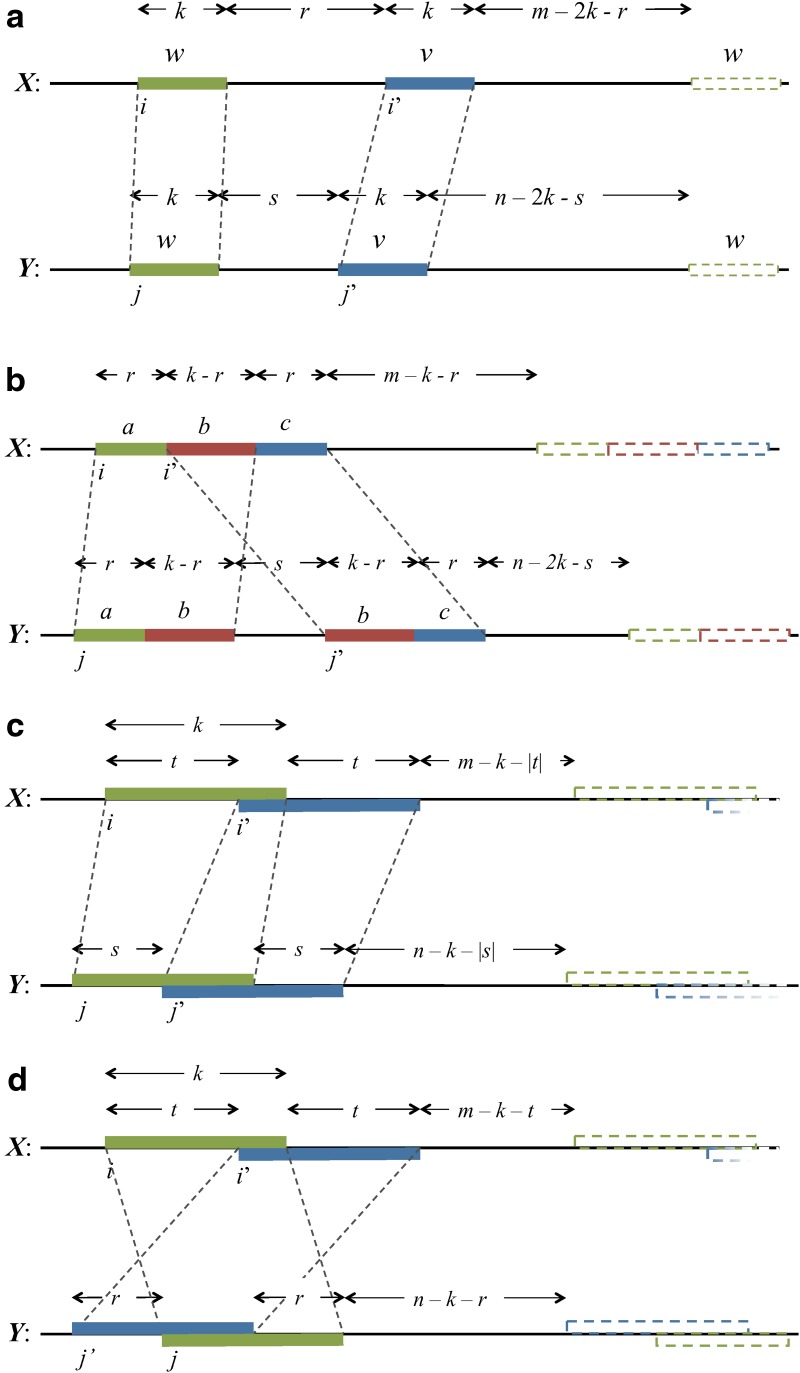
Consider first the case where k ≥ θ. The required probability is calculated by summing Equation (11) over all sequences x subject to the restriction that . The definition of the matrix , Equation (6), ensures that it is sufficient to restrict only those θ-tuples 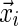located within the word w, because contributions to the sum from any partially overlapping θ-tuples will be zero unless the overlap letters match those of w (see Fig. 1a). Thus

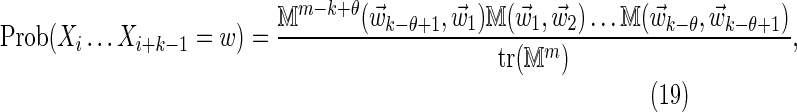FIG. 1.

Covering of the sequence X with θ-mers for the calculation of 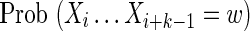(a) in the case where k ≥ θ, and (b) in the case where k < θ.

where the θ-tuples 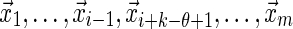have been summed over. Similarly we have

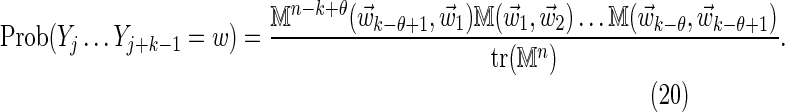The definition Equation (6) of the matrix M ensures that the sum over the k-word w in Equation (18) is equivalent to a sum over a set of independent θ-tuples 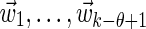. Thus, substituting Equations (19) and (20) into Equation (18) gives

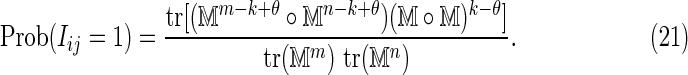Equation (17) then gives the required result for the case k ≥ θ.

For the case k < θ, the 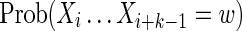is again calculated by summing Equation (11) over all sequences x such that 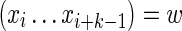. In this case, it is sufficient to restrict any one of the θ-tuples overlapping w to equal w on the overlap, and the structure of 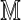will ensure that only terms in which the other overlapping θ-tuples match w will contribute to the sum. Accordingly set 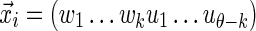, where the 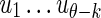are not fixed (see Fig. 1b). Then

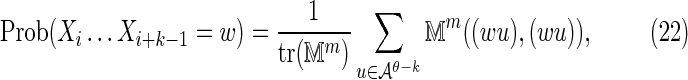and similarly

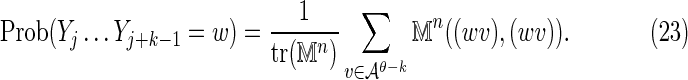Substituting these two probabilities into Equations (18) and (17) gives the required result.   ■

3.3. D₂ variance for k ≥ θ

For k ≥ θ, Equation (14) ensures that any θ > 1 case can be reduced to an equivalent θ = 1 case via the relation

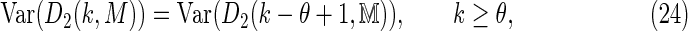where 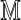is a square first-order Markov matrix. Even for θ = 1, the exact variance of D₂ for Markovian sequences with PBCs requires an extensive calculation. Here we give a summary of the θ = 1 result, and leave the technical details of the derivation to the Appendix. The case k < θ remains intractable.

For the remainder of this section, we take M to be a square d × d first-order Markov matrix. We have

The second term can be calculated from Equation (16). The first term is a sum of contributions obtained from Equation (12) by partitioning a sum over words beginning at positions i and i′ in sequence X and beginning at j and j′ in sequence Y,

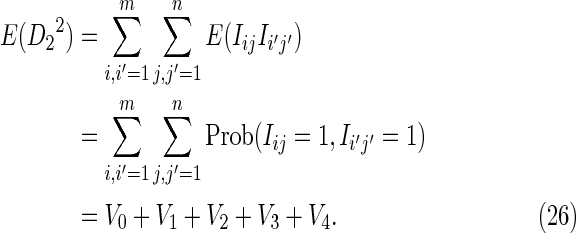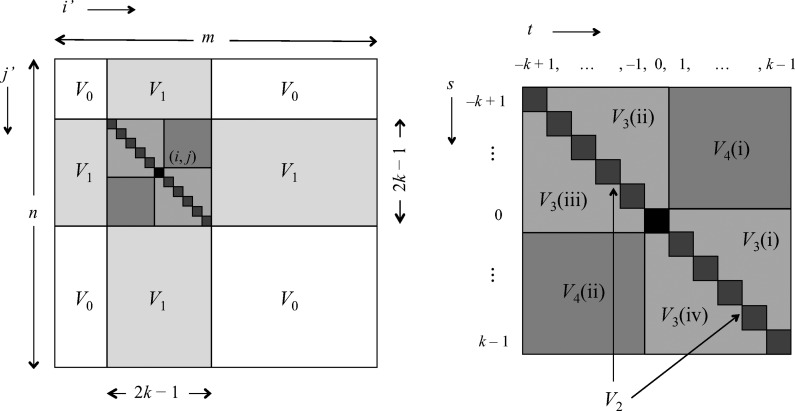
The partitioning reflects the degree of overlap between words in each of the two sequences, and is illustrated in Figure 2. We assume m,n ≥ 2k, which will almost certainly be the case in any biological application.

FIG. 2.

Contributions to Var(D₂) via the sum in Equation (26). The left-hand diagram shows the (i′, j′)-plane for a fixed value of (i, j), shown as the black square. The right-hand diagram is an expanded view of the “accordion” region −k + 1 ≤ s, t ≤ k − 1, where t = i′ − i and s = j′ − j up to PBCs [see Equations (41) and (42)].

We will write a Hadamard product of q factors, 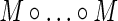, using the shorthand notation M^∘q. With this notation, the contributions to E(D ₂²) are:

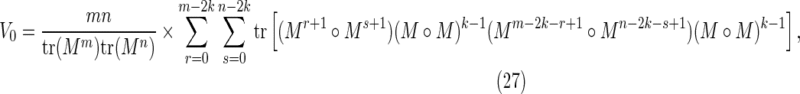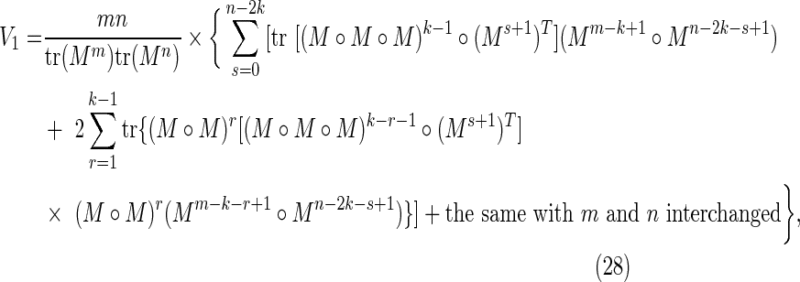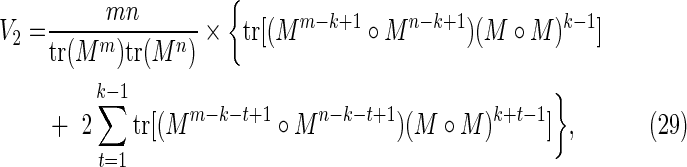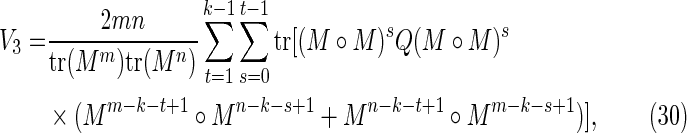where

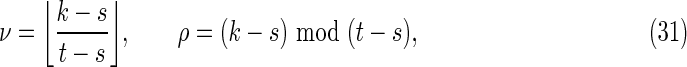and

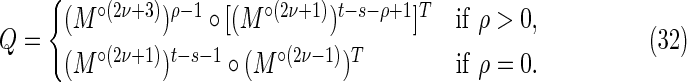Finally,

where

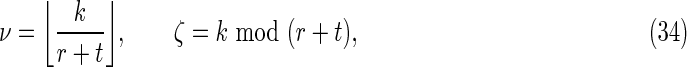and

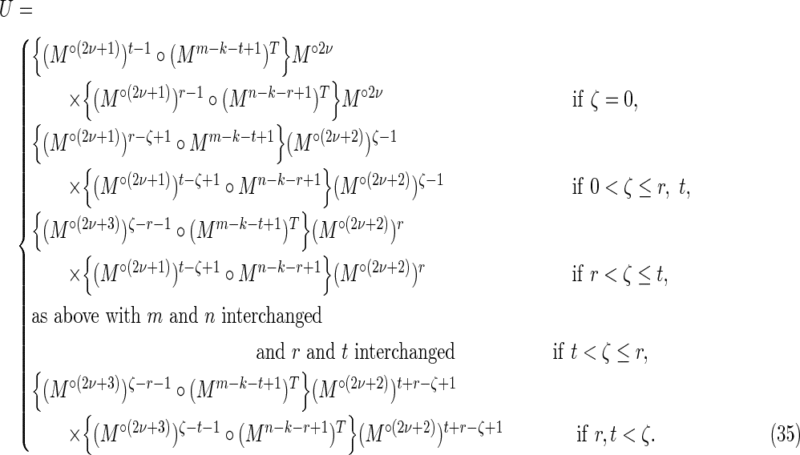A full derivation of these contributions is given in the Appendix.

3.4. Computational advantages of PBCs

One could, in principle, define D₂ more conventionally without imposing PBCs by considering standard Markov chains and stopping the sums in Equation (12) at n − k + 1 and m − k + 1, respectively. This is the approach used by Kantorovitz et al. (2007). However, the PBCs confer two computational advantages that allow the mean and variance to be calculated to higher orders and without further approximation.

Firstly, the “no privileged starting point” condition implies that the summands in Equation (17) for the mean and Equation (26) for the variance are independent of the word positions i and j, which reduces the sums to multiplicative factors of m and n, respectively. The variance summand in particular depends only on the relative word positions i′ − i and j′ − j. Kantorovitz et al. (2007) deal with this by assuming the first word occurrence in each random sequence to have a stationary distribution. This amounts to neglecting end effects, which introduces roughly the same order of approximation as PBCs.

Secondly, and more importantly, calculation of the variance via the Kantorovitz et al. (2007) approach entails multiple sums over sets of all possible words up to length 2k − 1, whereas the PBCs reduce these sums to traces of powers of matrices that are readily computed. In particular, the terms V ₂ to V ₄ above can be computed very rapidly, whereas Kantorovitz et al. (2007) suggest that the equivalent terms be omitted to save computation.

3.5. Differing Markov models

It may be necessary in some biological situations to consider a situation in which the sequences X and Y are generated by differing transition matrices, say M₁ and M₂, respectively. In this case, the formula for the mean easily generalizes to

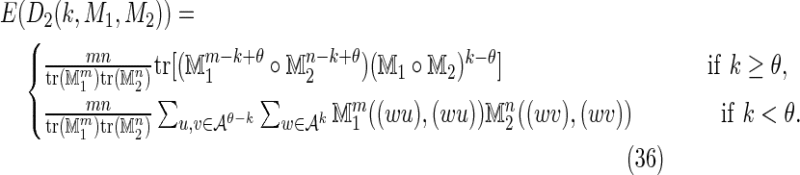A detailed formula for the variance in this case is beyond the scope of this article, but the key points of difference arising between this case and the case of a single common Markov matrix are clear. To summarize, the terms V ₀, V₁, and V₂ generalize relatively easily, but the terms V ₃ and V ₄ require more attention. For instance, the symmetry between the subcases of V ₃ shown in Figure 2 is broken, and thus the factor M^∘(2ν+1) in Equation (32) becomes either M₁^∘ν ∘ M₂^∘(ν+1) or M₁^∘(ν+1) ∘ M₂^∘ν, thus doubling the number of terms.

4. Numerical Results

4.1. Computer implementation of the mean and variance

In the Supplementary Material, we provide an R implementation (R Core Development Team, 2012) of E(D₂(k, M)) for arbitrary k and of Var (D₂(k, M)) for k ≥ θ using the formulas derived above. The k > θ means and variances are calculated by reducing the problem to the equivalent θ = 1 calculation with effective d^θ × d^θ Markov matrix M and effective word length k − θ + 1 [see Equation (24)].

The computationally most expensive parts of the computation of Var (D₂) are the sums over r and s occurring in Equation (27) and the first line of Equation (28). These sums are implemented efficiently for large sequence lengths m and n by storing powers of 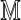out to convergence and by making use of the fact that the summand is essentially constant over parts of the domain of summation for which these matrix powers have converged. Although the programs are not yet fully optimized, they calculate Var (D₂) in about 30 sec on a standard laptop computer for an alphabet of size d = 4, Markovian order θ = 3, word lengths up to k = 20, and arbitrarily large sequence lengths m and n. The variance program slows for higher order Markov models as the size of 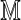grows exponentially with θ. Considerable gains are possible for the case k = θ, as the terms V₂, V₃, and V₄ in the equivalent θ = 1 calculation are automatically zero, and double sum in the term V₀ can be computed more efficiently by using the identity

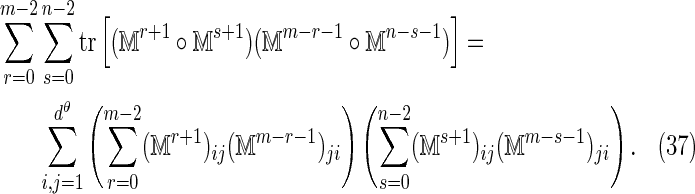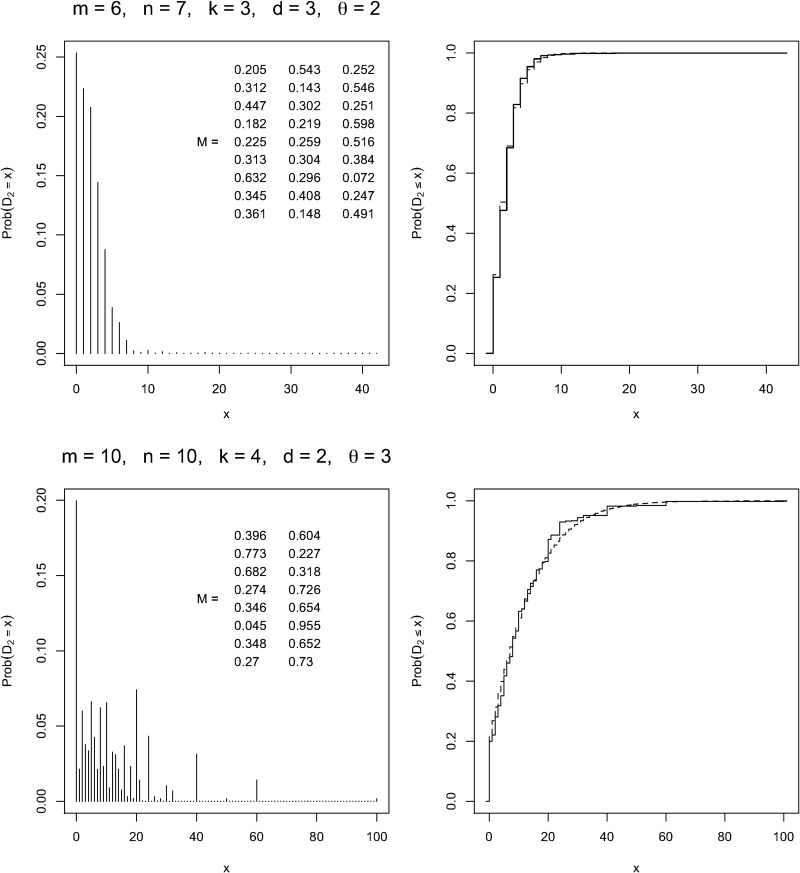
Also included in the Supplementary Material is a test program that generates the complete distribution of D₂ for short sequences for a randomly chosen Markovian model created by choosing each matrix element from a uniform distribution on the interval [0, 1] and then normalizing each row sum to 1. Using this program, we have confirmed the accuracy of the above mean and variance formulas to 13 significant figures for sequences up to length m = n = 10 for various values of the alphabet size d, Markov order θ, and word length k. Two examples of the exact D₂ distribution for short sequences are shown in Figure 3.

FIG. 3.

The exact distribution of the D₂ statistic for short sequences of length m, n and words of length k from a Markov model of order θ and alphabet of size d. The Markov matrix M has been generated randomly in each case, and the exact distribution has been calculated by enumerating all d^m+n possible sequence pairs. Also shown (dashed curve) is the cumulative distribution of the Pólya-Aeppli distribution with mean and variance set to the theoretical values using the formulas of Section 3.

For the case of sequences composed of i.i.d. letters, certain rigorous results are known for the asymptotic distribution of D₂ as the sequence lengths m, n → ∞ . For m = n, it has been shown that the limiting distribution is normal in the regime k < 1/2 log _b n + const. (Burden et al., 2008) and Pólya-Aeppli in the regime k > 2 log _b n + const. (Lippert et al., 2002). Here 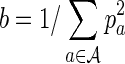where p_a is the probability of occurrence of letter a. A Pólya-Aeppli random variable is the sum of a Poisson number of geometric random variables, and is therefore an example of a compound Poisson random variable. It often arises in the study of random word counts as a Poisson number of clumps of overlapping words, each clump containing a geometric number of k-words (Reinert and Schbath, 1998; Reinert et al., 2005). In earlier work on i.i.d. sequences, Burden et al. (2012a) have found in general that, for simulations of D₂ for moderate to long sequences, the gamma distribution provides a good interpolation between the normal and Pólya-Aeppli regimes. Although the asymptotic results for D₂ are not proved for Markovian sequences, it is a reasonable experiment to compare our numerical simulations with these distributions as they may potentially provide an accurate estimate of p values in biological applications.

One would not expect the asymptotic distributions to be an accurate fit to the exact distributions for the short sequences considered in Figure 3. Nevertheless, we have added the Pólya-Aeppli distribution function with the mean and variance adjusted to their theoretical values to the plots, and find it to be a surprisingly close fit. Disagreement arises in the tail of the distribution because, for combinatoric reasons, certain values of D₂ within the range 0 to mn do not occur, whereas the Pólya-Aeppli has support over the whole range (and also out to ∞, albeit with very low probability).

4.2. Comparison with simulated distributions

For sequences of realistic biological length composed of the four-letter nucleotide alphabet, it is necessary to resort to Monte Carlo simulations to investigate the D₂ probability distribution.

We used a combination of R scripts and the SAFT program [Sequence Alignment-Free Tool, under development (Forêt, 2012)] to further verify the formulas for the mean and variance, and to compare the empirical distribution of the D₂ statistic with the conjectured asymptotic normal, Pólya-Aeppli, and gamma distributions. For this purpose, as well as using randomly generated Markov matrices, we used matrices obtained from DNA sequences occurring in nature. The Supplementary Material to Chor et al. (2009a) contains maximum likelihood estimates of Markov matrices for a number of species and for different regions within the human genome. As an example, we used the Markov matrices for human chromosome 1, with Markov orders 0, 1, 2, and 3 (Chor et al., 2009b). For each of these matrices, we used an R script that implements the algorithm of Section 2.1, using the built-in random number generator of R, via the function sample.int(), to generate 20,000 sequences of length 1,000, arranged as 10,000 pairs of cyclic sequences. The SAFT program calculated the D₂ statistic for each of these 10,000 pairs. We then used a second R script, based on the code in the Supplementary Material, to compare the mean and variance of the empirical distribution of the D₂ statistic with the theoretical values given by Equations (16) and (25) to (35), to compare the empirical cumulative distribution of the D₂ statistic with known distributions, and to plot results. Some simulations were also carried out for sequences of length 100 and 400.

As the purpose of these simulations is to verify the accuracy of the mean and variance formulas and to test the validity of certain functional approximations to the distribution function, the short to moderate sequence lengths are chosen to be in a range in which all terms in the variance formula are observed to make a noticeable contribution. The variance term V₀ is O(m²n²) in the sequence lengths, V₁ is O(mn(m + n)), and the remaining terms are O(mn), and so for longer sequences the term V₀ dominates. It happens that the sequence lengths in these simulations reflect typical sizes of cis-regulatory modules (Kantorovitz et al., 2007), but the theory will be applicable to biological sequences of any length.

Table 1 presents the results for the mean and variance for Markov orders 0 to 3. For the mean, the row labeled “Theoretical” is calculated from the corresponding Markov matrix using formula (16), the row labeled “Empirical” is estimated from the 10,000 values of D₂ obtained via SAFT, and the rows labeled “Lower 95%” and “Upper 95%” are obtained from the confidence interval returned by the R function t.test() that implements Student's t test. For the variance σ², the row labeled “Theoretical” is calculated from the corresponding Markov matrix using formulas (25) to (35), the row labeled “Empirical” is estimated from the 10,000 values of D₂ obtained via SAFT, and the rows labeled “Lower 95%” and “Upper 95%” are obtained via the χ² distribution, using the R quantile function qchisq and the inequality given by Snedecor and Cochran (1980; Section 5.10.2, p. 74),

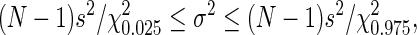Table 1.

Mean and Variance of D₂ Calculated from Theoretical Formulas

		Order
		0	1	2	3
Mean	Lower 95%	18.84	24.70	27.66	28.84
	Theoretical	18.92	24.73	27.79	28.97
	Empirical	18.95	24.83	27.80	29.00
	Upper 95%	19.07	24.96	27.95	29.15
Variance	Lower 95%	32.89	43.23	53.06	59.01
	Theoretical	33.24	44.69	55.56	60.53
	Empirical	33.81	44.44	54.54	60.65
	Upper 95%	34.77	45.70	56.09	62.37

Mean and variance of D₂ were calculated from the theoretical formulas derived in Section 3, and estimated from synthetically generated data (10,000 sequence pairs) for Markov models of order θ = 0, 1, 2, and 3 using Markov matrices estimated from human chromosome 1. Word length k = 8, alphabet size d = 4, sequence lengths m = n = 1,000.

where N = 10,000 in this case, and s² is the sample variance. In these and in a number of other simulations we have performed (data not shown), we find that in roughly the expected proportion of times the mean and variance calculated from the formulas of Section 3 lie within the 95% confidence intervals computed from the ensemble.

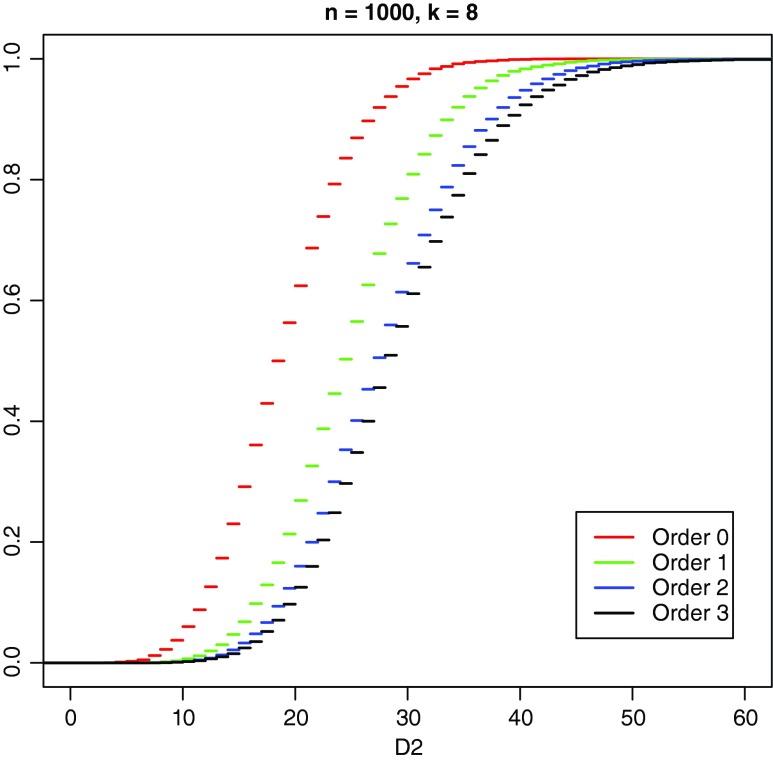
As a general rule, and as can be seen from Table 1, we observe that both the mean and variance of D₂ increase markedly as the Markov order increases for fixed word length k and sequence lengths m and n. The difference between the empirical cumulative distribution functions for the different Markov orders for the parameters of Table 1 is further illustrated in Figure 4.

FIG. 4.

Comparison of empirical cumulative distribution function for simulated D₂ using Markov matrices for human chromosome 1 from Chor et al. (2009a,b), for orders θ = 0, 1, 2, and 3. 10,000 pairs per order, word length k = 8, alphabet size d = 4, sequence lengths m = n =1,000.

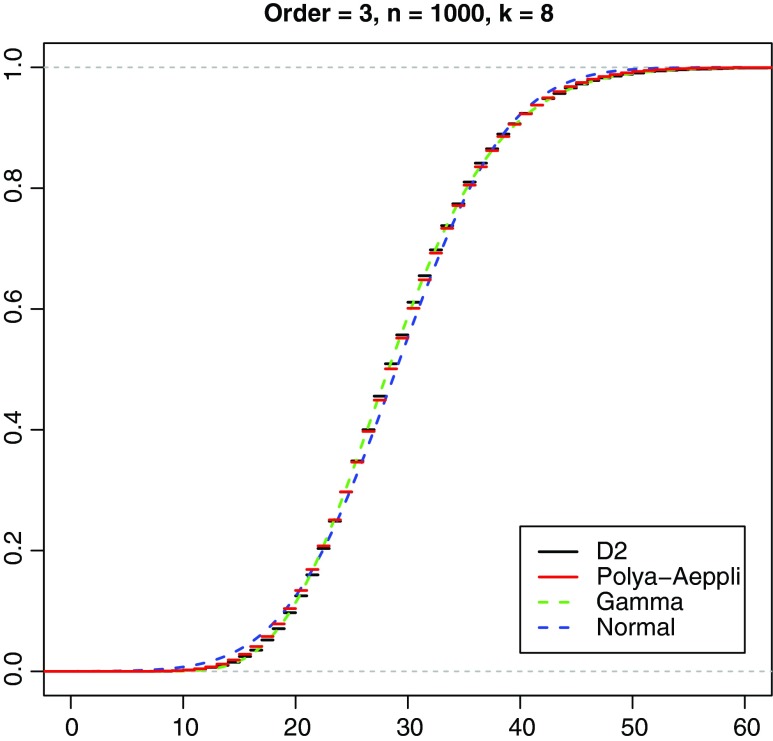
We compared the empirical distribution of D₂ for each Markov order with conjectured asymptotic distributions based on the theoretical mean and variance calculated via Equations (16) and (25) to (35). For Markov order 3, this is illustrated by Figure 5. Here the cumulative gamma and normal distributions are plotted using the built-in R functions pgamma() and pnorm(), respectively, and the cumulative Pólya-Aeppli distribution is plotted using the function pPolyaAeppli() included in the Supplementary Materials. We observe that, for these parameter values, the three conjectured distributions do not differ greatly from one another, although the Pólya-Aeppli clearly gives the best fit, particularly in the important tail of the distribution relevant to estimating p values. This trend is also observed for the other Markov orders and sequence lengths simulated including the simulations in Figure 4. In general, the Pólya-Aeppli behavior that is expected to apply asymptotically for large sequence lengths is reached within the accuracy expected of our Monte Carlo simulations at sequence lengths of some hundreds of letters. For parameters leading to large values of E(D₂), the continuous normal and gamma distributions are more readily computable, although slightly less accurate, than the Pólya-Aeppli, and of these two the gamma is invariably observed to give a better fit.

FIG. 5.

Comparison of Pólya-Aeppli, gamma, and normal cumulative distributions with empirical cumulative distribution function for simulated D₂ using Markov order 3 matrix for human chromosome 1 from Chor et al. (2009a,b). 10,000 pairs, word length k = 8, sequence lengths m = n = 1,000.

4.3. Comparison with chromosomal DNA

Ultimately, one hopes to use D₂ or similarly defined statistics as an alignment-free tool to assess the relatedness of biological sequences. To this end, it is helpful to know to what extent genomic sequences can be modeled as Markovian sequences for the purpose of defining a null-hypothesis distribution for the D₂ statistic. With this in mind, we have performed some exploratory comparisons between the D₂ distributions obtained via simulating the Markov processes using maximum likelihood estimates of Markov matrices and the D₂ distribution obtained by sampling original DNA data, for example, the DNA sequence from human chromosome 1 from Ensembl (Wellcome Trust Sanger Institute and European Bioinformatics Institute, (2012). For consistency with the range of parameters used in the simulations of the previous section, the comparisons were done for sequence lengths m = n = 300 and 1,000.

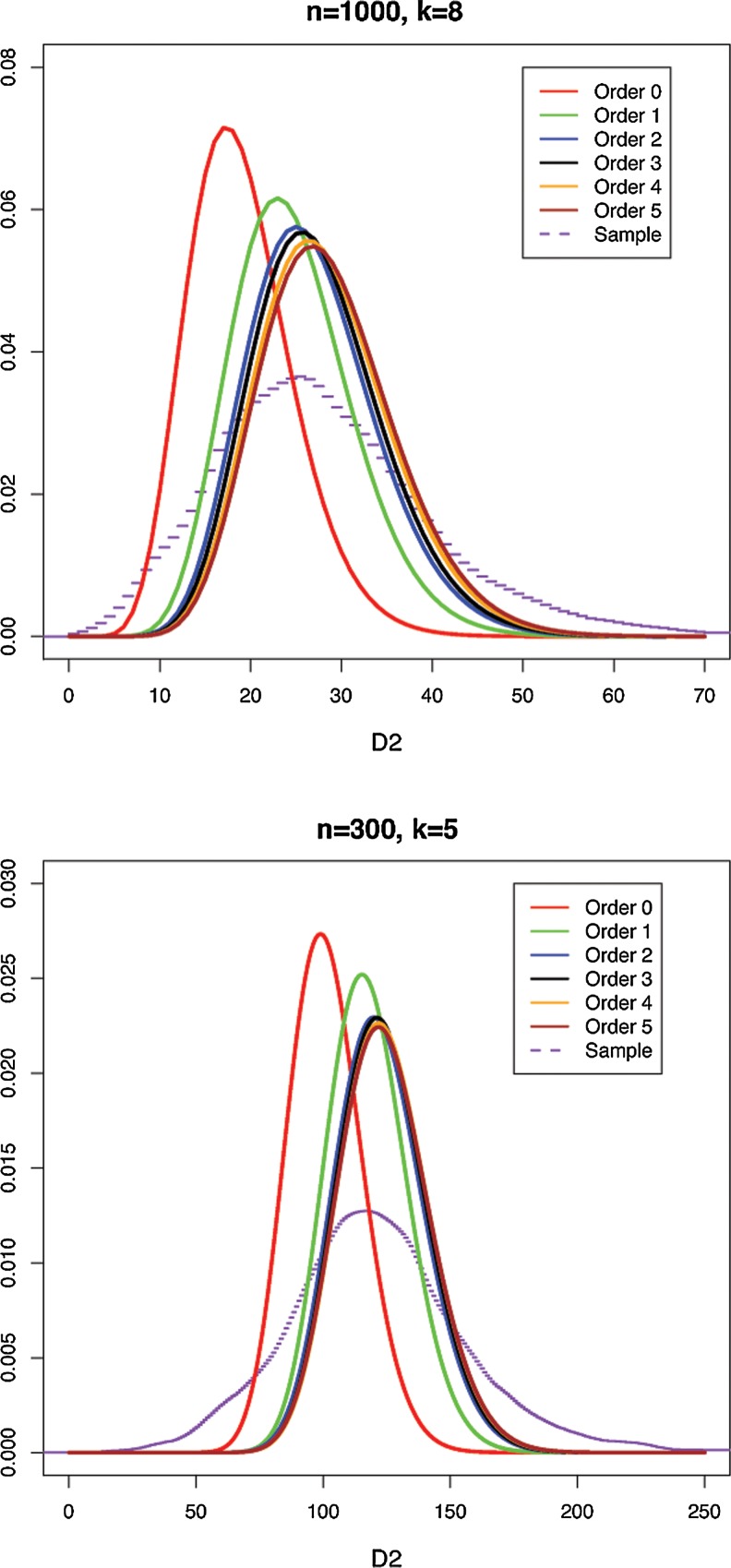
Figure 6 illustrates the comparison between D₂ distributions approximated by gamma distributions with exact means and variances calculated under Markovian hypotheses of various orders, and the empirical density of the D₂ distribution obtained from sampling human chromosome 1. The Markov transition matrices used for calculating the mean and variance at each order were estimated using maximum likelihood from the same subset of human chromosome 1 as that used for obtaining the empirical D₂ density (see below). The gamma representation was demonstrated to provide a very accurate approximation to the D₂ distribution (as estimated from Monte Carlo simulations) for m = n = 1,000 and Markov order θ = 0, 1, 2, and 3 in the previous Section (see Fig. 5). Here we also assume the gamma approximation to the D₂ distribution for θ and up to 5 to avoid further Monte Carlo simulations, as the computational demands of the algorithm of Section 2.1 for generating sequences with PBCs become prohibitive for higher Markov orders.

FIG. 6.

Density of the empirical distribution of D₂ from human chromosome 1 sample data from Ensembl compared with gamma distributions with calculated mean and variance, based on Markov models of various orders θ. 10,000 sample pairs, word length k = 8, and sequences lengths m = n = 1,000 (upper plot), word length k = 5 and sequences lengths m = n = 300 (lower plot).

To obtain the empirical density, we took the soft-masked DNA sequence for human chromosome 1 from Ensembl, and took uniform random samples of subsequences of length 300 or 1,000, according to Knuth's Algorithm S (Knuth, 1981, Section 3.4.2), but avoiding all ambiguous and masked regions. Ensembl's masking removes repetitive regions including tandem repeats. This data source and procedure for estimating Markov transition matrices correspond to those described by Chor et al. (2009a), except that the Markov matrices have been estimated from Ensembl's “soft-masked” sequences with the repeat regions (i.e., the lowercase letters) ignored, whereas Chor et al. include the repeat regions. We find that, as expected, including the repeat regions leads to a skewed empirical D₂ distribution with an extremely heavy right-hand tail corresponding to repetitive regions.

The sample mean and variance from the soft-masked DNA sequence, together with the theoretical values, are shown in Table 2. In general, agreement between the Markovian model and the empirical distribution improves as the Markovian order increases. For higher orders, the Markovian mean overshoots slightly. The Markovian variance, on the other hand, severely underestimates the empirical variance at any order. This is consistent with earlier observations by Csűrös et al. (2007) that genomic word count distributions tend to have heavier tails than that predicted by Markovian models, or, to put it another way, certain k-mers are “under-” or “over-represented” within genomes.

Table 2.

Empirical Estimates of Mean and Variance of D₂ from Human Chromosome 1

	Theoretical values
	θ = 0	1	2	3	4	5	Sample estimate
m = n = 1,000, k = 8
Mean	19.08	24.74	26.90	27.55	28.30	28.74	27.66
Variance	33.58	44.62	50.99	52.19	54.37	56.01	181.1
Std. Dev.	5.795	6.680	7.141	7.224	7.373	7.484	13.46
m = n = 300, k = 5
Mean	101.1	117.4	122.4	123.5	124.3	124.3	120.7
Variance	216.6	254.4	307.5	307.8	315.6	321.9	1,258.
Std. Dev.	14.71	15.95	17.53	17.55	17.77	17.94	35.47

Empirical estimates of the mean and variance of D₂ from human chromosome 1 sample data from Ensembl (right-hand column) were compared with the theoretical mean and variance based on Markov models of various orders using estimated Markov matrices for human chromosome 1. The variance for k = θ = 5 was calculated by implementing Equation (37).

Note also that the Markovian plots in Figure 6 suggest that θ = k may be in some sense a limiting case. Recall that the formula for the mean takes a different form for θ > k [see Equation (16)], and that the formula derived for the variance is only valid for θ ≤ k and remains intractable for θ > k. We suspect that this is related to the fact that, for sufficiently long sequences, θ-mer frequencies are determined by the stationary eigenvector of the Markov matrix, and that the statistics of k-mers for k < θ is implicit with the statistics of θ-mers.

5. Discussion

The primary purpose of this article is to demonstrate that it is possible to construct accurate representations of the distribution of the D₂ statistic under the null hypothesis of periodic Markovian sequences without the need to resort to computationally expensive Monte Carlo simulations or to asymptotic approximations valid only when log n ≫ k. Our method consists of deriving exact formulas for the mean and variance of D₂ that are readily computable for any sequence lengths, to which we fit functional forms based on asymptotic distributions typically observed for word count statistics. We have demonstrated that, for sequences of moderate length of up to only a few hundred letters, and for which log n ≈ k, the Pólya-Aeppli distribution with parameters determined by the exact formulas for the mean and variance developed herein accurately represents the true D₂ distribution for Markovian sequences of any order (see Fig. 5). For comparatively longer sequences with higher E(D₂), for which evaluating the Pólya-Aeppli distribution may be slow, the gamma distribution provides an acceptable approximation that is more accurate than the normal distribution.

It is known that the D₂ statistic itself, if used directly as a measure of sequence similarity, may perform poorly as the signal of over-representation of the same words in the query and target sequences is masked by the natural variability of word counts in each of the two sequences (Lippert et al., 2002). Variations on the theme of the D₂ statistic, such as the weighted, centered statistic 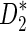studied by Reinert et al. (2009), have been developed to circumvent this problem. Burden et al. (2012a,b) have extended calculations of the exact mean and variance for i.i.d. sequences to weighted and centered versions of D₂, and it is expected that the analogous calculation for Markovian sequences will be entirely feasible.

The secondary purpose of this article is a preliminary comparison of the approximate D₂ distribution computed with the theoretical mean and variance under a Markovian hypothesis with an empirical genomic D₂ distribution. As a test example, we have considered the empirical distribution of the D₂ statistic between randomly chosen segments of a single human chromosome, avoiding highly repetitive parts of the chromosome such as stretches of tandem repeats. In general, we find that the empirical distribution has much heavier tails than the D₂ distribution for a Markovian sequence of any order up to θ = 5 (see Fig. 6). We interpret this as a signal that the chromosome, taken as a whole, contains a number of strongly over- and under-represented k-mers, relative to a Markovian sequence. Thus, one is tempted to conclude that a Markov model will tend to overestimate significance and give an inflated false-positive rate when attempting to detect relatedness of genomic sequences.

However, this test is preliminary, and takes no account of the structure of the genome. In particular, we have not restricted ourselves to non–protein-coding segments. As current opinion is that even the noncoding part of the human genome may be up to 80% functional (ENCODE Project Consortium, 2012), the possibility exists that the over- and under-represented words are restricted to segments of genome with specific, possibly yet unknown, functions. Thus, the potential exists, for instance, to use D₂ as an exploratory probe to detect functional regions within the noncoding part of the genome: Using a randomly generated Markovian probe sequence (a random probe of length m = 10,000, say, would contain almost all 6-mers), one could calculate D₂ between the probe and a moving window running along the genome. This exercise would expose whether, for instance, the genome consists of a sea of “null hypothesis” Markovian sequence containing islands of repeated motifs, or whether the genome is uniformly peppered with a particular set overexpressed words. The ability to easily calculate the null D₂ distribution as a function of sequence and word lengths enables the experiment to be performed readily at different resolutions. Furthermore, the property of D₂ that it is dominated by the natural variability in either of the two sequences being compared becomes an advantage. If a subset of words is over-represented within the moving window at a specific location in the genome, provided that subset contains some words also present in the probe sequence, its over-representation within the window will manifest as an extreme D₂.

6. Appendix: Contributions to Var (D₂)

We derive the contributions V₀ to V₄ to Var (D₂) when θ = 1 given in Section 3.3. These contributions are the partial sums 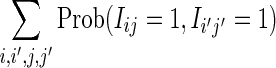contributing to Equation (26) where, for given (i, j), the indices (i′, j′) range over the regions shown in Figure 2. The event “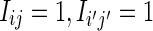” means that the k-words beginning at sites i and i′ in sequence X match the k-words beginning at sites j and j′ in sequence Y, respectively.

Nonoverlapping words in both sequences: V₀

Taking into account the PBCs, these are the contributions from the cases for which both 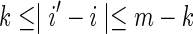and 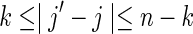occur simultaneously. Consider the situation

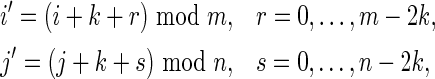shown in Figure 7a. As the two sequences are independent, applying Equation (11) gives

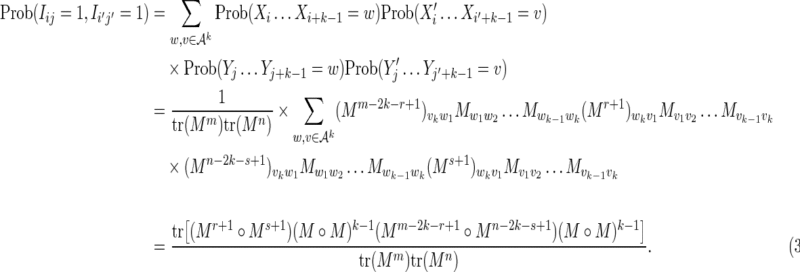FIG. 7.

Arrangements of word matches contributing to (a) nonoverlapping words, V₀, (b) crabgrass V₁, (c) accordions V₂, V₃, and (d) accordion V₄. Images of words due to periodic boundary conditions are shown as a dashed outline.

Summing over r and s, and including a factor of mn to account for the sum over i and j then gives Equation (27).

Overlaps in one sequence only: V₁

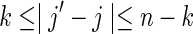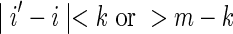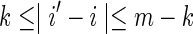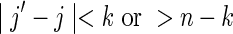These are cases for which either and (overlaps in X but not in Y), or and (overlaps in Y but not in X). This region is referred to as the “crabgrass” by Waterman (1995). Figure 7b shows the case of overlaps in X but not Y, where we have set

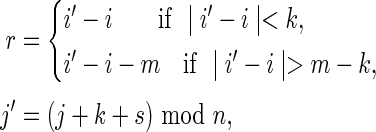for 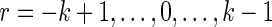and 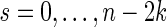. We split the common word beginning at i and j into a piece a of length r and a piece b of length k − r, and split the common word beginning at i′ and j′ into the piece b and a piece c of length r.

Then

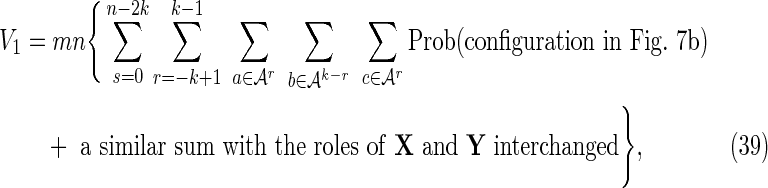where the sums over r and s arise from sums over i′ and j′ for fixed i and j, and the factor of mn arises from the outer sum over i and j. Using Equation (11),

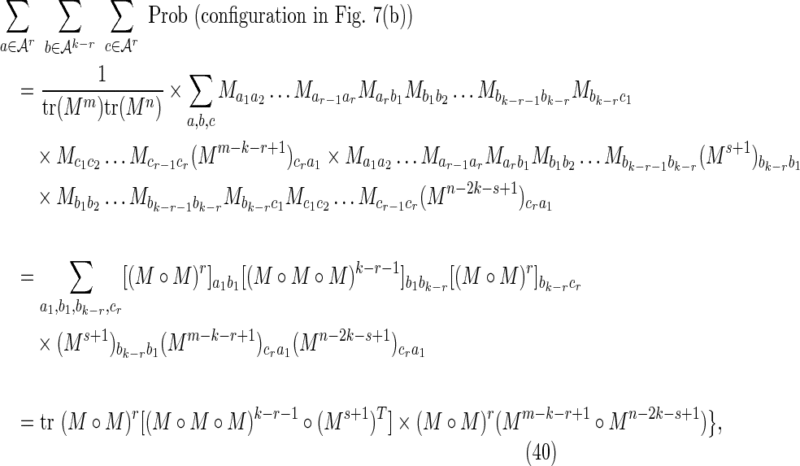where the superscript T indicates the matrix transpose. Equations (39) and (40) combine to give the crabgrass contribution Equation (28).

Overlaps in both sequences

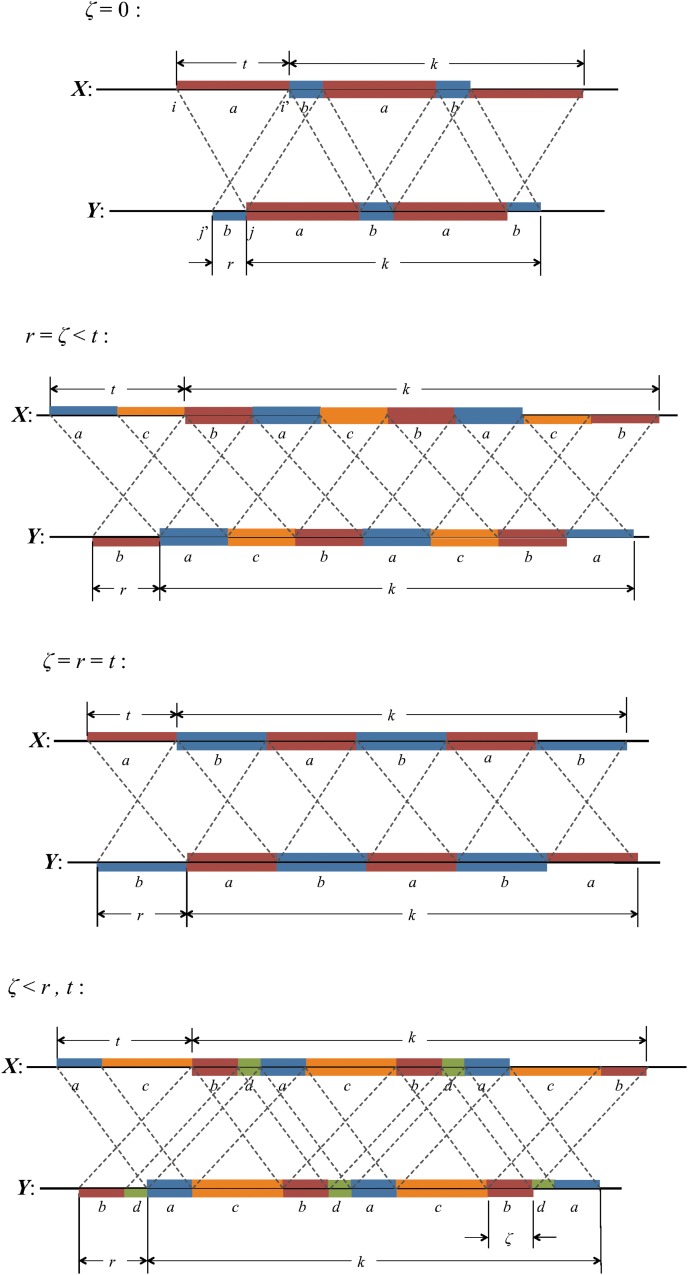
The set of configurations for which the words at positions i, i′, j, and j′ overlap in both sequences simultaneously is referred to as the “accordion” by Waterman (1995). For convenience, we define the following overlap distances (illustrated in Fig. 7c):

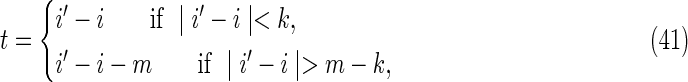in sequence X and

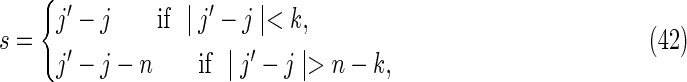in sequence Y. These definitions ensure that −k + 1 ≤ t, s ≤ k − 1. The remaining three contributions are from the accordion.

Diagonal part of the accordion: V₂

This is the contribution from those cases with s = t, in which case Figure 7c becomes a match between the (k + |t|)-letter word at position i in X and the (k + |t|)-letter word at position j in Y. Noting that the probability of this match is independent of i and j, we have

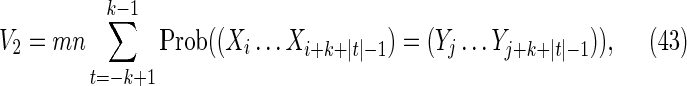where, by analogy with Equation (21),

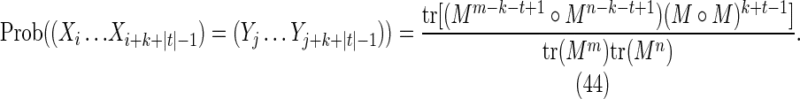Combining Equations (43) and (44) gives Equation (29).

Off-diagonal part of the accordion: subcases contributing to V₃

The off-diagonal part of the accordion is divided into a number of subcases. Consider first the contribution from the four subcases making up the region V₃ in Figure 2:

• 3(i): 0 ≤ s < t ≤ k − 1;

• 3(ii): − k + 1 ≤ s < t ≤ 0;

• 3(iii): − k + 1 ≤ t < s ≤ 0; and

• 3(iv): 0 ≤ t < s ≤ k − 1.

By symmetry, each subcase makes an equivalent contribution to the variance. Subcase 3(i) is shown in Figure 8, and the required contribution takes the form

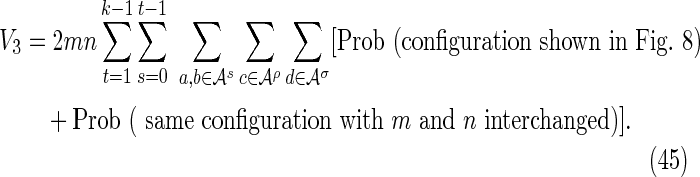FIG. 8.

Arrangements of word matches contributing to subcase 3(i) when ρ = (k − s) mod (t − s)> 0 (upper figure) and ρ = 0 (lower figure).

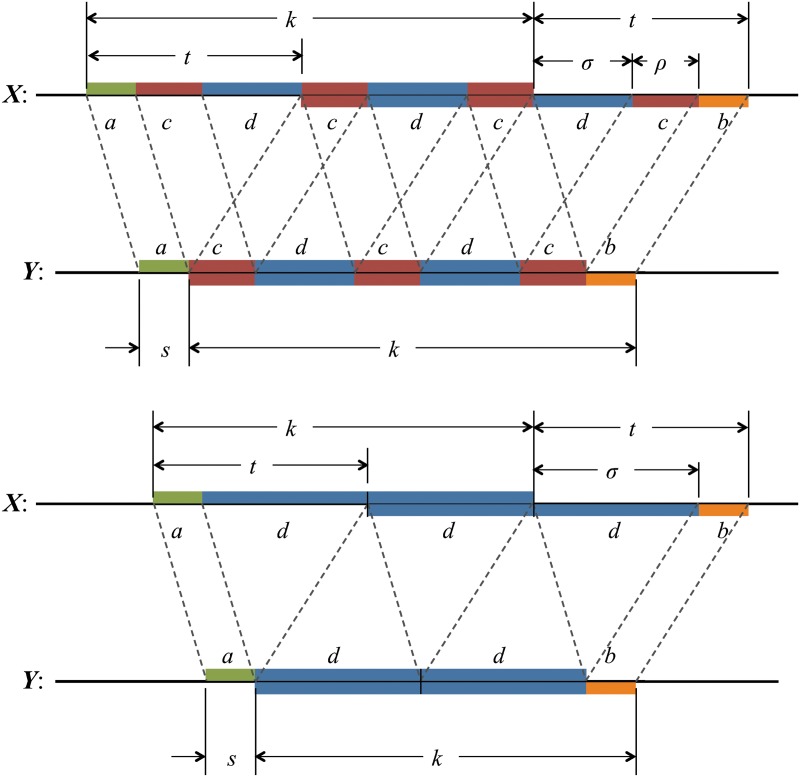
To calculate the probability of the configuration, the overlapping words have been divided into repeating independent elements. Elements a and b are the nonoverlapping parts of length s at either end of the words at j and j′ in Y. The nonoverlapping part of the words at i and i′ in X are segmented into elements (acd) and (dcb) shown in the upper part of Figure 8. The segment (cd) repeats an integer number ν times within the overlapping part in sequence Y, with a segment c of length ρ left over. We set the length of element d equal to σ. Thus

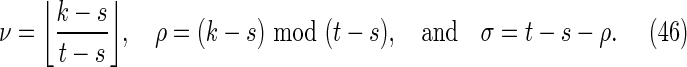When ρ = 0 the element c does not occur (lower part of Fig. 8).

Using arguments similar to those for the crabgrass contribution, we have, for ρ > 0,

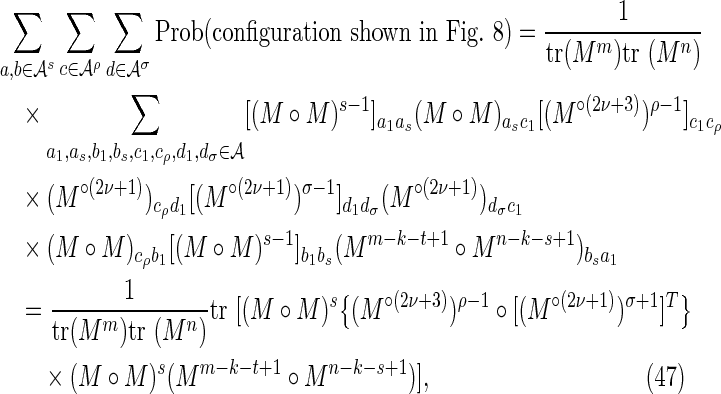whereas for ρ = 0 we have

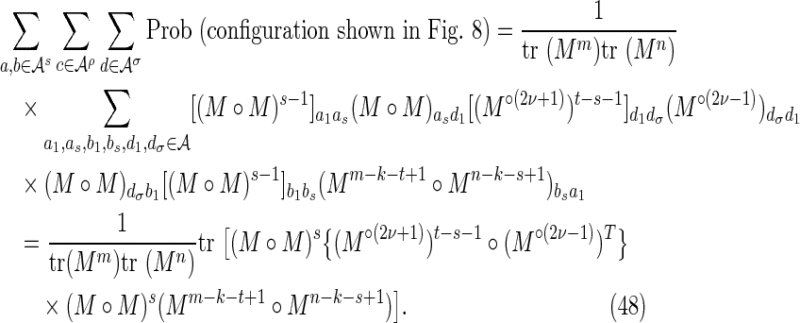Combining Equations (45) to (48) gives Equations (30) to (32).

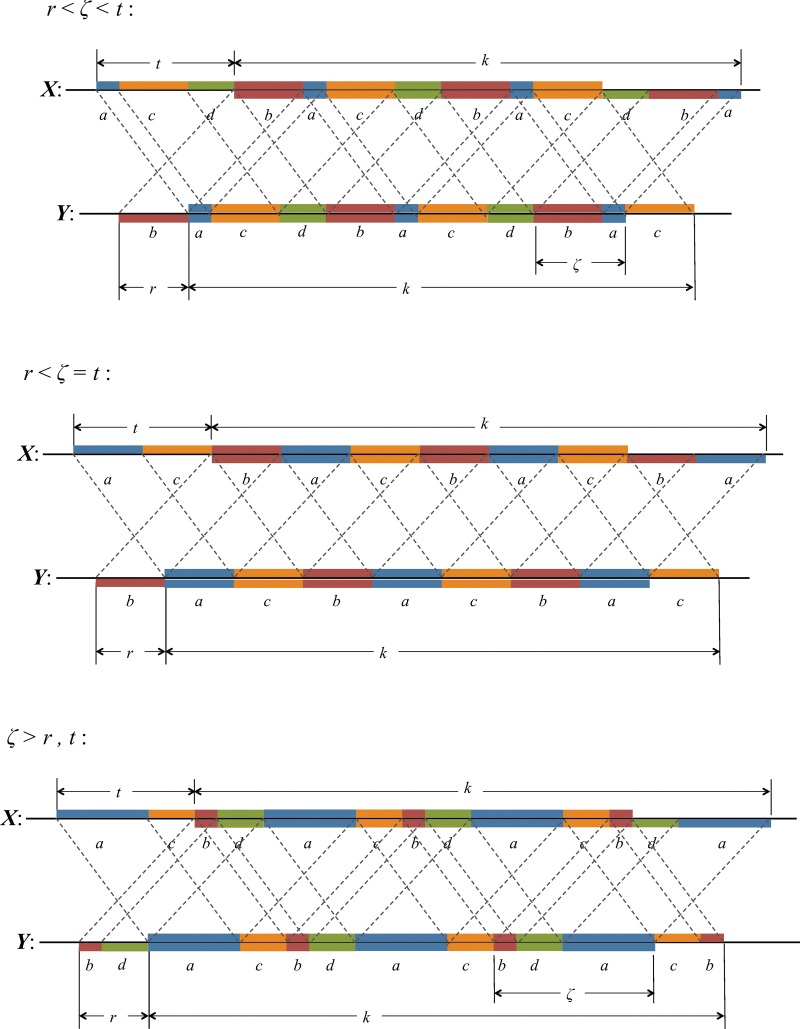
Off-diagonal part of the accordion: subcases contributing to V₄

These are contributions from the subcases

• 4(i): 1 ≤ t ≤ k − 1, − k + 1 ≤ s ≤ − 1; and

• 4(ii): 1 ≤ s ≤ k − 1, − k + 1 ≤ t ≤ − 1,

labeled V₄ in Figure 2. In these cases, either t or s is negative. By symmetry, each of these two subcases makes an equivalent contribution to V₄, so we consider subcase 4(i) and for convenience set r = −s (see Fig. 7d). Then

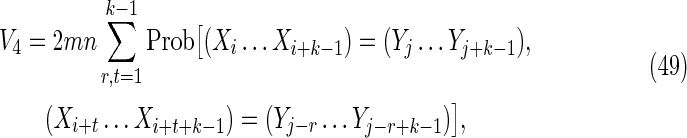where the factor mn arises from a sum over i and j, and we make use of the fact that for periodic Markovian sequences the summand is independent of i and j.

It is convenient to define

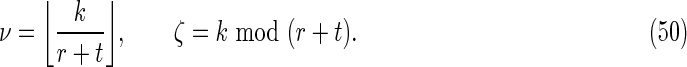Here ν is the integer number of times the complete repeat unit 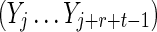fits inside the k-word 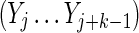, and ζ is the number of letters remaining (see Figs. 9 and 10). Calculation of the probability occurring in Equation (49) then proceeds in a similar fashion to that for V₃ by dividing the overlapping words into independent nonoverlapping elements. It turns out that the configuration of elements depends on the relationship between ζ, r, and t. The complete set of configurations is enumerated in Figures 9 and 10, with the repeated elements labeled a, b, etc. The calculation is lengthy and repetitive but straightforward, and yields Equations (33) and (35) after recombining cases that give the same algebraic formula.

FIG. 9.

Arrangements of word matches contributing to V4 (first four cases).

FIG. 10.

Arrangements of word matches contributing to V4 (final three cases).

Acknowledgment

This work was supported in part by ARC Discovery grant DP120101422.

Disclosure Statement

The authors declare that no competing financial interests exist.