Muscle Oxygen Uptake Differs from Consumption Dynamics During Transients in Exercise

Abstract

Relating external to internal respiration during exercise requires quantitative modeling analysis for reliable inferences with respect to metabolic rate. Often, oxygen transport and metabolism based on steady-state mass balances (Fick principle) and passive diffusion between blood and tissue are applied to link pulmonary to cellular respiration. Indeed, when the work rate does not change rapidly, a quasi-steady-state analysis based on the Fick principle is sufficient to estimate the rate of O₂ consumption in working muscle. During exercise when the work rate changes quickly, however, non-invasive in vivo measurements to estimate muscle O₂ consumption are not sufficient to characterize cellular respiration of working muscle. To interpret transient changes of venous O₂ concentration, blood flow, and O₂ consumption in working muscle, a mathematical model of O₂ transport and consumption based on dynamic mass balances is required. In this study, a comparison is made of the differences between simulations of O₂ uptake and O₂ consumption within working skeletal muscle based on a dynamic model and quasi-steady-state approximations. The conditions are specified under which the quasi-steady-state approximation becomes invalid.

36.1 Introduction

During exercise, oxygen transport and metabolism within muscle in healthy and disease states (e.g., heart failure and diabetes) can be studied under various experimental protocols with non-invasive measurements. Measurement methods include pulmonary O₂ uptake by indirect calorimetry, muscle oxygenation by near-infrared spectroscopy and microvascular oxygenation by phosphorescence quenching. Muscle O₂ consumption (UO_2m) during a fast transient change (e.g., exercise) cannot be directly evaluated by measuring oxygen uptake in the lungs (VO_2p). Consequently, a mathematical model is needed to relate these variables. Often, a quasi-steady-state model (e.g., Fick principle) is used to analyze dynamic responses at the onset of exercise in order to quantify relationships between the oxygen uptake, blood flow, and O2 concentration dynamics in the capillary bed (or index of extraction) within muscle [1–3]. Although this method is strictly applicable only under steady-state conditions [4], it could provide a reasonable approximation under some conditions [5]. More generally, interpretation of non-invasive measurements related to O₂ transport and metabolism in tissue can be made using dynamic mass balances if the tissue volume can be determined. Nevertheless, this has limitations also. At the microvascular level, the volume of tissue supplied with oxygen by the blood vessels is uncertain. Furthermore, in a macroscopic tissue volume, the heterogeneous spatial distribution and temporal variation of blood flow and O₂ concentration in tissue can have a significant effect on the interpretation of measurements. In this study, simulations using a quasi-steady-state model [3] and those using a multi-compartment dynamic model [6] are compared to experimental measurements during exercise. The effect of changes in muscle blood flow on the dynamic responses of venous oxygen concentration was investigated during exercise assuming specific dynamics of muscle O₂ consumption.

36.2 Methods

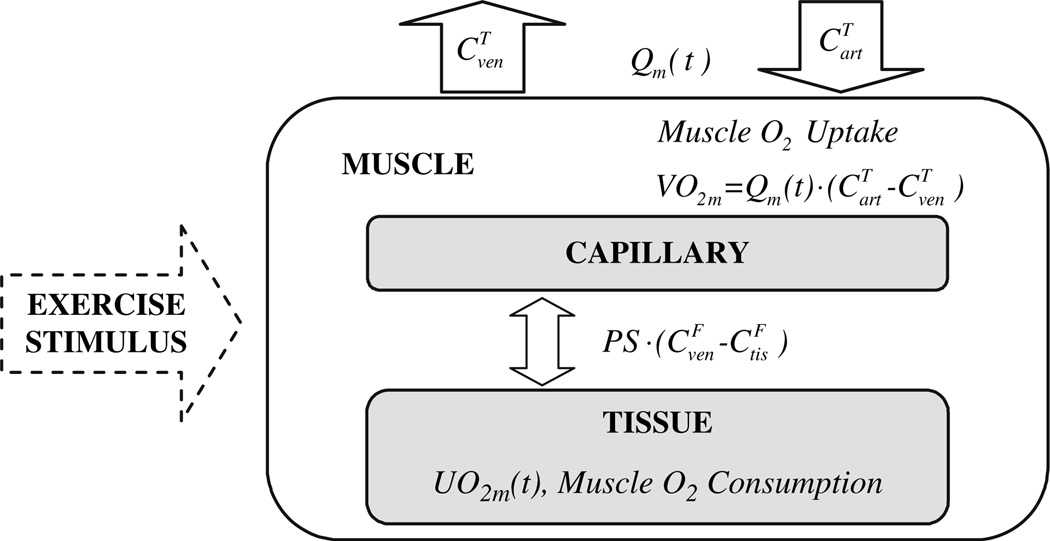
We consider oxygen transport and consumption in muscle to occur in a system of perfectly mixed blood and tissue compartments (Fig. 36.1) as developed previously [6]. In the blood compartment, the oxygen concentration C(t) changes with time depending on flow Q_m(t) through the capillary bed of volume V_cap and diffusion between blood and tissue with rate coefficient PS according to the dynamic mass balance:

$$V_{\mathit{\text{cap}}}\frac{d{C}_{\mathit{\text{ven}}}^T}{dt}=Q_m(t)(C_{\mathit{\text{art}}}^T-C_{\mathit{\text{ven}}}^T)-PS(C_{\mathit{\text{ven}}}^F-C_{\mathit{\text{tis}}}^F)$$ (36.1)

where $C_j^T$ and $C_j^F$ represent the total and free oxygen concentrations in compartment j, which are related by nonlinear equations [6]. In the tissue compartment, the oxygen concentration C(t) changes with time depending on the rates of diffusion between blood and tissue cells and oxygen consumption in muscle UO_2m(t):

$$V_{\mathit{\text{tis}}}\frac{d{C}_{\mathit{\text{tis}}}^T}{dt}=PS(C_{\mathit{\text{ven}}}^F-C_{\mathit{\text{tis}}}^F)-U{O}_{2m}(t)$$ (36.2)

Fig. 36.1.

Oxygen consumption and transport in skeletal muscle.

At steady state, these equations can be combined to yield the Fick principle for oxygen uptake of skeletal muscle:

$$V{O}_{2m}=Q_m(C_{\mathit{\text{art}}}^T-C_{\mathit{\text{ven}}}^T)=PS(C_{\mathit{\text{ven}}}^F-C_{\mathit{\text{tis}}}^F)=U{O}_{2m}$$ (36.3)

In response to a step increase in work rate, the oxygen consumption has typically an exponential response [3]:

$$U{O}_{2m}(t)=U{O}_{2m}^{BL}+\mathrm{\Delta }U{O}_{2m}[1-{\text{exp}}^{t_0-t/{\tau }_{U{O}_{2m}}}]$$ (36.4)

Also, the blood flow has two phases (I, II) with different amplitudes and time constants [3]:

$$Q_m(t)=Q_m^{BL}+\mathrm{\Delta }{Q}_{m,1}[1-{\text{exp}}^{(t_0-t)/{\tau }_{Q_{m,l}}}]+\mathrm{\Delta }{Q}_{m,2}[1-{\text{exp}}^{(t_0+T{D}_2-t)/{\tau }_{Q_{m,11}}}]$$ (36.5)

To simulate the oxygen concentration dynamics of skeletal muscle to a step change in work rate from baseline (BL), we must specify initial conditions at t₀: $C_{\mathit{\text{ven}}}^F(t_0)=C_{\mathit{\text{ven}}}^{F,BL};C_{\mathit{\text{tis}}}^{F,BL}(t_0)=C_{\mathit{\text{tis}}}^{F,Bl}$. Responses of venous oxygen concentration were simulated between two steady states assuming different values of muscle volume (V_m) engaged during exercise with different dynamic changes of blood flow in muscle. The differential equations of the model were solved numerically using a robust algorithm for stiff systems [7].

For comparison with the results of Ferreira [3], we used the same initial conditions, muscle blood flows (τ_Qm,I and τ_Qm,II), and oxygen consumption time constant τUO_2m = 30s). Except for the parameter values in Table 36.1, values of other model parameters were obtained from previous studies [6].

Table 36.1.

Initial conditions and model parameters

$C_{\mathit{\text{ven}}}^{F,BL}$ [mM]	$C_{\mathit{\text{tis}}}^{F,BL}$ [mM]	$C_{\mathit{\text{art}}}^{F,BL}$ [mM]	PS [L min−1]
3.48 ·10−2	3.37· 10−2	1.05 · 10−1	2026

Following Ferreira [3] we chose values for the arterial oxygen concentration, $C_{\mathit{\text{art}}}^T$, and free oxygen concentration $C_{\mathit{\text{ven}}}^{F,BL}$ . The free oxygen concentration intissue was determined based on PO₂=25 mmHg. The value of PS was computed from Eq. (36.3) at steady state.

36.3 Results

The effects of various blood flow time profiles on venous oxygen concentration for a specific oxygen consumption dynamics are simulated.

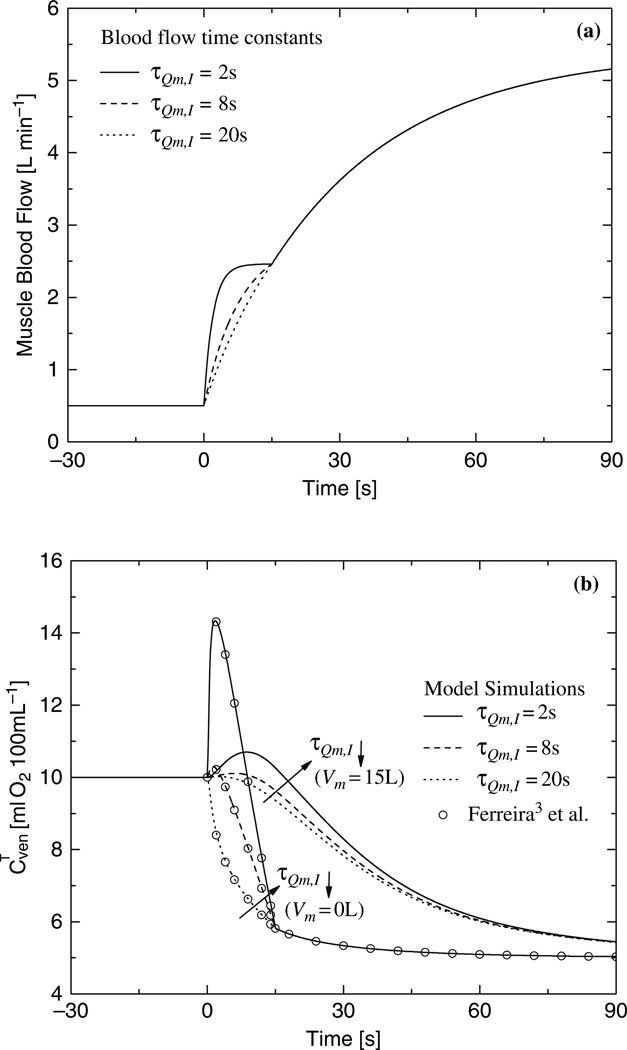
Figure 36.2 shows dynamic changes in phase I of muscle blood flow (Fig. 36.2a) and corresponding dynamic responses of venous oxygen concentration (Fig. 36.2b). The dynamic response of the venous oxygen concentration is faster when the transient term (i.e., rate of oxygen change) is negligible (V_m≈0L) than when it is significant (V_m = 15L). The overshoot of the venous oxygen concentration is greater with a smaller muscle volume and with a shorter time constant of phase I (τ_Qm,1). Even when the time constant of phase I is long, the dynamics of the venous oxygen concentration depends on the muscle volume.

Fig. 36.2.

(a) Blood flow dynamic for different time constants τ_Qm,I, (τ_Qm,II = 30 s); (b) Effect of blood flow dynamic on the dynamic response of the venous O₂ concentration obtained with quasi-steady-state and dynamic model.

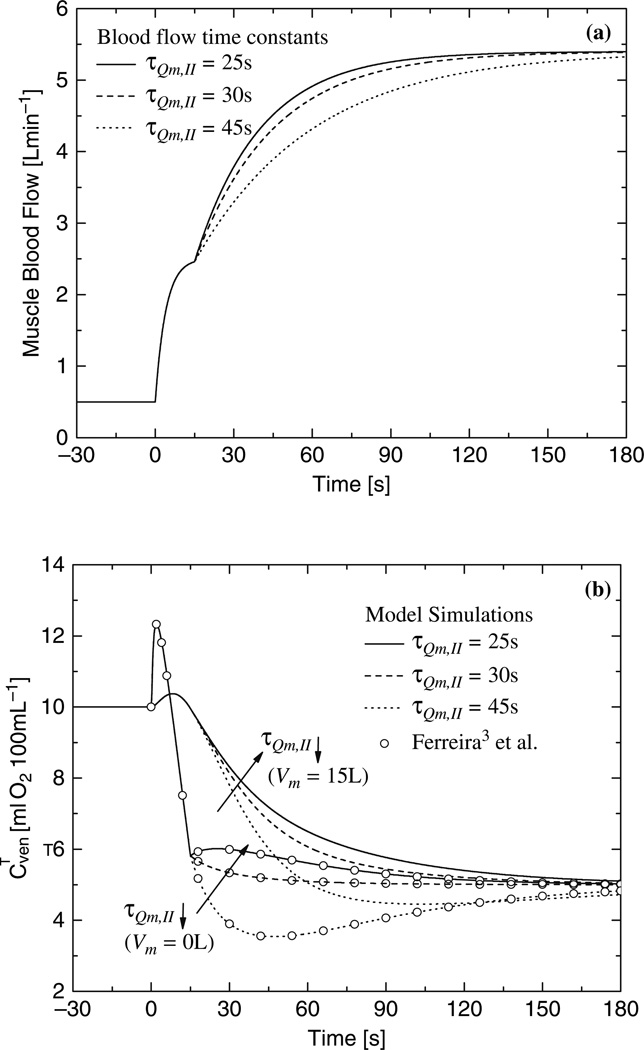
Figure 36.3 shows dynamic changes in phase II of muscle blood flow (Fig. 36.3a) and corresponding dynamic responses of venous oxygen concentration (Fig. 36.3b). The dynamic response of the venous oxygen concentration is faster when the transient term is negligible (V_m≈0L) than when the transient term is significant (V_m = 15L). The undershoot of the venous oxygen concentration is greater with a smaller muscle volume and with a longer time constant of phase II (τ_Qm,1I). Even when the time constant of phase II is small, the dynamics of the venous oxygen concentration depends on the muscle volume.

Fig. 36.3.

(a) Blood flow dynamic for different time constants τ_Qm,II, (τ_Qm,I = 4 s); (b) Effect of blood flow dynamic on the dynamic response of the venous O₂ concentration obtained with quasi-steady-state and dynamic model.

36.4 Discussion

Model simulations of the time response of venous oxygen concentration in working skeletal muscle were obtained with a dynamic computational model for quasi-steady-state (e.g., negligible muscle volume) and transient conditions. The simulations under quasi-steady-state conditions are equivalent to those of Ferreira [3], who applied a steady-state (Fick principle) analysis.

With a larger muscle volume, a change of muscle blood flow has less effect on the time profile of the venous oxygen concentration. In any case, an overshoot in venous oxygen concentration can occur during phase I of muscle blood flow as reported in human exercise studies [8]. Corresponding to simulations in venous oxygen concentration during phase II of muscle blood flow, experiments with rat muscle contractions show a similar undershoot response [9]. In these studies with diabetic rats where the disease induces a mismatch between oxygen delivery and oxygen consumption, an undershoot can occur in microvascular O₂ pressure at the onset of exercise.

Based on the Fick principle, the red blood cell flux (or oxygen delivery) and microvascular O₂ pressure measurements are used to compute oxygen consumption in the diabetic state [2]. This simplified analysis shows a mismatch between oxygen delivery and oxygen consumption, which accounts for the observed undershoot in microvascular O₂ pressure. Correct interpretation of this mismatch requires quantitative analysis with a more general dynamic model to determine the effect of muscle volume in the transient term of the oxygen balance. Furthermore, a dynamic model is essential to analyze the response of microvascular oxygen pressure in muscle at the onset of contraction in heart failure [10] and aging [11], where O₂ delivery is impaired.

Generally, venous oxygen concentration during exercise depends on the rate of oxygen mass accumulation within muscle that results from a dynamic interplay of convection, diffusion, and metabolism. Consequently, the dynamics of muscle oxygen uptake and muscle oxygen consumption differ during transient changes in exercise [6]. In this regard the extent of muscle involvement (i.e., muscle volume), which is often uncertain (especially at the microvascular level), plays a relevant role during exercise.

The more general dynamic model applied in this study consists of spatially lumped, dynamic mass-balance equations. A special case of this dynamic model is the quasi-steady-state-model, which is commonly used to analyze oxygen exchange in capillary blood and in tissue of the working muscle. Although this dynamic model of oxygen consumption in skeletalmuscle [6] is sufficient for some purposes, modifications are needed to reflect more physiological conditions. For example, the product of permeability and surface area should be a function of blood flow due to the capillary recruitment occurring at the onset of exercise [12]. Furthermore, this dynamic model assumes an exponential function to describe cellular oxygen consumption [13]. While this simple expression is sufficient to make some inferences about dynamic responses, key metabolic processes should be incorporated into the model to provide a mechanistic basis for oxygen consumption dynamics. For this purpose, future models should incorporate substrates and enzymes participating in mitochondrial oxidative phosphorylation during exercise.

The dynamics of the oxygen concentration in blood depend on the spatial distribution and temporal variation of the variables such as blood flow and hemoglobin oxygen saturation that affect convective and diffusive transport of oxygen in the micro circulation. Although these effects are not directly measurable during muscle contraction [14], more general models have been applied to account for heterogeneities of blood flow and oxygen consumption of the muscle [15–18].

In conclusion, physiological relations between oxygen transport and consumption within skeletal muscle during exercise require a model based on dynamic mass balances for oxygen in blood and tissue. Such a model can be used together with non-invasive or minimally invasive experiments to study capillary oxygen exchange during an exercise stimulus where active muscle, convection and diffusion have a significant effect. This could contribute to quantifying changes associated with aging in healthy subjects, as well as with potential pathological alterations of oxygen transport and metabolism in unhealthy subjects suffering from diabetes and heart failure [19].