Estimation and Testing Based on Data Subject to Measurement Errors: From Parametric to Non-Parametric Likelihood Methods

Abstract

Measurement error problems can cause bias or inconsistency of statistical inferences. When investigators are unable to obtain correct measurements of biological assays, special techniques to quantify measurement errors (ME) need to be applied. The sampling based on repeated measurements is a common strategy to allow for ME. This method has been well-addressed in the literature under parametric assumptions. The approach with repeated measures data may not be applicable when the replications are complicated due to cost and/or time concerns. Pooling designs have been proposed as cost-efficient sampling procedures that can assist to provide correct statistical operations based on data subject to ME. We demonstrate that a mixture of both pooled and unpooled data (a hybrid pooled-unpooled design) can support very efficient estimation and testing in the presence of ME. Nonparametric techniques have not been well investigated to analyze repeated measures data or pooled data subject to ME. We propose and examine both the parametric and empirical likelihood methodologies for data subject to ME. We conclude that the likelihood methods based on the hybrid samples are very efficient and powerful. The results of an extensive Monte Carlo study support our conclusions. Real data examples demonstrate the efficiency of the proposed methods in practice.

1. Introduction

Commonly, many biological and epidemiological studies deal with data subject to measurement errors (ME) attributed to instrumentation inaccuracies, within-subject variation resulting from random fluctuations over time, etc. Ignoring the presence of ME in data can result in the bias or inconsistency of estimation or testing. The statistical literature proposed different methods for ME bias correction (e.g., Carroll et al. [1-2]; Carroll and Wand [3]; Fuller [4]; Liu and Liang [5]; Schafer [6]; Stefanski [7]; Stefanski and Carroll [8-9]). Among others, one of the common methods is to consider repeated measurements of biospecimens collecting sufficient information for statistical inferences adjusted for ME effects (e.g., Hasabelnaby et al. [10]). In practice, measurement processes based on bioassays can be costly and time-consuming and can restrict the number of replicates of each individual available for analysis or the number of individual biospecimens that can be used. It can follow that investigators may not have enough observations to achieve the desired power or efficiency in statistical inferences.

Dorfman [11], Faraggi et al. [12], Liu and Schisterman [13], Liu et al. [14], Mumford et al. [15], Schisterman and Vexler et al. [16-17], Vexler et al. [18-21] addressed pooling sampling strategies as an efficient approach to reduce the overall cost of epidemiological studies. The basic idea of the pooling design is to pool together individual biological samples (e.g., blood, plasma, serum or urine) and then measure the pooled samples instead of each individual biospecimen. Since the pooling design reduces the number of measurements without ignoring individual biospecimens, the cost of the measurement process is reduced, but relevant information can still be derived. Recently, it has been found that a hybrid design that takes a sample of both pooled and unpooled biospecimens can be utilized to efficiently estimate unknown parameters, allowing for ME’s presence in the data without requiring repeated measures (Schisterman and Vexler et al. [17]).

In the context of the hybrid strategy, Schisterman and Vexler et al. [17] evaluated data that follow normal distribution functions. In this article, we consider general cases of parametric and nonparametric assumptions, comparing efficiency of pooled-unpooled samples and data consisting of repeated measures. It should be noted that the repeated measurement technique proposes to collect a large amount of information regarding just nuisance parameters related to distribution functions of ME, whereas the pooled-unpooled design provides observations that are informative regarding target variables allowing for ME. Therefore, we show that the pooled-unpooled sampling strategy is more efficient than the repeated measurement sampling procedure. We construct parametric likelihoods based on both the sampling methods. Additionally, in order to preserve efficiencies of both strategies without parametric assumptions, we consider a nonparametric approach using the empirical likelihood (EL) methodology (e.g., DiCicco et al. [22]; Owen [23-25]; Vexler et al. [26-27]; Vexler and Gurevich [28]; Yu et al. [29]). We develop and apply novel EL ratio test statistics creating the confidence interval estimation based on pooled-unpooled data and repeated measures data. Despite the fact that many statistical inference procedures have been developed to operate with data subject to ME, to our knowledge, relevant nonparametric likelihood techniques and parametric likelihood methods have not been well addressed in the literature.

The paper is organized as follows. In Section 2, we present a general form of the likelihood function based on repeated measures data and pooled-unpooled data. We propose the EL methodology to make nonparametric inferences based on repeated measures data and pooled-unpooled data in Section 3. We claim that the EL technique based on the hybrid design provides a valuable technique to construct statistical tests and estimators of parameters when MEs are present. To evaluate the proposed approaches, Monte Carlo simulations are utilized in Section 4. An application to cholesterol biomarker data from a study of coronary heart disease is presented in Section 5. In Section 6, we provide some concluding remarks.

2. Parametric inferences

In this section, we derive general forms of the relevant likelihood functions. In each case, we assume the total measurements of the biomarkers are fixed, say N, e.g., N is a total number of measurements that a study budget allows us to execute.

2.1 Parametric likelihood functions

2.1.1. Parametric likelihood based on repeated measures data

Suppose that we measure a biospecimen observing score Z_ij = X_i + ε_ij, where true values of biomarker measurements X_i are independent identically distributed (i.i.d.) and ε_ij are i.i.d. values of ME, i = 1, …, t; j = 1, …, n_i; $N={\sum }_{i=1}^t{n}_i$. Thus, we assume that there is a subset of t distinct biosassays and each of them is n_i times repeatedly measured. In this case, the total number of available individual bioassays can be defined to be T, T>t, when obtaining a large number of individual biospecimens can be considered to have a low cost with respect to a high cost of measurement processes. We assume that X and ε are independent. Firstly, we consider the simple normal case, say $X_i~N({\mu }_x,{\sigma }_x^2)$ and ${\epsilon }_{\mathit{ij}}~N(0,{\sigma }_m^2)$. Accordingly, we observe $Z_{\mathit{ij}}~N({\mu }_x,{\sigma }_x^2+{\sigma }_m^2)$. In this case, one can show that if n_i = 1, there are no unique solutions of estimation of ${\sigma }_m^2$ and ${\sigma }_x^2$ (non-identifiability). The observations Z’s in each group i are dependent, since they are measured using the same bioarray. Note that if we fix the value of X_i, Z_ij conditioned on X_i is independent of each other, e.g., in the case of ${\epsilon }_{\mathit{ij}}~N(0,{\sigma }_m^2)$, we have $Z_{\mathit{ij}}\mid X_i~N(X_i,{\sigma }_m^2)$. In a general case, the likelihood function based on the repeated measures data has the general form of

$$L_R(Z\mid {\mu }_x,{\sigma }_x^2,{\sigma }_m^2)=\prod _{i=1}^t{\mathit{\int }}_{-\infty }^{\infty }\left[f_X\left(x\right)\prod _{j=1}^{n_i}{f}_{\mathit{z}}(z_{\mathit{ij}}\mid x)\right]\mathit{dx}.$$

When the distribution of X_i and ε_ij are known, we can obtain the specific likelihood functions, and further, we can also derive the maximum likelihood estimators of μ_x, ${\sigma }_x^2$ and ${\sigma }_m^2$. Well-known asymptotic results related to the maximum likelihood estimation give evaluations of properties of estimators based on the likelihood $L_R(Z\mid {\mu }_x,{\sigma }_x^2,{\sigma }_m^2)$.

2.1.2. Parametric likelihood based on pooled and unpooled data

We briefly address the basic concept of the pooling design. Let T be the number of individual biospecimens available and N be the total number of measurements that can be obtained due to limited study budget. The pooling samples are obtained by randomly grouping individual samples into groups of size p, where p = [T/N], the number of individual samples in a pooling group and [x] is the integral part of x. The pooling design requires a physical combination of specimens of the same group and a test of each pooled specimen, obtaining a single observation, when the pooled sample is measured. Since the measurements are generally per unit of volume, we assume that the true measurement for a pooled set is the average of the true individual marker values in that group. In this case, taking into account that instruments applied to the measurement process can be sensitive and subject to some random exposure measurement error, we define a single observation to be a sum of the average of individual marker values and a value of measurement error. Note that, in accordance with the pooling literature, we assume that analysis of the biomarkers is restricted by the high cost of the measurement process, whereas access to a large number of individual biospecimens can be considered to have a relatively low cost.

In this subsection of hybrid design, we assume T distinct individual bioassays are available, but still we can provide just N measurements (N<T). The ratio of pooled and upooled samples is α/(1 − α), α ∈ [0, 1] and the pooling group size is p. Namely, T = αNP + (1 − α)N. Specifically, pooled data can be obtained by mixing p individual bioassays together and the αNp bioassays are therefore divided into n_p groups, where n_p = αN. The grouped biospecimens are measured as n_p single observations. Let $Z_i^p$, i = 1, …, n_p denote measurements of pooled bioassays. In accordance with the literature, we have

$$Z_i^p=\frac{1}{p}\sum _{k=(i-1)p+1}^{\mathit{ip}}{X}_k+{\epsilon }_{i1},i=1,\dots ,n_p=\mathit{\alpha N},$$

(see, e.g., Faraggi et al. [12], Liu and Schisterman [13], Liu et al. [14], Schisterman and Vexler et al. [16-17], Vexler et al. [18-21]). Hence, we can obtain that $Z_i^p$ are independent, identically distributed (i.i.d.) with the mean μ_x and the variance ${\sigma }_x^2/p+{\sigma }_m^2$, namely,

$$Z_i^p~\mathit{i.\; i.\; d.}({\mu }_x,{\sigma }_x^2/p+{\sigma }_m^2).$$

The unpooled samples are based on n_up = (1 − α)N independent observations

$$Z_j=X_{p{n}_p+j}+{\epsilon }_{j1},j=1,\dots ,n_{\mathit{up}}=(1-\alpha )N.$$

In this case, we have $Z_j~\mathit{i.\; i.\; d.}({\mu }_x,{\sigma }_x^2+{\sigma }_m^2)$.

Note that the pooled and unpooled samples are independent of each other. As a result, the likelihood function based on the combination of pooled and unpooled data has the form of

$$L_H(Z^p,Z\mid {\mu }_x,{\sigma }_x^2,{\sigma }_m^2)=\prod _{i=1}^{n_p}{f}_{z^p}\left(z_i^p\right)\prod _{j=1}^{n_{\mathit{up}}}{f}_z(z_j).$$

If the distribution functions of X_i and ε_ij are known, the likelihood functions can be derived according to the distribution of $Z_i^p$ and Z_j. Therefore, the corresponding theoretical maximum likelihood estimators of (μ_x, ${\sigma }_x^2$, ${\sigma }_m^2$) can also be obtained. Since the estimators follow the maximum likelihood methodology, the asymptotic properties of the estimators can be easily shown.

2.2. Normal case

In this subsection, we assume $X_i~N({\mu }_x,{\sigma }_x^2)$ and ${\epsilon }_{\mathit{ij}}~N(0,{\sigma }_m^2)$. Then closed-form analytical solutions for the maximum likelihood estimators of the unknown parameters, μ_x, ${\sigma }_x^2$, and ${\sigma }_m^2$, are obtained.

2.2.1. Maximum likelihood estimators based on repeated measures

Assume that i = 1, …, t; j = 1, …, n_i; $N={\sum }_{i=1}^t{n}_i$. By the additive property of the normal distribution, we have $Z_{\mathit{ij}}=X_i+{\epsilon }_{\mathit{ij}}~N({\mu }_x,{\sigma }_x^2+{\sigma }_m^2)$.

Referring to Searle et al. [30], the likelihood function is a well-known result that can be expressed by

$$L_R(Z\mid {\mu }_x,{\sigma }_x^2,{\sigma }_m^2)=\frac{\mathit{exp}\left\{-\left[\frac{{\sum }_i{\sum }_j{(Z_{\mathit{ij}}-{\mu }_x)}^2}{2{\sigma }_m^2}-{\sum }_i\frac{n_i^2{\sigma }_x^2{({\overline{Z}}_{i·}-{\mu }_x)}^2}{2{\sigma }_m^2(n_i{\sigma }_x^2+{\sigma }_m^2)}\right]\right\}}{{\left(2\pi \right)}^{\frac{N}{2}}{\sigma }_m^{2[\frac{1}{2}(N-t)]}{\prod }_i{(n_i{\sigma }_x^2+{\sigma }_m^2)}^{\frac{1}{2}}},$$

where ${\overline{Z}}_{i·}=n_i^{-1}{\sum }_{j=1}^{n_i}{Z}_{\mathit{ij}}$.

Under the assumption that n_i’s are equal (i.e. assuming balanced data), the log likelihood function is in the form of

$$\begin{array}{c}{l}_R(Z\mid {\mu }_x,{\sigma }_x^2,{\sigma }_m^2)=-\frac{N}{2}\mathit{log}(2\pi )-\frac{t(n-1)}{2}\mathit{log}{\sigma }_m^2-\frac{t}{2}\mathit{log}(n{\sigma }_x^2+{\sigma }_m^2)\\ -\frac{\mathit{SSE}}{2{\sigma }_m^2}-\frac{\mathit{SSA}}{2(n{\sigma }_x^2+{\sigma }_m^2)}-\frac{\mathit{tn}{(\overline{Z}..-{\mu }_x)}^2}{2(n{\sigma }_x^2+{\sigma }_m^2)},\end{array}$$

where $\overline{Z}..={(\mathit{nt})}^{-1}{\sum }_{i=1}^t{\sum }_{j=1}^n{Z}_{\mathit{ij}}$, $\mathit{SSE}={\sum }_i{\sum }_j{(Z_{\mathit{ij}}-{\overline{Z}}_{i·})}^2$, and $\mathit{SSA}={\sum }_{i}n{({\overline{Z}}_{i·}-\overline{Z}\mathrm{..})}^2$.

Let $\lambda =n{\sigma }_x^2+{\sigma }_m^2$. By taking the partial derivatives of l_R with respect to μ_x, ${\sigma }_m^2$ and λ and setting the equations equal to zero, we obtain the maximum likelihood equations with the roots

$${\stackrel{\sim }{\mu }}_x=\overline{Z}\mathrm{..},{\stackrel{\sim }{\sigma }}_m^2=\frac{\mathit{SSE}}{t(n-1)},\stackrel{\sim }{\lambda }=\frac{\mathit{SSA}}{t},\mathrm{and}{\stackrel{\sim }{\sigma }}_x^2=\frac{\mathit{SSA}}{\mathit{nt}}-\frac{\mathit{SSE}}{\mathit{nt}(n-1)}.$$

Thus, the maximum likelihood estimator of μ_x is μ̂_x = μ̃_x = Z̄.. and the maximum likelihood estimators of ${\sigma }_x^2$ and ${\sigma }_m^2$ are ${\widehat{\sigma }}_x^2={\stackrel{\sim }{\sigma }}_x^2$ and ${\widehat{\sigma }}_m^2={\stackrel{\sim }{\sigma }}_m^2$, respectively, when ${\stackrel{\sim }{\sigma }}_x^2\ge 0$; ${\widehat{\sigma }}_x^2=0$ and ${\widehat{\sigma }}_m^2={(\mathit{tn})}^{-1}{\sum }_{i=1}^t{{\sum }_{j=1}^n(Z_{\mathit{ij}}-\overline{Z}\mathrm{..})}^2$, respectively, when ${\stackrel{\sim }{\sigma }}_x^2<0$.

Also, the large-sample variances and covariance of ${\widehat{\sigma }}_x^2$ and ${\widehat{\sigma }}_m^2$ are given by

$$\begin{array}{c}\mathrm{var}({\widehat{\sigma }}_x^2)=\frac{2{\sigma }_m^4}{n^2}\left[\frac{{(n{\sigma }_x^2+{\sigma }_m^2)}^2/{\sigma }_m^4}{t}+\frac{1}{t(n-1)}\right],\mathrm{var}({\widehat{\sigma }}_m^2)=\frac{2{\sigma }_m^4}{t(n-1)},\\ \mathrm{cov}({\widehat{\sigma }}_x^2,{\sigma }_m^2)=-\frac{\mathrm{var}({\widehat{\sigma }}_m^2)}{n}\end{array}$$

(for details, see Searle et al. [30])

By the property of the maximum likelihood estimators, it is clear that asymptotically those estimators follow a multivariate normal distribution as

$$\sqrt{N}{[{\widehat{\mu }}_x-{\mu }_x{\widehat{\sigma }}_x^2-{\sigma }_x^2{\widehat{\sigma }}_x^2-{\sigma }_x^2]}^T~\mathit{MVN}(\mathbf{0},\mathbf{\sum }),\mathrm{as}t\to \infty ,$$

where

$$\mathbf{\sum }=\left[\begin{array}{ccc}n{\sigma }_x^2+{\sigma }_m^2& 0& 0\\ 0& \frac{2{\sigma }_m^4}{n}\left[\frac{{(n{\sigma }_x^2+{\sigma }_m^2)}^2}{{\sigma }_m^4}+\frac{1}{(n-1)}\right]& -\frac{2{\sigma }_m^4}{(n-1)}\\ 0& -\frac{2{\sigma }_m^4}{(n-1)}& \frac{2n{\sigma }_m^4}{(n-1)}\end{array}\right].$$

2.2.2. Maximum likelihood estimators followed the hybrid design

Since we assume that $X_i~N({\mu }_x,{\sigma }_x^2)$ and ${\epsilon }_{i1}~N(0,{\sigma }_m^2)$, i = 1, …, n_p, we can write $Z_i^p~N({\mu }_x,{\sigma }_x^2/p+{\sigma }_m^2)$ and $Z_j~N({\mu }_x,{\sigma }_x^2+{\sigma }_m^2)$, i = 1, …, n_p, j = 1, …, n_up, n_p + n_up = N.

The likelihood function based on pooled-unpooled data then takes the form

$$L_H(Z\mid {\mu }_x,{\sigma }_x^2,{\sigma }_m^2)={(2\pi )}^{-N/2}{({\sigma }_m^2+{\sigma }_x^2/p)}^{-n_p/2}{({\sigma }_m^2+{\sigma }_x^2)}^{-n_{\mathit{up}}/2}{e}^{-{\sum }_{i=1}^{n_p}\frac{{(Z_i^p-{\mu }_x)}^2}{2({\sigma }_m^2+{\sigma }_x^2/p)}-{\sum }_{j=1}^{n_{\mathit{up}}}\frac{{(Z_j-{\mu }_x)}^2}{2({\sigma }_m^2+{\sigma }_x^2)}}.$$

Differentiating the log likelihood function, $\log L_H(Z\mid {\mu }_x,{\sigma }_x^2,{\sigma }_m^2)$, with respect to μ_x, ${\sigma }_x^2$ and ${\sigma }_m^2$, respectively, we obtain the maximum likelihood estimators of μ_x, ${\sigma }_x^2$ and ${\sigma }_m^2$ given by

$$\begin{array}{c}{\widehat{\mu }}_x=\frac{({\widehat{\sigma }}_m^2+{\widehat{\sigma }}_x^2){\sum }_{i=1}^{n_p}{Z}_i^p+({\widehat{\sigma }}_m^2+{\widehat{\sigma }}_x^2/p){\sum }_{j=1}^{n_{\mathit{up}}}{Z}_j}{n_{\mathit{up}}({\widehat{\sigma }}_m^2+{\widehat{\sigma }}_x^2/p)+n_p({\widehat{\sigma }}_m^2+{\widehat{\sigma }}_x^2)},\\ {\widehat{\sigma }}_x^2=\frac{p}{p-1}\left[\frac{{\sum }_{j=1}^{n_{\mathit{up}}}{(Z_j-{\widehat{\mu }}_x)}^2}{n_{\mathit{up}}}-\frac{{\sum }_{i=1}^{n_{\mathit{up}}}{(Z_i^p-{\widehat{\mu }}_x)}^2}{n_p}\right],{\widehat{\sigma }}_m^2=\frac{{{\sum }_{i=1}^{n_p}(Z_i^p-{\widehat{\mu }}_x)}^2}{n_p}-\frac{{\widehat{\sigma }}_x^2}{p}.\end{array}$$ (1)

Note that the estimator of μ has a structure that weighs estimations based on pooled and unpooled data in a similar manner to a Bayes point estimator used in normal-normal models (see Carlin and Louis [31]). In this case, we show that inference regarding the parameters can be obtained by using this hybrid approach without repeating measures on the same individual, which is the most common strategy to solve measurement error problems.

By the virtue of the properties of the maximum likelihood estimators, the asymptotic distribution of the estimators (1) is asymptotically $\sqrt{N}{[\begin{array}{ccc}{\widehat{\mu }}_x-{\mu }_x& {\widehat{\sigma }}_x^2-{\sigma }_x^2& {\widehat{\sigma }}_x^2-{\sigma }_x^2\end{array}]}^T~\mathit{MVN}(\mathbf{0},\mathbf{\sum })$, where Σ is the inverse of the Fisher Information matrix, I,

$$\begin{array}{c}\mathbf{I}=-\underset{N\to \infty }{\lim }\frac{1}{N}E\left[\begin{array}{ccc}\frac{{\partial }^2{l}_H}{\partial {({\mu }_x)}^2}& \frac{{\partial }^2{l}_H}{\partial {\mu }_x\partial {\sigma }_x^2}& \frac{{\partial }^2{l}_H}{\partial {\mu }_x\partial {\sigma }_m^2}\\ \frac{{\partial }^2{l}_H}{\partial {\sigma }_x^2\partial {\mu }_x}& \frac{{\partial }^2{l}_H}{\partial {({\sigma }_x^2)}^2}& \frac{{\partial }^2{l}_H}{\partial {\sigma }_x^2\partial {\sigma }_m^2}\\ \frac{{\partial }^2{l}_H}{\partial {\sigma }_m^2\partial {\mu }_x}& \frac{{\partial }^2{l}_H}{\partial {\sigma }_m^2\partial {\sigma }_x^2}& \frac{{\partial }^2{l}_H}{\partial {({\sigma }_m^2)}^2}\end{array}\right]\\ =\left[\begin{array}{ccc}\frac{\alpha }{{\sigma }_m^2+{\sigma }_x^2/p}+\frac{1-\alpha }{{\sigma }_m^2+{\sigma }_x^2}& 0& 0\\ 0& \frac{\alpha }{2p^2{({\sigma }_m^2+{\sigma }_x^2/p)}^2}+\frac{1-\alpha }{2{({\sigma }_m^2+{\sigma }_x^2)}^2}& \frac{\alpha }{2p{({\sigma }_m^2+{\sigma }_x^2/p)}^2}+\frac{1-\alpha }{2{({\sigma }_m^2+{\sigma }_x^2)}^2}\\ 0& \frac{\alpha }{2p{({\sigma }_m^2+{\sigma }_x^2/p)}^2}+\frac{1-\alpha }{2{({\sigma }_m^2+{\sigma }_x^2)}^2}& \frac{\alpha }{2{({\sigma }_m^2+{\sigma }_x^2/p)}^2}+\frac{1-\alpha }{2{({\sigma }_m^2+{\sigma }_x^2)}^2}\end{array}\right],\end{array}$$

where $l_H=\log L_H(Z\mid {\mu }_x,{\sigma }_x^2,{\sigma }_m^2)$ is the corresponding log likelihood function (for details, see Appendix A1 of the supplementary material).

2.2.3. Remarks on the normal case

As shown above, when biomarkers’ values and measurement errors are normally distributed, the maximum likelihood estimators exist and can be easily obtained. It is also clear that these estimators can be considered as the least square estimators in a nonparametric context.

However, when data are not from normal distributions, it may be very complicated or even be infeasible to extract the distributions of repeated measures data or pooled and unpooled data (e.g., Vexler et al. [21]). For example, in various situations, closed analytical forms of the likelihood functions cannot be found based on pooled data, since the density function of the pooled biospecimen values involves complex convolutions of p-individual biospecimen values. Consequently, efficient nonparametric inference methodologies based on the repeated measures data or pooled-unpooled data are reasonable to be considered.

3. Empirical likelihood method

In this section, we apply the empirical likelihood (EL) methodology to the statement of the problem in this article. The EL technique has been extensively proposed as a nonparametric approximation of the parametric likelihood approach (e.g., DiCiccio et al. [22]; Owen [23-25]; Vexler et al. [26-27]; Vexler and Gurevich [28]; Yu et al. [29]). We begin by outlining the EL ratio method and then modifying the EL ratio test to apply to construct confidence interval estimations and tests based on data with repeated measures and pooled-unpooled data.

3.1. The EL ratio test

Consider the following simple testing problem that is stated nonparametrically. Suppose i.i.d. random variables Y₁, Y₂, …, Y_n with E(Y₁) = μ and E|Y₁|³ < ∞ are observable. The problem of interest, for example, is to test the hypothesis

$$H_0:E(Y_1)={\mu }_0\mathrm{vs}.H_1:E(Y_1)\ne {\mu }_0,$$ (2)

where μ₀ is fixed and known. To test for the hypothesis at (2), the EL function can be written as

$$L_n=\prod _{i=1}^n{p}_i,\sum _{i=1}^n{p}_i=1,0\le p_1,\dots ,p_n\le 1,$$

where p_i’s are assumed to have values that maximize L_n given empirical constraints. The empirical constraints correspond to hypotheses settings. Then, under the null hypothesis at (2), we maximize L_n subject to ${\sum }_{i=1}^n{p}_i{Y}_i={\mu }_0$. Here the condition ${\sum }_{i=1}^n{p}_i{Y}_i={\mu }_0$ is an empirical form of EY₁ = μ₀. Using the Lagrange multipliers, one can show the maximum EL function has the form of

$$L({\mu }_0)=\underset{\begin{array}{c}0\le p_1,\dots ,p_n\le 1\\ {\sum }_{i=1}^n{p}_i=1,{\sum }_{i=1}^n{p}_i{Y}_i={\mu }_0\end{array}}{\sup }\prod _{i=1}^n{p}_i=\prod _{i=1}^n\frac{1}{n}\frac{1}{1+\lambda (Y_i-{\mu }_0)},$$

where λ is a root of

$$\sum _{i=1}^n\frac{Y_i-{\mu }_0}{1+\lambda (Y_i-{\mu }_0)}=0.$$

Similarly, under the alternative hypothesis, the maximum EL function has the simple form

$$L=\underset{\begin{array}{c}0\le p_1,\dots ,p_n\le 1\\ {\sum }_{i=1}^n{p}_i=1\end{array}}{\sup }\prod _{i=1}^n{p}_i=\prod _{i=1}^n\frac{1}{n}=n^{-n}.$$

As a consequence, the 2log EL ratio test for (2) is

$$l({\mu }_0)=2[\log (L)-\log (L({\mu }_0))]=2\sum _{i=1}^n\log [1+\lambda (Y_i-{\mu }_0)].$$

It is proven in Owen [25] that the 2log EL ratio, l(μ₀), follows asymptotically ${\chi }_1^2$ distribution as n → ∞. Thus, we reject the null hypothesis at a significance level α if $l({\mu }_0)>{\chi }_{1,1-\alpha }^2$. Furthermore, we also can construct the confidence interval estimator of EY₁ as

$$\mathrm{CI}=\{\mu :l(\mu )\le C_{1-\alpha }\}.$$

(Here, C_1−α is the 100(1 − α)% percentile of a ${\chi }_1^2$ distribution with one degree of freedom.)

3.2. The EL method based on repeated measures data

Following the statement mentioned in Section 2, we have correlated data with repeated measures. In order to obtain an i.i.d. sample, we utilize the fact that Z_ij is independent of Z_kl when i ≠ k. Therefore, we give an EL function for the block sample mean ${\overline{Z}}_i=n_i^{-1}{\sum }_{j=1}^{n_i}{Z}_{\mathit{ij}}$, i = 1, …, t, $N={\sum }_{i=1}^t{n}_i$, in a similar manner to the blockwise EL method given in Kitamura [32]. Then, the random variables become Z̄₁, Z̄₂ …, Z̄_t and the corresponding EL function for μ_x is given by

$$L_R({\mu }_x)=\underset{\begin{array}{c}0\le p_1,\dots ,p_t\le 1\\ {\sum }_{i=1}^t{p}_i=1,{\sum }_{i=1}^t{p}_i{\overline{Z}}_i={\mu }_x\end{array}}{\sup }\prod _{i=1}^t{p}_i=\prod _{i=1}^t\frac{1}{t}\frac{1}{1+\lambda ({\overline{Z}}_i-{\mu }_x)},$$

where λ is a root of

$$\sum _{i=1}^t\frac{{\overline{Z}}_i-{\mu }_x}{1+\lambda ({\overline{Z}}_i-{\mu }_x)}=0.$$

In this case, the 2log EL ratio test statistic is in the form of

$$l_R({\mu }_x)=2\sum _{i=1}^t\log [1+\lambda ({\overline{Z}}_i-{\mu }_x)].$$

Proposition 3.2.1

Assume E|Z₁₁|³ < ∞. Then the 2log EL ratio, l_R (μ_x), distributes ${\chi }_1^2$, when ${\sum }_{i=1}^t{n}_i^{-1}\to \infty$, as t → ∞.

(Proof in Appendix A2.1 of the supplementary material.)

The associated confidence interval estimator is then given by CI_R = {μ_x : l_R (μ_x) ≤ C_{1 −α}}, where C_{1 −α} is the 100(1 − α)% percentile of a ${\chi }_1^2$ distribution with one degree of freedom.

3.3. The EL method based on pooled-unpooled data

In this section, we consider two distribution-free alternatives to the parametric likelihood method mentioned in Section 2.1.2. To this end, we apply the EL technique. Note that, in contrast to data that consists of repeated measures, in this section we use data that are based on independent observations. Consequently, we can introduce a combined EL function for the mean μ_x based on two independent samples, i.e. i.i.d. $Z_1^p$, $Z_2^p$, …, $Z_{n_p}^p$ and i. i. d. Z₁, Z₂, …, Z_nup (N = n_p + n_up), representing measurements that correspond to pooled and unpooled biospecimens, respectively. Under the null hypothesis, the EL function for μ_x can be presented in the form of

$$\begin{array}{lll}{L}_H({\mu }_x)& =& \underset{\begin{array}{c}0\le p_1,\dots ,p_{n_p}\le 1;0\le q_1,\dots ,q_{n_{\mathit{up}}}\le 1;\\ {\sum }_{i=1}^{n_p}{p}_i=1,{\sum }_{i=1}^{n_p}{p}_i{Z}_i^p={\mu }_x;{\sum }_{j=1}^{n_{\mathit{up}}}{q}_j=1,{\sum }_{j=1}^{n_{\mathit{up}}}{q}_j{Z}_j={\mu }_x\end{array}}{\sup }\prod _{i=1}^{n_p}{p}_i\prod _{j=1}^{n_{\mathit{up}}}{q}_j\\ & =& \prod _{i=1}^{n_p}\frac{1}{n_p}\frac{1}{1+{\lambda }_1(Z_i^p-{\mu }_x)}\prod _{j=1}^{n_{\mathit{up}}}\frac{1}{n_{\mathit{up}}}\frac{1}{1+{\lambda }_2\left(Z_j-{\mu }_x\right)},\end{array}$$

where λ₁ and λ₂ are roots of the equations

$$\sum _{i=1}^{n_p}\frac{Z_i^p-{\mu }_x}{1+{\lambda }_1\left(Z_i^p-{\mu }_x\right)}=0\mathrm{and}\sum _{j=1}^{n_{\mathit{up}}}\frac{Z_j-{\mu }_x}{1+{\lambda }_2(Z_j-{\mu }_x)}=0.$$

Finally, the 2log EL ratio test statistic can be given in the form of

$$l_H({\mu }_x)=2\sum _{i=1}^{n_p}\log [1+{\lambda }_1(Z_i^p-{\mu }_x)]+2\sum _{j=1}^{n_{\mathit{up}}}\log [1+{\lambda }_2(Z_j-{\mu }_x)].$$ (3)

In a similar manner to common EL considerations, one can show that the statistics $2{\sum }_{i=1}^{n_p}\log \left[1+{\lambda }_1(Z_i^p-{\mu }_x)\right]$ and $2{\sum }_{j=1}^{n_{\mathit{up}}}\log \left[1+{\lambda }_2(Z_j-{\mu }_x)\right]$ follow asymptotically a ${\chi }_1^2$ distribution, respectively. By virtue of the additive property of χ² distributions, the 2log EL ratio, l_H (μ_x), has an asymptotic ${\chi }_2^2$ distribution with two degrees of freedom. Thus, we formulate the next proposition.

Proposition 3.3.1

Let E|Z₁|³ < ∞. Then the 2log EL ratio, l_H (μ_x), has a ${\chi }_2^2$ distribution as n_p, n_up → ∞.

The corresponding confidence interval estimator is

$${\mathrm{CI}}_H=\left\{{\mu }_x:l_H({\mu }_x)\le H_{1-\alpha }\right\},$$ (4)

where H_1−α is the 100(1 − α)% percentile of a ${\chi }_2^2$ distribution with two degrees of freedom.

In practice, to execute the procedure above, we can directly use standard programs related to the c assica EL ratio tests, e.g., the code “el.test” of the R software can be utilized to conduct the EL confidence interval estimator (4).

The EL technique mentioned above does not use an empirical version of the rule

$$E{\left(Z_i^p\right)}^2=E{\left(Z_j\right)}^2-\frac{p}{p-1}{\sigma }_x^2$$ (5)

that connects the second moments derived from pooled and unspooled observations. Intuitively, using a constraint related to (5), one can increase the power of the EL approach. Consider the EL function for μ_x under the null hypothesis,

$$\begin{array}{lll}{L}_H^{\prime }({\mu }_x,{\widehat{\sigma }}_x^2)& =& \underset{\begin{array}{c}0\le p_1,\dots ,p_{n_p}\le 1;0\le q_1,\dots ,q_{n_{\mathit{up}}}\le 1;\\ {\sum }_{i=1}^{n_p}{p}_i=1,{\sum }_{i=1}^{n_p}{p}_i{Z}_i^p={\mu }_x;{\sum }_{j=1}^{n_{\mathit{up}}}{q}_j=1,{\sum }_{j=1}^{n_{\mathit{up}}}{q}_j{Z}_j={\mu }_x;\\ {\sum }_{i=1}^{n_p}{p}_i{(Z_i^p)}^2={\sum }_{j=1}^{n_{\mathit{up}}}{q}_j{(Z_j)}^2-\left(\frac{p-1}{p}\right){\widehat{\sigma }}_x^2\end{array}}{\sup }\prod _{i=1}^{n_p}{p}_i\prod _{j=1}^{n_{\mathit{up}}}{q}_j\\ & =& \prod _{i=1}^{n_p}{\left({\lambda }_1+{\lambda }_3{Z}_i^p+{\lambda }_5{\left(Z_i^p\right)}^2\right)}^{-1}\prod _{j=1}^{n_{\mathit{up}}}{\left({\lambda }_2+{\lambda }_4{Z}_j+{\lambda }_5{(Z_j)}^2\right)}^{-1}\end{array}$$

as an alternative to the simple EL function L_H (μ_x). Here, ${\widehat{\sigma }}_x^2$ is the estimator from (1) that is defined under the null hypothesis,

$${\left({\widehat{\sigma }}_x^2\right)}^2=\frac{p}{p-1}\left[\frac{{\sum }_{j=1}^{n_{\mathit{up}}}{\left(Z_j-{\mu }_x\right)}^2}{n_{\mathit{up}}}-\frac{{\sum }_{i=1}^{n_p}{\left(Z_i^p-{\mu }_x\right)}^2}{n_p}\right],$$

λ₁, λ₂, λ₃, and λ₄ are roots of the equations mentioned under the operator sup in the definition of $L_H^{\prime }\left({\mu }_x,{\widehat{\sigma }}_x^2\right)$ with $p_i={\left({\lambda }_1+{\lambda }_3{\left(Z_i^p\right)}^2\right)}^{-1}$ and q_j = (λ₂ − λ₄(Z_j)²)⁻¹. Likewise, under the alternative hypothesis, we maximize the EL function, $\prod _{i=1}^{n_p}{p}_i\prod _{j=1}^{n_{\mathit{up}}}{q}_j$, subject to

$$\begin{array}{c}0\le p_1,\dots ,p_{n_p}\le 1,0\le q_1,\dots ,q_{n_{\mathit{up}}}\le 1,\\ \sum _{i=1}^{n_p}{p}_i=1,\sum _{j=1}^{n_{\mathit{up}}}{q}_j=1,\sum _{i=1}^{n_p}{p}_i{\left(Z_i^p\right)}^2=\sum _{j=1}^{n_{\mathit{up}}}{q}_j{\left(Z_j\right)}^2-\left(\frac{p-1}{p}\right){\left({\widehat{\sigma }}_x^1\right)}^2,\end{array}$$ (6)

where

$${({\widehat{\sigma }}_x^1)}^2=\frac{p}{p-1}\left[\frac{{\sum }_{j=1}^{n_{\mathit{up}}}{(Z_j-{\widehat{\mu }}_x)}^2}{n_{\mathit{up}}}-\frac{{\sum }_{i=1}^{n_p}{(Z_i^p-{\widehat{\mu }}_x)}^2}{n_p}\right].$$

Thus, the EL under the alternative hypothesis that depends on ${({\widehat{\sigma }}_x^1)}^2$ is given by

$$L_H^{\prime H_1}({({\widehat{\sigma }}_x^1)}^2)=\prod _{i=1}^{n_p}{p}_i\prod _{j=1}^{n_{\mathit{up}}}{q}_j=\prod _{i=1}^{n_p}\frac{1}{{\lambda }_1^{\ast }+{\lambda }_3^{\ast }{(Z_i^p)}^2}\prod _{j=1}^{n_{\mathit{up}}}\frac{1}{{\lambda }_2^{\ast }-{\lambda }_4^{\ast }{(Z_j)}^2},$$

where $p_i={\left({\lambda }_1^{\ast }+{\lambda }_3^{\ast }{(Z_i^p)}^2\right)}^{-1}$, $q_j={\left({\lambda }_2^{\ast }-{\lambda }_4^{\ast }{(Z_j)}^2\right)}^{-1}$ as well as ${\lambda }_1^{\ast }$, ${\lambda }_2^{\ast }$, ${\lambda }_3^{\ast }$, and ${\lambda }_4^{\ast }$ should be numerically derived using the equations (6). As a result, the corresponding 2log EL ratio test statistic is

$$l_H^{\prime }({\mu }_x)=2\left[\log (L_H^{\prime H_1}({({\widehat{\sigma }}_x^1)}^2))-\log \left(L_H^{\prime }({\mu }_x,{\widehat{\sigma }}_x^2)\right)\right].$$ (7)

Note that, following Qin and Lawless [33], $l_H^{\prime }({\mu }_x)$ is asymptotically equivalent to the maximum log EL ratio test statistic. By virtue of results mentioned in Qin and Lawless [33], $l_H^{\prime }({\mu }_x)$ asymptotically follows a ${\chi }_2^2$ distribution. Then we reject the null hypothesis at a significance level α when

$$l_H^{\prime }({\mu }_x)>C_{1-\alpha }^{\prime },$$ (8)

where $C_{1-\alpha }^{\prime }$ is the 100(1 − α)% percentile of a ${\chi }_2^2$ distribution. Moreover, the corresponding confidence interval is ${\mathrm{CI}}_H^{\prime }=\{{\mu }_x:l_H^{\prime }({\mu }_x)\le C_{1-\alpha }^{\prime }\}$, where $C_{1-\alpha }^{\prime }$ is the 100(1 − α)% percentile of a ${\chi }_2^2$ distribution.

The Monte Carlo simulation study presented in the next section examines the performance of each EL method mentioned above.

4. Monte Carlo experiments

In this section, we conduct an extensive Monte Carlo study to evaluate the performance of the parametric and nonparametric likelihood methods proposed in Sections 2 and 3.

4.1. Simulation settings

Examining the repeated measures sampling method, we randomly generated samples of x₁, …, x_t values from a normal distribution with mean E(X₁) = μ_x and variance $\mathrm{var}(X_1)={\sigma }_x^2$. Let n_i, i = 1, …, t, denote the number of replicates for each subject. For simplicity, we assume each subject has the same number of replicates n₁ = ⋯ = n_t (i.e. assuming balanced data). Then, in a similar manner, we randomly generate normally distributed measurement errors, ε_ij’s, having E(ε_ij) = 0 and $\mathrm{var}({\epsilon }_{\mathit{ij}})={\sigma }_m^2$, i = 1, …, t; j = 1, …, n. Therefore, we conducted samples of z_ij = x_i + ε_ij. Each sample had N = tn observations.

To obtain the hybrid samples, we first generate a sample of size T, where T = αNp + (1 − α)N, n_p = αN, n_up = (1 − α)N, to represent available individual bioassays. Then we proceed to generate pooled data. To this end, we pool αNp, α ∈ [0, 1], samples of x_i’s to constitute pooled data, where αNp is assumed to be an integer and x_i’s, i = 1, …, T, are i.i.d. random samples from a normal distribution with mean E(X₁) = μ_x and $\mathrm{var}(X_1)={\sigma }_x^2$. Following the pooling literature, if there are no measurement errors, the average values of the pooled biospecimens, $p^{-1}{\sum }_{k=(i-1)p+1}^{\mathit{ip}}{x}_k$, i = 1, …, n_p, are assumed to be observed and can be represented as the n_p measurements of pooled bioassays. The remaining (1 − α)N observations x_{pnp + j}, j = 1, …, n_up, are taken as individual measurements. For each observation, we randomly generate a measurement error ε_i1 from a normal distribution. Combining the pooled sample, $z_i^p=p^{-1}{\sum }_{k=(i-1)p+1}^{\mathit{ip}}{x}_k+{\epsilon }_{i1}$, i = 1, …, n_p, with the unpooled sample, z_j = x_{pnp + j} + ε_j1, j = 1, …, n_up, we obtain pooled-unpooled data with the total sample size N = n_p + n_up equal to that in the Monte Carlo evaluations related to the repeated measures approaches.

To evaluate the performance of proposed methods, the following simulation setting was applied: the fixed significance level was 0.05; μ_x =1 and ${\sigma }_x^2=1$; ${\sigma }_m^2=0.4$, 1; n =2, 5, 10; the pooling group size p= 2, 5, 10; the pooling proportion α=0.5; the total sample size N=100, 300. For each set of parameters, there were 10,000 data generations (Monte Carlo). In this section, following the pooling literature, we assume that the simulated analysis of biomarkers is restricted to execute just N measurements and T = 0.5N(p + 1) individual biospeciaments are available, when the hybrid design is compared with the repeated measures sampling method. The Monte Carlo simulation results are presented in the next subsection.

4.2. Monte Carlo outputs

Table 1 shows the estimated parameters based on the repeated measures data using the parametric likelihood method. The results show that as the replicates increase, the standard errors of the estimates of ${\sigma }_m^2$ decrease, indicating that the estimations of ${\sigma }_m^2$ appear to be better as the number of replicates increases. Apparently, the Monte Carlo standard errors of the estimators of μ_x and ${\sigma }_x^2$ increase when the number of replicates is increased.

Table 1.

The Monte Carlo Evaluations of the Maximum Likelihood Estimates Based on Repeated Measurements and the Hybrid Design

Sample Size	Replicates n; Pooling Size p	Parameters (μx, ${\sigma }_x^2$, ${\sigma }_m^2$)	Estimates			Standard Errors
			μ̂x	${\widehat{\sigma }}_x^2$	${\widehat{\sigma }}_m^2$	SE(μ̂x)	$\mathrm{SE}({\widehat{\sigma }}_x^2)$	$\mathrm{SE}({\widehat{\sigma }}_m^2)$
Repeated Measurements:
N=100	n=2	(1, 1, 0.4)	1.0021	0.9781	0.3997	0.1553	0.2410	0.0790
		(1, 1, 1.0)	1.0006	0.9688	0.9984	0.1726	0.3106	0.1994
	n=5	(1, 1, 0.4)	0.9966	0.9462	0.3990	0.2328	0.3305	0.0623
		(1, 1, 1.0)	1.0015	0.9362	0.9998	0.2442	0.3688	0.1570
	n=10	(1, 1, 0.4)	1.0026	0.8951	0.3999	0.3209	0.4346	0.0597
		(1, 1, 1.0)	1.0044	0.8917	0.9995	0.3299	0.4690	0.1501
N=300	n=2	(1, 1, 0.4)	0.9987	0.9921	0.3999	0.0889	0.1405	0.0455
		(1, 1, 1.0)	1.0005	0.9883	0.9999	0.0995	0.1803	0.1162
	n=5	(1, 1, 0.4)	0.9995	0.9797	0.3998	0.1356	0.1950	0.0365
		(1, 1, 1.0)	0.9990	0.9766	0.9990	0.1409	0.2181	0.0906
	n=10	(1, 1, 0.4)	0.9985	0.9682	0.3997	0.1864	0.2633	0.0344
		(1, 1, 1.0)	0.9985	0.9660	1.0002	0.1914	0.2782	0.0861
Hybrid Design:
N=100	p=2	(1, 1, 0.4)	1.0015	1.0160	0.4365	0.1048	0.6712	0.4579
		(1, 1, 1.0)	1.0007	1.0754	1.0098	0.1327	1.0058	0.7275
	p=5	(1, 1, 0.4)	0.9994	1.0045	0.3889	0.0924	0.3857	0.1662
		(1, 1, 1.0)	1.0008	1.0053	0.9880	0.1240	0.5932	0.3217
	p=10	(1, 1, 0.4)	0.9993	1.0049	0.3918	0.0871	0.3341	0.1164
		(1, 1, 1.0)	0.9996	1.0050	0.9836	0.1197	0.5082	0.2486
N=300	p=2	(1, 1, 0.4)	0.9999	0.9974	0.4066	0.0608	0.3868	0.2652
		(1, 1, 1.0)	1.0002	1.0069	0.9982	0.0758	0.5788	0.4179
	p=5	(1, 1, 0.4)	0.9995	1.0013	0.3969	0.0534	0.2197	0.0954
		(1, 1, 1.0)	0.9993	1.0076	0.9910	0.0711	0.3386	0.1819
	p=10	(1, 1, 0.4)	0.9995	0.9995	0.3972	0.0497	0.1935	0.0671
		(1, 1, 1.0)	0.9992	1.0059	0.9922	0.0688	0.2928	0.1436

To accomplish the efficiency comparison between the repeated measures strategy and the hybrid design strategy, the Monte Carlo properties of the maximum likelihood estimates based on pooled-unpooled data are provided in Table 1. Table 1 shows that the Monte Carlo standard errors of the estimates for μ_x based on pooled-unpooled data are clearly less than those of the corresponding estimates that utilize repeated measures, when p ≥ 2 (respectively, n ≥ 2). One observed advantage is that the estimation for ${\sigma }_x^2$ based on pooled-unpooled data is very accurate when the total number of measurements is fixed at the same level. Another advantage is that the standard errors of the estimates for the mean are much smaller than those shown in Table 1.

Table 2 displays the coverage probabilities of the confidence interval estimators constructed by the parametric likelihood and EL method based on repeated measures data and the mixed data, respectively. Table 2 shows that the EL ratio test statistic is as efficient as the traditional parametric likelihood approach in the context of constructing confidence intervals, since the coverage probabilities and the interval width of the two methods are very close.

Table 2.

Coverage Probabilities and Confidence Intervals Based on Repeated Measurements and the Hybrid Design

Sample Size	Replicates n; Pooling Size p	Parameters (μx, ${\sigma }_x^2$, ${\sigma }_m^2$)	Parametric Likelihood		Empirical Likelihood
			Coverage	CI	Coverage	CI
Repeated Measurements:
N=100	n=2	(1, 1, 0.4)	0.9420	(0.7028, 1.3014)	0.9496	(0.6980, 1.3049)
		(1, 1, 1.0)	0.9423	(0.6665, 1.3347)	0.9466	(0.6613, 1.3394)
	n=5	(1, 1, 0.4)	0.9305	(0.5584, 1.4348)	0.9327	(0.5519, 1.4466)
		(1, 1, 1.0)	0.9289	(0.5404, 1.4626)	0.9353	(0.5298, 1.4752)
	n=10	(1, 1, 0.4)	0.9044	(0.4193, 1.5859)	0.8985	(0.4158, 1.5876)
		(1, 1, 1.0)	0.9042	(0.4040, 1.6047)	0.9030	(0.4054, 1.6065)
N=300	n=2	(1, 1, 0.4)	0.9477	(0.8243, 1.1731)	0.9517	(0.8240, 1.1753)
		(1, 1, 1.0)	0.9469	(0.8056, 1.1955)	0.9479	(0.8034, 1.1962)
	n=5	(1, 1, 0.4)	0.9400	(0.7401, 1.2588)	0.9467	(0.7360, 1.2628)
		(1, 1, 1.0)	0.9448	(0.7257, 1.2722)	0.9467	(0.7210, 1.2763)
	n=10	(1, 1, 0.4)	0.9396	(0.6422, 1.3547)	0.9379	(0.6318, 1.3582)
		(1, 1, 1.0)	0.9336	(0.6321, 1.3648)	0.9417	(0.6245, 1.3712)
Hybrid Design:
N=100	p=2	(1, 1, 0.4)	0.9512	(0.7939, 1.2090)	0.9492	(0.7725, 1.2303)
		(1, 1, 1.0)	0.9463	(0.7422, 1.2592)	0.9421	(0.7146, 1.2869)
	p=5	(1, 1, 0.4)	0.9424	(0.8230, 1.1757)	0.9490	(0.7978, 1.2010)
		(1, 1, 1.0)	0.9439	(0.7644, 1.2372)	0.9509	(0.7314, 1.2703)
	p=10	(1, 1, 0.4)	0.9393	(0.8339, 1.1646)	0.9498	(0.8099, 1.1887)
		(1, 1, 1.0)	0.9431	(0.7701, 1.2290)	0.9478	(0.7376, 1.2614)
N=300	p=2	(1, 1, 0.4)	0.9482	(0.8817, 1.1182)	0.9551	(0.8660, 1.1337)
		(1, 1, 1.0)	0.9469	(0.8525, 1.1479)	0.9520	(0.8334, 1.1672)
	p=5	(1, 1, 0.4)	0.9478	(0.8963, 1.1026)	0.9532	(0.8822, 1.1166)
		(1, 1, 1.0)	0.9463	(0.8616, 1.1371)	0.9506	(0.8433, 1.1556)
	p=10	(1, 1, 0.4)	0.9462	(0.9030, 1.0961)	0.9584	(0.8896, 1.1095)
		(1, 1, 1.0)	0.9484	(0.8652, 1.1332)	0.9532	(0.8475, 1.5080)

It is clearly shown that when sample sizes are greater than 100, the coverage probabilities obtained via the pooled-unpooled design are closer to the expected 0.95 value than those based on repeated measurements. This, again, demonstrates that mixed data are more efficient than repeated measures data.

To compare the Monte Carlo type I errors and powers of the tests based on the test statistics l_H (μ_x) and $l_H^{\prime }({\mu }_x)$ by (3) and (7), we performed 10,000 simulations for each parametric setting and sample size. To test the null hypothesis H₀: μ_x = 0, we use the statistics l_H (μ_x) and $l_H^{\prime }({\mu }_x)$ by (3) and (7). Table 3 depicts results that correspond to the case when X_i~N(μ_x, 1). The outputs show that the Monte Carlo type I errors and powers of the test statistic l_H (μ_x) are slightly better than those corresponding to the test statistic $l_H^{\prime }({\mu }_x)$. This indicates that the test based on the simple statistic l_H (μ_x) outperforms that based on the statistic $l_H^{\prime }({\mu }_x)$, in the considered cases.

Table 3.

The Monte Carlo Type I Errors and Powers of the EL ratio test statistics (3) and (7) for testing H₀: μ_x = 0 Based on Data Following the Hybrid Design (X_i ~ N(μ_x, 1), ${\epsilon }_i~N(0,{\sigma }_m^2)$. The pooling proportion α = 0.5; the expected significance level was 0.05).

Sample Size (N)	Pooling Group Size (p)	Parameters ${\sigma }_m^2$	ELR Test Statistic (3)			ELR Test Statistic (7)
			Type I Error	Power		Type I Error	Power
			μx =0	μx =0.5	μx =1.0	μx =0	μx =0.5	μx =1.0
N=100	p=2	0.4	0.0587	0.9919	1.0000	0.0580	0.9718	0.9990
		1.0	0.0558	0.9373	1.0000	0.0611	0.9230	0.9986
	p=5	0.4	0.0555	0.9989	1.0000	0.0530	0.9512	0.9992
		1.0	0.0587	0.9626	1.0000	0.0604	0.9446	0.9976
	p=10	0.4	0.0588	0.9995	1.0000	0.0595	0.9531	0.9999
		1.0	0.0556	0.9684	1.0000	0.0621	0.9680	0.9992
N=200	p=2	0.4	0.0495	0.9999	1.0000	0.0594	0.9990	0.9985
		1.0	0.0536	0.9991	1.0000	0.0593	0.9983	0.9995
	p=5	0.4	0.0540	1.0000	1.0000	0.0524	0.9952	0.9996
		1.0	0.0511	0.9997	1.0000	0.0543	0.9981	0.9999
	p=10	0.4	0.0549	1.0000	1.0000	0.0546	0.9950	0.9996
		1.0	0.0536	0.9999	1.0000	0.0551	0.9979	1.0000

Table 4 displays the Monte Carlo simulation results of testing the null hypothesis H₀: μ_x = 2 when $X_i~{\chi }_2^2+a$, where ${\chi }_2^2$ is a chi-squared distribution with two degrees of freedom and a is an effect size. Again, in this case, it is obvious that the type I errors (when a=0) of the test statistic l_H (μ_x) are much better controlled by 0.05 than those based on the test statistic $l_H^{\prime }({\mu }_x)$. In addition, the Monte Carlo powers of the test based on the test statistic l_H (μ_x) are higher than those based on the statistic $l_H^{\prime }({\mu }_x)$ when the effect size a is large than 0.5. On the contrary, as the effect size a is small such as 0.1 and 0.2, the Monte Carlo powers of the tests based on the test statistic $l_H^{\prime }({\mu }_x)$ seem higher than those based on the statistic l_H (μ_x). This shows that when the effect size a is large, the test based on the simple statistic l_H (μ_x) is preferable to that based on the statistic $l_H^{\prime }({\mu }_x)$.

Table 4.

The Monte Carlo Type I Errors and Powers of the EL ratio test statistics (3) and (7) for testing H₀: μ_x = 2 Based on Data Following the Hybrid Design ( $X_i~{\chi }_2^2+a$, ${\epsilon }_i~N(0,{\sigma }_m^2)$, and EX_i = 2 + a. The pooling proportion α = 0.5; the expected significance level was 0.05).

Sample Size (N)	Pooling Group Size (p)	Parameters ${\sigma }_m^2$	ELR Test Statistic (3)				ELR Test Statistic (7)
			Type I Error	Power			Type I Error	Power
			a = 0	a = 0.1	a = 0.2	a = 0.5	a = 0	a = 0.1	a = 0.2	a = 0.5
N=100	p=2	0.4	0.0687	0.0862	0.2021	0.8567	0.0724	0.0989	0.2144	0.7446
		1.0	0.0654	0.0792	0.1579	0.6978	0.0690	0.0936	0.1696	0.6417
	p=5	0.4	0.0649	0.1123	0.3133	0.9808	0.0985	0.1583	0.3552	0.9084
		1.0	0.0670	0.0906	0.1901	0.8141	0.0862	0.1131	0.2338	0.8171
	p=10	0.4	0.0646	0.1454	0.4460	0.9990	0.1016	0.1724	0.4416	0.9269
		1.0	0.0623	0.0916	0.2253	0.8776	0.0933	0.1241	0.2693	0.8744
N=200	p=2	0.4	0.0587	0.1137	0.3381	0.9907	0.0555	0.1210	0.3294	0.8227
		1.0	0.0544	0.0940	0.2583	0.9427	0.0534	0.1044	0.2612	0.8147
	p=5	0.4	0.0559	0.1699	0.5557	0.9998	0.0857	0.1903	0.5215	0.8944
		1.0	0.0538	0.1134	0.3366	0.9860	0.0770	0.1468	0.3687	0.9436
	p=10	0.4	0.0572	0.2279	0.7539	1.0000	0.0801	0.2027	0.6158	0.8875
		1.0	0.0568	0.1233	0.3988	0.9935	0.0815	0.1629	0.4219	0.9527

5. An example

In this section, the proposed methods are illustrated via data from the Cedars-Sinai Medical Center. This study on coronary heart disease investigated the discriminatory ability of a cholesterol biomarker for myocardial infarction (MI). We have 80 individual measurements of cholesterol biomarker in total. Half of them were collected on cases, who recently survived a myocardial infarction (MI), and the other half on controls, who had a normal rest ECG and were free of symptoms having no previous cardiovascular procedures or MIs. Additionally, the blood specimens were randomly pooled in groups of p = 2, keeping cases and controls separate, and then re-measured. Consequently, we have measurements for 20 samples of pooled cases and 20 samples of pooled controls, allowing us to form the hybrid design.

The p-value of 0.8662 for Shapiro-Wilk test indicates that we can assume a cholesterol biomarker follows a normal distribution. A histogram and normal Q-Q plot in Figure 1 confirm that the normal distributional assumption for the data is reasonable.

Figure 1.

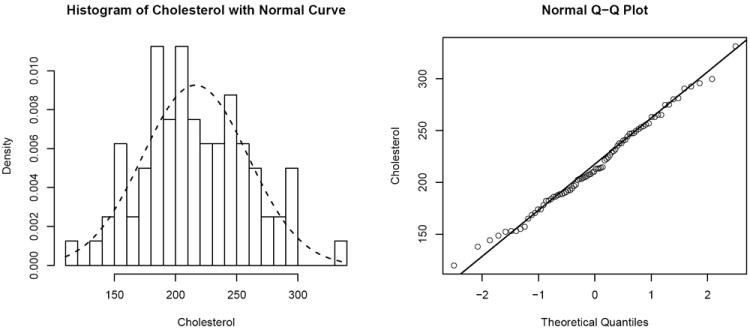
The Histogram and the Normal Q-Q plot of Cholesterol Data

Hybrid samples are formed by taking combinations of 20 unpooled samples and 10 pooled samples from different individuals for cases and controls, separately. In this example, we focused on the means of cholesterol measurements and therefore we calculated these means based on 40 individual samples for cases and controls, separately. The obtained means were 226.7877 and 205.5290, respectively. Using a bootstrap strategy, we compared the confidence interval estimators and the coverage probabilities of the EL method with those of the parametric method. To execute the bootstrap study, we proceeded as follows. We randomly selected 10 pooled assays of group size p = 2 with replacement. We then randomly sampled 20 assays from the individual assays, excluding those performed on individual biospecimens that contributed to the 10 chosen pooled assays. With our 20 sampled individual and 10 pooled assays, we applied a parametric likelihood method assuming a normal distributional assumption and an EL ratio test (3) to calculate the 95% confidence interval of the mean of cholesterol biomarkers. We repeatedly sampled and calculated the confidence interval of the cholesterol mean 5,000 times, obtaining 5,000 values for the confidence interval of the mean value of cholesterol measurements for both case and control. Table 5 depicts the outputs of the bootstrap evaluation.

Table 5.

Bootstrap Evaluations of the Confidence Interval Estimators Based on Parametric Likelihood Ratio Test and the EL ratio Test

	Health		MI
Parametric (Normal)	CI	Length	CI	Length
	(192.5738, 220.8708)	28.29704	(210.0585, 239.4560)	29.39748
Empirical	(192.9715, 221.1471)	28.17561	(210.4337, 240.5975)	30.16376

The bootstrap coverage probabilities of the Cholesterol mean were computed as 0.9999 (Healthy controls), 1 (MI cases), utilizing the parametric (normal) likelihood method and as 0.955 (Healthy controls), 0.966 (MI cases) based on the EL technique, respectively. Also, we calculated the coverage probabilities of the intersections of the 95% confidence intervals for each case (MI) and control (healthy). The obtained coverage probabilities were 0.9987 and 0.9324, corresponding to applications of the parametric method and the EL approach, respectively.

In accordance with these results, the confidence intervals of estimators of the cholesterol mean via the EL ratio method are close to those corresponding to the parametric approach; therefore, we cannot observe a significant difference in the confidence intervals related to the approaches. However, differences between the parametric method and the EL ratio approach in the coverage probability of mean of cholesterol biomarker are much more appreciable. The EL ratio method provided a good result in that the coverage probability of the cholesterol mean is close to the expected 0.95, whereas the corresponding result of the parametric method gave 1 as the coverage probability. This result shows that, in this example, the proposed EL approach outperforms the traditional parametric method.

6. Conclusions

In this article, we proposed and examined different parametric and distribution-free likelihood methods to evaluate data subject to measurement errors. The common sampling strategy based on repeated measures and the novel hybrid sample procedure were evaluated. When the measurement error problem is in effect, we pointed out that the repeated measurements strategy may not perform well. The proposed hybrid design utilizes the cost-efficient pooling approach and combines the pooled and unpooled samples.

The study done in this paper has confirmed that the strategy to repeat measures provides a lot of information just related to ME distributions, reducing efficiency of this procedure compared to the hybrid design in the context of the eva uation of biomarker’s characteristics. The EL techniques, very efficient nonparametric methods, were proposed to apply to data subject to ME.

To verify the efficiency of the hybrid design and the EL methodology, theoretical propositions as well as the Monte Carlo simulation results were provided.

The numerical studies have supported our arguments that the likelihood based on pooled-unpooled data are more efficient than those based on the repeated measures data. We showed the EL method can be utilized as a very powerful tool in statistical inference involving measurement errors.