MARGINAL EMPIRICAL LIKELIHOOD AND SURE INDEPENDENCE FEATURE SCREENING

Abstract

We study a marginal empirical likelihood approach in scenarios when the number of variables grows exponentially with the sample size. The marginal empirical likelihood ratios as functions of the parameters of interest are systematically examined, and we find that the marginal empirical likelihood ratio evaluated at zero can be used to differentiate whether an explanatory variable is contributing to a response variable or not. Based on this finding, we propose a unified feature screening procedure for linear models and the generalized linear models. Different from most existing feature screening approaches that rely on the magnitudes of some marginal estimators to identify true signals, the proposed screening approach is capable of further incorporating the level of uncertainties of such estimators. Such a merit inherits the self-studentization property of the empirical likelihood approach, and extends the insights of existing feature screening methods. Moreover, we show that our screening approach is less restrictive to distributional assumptions, and can be conveniently adapted to be applied in a broad range of scenarios such as models specified using general moment conditions. Our theoretical results and extensive numerical examples by simulations and data analysis demonstrate the merits of the marginal empirical likelihood approach.

1. Introduction

High-dimensional data are more frequently encountered in current practical problems of finance, biomedical sciences, geological studies and many more areas. Statistical methods for high-dimensional data analysis have received increasing interests to deal with large volume of data containing considerably many features; see Bühlmann and van de Geer (2011), Hastie, Tibshirani and Friedman (2009) and Fan and Lv (2010) for overviews. A fundamental objective of statistical analysis with high-dimensional data is to identify relevant features, so that effective models can be subsequently constructed and applied to solve practical problems.

Recently, independence feature screening methods have been considered, see, for example, Fan and Lv (2008), Fan and Song (2010) and Fan, Feng and Song (2011) for linear models, generalized linear models and nonparametric additive models, respectively. Fan and Lv (2008) and Fan and Song (2010) performed screening by ranking the absolute values of marginal estimates of model coefficients, and Fan, Feng and Song (2011) carried out screening by ranking integrated squared marginal nonparametric curve estimates. Fan and Song (2010) also discussed independence screening by examining the magnitudes of the likelihood ratios. More recently, Wang (2012) considered a sure independence screening by a factor profiling approach; Xue and Zou (2011) studied sure independence screening and sparse signal recovery; see also Zhu et al. (2011) and Li, Zhong and Zhu (2012) for recent development using model-free approaches for feature screening, Li et al. (2012) for a robust rank correcation based approach, and Zhao and Li (2012) for an estimating equation based feature screening approach.

The empirical likelihood approach [Owen (1988, 2001)] is demonstrated effective in scenarios with less restrictive distributional assumptions for statistical inferences; see Qin and Lawless (1994), Newey and Smith (2004) and reference therein. We refer to Chen and Van Keilegom (2009) as a review and discussion of recent development in the empirical likelihood approach. The scope of the empirical likelihood approach recently has also been extended to deal with high-dimensional data; see Hjort, McKeague and Van Keilegom (2009), Chen, Peng and Qin (2009), Tang and Leng (2010), Leng and Tang (2012), and Chang, Chen and Chen (2013). Though demonstrated effective in statistical inferences, the empirical likelihood approach encounters substantial difficulty when data dimensionality is high. More specifically, the data dimensionality p cannot exceed the sample size n in the conventional empirical likelihood construction. In addition, p can be at most o(n^1/2) or even slower under which asymptotic properties are established [Chang, Chen and Chen (2013), Chen, Peng and Qin (2009), Hjort, McKeague and Van Keilegom (2009), Leng and Tang (2012), Tang and Leng (2010)]. Therefore, to practically more effectively apply the empirical likelihood approach, a pre-screening procedure is necessary to reduce the candidates of target features.

In this study, we systematically examine the properties of a marginal empirical likelihood approach where the available features are assessed one at a time individually. The marginal empirical likelihood approach only involves univariate optimizations, so that it provides a convenient device for both theoretical analysis and practical implementation. Our analysis reveals the probabilistic behavior of the marginal empirical likelihood ratios as functions of the parameters of interest that can be evaluated at arbitrary values, which itself is a problem of individual interest because existing studies of the empirical likelihood approach generally focus on its properties when evaluated at the truth, or at values in a small neighborhood of the truth. Based on our finding, we propose to conduct feature screening by using the marginal empirical likelihood ratio evaluated at zero. We find that a unified screening procedure can be applied in both linear models and generalized linear models. We also demonstrate how the marginal empirical likelihood approach can be conveniently adapted to solve a broad range of problems for models specified by general moment conditions. Hence, the marginal empirical likelihood approach provides a general and adaptive procedure for solving a broad class of practical problems for feature screening. Our theoretical analyses show that the proposed screening procedure based on the marginal empirical likelihood approach is selection consistent—that is, being able to identify the features that contribute to the response variable when the number of explanatory variables p grows exponentially with sample size n.

Our study contributes to the sure independence feature screening for high-dimensional data analysis from the following two substantial aspects. First of all, a fundamental difference of our approach to all existing approaches is that the marginal empirical likelihood ratio statistic is a self-studentized quantity [Owen (2001)] while other existing screening methods generally rely on the ranking of features based on magnitudes of some marginal estimators. Therefore, our approach is able to incorporate additionally the level of uncertainties associated with the estimators to conduct feature screening. This clearly extends the scope of existing feature screening approaches by considering more aspects of marginal statistical approaches. We show in our simulation studies that when heterogeneity exists in the conditional variance, our approach performs much better than a least-squares based approach. Second, our screening procedure inherits the non-parametric merits of the empirical likelihood approach. Specifically, our approach requires no strict distributional assumptions such as normally distributed errors in the linear models, or exponential family distributed response in the generalized linear models. This generalizes the scope and applicability of our approach. As a result, we show that the marginal empirical likelihood approach provides a unified framework for feature screening in linear regression models and generalized linear models, and can be conveniently applied for solving a broad class of general problems.

The rest of this paper is organized as follows. We elaborate the method of the marginal empirical likelihood approach in Section 2. Properties of the proposed approach are given in Section 3. Section 4 extends the marginal empirical likelihood approach to a broad framework including models specified by general moment conditions, and presents an iterative sure screening procedure using profile empirical likelihood. Numerical examples are given in Section 5. We conclude with some discussions in Section 6. All technical details are contained in the supplementary material of this paper [Chang, Tang and Wu (2013)].

2. Methodology

2.1. Marginal empirical likelihood for linear models

Let us motivate the marginal empirical likelihood approach by first considering the multiple linear regression model

$$Y={\mathbf{X}}^{\mathrm{T}}\mathit{\beta }+\epsilon ,$$ (2.1)

where X = (X₁, …, X_p)^T is the vector of explanatory variables, ε is the random error with zero mean, and β = (β₁,…, β_p)^T is the vector of unknown parameters. Hereinafter, we also use β to denote the truth of the parameter whenever no confusion arises. Without loss of generality, we assume hereinafter that the explanatory variables are standardized such that 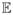(X_j) = 0 and $\mathbb{E}(X_j^2)=1$ (j = 1,…, p). For effective and interpretable practical applications, one may reasonably expect that among the large number of explanatory variables, only a small fraction of them contribute to the response variable. We therefore denote by = {1 ≤ j ≤ p :β_j ≠ 0} the collection of the effective explanatory variables in the true sparse model whose size is characterized by its cardinality s = | |. Here we assume that s is much smaller than p, reflecting the case in many practical applications like in finance, biology and clinical studies.

In the recent literature of high-dimensional data analysis, various marginal approaches have been applied for locating the true model ; see, for example, Fan and Lv (2008), Fan and Song (2010) and Fan, Feng and Song (2011). Among those approaches, a popular way is to assess the marginal contribution from a given explanatory variable X_j. Commonly applied criteria for measuring the marginal contribution are the magnitudes of some marginal estimators [Fan, Feng and Song (2011), Fan and Lv (2008), Fan and Song (2010)]. Subsequently, the candidate models are chosen from the top ranked explanatory variables.

To apply a marginal empirical likelihood approach for the linear regression model (2.1), let us consider the marginal moment condition of the least squares estimator:

$$\mathbb{E}\{X_j(Y-X_j{\beta }_j^M)\}=0(j=1,\dots ,p),$$ (2.2)

where ${\beta }_j^M$ is interpreted as the marginal contribution of covariate X_j to Y. From (2.2), we can see that ${\beta }_j^M=\mathbb{E}(X_{j}Y)$ is the covariance between X_j and Y so that ${\beta }_j^M=0$ is equivalent to that Y and X_j are marginally uncorrelated. Here we note the remarkable difference between ${\beta }_j^M$ and β_j where the latter is the truth of the parameter in (2.1). In general, ${\beta }_j^M\ne {\beta }_j$ unless 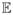(X_iX_j) = 0 for all i ≠ j. In addition to that from β_j in the model (2.1), ${\beta }_j^M$ also contains aggregated contribution from other components that may be correlated with X_j. Thus, the correlation level among covariates has significant impact on the performance of a screening procedure based on (2.2); more discussions on this are given in a later section containing the main results.

A marginal empirical likelihood for linear models can be constructed as follows. Note that $\mathbb{E}(X_j^2)=1$, therefore (2.2) is equivalent to

$$\mathbb{E}(X_{j}Y-{\beta }_j^M)=0.$$ (2.3)

Let ${\{({\mathbf{X}}_i,Y_i)\}}_{i=1}^n$ be collected independent data, g_ij(β) = X_ijY_i−β (j = 1,…, p) and X_ij means the j th component of the ith observation X_i. Based on (2.3), we define the following marginal empirical likelihood:

$${\text{EL}}_j(\beta )=sup\left\{\prod _{i=1}^n{w}_i:w_i\ge 0,\sum _{i=1}^n{w}_i=1,\sum _{i=1}^n{w}_i{g}_{ij}(\beta )=0\right\}$$ (2.4)

for j = 1,…, p. For any given β in the convex hull of ${\{X_{ij}{Y}_i\}}_{i=1}^n$, the marginal empirical likelihood ratio is defined as

$${\ell }_j(\beta )=-2log\{{\text{EL}}_j(\beta )\}-2\mathit{n}logn=2\sum _{i=1}^{n}log\{1+\lambda g_{ij}(\beta )\},$$ (2.5)

where λ is the Lagrange multiplier satisfying

$$0=\sum _{i=1}^n\frac{g_{ij}(\beta )}{1+\lambda g_{ij}(\beta )}.$$ (2.6)

2.2. Extended coverage to generalized linear models

A merit of the marginal empirical likelihood approach is that the formulation by (2.4) and (2.5) only requires the moment condition (2.3), rather than specific distributional assumption of ε in model (2.1). This entitles our approach robustness against the violation of distributional model assumptions, and thus it can be extended and adapted to a broader framework. Now we elaborate how the above marginal empirical likelihood approach can be equally applied when the response variable Y is in the exponential family with the density function taking the canonical form [McCullagh and Nelder (1989)]:

$$f(y)=exp\{y\theta -b(\theta )+c(y)\}$$ (2.7)

for some suitable known functions b(·), c(·) and canonical parameter θ. Further extensions of the marginal empirical likelihood approach are discussed in a later section. We refer to Kolaczyk (1994) and Chen and Cui (2003) for conventional applications of the empirical likelihood to generalized linear models. Following the convention of generalized linear models, we denote the mean function by μ = 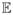(Y |X) = b′(θ) where θ is modeled by a linear function β₀ + X^Tβ with β = (β₁,…, β_p)^T, and use V(μ) to denote the variance of Y expressed as a function of μ.

For any j = 1,…, p, the moment condition based on the marginal likelihood approach in Fan and Song (2010) for β_j is

$$\mathbb{E}\left\{\frac{Y-{\mu }_j}{V({\mu }_j)}\frac{\partial {\mu }_j}{\partial {\beta }_j}\right\}=0,$$ (2.8)

where ${\mu }_j=b^{\prime }({\beta }_0+{\beta }_j^M{X}_j)$ is the implied mean function that is modeled marginally only using X_j. Here the ${\beta }_j^M$ is again interpreted as the marginal contribution of X_j to the response variable Y ; see also Fan and Song (2010). By the property of the exponential family distribution, $\frac{\partial \mu }{\partial {\beta }_j}=X_j{b}^{″}(\theta )$ and V(μ) = b″(θ). Then (2.8) becomes

$$\mathbb{E}\{X_j(Y-{\mu }_j)\}=0.$$ (2.9)

For linear models, $b(\theta )=\frac{{\theta }^2}{2}$, then b′ (θ) = θ, so that (2.9) becomes $\mathbb{E}\{X_j(Y-X_j{\beta }_j^M)\}=0$ by noting that β₀ = 0 in the linear model case, which is exactly (2.2). Hence, (2.9) is a natural extension of (2.2) in the generalized linear models.

One way to apply the marginal approach can be generalizing the definition in (2.4) to be g_ij (β) = X_ij{Y_i − b′(β₀ + βX_ij)} (j = 1,…, p). However, such a modification is actually not necessary. To see this, we note that when the marginal contribution ${\beta }_j^M=0$, then the marginal moment condition (2.9) becomes 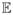[X_j {Y − b′(β₀)}] = 0. Hence, it implies that the covariance between X_j and Y is 0, which exactly shares the same implication of (2.3) as in the linear models. From this perspective, (2.9) and (2.3) are essentially equivalent. Additionally, the response variable in practice can always be centered to have zero mean. This fact eliminates the concern on the intercept β₀ in the generalized linear models when considering a marginal empirical likelihood approach. As a result, we conclude that a unified marginal empirical likelihood construction (2.4) with the same g_ij (β) = X_ijY_i −β can be equally applied for both linear models and generalized linear models with centered response variable Y. The implication of this unified construction is also intuitively very clear by interpreting β as the covariance between a covariate and the response variable.

Furthermore, we note that the distributional assumption (2.7) is actually not required in our marginal empirical likelihood approach. Therefore our approach is not restricted to the exponential family (2.7). Since we only require the marginal moment condition (2.9), our approach can be applied with the quasi-likelihood approach and it also works with misspecified variance functions [McCullagh and Nelder (1989)].

The marginal empirical likelihood ratio (2.5) with g_ij(β) = X_ijY_i −β evaluated at β = 0—that is, ℓ_j (0)—has a very clear practical interpretation by noting that it can be used to test the null hypothesis $H_0:{\beta }_j^M=0$. By noting additionally the intuitively clear fact that ℓ_j (0) should not be large if ${\beta }_j^M=0$, we can see that ℓ_j (0) can be used as a device for feature screening. More specifically, we have the following procedure:

• Step 1: Evaluating ℓ_j (0) for all j = 1,…, p, where ℓ_j (·) is defined in (2.5) with g_ij (β) = X_ijY_i − β. If 0 is not in the convex hull of ${\{X_{ij}{Y}_i\}}_{i=1}^n$, we define ℓ_j (0)=∞ as a strong evidence of significance in predicting Y using X_j.

• Step 2: Given a threshold level γ_n, select a set of variables by

$${\widehat{\mathcal{M}}}_{{\gamma }_n}=\{1\le j\le p:{\ell }_j(0)\ge {\gamma }_n\}.$$

We specify in the next section the requirement for γ_n so that the screening procedure is consistent. On the other hand, however, explicitly identifying γ_n in practice is generally difficult because it involves unknown constants. Thus, a screening procedure can be practically implemented in a way such that 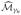recruits candidate features until certain size such as n^1/2 is achieved.

We remark that the evaluation of ℓ_j (β) in (2.5) in practice is actually very easy by noting that all optimizations involved are univariate, which is very convenient for practical applications. On the other hand, our procedure only needs to evaluate the marginal empirical likelihood ratio (2.5) at β = 0 and avoids the estimation of ${\beta }_j^M$ when conducting the feature screening.

3. Main results

Now we present main results for the marginal empirical likelihood ratio in (2.5) with the unified specification g_ij (β) = X_ijY_i − β that are generally applicable for both linear models and generalized linear models. In our discussion hereinafter, let ρ_j = 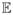(X_jY). If ρ_j = 0, it is well known that ℓ_j (0) is asymptotically chi-square distributed with 1 degree of freedom [Owen (1988, 2001)]. If ρ_j ≠ 0, however, the properties of ℓ_j (0) is generally less clear, which is also a question of independent interest. Specifically, if β = ρ_j +τσn^−1/2 where σ² = var(X_jY), it can be shown following the same argument of Owen (1988) that ${\ell }_j(\beta )\stackrel{d}{\to }{\chi }_1^2({\tau }^2)$ as n→∞ under some regularity conditions where τ² is a noncentrality parameter. But if β − ρ_j converges to zero at a rate slower than n^−1/2, the exact diverging rate of ℓ_j(β) is less clear in existing literature.

We first present a general result that shows that the empirical likelihood ratio ℓ_j(β) is no longer O_p(1) when β −ρ_j converges to 0 but n^1/2(β −ρ_j) diverges.

Proposition 1

Suppose that U₁,…, U_n are independent and identically distributed random variables with 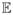(|U_i |^ν) <∞ for some ν ≥ 3. Replacing g_ij (β) in (2.5) and (2.6) by U_i − μ for all i = 1,…, n, we obtain ℓ(μ). If |μ − μ₀| = O(n^−w) for some $w\in (\frac{1}{\nu },\frac{1}{2})$, then

$$\frac{\ell (\mu )}{n{(\mu -{\mu }_0)}^2{\sigma }^{-2}}\stackrel{p}{\to }1asn\to \infty ,$$

where μ₀ = 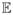(U_i) and σ² = 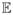{(U_i −μ₀)²}.

We note that Chen, Gao and Tang (2008) contains a related result showing that the empirical likelihood ratio is diverging when evaluated at values far enough from the truth. Our Proposition 1 contains the specific diverging rate of the empirical likelihood ratio. Proposition 1 implies that if β − ρ_j converges to zero at a rate slower than n^−1/2, ℓ_j (β) = O_p{n(β − ρ_j)²}. On the other hand, if β − ρ_j does not weaken to zero, our Theorem 1 presented later shows that ℓ_j(β) has high probability to take large value. On the other hand, as clearly shown in our proof of Proposition 1 given in Chang, Tang and Wu (2013), the statistics ℓ_j (0) is self-studentized, and hence it incorporates the level of uncertainties from using the finite sample moment conditions. Such a feature is desirable because in practice levels of uncertainties corresponding to different covariates can be different when contributing to the response variable of interest. This may confound the ranking for feature screening based on marginal estimators themselves without considering their standard errors, not mentioning incorporating the level of uncertainties is difficult especially when handling high-dimensional statistical problems.

An effective marginal screening procedure requires two conditions: (i) if j ∈ , then ρ_j takes nonnegligible value; and (ii) if j ∉ , then ρ_j takes negligible value. Actually, the first requirement is closely related to recruiting the true signals that contribute to the response, and the second one affects the size of selected variable set that may contain false signals. Fan and Lv (2008) shows that under the identification condition min_j∈ 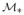|ρ_j| ≥ f_n > 0 for some function f_n, the first requirement is fulfilled. A common assumption for f_n is f_n = O(n^−κ) for some $\kappa \in (0,\frac{1}{2})$.

Our next theoretical analysis imposes the following two assumptions:

• A.1: The random variable Y has bounded variance and there exists a positive constant c₁ such that

  $$\underset{j\in {\mathcal{M}}_{\ast }}{min}\mid \mathbb{E}(X_{j}Y)\mid =\underset{j\in {\mathcal{M}}_{\ast }}{min}\mid cov(Y,X_j)\mid \ge c_1{n}^{-\kappa }$$

  for some $\kappa \in [0,\frac{1}{2})$.

• A.2: There are positive constants K₁, K₂, γ₁ and γ₂ such that

  $$\begin{array}{ll}\mathbb{P}\{\mid X_j\mid \ge u\}\le K_{1}exp(-K_2{u}^{{\gamma }_1})\hfill & \text{for}\text{each}j=1,\dots ,p\text{and}\text{any}u>0,\hfill \\ \mathbb{P}\{\mid Y\mid \ge u\}\le K_{1}exp(-K_2{u}^{{\gamma }_2})\hfill & \text{for}\text{any}u>0.\hfill \end{array}$$

Assumption A.1 can be viewed as a requirement for the minimal signal strength, and we call it the identification condition for j ∈ . For linear models, the assumption A.1 is same as condition 3 in Fan and Lv (2008) that is commonly assumed in sure independence feature screening. For generalized linear models, Fan and Song (2010) imposes the identification condition as min_j∈ 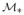|cov(b′(X^Tβ), X_j)| ≥ c₁n^−κ. By noticing that cov(b′(X^Tβ), X_j) = 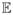(X_jY), their identification condition for j ∈ is also same as A.1. Since we impose no distributional assumptions, A.2 is assumed to ensure the large deviation results that are used to get the exponential convergence rate. The first part of A.2 is same as the first part of condition D in Fan and Song (2010). For linear regression model, the second part of condition D in Fan and Song (2010) is equivalent to that X^Tβ satisfies the Cramér condition such that there exists a positive constant H such that {exp(tX^Tβ)} <∞ for any |t |<H. If the error ε is independent of covariates and satisfies the Cramér condition, then we can obtain that the variable Y also satisfies the Cramér condition. From Lemma 2.2 in Petrov (1995), a random variable W satisfies Cramér condition is equivalent to that there are positive constants b₁ and b₂ such that ℙ{|W| ≥ u} ≤ b₁ exp(−b₂u) for any u > 0. Therefore, our assumption here is actually weaker than that in Fan and Song (2010). On the other hand, A.2 is also a general technical assumption in the literature of large derivations. For example, γ₁ = 2 if X_j’s follow normal distribution or sub-Gaussian distribution, and γ₁=∞ if X_j’s have compact support.

We now establish the following general result for the distribution of empirical likelihood ratio which is the foundation for our future theoretical results.

Theorem 1

Suppose that U₁,…, U_n are independent and identically distributed random variables. Assume that there exist three positive constants K̃₁, K̃₂ and γ such that ℙ{|U_i|>u} ≤ K̃₁ exp(−K̃₂u^γ) for all u>0. Define μ₀ = (U_i), $\delta =max\{\frac{2}{\gamma }-1,0\}$, H = 2^1+δ and $\overline{\mathrm{\Delta }}=\frac{n^{1/2}\sigma }{2K}$, where σ² = {(U_i − μ₀)²} and K >σ is a sufficiently large positive constant depending only on K̃₁, K̃₂, γ and μ₀, then for L → ∞, there exists a positive constant C only depending on K̃₁, K̃₂ and γ such that

$$\mathbb{P}\left\{\ell (\mu )<\frac{n{(\mu -{\mu }_0)}^2}{L^2}\right\}\le \{\begin{array}{ll}exp\left\{-\frac{n{(\mu -{\mu }_0)}^2}{4H{\sigma }^2}\right\}+exp(-{CL}^{\gamma }),\hfill & if{n}^{1/2}\mid \mu -{\mu }_0\mid \le \sigma {(H^{1+\delta }\overline{\mathrm{\Delta }})}^{1/(1+2\delta )};\hfill \\ exp\left\{-\frac{1}{4}{\left(\frac{n\mid \mu -{\mu }_0\mid }{2K}\right)}^{1/(1+\delta )}\right\}+exp(-{CL}^{\gamma }),\hfill & if{n}^{1/2}\mid \mu -{\mu }_0\mid >\sigma {(H^{1+\delta }\overline{\mathrm{\Delta }})}^{1/(1+2\delta )};\hfill \end{array}$$

where ℓ(μ) is defined in Proposition 1.

The proof of Theorem 1 is given in Chang, Tang and Wu (2013), where the main idea is applying large deviation theory [Petrov (1995), Saulis and Statulevičius (1991)].

Theorem 1 reveals the magnitude of the empirical likelihood ratio statistic evaluated at arbitrary values. When μ −μ₀ does not diminish to 0, Theorem 1 implies that the empirical likelihood ratio statistic diverges with large probability where the diverging rate synthetically depends on the sample size n, some diverging L and the deviation of μ from the truth. Here L is a general technical device whose diverging rate is arbitrary. As a direct result of Theorem 1, we have the following proposition for ℓ_j (0).

Proposition 2

Under assumptions A.1 and A.2, there exists a positive constant C₁ depending only on K₁, K₂, γ₁ and γ₂ appeared in assumption A.2 such that for any j ∈ and L→∞,

$$\mathbb{P}\left\{{\ell }_j(0)<\frac{c_1^2{n}^{1-2\kappa }}{L^2}\right\}\le \{\begin{array}{ll}exp(-C_1{n}^{1-2\kappa })+exp(-C_1{L}^{\gamma }),\hfill & if(1-2\kappa )(1-2\delta )<1;\hfill \\ exp(-C_1{n}^{(1-\kappa )/(1+\delta )})+exp(-C_1{L}^{\gamma }),\hfill & if(1-2\kappa )(1+2\delta )\ge 1;\hfill \end{array}$$

where $\gamma =\frac{{\gamma }_1{\gamma }_2}{{\gamma }_1+{\gamma }_2}$ and $\delta =max\{\frac{2}{\gamma }-1,0\}$.

Proposition 2 is a uniform result for all features contributing in the true model. Specifically, with large probability and uniformly for all j ∈ , the diverging rate of ℓ_j (0) is not slower than n^1−2κL⁻². From Proposition 1, if | (X_jY)| = O(n^−w) for some $w\in (0,\frac{1}{2})$ and some j ∈ , then ${\ell }_j(0)\stackrel{p}{\to }\infty$. This can be viewed as a requirement such that the signal strength cannot diminish to 0 at a too fast rate. Therefore, n^1/2−κL⁻¹→∞ as n→∞ is required for sure independence screening. By choosing L = n^{1/2−κ−τ} for some $\tau \in (0,\frac{1}{2}-\kappa )$, we obtain the following corollary more specifically summarizing that the set can be distinguished by examining the marginal empirical likelihood ratio ℓ_j (0) (j = 1,…, p).

Corollary 1

Under assumptions A.1 and A.2, there exists a positive constant C₁ depending only on K₁, K₂, γ₁ and γ₂ appeared in assumption A.2 such that, for any $\tau \in (0,\frac{1}{2}-\kappa )$,

$$\underset{j\in {\mathcal{M}}_{\ast }}{max}\mathbb{P}\{{\ell }_j(0)<c_1^2{n}^{2\tau }\}\le \{\begin{array}{ll}exp\{-C_1{n}^{(1-2\kappa )\wedge ((1-2\kappa -2\tau )\gamma /2)}\},\hfill & if(1-2\kappa )(1+2\delta )<1;\hfill \\ exp\{-C_1{n}^{((1-\kappa )/(1+\delta ))\wedge ((1-2\kappa -2\tau )\gamma /2)}\},\hfill & if(1-2\kappa )(1+2\delta )\ge 1;\hfill \end{array}$$

where $\gamma =\frac{{\gamma }_1{\gamma }_2}{{\gamma }_1+{\gamma }_2}$ and $\delta =max\{\frac{2}{\gamma }-1,0\}$.

Summarizing above results, we formally establish the screening properties of the marginal empirical likelihood approach.

Theorem 2

Under assumptions A.1 and A.2, there exists a positive constant C₁ depending only on K₁, K₂, γ₁ and γ₂ appeared in assumption A.2 such that, for any $\tau \in (0,\frac{1}{2}-\kappa )$ and ${\gamma }_n=c_1^2{n}^{2\tau }$,

$$\mathbb{P}\{{\mathcal{M}}_{\ast }\subset {\widehat{\mathcal{M}}}_{{\gamma }_n}\}\ge \{\begin{array}{ll}1-sexp\{-C_1{n}^{(1-2\kappa )\wedge ((1-2\kappa -2\tau )\gamma /2)}\},\hfill & if(1-2\kappa )(1+2\delta )<1;\hfill \\ 1-sexp\{-C_1{n}^{((1-\kappa )/(1+\delta ))\wedge ((1-2\kappa -2\tau )\gamma /2)}\},\hfill & if(1-2\kappa )(1+2\delta )\ge 1;\hfill \end{array}$$

where $\gamma =\frac{{\gamma }_1{\gamma }_2}{{\gamma }_1+{\gamma }_2}$ and $\delta =max\{\frac{2}{\gamma }-1,0\}$.

Theorem 2 implies the sure screening property for our procedure with nonpolynomial dimensionality:

$$logp=\{\begin{array}{ll}o(n^{(1-2\kappa )\wedge ((1-2\kappa -2\tau )\gamma /2)}),\hfill & \text{if}(1-2\kappa )(1+2\delta )<1;\hfill \\ o(n^{((1-\kappa )/(1+\delta ))\wedge ((1-2\kappa -2\tau )\gamma /2)}),\hfill & \text{if}(1-2\kappa )(1+2\delta )\ge 1.\hfill \end{array}$$

When the covariates and error are normal, γ₁ = 2 and γ₂ = 2. Then γ = 1, δ = 1 and log p = o(n^1/2−κ) which is weaker than that in Fan and Lv (2008) where log p = o(n^1−2κ) is allowed. This can be viewed as a price paid for allowing nonnormal covariate and more general error distribution. Furthermore, we compare our result and that in Fan and Song (2010). The Lemma 1 in Fan and Song (2010) means that γ₂ = 1. The corresponding parameters under their this setting are $\gamma =\frac{{\gamma }_1}{{\gamma }_1+1}$ and $\delta =\frac{{\gamma }_1+2}{{\gamma }_1}$, respectively. Then, we can handle the nonpolynomial dimensionality

$$logp=o\left(n^{(1-2\kappa ){\gamma }_1/(2{\gamma }_1+2)}\right)$$

in this setting, which is actually a stronger result than that in Fan and Song (2010) where log p = o(n^{(1−2κ)γ₁/A)} and A = max{γ₁ + 4, 3γ₁ +2}.

Now we investigate how large the set 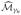is. This question is closely related to the asymptotic property of ℓ_j (0) for j ∉ . Essentially, we need to know the magnitudes of ℓ_j (0) for j ∉ . We first consider the simple case ρ_j = 0 for any j ∉ and have the following result.

Proposition 3

Under assumptions A.1 and A.2, if ρ_j = 0, there is a positive constant C₂ depending only on K₁, K₂, γ₁ and γ₂ appeared in assumption A.2 such that, for any $\tau \in (0,\frac{1}{2}-\kappa )$,

$$\mathbb{P}\{{\ell }_j(0)\ge c_1^2{n}^{2\tau }\}\le \{\begin{array}{ll}exp(-C_2{n}^{2\tau }),\hfill & if\gamma <4\mathit{and}\tau \le \frac{\gamma }{12};\hfill \\ exp(-C_2{n}^{\gamma /6}),\hfill & if\gamma <4\mathit{and}\tau >\frac{\gamma }{12};\hfill \\ exp(-C_2{n}^{2\tau }),\hfill & if\gamma \ge 4\mathit{and}\tau \le \frac{\gamma }{2\gamma +4};\hfill \\ exp(-C_2{n}^{\gamma /(\gamma +2)}),\hfill & if\gamma \ge 4\mathit{and}\tau >\frac{\gamma }{2\gamma +4};\hfill \end{array}$$

where $\gamma =\frac{{\gamma }_1{\gamma }_2}{{\gamma }_1+{\gamma }_2}$.

The assumption ρ_j = 0 for any j ∉ can be guaranteed by the partial orthogonality condition, that is, {X_j :j ∉ } is independent of {X_j : j ∈ }. The orthogonality condition is essentially the assumption made in Huang, Horowitz and Ma (2008) who showed the model selection consistency in the case with the ordinary linear model and bridge regression. This proposition gives the property of ℓ_j (0) for any j ∉ which can be used to establish the theoretical result for the size of 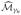where ${\gamma }_n=c_1^2{n}^{2\tau }$. Note that

$$\begin{array}{l}\mid {\widehat{\mathcal{M}}}_{{\gamma }_n}\mid =\sum _{j\in {\mathcal{M}}_{\ast }}I\{{\ell }_j(0)\ge c_1^2{n}^{2\tau }\}+\sum _{j\notin {\mathcal{M}}_{\ast }}I\{{\ell }_j(0)\ge c_1^2{n}^{2\tau }\}\\ \le s+\sum _{j\notin {\mathcal{M}}_{\ast }}I\{{\ell }_j(0)\ge c_1^2{n}^{2\tau }\},\end{array}$$

then

$$\mathbb{P}\{\mid {\widehat{\mathcal{M}}}_{{\gamma }_n}\mid >s\}\le \sum _{j\notin {\mathcal{M}}_{\ast }}\mathbb{P}\{{\ell }_j(0)\ge c_1^2{n}^{2\tau }\}.$$

By Proposition 3, we obtain the following theorem.

Theorem 3

Under assumptions A.1 and A.2, if ρ_j = 0 for any j ∉ , then there exists a positive constant C₂ depending only on K₁, K₂, γ₁ and γ₂ appeared in assumption A.2 such that, for any $\tau \in (0,\frac{1}{2}-\kappa )$ and ${\gamma }_n=c_1^2{n}^{2\tau }$,

$$\mathbb{P}\{\mid {\widehat{\mathcal{M}}}_{{\gamma }_n}\mid >s\}\le \{\begin{array}{ll}pexp(-C_2{n}^{2\tau }),\hfill & if\gamma <4\mathit{and}\tau \le \frac{\gamma }{12};\hfill \\ pexp(-C_2{n}^{\gamma /6}),\hfill & if\gamma <4\mathit{and}\tau >\frac{\gamma }{12};\hfill \\ pexp(-C_2{n}^{2\tau }),\hfill & if\gamma \ge 4\mathit{and}\tau \le \frac{\gamma }{2\gamma +4};\hfill \\ pexp(-C_2{n}^{\gamma /(\gamma +2)}),\hfill & if\gamma \ge 4\mathit{and}\tau >\frac{\gamma }{2\gamma +4};\hfill \end{array}$$

where $\gamma =\frac{{\gamma }_1{\gamma }_2}{{\gamma }_1+{\gamma }_2}$.

From Theorem 3, we have ℙ{| 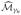| > s} ≤ p exp{−C₂n^{(2τ)^(γ/6)^(γ/(γ+2))}} which means that the event {| 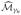| ≤ s} occurs with probability approaching to 1 if log p = o(n^{(2τ)^(γ/6)^(γ/(γ+2))}). On the other hand, following Theorem 2, we have ℙ{ ⊂ 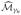} → 1 provided log p = o(n^{((1−2κ−2τ)γ/2)^(1−2κ)}). Combining these two results together, we can obtain that

$$\mathbb{P}\{{\widehat{\mathcal{M}}}_{{\gamma }_n}={\mathcal{M}}_{\ast }\}\to 1\text{if}logp=o(n^{(\gamma /6)\wedge ((1-2\kappa )\gamma /(\gamma +2))})$$

and

$$\tau =\frac{(1-2\kappa )\gamma }{2\gamma +4}.$$

This property shows the selection consistency of our procedure. In a more general case without partial orthogonality condition, we could consider the size of the set 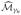under the setting

$$\underset{j\notin {\mathcal{M}}_{\ast }}{max}\mid {\rho }_j\mid =o\left(n^{-\kappa }\right),$$

which is an assumption imposed in Fan and Song (2010).

Proposition 4

Under assumptions A.1 and A.2, if max_j∉ 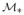|ρ_j| = O(n^−η) where η > κ and ${min}_{j\notin {\mathcal{M}}_{\ast }}\mathbb{E}(X_j^2{Y}^2)\ge c_2$ for some c₂ > 0, there exists a positive constant C₃ depending only on K₁, K₂, γ₁ and γ₂ appeared in assumption A.2 and c₂ such that, for any j ∉ and $\tau \in (\frac{1}{2}-\eta ,\frac{1}{2}-\kappa )$,

$$\mathbb{P}\{{\ell }_j(0)\ge c_1^2{n}^{2\tau }\}\le \{\begin{array}{ll}exp(-C_3{n}^{2\tau })+exp(-C_3{n}^{\gamma /6}),\hfill & if\gamma <2\mathit{and}\eta >\frac{1}{4};\hfill \\ exp(-C_3{n}^{\gamma \eta })+exp(-C_3{n}^{\gamma /6}),\hfill & if\gamma <2\mathit{and}\eta \le \frac{1}{4};\hfill \\ exp(-C_3{n}^{\gamma \eta })+exp(-C_3{n}^{\gamma /6}),\hfill & if\gamma \ge 2\mathit{and}\eta \le \frac{1}{\gamma +2};\hfill \\ exp(-C_3{n}^{\gamma /(\gamma +2)})+exp(-C_3{n}^{2\tau }),\hfill & if\gamma \ge 4\mathit{and}\eta >\frac{1}{\gamma +2};\hfill \\ exp(-C_3{n}^{\gamma /6})+exp(-C_3{n}^{2\tau }),\hfill & if2\le \gamma <4\mathit{and}\eta >\frac{1}{\gamma +2};\hfill \end{array}$$

where $\gamma =\frac{{\gamma }_1{\gamma }_2}{{\gamma }_1+{\gamma }_2}$.

If ρ_j = 0 for any j ∉ , then η = ∞. Hence, this proposition reduces to Proposition 3. Following the same argument between Proposition 3 and Theorem 3, we can obtain the following theorem related to the size of .

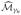Theorem 4

Under assumptions A.1 and A.2, if max_{j ∉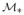} |ρ_j| = O(n^−η) where η > κ and ${min}_{j\notin {\mathcal{M}}_{\ast }}\mathbb{E}(X_j^2{Y}^2)\ge c_2$ for some c₂ > 0, then there exists a positive constant C₃ only depending on K₁, K₂, γ₁ and γ₂ appeared in assumption A.2 and c₂ such that, for any $\tau \in (\frac{1}{2}-\eta ,\frac{1}{2}-\kappa )$ and ${\gamma }_n=c_1^2{n}^{2\tau }$,

$$\mathbb{P}\{\mid {\widehat{\mathcal{M}}}_{{\gamma }_n}\mid >s\}\le \{\begin{array}{ll}pexp(-C_3{n}^{2\tau })+pexp(-C_3{n}^{\gamma /6}),\hfill & if\gamma <2\mathit{and}\eta >\frac{1}{4};\hfill \\ pexp(-C_3{n}^{\gamma \eta })+pexp(-C_3{n}^{\gamma /6}),\hfill & if\gamma <2\mathit{and}\eta \le \frac{1}{4};\hfill \\ pexp(-C_3{n}^{\gamma \eta })+pexp(-C_3{n}^{\gamma /6}),\hfill & if\gamma \ge 2\mathit{and}\eta \le \frac{1}{\gamma +2};\hfill \\ pexp(-C_3{n}^{\gamma /(\gamma +2)})+pexp(-C_3{n}^{2\tau }),\hfill & if\gamma \ge 4\mathit{and}\eta >\frac{1}{\gamma +2};\hfill \\ pexp(-C_3{\eta }^{\gamma /6})+pexp(-C_3{n}^{2\tau }),\hfill & if2\le \gamma <4\mathit{and}\eta >\frac{1}{\gamma +2};\hfill \end{array}$$

where $\gamma =\frac{{\gamma }_1{\gamma }_2}{{\gamma }_1+{\gamma }_2}$.

In summary, our results show that the marginal empirical likelihood approach has a very good control of the size of the recruited variables. With large probability, the set of the recruited variables is not larger than the true contributing explanatory variables. As shown later in our simulation results, the marginal empirical likelihood approach perform very well in terms of the set of false selected variables by the marginal empirical likelihood approach.

4. Extensions

4.1. A broad framework

The marginal empirical likelihood can be applied in a general framework besides the linear models and generalized linear models. Based on general estimating equations approach [Hansen (1982), Qin and Lawless (1994)], we can also apply the screening procedure based on the marginal empirical likelihood. We will demonstrate that the marginal empirical likelihood approach provides an effective device to combine information that can be used to enhance the performance of a screening procedure.

Let Z_i ∈ ℝ^d (i = 1, …, n) be generic observations, β = (β₁, …, β_p)^T ∈ ℝ^p be parameter of interest and g(Z; β) = (g₁(Z; β), …, g_r(Z; β))^T be the r-dimensional estimating function such that 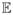{g(Z; β)} = 0. Let = {1 ≤ j ≤ p : β_j ≠ 0} be the true model with size | | = s. We are interested in how to construct a sure feature screening procedure to recover in the general estimating equation setting. To motivate the marginal empirical likelihood approach, let us consider the estimating function evaluated at

$${\mathit{\beta }}^{(j)}={(\underset{j-1}{\underbrace{0,\dots ,0}},\beta ,\underset{p-j}{\underbrace{0,\dots ,0}})}^{\mathrm{T}}(j=1,\dots ,p).$$

In practice, many components in g(Z; β^(j)) do not involve the unknown parameter; see, for example, the estimating function constructed from the least-squares method and our example given later. Therefore, we denote by

$${\mathbf{g}}^{(j)}(\mathbf{Z};\beta )={(g_1^{(j)}(\mathbf{Z};\beta ),\dots ,g_{r_j}^{(j)}(\mathbf{Z};\beta ))}^{\mathrm{T}}$$

an r_j (r_j ≥ 1)-dimensional estimating function collecting the components in g(Z; β^(j)) that depend on the unknown parameter. Usually r_j > 1 is small and not all components of Z are involved in g^(j)(Z; β). A remarkable advantage of this broad framework is that it provides a device for feature screening using more flexibly constructed conditions so that additional data information can be more effectively incorporated.

Correspondingly, we define the marginal empirical likelihood for β as

$${\text{EL}}_j(\beta )=sup\left\{\prod _{i=1}^n{w}_i:w_i\ge 0,\sum _{i=1}^n{w}_i=1,\sum _{i=1}^n{w}_i{\mathbf{g}}^{(j)}({\mathbf{Z}}_i;\beta )=\mathbf{0}\right\}.$$ (4.1)

Then screening can be done based on the ranking of EL_j(0) or equivalently using the corresponding marginal empirical likelihood ratio evaluated at 0—that is, ℓ_j(0). The steps of the procedure are the same as those described earlier. A concrete example of this scenario is given as follows.

Example (Quadratic inference function (QIF) approach [Qu, Lindsay and Li (2000)])

Longitudinal data arise commonly in biomedical research with repeated measurements from the same subject or within the same cluster. Let Y_it and X_it(i = 1, …, n, t = 1, …, m_i) be the response and covariates of the ith subject measured at time t. Let $\mathbb{E}(Y_{it})=\mu ({\mathbf{X}}_{it}^{\mathrm{T}}\mathit{\beta })={\mu }_{it}$ where β ∈ ℝ^p is the parameter of interest. Incorporating the dependence among the repeated measurements is essential for efficient inference. Liang and Zeger (1986) proposed to estimate β by solving $0={\sum }_{i=1}^n{\stackrel{.}{\mathit{\mu }}}_i^{\mathrm{T}}{\mathbf{W}}_i^{-1}({\mathbf{Y}}_i-{\mathit{\mu }}_i)$. Here for the ith subject, Y_i = (Y_i1, …, Y_imi)^T, μ_i = (μ_i1, …, μ_imi)^T, ${\stackrel{.}{\mathit{\mu }}}_i=\frac{\partial {\mathit{\mu }}_i}{\partial \mathit{\beta }}$ and ${\mathbf{W}}_i={\mathbf{v}}_i^{1/2}{\mathbf{Rv}}_i^{1/2}$, where v_i is a diagonal matrix of the conditional variances of subject i and R is a working correlation matrix that may depend on some unknown parameter. This approach uses estimating function $\mathbf{g}({\mathbf{Z}}_i;\mathit{\beta })={\stackrel{.}{\mathit{\mu }}}_i^{\mathrm{T}}{\mathbf{W}}_i^{-1}({\mathbf{Y}}_i-{\mathit{\mu }}_i)$, where ${\mathbf{Z}}_i={({\mathbf{Z}}_{i1}^{\mathrm{T}},\dots ,{\mathbf{Z}}_{{im}_i}^{\mathrm{T}})}^{\mathrm{T}},{\mathbf{Z}}_{it}={(Y_{it},{\mathbf{X}}_{it}^{\mathrm{T}})}^{\mathrm{T}}$ and r = p. More recently, Qu, Lindsay and Li (2000) proposed to model R⁻¹ by ${\sum }_{i=1}^m{a}_i{\mathbf{M}}_i$, where M₁, …, M_m are known matrices and a₁, …, a_m are unknown constants. Then β can be estimated by the quadratic inference functions approach [Qu, Lindsay and Li (2000)] that uses

$$\mathbf{g}({\mathbf{Z}}_i;\mathit{\beta })=\left(\begin{array}{c}{\stackrel{.}{\mathit{\mu }}}_i^{\mathrm{T}}{\mathbf{v}}_i^{-1/2}{\mathbf{M}}_1{\mathbf{v}}_i^{-1/2}({\mathbf{Y}}_i-{\mathit{\mu }}_i)\\ ⋮\\ {\stackrel{.}{\mathit{\mu }}}_i^{\mathrm{T}}{\mathbf{v}}_i^{-1/2}{\mathbf{M}}_m{\mathbf{v}}_i^{-1/2}({\mathbf{Y}}_i-{\mathit{\mu }}_i)\end{array}\right)(i=1,\dots ,n).$$ (4.2)

This falls into our framework with r > p when m > 1, and with r = p if m = 1. When applying the marginal approach, we note that g^(j)(Z; β) is an m-dimensional estimating function. The marginal screening by empirical likelihood can be conveniently applied to this scenario, and we note that the existing independence screening methods cannot be directly applied when m > 1.

In a concurrent and independent work, Zhao and Li (2012) considered feature screening using estimating functions when r = p. By using our notations, their approach are based on g^(j)(Z; 0)—the marginal estimating function evaluated at 0. Their screening procedure are based on ranking the absolute value of g^(j)(Z; 0) for j = 1, …, p. Our approach is different as seen from the above marginal empirical likelihood construction. In addition, analogous to that in linear models and generalized linear models, the marginal empirical likelihood constructed from using the marginal estimating function is also capable of incorporating the level of uncertainties associated with finite sample estimating functions.

We now characterize the properties of the screening procedure in the framework of models specified by estimating equations. For any vector a =(a₁, …, a_q)^T ∈ ℝ^q, we use ||a||_∞ = max_{i=1, …, q} |a_q| and ${\Vert \mathbf{a}\Vert }_2={({\sum }_{i=1}^q{a}_i^2)}^{1/2}$ to denote its L_∞ and L₂ norms, respectively. Aiming to establish the theoretical results, we need the following two assumptions.

• A.3: There exists a positive constant c₃ such that

  $$\underset{j\in {\mathcal{M}}_{\ast }}{min}{\Vert \mathbb{E}\{{\mathbf{g}}^{(j)}(\mathbf{Z};0)\}\Vert }_{\infty }\ge c_3{n}^{-\kappa }$$

  for some $\kappa \in [0,\frac{1}{2})$.

• A.4: There are positive constants K₃, K₄ and γ₃ such that

  $$\mathbb{P}\{{\Vert {\mathbf{g}}^{(j)}(\mathbf{Z};0)\Vert }_2\ge u\}\le K_{3}exp(-K_4{u}^{{\gamma }_3})$$

  for each j = 1, …, p and any u > 0.

Assumption A.3 is a general identification condition for the set when considering the broad framework of models specified by general estimating equations. It means that the weakest signals reflected by || 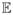{g^(j)(Z; 0)}||_∞ (j ∈ ) cannot vanish at a rate faster than n^−1/2. Assumption A.3 is not stringent, and it reduces to A.1 in special cases of linear models and generalized linear models. A similar assumption is also made in Zhao and Li (2012). Assumption A.4, which is a counterpart of A.2 in general cases, is required for establishing exponential inequality when analyzing large deviations. Zhao and Li (2012) assumed boundness of all components in g^(j)(Z; 0), which implies A.4.

Theorem 5

Under assumptions A.3–A.4, there exists a positive constant C₄ depending only on K₃, K₄ and γ₃ appeared in assumption A.4 such that, for any $\tau \in (0,\frac{1}{2}-\kappa )$ and ${\gamma }_n=c_3^2{n}^{2\tau }$,

$$\mathbb{P}\{{\mathcal{M}}_{\ast }\subset {\widehat{\mathcal{M}}}_{{\gamma }_n}\}\le \{\begin{array}{ll}1-sexp\{-C_4{n}^{(1-2\kappa )\wedge ((1-2\kappa -2\tau ){\gamma }_3/2)}\},\hfill & if(1-2\kappa )(1+2\delta )<1;\hfill \\ 1-sexp\{-C_4{n}^{((1-\kappa )/(1+\delta ))\wedge ((1-2\kappa -2\tau ){\gamma }_3/2)}\},\hfill & if(1-2\kappa )(1+2\delta )\ge 1;\hfill \end{array}$$

where $\delta =max\{\frac{2}{{\gamma }_3}-1,0\}$.

This theorem is a natural extension of Theorem 2 in the broad framework for models specified by general estimating equations. In special cases, we have considered for linear models and generalized linear models, g^(j)(Z; 0) = X_j Y(j = 1, …, p), and γ₃ in assumption A.4 is equal to $\frac{{\gamma }_1{\gamma }_2}{{\gamma }_1+{\gamma }_2}$ where γ₁ and γ₂ are specified in A.2.

Let

$${\mathbf{u}}_j=\mathbb{E}\{{\mathbf{g}}^{(j)}(\mathbf{Z};0)\}\text{for}\text{each}j=1,\dots ,p.$$

We now consider the size of 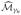in the setting

$$\underset{j\notin {\mathcal{M}}_{\ast }}{max}{\Vert {\mathbf{u}}_j\Vert }_{\infty }=o(n^{-\kappa }).$$

This specification also reduces to those considered in special cases of linear models and generalized linear models. The counterpart of Theorem 4 for establishing the selection consistency is given as follows.

Theorem 6

Under assumptions A.3 and A.4, if max_{j ∉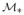} ||u_j||_∞ = O(n^−η) where η > κ and min_{j ∉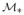} λ_min( 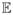{g^(j)(Z; 0)g^(j)(Z; 0)^T}) ≥ c₄ for some c₄ > 0, where λ_min(A) means the smallest eigenvalue of A, then there exists a positive constant C₅ depending only on K₃, K₄ and γ₃ appeared in assumption A.4 and c₄ such that, for any $\tau \in (\frac{1}{2}-\eta ,\frac{1}{2}-\kappa )$and, γ_n=c₃,n^2τ

$$\mathbb{P}\{\mid {\widehat{\mathcal{M}}}_{{\gamma }_n}\mid >s\}\le \{\begin{array}{ll}pexp(-C_5{n}^{2\tau })+pexp(-C_5{n}^{{\gamma }_3/6}),\hfill & if{\gamma }_3<2\mathit{and}\eta >\frac{1}{4};\hfill \\ pexp(-C_5{n}^{{\gamma }_3\eta })+pexp(-C_5{n}^{{\gamma }_3/6}),\hfill & if{\gamma }_3<2\mathit{and}\eta \le \frac{1}{4};\hfill \\ pexp(-C_5{n}^{{\gamma }_3\eta })+pexp(-C_5{n}^{{\gamma }_3/6}),\hfill & if{\gamma }_3\ge 2\mathit{and}\eta \le \frac{1}{{\gamma }_3+2};\hfill \\ pexp(-C_5{n}^{{\gamma }_3/({\gamma }_3+2)})+pexp(-C_5{n}^{2\tau }),\hfill & if{\gamma }_3\ge 4\mathit{and}\eta >\frac{1}{{\gamma }_3+2};\hfill \\ pexp(-C_5{n}^{{\gamma }_3/6})+pexp(-C_5{n}^{2\tau }),\hfill & if2\le {\gamma }_3<4\mathit{and}\eta >\frac{1}{{\gamma }_3+2}.\hfill \end{array}$$

Combining the Theorems 5 and 6, we can see that the screening procedure using the marginal empirical likelihood ratio is valid in a broad framework for identifying the set of the effective features.

4.2. Iterative screening procedure

As we can see from the main results, the proposed marginal empirical likelihood screening procedure works ideally for the case with explanatory variables that are independent of each other. To deal with challenging situations with correlated explanatory variables, we propose to use the following iterative sure independence screening procedure.

• Step 1: Rank explanatory variables according to ℓ_j(0) by (2.5) and select top ranked explanatory variables with largest values of ℓ_j(0)’s until some desirable number of features are included. Denote the set of select explanatory variables by .

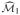• Step 1′: Apply penalized empirical likelihood [Leng and Tang (2012), Tang and Leng (2010)] to explanatory variables in 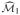and denote the final model by .

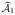• Step 2: Let 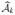⊂{1, …, p} be the selected model at the kth step. At the kth iteration, for each j ∉ 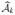, denote by

  $${\text{EL}}_{\{j\}\cup {\widehat{\mathcal{A}}}_k}(\mathit{\mu })=sup\left\{\prod _{i=1}^n{w}_i:w_i\ge 0,\sum _{i=1}^n{w}_i=1,\sum _{i=1}^n{w}_i{\mathbf{X}}_{i,\{j\}\cup {\widehat{\mathcal{A}}}_k}{Y}_i=\mathit{\mu }\right\}$$
  the empirical likelihood for the combined covariates, and denote by

  $${\stackrel{\sim }{\text{EL}}}_j(\mu )=\underset{{\mu }_j=\mu }{sup}\{{\text{EL}}_{\{j\}\cup {\widehat{\mathcal{A}}}_k}(\mathit{\mu })\}$$

  the profile empirical likelihood evaluated at μ. Rank explanatory variable j in ${\widehat{\mathcal{A}}}_k^c$ according to ${\stackrel{\sim }{\text{EL}}}_j(0)$ and select the top ranked until some desirable number of features are included. Denote the selected set by .

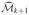• Step 2′: Apply penalized empirical likelihood to explanatory variables in 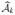∪ 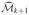and denote the final model by .

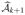• Step 3: Repeat steps 2 and 2′ when either 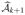= 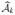or the size of 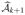reaches a pre-specified number.

The above iterative screening procedure incorporates the profile empirical likelihood. The rationale behind it is to capture the joint impact that may be invisible using the marginal screening procedure if correlations exist among those covariates. Our iterative screening procedure shares some similar features of the analogous ones in Fan and Lv (2008) and Fan and Song (2010). However, on the other hand, the iterative procedure using the profile empirical likelihood ratio shares the feature of the marginal empirical likelihood approach by incorporating the level of uncertainties. In addition, we note that the above iterative procedure is generally applicable in a broad framework.

5. Numerical examples

In this section, we use five simulation examples and a real data example to demonstrate the performance of the proposed empirical likelihood-based screening procedure (denoted by EL-SIS) and corresponding iterative procedure (denoted by EL-ISIS). Depending on the example setting, we compare it with the screening methods proposed in Fan and Lv (2008) (denoted by LS-SIS and LS-ISIS) and Fan and Song (2010) (denoted by GLM-SIS and GLM-ISIS) for linear regression models and generalized linear models, respectively. Whenever appropriate, we compare to the robust rank correlation based screening (RRC-SIS and RRC-ISIS) studied by Li et al. (2012). For all simulation examples, we begin with p = 1000 explanatory variables and screen to a much smaller number d of explanatory variables. The respective SCAD penalized variable selection is further applied to these selected explanatory variables to get the corresponding final model. Results over 200 repetitions are reported. For each case, we report the number of repetitions that each important explanatory variable is selected in the final model and also the average number of unimportant explanatory variables being selected.

Example 1

This example has a very standard setting with three important explanatory variables and is taken from Fan and Lv (2008). Covariates are generated as X_j ~ N(0, 1) and cov(X_j, X_j′) = 1 if j = j′ and 0.3 otherwise. The response is generated as Y = 5X₁ + 5X₂ + 5X₃ + ε with error being independent of the explanatory variables. We consider three different error distribution N(0, 1), N(0, 2²), and t₄ for ε. Random samples of size n = 100 are used and we set d = ⌊n/(2 log n)⌋ = 10, where ⌊a⌋ denotes the largest integer that is less than or equal to a. Results over 200 repetitions are reported in Table 1, where we report the number of repetitions that each of the important explanatory variables X₁, X₂ and X₃ is selected. For unimportant explanatory variables, Table 1 reports their average number of repetitions for each being selected. It shows that the proposed empirical likelihood-based screening methods perform very competitively when compared to the least squares-based screening or the robust rank correlation-based screening.

Table 1.

Simulation result for Example 1

ε	Method	X1	X2	X3	Unimportant explanatory variables
N(0, 1)	LS-SIS	199	199	200	1.406219
	RRC-SIS	199	199	199	1.407222
	EL-SIS	194	183	185	1.442327
	LS-ISIS	200	200	200	0.965898
	RRC-ISIS	200	200	200	0.800401
	EL-ISIS	200	200	200	0.659980
N(0, 22)	LS-SIS	199	199	200	1.406219
	RRC-SIS	198	198	199	1.409228
	EL-SIS	192	182	183	1.447342
	LS-ISIS	200	200	200	1.404213
	RRC-ISIS	200	200	200	1.403210
	EL-ISIS	200	200	200	0.980943
t4	LS-SIS	199	199	200	1.406219
	RRC-SIS	198	199	199	1.408225
	EL-SIS	193	186	187	1.438315
	LS-ISIS	200	200	200	1.383149
	RRC-ISIS	200	200	200	1.362086
	EL-ISIS	200	199	200	0.635908

Example 2

The second example is also from Fan and Lv (2008) and has a hidden important explanatory variable, which is important but marginally uncorrelated with the response. This example is to illustrate that the proposed iterative empirical likelihood-based screening works effectively in such challenging cases. Covariates are generated as X_j ~ N(0, 1) and cov(X_j, X_j′) = 1 if j = j′ and 0.3 otherwise except $cov(X_4,X_j)=\sqrt{0.3}$ for j ≠ 4. The response is generated as $Y=5X_1+5X_2+5X_3-15\sqrt{0.3}{X}_4+\epsilon$ with ε being independent of explanatory variables. We consider three different error distribution N(0, 1), N(0, 2²), and t₄. Results over 200 repetitions with n = 100 and d = ⌊n/(2 log n)⌋ = 10 are reported in Table 2. It shows that the empirical likelihood-based screening is challenged by the hidden important explanatory variable X₄ but the corresponding iterative screening can easily pick it up. Overall the performance of the empirical likelihood-based screening methods is very similar to that of the least squares-based screening methods and is better than the robust rank correlation-based screening. Note that iterative version of the robust rank correlation-based screening is residual-based. This explains the improvement of the robust rank correlation-based screening.

Table 2.

Simulation result for Example 2 with a hidden important explanatory variable X₄

ε	Method	X1	X2	X3	X4 (hidden)	Unimportant explanatory variables
N(0, 1)	LS-SIS	198	197	195	0	1.415663
	RRC-SIS	196	197	194	0	1.418675
	EL-SIS	198	198	197	0	1.412651
	LS-ISIS	200	200	199	196	1.125502
	RRC-ISIS	200	199	200	111	1.157631
	EL-ISIS	199	199	200	193	0.853414
N(0, 22)	LS-SIS	198	197	194	0	1.416667
	RRC-SIS	196	196	194	0	1.419679
	EL-SIS	198	196	194	0	1.417671
	LS-ISIS	199	200	199	196	1.210843
	RRC-ISIS	199	199	200	96	1.311245
	EL-ISIS	200	200	198	188	0.912651
t4	LS-SIS	197	197	197	0	1.414659
	RRC-SIS	195	198	196	0	1.416667
	EL-SIS	197	198	196	0	1.414659
	LS-ISIS	199	200	200	196	1.209839
	RRC-ISIS	200	200	199	100	1.305221
	EL-ISIS	200	198	200	185	0.824297

Example 3

The performances of the empirical likelihood-based screening and the least squares-based screening methods are very similar in the previous two examples. It is known that the empirical likelihood approach requires a less restrictive distributional assumption. We next use a heteroscedastic example to show the advantage of the empirical likelihood-based screening. Explanatory variables are generated as X_j ~ N(0, 1) with cov(X_j, X_j′) = 0 for j ≠ j′. The response is generated as $Y=c(X_1-X_2+X_3)+\epsilon /(X_1^2+X_2^2+X_3^2)$ with independent ε ~ N(0, 1) and c > 0 controls the signal level. Results over 200 repetitions with n = 70 and d = ⌊n/(2 log n)⌋ = 8 are reported in Table 3 for three different values of c. It shows that the performance of the least squares-based screening is severely affected by the heteroscedasticity especially when the signal level is low. On the other hand, the proposed empirical likelihood-based screening works much better and similarly as the robust rank correlation-based screening.

Table 3.

Simulation result for Example 3

c	Method	X1	X2	X3	Unimportant explanatory variables
1	LS-SIS	149	147	156	1.151454
	RRC-SIS	191	185	190	1.037111
	EL-SIS	190	184	191	1.038114
1.5	LS-SIS	173	171	174	1.085256
	RRC-SIS	194	191	193	1.025075
	EL-SIS	196	192	194	1.021063
2	LS-SIS	182	182	180	1.059178
	RRC-SIS	194	194	195	1.020060
	EL-SIS	199	195	194	1.015045

Example 4

We now consider an example with the extended scope. In this example, we generate data from the longitudinal data example as in Section 4.2 with m = 4 means 4 repeated measurements generated. In particular, the following model is generated:

$$Y_{il}={\mathbf{X}}_{il}^{\mathrm{T}}\mathit{\beta }+{\epsilon }_{il}(i=1,\dots ,n;l=1,\dots ,m).$$

Here X_il is generated from multivariate normal N(0, Σ) with Σ = (σ_jk)_{j,k=1, …, p} and σ_jk = 0.5^|j−k|. The error vector ε_i = (ε_i1, …, ε_im)^T is generated from multivariate normal distribution with unit variance. The correlation structure of ε is specified as AR(1) with parameter 0.8; see Diggle et al. (2002) for reference for the correlation structure. The first five components of the true β is set to be c · (2.0, −2.0, 0, 0, 2.0)^T where c is used to control the signal strength, and all other components of β are zero. We use two sets of basis matrices in (4.2). We take M₁ = I as the identity matrix. The second basis matrix M₂ is a matrix with two main off-diagonals being 1 and 0 elsewhere corresponding to the AR(1) working correlation [Qu, Lindsay and Li (2000)]. We then apply the marginal empirical likelihood procedure as in Section 4 using the marginal estimating function of (4.2). Here we note that the marginal estimating function is 4-dimensional. By ignoring the correlation structure of the longitudinal data, the least squares-based screening and robust rank correlation-based screening procedures can be applied. Results over 200 repetitions with n = 60 and d = 15 are reported in Table 4. From Table 4, we clearly see that the marginal empirical likelihood approach works much better than the alternative ones, especially when signal is relatively weak. The improvement can be seen as the results of incorporating additional data structural information. Hence, we demonstrate an advantage of the marginal empirical likelihood approach of being adaptive and flexible.

Table 4.

Simulation result for the longitudinal data estimation function example with c controlling the signal strength

c	Method	X1	X2	X5	Unimportant explanatory variables
1	LS-SIS	90	73	153	2.692076
	GEE-SIS	111	111	168	2.617854
	RRC-SIS	84	66	136	2.722166
	EL-SIS	135	128	191	2.553661
1.5	LS-SIS	153	153	195	2.506520
	GEE-SIS	165	160	196	2.486459
	RRC-SIS	142	136	193	2.536610
	EL-SIS	176	187	199	2.445336
2	LS-SIS	183	183	200	2.441324
	GEE-SIS	183	184	200	2.440321
	RRC-SIS	179	176	200	2.452357
	EL-SIS	192	196	200	2.419258
2.5	LS-SIS	195	195	200	2.417252
	GEE-SIS	196	195	200	2.416249
	RRC-SIS	192	190	200	2.425276
	EL-SIS	198	197	200	2.412237
3	LS-SIS	199	198	200	2.410231
	GEE-SIS	198	197	200	2.412237
	RRC-SIS	199	198	200	2.410231
	EL-SIS	200	198	200	2.409228

In the review process, one referee pointed out that our comparison to the LS-SIS is not fair as it is based on the ordinary least squares. It is more reasonable to compare to a weighted least squares-based screening by adjusting to correlation among longitudinal observations. To address this issue, we implement this weighted least squares-based screening by using the R package “geepack,” which can estimate both the correlation structure and regression parameter once a parametric form of the correlation structure is specified. Table 4 is updated accordingly with GEE-SIS denoting this weighted least squares-based screening method. It shows that our newly proposed EL-SIS still does better than the GEE-SIS even though a correct parametric correlation structure, AR(1), is specified.

Example 5

This is an extension of Example 2 to the case with a binary response using logistic regression. Covariates are generated as X_j ~ N(0, 1) and cov(X_j, X_j′) = 1 if j = j′ and 0.3 otherwise except $cov(X_4,X_j)=\sqrt{0.3}$ for j ≠ 4. The binary response is generated from Bernoulli distribution with success probability given by ${\{1+exp(-4X_1-4X_2-4X_3+12\sqrt{0.3}{X}_4)\}}^{-1}$. Results over 200 repetitions with n = 400 and d = 10 are reported in Table 5. A similar performance pattern is observed. For this example, the result for the iterative version of the robust rank correlation-based screening is not presented since it is not clear how to define a residual-based iterative procedure.

Table 5.

Simulation result for Example 5

Method	X1	X2	X3	X4 (hidden)	Unimportant explanatory variables
GLM-SIS	200	200	200	0	1.405623
RRC-SIS	200	200	200	0	1.405623
EL-SIS	200	200	200	0	1.405623
GLM-ISIS	200	200	200	200	0.324297
EL-ISIS	199	200	200	199	0.764056

A real data example

Glioblastoma is the most common primary malignant brain tumor of adults and one of the most lethal of all cancers [Horvath et al. (2006)]. The median survival of glioblastoma patients is 15 months from the time of diagnosis. We next apply our proposed methods to a microarray gene expression dataset of glioblastoma patients reported in Horvath et al. (2006). The dataset has been analyzed by Pan, Xie and Shen (2010) and Li and Li (2008) among many others. Drawn from two different studies, the data consist of two independent sets. We use the set with 50 samples. We use the log survival time, measured in years, as the response. The second sample with a outlier response is excluded and the other 49 samples are used in our analysis. Explanatory variables are gene expression profiles of 1523 genes measured on Affymetrix HG-U133A arrays.

We apply the least squares-based and empirical likelihood-based screening methods with d = 6. LS-SIS selects “GSN”, “FOS”, “COL11A1”, “AVPR1A”, “SELE”, and “TBL1X” as important gene explanatory variables while EL-SIS selects “GSN”, “JAK2”, “COL11A1”, “CDK6”, “ADCYAP1R1”, and “TBL1X”. Note that they select some common genes (“GSN” and “COL11A1”) and some different genes. LS-ISIS selects “GSN”, “COL11A1”, “THBS1”, “SELE”, “TBL1X”, and “GCGR”. EL-ISIS selects “DUSP7”, “COL11A1”, “BST1”, “ADCYAP1R1”, “TBL1X”, and “GCGR”. Similarly two genes (“TBL1X” and “GCGR”) are recruited by the iterative screening methods based on both the least squares and empirical likelihood. The robust rank correlation-based screening performs similarly with 2–3 overlapping genes.

6. Discussion

Screening based on marginal model fitting has enjoyed great popularity in the recent literature. However, most, if not all, of the marginal screening methods studied thus far are based on some restrictive distributional assumptions. Yet these assumptions may not be realistic in applications. Thus motivated we propose a new screening method based on marginal empirical likelihood, which is known to be less restrictive. It has been demonstrated to be effective using both theoretical sure screening property and numerical evidences. Further extensions using empirical likelihood are being investigated.