Abstract
Miscarriage, even if biologically random, is not socially random. Willingness to abort reduces miscarriage risk. Because abortions are favorably selected among pregnant teens, those miscarrying are less favorably selected than those giving birth or aborting but more favorably selected than those giving birth. Therefore, using miscarriage as an instrument is biased towards a benign view of teen motherhood while OLS on just those giving birth or miscarrying has the opposite bias. We derive a consistent estimator that reduces to a weighted average of OLS and IV when outcomes are independent of abortion timing. Estimated effects are generally adverse but modest.
While policy-makers have consistently cited teenage childbearing as an important social issue, labour economists have generally struggled over the past thirty years to disentangle the causal impact of childbearing on future labour market and fertility outcomes from adverse selection. In particular, the counterfactual outcomes of women who chose to have children when they are younger might be less favourable than those who have children when they are older, making it difficult to measure the impact of delaying childbearing on those outcomes. Academic studies relying on regression or matching estimators generally conclude there is a modest but nontrivial adverse impact of childbearing on a range of outcomes. In contrast, the literature focussed on using instrumental variables (IV) draws mixed conclusions.
Early literature focussed on using differences in timing of teenage birth between sisters to mitigate selection issues. A summary of work using the National Longitudinal Survey of Youth (NLSY) and Panel Study of Income Dynamics (PSID) by Hoffman et al (1993) suggests that the positive impact of teen fertility on future childbearing and negative impact on educational and labour market outcomes is reduced but not eliminated when controlling for unobserved heterogeneity. Studying a panel of Swedish sisters, Holmlund (2005) finds modest effects of birth timing on educational attainment once she controls for educational performance before pregnancy. More recent work has used other matching techniques. Sanders et al (2007) find adverse effects on educational attainment in the NLSY using propensity score techniques. Levine and Painter (2003) document adverse effects on both earnings and education when matching women within schools using the National Education Longitudinal Survey (NELS).
Turning to the instrumental variables literature, a number of studies use cross-sectional variation in age at menarche as a source of exogenous variation in the timing of childbearing. Ribar (1994) uses age at menarche (in addition to the local area abortion rate and ob-gyn availability) in the NLSY, estimating insignificant or beneficial effects of early childbearing on educational attainment. In contrast, Chevalier and Viitanen (2003) as well as Klepinger et al (1999) document more adverse effects. Using a survey of British women (the National Child Development Survey), the former conclude that endogeneity is relatively unimportant and that the consequences of teen motherhood are dire. The latter combine menarche with county-level instruments in NLSY data and also find large negative effects. Using a different set of instruments, Walker and Zhu (2009) exploit variation in school-leaving age and age within school cohort and find no effects on employment. A final strand of this literature uses miscarriage as an exogenous delay in birth timing. Hotz, McElroy and Sanders (1998,2005), hereafter HMS, use miscarriage during teenage pregnancy in the NLSY data to document that teenage motherhood has only a small effect on completed fertility and modest negative impact on educational or labour market outcomes. Using a survey of British women, Goodman et al (2004) and Ermisch and Pevalin (2003) each use miscarriage as an instrument, finding small and generally insignificant results.
Related labour literature suggests that the presence of young children reduces female labour supply. Angrist and Evans (1998) use the randomness of sex mix of the first two children as an instrument for having a third child and find that motherhood has a small but notable effect on female labour supply. Similarly, Bronars and Grogger (1994) use the randomness of twins at first birth as a natural experiment and conclude there are small, albeit short-lived, effects on the labour supply of unwed mothers although the effects on blacks are larger. Consequently, we should not be surprised that, as HMS find, delaying childbirth initially raises labour supply but later decreases it. In a Ben-Porath style human capital investment model, early childbirth can be a wealth maximizing strategy (Buckles, 2005).
Looking at the literature as a whole, we do note that the balance of evidence in favour of a benign view of teenage childbearing relies on variation in birth timing driven by miscarriage. One potential concern with the strategy is that miscarriage may not be random. In order to account for the presence of non-random miscarriages, Hotz et al (1997) use the NLSY to implement non-parametric bounds, confirming earlier results. However, as these bounds make relatively weak assumptions, they are large and do not rule out economically significant adverse outcomes. Another potential concern with using miscarriage as an instrument is that while the assignment of miscarriage might be random conditional on key risk factors, the event of miscarriage is frequently censored by a woman having an abortion. In particular, when abortion is an option, teenagers who miscarry are less likely to be girls who would otherwise abort their pregnancy than are teenagers who either abort or carry the child to term. Building on an earlier version of this paper (Ashcraft and Lang, 2006), Fletcher and Wolfe (2009) show that miscarriage is nonrandom and can be predicted by the frequency of abortion in the individual’s neighbourhood. Since, as we will see, pregnant teenagers who have abortions, on average, come from more favoured backgrounds than those who do not, girls who miscarry are not a random sample of pregnant teenagers but are, instead, drawn from more disadvantaged backgrounds. The IV estimator therefore underestimates the true costs of teenage childbearing. When miscarriage serves as an instrument for the timing of birth, the estimates are biassed towards a benign view of teenage childbearing. Ashcraft and Lang (2006) and Fletcher and Wolfe (2009) use this insight to bound the effects of teen births using ordinary least squares (OLS) on miscarriages and births only to get an upward biassed estimate of the adverse effect and using miscarriage as an instrument for delay on a sample of all pregnancies to get a downward biassed estimate. As expected in almost all cases the OLS estimates suggest a more adverse effect. Unfortunately, in neither paper are the bounds consistently small.
In this paper, we show that if the timing of miscarriage is random conditional on some controls, we can obtain a consistent estimator of the effect of giving birth on pregnant teens who would not choose to abort. In essence our approach is to calculate the proportion of abortion types who miscarry and remove their influence from the estimated miscarriage outcome. In a special case, where abortion outcome is independent of abortion timing, the consistent estimator is a linear combination of OLS on only those who give birth or miscarry and IV on the entire sample. Since the assumption of constant abortion outcomes is not rejected in our data, this provides us with a relatively simple consistent estimator.
In most dimensions our results suggest a modest adverse effect on adult outcomes from giving birth as a result of a first teen pregnancy. The probability of getting a high school diploma is unaffected but the probability of getting a General Educational Development (GED) test is reduced by about five percentage points and average education is lower by about 0.15 years. The probability of working is reduced by about five percentage points and weekly hours by about four, but the effect on income conditional on working is close to zero. Women who gave birth as teens are about three percentage points less likely to be currently married, but conditional on being married have husbands who earn more than the husbands of women who did not give birth as teens. Overall, there is almost no effect on family income but since women who gave birth as teens have larger families, their income relative to an index of family needs is marginally lower. Few of these differences approach statistical significance. The one exception is number of children, where we find that having a child as a teenager increases the expected number of live births by about eight-tenths.
As an additional check on our results, we use an expanded sample with more late miscarriages and still-births. We first show that such “late miscarriages” are statistically random. Since late induced abortions are very rare, OLS on this sample is an (almost) consistent estimator. Albeit for a more restrictive set of outcomes, we again find no evidence of strong adverse effects on the teen mothers.
The next section explains the econometric issues. Section two describes the data we use. In section three we present evidence in support of the argument that miscarriages are conditionally random. The fourth section presents the results and a variety of robustness checks. Section five concludes. The on-line appendix contains the proofs of the main results and the formal analysis for some results that are outlined in the paper.
1 Methods
We begin with a largely intuitive explanation of the econometric issues. For the moment we ignore any control variables. The results here are developed more formally and more generally in the next subsections.
Teens who become pregnant may be birth types (A* = 0) or abortion types (A* = 1). They may also be miscarriage (M* = 1) or non-miscarriage (M* = 0) types. The outcome of their pregnancy may be a birth (D = 1), miscarriage (M = 1) or abortion (A = 1). Note that if a teen miscarries, we do not know if she was a birth or abortion type, and if she has an abortion, we do not know whether she was a miscarriage type.
Define YD = E[Y | D = 1] as the expected outcome for those giving birth, YM =
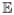 [Y | M = 1] as the expected outcome for those miscarrying, YA =
[Y | M = 1] as the expected outcome for those miscarrying, YA =
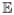 [Y | A = 1] as the expected outcome for those having abortions,
as the expected outcome for birth types who give birth, and
as the expected outcome for birth types who miscarry. The causal effect of teen motherhood on birth types is
.
[Y | A = 1] as the expected outcome for those having abortions,
as the expected outcome for birth types who give birth, and
as the expected outcome for birth types who miscarry. The causal effect of teen motherhood on birth types is
.
If abortions are positively selected, as appears to be the case among pregnant teens, , and if miscarriage is medically random, . Note that we assume that the abortion outcome is independent of its timing. We relax this assumption below.
The assumption that miscarriage is medically random implies that
, and that
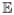 [Y | M = 1 & A* = 1] = YA. It is convenient to let γ
* be the probability that miscarriage occurs before abortion for women of abortion and miscarriage type, and m* and a* be the proportion of teens who are miscarriage and abortion types, respectively. The expected outcome for those miscarrying is
[Y | M = 1 & A* = 1] = YA. It is convenient to let γ
* be the probability that miscarriage occurs before abortion for women of abortion and miscarriage type, and m* and a* be the proportion of teens who are miscarriage and abortion types, respectively. The expected outcome for those miscarrying is
| (1) |
Equation (1) points to our first approach to estimation. Rearranging terms gives
| (2) |
The averages YA and YM can be estimated directly from the data. The remaining parameters can be estimated from a competing risks model for miscarriage and abortion weeks. So we can simply adjust the average outcome for teens who miscarry to get , and subtract this from YD to get Δ.
If we compute the effect of teen motherhood by comparing teens who give birth with those who miscarry, we get
| (3) |
Since YM < YA, comparing teens who miscarry with those who give birth is biassed towards an adverse view of the effects of teen motherhood.
Now consider the more common practice of using miscarriage as an instrument for (the absence of a) teen birth. Then
| (4) |
But YD − YM is Δols and therefore
| (5) |
Since YA > YM, IV is biassed towards a benign view of teen motherhood.
From (3) and (5) we have two linear equations in Δ and YA − YM. We can therefore solve for the causal effect as a linear combination of Δols and Δiv,
| (6) |
The averages YD, YM, and YA and therefore Δols and Δiv can be estimated directly from the data, while m* and γ * can be estimated from a competing risks model.
Note that we could also adjust the IV estimator to get a consistent estimator of Δ by obtaining the values of a*, γ * and m* from a competing risks model and the estimators of YA and YM, an approach we do not pursue. More importantly, IV adds a multiple of YA − YM to the true causal effect and OLS subtracts a multiple of this difference. Weighting the two estimators provides a simple way of doing the requisite adjustment.
1.1 Model and Parameters of Interest
We use a potential outcomes model for the econometric analysis. This model is useful to formulate assumptions and to define the parameters of interest. Our population consists of women who became pregnant as teenagers. Let T̄ denote the maximum number of weeks of pregnancy, e.g. T̄ = 41. The structural variables of the model are:
The treatment indicator, D, where D = 1 for women who gave birth as teens and D = 0 otherwise.
The potential outcomes indexed by treatment status, Y *(d) = Y *(D = d), d ∈ {0, 1}.
The scheduled abortion week, , where we set for women who would not abort.
The scheduled miscarriage week, , where we set for women who would not miscarry.
An indicator for abortion occurring first, , when abortion and miscarriage are scheduled for the same week, i.e. when .
A vector of individual characteristics, X, which are related to and might affect potential outcomes.
Variables with asterisk are latent because they are unobservable for some part of the population. For example, is not observed for women such that , that is we do not observe the timing of the scheduled abortion for women who were scheduled to miscarry before the abortion. The potential outcomes of interest include adult demographic and economic outcomes such as educational attainment, marital status, fertility, labour force participation, labour supply, earnings, and family income. For the indicator , we consider two polar cases: abortion always precedes miscarriage, ; and miscarriages always precede abortion, 1 The vector X includes risks factors for miscarriage such as smoking during pregnancy, age at conception, parents presence and their education. Based on and , we define the abortion and miscarriage types as and .
We assume that the following variables are observed:
Assumption 1 (Observed variables)
The observed variables are
Treatment indicator: D.
Realized outcome: Y = (1 − D)Y *(0) + DY *(1).
- Realized abortion week:
(7) - Realized miscarriage week:
(8) Individual characteristics: X.
Based on TA and TM, we can construct the realized abortion and miscarriage indicators A = 1(TA < T̄) and M = 1(TM < T̄).2
The parameters of interest in this model are characteristics of the potential outcome distributions for women of the non-abortion type. In particular, we are interested in the average treatment effect (ATE)
| (9) |
where μ(d) is the average structural function (ASF) at d, which gives the average potential outcome when everyone in the population receives the treatment assignment D = d. We exclude the abortion types because we cannot hope to point identify the ATE for them, since we never observe these women under the treatment, i.e. having a child.3 Moreover, for many policy purposes, notably the value of teen pregnancy prevention programs, the parameter we wish to measure is Δ: the ATE of giving birth on a teen who becomes pregnant and would choose to have the child. Although we focus on the ATE, the analysis can be extended to other effects such as distribution and quantile treatment effects. We leave this extension to future work.
The ATE is not directly identifiable because we do not observe potential outcomes and abortion type. We impose conditions on the relation between potential outcomes and scheduled weeks to identify the ATE. In particular, we assume that, among women with the same observable characteristics X, the event and the timing of a scheduled miscarriage are randomly assigned relative to potential outcomes conditional on the scheduled abortion week, and that the scheduled miscarriage and abortion weeks are independent.
Assumption 2 (Conditionally random miscarriage)
where ⫫ denotes statistical independence.
The independence condition for potential outcomes can be weakened to mean independence since we are interested only in the ATE. The independence condition for scheduled weeks cannot be weakened in this way. We discuss the plausibility of Assumption 2 in our application, together with the choice of X, in Section 3.
We assume that the potential outcomes have finite means and that there is a positive mass of women of the abortion, miscarriage and birth types for each value of X and . These regularity conditions ensure that all the quantities that we will use to identify the ATE are well-defined.
Assumption 3 (Moments)
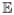 [|Y|] < ∞,
, and
[|Y|] < ∞,
, and
The ATE is identified under Assumptions 1–3. Under additional assumptions, we relate the ATE with the OLS and IV approaches that have been previously used to estimate the ATE. Thus, we find that a linear combination of OLS and IV consistently estimates the ATE under the following independence condition between the abortion timing and potential outcomes:
Assumption 4 (Conditionally random abortion timing)
Statistical independence can be weakened to mean independence. An implication of this condition is that
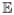 [Y | TA = t, X] =
[Y | TA = t, X] =
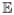 [Y | TA = s, X] a.s. for all s, t ∈ {1, …, T̄ − 1}, which is directly testable because it involves only moments of observed variables.
[Y | TA = s, X] a.s. for all s, t ∈ {1, …, T̄ − 1}, which is directly testable because it involves only moments of observed variables.
We also use a non-random selection assumption to sign the bias of the OLS and IV estimators.
Assumption 5 (Selection)
| (10) |
This assumption requires that women of the abortion type are positively selected from the population in terms of potential outcomes even after conditioning on characteristics.4 It can be interpreted as the monotone instrumental variable assumption of Manski and Pepper (2000), although the “instrument” A* is not fully observable. In Section 2, we give evidence of Assumption 5 in our application.
For estimation and inference purposes, it will be convenient to work with discrete individual characteristics X. This is the case in our application where X will include indicators for smoking/conception before age 15 or indicators for father’s presence/education. Let
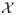 denote the support of X.
denote the support of X.
Assumption 6 (Discrete X)
The set
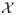 is finite.
is finite.
1.2 Identification Analysis
In this section, we show that the ATE is identified by moments of the observed variables under the stated assumptions. The proofs of all the results are relegated to the on-line appendix. In the absence of abortions, [Y *(0), Y *(1)] ⫫ D | X if miscarriages are randomly assigned and we could identify the ATE by comparing average realized outcomes for those who gave birth with those who miscarried. The identification problem arises because D is no longer randomly assigned if there is the possibility of abortion. Thus, in the absence of miscarriage, the decision between carrying the pregnancy to term and having an abortion is related to potential outcomes under our selection assumption.
Assumption 2 helps deal with the endogeneity problem of D. To see the implications of this assumption, it is convenient to bring in some standard notation for duration models. For j ∈ {A, M} and f ∈ {0, 1}, let , pj(x, t) = ℙ[Tj = t | X = x], and Sj(x, t) = ℙ[Tj > t | X = x] denote the probability and survival functions for the scheduled and realized abortion and miscarriage weeks when . Furthermore, let denote the hazard functions for the scheduled abortion and miscarriage. While clearly the assumption about the within-week timing of abortions and miscarriages does not affect the realized scheduling of miscarriages and abortions, it affects the functions for the scheduled weeks that we can identify from the functions for realized weeks. Thus, and depend on f, the value of , because the values of these functions compatible with the population values of pj(x, t) and Sj(x, t) depend on the choice of f. For example, is the survival function for scheduled miscarriage week when the tie-breaking rule is that abortion precedes miscarriage when both are scheduled for the same week.
We are now ready to present the main identification results linking moments of the observed variables to moments of the structural variables. We start by analysing the probability and survival functions for scheduled weeks. These functions will be the key ingredient to remove the selection bias in the identification of the ATE. The following proposition gives a recursive system for the probability and survival functions in terms of observed functions. It follows from standard results for competing risks models in discrete time with independent risks (e.g., Kalbfleisch and Prentice, 2002).
Proposition 1 (Competing risk model)
Under Assumptions 1–3, for t ∈ {1, …, T̄ − 1} and ,
| (11) |
a.s., where
| (12) |
and
| (13) |
It is apparent from the expressions in Proposition 1 that and , since survival functions SM and SA are decreasing in t so that and . In other words, holding the observed probabilities fixed, assuming that abortion precedes miscarriage in the case of tie reduces the survival probability of the scheduled abortion week because it increases its hazard. The opposite effect holds for the scheduled miscarriage week.
For the ATE, it is convenient to carry out the analysis conditional on X. We decompose the ASF into
| (14) |
where μ(d, X) =
 [Y
*(d) | A* = 0, X] is the conditional ASF given characteristics X, and FX(·| A*) is the conditional distribution of X given A*. Then, we characterize the conditional ASF when
, using the observed outcomes and the probability and survival functions for the scheduled weeks. Define YM (X) =
[Y
*(d) | A* = 0, X] is the conditional ASF given characteristics X, and FX(·| A*) is the conditional distribution of X given A*. Then, we characterize the conditional ASF when
, using the observed outcomes and the probability and survival functions for the scheduled weeks. Define YM (X) =
 [Y | M = 1, X], the average outcome for women with characteristics X who had a miscarriage, and YA(X, t) =
[Y | M = 1, X], the average outcome for women with characteristics X who had a miscarriage, and YA(X, t) =
 [Y | TA = t, X], the average outcome for women with characteristics X who had an abortion at week t.
[Y | TA = t, X], the average outcome for women with characteristics X who had an abortion at week t.
Theorem 1 (Conditional ASF)
Under Assumptions 1–3, if ,
| (15) |
and, a.s.,
| (16) |
The average outcome for women with characteristics X who gave birth identifies μ(1, X), since these women only include non-abortion types that are randomly selected not to miscarry. To identify μ(0, X) from the average outcome for women with characteristics X who miscarried, we need to remove the contribution of the abortion types to the average of this group. The composition of abortion and non-abortion types is obtained using the competing risk model for abortion and miscarriage, and the average outcome of abortion types at each week is obtained from the average outcome of the women who aborted at the same week. For example, when miscarriages precede abortions in the same week, for miscarriages in week 7, we use the hazard model to calculate the probability of having an abortion scheduled in each week starting with the eighth and calculate the average outcome among those having an abortion in each of these weeks. We use this information to adjust the mean outcome for women miscarrying in week 7.
The conditional ATE, Δ(X) = μ(1, X) − μ(0, X), is identified by
| (17) |
if . The next theorem is the main result of this section. It shows that under the independence of potential outcomes and scheduled abortion weeks in Assumption 4, the conditional ATE has a convenient representation as a weighted average of the probability limits of two estimators. Let
| (18) |
the OLS estimand of Y on D in the sample of women who gave birth or had a miscarriage. Let
| (19) |
the IV estimand when no miscarriage is used as an instrument for birth in the entire population. We find that Δf (X) is a weighted average of Δols(X) and Δiv(X). Moreover, under the non-random abortion selection of Assumption 5, Δols(X) ≤ Δf (X) ≤ Δiv(X), i.e., OLS is biassed towards a negative view of teen motherhood, whereas IV is biassed towards a benign view. For OLS, the women who miscarried are a mixture of abortion and non-abortion types, and therefore are drawn from a more favoured population than the women who gave birth, who are non-abortion types.
Let , the probability that miscarriage occurs before abortion for women of abortion and miscarriage type and characteristics X when .
Theorem 2 (Conditional ATE, OLS and IV)
Under Assumptions 1–4, if ,
| (20) |
where
| (21) |
If in addition Assumption 5 holds
| (22) |
Theorems 1 and 2 show that the conditional ATEs are identified from moments of the observed variables. We next extend the result to the overall ATE. We show that this ATE is a weighted average of the conditional ATEs. The weights in the average are determined by the mass of non-abortion types for each value of the characteristics X. Here it is convenient to assume that X is discrete, although this condition is not necessary and the result can be extended to the continuous case with an obvious change of notation.
Theorem 3 (Overall ATE)
Under Assumptions 1–3, and 6, if ,
| (23) |
1.3 Estimation and Inference
Assume that we have a random sample of the observed variables {(Di, Yi, TAi, TMi, Xi): 1 ≤ i ≤ n}. Estimation is straightforward and follows directly identification in the case where X is discrete. Since the ATE is exactly identified by the moment conditions considered, we can replace expectations and probabilities by their sample analogs. In particular, we replace
 and ℙ in the expressions of Proposition 1, and Theorems 1–3, by the empirical versions
and ℙ in the expressions of Proposition 1, and Theorems 1–3, by the empirical versions
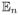 and ℙn, where
and
.
and ℙn, where
and
.
We use bootstrap to obtain standard errors. Since all the estimators are based on sample moments, bootstrap is consistent to approximate their distributions under standard regularity conditions (Mammen, 1992). These conditions include the existence of second moments for the outcome variables, and the conditional probabilities of the abortion, miscarriage and birth types being bounded away from zero and one. We implement a version of the bootstrap called weighted bootstrap. This method, in principle, consists of drawing n weights i.i.d. from the standard exponential distribution (or any other distribution with unit mean and variance), and including these weights, multiplied by the original sampling weights, as sampling weights in all the estimation steps. We refer to van Barbe and Bertail (1995) for a more detailed discussion of this method. This version of bootstrap is convenient for our application because the discrete characteristics X have small cell sizes. In cases with small cell sizes, the weighted bootstrap is less sensitive to singular designs than the standard nonparametric bootstrap, because it uses a smoother data generating process in the resampling (the exponential distribution instead of the multinomial distribution).
1.4 Underreporting of Abortions
Data exist for legal abortions experienced by teens since 1972 (Guttmacher Institute, 2010, table 2.2). We weight the fraction of pregnancies ending in abortion for each year, starting in 1972, by the proportion of our sample conceiving in that year. Based on this estimate, 37% of the pregnancies in our sample should have ended in an abortion compared with the 28% in our data over this period. The Guttmacher data are for teens who were age 15–17 when the pregnancy ended while our data are for teens less than 18 when they conceived, but we would not expect the bias from the age differences to be large in either direction. So we are probably missing close to one-fourth of abortions in our sample.
We might be concerned that this explains our inability to detect significant adverse impacts from teen births. In fact, underreporting probably leads us to overestimate the magnitude of any negative effects. If underreporting of abortions is random, then as the proportion of abortions that are not reported goes up, the favourable bias of the IV estimator diminishes and may even be reversed and our weighted average of OLS and IV becomes biassed for the conditional ATEs towards finding adverse effects. The intuition is as follows. The IV estimator is biassed towards finding benign effects of births because the proportion of abortion-types is higher among the abortion/birth group than is the proportion of abortion types among the miscarriage group. But if abortions are underreported this discrepancy is diminished and possibly reversed. In the extreme case where no abortions were reported, the restricted sample and the IV sample would be identical and both would be biassed towards overestimating the adverse effect of teen births.
This argument is exacerbated if some women report abortions as miscarriages since this will simultaneously reduce the proportion of abortion-types in the birth/abortion group and increase the proportion in the miscarriage group, thereby reducing the favourable bias of the IV estimator and increasing the unfavourable bias of the OLS estimator. As discussed in the next sub-section, however, we doubt that this is an important issue. We formalize the previous arguments about the effects of underreporting abortions and misreporting abortions as miscarriages in the on-line appendix.
It is, of course, possible that nonreporting is nonrandom in a way that creates a different bias. We know of no obvious way to address this concern.
1.5 Underreporting of Miscarriages
The risk of miscarriage may be as high as 25% during the first six weeks following the last menstrual period (Wilcox et al., 1999), but at this stage miscarriages are often asymptomatic (Pandya et al., 1996). There is little chance of a woman recognizing a miscarriage that occurs in the first four weeks following her last menstrual period. While from a statistical power perspective it is unfortunate that such miscarriages go unreported, there is little reason to believe that this underreporting is nonrandom.
The Guttmacher Institute data cited above imply that close to 14% of our sample should have experienced a miscarriage instead of the roughly 11% who report one. Given that we have fewer miscarriages than we should, we think it is unlikely that we have large numbers of abortions misreported as miscarriages. The more likely hypothesis is that many teens simply never notice a miscarriage but simply conclude that they were “late” since their menstrual periods are often erratic anyway. Unfortunately, awareness of miscarriage is unlikely to be random. Lang and Nuevo (2012) find that older and more educated women are more likely to report that they experienced a miscarriage in the early weeks of pregnancy. To the extent that more advantaged women are more likely to recognize an early miscarriage, this biases us towards finding adverse effects of birth. We address this issue with the inclusion of the characteristics X, which divide the sample based on four categories of father’s education (which does predict miscarriage in our data) in addition to the more standard smoker/early conception categories (which do not predict miscarriage in our data). If underreporting is random conditional on X, we show in the on-line appendix that the weighted average of OLS and IV consistently estimates the conditional ATEs. The overall ATE, however, might be affected by the misreporting in a way that is difficult to sign unless there is no heterogeneity in the conditional ATEs, i.e. Δ(X) = Δ a.s. In this case, underreporting miscarriages does not affect the overall ATE.
2 Data
The primary data employed in this analysis are from the 1995 wave of the National Survey of Family Growth (NSFG), a survey administered by the National Center for Health Statistics (NCHS), an agency of the Department of Health and Human Services. The purpose of the survey is to produce national estimates and information on factors affecting pregnancy, including sexual activity, contraceptive use, infertility, and sources of family planning services, and on the health of women and infants.
A national stratified sample of 10,847 civilian non-institutionalized women ages 15 to 44 was interviewed between mid-January and October 1995. The interviews were conducted in person by trained female interviewers using laptop or notebook computers. The interview, which lasted an average of 105 minutes, collected data on each pregnancy; contraceptive use by the interviewee and her partner; her ability to bear children; the use of medical services for contraception; infertility and prenatal care; her marriage, cohabitation, living situation, and work history; and a variety of demographic and economic characteristics. Additional data were collected in a short self-administered interview in which the respondent heard questions over headphones and entered her own answers into the notebook computer. This approach is designed to reduce the underreporting of abortions which is a serious problem that must be acknowledged in any study using fertility microdata.
Since we are using recall data, there may be a concern that women forget miscarriages that occurred a long time ago. Lang and Nuevo (2012) examine this issue by comparing miscarriage rates by calendar year in different waves of the NSFG. They argue that if recall bias were a problem, then the miscarriage rate in, for example, 1992 should be higher in the 1995 wave than in the 2002 wave. They find no support for this hypothesis either for all miscarriages taken together or for early miscarriages.
We focus on twelve outcome variables. The first three are measures of education: whether the individual has a high school diploma, has a GED and years of educational attainment. The next two concern marital status: whether the woman is currently married and whether she is currently divorced or separated. We also examine spouse’s earnings conditional on the woman being married or living with a partner. We examine whether the woman is working, and conditional on working, how many hours she works per week and what she earns annually. In addition, we look at total family income and income relative to the poverty line given family composition. The data set contains imputed family income for those who do not answer the question.5 Our early experiments showed little difference between the results with and without the imputed data. There are well known advantages and disadvantages to relying on imputed data. We compromise by using only actual data when examining family income and including the imputed data when reporting income relative to the poverty line. Unfortunately, income data are reported only in intervals. We impute income using these intervals.6 Finally, we examine the number of live births.
We supplement our investigation with data from the 1982, 1988 and 2002 waves of the NSFG. Each of these waves is less suitable for our purposes than the 1995 wave is, but by combining all four waves, we can obtain an adequate number of observations of teens experiencing a stillbirth or a miscarriage after the fourth month of pregnancy. Combining data from all four waves reduces the number of outcomes we can study and also the set of potential medical predictors of miscarriage we can consider.7
Table 1 presents weighted means and standard deviations for key variables. The first two columns show means for all women who were at least 20 years old at the time of the survey and for the teen pregnancy sub-sample, which consists of women who started their first pregnancy before their 18th birthday.8 Both the miscarriage rate on first pregnancy and proportion having given birth by roughly 18.75 years are consistent with published sources using other data.9 The last two columns describe those whose pregnancies lasted more than four months (or seventeen weeks) regardless of wave. Note that most such pregnancies end in birth. Only about 4% of teens whose first pregnancy lasted at least four months did not give birth as a teen. Note also, however, that not all of the women in the teen pregnancy sample were teen mothers. On average, members of the 1995 teen sample first gave birth at eighteen, approximately four and half years earlier than the average for the full sample.
Table 1.
Descriptive Statistics
| 1995 | PREGNANCY > 17 WEEKS | |||
|---|---|---|---|---|
| Full Sample | Teen Pregnancy | All | Teens | |
| Teen Pregnancy | 0.18 (0.38) | 1.00 (0.00) | 0.15 (0.36) | 1.00 (0.00) |
| Teen Birth | 0.12 (0.32) | 0.65 (0.48) | 0.15 (0.35) | 0.96 (0.19) |
| High School Diploma | 0.82 (0.38) | 0.50 (0.50) | ||
| GED | 0.06 (0.24) | 0.19 (0.39) | ||
| Education | 13.2 (2.73) | 11.3 (2.58) | 13.1 (2.62) | 10.9 (2.40) |
| Currently Married | 0.57 (0.49) | 0.53 (0.50) | 0.58 (0.49) | 0.55 (0.50) |
| Currently Divorced or Separated | 0.14 (0.35) | 0.24 (0.43) | 0.12 (0.33) | 0.22 (0.41) |
| Currently Working | 0.73 (0.45) | 0.63 (0.48) | 0.77 (0.42) | 0.71 (0.46) |
| Current Hours | 27.6 (19.7) | 24.0 (20.7) | ||
| Current Income if Working | 21,986 (16,985) | 18,107 (12,152) | ||
| Current Spouse Income if with Partner | 36,243 (24,466) | 29,585 (20,112) | ||
| Current Family Income | 43,595 (30,779) | 33,693 (26,212) | 37,624 (26,267) | 27,852 (22,558) |
| Percent Poverty Level Income | 339 (225) | 250 (195) | 286 (155) | 206 (145) |
| Number of Children | 1.45 (1.35) | 2.31 (1.41) | 1.54 (1.44) | 2.74 (1.40) |
| Age at Interview | 32.4 (7.00) | 32.3 (6.92) | 31.8 (7.17) | 32.4 (7.08) |
| White | 0.71 (0.45) | 0.59 (0.49) | 0.71 (0.45) | 0.53 (0.50) |
| Hispanic | 0.11 (0.31) | 0.14 (0.34) | 0.11 (0.32) | 0.16 (0.37) |
| Black | 0.13 (0.34) | 0.24 (0.43) | 0.13 (0.34) | 0.27 (0.45) |
| Protestant | 0.54 (0.50) | 0.59 (0.49) | 0.56 (0.50) | 0.64 (0.48) |
| Roman Catholic | 0.35 (0.48) | 0.30 (0.46) | 0.34 (0.47) | 0.27 (0.44) |
| No Mother | 0.01 (0.08) | 0.01 (0.11) | ||
| No Father | 0.05 (0.21) | 0.09 (0.29) | ||
| Mother’s Education | 11.4 (3.55) | 10.4 (3.66) | ||
| Father’s Education | 11.7 (4.02) | 10.3 (4.19) | ||
| Working Mother | 0.43 (0.50) | 0.50 (0.50) | 0.44 (0.50) | 0.49 (0.50) |
| Age at First Birth | 22.6 (4.86) | 18.0 (2.95) | 21.9 (4.47) | 16.9 (1.40) |
| Observations | 9,431 | 1,913 | 23882 | 4675 |
Notes: Sample means and standard deviation using sample weights. The Full Sample corresponds to all of the women surveyed in the 1995 National Survey of Family Growth while the Teen Pregnancy Sample represents women having a pregnancy before their 18th birthday. In both samples only women at least 20 years old when surveyed in 1995 were included. The Pregnancy > 17 Weeks sample includes all four NSFG cohorts but includes only those whose first pregnancy lasted at least seventeen weeks. Within year sampling weights are calculated so that the mean weight in each year is 1 for the full sample (including those with shorter first pregnancies
The top rows of table 1 illustrate the well-known differences in outcomes for women who were teen mothers and women as a whole. Relative to the full sample, women in the teen pregnancy sample are more likely to be divorced and less likely to be currently married and have lower spousal income conditional on being married or with a long-term partner, are less likely to be working and work fewer hours and have lower personal income conditional on working, have lower family income, are less likely to have obtained a high school diploma, a difference that is not fully offset by their greater tendency to have a GED.
The lower rows of table 1 confirm that there are also significant differences in family background between the women who became pregnant as teens and the sample as a whole. The teen pregnancy sample contains a higher proportion of blacks and a somewhat higher proportion of Hispanics than the full sample. It is somewhat more Protestant and less Catholic than the full sample. Women in the teen pregnancy sample are much more likely to have had an absent father and/or mother and had less educated parents on average.10 Their mothers were more likely to have worked.
Since women who become pregnant as teens are not a representative sample of the teen population, differences in adult outcomes between those who become pregnant as teens and those who do not should not be ascribed to their pregnancy. More significantly, we are measuring the effect of teen childbearing on a select group, not on a random teen, and, as we emphasized in the previous section, within this select group on those who would not choose to have an abortion.
Table 2 contains similar information by pregnancy outcome. Miscarriage occurred in about 10% of first teen pregnancies, abortion in 25%, and birth in 65%. Outcomes are generally similar for women who gave birth or miscarried. Those who miscarried have a slightly higher probability of having a high school diploma or GED and marginally higher personal and family incomes. They are also marginally more likely to be currently working, married and work somewhat more hours per week. They had their first child three years later than those who gave birth but actually have their next pregnancy somewhat earlier.
Table 2.
Descriptive Statistics by Pregnancy Outcome
| Birth | Miscarriage | Abortion | Early Abortion | Late Abortion | |
|---|---|---|---|---|---|
| High School Diploma | 0.41 (0.49) | 0.45 (0.50) | 0.73 (0.45) | 0.75 (0.44) | 0.65* (0.48) |
| GED | 0.21 (0.41) | 0.25 (0.43) | 0.12 (0.32) | 0.10 (0.30) | 0.17* (0.38) |
| Education | 10.8 (2.53) | 11.1 (2.51) | 12.6 (2.28) | 12.5 (2.28) | 12.7 (2.29) |
| Currently Married | 0.53 (0.50) | 0.55 (0.50) | 0.51 (0.50) | 0.50 (0.50) | 0.54 (0.50) |
| Divorced or Separated | 0.25 (0.43) | 0.22 (0.42) | 0.22 (0.42) | 0.24 (0.43) | 0.15** (0.36) |
| Currently Working | 0.60 (0.49) | 0.65 (0.48) | 0.68 (0.47) | 0.69 (0.46) | 0.66 (0.48) |
| Current hours | 22.8 (20.6) | 26.4 (21.8) | 26.1 (20.2) | 26.1 (20.0) | 26.0 (21.0) |
| Annual Income if Working | 16,881 (11,128) | 17,370 (13,418) | 21,212 (13,313) | 21,317 (13,535) | 20,814 (12,532) |
| Spouse Annual income if with Partner | 27,344 (18,141) | 26,353 (15,574) | 36,612 (24,510) | 37,119 (25,115) | 34,759 (22,303) |
| Family Annual Income | 30,928 (24,710) | 31,749 (24,435) | 41,692 (29,005) | 42,528 (29,211) | 38,726 (28,219) |
| Poverty | 221 (177) | 242 (186) | 329 (219) | 335 (217) | 307 (227) |
| Number of Children | 2.71 (1.31) | 1.86 (1.40) | 1.44 (1.22) | 1.41 (1.21 | 1.58 (1.27) |
| Age at first birth | 16.7 (1.17) | 19.7 (3.08) | 21.6 (3.86) | 21.6 (3.79) | 21.8 (4.13) |
| Age at next pregnancy | 19.7 (3.36) | 18.4 (2.75) | 20.0 (3.84) | 20.0 (3.71) | 20.2 (4.28) |
| Teen birth ever | 1.00 (0.00) | 0.29 (0.45) | 0.13 (0.33) | 0.13 (0.33) | 0.13 (0.34) |
| White | 0.521 (0.50) | 0.68 (0.47) | 0.74 (0.44) | 0.76 (0.43) | 0.69 (0.46) |
| Hispanic | 0.17 (0.38) | 0.11 (0.31) | 0.06 (0.24) | 0.06 (0.25) | 0.06 (0.24) |
| Black | 0.28 (0.45) | 0.19 (0.39) | 0.17 (0.38) | 0.15 (0.36) | 0.24* (0.43) |
| Protestant | 0.63 (0.48) | 0.58 (0.49) | 0.48 (0.50) | 0.47 (0.50) | 0.51 (0.50) |
| Roman Catholic | 0.28 (0.45) | 0.31 (0.46) | 0.35 (0.48) | 0.39 (0.49) | 0.22*** (0.42) |
| No Mother | 0.01 (0.08) | 0.05 (0.22) | 0.01 (0.08) | 0.01 (0.09) | 0.00 (0.00) |
| No Father | 0.10 (0.31) | 0.10 (0.31) | 0.06 (0.25) | 0.06 (0.24) | 0.08 (0.28) |
| Mother’s Education | 9.69 (3.82) | 10.7 (3.42) | 12.0 (2.65) | 12.0 (2.72) | 12.0 (2.42) |
| Father’s Education | 9.51 (4.31) | 11.0 (3.90) | 12.0 (3.35) | 12.1 (3.31) | 11.6 (3.50) |
| Working Mother | 0.49 (0.50) | 0.54 (0.50) | 0.53 (0.50) | 0.49 (0.50) | 0.68*** (0.47) |
| Father of pregnancy’ age | 19.8 (3.96) | 19.9 (3.50) | 18.7 (3.38) | 18.7 (3.38) | 18.8 (3.39) |
| Observations | 1,313 | 186 | 414 | 311 | 103 |
Notes: Sample means and standard deviations for Teen Pregnancy Sample. All statistics employ sample weights. Miscarriage includes stillbirths and ectopic pregnancies. Asterisks represent a test of whether outcomes for early and late abortions are the same at 10%(*), 5%(**) or 1%(***).
The group that stands out as distinct in table 2 is the set of women who terminated their first pregnancy by having an abortion. This group is much more likely than the others to have obtained a high school diploma, has substantially higher personal and family income, is somewhat more likely to be working and works more hours. Both their next pregnancy and their first birth occurred later than for the other two groups. This highlights the importance of how abortions are treated in the analysis.
The lower part of the table shows that there are also big differences in the family backgrounds of teens associated with the outcomes of their pregnancies. In particular, teens whose pregnancy ends in abortion are more likely to be white and have more educated parents and are less likely to have grown up without a mother or a father. Consistent with our argument that some of the women who miscarry would otherwise have had abortions, the women who miscarry are somewhat more advantaged than those who give birth but less advantaged than those who have abortions. In particular, they are more likely to be white than those who give birth but less likely than those who have abortions. Their parents’ education levels fall between those of the other two groups. The only exception is that women who miscarry are more likely to have grown up without their mother than are either of the other two groups.
We have shown that under Assumption 4, i.e., early and late abortions are drawn from the same pool, our estimator simplifies to a weighted average of the OLS and IV estimators. The two right-hand columns of table 2 present some evidence on this. Outcomes appear to be somewhat more favourable for women who had early abortions than for women who had late abortions as teens, but most of the differences are statistically insignificant. In fact, the only difference in outcomes that achieves significance at the 0.05 level is that those who had late abortions are less likely to be divorced or separated. There is also some evidence that they are less likely to have a high school diploma and more likely to have a GED. On the other hand, their average education level is higher. Given that we are looking at twelve different outcomes, we find table 2 supportive of Assumption 4, but we address this directly by presenting estimates both with and without this assumption.
3 Are Miscarriages Random?
The NSFG asks women if they have smoked more than 100 cigarettes in their life, and if so when they started smoking. A smoker is defined as a woman who started smoking before the age at which the pregnancy started. There is more detailed data on smoking during pregnancy, but these questions were not asked of women who end the pregnancy with an abortion. Therefore, we use the “smoked before pregnancy” variable. While over 60% of girls had smoked 100 cigarettes in their lifetime, only 27% started smoking before the pregnancy, generally viewed as a risk factor for miscarriage.11
In addition to smoking, using certain drugs (notably cocaine and heroin, possibly caffeine, but probably not marijuana), using an IUD before pregnancy (in some studies) and being less than fifteen years old at conception are believed to be risk factors for miscarriage. Unfortunately, the NSFG does not include data on drinking behaviour before pregnancy. The NSFG does include information on use of an IUD before pregnancy but only three members of our teen pregnancy sample had used an IUD before their pregnancy and none of these reported miscarrying.
At the same time, it must be recognized that the epidemiological literature has largely ignored the potential for abortion to influence these outcomes. If smokers and cocaine users are less likely to terminate their pregnancies through an abortion, they will be more likely to miscarry. Therefore, we consider this issue directly in a model that accounts for abortion. Below we present some direct evidence on the determinants of miscarriage, but we begin by pointing out that the difference in outcomes between early and late abortions already provides some indirect evidence.
Early abortions contain a higher fraction of teens who are also miscarriage types than do late abortions. If conditional on being an abortion type, miscarriage types are selectively drawn from teens with worse expected outcomes, then we would expect that early abortions would be associated with worse outcomes than are late abortions. We have seen that, if anything, they are associated with somewhat better outcomes. Of course, it is possible that late abortions are more adversely selected than early abortions and that this outweighs the negative effect of including miscarriage types among the early abortions. But Occam’s razor pushes us to the simpler explanation that there are no large differences in outcomes between early and late abortions and between latent-miscarriage and latent-nonmiscarriage types. Still, we turn now to direct evidence.
We estimate a semiparametric version of the competing risk model in Proposition 1 with hazard functions and . This proportional hazard formulation is restrictive but standard in the literature.12
Table 3 shows the results under the miscarriage-first assumption. The first column shows that a number of variables predict abortion. Whites are substantially more likely to have abortions than are either blacks or “other” racial/ethnic groups. Those describing themselves as Protestant or Catholic are less likely to have an abortion. Teens with more educated parents, working mothers and who conceive before age fifteen are more likely than other teens to have an abortions.
Table 3.
Estimates of the Relation between Individual Characteristics and Miscarriage
| Competing Risks | Weeks Pregnant > 17 (Probit Coefficients) | |||
|---|---|---|---|---|
| Abortion | Miscarriage | Full Sample | Teens | |
| White | 0.56 (0.27) | 0.13 (0.41) | −0.07 (0.26) | −0.13 (0.26) |
| Hispanic | −0.15 (0.31) | −0.28 (0.47) | −0.07 (0.28) | −0.31 (0.28) |
| Black | 0.16 (0.28) | −0.34 (0.44) | 0.17 (0.23) | 0.02 (0.27) |
| Protestant | −0.65 (0.10) | −0.04 (0.23) | 0.25 (0.22) | −0.15 (0.17) |
| Roman Catholic | −0.26 (0.10) | 0.12 (0.25) | 0.12 (0.23) | −0.04 (0.19) |
| No Mother | 0.87 (0.55) | 1.57 (0.37) | 0.02 (0.48) | - |
| No Father | 0.09 (0.21) | 0.48 (0.31) | −0.03 (0.23) | - |
| Mother’s Education | 0.09 (0.01) | 0.01 (0.02) | −0.01 (0.01) | Categorical variable |
| Father’s Education | 0.04 (0.01) | 0.04 (0.02) | 0.003 (0.01) | - |
| Working Mother | 0.13 (0.07) | 0.16 (0.14) | 0.01 (0.09) | 0.09 (0.10) |
| Smoking | −0.07 (0.08) | 0.07 (0.15) | 0.21 (0.10) | - |
| Conception before 15 | 0.26 (0.08) | 0.19 (0.19) | 0.33 (0.23) | 0.21 (0.13) |
| IUD before 1st pregnancy | - | - | 0.64 (0.35) | - |
|
| ||||
| Wald chi2 (p-value) | <.001 | <.001 | .064 | .137 |
| Observations | 1913 | 5,444 | 4,598 | |
Notes: Only women at least 20 years old when surveyed were included. First three columns are from the 1995 cycle of the National Survey of Family Growth. Teen sample is from all 1982, 1988, 1995 and 2002 cycles of the NSFG.
Column four also controls for year of pregnancy and year of survey.
The variables in table 3 have some power to predict miscarriage, but there is no consistent pattern that suggests more or less advantaged teens have a greater probability of miscarrying. The very small number of teens who have no mother figure for whom they report education are noticeably more likely to miscarry. In contrast, the probability of miscarrying is increasing in father’s education. For the remaining (individually and jointly insignificant) variables, there is no consistent pattern relating the sign of the coefficient to whether the variable is associated with a more favourable or unfavourable background.
Since the number of women who report having no mother figure in their lives is small, it is unlikely that a positive relation between this report and miscarriage has any effect on the results (and recall that such individuals have zeros for mother’s, and often father’s, variables). However, in order to ensure that our later results were not driven by the very small number of women with no mother figure, we replicated our principal estimates dropping from the sample all women reporting no mother figure. The results do not change in any substantive way. When these observations are dropped from the competing risks model, the coefficients on the factors explaining miscarriage are jointly significant at the 0.05 level but not the 0.01 level. The only variable to be individually significant is father’s education which shows a positive correlation with miscarriage.13 If anything, the results of the competing risks model therefore suggest a positive correlation between miscarriage and family background (at least once the observations without mother figures are dropped). We therefore find no evidence that our approach underestimates the adverse effects of teen motherhood on the mothers by relying on an adversely selected comparison group.
It might be argued that the teen pregnancy sample is too small to allow us to examine directly the relation between individual characteristics and miscarriage. There may also be concerns about the power of the competing risks model to detect any relations. Therefore, we turn to the entire 1995 pregnancy sample, not just the sample of women who first became pregnant as teens. We estimate the probability of a miscarriage using standard probit but restrict the sample to women who have been pregnant for more than seventeen weeks and are therefore unlikely to have an abortion. The choice of seventeen weeks is a compromise. Longer periods are more effective at eliminating concerns about abortion but reduce the sample of miscarriages.14 Only about 1% of women who are pregnant after seventeen weeks have an abortion, so the risk of bias from future miscarriages being selectively preempted by abortions is small. Seventeen weeks is also the latest period for which we can obtain meaningful estimates for the teen sample.
The results here are consistent with our expectations from reading the literature. Girls who conceive while less than fifteen are more likely to miscarry although the effect fall short of statistical significance at conventional levels. Smoking is also a risk factor. Women who used an IUD before pregnancy are also more likely to miscarry. This effect is large but significant only at the 10% level. The remaining characteristics are insignificant individually and jointly.15
In column four, we replicate column three for our teen pregnancy sample from all waves except that we drop IUD (which in any event is extremely rare among teens) and cannot control for smoking.16 Although, the t-statistic indicates that the effect of conceiving prior to age fifteen is statistically significant at the 0.1 level, we cannot reject the hypothesis that all the coefficients in column four are jointly insignificant. Thus late miscarriage does not appear to be strongly related to other factors that are likely to be correlated with adult outcomes. Therefore, as a robustness check, we will present evidence based only on births and late miscarriages.
In what follows, we focus on estimates in which we assume that miscarriages are random conditional on smoking behaviour and age at conception since this is consistent with the literature and what we find in columns (3) and (4). However, as a check on our results and because it is consistent with the competing risks model in columns (1) and (2) and with Lang and Nuevo (2012), we also present the principal results for the case where miscarriage is random conditional on father’s education (divided into no father figure, less than 12 years, exactly 12 years and more than 12 years). As a final check, we also experiment with limiting our OLS (birth v. miscarriage) results to late miscarriages.
We do not, however, present results in which we control for other known correlates of outcomes such as race and parental education in our OLS and IV estimation. Since these factors also predict abortion, it is easy to develop examples in which including them as controls worsens the bias or changes the sign of the bias.17 This argument does not apply to late miscarriages because we do not have to worry about abortions. Therefore we control for other variables in our estimates using only late miscarriages. Of course if late miscarriage is truly random, adding covariates will only affect the efficiency and not the consistency of the estimates.
4 Results
Table 4 gives the results of the competing risk model of Proposition 1 with nonparametric hazard functions in X, which includes four indicators for all the combinations of smoker/conception before age 15. The results with and without conditioning on X are indistinguishable to two decimal places. The results for X including the four categories of father’s education are trivially different and not shown.
Table 4.
Estimates from Competing Risks Model
| Miscarriage First | Abortion First | |
|---|---|---|
| Proportion Latent Abortion | 0.26 (0.01) | 0.26 (0.01) |
| Proportion Latent Miscarriage | 0.12 (0.01) | 0.12 (0.01) |
| Proportion Latent Birth | 0.74 (0.01) | 0.74 (0.01) |
| Proportion Latent Abort & Misc. who Miscarry | 0.47 (0.03) | 0.38 (0.03) |
| Proportion who Miscarry | 0.10 (0.01) | 0.10 (0.01) |
| Proportion who Abort | 0.25 (0.01) | 0.25 (0.01) |
| Proportion who give Birth | 0.65 (0.01) | 0.65 (0.01) |
Standard errors using exponential (weighted) bootstrap are in parentheses.
Estimates use sampling weights.
The “abortion first” assumption, , leads to the conclusion that 26% of teens are abortion types and 12% are miscarriage types. With the opposite assumption, , , the figures are unchanged. Again, with the latter assumption, 47% of women who are both abortion types and miscarriage types have miscarriages while with the former, the estimate is 38%. These estimates imply that only a little over 3% of our sample were both abortion and miscarriage types and that roughly one-seventh of teens having miscarriages are abortion types although OLS requires that the miscarriage group include only birth types. Similarly, for IV to be consistent, a little over 26% of those having miscarriages should be abortion types, substantially more than the one-seventh figure.
Perhaps most significantly, compared with the abortion-first assumption, the miscarriage-first assumption implies that there are close to 25% more abortions that have to be “purged” from the miscarriage outcomes. Thus it will tend to imply larger adverse effects than the abortion-first assumption does as we show in Theorem 2. Moreover, recall that we believe that about one-quarter of abortions are unreported in our data. If nonreporting is random, then in very rough terms, the estimated effect of “putting the missing abortions back into the data” would be comparable to switching from the abortion-first to the miscarriage-first assumption. As we will see, the differences between the estimates under the two assumptions are not very large, suggesting that missing abortions are not likely to bias the results greatly.
Table 5 presents the principal results of the paper. The first two columns present the estimates based on Theorems 1 and 3 without imposing Assumption 4, that is, in these estimates we allow women who are scheduled to have late abortions to be more or less favourably selected than those with early scheduled abortions. The third and fourth columns are based on Theorems 2 and 3 which impose that the potential outcomes of abortion types are independent of the timing of the abortion (Assumption 4). Within each pair, the first column gives the estimates under the assumption that in any week a scheduled miscarriage occurs before a scheduled abortion; the second column makes the opposite assumption. It will be apparent that the choice of miscarriage or abortion first has little effect on the results, and therefore we generally discuss each pair without distinguishing between the miscarriage and abortion first results.
Table 5.
Effect of Teen Motherhood on Adult Outcomes Controlling for Conception before Age 15 and Smoking before Conception
| Abortion Outcomes Vary | Abortion Outcomes Constant | Biased Estimates | ||||
|---|---|---|---|---|---|---|
|
| ||||||
| Outcome | Miscarriage First | Abortion First | Miscarriage First | Abortion First | IV | Birth v Miscarriage |
| High School Diploma | −0.01 (0.05) | −0.02 (0.05) | −0.01 (0.05) | −0.01 (0.04) | 0.06 (0.05) | −0.05 (0.04) |
| GED | −0.05 (0.04) | −0.04 (0.04) | −0.05 (0.04) | −0.05 (0.04) | −0.08 (0.04) | −0.03 (0.03) |
| Years of Education | −0.13 (0.24) | −0.17 (0.23) | −0.15 (0.24) | −0.19 (0.24) | 0.19 (0.27) | −0.37 (0.19) |
| Married | −0.04 (0.05) | −0.03 (0.05) | −0.03 (0.05) | −0.03 (0.05) | −0.04 (0.05) | −0.03 (0.04) |
| Divorced or Separated | 0.04 (0.04) | 0.04 (0.04) | 0.04 (0.04) | 0.04 (0.04) | 0.04 (0.05) | 0.04 (0.03) |
| Working | −0.05 (0.05) | −0.05 (0.05) | −0.05 (0.05) | −0.05 (0.05) | −0.04 (0.05) | −0.05 (0.04) |
| Hours Worked per Week | −4.02 (2.27) | −4.02 (2.15) | −3.94 (2.12) | −3.92 (2.07) | −4.01 (2.17) | −3.84 (1.57) |
| Annual Earnings if Working | −1104 (1383) | −1208 (1311) | −73.6 (1,612) | −204 (1,566) | 961 (1,697) | −658 (1,112) |
| Spouse Annual Earnings if with Partner | −326 (1706) | −428 (1686) | 2,548 (2,008) | 2,238 (1,944) | 5,045 (2,911) | 889 (1,794) |
| Total Annual Family Income | −242 (2502) | −480 (2375) | 638 (2,446) | 333 (2,381) | 2,782 (2,869) | −1,096 (1,921) |
| Percent Poverty Level Income | −9.40 (19.36) | −12.0 (18.06) | −8.34 (18.5) | −11.0 (18.8) | 11.2 (20.5) | −22.7 (13.4) |
| Number of Live Births | 0.78 (0.13) | 0.79 (0.13) | 0.77 (0.14) | 0.78 (0.13) | 0.69 (0.14) | 0.85 (0.10) |
Exponential (weighted) bootstrapped standard errors are shown in parenthesis in columns 1–4.
Traditional standard errors are displayed in columns 5 and 6.
When we allow the potential outcomes to vary by scheduled abortion week, the estimated causal effects of giving birth are consistently adverse but generally negligible although in some cases the confidence intervals include modest impacts. There is no difference in the probability of having a high school diploma and only about one-sixth year difference in average education although there is a four or five percentage point difference in the probability of having a GED. We can rule out mean education effects of more than seven-tenths of a year. Similarly, the estimated effects on marriage are modest, a three to four percentage point reduction in the probability of being married with a corresponding increase in the probability of being divorced or separated.
The teen mothers are less likely to be working, by about five percentage points. On average, they work about four fewer hours per week, compared with a mean of twenty-four. They also earn about $1,200 less if working or about 6% less than the overall mean. The point estimate of the effect of a teen birth on spouse’s earnings, conditional on having a partner is trivial although the standard error is large. The point estimate of the effect on family income is similarly small, and we can rule out effects that exceed about 15% of mean income for this group. Similarly, the estimate of the effect on income relative to the poverty line suggests that teen mothers lose less than 5% of family-size adjusted income although the 95% confidence interval goes up to about 19%.
Finally, the estimates do suggest that having a teen birth significantly increases parity. However, this result should be treated with caution. One strong result in the literature (e.g. Lang and Nuevo, 2012) is that past miscarriage predicts future miscarriage. Thus the exogeneity of miscarriage with respect to total parity is suspect.
We turning now to columns 3 and 4 of table 5. Recall that table 2 reveals that outcomes for early and late abortions are similar but possibly somewhat more adverse for the latter. Consistent with both interpretations of table 2, the results are similar regardless of whether we impose Assumption 4, but imposing this assumption has a very slight tendency to diminish the estimated adverse effects of teen births. The most notable differences concern the income variables. The point estimate of the effect on income conditional on working becomes trivial, and the effects on spousal earnings and total family income turn positive, but nothing substantive changes. The confidence interval still includes modest but nontrivial effects.
The last two columns of table 5 present the IV and OLS results when we control for smoking before pregnancy and conception before age 15. These estimates are not precisely the parameters from which we derive the estimates in columns 3 and 4. The latter estimates are derived from four separate IV and four separate OLS estimates. Nevertheless, they are similar. Comparing the estimates in columns 3 and 4 with those in 5 and 6 underscores our result in Theorem 2 about OLS being biassed towards adverse and IV towards benign views under Assumption 5.
Table 6 replicates the first four columns of table 5 but instead controls for father’s education. The results in the first columns of tables 5 and 6 do not differ noticeably. The point estimate of the effect of a birth on obtaining a high school diploma is now insignificantly positive instead of insignificantly negative but the effect on years of education is slightly more negative but still statistically insignificant. These differences are similarly unremarkable. The differences in column (2)–(4) are similarly small although there is a clearer pattern of less adverse outcomes when we control for father’s education than when we control for smoking and age at conception. The fact that the differences between the first and third columns in table 6 are more pronounced than in the prior set of estimates suggests that we cannot completely ignore differences in outcomes for early and late abortion types, that is the evidence supporting Assumption 4 is stronger for smoking before pregnancy and conception before age 15 than for father’s education.
Table 6.
Effect of Teen Motherhood on Adult Outcomes Controlling for Father’s Education (No Father Figure, <12 Years, 12 Years, >12 Years)
| First Pregnancies Only | ||||
|---|---|---|---|---|
| Abortion Outcomes Vary | Abortion Outcomes Constant | |||
|
| ||||
| Outcome | Miscarriage First | Abortion First | Miscarriage First | Abortion First |
| High School Diploma | 0.02 (0.05) | 0.03 (0.05) | 0.04 (0.05) | 0.03 (0.05) |
| GED | −0.06 (0.04) | −0.05 (0.04) | −0.06 (0.04) | −0.06 (0.04) |
| Years of Education | −0.26 (0.25) | 0.10 (0.25) | 0.11 (0.25) | 0.06 (0.23) |
| Married | −0.04 (0.05) | −0.03 (0.05) | −0.02 (0.05) | −0.02 (0.05) |
| Divorced or Separated | 0.01 (0.04) | 0.02 (0.04) | 0.02 (0.05) | 0.02 (0.04) |
| Working | −0.05 (0.05) | −0.03 (0.05) | −0.03 (0.05) | −0.03 (0.04) |
| Hours Worked per Week | −4.41 (2.17) | −3.56 (2.12) | −3.41 (2.19) | −3.41 (2.08) |
| Annual Earnings if Working | −1000 (1252) | −626 (1246) | 369 (1,646) | 263 (1,684) |
| Spouse Annual Earnings if with Partner | −460 (1734) | 84 (1714) | 3,377 (2,219) | 3,020 (1,896) |
| Total Annual Family Income | −39 (2483) | 905 (2345) | 2164 (2,610) | 1787 (2,348) |
| Percent Poverty Level Income | −8.76 (18.46) | −0.84 (17.26) | 3.57 (19.28) | 0.52 (17.13) |
| Number of Live Births | 0.65 (0.13) | 0.71 (0.12) | 0.70 (0.14) | 0.71 (0.13) |
Exponential (weighted) bootstrapped standard errors are shown in parenthesis.
4.1 Late Miscarriages
In Theorem 2 we find that if all abortions preceded all miscarriages, then OLS on the sample of teens who either miscarried or gave birth would estimate the effect of teen motherhood. We can approximate this by limiting our sample to pregnancies that lasted sufficiently long that there are (almost) no subsequent abortions that preempt scheduled miscarriages. Note that excluding the abortions is not problematic because the goal of the econometrics is to purge the estimates of the confounding effects of abortion-types. Excluding early miscarriages is not problematic because the timing of miscarriage is random under Assumption 2.
There are very few abortions after four months. In table 3 we saw that miscarriages occurring this late were largely random. There is weak evidence that smokers, women who use IUDs and very young girls are more likely to have late miscarriages but the evidence of a relation to family background is very weak. Moreover, because we no longer have to worry about miscarriages preempting abortions, we can control for family background. Therefore, in principle, we can get (nearly) unbiassed estimates of the effect of birth by using women with late miscarriages as the comparison group for those who gave birth as teens.
Table 7 shows the results of restricting the sample to those whose first pregnancy lasted more than seventeen weeks and who did not have an abortion using data from four waves of the NSFG. The first column controls only for survey year. The second column adds a full set of controls. Consistent with the argument that late miscarriage is random, the point estimates in the two columns are virtually identical although adding controls improves the efficiency of the estimators. All of the estimates are relatively imprecise, but in most cases we can rule out large adverse effects. For example, the lower end of the 95% confidence interval is that teen motherhood reduces average educational attainment by less than one-quarter year and reduces family income by no more than about 11% or one-sixth of the poverty threshold.
Table 7.
Effect of a Teen Birth on Selected Outcomes: First Pregnancy Lasted More than 17 Weeks: OLS Estimates
| Outcomes | Controls only for Survey Year | All Controls |
|---|---|---|
| Years Education | 0.12 (0.19) | 0.14 (0.18) |
| Married | 0.01 (0.05) | −0.02 (0.04) |
| Divorced or Separated | 0.03 (0.04) | 0.03 (0.04) |
| Working | 0.05 (0.04) | 0.04 (0.04) |
| Log Total Annual Family Income | 0.10 (0.09) | 0.05 (0.08) |
| Percent Poverty Level Income | 15.6 (13.7) | 8.08 (12.7) |
| Number of Live Births | 0.55 (0.13) | 0.55 (0.12) |
Teen pregnancies from the 1982, 1988, 1995 and 2002 cycles of the National Survey of Family Growth. N=4,598.
Weights reflect within year sampling weights but are adjusted so that weighted sample size from each year equals actual sample size from that cycle.
Controls: Survey year, age, age at conception, Hispanic, black, white, catholic, protestant, mother’s education (three dichotomous variables), mother worker full-time and age at conception before 15.
Abortions after seventeen weeks have been dropped from the sample.
Perhaps most significantly where the results in table 5 tend to show adverse effects, those in table 7 tend to show positive effects. We noted that in many cases the confidence intervals in table 5 included modest but nonneglible adverse effects. The more favourable results in table 7 make it less plausible that the true effects are towards the lower bounds of the confidence intervals in table 5.
Beyond this, what should we make of the differences between the results in the two tables? On the one hand, there may be nothing to explain. With the possible exception of the estimated effect of a birth on total parity, it is unlikely that any of the differences is statistically significant.18 On the other hand, the direction of the differences between both table 5 and table 7 and the second column of tables 5 and 6 is consistent with the view that early miscarriages are favourably selected and that our principal estimates are therefore biassed towards an adverse view of teen motherhood.
4.2 Changing Effects with Age
One of the messages of the HMS paper is that teen births are largely a matter of timing. Teens who give birth have only slightly more live births over their lifetimes. They suffer the disadvantages of having children when they are young but fare better than their counterparts when they are older because they no longer have children. Depending on the model of wage determination and the relation between the discount rate and the rate of growth of wages, either delaying childbirth or advancing it could be the optimal strategy for maximizing lifetime income (see Buckles, 2005). Of course, there are other reasons for choosing the timing of births, but if giving birth as a teen only changes the timing of births, one could reasonably argue that for the women who gave birth as teens, early child-bearing is an optimal strategy.
To address this issue, we interact the effect of a teen birth with the current age of the mother. In general the interaction effects did not approach statistical significance and are therefore not shown. Either such age effects do not exist in our data, they are too small to be estimated with any precision or cohort effects counteract age effects.
There are two somewhat noteworthy exceptions. The first is total number of live births. When we use the estimates from “miscarriage-first,” the interaction falls just short of statistical significance at the 0.1 levels (and achieves significance at this level if we drop the small sample of teens who both smoked and conceived before age 15). The point estimate implies that women who miscarry on their first teen pregnancy subsequently have about 0.03 more children per year. The estimate using “abortion-first” is similar but does not approach significant at conventional levels. In both cases, the estimates imply that at age 20, a teen who gave birth rather than miscarried has just about one more child. However, by age 45 this difference has fallen to about 0.3. Much of the effect of a teen birth is on timing rather than on completed fertility.
The second exception is total family income relative to the poverty. In this case, the interaction is significant at the 0.1 level when we use the “abortion-first” estimates but not the “miscarriage-first” estimates. In both cases, the point estimate is that the adverse effect on income relative to the poverty line falls by about 3.5 percentage points per year as the women age so that by their late thirties women who gave birth have caught up with those who miscarried. This is consistent with the difference in family size falling with age and therefore, the women who gave birth having smaller households by their late thirties.
With this one important exception, our results point towards modest but age invariant adverse impacts of giving birth as a teen. The fact that we are able to detect an effect that diminishes with age when we would most expect it, total number of live births, reinforces our confidence that we are not missing important age interactions.
4.3 Multiple Teen Pregnancies
One reason that the effect of giving birth might be small is that many teens who have an initial pregnancy also have a second, and birth types might therefore be likely to give birth as a teen even if their first pregnancy ends in miscarriage. In fact, almost 30% of teens who miscarry on first pregnancy give birth as teens. Surprisingly, about an eighth of teens who terminate their first pregnancy also give birth as teens. Using the data in table 4, allows us to back out that 31% of birth types who miscarry give birth as teens.19 If we view the treatment as “any teen birth” rather than initial pregnancy ended in birth, this suggests that we should multiply the estimates in table 5 by a factor of about 1.45.20
4.4 Adoptions
One explanation for the small impact of teen births on mothers might be that many teen mothers give their babies up for adoption. In fact, relatively few teen mothers do so (although the children may be brought up by grandparents). In preliminary work, we experimented with making the explanatory variable “giving birth and keeping the child.” The results were unaffected.
4.5 Timing of Births
It has been suggested to us that women who gave birth may be more likely to have a second pregnancy because it is optimal to space births relatively close together. Of course, the physical limitations on second pregnancy and the contraceptive effect of breast-feeding work in the opposite direction. We examined the relation between the pregnancy outcome and the probability of a second conception before age twenty. Women who miscarried were most likely (68%) and those who had an abortion were least likely (51%) to have a second pregnancy before age twenty. Those who gave birth were significantly less likely (55%) than those who miscarried to have a second pregnancy by age twenty. The difference between those aborting and those giving birth is not statistically significant at conventional levels.
5 Conclusions
Teens who choose to abort are favourably selected from the set of teens who become pregnant. At the same time, teens who would choose to abort are less likely than other teens to miscarry. Therefore, instrumental variables estimation using miscarriage as an instrument for the absence of a birth is biassed towards a benign view of the ATE of teen motherhood on the adult outcomes for those who give birth. We show first that OLS on only those teens who give birth or miscarry is biassed in the opposite direction. Under plausible assumptions, if the outcomes of abortion types are independent of the planned timing of the abortion, a weighted average of the OLS and IV estimators is consistent for the ATE. We also derive a consistent estimator when the outcomes for abortion types differ by planned timing.
Our results reinforce recent research that finds at most modest adverse causal effects of teen births on the mothers’ adult outcomes. Moreover, they support the conclusion that the even more benign view rests on the use of a positively biassed estimator.
Our conclusions rest on a set of key assumptions. The first is that, in the absence of abortion, women who miscarry and women who do not miscarry would have similar outcomes in the absence of a birth. In other words, in the absence of abortion, miscarriage would be random, at least conditional on a small number of measured factors. We provide direct evidence to support this assumption and indirect evidence in the form of similar outcomes for teens having early and late abortions. To the extent that the assumption is violated, it appears that more advantaged women are more likely to recognize early miscarriages so that our results would be biassed towards finding a larger adverse effect of teen motherhood.
Our second key assumption, that we observe all abortions, is obviously false. Unreported abortions will tend to reduce the upward bias of the IV estimator. Since one of our estimators is a weighted average of the IV and restricted-OLS estimators, we expect that nonreporting biases us towards finding more adverse effects of births.
Given this evidence, we conclude that the adverse effects of birth on the mothers who would choose to give birth are modest. This, of course, does not preclude the existence of potentially large adverse effects on their children and/or on those who choose abortion or who avoid pregnancy altogether.
Supplementary Material
Acknowledgments
We are grateful to Carlos Sepulveda-Rico and Greg Hutko for excellent research assistance and to Joshua Angrist, Mingli Chen, Donna Ginther, Jonathan Guryan, John Johnson IV, Karen Norberg, Robert Pollak, Steve Pischke and two anonymous referees, and participants in informal labor lunches at Boston University and MIT and workshops and seminars at George Washington University, Harvard, the NBER and Washington University for helpful comments and suggestions. This research was supported in part by NSF grant SEC-0339149 and NIH grant R03 HD056056-1. The opinions expressed are those of the authors and not necessarily those of the Federal Reserve Bank of New York or of the funding agencies.
Footnotes
The analysis can be extended to the case where the indicator is random, provided that it is independent of potential outcomes and scheduled weeks.
We ignore for the moment the problem of multiple pregnancies.
Under our assumptions, the ASF at 0 for women of the abortion type is identified by the average outcome of the women with realized abortions. If in addition the potential outcome takes values in a bounded interval, the identified ASF at 0 can be combined with bounds on the ASF at 1 to partially identify the ATE for women of abortion type (e.g., Manski, 2007).
For fertility outcomes such as the number of live births, positive selection refers to having fewer children and the assumption applies to minus the outcome.
The imputation relies on reports on family income in 1993 and uses a regression procedure to update. For details see Potter et al (1998).
There are eighteen intervals which we impute as follows: less than $7,000 ($3500), $7,000–$8,499 ($7,750), $8,500–$9,999 ($9,250), $10,000–$11,999 ($10,999), $12,000–$13,999 ($12,999), $14,000–$15,999 ($14,999), $16,000–$17,999 ($16,999), $18,000–$19,999 ($18,999), $20,000–$24,999 ($22,499), $25,000–$29,999 ($27,499), $30,000–$39,999 ($34,499), $40,000–$49,999 ($44,499), $50,000–$59,999 ($54,499), $60,000–$69,999 ($64,499), $70,000–$79,999 ($74,499), $80,000–$89,999 ($84,499), $90,000–$99,999 ($94,499), $100,000 and up ($124,499).
We weight the data by the sampling weights for each year normalized so that the weighted sample size in each year equals the actual sample size in that year.
Some papers (e.g. Fletcher and Wolfe, 2009) have timed pregnancy by the end date (e.g. eighteen years, nine months). This is slightly problematic in that it means that some women who miscarried or had abortions but essentially none of the women who gave birth were over eighteen at the time of conception. We doubt that this is an important issue.
In very rough numbers, the number of live births to 15 to 17 year old girls each year during this period was roughly 33 per thousand (Guttmacher Institute, 2010, table 2.2) so that the cumulative number of live births by age eighteen is roughly 100. Similarly teen girls and 18 and 19 had roughly 82 annual live births per thousand (table 2.3). Since live births increase with age, total live births by age 18 years, nine months should be in the range 125 to 160 per thousand including second and third births, making 12% a plausible estimate of the proportion having at least one birth by this age.
The no mother and no father variables are drawn from responses to parental education questions that are coded no mother (father) figure.
Our summary of the literature relies primarily on Regan and Rai (2000) and Garcia-Enguidanos et al. (2002) but also on Porter and Hook, 1980 and Kline et al. (1989) and conversations with physicians. The consensus is that about 75% of conceptions do not result in a live birth and that the vast majority of these conceptions are never recognized. About 12–15% of miscarriages are clinically recognized. The risk factors for miscarriage are not well-established, in part because there are few prospective studies, and because some of the recognized risk factors are highly collinear. For example, almost all cocaine users smoke, recognized as a risk factor, but studies of the effect of cocaine have generally not controlled for smoking. Similarly, among adult women age does appear to be a risk factor but its importance may be exaggerated by women who have had miscarriages being more likely to continue to conceive later in life. The summary in this section is, of necessity, subject to these limitations.
The approach here parallels the semi-parametric Cox proportional hazard model (1972) but most parametric models also imply a proportional hazard.
In a much larger sample of women who conceived between ages 13 and 25, Lang and Nuevo (2012) use a competing risks model of miscarriage and abortion. The only sociodemographic factors that predict miscarriage risk are education and age at conception. Since education is an outcome variable in this study, it is not appropriate as a control but the positive finding suggests that, if anything, reported miscarriages are favorably selected, consistent with the conclusion we reach here.
Pregnancies that last more than twenty-two weeks are not considered miscarriages (spontaneous abortions in medical terminology). We use the term miscarriage for simplicity.
We also tried restricting the full 1995 pregnancy sample to those who were pregnant for more than twenty-four weeks. There are only four abortions recorded after the twenty-fourth week of pregnancy in our data. Such abortions are sufficiently rare that we expect that they are either errors or cases where the mother’s life was in danger or the fetus was not viable. These four cases are excluded from the sample in column three. Strikingly the equation has no explanatory power for miscarriages in the last trimester of pregnancy. None of the personal characteristics is individually statistically significant and the estimated magnitudes are generally small. The likelihood ratio χ2 for the equation is 14.5, well short of statistical significance.
Not all waves had information on father’s education, and the 1982 and 1988 waves do not have a code for “no mother figure.” We drop observations who reported no mother figure in the later waves.
The simplest case is when there are two groups of abortion types, some with potential outcomes that are better than those of the birth types in the absence of a birth and some whose outcomes are worse. In this case, if we can only predict one abortion type, the IV estimator will be either more biased or biased in the opposite direction depending on which type of abortion we can predict.
Since the samples have some small overlap, the two sets of estimates are likely to be somewhat positively correlated. However, unless this correlation is quite large, none of the differences would be significant.
For details see the on-line appendix.
This is 1/(1 − .31) and should be regarded as an approximation. As shown in the on-line appendix, to adjust the estimate correctly would require calculating a separate scale factor for each of our four groups, multiplying the effect on that group by the group-specific scale factor and then adding the coefficients. Our sample of miscarriages is too small for us to carry out this exercise with confidence. The scale factor of 1.45 will be correct if, among birth types, the probability of birth following miscarriage is independent of X.
References
- Angrist JD, Evans WN. Children and their parents’ labor supply: evidence from exogenous variation in family size. American Economic Review. 1998;88(3):450–77. [Google Scholar]
- Ashcraft A, Lang K. National Bureau of Economic Research Working Paper No 12485. 2006. The Consequences of teenage childbearing. [Google Scholar]
- Barbe P, Bertail P. The Weighted Bootstrap. New York: Springer; 1995. [Google Scholar]
- Bronars SG, Grogger J. The economic consequences of unwed motherhood: using twin births as a natural experiment. American Economic Review. 1994;84(5):1141–56. [Google Scholar]
- Buckles K. working paper. University of Notre Dame; 2005. Stopping the biological clock: fertility therapies and the career/family tradeoff. [Google Scholar]
- Chevalier A, Viitanen TK. The long-run labour market consequences of teenage motherhood in Britain. Journal of Population Economics. 2003;16(2):323–343. [Google Scholar]
- Cox David R. Regression models and life tables (with discussion) Journal of the Royal Statistical Society, Series B. 1972;34(2):187–220. [Google Scholar]
- Ermisch J, Pevalin DJ. Institute for Social and Economic Research Working Paper 2003–28. 2003. Does a ‘teen-birth’ have longer-term impacts on the mother? evidence from the 1970 British Cohort Study. [Google Scholar]
- Fletcher JB, Wolfe BL. Education and labor market consequences of teenage childbearing: evidence using the timing of outcomes and community fixed effects. Journal of Human Resources. 2009;44(2):303–25. [Google Scholar]
- Garcia-Enguidanos A, Calle ME, Valero J, Luna S, Dominguez-Rojas V. Risk factors in miscarriage: a review. European Journal of Obstetrics and Gynecology and Reproductive Biology. 2002;102(2):111–119. doi: 10.1016/s0301-2115(01)00613-3. [DOI] [PubMed] [Google Scholar]
- Geronimus A, Korenman S. The socioeconomic consequences of teen child-bearing reconsidered. Quarterly Journal of Economics. 1992;107(4):1187–214. [Google Scholar]
- Goodman A, Kaplan G, Walker I. IZA Discussion Paper No 1131. 2004. Understanding the effects of early motherhood in Britain: the effects on mothers. [Google Scholar]
- Guttmacher Institute. [last accessed January 27, 2012];US teenage pregnancies, birth and abortions: national and state trends and trends by race and ethnicity. 2010 http://www.guttmacher.org/pubs/USTPtrends.pdf.
- Henshaw SK. Teenage abortion and pregnancy statistics by state, 1992. Family Planning Perspectives. 1997;29(3):115–22. [PubMed] [Google Scholar]
- Hoffman SD. University of Delaware Economics Department Working Paper No 2003-08. 2003. The socio-economic effects of teen childbearing re-considered: a reanalysis of the teen miscarriage experiment. [Google Scholar]
- Hoffman SD, Foster EM, Furstenberg FF., Jr Reevaluating the costs of teenage childbearing. Demography. 1993;30(1):1–13. [PubMed] [Google Scholar]
- Holmlund H. Estimating long-term consequences of teenage childbearing. Journal of Human Resources. 2005;40(3):716–43. [Google Scholar]
- Hotz VJ, McElroy SW, Sanders SG. The impacts of teenage childbearing on the mothers and the consequences of those impacts for government. In: Maynard R, editor. Kids Having Kids: Economic Costs and Social Consequences of Teen Pregnancy. Washington, DC: Urban Institute; 1998. pp. 55–94. [Google Scholar]
- Hotz VJ, McElroy SW, Sanders SG. Teenage childbearing and its life cycle consequences. Journal of Human Resources. 2005 Summer;40:683–715. [Google Scholar]
- Hotz VJ, Mullin CH, Sanders SG. Bounding causal effects using data from a contaminated natural experiment: analyzing the effects of teenage childbearing. Review of Economic Studies. 1997;64(4):575–603. [Google Scholar]
- Kalbfleisch JD, Prentice RL. The Statistical Analysis of Failure Time Data. 2. Hoboken, New Jersey: John Wiley; 2002. [Google Scholar]
- Klepinger D, Lundberg S, Plotnick R. How Does Adolescent Fertility Affect the Human Capital and Wages of Young Women? Journal of Human Resources. 1999;34(3):421–448. [Google Scholar]
- Kline J, Stein Z, Susser M. Conception to Birth: Epidemiology of Prenatal Development. New York: Oxford University Press; 1989. [Google Scholar]
- Kost K, Henshaw S, Carlin L. US Teenage Pregnancies, Births and Abortions: National and State Trends and Trends by Race and Ethnicity. New York: Guttmacher Institute; 2010. [Google Scholar]
- Lang K, Nuevo Chiquero A. Trends in self-reported spontaneous abortions: 1970–2000. Demography. 2012;49(3):989–1009. doi: 10.1007/s13524-012-0113-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levitt S, Donohue JJ., III The impact of legalized abortion on crime. Quarterly Journal of Economics. 2001;116(2):379–420. [Google Scholar]
- Levine DI, Painter G. The schooling costs of teenage out-of-wedlock childbearing: analysis with a within-school propensity-score-matching estimator. Review of Economics and Statistics. 2003;85(4):884–900. [Google Scholar]
- Mammen E. When Does Bootstrap Work? Asymptotic Results and Simulations. New York: Springer; 1992. [Google Scholar]
- Manski CF, Pepper JV. Monotone instrumental variables, pp.with an application to returns to schooling. Econometrica. 2000;68(4):997–1010. [Google Scholar]
- Manski CF. Identification for Prediction and Decision. Princeton: Princeton University Press; 2007. [Google Scholar]
- Pandya PP, Snijders JM, Psara N, Hilbert L. The prevalence of non-viable pregnancy at 10–13 weeks of gestation. Ultrasound in Obstetrics and Gynecology. 1996;7(1):1–4. doi: 10.1046/j.1469-0705.1996.07030170.x. [DOI] [PubMed] [Google Scholar]
- Porter IH, Hook EB, editors. Human Embryonic and Fetal Death. New York: Academic Press; 1980. [Google Scholar]
- Regan L. Epidemiology and the medical causes of miscarriage. Balliere’s Best Practice and Research: Clinical Obstetrics and Gynaecology. 2000;14(5):839–54. doi: 10.1053/beog.2000.0123. [DOI] [PubMed] [Google Scholar]
- Ribar DC. Teenage fertility and high school completion. Review of Economics and Statistics. 1994;76(3):413–24. [Google Scholar]
- Sanders S, Smith J, Zhang Y. working paper. University of Maryland; 2007. Teenage childbearing and maternal schooling outcomes: evidence from matching. [Google Scholar]
- Walker I, Zhu Y. University of Kent School of Economics Discussion Paper 0917. 2009. The causal effect of teen motherhood on worklessness. [Google Scholar]
- Wilcox AJ, Baird DD, Weinberg CR. Time of implantation of conceptus and loss of pregnancy. New England Journal of Medicine. 1999;340(23):1796–99. doi: 10.1056/NEJM199906103402304. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


