Wires in the soup: quantitative models of cell signaling

Abstract

Living cells are capable of extracting information from their environments and mounting appropriate responses to a variety of associated challenges. The underlying signal transduction networks enabling this can be quite complex, necessitating for their unraveling by sophisticated computational modeling coupled with precise experimentation. Although we are still at the beginning of this process, some recent examples of integrative analysis of cell signaling are very encouraging. This review highlights the case of the NF-κB pathway in order to illustrate how a quantitative model of a signaling pathway can be gradually constructed through continuous experimental validation, and what lessons one might learn from such exercises.

Introduction

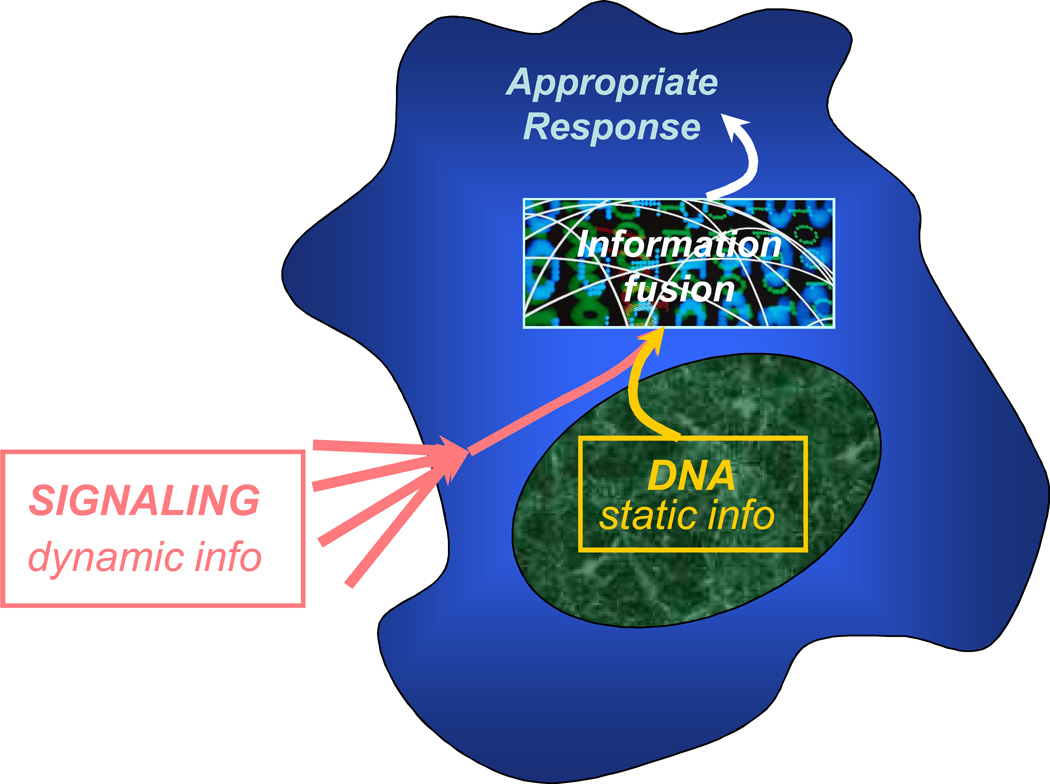
A critical ability of and the grand challenge for a living cell is information fusion. Cells are faced with a continuous stream of information reflecting changes in their micro-environment, information that demands adequate processing resulting in appropriate decision making. To engender a correct decision, this dynamic and multi-faceted type of information needs to be channeled to and merged with another, much more static, sort of information, the information encoded in the cell genome (Fig. 1). Successful coupling of these information sources is at the core of the very survival of the cell and often of the organism of which the cell is but a small part. One of the formidable problems of modern biology is to develop an understanding of how the dynamic and static information types are integrated in a manner appropriate for cell function and what can go wrong in this process.

Figure 1.

Information fusion in signal transduction. The life cycle of all cells appears to involve the process of continuous assessment of the immediate micro-environment outside (and inside) the cell and merger of this dynamic and fluid information with more static information contained in the cell genome. The appropriateness of the decision making arising from this information fusion might determine the cell’s very survival.

Fortunately, now might be the perfect time to start approaching the solution of this problem. The ways that biological research is done are rapidly changing. Not only are we in possession of the blueprints of one type of information – the encoded information in the form of various sequenced genomes – we are also beginning to understand how this encoded information helps cells decode the dynamic and fluid information that the cell perceives in the extracellular world. In this review, we will briefly illustrate the evolution of our understanding of biological information processing, using an example of a broadly studied signaling ‘module’: the NF-κB response to cytokine stimulation in a variety of mammalian cell types. In particular, we will recount the story of a gradual integrative development of the quantitative understanding of this pathway as well as suggesting some general principles of signal transduction arising from quantitative model analysis.

The NF-κB pathway

Nuclear factor-kappaB (NF-κB) is a conserved transcription factor that has been a paradigm for gene regulation for more than 20 years [1]. It is the central mediator of inflammation and also has roles in apoptosis, adaptive immunity, immune system development, and neurological memory [2]. NF-κB is implicated in a myriad of common diseases especially those with inflammatory or autoimmune components like septic shock, cancer, arthritis, asthma, diabetes, and atherosclerosis to name a few [3]. With such broad implications for basic biology and the clinic, it is easy to see that understanding NF-κB is of intense interest.

NF-κB is a dimer of two of five possible subunits, but is most commonly found as a p50-p65 heterodimer. It is held latent in the cytoplasm by binding to its inhibitor, IκB, of which there are three major isoforms: IκBα, IκBβ, and IκBε [4]. Almost all cues known to activate NF-κB do so through the IκB kinase (IKK) complex [5]. For example, the inflammatory cytokine tumor necrosis factor alpha (TNFα), which is a principle activator of NF-κB, binds to its receptor TNFRI which initiates assembly of the IKK complex at the receptor [6]. Active IKK then phosphorylates IκB, marking it for subsequent ubiquitination and proteasomal degradation [7]. This releases free NF-κB which translocates into the nucleus where it activates its target genes. Among these target genes is the gene coding for IκBα. Newly synthesized IκBα enters the nucleus and binds to NF-κB, which promotes its dissociation from DNA and subsequent export to the cytoplasm. In this way, NF-κB pathway activity can be brought back to the baseline.

A puzzling question suggested by this basic outline of the TNFα-NF-κB signaling pathway is how specificity is maintained. NF-κB can be activated by many ligands, has hundreds of target genes [8] and its consensus binding sequence is notoriously permissive [9]. Cellular and organismal disaster would ensue if all of these genes were activated simultaneously. Various controls over specificity have been demonstrated, such as differential gene regulation due to different cytokine stimuli [10, 11], dimer compositions [12], NF-κB binding sequences [13], cofactors [9], and NF-κB post-translational modifications [14]. However, another form of specificity—through signaling temporal dynamics—has been largely ignored. Stimulus-induced NF-κB activity is not constant, rather it rises and falls in time in a highly regulated fashion and the peculiarities of these dynamics depend on the stimulus. This suggests that signaling dynamics plays an important role in determining the cellular response. Investigating this form of control is especially suited to combined quantitative experimental and computational techniques, which has only recently been undertaken despite relatively detailed knowledge of the pathway’s biochemistry.

Initial integrated modeling and experiments of NF-κB pathway dynamics

Dynamics in unstimulated cells

An early indication of the importance of pathway dynamics in the control of NF-κB came from the studies of constitutive nucleocytoplasmic shuttling. In the classical view of NF-κB signaling, translocation of NF-κB to the nucleus and subsequent changes in gene expression occur in response to a specific stimulus. So, it came as some surprise when multiple groups reported that leptomycin B, which is not a specific activator of NF-κB but rather is an inhibitor of IκB-mediated export of NF-κB out of the nucleus, also showed nuclear-localized NF-κB in otherwise unstimulated cells. This result implied that NF-κB enters the nucleus in the absence of a specific stimulus and is simultaneously subject to IκB-mediated export to the cytoplasm. This idea stirred a small controversy [15] because this was at odds to the established model in which IκB tethers NF-κB to the cytoplasm.

The paradox between shuttling and tethering was eventually resolved by a quantitative study of shuttling dynamics [16]. Nonstimulated cells expressing fluorescent protein-labeled NF-κB or IκBα were used to measure concentrations of these proteins in the nucleus and cytoplasm and their rates of nuclear import and export. When treated with leptomycin B, those cells with lower levels of cytoplasmic IκB had higher levels of NF-κB import. This result is inconsistent with shuttling of the whole IκB-NF-κB complex for then lower IκB levels would lower and limit the rate of NF-κB import. On the other hand, if the complex must dissociate prior to import of NF-κB, then from consideration of chemical equilibria, lower IκB levels would promote the dissociation of complex leading to greater NF-κB import. A consequence of this mechanism is that free NF-κB might accumulate in the nucleus when not stimulated, leading to aberrant gene expression. However, a high rate of IκB-mediated export can keep resting levels of nuclear NF-κB, as demonstrated through a model in which the combined events of dissociation, import, and export are represented with straightforward mass-action rate laws. Furthermore, the model drew attention to the fact that even though IκB binds to NF-κB tightly (i.e. low dissociation constant), dissociation does occur at some finite rate. Thus, the high rate of IκB-mediated export compensates for IκB’s inevitable imperfection as a cytoplasmic tether. This concept, borne out of the initial experimental-modeling study, not only resolved the paradox between shuttling and tethering, but also suggested that shuttling is a general mechanism to deal with inhibitor dissociation. Indeed, shuttling can be found in the structurally similar Nrf2 signaling pathway [17].

Dynamics in TNFα-stimulated cells

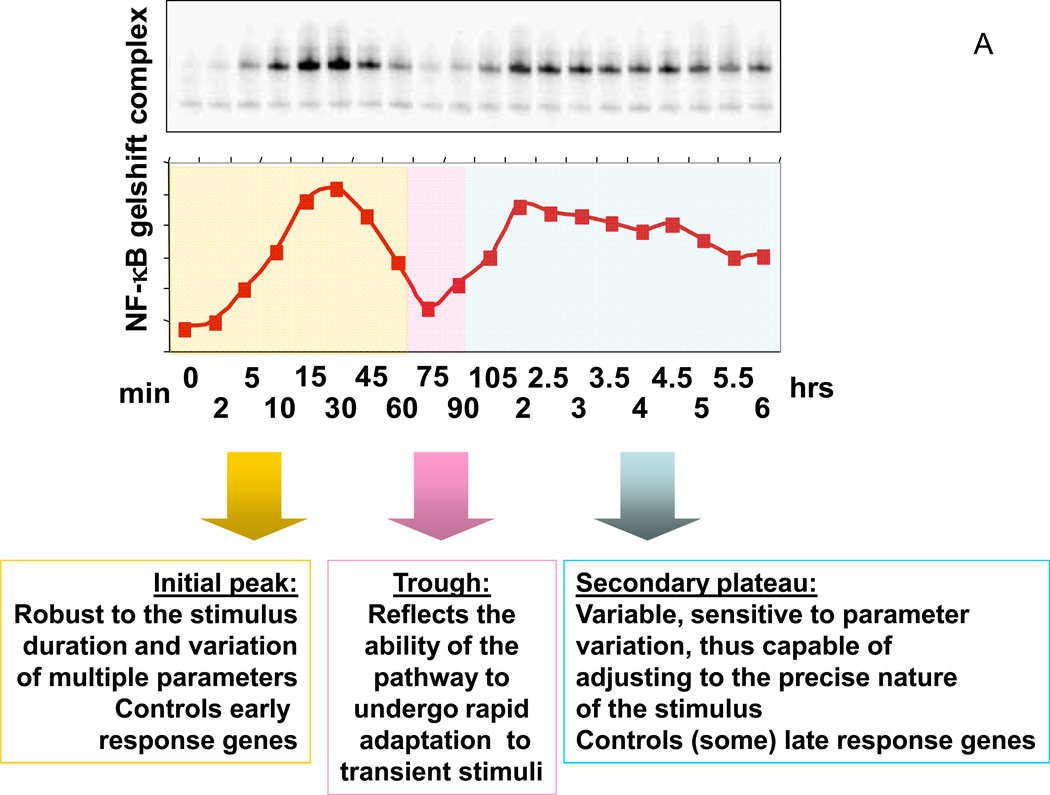
A major development in understanding how temporal dynamics control NF-κB specificity came in 2002 in the first extensive experimental-computational analysis of oscillations in NF-κB activity [18]. Most cell types display biphasic NF-κB activity (as measured by electrophoretic mobility shift assay) in response to persistent TNFα stimulus: activity peaks around 30 minutes, declines to near basal levels at around 60 minutes, and returns to steady, intermediate level from 90 minutes onward (Fig. 2A) [18–20]. However, when two of the three IκB isoforms are knocked out in mouse embryonic fibroblasts the response is quite different. When IκBα is the only inhibitor present, NF-κB activity is strongly oscillatory with a period of about 1 hr, but when IκBβ or IκBε is the only inhibitor then NF-κB remains persistently activated [18]. Since IκBα is the isoform whose gene is most strongly NF-κB-responsive, these observations can be reconciled by the idea that the negative feedback provided by IκBα has a strong propensity to oscillate but the oscillations are heavily damped into a biphasic response by the other isoforms.

Figure 2.

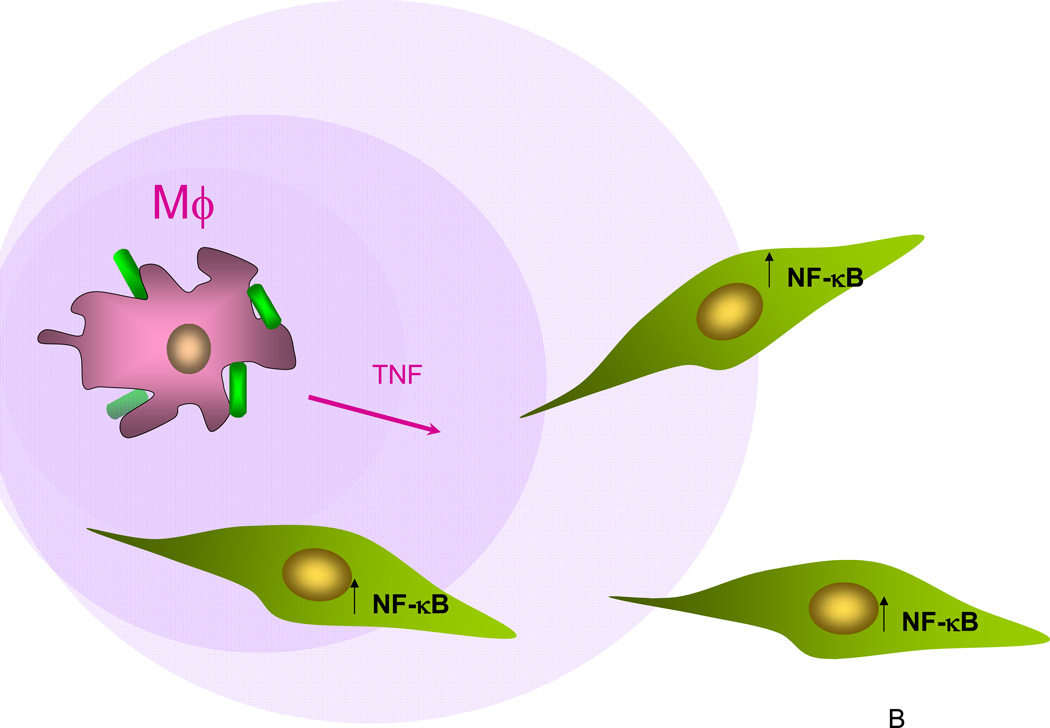
Role of dynamics in NF-κB signaling. (A) In the NF-κB pathway triggered by a cytokine, such as TNF, the constant signal outside the cell is transduced into a complex signal arriving at the cell’s nucleus, with the peak, trough and the secondary plateau dictating to diverse genes an appropriate program of their expression; (B) The computational models not only reveal the underpinnings of the particular signal shape in (A), but also predict that the particular robustness of the first peak of the response might be related to how TNF signal secreted by macrophages exposed to infection (depicted as bacteria bound to the macrophage surface as blue and green cylinders) can be robustly sensed by cells at or below a threshold TNF concentration (purple gradient). All signal receiving cells, e.g., endothelial or smooth muscle cells, generate a full fledged response peak with the amplitude proportional to the distance to the signal source (the macrophage).

Our detailed model of the pathway incorporating these and other known biochemical interactions between IKK, NF-κB, and the three IκB isoforms was able to quantitatively reproduce all of this data, thus demonstrating that the idea of damped oscillations was sufficient to explain the observed dynamics (Text Box). Furthermore, the model predicted that transient TNFα stimulation—even very short stimuli— should result in a full response of the first phase of NF-κB activity, and it was verified experimentally [18]. Such a prediction cannot be made by simple qualitative knowledge of biochemical interactions in the pathway and serves as an excellent example of how quantitative modeling can lead to unexpected insight. Finally, returning to experiments, the biphasic temporal dynamics was definitively shown to be a form of regulation in the NF-κB pathway because some NF-κB-responsive genes were specifically activated in the first phase of activity, but other genes were not activated until the second phase [18].

TEXT BOX.

Mathematical modeling of signaling pathways

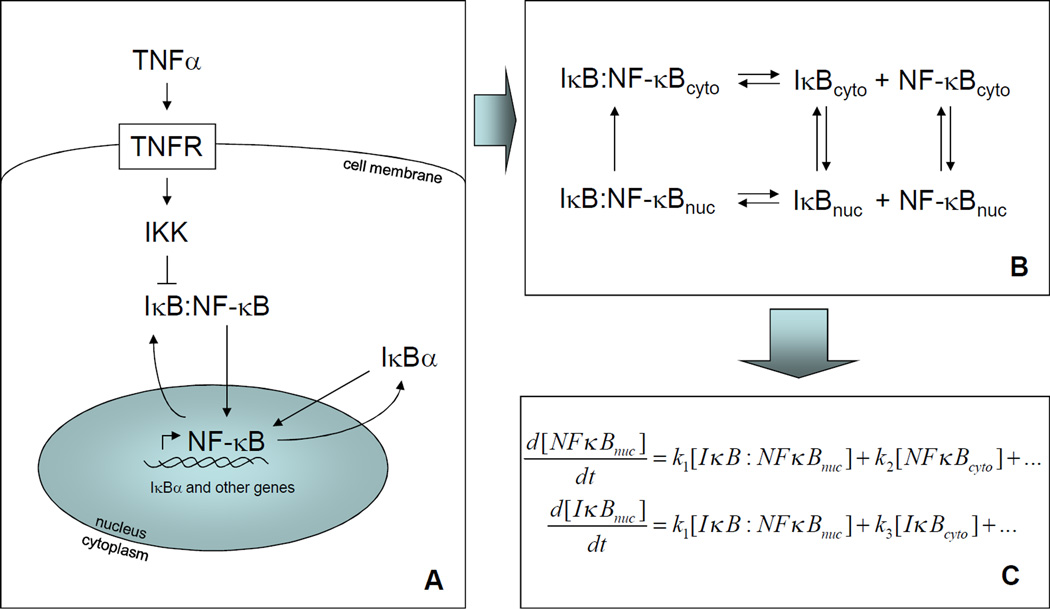
One method to mathematically model a signaling pathway is through the use of differential equations that describe how the concentrations of each signaling species changes over time. This strategy has been employed to great effect in the NF-κB pathway. The process begins by setting the scope of the pathway in terms of the signaling species and interactions to be considered (A). In most models of the NF-κB pathway to date, the species involved are IKK, NF-κB, and the various IκB isoforms. The main interactions are IKK-induced degradation of IκB, IκB inhibition of NF-κB, NF-κB-induced expression of certain IκB isoforms, and transport into and out of the nucleus. Next, these interactions are recast as a set of biochemical reactions that are linked together (B). For example, IκB-mediated inhibition of NF-κB can be represented as a binding reaction and export of IκB:NF-κB complex out of the nucleus, resulting in NF-κB tethered to IκB in the cytoplasm. Then, simple mass-action chemical kinetics are used to convert these reactions into equations for the rate of change in the concentration of each species (C). For example, dissociation of IκB:NF-κB contributes to the rate of change of [IκB] and [NF-κB] proportional to the concentration of IκB:NF-κB. An equation for the rate of change is written for each species, and each equation may have many terms depending on the number of reactions in which that species participates. The values for parameters in these equations is taken from biochemical measurements or fit to the data. Finally, a numerical differential equation solver (e.g. NDSolve in Mathematica or ode45 in Matlab) provides the solution to the equations, i.e. a timecourse for each species, including nuclear NF-κB, which can then be compared to experiments.

Some of the pathway models constructed in this way and their resulting insights are summarized in the following table:

Reference	Main model assumptions	Principle resulting dynamic behavior	Biological implications
[18]	IκBα negative feedback with damping due to IκBβ and IκBε	Biphasic NF-κB dynamics in wildtype cells and highly oscillatory dynamics in IκBβ−/−IκBε−/− cells	Biphasic dynamics determine expression of early and late responding genes
[19]	Sharply peaked IKK activity in response to persistent TNF	Across a wide range of doses, TNF induces the full initial phase of NF-κB activity	TNF can signal over long distances because even low TNF doses elicit NF-κB responses
[32]	Stimulus-specific IKK activity timecourses	Biphasic NF-κB dynamics in response to TNF but monophasic dynamics in response to LPS	Distinct NF-κB responses to different stimuli may result from differential regulation of IKK
[34]	IκBα negative feedback and IκBα delayed negative feedback	Oscillations underlying IκBα and IκBα feedback are out of phase and cancel each other out, resulting in steady NF-κB activity	Double feedback control allows for a rapid yet fine-tuned cellular response

NF-κB oscillations

The findings of our integrative analysis of the NF-κB pathway sparked an experimental study that thrust NF-κB oscillations into the limelight. HeLa (cervical carcinoma) or SK-N-AS (neuroblastoma) cells expressing fluorescent protein-labeled NF-κB and/or IκB showed dramatic periodic spikes in NF-κB activity and the amplitude and frequency of the spikes varied from cell to cell [21]. It is unclear whether oscillations have any physiologic role (compared to the more sustained temporal dynamics described above), as there is no difference in the temporal expression of various genes in oscillatory versus persistent NF-κB activity [22]. In addition, at the level of the population average, wildtype cells do not show spiky behavior. Currently, tracking NF-κB activity in a single live cell requires genetic manipulation, so timecourses of NF-κB activity in single wildtype cells cannot be measured. However, immunocytochemistry can be used to measure NF-κB activity in an ensemble of cells at at single points in time. Distributions of NF-κB activity obtained in this way are inconsistent with those expected from spiky behavior, strongly suggesting that single wildtype cells do not oscillate [22]. So, the interpretation of dynamic behavior, and spiky oscillations in the NF-κB pathway in particular, must be made with care.

Nonetheless, the intrinsic beauty of oscillations and the available template mathematical model for the TNF-NF-κB pathway spurred multiple computational studies of NF-κB oscillations. One use of models in general is to test the potential effects of drugs, with the long term goal of developing reliable models that can predict potency and side effects. In a step toward this direction, one study simulated the effects of a clinical proteasome inhibitor, and two hypothetical drugs that acted at different points in the pathway. This revealed that different inhibitors might alter the NF-κB profile in different ways, especially with respect to the quality and presence of oscillations [23]. While the predicted effects on NF-κB dynamics are certainly experimentally testable, their physiologic significance is unclear. Additionally, the effects are likely different in wildtype cells because the analysis was made on a simplified model in which the only IκB isoform was IκBα. Removal of the other isoforms is a common simplification in computational analysis of the pathway [24–27], but this overlooks the fact that IκBα negative feedback alone exaggerates oscillations [18]. Another caveat of some NF-κB pathway models is that feedback is missing, but this is typically done in simple examples to illustrate the utility of new modeling tools [28, 29]. In general, the interpretation of these analyses should be made in the context of the assumptions incorporated into the model.

Further computational studies of oscillations delved into the origin of the variable amplitude and frequency of the NF-κB oscillations between individual cells as observed in the live cell experiments. A model in which every step in the pathway is activated stochastically suggests that variation is due mostly to extrinsic factors like different IKK or NF-κB concentrations from cell to cell and not intrinsic noise resulting from biochemical reactions, unless parameters related to transcription and translation are very different than the usual estimates [27]. Hence, this model suggests that responses vary from cell to cell because of inherent differences from cell to cell, rather than because of random fluctuations in pathway activation in otherwise identical cells. However, another model in which only transcription and translation are stochastic gives spiky behavior and distributions of period and amplitude that match the live cell experiments [25]. This suggests that random fluctuations in otherwise identical cells are sufficient to generate the variation observed in the live cell experiments. One major difference between these two models that might explain these differing conclusions is that the latter model adds an A20 negative feedback loop on top of the IκB negative feedback loop, whereas the former model only has IκB feedback. A20 is an NF-κB-responsive gene that deactivates TNF receptor complexes, and the latter model proposes that A20 is an important regulator of NF-κB activity, although the role of A20 is exaggerated compared to later experiments [19]. In principle, the contribution of different pathway steps to cell-cell variability can be measured to distinguish these models [30, 31] but experimental data is currently lacking.

Further insights from integrated studies of NF-κB pathway dynamics

Although many of the above examples of pure modeling of the NF-κB pathway are interesting, it is arguable that the most insightful results have come from true integration of experiments and computer models. For example, experimental demonstration that the temporal profile of NF-κB activity is unchanged at different, even very low, TNFα doses inspired model analysis that unexpectedly suggested that fast IKK inactivation was responsible for this phenomenon [19]. This was experimentally verified at all doses and highlighted the critical role of IKK regulation in control of NF-κB activity whose mechanism is currently poorly understood. All of these results were then reanalyzed computationally in the context of innate immune signaling, which suggested that one biological role of such pathway dynamics is to ensure that an inflammatory signal can be transmitted with fidelity across a long distance (Fig. 2B) [19]. These two complete experimental-computational cycles are excellent examples of how integrated analysis can lead to surprising and unpredictable insight.

Additional integrated research continues to deepen our understanding of NF-κB signaling dynamics. Challenging the pathway model with different IKK temporal profiles results in distinct NF-κB dynamics and indeed the different NF-κB profiles resulting from wildtype mouse embryonic fibroblasts (MEFs) stimulated with TNF or LPS, or A20^−/− MEFs stimulated with TNF can be predicted from their respective IKK activity timecourses [32]. Interestingly, in contrast to TNFα, LPS-induced NF-κB activity rises over 30 minutes then remains steady. An integrated analysis revealed that this timecourse can be broken down into an early phase of LPS-induced NF-κB activity that results in TNFα production and subsequent autocrine signaling to ensure continued late phase NF-κB activity [32]. Some NF-κB-responsive genes are only activated by the TNF signal at later times, again demonstrating how signaling dynamics are carefully controlled to give specific gene expression programs.

Interestingly, the underlying NF-κB signals induced by LPS and TNFα oscillate out of phase with one another, so when they are overlapped the overall activity pattern is steady [33]. This theme is repeated in the TNFα-NF-κB pathway alone. IκBε is an NF-κB-responsive gene under TNFα stimulation, giving rise to an oscillatory NF-κB signal that is out of phase with IκBα-induced oscillations and helps keep the late phase of TNFα-induced NF-κB activity steady [34]. All of these observations can be recapitulated in well-grounded models of the NF-κB pathway, suggesting that no other mechanisms must be invoked to explain the data. Thus, it seems that oscillations are a tradeoff for rapid responses to inflammatory signals and additional feedback is needed to compensate to provide a steady supply of active NF-κB. Similar compensation may be present in other pathways.

In summary, integration of experiments and computer models has opened new ground in understanding the control of NF-κB dynamics by inflammatory stimuli and its effects on specificity of gene expression. As LPS and TNF are but a few of the signals that can activate NF-κB, we expect models to continue to be helpful in understanding the effects of other inflammatory stimuli. Furthermore, NF-κB pathways are affected by other major signaling pathways [35], which may provide a way to modulate NF-κB appropriate to the broader context of the cell or organism. As such, modeling may help to understand why inflammatory responses vary from individual to individual, and provide a mechanism to predict optimal therapies and clinical outcomes.

Analysis of organizational motifs common to different pathways

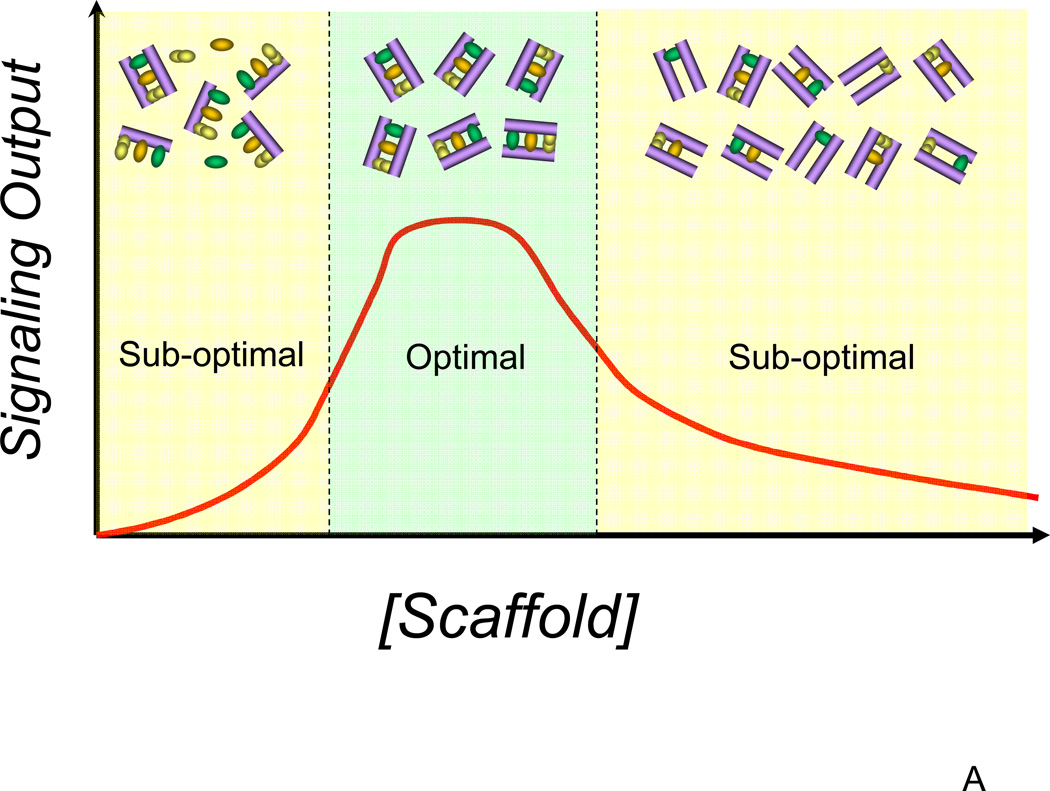
In spite of a dizzying diversity of the means to encode and transfer the information about changes in the cell microenvironment, signaling pathways appear to depend in their function on common principles that might inform their investigators about fundamental constraints on biochemical signal processing. One such principle is scaffolding and anchoring the signaling molecules at appropriate cellular locations. The NF-κB signaling module appears to have at least one such scaffold/anchor. NEMO (also known as IKKγ), a scaffold molecule that binds both IKKα and IKKβ isoforms, appears to facilitate the translocation of the multi-meric, multi-isoform IKK complex to several types of NF-κB activating receptors [36]. NEMO also serves as a platform for binding several other pathway modifiers, including A20. In this regard, NEMO is similar to scaffolding proteins in other pathways. For instance, β-arrestins and Ste5 can nucleate assembly of the members of the MAPK cascades in mammalian and yeast cells respectively, targeting the signaling complexes to the membrane, in the immediate vicinity of activated receptors [37]. Similarly, axin can nucleate formation of the GSK-3, APC, β-catenin complex and its translocation to the membrane [38]. Additional examples of similar scaffold activities in MAPK and other pathways abound. By means of computational modeling, we and others have shown that there is an optimal scaffold concentration, allowing maximal pathway activation for given concentrations of other signaling molecules (Fig. 3A) [38, 39]. This mathematically derived result, confirmed in multiple signaling systems, allowed resolution of paradoxical observations suggesting that scaffolds can be both enhancers and inhibitors of signaling. This, in particular, is true for NEMO, as has been e.g., demonstrated by cell transfection with various levels of NEMO cDNA [36].

Figure 3.

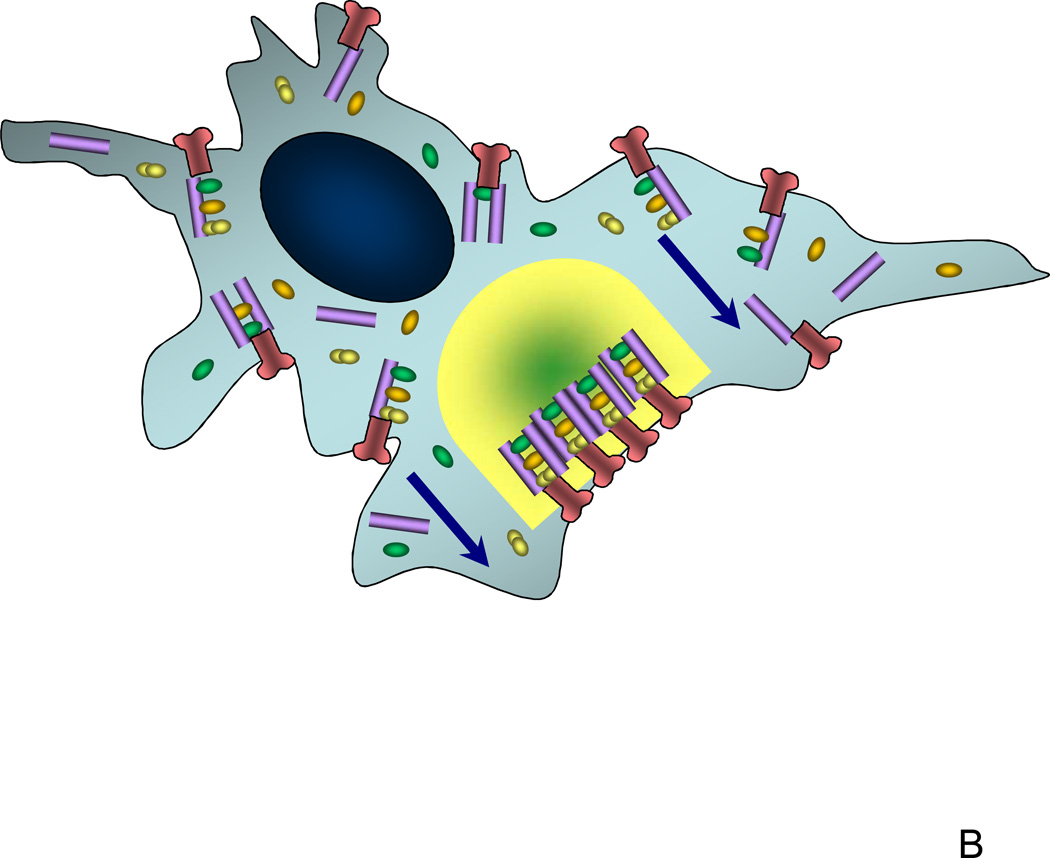
The role of scaffolds in cell signaling. (A) In many types of signaling pathways, scaffolds serve to bring together most of the members of the signaling pathway and localize them close to the receptor. This cross-linking property of scaffold molecules ensures that there is an optimal scaffold concentration for the given concentrations of other signaling molecules, potentially allowing for controlling where in the cell the signaling will be most efficient; (B) Preferential localization of scaffolds to particular membrane compartments can ensure that the signaling is relatively high only around those compartments but not elsewhere, the property that might be crucial for cell polarization and directed cell extension or migration. This image shows a signaling scaffold at the leading edge of a migrating cell and the subsequent compartmentalization to the leading edge of its signal (depicted as green gradient).

The scaffold-mediated translocation of the signaling complexes to the plasma membrane within a vicinity of the activated receptor can result in formation of signaling super-complexes encompassing most pathway members, activated in appropriate spatially confined compartments. According to modeling results [39], in addition to facilitating signal propagation due to juxtaposition of signaling partners, this tightly regulated spatial localization can facilitate cell polarization. In chemotaxis, for example scaffolding may promote localization of receptor-linked kinases at the leading edge which signal to the migratory machinery enabling directed movement as well as protect pathway members from inactivation in the phosphatase-rich cytosol (Fig. 3B). Indeed, if the concentration of the scaffold proteins is highest only in specific areas of the plasma membrane, it is predicted to be sub-optimal elsewhere, in a fashion predicted by the model. These locally active signalosomes thus solve the problem of how to regulate a very complex signaling pathway in a highly uncertain and equally sophisticated intracellular chemical environment.

Another major insight from modeling studies, possibly universally relevant to signal transduction pathways, is that signaling activation, inactivation and continuous steady state activity are predominantly determined by the properties of receptor down-regulation, re-synthesis and ligand availability through secretion and proteolysis. This has been extensively demonstrated in the modeling and experimental analyses of the EGF pathway signaling [40], and long-term evaluation of the TNF and TGFβ signaling events [35, 41]. Interestingly, the kinetic constants and other parameters characterizing enzymatic reactions constituting the core of pathway reactions appear to have lower ‘importance’ for the ultimate pathway read-out, with mathematical model outputs frequently displaying lower sensitivity to variation of the corresponding parameter values.

Paradoxes of integrative analysis: the NF-κB module and beyond

The previous sections present a testament to the predictive power of mathematical models and demonstrate their utility. However, the truth to the matter is that we do not know why the models work so successfully. The intracellular milieu is extremely varied and complex, raising questions about the commonly assumed view of a cell as a well mixed bag (more imaginatively soup) of enzymes. Contrary to this notion, the last few decades painted a picture of the cell interior more resembling a well organized engine of a race car, filled with cytoskeletal components and dynamic organelles. Why then, the models clearly over-simplifying the reality have nevertheless proven so useful and effective? Although the answer to this, somewhat provocative question, is not entirely clear, one possibility could be that the ability by the cells to develop the highly spatially separated and integrated signaling platforms simplifies the underlying chemistry and allows the signals to navigate through the intermediate stations in a facilitated fashion, permitting a simple kind of a model. This idea combined with the overriding importance of controlling intra- and extra-cellular feedback interactions can make the specific details of cell organization and its biochemical consequences of significantly lower import. Regardless of the actual reason, the models we have already approximate the reality astonishingly well, giving us useful tools for the ultimate control of signaling function.

Future directions (conclusion)

Signal transduction pathways are dedicated sets of chemical reactions responsible for detection, processing and delivery of the information about changes in the cell environment to the ‘decision centers’ of a cell. Unlike wires and antennas used in human built devices designed for information transfer, cells are limited to using chemistry as the basis for sophisticated and robust passing of signals within complex and convoluted intracellular spaces. The underlying complexity may thus be foreign to our anthropomorphic attempts to confer the ideas of wires, transistors and resistors to the sophisticated liquidity of biological processes. Nevertheless, the only way to understand the intricacy of signal transduction is to resort to help of computational techniques, hoping in the process that they can be useful approximations and predictive constructs allowing us to penetrate further into the strange world of cellular biology. Arguably, the best way to achieve this is to tightly integrate theory and experiment into an iterative program, emblematic of both the generally defined Scientific Method and its particular incarnation, Systems Biology. If the last few years are any indicator, we will probably see a lot of important qualitative insights into the nature of signaling pathways and beyond coming from inherently quantitative research, rather than more classical qualitative essays. As our understanding becomes more sophisticated, we might begin to see how the chemistry of the cells has evolved to effectively pass and fuse information through the ‘wires’ very different from the ones we are used to in a ‘soup’ feeding the life itself.