Time-based reward maximization

Abstract

Humans and animals time intervals from seconds to minutes with high accuracy but limited precision. Consequently, time-based decisions are inevitably subjected to our endogenous timing uncertainty, and thus require temporal risk assessment. In this study, we tested temporal risk assessment ability of humans when participants had to withhold each subsequent response for a minimum duration to earn reward and each response reset the trial time. Premature responses were not penalized in Experiment 1 but were penalized in Experiment 2. Participants tried to maximize reward within a fixed session time (over eight sessions) by pressing a key. No instructions were provided regarding the task rules/parameters. We evaluated empirical performance within the framework of optimality that was based on the level of endogenous timing uncertainty and the payoff structure. Participants nearly tracked the optimal target inter-response times (IRTs) that changed as a function of the level of timing uncertainty and maximized the reward rate in both experiments. Acquisition of optimal target IRT was rapid and abrupt without any further improvement or worsening. These results constitute an example of optimal temporal risk assessment performance in a task that required finding the optimal trade-off between the ‘speed’ (timing) and ‘accuracy’ (reward probability) of timed responses for reward maximization.

1. Introduction

Many organisms ranging from pigeons [1] to humans [2] share the ability to time intervals in the seconds-to-minutes range. This ability, called interval timing, plays a crucial role in adaptive behaviours such as optimal foraging [3,4] and keeping track of reward rates [5]. Behavioural data show that animals on average are flexibly accurate in their timing behaviour; however, flexibility in accuracy comes at a cost of imprecision reflected by the substantial trial-to-trial variability in timed responses. Imprecision in timed responses is assumed to originate primarily from the endogenous noise in timing processes that underlay temporal control over responding and to have well-defined statistical properties. For instance, responding in different interval timing tasks across species conforms to Weber's law, which points at the proportionality of timing imprecision (endogenous timing uncertainty) to targeted intervals. Scalar property, a well-established property of interval timing [6], indeed shows that the standard deviation (s.d.) of time estimates is proportional to the target time intervals [7]. Consequently, every action or decision that relies on interval timing is by default subjected to temporal uncertainty and its statistical properties, which dictates that timing tasks inherently require adapting decisions to the noise characteristics of interval timing for reward maximization. To this end, integrating a psychophysically plausible model of endogenous timing uncertainty into the framework of reward maximization may help define a valid optimal solution to time-dependent decisions by accounting for the organisms’ time-representational constraints.

Findings from earlier studies that adopted such an analytical approach [8–12] showed that both humans and rodents can adopt nearly optimal strategies by taking account of their endogenous uncertainty in tasks that required various decisions. In one of these experiments [8], humans and mice were trained in a temporal discrimination task that was composed of two types of trials (short latency trial and long latency trial) presented probabilistically. If a given trial was a short latency trial, responding at or after the short duration at one of the two locations (short location) was reinforced. On the other hand, if that trial was instead a long latency trial, responding at or after long duration at the other location (long location) was reinforced. If in long latency trials a subject's first response at or after the long duration was at the short location, or in short latency trials a subject's first response at or after the short duration was at the long location, the subject did not receive reward or suffered a penalty depending on the payoff matrix. The emergent response pattern in this task was initiating anticipatory responding at the short location and if the short interval had elapsed without reward delivery there, switching to the long location. The trial time at which the subject stopped responding at the short location for responding at the long location (i.e. switch latency) was treated as the critical temporal decision output (see also [13]).

Responding in this task leads to four possible consequences: earning reward in short latency trials by not switching; earning reward in long latency trials by switching prior to the long duration; missing the reward (or suffering penalty) in short latency trials by switching prior to the short duration; and missing the reward (or suffering penalty) in long latency trials by not switching prior to the long duration. The expected gain (equation (2.1)) here depends on the short and long latency trial probabilities, target switch latency (mean switch latency), and the level of the subject's timing uncertainty (coefficient of variation of switch latencies) in addition to other task parameters described below:

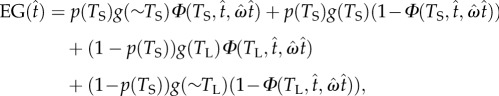2.1

where is the estimate of a subject's target switch latency, is the coefficient of variation of switch latencies, T_S is the short duration, T_L is the long duration, p(T_S) is the probability of short latency trial and g defines the payoff matrix (e.g. g(T_S) shows the gain associated with a correct short latency trial), and 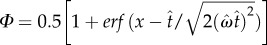, where 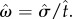Optimal target switch latency for a given subject can be determined by finding the t-value that maximizes the output of equation (2.1) for that subject's level of timing uncertainty (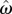). Balcı et al. [8] manipulated the probability of trial types (for both humans and mice) and the payoff matrix (for humans only) between different conditions and evaluated the optimality of the empirical performance. They showed that humans and mice closely tracked the changes in the optimal target switch latency as a function of endogenous timing uncertainty and exogenous probabilities, and earned over 98% of the maximum possible expected gain that could be attained given the level of their endogenous timing uncertainty. These findings were recently replicated by Kheifets & Gallistel [11]. Different from Balcı et al. [8], Kheifets & Gallistel [11] changed the probability of short and long latency trials during testing and found that mice adjusted their target switch latencies rapidly and abruptly in an optimal fashion, which could not be accounted for by slow reinforcement learning. These findings overall suggested that not only humans but also mice could maximize reward by integrating their endogenous timing uncertainty as well as exogenous probabilities into their decisions in a normative fashion.

The reward maximization problem that characterizes the switch task also applies to other temporal discrimination tasks such as the traditional temporal bisection task [14]. In the temporal bisection task, participants are trained to categorize durations as short or long depending on their subjective similarity to short and long reference durations that de-limit the range of to-be-judged durations; however, different from the switch task, choice behaviour is manifested only after the termination of the to-be-judged duration. Machado & Keen [15] tested pigeons in this task using a long-box apparatus and reported behavioural patterns similar to our observations in the switch task; contingent upon the onset of the timing, signal pigeons moved to the location associated with short duration and switched to the location associated with long duration if the timing signal lasted longer than the short reference duration. This observation suggests that the decision dynamics that underlay choice behaviour in the temporal bisection task are similar to those that underlay timed switching behaviour. We recently tested human participants on the temporal bisection task changing the probability of short and long reference durations, and computed the optimal target bisection point (duration that the participant is equally likely to categorize as short or long) based on experienced exogenous probabilities and their level of endogenous timing uncertainty (estimated from choice functions). Consistent with our earlier findings in the switch task, human participants closely tracked the optimal bisection point, earning nearly (over 98%) the maximum possible expected gain they could attain given the level of their timing uncertainty and exogenous probabilities [16].

There are other tasks in which optimal temporal strategy depends on the level of endogenous timing uncertainty but in the absence of exogenous probabilistic relations [9,12]. Beat-the-clock constitutes one of these tasks [12]. In this task, participants are asked to respond as close as possible to a fixed duration but no later, in order to earn reward. The magnitude of reward that can be earned increases exponentially with time until a fixed duration and drops to zero from thereafter. Endogenous timing uncertainty dictates that in order to maximize reward, participants should aim at a time point earlier than the fixed duration and how early they should aim for depends on the level of their timing uncertainty. Equation (2.2) defines the expected gain and its dependence on the level of timing uncertainty in this task:

2.2

where t is a possible response time, 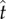is the estimate of target response time, g is the right truncated exponential reward function and p is the probability of responding at t given 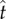and the level of endogenous timing uncertainty (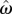). Optimal target response time can be determined by finding 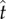that maximizes the output this function.

Consistent with earlier studies described above, participants in this task closely tracked the optimal target response time that changed as a function of the level of timing uncertainty, and earned 99% of the maximum possible expected gain they could attain given the level of their timing uncertainty. There is also evidence for reward maximization in the sub-second range as a result of integrating timing uncertainty in temporal reproduction and motor timing decisions [9,10].

These findings overall suggest that humans can take normative account of their endogenous timing uncertainty along with experienced exogenous probabilities (when dictated by the task) in order to maximize the reward earned. However, the scenarios described above constitute discrete-trial paradigms that do not impose a trade-off between speed and accuracy of timed responses with respect to reward maximization. On the other hand, many daily decisions are characterized by this fundamental trade-off. One of the tasks that captures speed–accuracy trade-off in the domain of temporal decision-making is the differential reinforcement of low rates of responding (DRL), which is traditionally used in the field of psychopharmacology to test the efficacy of putative anti-depressant agents [17,18].

In the DRL task, subjects are trained to respond after a fixed minimum time interval has elapsed (not signalled) since their previous response. Subjects receive reward only when they respond after this fixed interval and each response resets the trial time. Reward rate in this task can be expressed as p(reward)/mean(IRT) and thus reward maximization depends on the trade-off between two time-dependent quantities: the reward probability and the inter-response time (IRT). Probability of receiving reward increases with IRT in a nonlinear fashion due to timing uncertainty (increasing the reward rate) whereas time cost increases linearly with IRT (decreasing the reward rate). Importantly, the optimal (i.e. reward maximizing) trade-off between the reward probability and IRT depends on the DRL schedule (i.e. scheduled minimum wait time) and the level of the subject’s endogenous timing uncertainty. To that end, as in tasks described earlier, well-established psychophysical properties of interval timing should be included in the optimality analysis of timed response inhibition in DRL. Dependence of reward rate on the level of timing uncertainty and its scalar property [19] (assuming an inverse-Gaussian distributed response¹) in the DRL task can be expressed by equation (2.3):

2.3

where 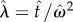, T denotes the DRL schedule, 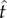is mean IRT and 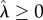is the Wald shape parameter; waldcdf(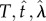) is defined by equation (2.4):

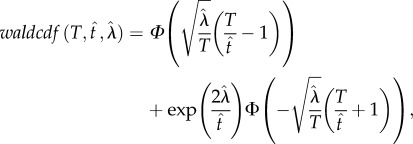2.4

where .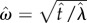

Optimal target IRT can be determined by finding the t that maximizes the output of equation (2.3) for a given level of timing uncertainty, 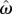. We have recently derived a closed form solution to optimality in this task, which defined the optimal performance curve (OPC) for the DRL task (equation (2.5); see electronic supplementary material, File 2 for the derivation). The t-value that satisfies equation (2.5) is the optimal wait time for the corresponding level of timing uncertainty (figure 1):

2.5

Figure 1.

Family of OPCs for the DRL task parametrized by the relative penalty for errors based on equation (2.7). Inc., increment. (Online version in colour.)

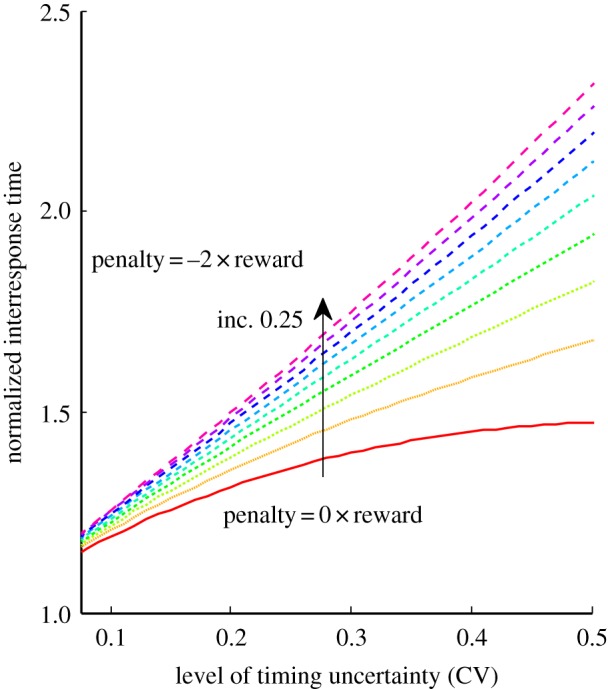
This approach captures exclusively those cases in which payoff structure does not contain penalties. On the other hand, many daily scenarios contain explicit penalties for errors and a more generalized solution to the reward maximization problem should also account for these costs. Equation (2.6) defines the generalized form of expected reward rate when errors were penalized:

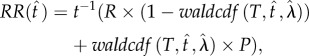2.6

where R is the reward magnitude and P is the penalty magnitude associated with correct and erroneous responses, respectively. The closed form solution to this problem is shown in equation (2.7) (see electronic supplementary material, File 2 for the derivation), which defines OPCs for the DRL task parametrized by the relative penalty for errors (figure 1):

2.7

Building upon our earlier findings regarding reward maximization in the DRL task [9], we conducted two experiments that addressed important questions regarding optimal temporal risk assessment in the context of timed response inhibition. Earlier studies showed nearly optimal human performance in the DRL task when participants were provided with instructions regarding task rules and given the opportunity to experience the minimum wait time explicitly prior to testing. On the other hand, studies conducted with rodents did not allow this for obvious reasons. In the current experiments, in order to constitute a better analogue to the animal studies, we tested human participants on the DRL task without providing any instructions or prior experience with the minimum wait time and evaluated their performance within the framework of optimality described above. Current experiments also differ from the limited number of earlier human DRL experiments in that they extended the degree of training from single-session testing to multiple-session testing. Extensive training (i.e. eight sessions) coupled with lack of instructions allowed us to characterize the acquisition patterns that lead to optimal/steady-state DRL performance. Finally, earlier studies did not contain any penalty for early responses and thus captured only a limited scope of temporal risk assessment. The second experiment of this study addressed this issue by introducing penalty for premature responses and allowed for the evaluation of DRL performance according to the generalized expected reward rate function.

2. Material and methods

(a). Subjects

Twenty-four adult participants were tested: Experiment 1 (five males and seven females with mean age of 20.50 years, s.d. = 1.7) and Experiment 2 (three males and nine females with mean age of 19.16 years, s.d. = 2.1). Participants were recruited through a publicly available newsletter published on the Koç University website. The experiment was composed of eight 50-min (fixed test duration) daily DRL sessions and one 20-min working memory task given after DRL testing. Participants received monetary reward based on their performance in each DRL session and fixed monetary compensation for the working memory task. The experiment was approved by the Institutional Review Board at Koç University and all participants provided written consent prior to testing.

(b). Stimuli and apparatus

The visual stimulus consisted of a white square on a black background. The square briefly changed its colour to red or green to provide feedback after premature responses (errors) and responses emitted after the minimum wait time (correct responses), respectively. The display was generated in MATLAB on a Macintosh computer, using the Psychophysics Toolbox extension [20,21]. Responses were collected with a standard computer keyboard.

(c). Procedure of DRL task

Each participant was tested with either a 5 or a 10 s DRL schedule over eight sessions. In Experiment 1, participants earned a reward when they hit the space key after the minimum wait time. There was no penalty for responding earlier than this minimum time. In Experiment 2, participants earned a reward upon hitting the space key after the DRL schedule; however, they were penalized for half of the reward amount if they responded prematurely. The only explicit instruction was to press the designated key for the opportunity to earn a reward and to try to maximize reward earned. In Experiment 1, participants were told that it was possible for them not to receive a reward upon a key press. In Experiment 2, participants were told that it was possible to earn reward or suffer penalty upon a key press. Participants were not provided any other instructions regarding the DRL task rules and parameters. On the contrary in the earlier work [9], participants were provided with these critical instructions regarding the DRL task rules and parameters. For instance, participants were told that they would earn reward for their each response emitted following a minimum wait duration since their previous response and that this response would reset the trial clock. They were also told that any response prior to the minimum wait duration would reset the trial clock without the reward delivery. In the earlier work [9], participants were also provided with prior experience with the critical task parameter prior to DRL testing, namely the minimum withhold duration. Specifically, participants were presented with the time interval that was equal to the DRL schedule. They were allowed to reproduce this interval for 50 times and received parametric feedback regarding the accuracy of each reproduction. This provided prior experience with the DRL schedule in the earlier study, which was absent in this study.

As in the earlier work [9], participants were asked not to count. A secondary task was used to suppress chronometric counting during the DRL tests. At the beginning of each block, participants were presented with a four-digit number and at the end of that block a single-digit number. Participants were asked whether the four-digit number presented at the beginning of the block contained the single-digit number presented at the end of the block. The total reward earned from the DRL task-related responses was multiplied by the proportion correct from the secondary task. Participants were told that the reward earned from the primary task was going to be multiplied with the proportion correct in the secondary task. Working memory task was the automated version of the operational span task as described in [22].

(d). Data analysis

Cumulative Weibull distribution functions (with an extra scaling parameter) were fit to the IRTs ordered according to their actual order of occurrence. The onset of steady-state responding was defined in terms of the response that corresponded to the mean value plus three times the standard deviation estimated from the best-fit cumulative Weibull distribution. In order to quantify the abruptness of acquisition, we calculated the time it took to reach from 25 to 75% of the best-fit scaling parameter. Acquisition of steady-state performance by one participant in Experiment 1 (ID:19) and three participants in Experiment 2 (ID:27, ID:29 and ID:39) exhibited atypical patterns. Specifically, these participants tended to respond after the DRL schedule similar to other participants, but they initially waited much longer than the optimal IRT and then slowly converged on the optimal value gradually by speeding up their responses. Thus, these participants were excluded from the acquisition analysis (for these participants, the last three sessions were treated as the steady-state data for the other analyses). Representative atypical acquisition patterns as well as representative typical acquisition patterns from both Experiment 1 and Experiment 2 are presented in the electronic supplementary material, figures S1 and S2, respectively. Note that participants were excluded only from the acquisition analysis and not from the optimality analysis that is described next.

Steady-state IRTs were fit with an exponential inverse-Gaussian mixture function that has been previously shown to account for IRTs in the DRL task [9]. There were atypical response patterns of several participants at the session-level during the steady state. Individual sessions with such atypical responses were excluded from the analysis for four participants in Experiment 1 and two participants in Experiment 2 (participants were not excluded from the analysis). For completeness, response patterns of these participants with no omissions and omissions are presented in the electronic supplementary material, figures S3 and S4, respectively. In order to ensure that results gathered were not because of the exclusion of participants from the acquisition analysis and sessions from the optimality analysis, we estimated the parameters once more without any exclusions. All of the parameters (Speed and Abruptness of acquisition indices, optimal and empirical IRTs, CVs (coefficient of variance) and maximum possible expected reward rates) were not significantly different from the values obtained without any omissions in either experiments (at alpha level 0.05, not reported).

Best-fit mean and shape parameter of the inverse-Gaussian portion of the mixture distribution were used to calculate the optimal strategy for the corresponding participant. Mann–Whitney U-tests were used for the comparison of the acquisition indices (i.e. rapidness and abruptness), IRTs and CVs between experiments and schedules within each experiment. Wilcoxon signed-ranks test was used for all other analysis. Results based on t-test comparisons revealed the same results (not reported). Alpha level of 0.05 was used as the significance level in all analyses.

3. Results

(a). Acquisition

We first characterized the acquisition of the DRL responding, which was particularly relevant given the lack of instructions and multiple session testing in our experiments. To that end, we were interested in two different measures of acquisition: rapidness and abruptness of the acquisition of optimal/steady-state IRTs.

(i). Rapidness (speed) of acquisition

Average onset of steady state occurred around the 19th (s.e.m. = 5.87, median = 18.90, IQR = 33.00) minute of Experiment 1 (with no penalty for errors) and 6th (s.e.m. = 2.86, median = 0.60, IQR = 14.30) minute of Experiment 2 (with penalty for errors) and this difference was statistically significant (U = 21, Z =−2.17, p < 0.05). Rapidness of acquisition did not differ between the DRL schedules (5 and 10 s) in either Experiment 1 (U = 8, Z =−1.28, p = 0.25) or Experiment 2 (U = 6, Z =−0.98, p = 0.41). There was a significant negative correlation between working memory span and onset of steady state in Experiment 1, r(9) = −0.59, p < 0.05, although in the same direction this relation was not significant in Experiment 2, r(7) = −0.11, p = 0.38.

(ii). Abruptness of acquisition

The mean abruptness index normalized by the schedule was 14.28 (s.e.m. = 6.39, median = 4.54, IQR = 13.70) in Experiment 1 while it was 8.32 (s.e.m. = 3.99, median = 2.21, IQR = 15.11) in Experiment 2. This difference between two experiments was not significant (U = 41, Z =−0.65, p = 0.52). There was no significant correlation between working memory span and abruptness in either Experiment 1, r(11) = −0.33, p < 0.16 or Experiment 2, r(9) = 0.05, p = 0.45.

(b). Steady-state responding

We first evaluated whether the IRTs after acquisition (mean + 3 × s.d.) exhibited a trend for slowing or speeding. In both Experiment 1 and Experiment 2, the group average slope of the linear regression fits to post-acquisition data points were 0.00 (median 0.00) suggesting that IRTs remained very stable after the acquisition took place. An exponential inverse-Gaussian mixture distribution function was fit to steady-state IRTs in Experiment 1 (mean ω² = 0.91, s.e.m. = 0.03, median = 0.95, IQR = 0.09) and in Experiment 2 (mean ω² = 0.91, s.e.m. = 0.02, median = 0.94, IQR = 0.08). When an exponential-Gaussian mixture distribution function was fit to the same dataset, the ω² values decreased to 0.88 (s.e.m. = 0.03, median = 0.93, IQR = 0.11) and 0.85 (s.e.m. = 0.03, median = 0.88, IQR = 0.09) for Experiment 1 and Experiment 2, respectively. Wilcoxon signed-ranks test showed that this difference was significant for Experiment 1, Z =−2.90, p < 0.01, and Experiment 2, Z =−3.06, p < 0.01.

(c). Optimality analysis

The optimality analysis of steady-state responding in both experiments showed that participants aimed for the optimal IRT that was parametrized by the payoff structure and participants’ timing uncertainty level. Figure 2a,b depicts the performance of each participant tested with 5 or 10 s schedules in Experiment 1 and Experiment 2, respectively. These figures show the heat map of the expected reward rates (for normalized DRL schedules) expressed over a parameter space composed of target IRT and the level of timing uncertainty (CV). Ridges of these two ‘surfaces’ are indicated by the black curves, namely the OPCs for the DRL task with two different payoff structures. OPCs indicate how long participants should aim to wait (normalized by DRL schedule) before responding again given their level of timing uncertainty and payoff structure.

Figure 2.

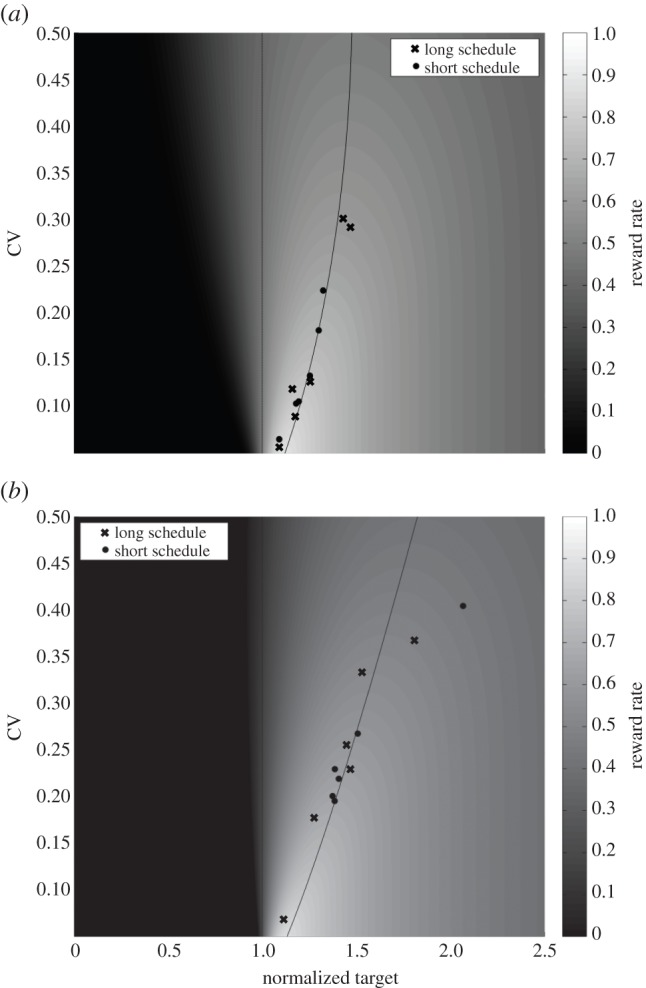
Heat map of expected reward rates for (a) Experiment 1 and (b) Experiment 2 for normalized DRL schedule. Curves denote the ridge of these surfaces indicating the optimal normalized target IRTs for different levels of timing uncertainty for no penalty (a) and penalty (b) conditions separately. Each data point corresponds to a participant and each symbol corresponds to a different schedule. Note that empirical IRTs were normalized by the corresponding DRL schedule. Short schedule, 5 s; long schedule, 10 s.

We calculated how much participants earned compared to how much they could maximally earn given these endogenous and exogenous parameters. In Experiment 1, participants achieved 99.1% (s.e.m. = 0.41%, median = 99.8%, IQR = 1.26%) of the maximum possible expected reward rate for their level of timing uncertainty. In Experiment 2, this value was 98.6% (s.e.m. = 0.62%, median = 99.7%, IQR = 1.95%). We also conducted this analysis adopting a more conservative approach. We divided the difference between the empirical expected reward rate and the expected reward rate if targeting the schedule (ER(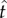) – ER(T)) by the difference between the maximum possible reward rate and empirical expected reward rate if targeting the schedule (ER(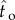) – ER(T), where 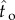is the optimal IRT). The average of this conservative estimate of proportion of the maximum possible reward rate was 97.9% (s.e.m. = 0.95%, median = 99.5%, IQR = 3.62%) in Experiment 1 and 98.0% (s.e.m. = 0.86%, median = 99.6%, IQR = 2.74%) in Experiment 2. The proportions of maximum expected reward rates gathered without excluding the sessions with atypical response patterns were nearly identical to the values reported above (means ranging between 97.8 and 99.1% and medians ranging between 99.2 and 99.7%). Briefly, participants nearly maximized their rewards in both experiments. Participant's reward rates were significantly higher than the reward rates they would attain if their mean IRT was equal to the DRL schedule (if they were targeting the DRL schedule) in Experiment 1 (Z =−3.06, p < 0.01) and in Experiment 2 (Z =−3.06, p < 0.01). There was no significant difference between the two schedules in terms of the percentage of maximum expected reward rate attained in either Experiment 1 or 2 (U = 13, Z =−0.80, p = 0.48 and U = 9, Z =−1.44, p = 0.18, respectively). Note that this comparison was conducted after normalization by the corresponding DRL schedule.

We then compared the empirical normalized IRTs of the participants with the corresponding optimal normalized IRTs using Wilcoxon signed-rank test; there were no significant differences between empirical and optimal values in either Experiment 1 (Z =−0.86, p = 0.39) or Experiment 2 (Z =−0.71, p = 0.48). Normalized empirical IRTs in Experiment 2 were significantly longer than the normalized IRTs in Experiment 1 (U = 24, Z =−2.77, p < 0.005). Coefficient of variations obtained in Experiment 2 were significantly higher than the CVs obtained in Experiment 1 (U = 31, Z =−2.37, p < 0.05).

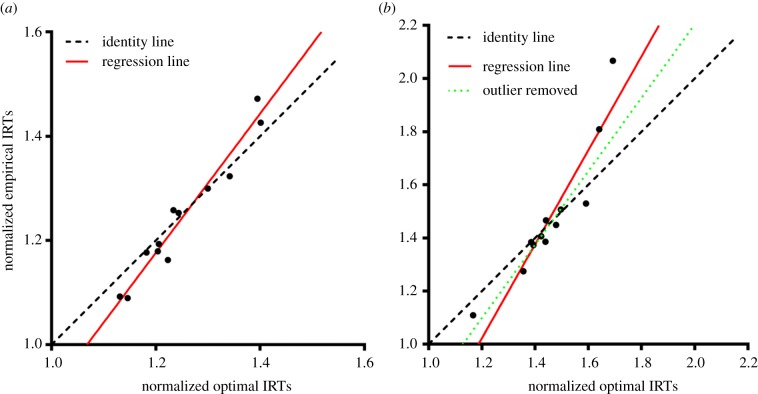
Deming regression fits revealed a significant relation between the optimal and empirical IRTs for both Experiment 1 (figure 3a) and Experiment 2 (figure 3b): F_1,10 = 188.4, p < 0.001, slope = 1.34 in Experiment 1 and F_1,10 = 61.46, p < 0.001, slope = 1.77 in Experiment 2. When we excluded the participant that had empirical IRT longer than two standard deviations from the mean in Experiment 2, the slope decreased to 1.38, F₉ = 75.74, p < 0.001. Note that best-fit regression lines crossed over the identity line in both experiments. This observation suggests that participants had a tendency to respond earlier than the optimal when the optimal IRT was closer to the DRL schedule and later than the optimal when the optimal IRT was farther from the DRL schedule. This pattern suggests an over-adjustment of IRTs in relation to the level of timing uncertainty. These small biases, however, resulted in only negligible costs in terms of the reward rate attained.

Figure 3.

Deming regression fits to empirical and optimal IRTs in (a) Experiment 1 and (b) Experiment 2. Data from Experiment 2 were fit twice: 1—full dataset and 2—after removing one participant based on −/+ two standard deviation exclusion rule. (Online version in colour.)

4. Discussion

This study aimed to expand the scope of temporal decision-making research by addressing novel questions to bridge the gap between interval timing and decision-making fields. To that end, we investigated the temporal risk assessment performance of human participants in the DRL task with two different schedules (5 and 10 s) and payoff structures (i.e. penalty versus no penalty for premature responses) and evaluated it within the framework of optimality based on the statistical decision theory.

Our results indicated that humans can maximize reward rate by taking normative account of their endogenous timing uncertainty even when instructions regarding the task rules were absent, when the exact minimum wait time itself was never experienced, and when premature responses were explicitly penalized. Observed performance was comparable, if not closer to optimality, when compared with earlier single-session DRL experiments with instructions, prior experience of the minimum wait time, and no penalty for errors [9]. Overall, our findings corroborated optimal (reward maximizing) performance of human and/or non-human animals in other timing tasks where time was an explicit component of the decisions: switch task [8,11], temporal bisection task [16], beat-the-clock task [12], temporal reproduction [10] and motor timing [23]. Different from these discrete-trial tasks, however, our experiments demonstrated the optimality of temporal decisions when the task rules imposed a trade-off between the ‘speed’ (i.e. response time) and ‘accuracy’ (i.e. probability of reward) of temporal decisions, a relation that has been shown to adaptively guide decisions in other free-response non-temporal tasks [9]. Thus, our findings also expanded the scope of optimal speed–accuracy trade-offs to the domain of interval timing and temporal decision-making.

Acquisition of the optimal DRL responding in the absence of instructions occurred early during training (mostly within the first session) in an abrupt fashion. This constituted one of the fundamental differences from the DRL acquisition pattern of rats, which is typically gradual. After the acquisition took place (as captured by cumulative Weibull fits), the performance was very stable and nearly optimal given the DRL schedule, payoffs and level of participants’ timing uncertainty. These findings support a model-based guidance of human timed behaviour in the DRL task and constitute a challenge for gradual reinforcement learning-based accounts of performance (see also [12]).

We expected earlier acquisition of timed responding when participants suffered monetary penalty (penalty > 0) for premature responding as this penalty would locally/transiently or globally motivate longer wait times, which would presumably facilitate the acquisition of the DRL task. This is exactly what was observed; participants learned the optimal wait time earlier in the second experiment (penalty > 0) compared with the first experiment (penalty = 0). It is of interest to examine whether similar manipulations (e.g. in the form of time-out period for premature responses) would lead to the same findings in non-human animals. There were no differences between schedules in terms of the rapidness of the acquisition of DRL responding, which does not corroborate the view that acquisition scales with the degree of temporal uncertainty (for review, see [24]). This discrepancy can be attributed to the peculiar features of the DRL task such as the acquisition of response inhibition and the absence of discrete timing cues.

Since the acquisition of task representation depended on experienced response-outcome contingencies, we also expected higher working memory capacity to facilitate the acquisition of optimal/steady-state responding. This expectation was confirmed by Experiment 1; participants with higher working memory span acquired time response inhibition earlier. However, this relation did not hold for Experiment 2. It is possible that differences in the effect of penalty on acquisition (e.g. owing to differential penalty processing) masked the effect of working memory span on the same measure in Experiment 2. It is also possible that the sample size was adequate for the timing study but not for the working memory task. Future studies can use larger sample sizes to investigate this relation.

Different from steady-state performance in non-human animals, human participants exhibited lower proportion of untimed responses despite the purely experiential nature of the current experiments. These responses are typically emitted very shortly after the previous response. Balcı et al. [9] argued that non-timed responses might help agents detect beneficial alterations in environmental statistics (e.g. shift to a shorter DRL schedule). This would constitute a long-term adaptive strategy in unstable environments particularly given the minimal time cost exerted by these responses [25]. The difference between rats and humans in terms of the frequency of non-timed responses might be related to their different expectations regarding the stability of the environmental conditions. Humans might be less willing to explore possible changes in the schedule based on their prior belief that task parameter values remain stable throughout the experiment. On the other hand, environmental statistics are less stable in nature, and for non-human animals and smaller organisms. Alternatively, these results can be explained by the superior inhibitory control of humans compared to the rats. These issues can be addressed empirically with experiments in which the DRL schedule (minimum wait time for reward) unpredictably shortens and lengthens without signalling. We are currently conducting such tests with humans in our laboratory.

This study has a number of methodological advantages over the previous studies with instructions and prior experience of the DRL schedule. Acquiring the task-relevant parameters purely based on experienced response-outcome contingencies with no instructions or experience of task parameters minimizes the likelihood of adopting task-related top-down auxiliary processes (at least early in training). Investigations of optimal temporal decision-making often consider steady-state performance. Our methodological approach on the other hand also allowed the characterization of acquisition of timed response inhibition in relation to optimality. Finally, lack of instructions minimized the gap between the human and non-human animal versions of the task, increasing the interspecies generalizability of the conclusions and emphasizing the translational nature of temporal risk assessment.

Optimal performance under uncertainty appears to be a common feature of human and animal time-based decision-making [9]. This is not surprising as time is a determinant of the amount of reward earned in many biologically critical situations humans and non-human animals have faced in their evolutionary history. Given that interval timing is a primitive and fundamental function observed in many different species with similar psychophysical properties, its noise characteristics might have indeed been well-integrated into decision-making mechanisms over the course of evolution. In other words, the nervous system of many vertebrates might be pre-wired to parametrically convert the endogenous timing noise into an adaptive bias signal during decision-making when reward maximization requires it.

DRL task's usefulness in psychopharmacology and its ability to characterize impulsive behaviour have attracted the attention of behavioural neuroscientists. The most prominent neuroanatomical target of these studies had been the limbic system, which is also implicated in interval timing [26–35]. For instance, hippocampus [27–29,33,35] and amygdala [33] lesions have been shown to result in clear impairments of DRL performance in the form of increased responses per reinforcer. Unfortunately, many of these reports did not present the complete response curves, which does not enable the characterization of observed deficiencies differentially as being due to an increase in frequency of non-timed responses (exponential portion of our mixture model) or due to a leftward shift of the timed response curve (inverse-Gaussian portion of our mixture model) or both.

Few studies that presented the response curves revealed that lesions of dentrate gyrus, a subregion of hippocampal formation [29] resulted in a leftward shift in the timed portion of the response curve. Bilateral hippocampus lesions showed similar effects but they also increased the frequency of non-timed responding (see fig. 3 in [28]). The leftward shift in IRT curves is consistent with the assumed role of hippocampus in timing accuracy [26,32,34]. For instance, hippocampal lesions have been observed to result in leftward shifts in bisection curves [32] and peak response curves [26,31,32]. Single cell recordings in DRL [35] and other tasks with time gaps [30] also revealed time-dependent activity of hippocampal cells. For instance, a subgroup of hippocampal cells gradually decreased their firing rate over the course of the trial until the emission of the response and went back to basal levels after responding in the DRL task [35].

On the other hand, the effect of hippocampal lesions on DRL performance might not be due to its effects on timing processes itself but primarily because of its disruption of inhibitory control over timed anticipatory responding. To that end, hippocampus might affect DRL responding by modulating nucleus accumbens (NAc) activity via gating its cortical inputs [36]. Based on previous studies, NAc core and its target structures indeed appear as possibly crucial structures in timed response inhibition. For instance, lesions of NAc core but not NAc shell cause a leftward shift in DRL response curve, which become more apparent with longer DRL schedules [37]. Biological and pharmacological manipulations of downstream regions of NAc core, such as blocking the NAc core–ventral pallidum GABAergic pathway [38] and lesions of subthalamic nucleus (STN) [39] also impair DRL performance. The effect of other downstream regions on DRL performance is not well investigated but an entopeduncular nucleus (or GPi in humans) inhibitory role on action (and increase in premature responses with its inactivation) has been shown using lesions and inactivation methods [40].

Excitatory and inhibitory connections between these basal ganglia structures and their effect on thalamus activity suggest that NAc core might modulate the output/manifestation of dorsal striatal temporal processing at multiple levels [7,41] (GPi/SNr and STN). Prefrontal inputs (e.g. anterior cingulate cortex, dorsal agranular insular areas, prelimbic cortex) to Nac core [42,43] are on the other hand potential candidates as the source of adaptive bias signal and its parametrization by timing uncertainty. Future neuroimaging studies can provide clues regarding the precise role of this network in adaptive timed response inhibition.

In summary, our results provided strong evidence for optimal temporal risk assessment performance of humans in a task that imposed a trade-off between the ‘speed’ and ‘accuracy’ of timed responses. This work further extended the scope of optimal temporal risk assessment performance to those conditions in which errors (i.e. premature responses) were penalized. These findings overall pointed at the robustness of reward maximization in the context of temporal decision-making. Importantly, optimal performance was observed in the absence of instructions and pre-training with task parameters, and purely based on experienced response-outcome contingencies constituting a better analogue of animal studies. Acquisition of optimal performance was rapid and abrupt; speed of acquisition was further facilitated by penalizing errors and higher working memory span. Future studies can investigate the neural correlates of timed response inhibition and its interaction with timing uncertainty focusing on the afferent and efferent projections of ventral striatum.

Funding statement

This work was supported by an FP7 Marie Curie grant PIRG08-GA-2010-277015 to F.B.