Imaging the wave functions of adsorbed molecules

Significance

In quantum mechanics, the electrons in a molecule are described by a mathematical object termed the wave function or molecular orbital. This function determines the chemical and physical properties of matter and consequently there has been much interest in measuring orbitals, despite the fact that strictly speaking they are not quantum-mechanical observables. We show how the amplitude and phase of orbitals can be measured in good agreement with wave functions from ab initio calculations. Not only do such measurements allow wave functions of complex molecules and nanostructures to be determined, they also open up a window into critical discussions of theoretical orbital concepts.

Abstract

The basis for a quantum-mechanical description of matter is electron wave functions. For atoms and molecules, their spatial distributions and phases are known as orbitals. Although orbitals are very powerful concepts, experimentally only the electron densities and -energy levels are directly observable. Regardless whether orbitals are observed in real space with scanning probe experiments, or in reciprocal space by photoemission, the phase information of the orbital is lost. Here, we show that the experimental momentum maps of angle-resolved photoemission from molecular orbitals can be transformed to real-space orbitals via an iterative procedure which also retrieves the lost phase information. This is demonstrated with images obtained of a number of orbitals of the molecules pentacene (C₂₂H₁₄) and perylene-3,4,9,10-tetracarboxylic dianhydride (C₂₄H₈O₆), adsorbed on silver, which are in excellent agreement with ab initio calculations. The procedure requires no a priori knowledge of the orbitals and is shown to be simple and robust.

As the electronic, optical, and chemical properties of nanostructures are defined by their electronic orbitals, in the last decades experimentalists have striven to image them. This is despite the fact that orbitals are not, strictly speaking, quantum-mechanical observables. Molecules are arguably the best-defined nanostructures, and for simple diatomic molecules, such as N₂, both the amplitude and the phase of the highest occupied molecular orbital (HOMO) in three-dimensional space have been recovered (1). This tomographic reconstruction requires higher harmonics generated from intense femtosecond laser pulses, focused on a series of molecular alignments, together with theoretical modeling (1). Although offering the exciting prospect of imaging orbitals on the time scale of chemical reactions, being both complex and only appropriate for simple molecules and orbitals, the technique is not generally applicable for the task of orbital reconstruction. Alternatively, scanning probe techniques offer real-space imaging of large molecules with submolecular resolution on surfaces. Although great advances have been made with understanding and controlling scanning probe tips, so-called “tip functionalization” (2), tips are still a factor of uncertainty. With an appropriate tip, the correct nodal structure of orbitals can be directly observed. Moreover, with tip molecules of p-wave structure the relative phase of the sample wave function may be inferred (3). Unfortunately, as the wave functions of the substrate generally spill out beyond the adsorbed molecules, decoupling layers such as NaCl are necessary to avoid direct tunneling into the substrate.

The full angle dependence of valence band UV photoelectron spectroscopy from molecular films has been shown to contain rich information on the orbital structure (4, 5). In the past few years a number of studies on molecular films have demonstrated a strong connection between the angular intensity distribution measured in UV photoemission experiments and the Fourier transform of the initial state orbitals (6–13). This relation can be justified in the so-called “one-step model” of the photoemission process, wherein the excitation occurs in a single step from an initial state to a final state (14). When approximating this final state by a free electron state, one can show that the photoemission intensity follows an angular dependence given by the Fourier transform of initial state wave function (15). Thus, it is tempting to use angle-dependent photocurrent data as measured in angle-resolved photoemission spectroscopy (ARPES) to recover the real-space distribution of the initial orbital by applying an inverse Fourier transform (6). However, this is not possible in general because the phase information of the wave function is lost in the measurement.

In this work, we develop an unbiased and widely applicable procedure, based on a scheme proposed for one-dimensional surface states confined by surface step edges of Au(111) (16), that can be used to regain the lost phase information and thereby enable the reconstruction of real-space orbitals. It only demands the wave function under study to be spatially confined. Here, we will assume that the wave functions are confined to a region defined by the van der Waals (vdW) size of the molecules, a requirement well-justified for many molecular adsorbate systems. Based on ARPES momentum maps of adsorbed monolayers on a Ag(110) surface, we demonstrate our method by reconstructing 2D orbital images of the lowest unoccupied molecular orbital (LUMO) and the HOMO of perylene-3,4,9,10-tetracarboxylic dianhydride (PTCDA), as well as of the LUMO, HOMO, and HOMO-1 of pentacene (5A) that are in remarkable agreement with one-electron wave functions from density functional theory (DFT). In the photoemission process it is not a priori clear that the one-electron orbitals should result. Indeed, in going from an N to an N − 1 final state, a Dyson orbital would be the more strictly correct description, a Dyson orbital representing the overlap between the N electron wave function with the N − 1 electron wave function before and after the ionization, respectively (17). In principle, Dyson orbitals should be based upon many-body perturbation theory and could include the molecule as well as the substrate. However, when computed within the framework of DFT and applied to isolated molecules, it has been shown that Dyson orbitals closely resemble one-electron initial state orbitals (9). Our results here also indicate that relaxation is often only playing a minor role and the frozen orbitals approximation is in fact reasonable.

Problem of the Phase

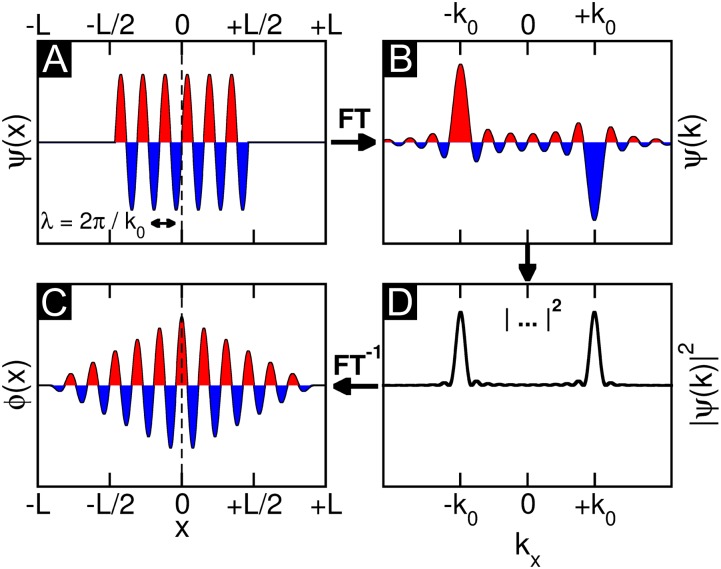
Fig. 1 illustrates the problem which one encounters when attempting to retrieve a real-space image of the orbital from an inverse Fourier transform of an experimental ARPES map. Fig. 1A shows a model wave function 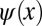in one dimension, which has a sinusoidal shape of wave number k₀ and is spatially confined to a region of length L. For instance, 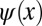could be viewed as a one-dimensional schematic representation of the HOMO of parasexiphenyl (6). When calculating its Fourier transform (FT) depicted in Fig. 1B, the wave function in momentum space 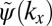is also antisymmetric and shows main peaks at ±k₀. Experimentally, the intensity distribution observed in angle-resolved photoemission experiments is proportional to the square of the absolute value 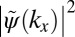. Thus, as evident from Fig. 1C, information on the sign of the wave function, or more generally on its phase, is lost in the measurement process. When attempting to obtain the spatial distribution of the orbital by performing an inverse Fourier transform (FT⁻¹) of its measured momentum distribution, one does not recover the original wave function 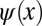, as can be seen from Fig. 1D. The resulting real-space function 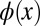has both the wrong phase (now being symmetric) and also a spatial extent which is twice as large (2L) as that of the original wave function 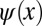. Mathematically, the so-obtained function 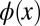is the autocorrelation of the wave function 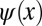with its complex conjugate. This shows that phase information is indeed crucial to obtain the correct real-space distribution of a molecular orbital from a momentum distribution measured via ARPES. In an earlier publication (6), we have suggested that in certain cases the missing phase information can be guessed and imposed onto the measured data, thereby enabling the reconstruction of real-space wave functions from ARPES data. However, such a procedure is biased and moreover not generally applicable.

Fig. 1.

Phase problem for a 1D wave function. (A) Model 1D wave function of sinusoidal shape with wave number k₀ and spatial extent L is Fourier transformed, yielding B. When taking the absolute value as in the measurement process (C) and subsequently transforming back to real space, the resulting real-space function D generally has the wrong phase and a spatial extent 2L, twice as large as the original wave function.

Iterative Phase Recovery

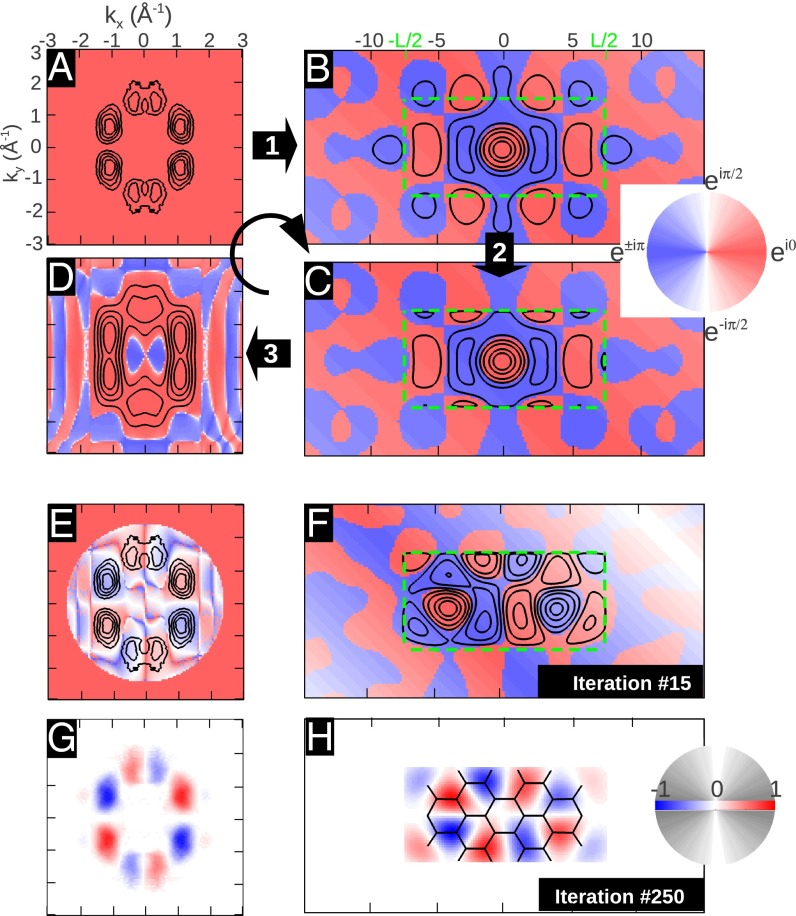
Fig. 2 illustrates how the phase information is recovered by an iterative procedure. The starting point is an experimental ARPES intensity map as shown in Fig. 2A. In this example, we use ARPES data taken from an ordered monolayer of PTCDA/Ag(110) containing only one molecule in the unit cell, recorded at a constant binding energy (CBE) of 1.9 eV below the Fermi level, which has been shown to correspond to the electron emission from the HOMO of PTCDA (7, 8). Note that the black isolines denote the square root of the ARPES intensity, i.e., the absolute value of the wave function 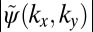, whereas the unknown complex phase 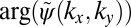is shown as a color map and arbitrarily set to a constant value in this case. In the first step of the iteration, an inverse FT leads to the real-space function displayed in Fig. 2B. As we have already noticed for the 1D example of Fig. 1, the resulting real-space function must be expected to have too large a spatial extent. Therefore, the second step consists of modifying outside a predefined spatial region. For simplicity, we choose a rectangular region (green dashed lines) of area 14.8 × 7.2 Ų, which roughly corresponds to the vdW size of PTCDA, and reduce 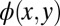by a given factor outside this confinement box. This leads to 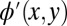shown in Fig. 2C. In the third step, an FT of 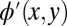yields the new momentum distribution 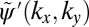in Fig. 2D, which differs from the original 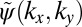in both absolute value (isolines) and phase (color map). To close the iteration loop, the new phase distribution of 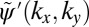is kept and imposed on the experimental ARPES map of Fig. 2A.

Fig. 2.

Iterative wave function reconstruction algorithm, using the example of the PTCDA HOMO. (A) Experimental ARPES momentum map. Black isolines represent the square root of the measured intensities, whereas the color indicates the phase. An inverse FT leads to B. The absolute value of the wave function is reduced to 10% outside the confinement box (green, dashed rectangle) in C; its FT leads to D. E and F, and G and H show the 15th and 250th step in the iterative procedure, respectively. In G and H, we show the real part of the reconstructed wave function, in k space and real space, respectively.

When continuing the steps of this iterative procedure, the resulting real-space function 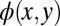gradually changes such that its probability density inside the confinement box is maximized. Interim results of the 15th and 250th iteration steps in momentum and real space are displayed in Fig. 2 E–H. Note that for the 250th iteration, after which no further change in the appearance of the wave function is seen, we have switched to a more conventional graphical representation of the wave function. Thus, Fig. 2 G and H display the real part of the wave function in momentum and real space, respectively, as a density plot, where red indicates positive and blue represents negative values.

Reconstructed Versus Theoretical Orbitals

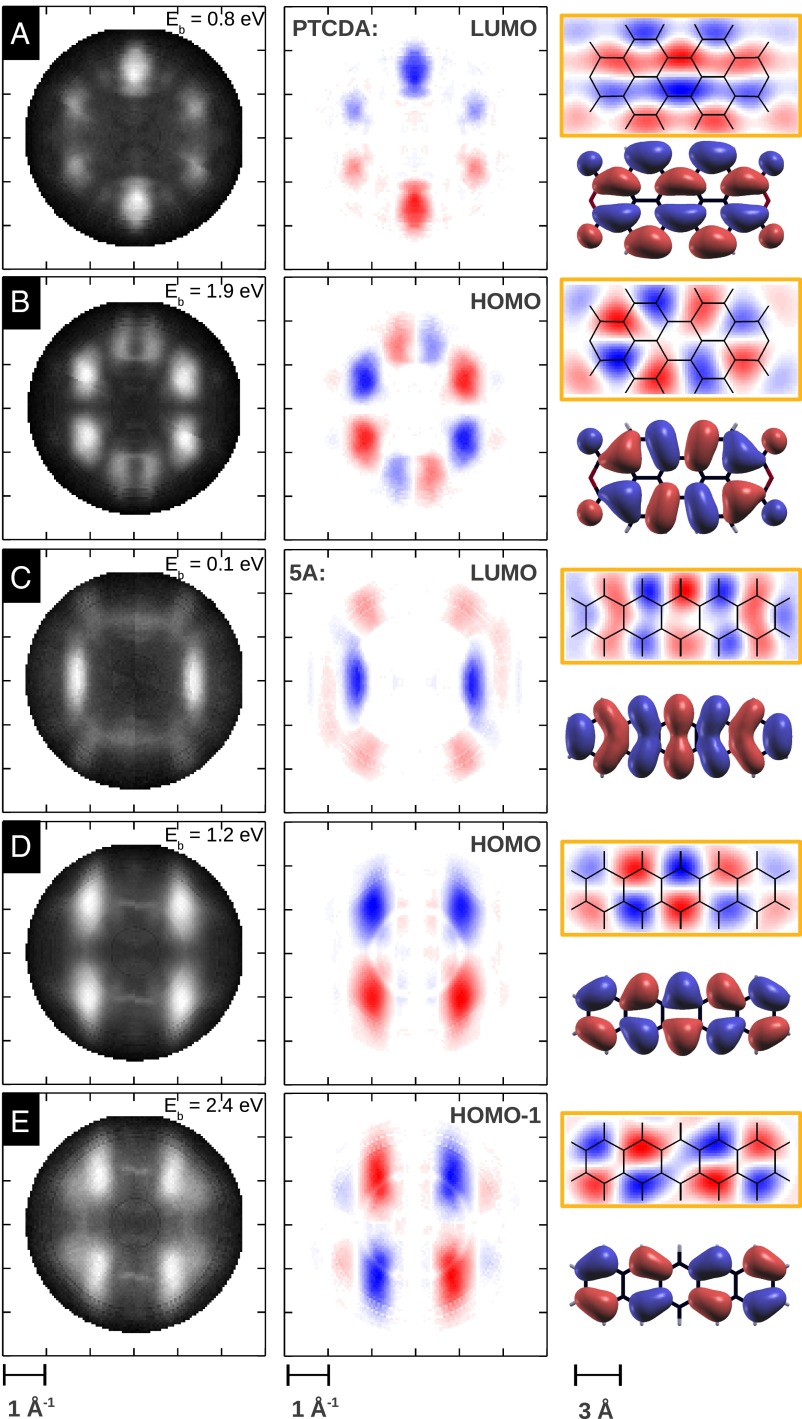
We have successfully applied this iterative procedure to a number of ARPES CBE 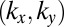maps of molecular monolayers adsorbed on metallic surfaces and retrieved the corresponding molecular orbitals. Fig. 3 compiles a set of five molecular orbitals which are discussed in this work. Fig. 3 A–E are CBE momentum maps of the PTCDA HOMO and LUMO (8), and of the HOMO-1, HOMO, and LUMO of pentacene. All data have been taken on well-ordered monolayers adsorbed on the Ag(110) surface. Upon bonding on the substrate, the molecular states are broadened into resonances where their full width at half maximum is only slightly broader than the 150–200-meV energy resolution of the toroidal electron energy analyzer. The CBE maps are taken at the binding energies indicated in Fig. 3 and show data integrated over an energy range of 60 meV. Due to energy resolution of the toroidal electron energy analyzer, however, the maps cover a somewhat larger energy window. Note that for both molecules, there is charge transfer from the metal into the molecule’s LUMO, thereby enabling its detection by the photoemission experiment.

Fig. 3.

Compilation of orbitals reconstructed from ARPES data in this work. (Left) Experimental CBE ARPES maps of the PTCDA LUMO (A) and HOMO (B), and the pentacene LUMO (C), HOMO (D), and HOMO-1 (E). (Center) CBE maps with the recovered phase information. (Right) Reconstructed real-space orbitals (orange box) which are compared with corresponding Kohn–Sham orbital images obtained from density functional theory (without box). The wave function confinement regions are 14.8 × 7.2 Ų and 14.8 × 5.4 Ų for PTCDA and pentacene, respectively.

When subjecting the experimental data to the iterative phase recovery, one obtains the orbital images depicted in Fig. 3 which are shown in comparison with the respective DFT orbitals calculated for the isolated PTCDA and pentacene. In all five cases, the reconstructed orbitals show an excellent agreement with the theoretical predictions, thereby demonstrating the power of the method. Comparing the experimental orbitals to the calculated one-electron orbitals of Fig. 3, two questions need to be considered: (i) What is actually displayed in a calculated orbital, and (ii) should it be expected to agree with the experimental orbitals? Clearly, in Fig. 3 not only are the nodal structures of the orbitals well reproduced, but also the sizes and shapes of the lobes in the patterns appear to be in excellent agreement between experiment and theory. Usually, 3D theoretical orbitals are represented by isosurfaces, where the sizes and shapes of the lobes in theoretical orbital images are influenced by the choice of the isovalue; isosurfaces displayed in Fig. 3 are 10% isosurfaces, as commonly used in displaying calculated orbitals, i.e., 90% of the charge density is located within the displayed surface. Clearly this fits our experimental data well, whereas for scanning tunneling microscopy (STM) images DFT orbitals with ∼1% isosurfaces (enclosing 99% of the charge) seem to match the HOMO and LUMO of 5A (18). This is presumably due to the STM tip probing the probability density well above the molecule. A comparison of our data with STM results can be found in Fig. S1. An alternative way of comparing the theoretical with the orbitals reconstructed from ARPES is to represent also the theoretical orbitals as 2D plots. For the π-orbitals of the planar molecules treated in this work, this can be accomplished by projecting out the z dependence of carbon p_z orbitals. This leads to the images shown in Fig. S2, which is a duplicate of Fig. 3 except for the theoretical orbital images which are replaced by the 2D projections mentioned above.

Of particular note in the shape agreement between the reconstructed orbitals and the calculated ones are, for instance, the asymmetric curvatures on each side of the lobes close to the long axis of the PTCDA LUMO, or the increasing bend in the lobes of the 5A LUMO moving from the center to the end of the molecule. The 5A HOMO data show clearly that the quasiperiodicity of the electron density is larger than the periodicity of the carbon backbone. This leads to the density shifting from the apex carbon sites in the center of the molecule to the bond between the apex and the terminal carbons at the end of the molecule. Such a shift would not be expected for an infinitely long acene. On careful inspection there are some features in the reconstructed orbitals which differ from those of the calculated orbitals of isolated molecules. For instance, the outermost lobes of the 5A LUMO, although showing a maximum on the long molecular axis, have extensions perpendicular to it that are greater than predicted by the calculation. Also, the lobe shape of the PTCDA HOMO is not in perfect agreement with the 10% isosurface DFT orbital. On assessing the agreement or disagreement of reconstructed orbitals with calculated ones in Fig. 3, it has to be kept in mind that an agreement with orbitals calculated for isolated molecules is perhaps remarkable, because reconstructed orbitals are for molecules adsorbed on a surface. Although the interaction with Ag is relatively weak, there is charge transfer to the LUMOs in both cases and thus orbital distortions cannot be ruled out.

As in the discussion above, generally the comparison of experimental and calculated orbitals has been subjective (1, 18). In contrast, our data, having both the phase information and more than one orbital for one molecule, allow a more critical analysis of how good the experimentally obtained wave functions are. Because orbitals of any particular system are orthogonal to each other, we can use this criterion to show that our reconstructed orbitals are indeed realistic in the quantum-mechanical sense. In the case of PTCDA, the calculated overlap between the experimental HOMO and LUMO is 10% (90% orthogonality). For 5A the three orbital combinations yield even better orthogonalities in the range of 93–99%. This not only suggests the orbitals to be objectively good, it also provides the possibility of introducing a further objective criterion in the reconstruction procedure, if deemed necessary.

How Can the Lost Phase Be Recovered?

Several questions may be posed concerning the mathematical procedure to recover the unknown phase: (i) How can the phase be restored from intensity information only? (ii) How stable is the procedure, e.g., do results depend on the chosen initial phase or the assumed confinement box size? (iii) How can 2D momentum maps be used to get information on 3D orbitals?

• i)At first glance, it appears that the phase information is created from nowhere, because intensity information in momentum space eventually leads to intensity and phase information in real space. However, considering the well-known properties of discrete FTs and the fact that the wave function goes to zero outside the confining box, this apparent underdeterminacy can be resolved. Our data resolution in momentum space of 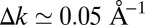converts to a real-space domain size of 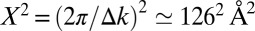. Comparing this with the area of the molecule A, the so-called oversampling ratio X²/A amounts to ≃ 150. By forcing the wave function to be zero in the large area outside the molecular region during the iterative procedure, the missing phase information is compensated. Successful orbital reconstruction requires an oversampling ratio of at least 2 but, as is the case here, the algorithm becomes more stable if the ratio is larger.
• ii)For starting the iterative phase recovery, an initial guess of the phase has to be made. In the example of Fig. 2, a constant k-independent phase has been chosen. However, a random k_x- and k_y-dependent starting phase leads essentially to the same result, as evidenced in Fig. S3. That such an extremely different and even unphysical starting point leads to the same result emphasizes the robustness of the orbitals shown in Fig. 3 with respect to the initial choice of phase. The question of how to select a suitable confinement region is slightly more subtle. Firstly, it is evident from the mathematical properties of FTs that the real-space orbitals 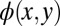are only determined up to an arbitrary translation vector 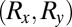. Because the FT of the translated orbital 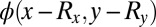differs from that of 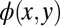only by a k-dependent phase factor, an incorrect confinement box results in orbitals 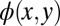which may be arbitrarily translated inside the confinement box. This can be seen clearly as a 0.3-Å shift in the 5A LUMO of Fig. 3C when using a box size appropriate for the HOMO wave function in Fig. 3D. The problem of cyclical translation within the confinement box is even more pronounced for the HOMO-1 of 5A (Fig. S4). For objectivity, and to emphasize the robustness of the procedure, we have chosen a simple rectangular box with constant size for all pentacene orbitals. Only for HOMO-1 is the orbital’s overall position fixed by imposing inversion symmetry in the iterative procedure.
• iii)The last question concerns the fact that the reconstructed orbital images shown in Fig. 3 are interpreted as planar 2D sections through 3D orbitals. Such a simplified relation is possible because all wave functions studied in this work are π-orbitals belonging to nearly planar molecules. In such cases, the 3D structure of orbitals in momentum space is dominated by features with a weak k_z dependence that is essentially equal to that of an atomic p_z state, as is exemplified for the HOMO of pentacene in figure 2B of ref. 6. Therefore, the hemispherical cut through 3D momentum space measured in ARPES may be interpreted as a 2D cut through the real-space π-orbital. We emphasize, however, that our phase recovery method is not restricted to such cases. By measuring CBE momentum maps for various photon energies, the full 3D structure of the orbital in momentum space may be mapped out, with which it should be possible to reconstruct the complete 3D orbital structure in real space.

Potentials and Limitations

The simple FT relation between real and reciprocal space strictly holds only for a plane wave (PW) final state. Note that the more complex independent atomic center description of the photoemission process reduces to the PW final state when the atomic sites have the same atomic orbitals and when the experimental geometry is such that the polarization vector and emitted electrons are close to each other (6). This is the case for the molecules investigated here. Moreover, as they contain only light atoms, scattering effects are expected to be small, and the results presented here for delocalized π-orbitals indicate that the PW final state approximation is in fact reasonable. Related to the issue of scattering, we have observed no differences for different molecular orientations and/or substrate surfaces. For instance, the reconstructed HOMOs of pentacene on silver and copper are essentially identical, although the molecules align across and along the atomic rows of the substrate, respectively. As yet we have come across no system in which the PW final state fails. However, it is possible that for molecules containing high-Z atoms scattering may become problematic.

As opposed to local scanning probe techniques, our photoemission momentum maps collect the emitted electrons from large sample areas. Thus, our method works best, without the need of deconvolution, when the molecules all have the same orientation. This is often the case on anisotropic substrates such as the (110) surfaces of face-centered cubic metals, as used in this work. The results here have been obtained for well-ordered monolayers. However, long-range order is not a prerequisite. Indeed, it can be detrimental, as significant intermolecular orbital overlap could lead to strongly dispersing bands, such that a description in terms of molecular orbitals is no longer appropriate. This is for instance the case for the LUMO of the monolayer of pentacene on Cu(110). Interestingly, however, at lower coverages the molecules remain aligned while diffusing over the surfaces at room temperature, and the orbital reconstruction is possible.

In conclusion, we have demonstrated that both the amplitude and the phase of the wave functions of adsorbed molecules can be simply recovered from angle-resolved photoemission data. The orbitals obtained are not only in qualitatively good agreement with calculated orbitals, they also possess the orthogonality required of true wave functions. As such, the results open up a window into discussions of theoretical orbital concepts. On the more applied side, as the phase recovery procedure makes almost no assumptions, we believe ultimately it should be possible to obtain the orbital structure even of unknown molecules such as species formed in surface reactions. We foresee that with the new generation of electron analyzers with large acceptance angles that are now commercially available, the technique of orbital reconstruction will find many applications.

Materials and Methods

Experimental Details.

Experiments were performed in situ in ultrahigh vacuum with the toroidal electron analyzer (19) attached to the U125/2-SGM beamline at the Helmholtz Zentrum Berlin - Electron Storage Ring BESSY II. A photon energy of 30 eV and a photon incidence angle of 40° with respect to the surface normal were used. The polarization direction is in the specular plane, containing the measured photoelectron trajectory. The toroidal energy analyzer collects photoelectrons in a kinetic energy window of 1-eV width over a polar emission angular range of θ = ±80° simultaneously. The full hemisphere of emitted electrons was obtained by rotating the azimuthal angle ϕ in 1° steps. The angular emission data were converted to parallel momentum components 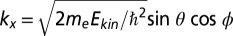and .

The Ag(110) substrate was cleaned in situ by standard sputter anneal cycles. The molecules were evaporated from effusion cells onto the substrate at room temperature and their monolayers controlled by low-energy electron diffraction. For pentacene a 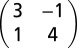monolayer structure was investigated where the majority of the molecules are oriented parallel to the [001] azimuth. For PTCDA the so-called brick wall monolayer structure c(4 × 6) was investigated with all of the molecules also parallel to [001].

Computational Details.

Theoretical orbitals are obtained within DFT using the ABINIT code (20). The all-electron potentials are replaced by extended norm-conserving, highly transferable Troullier–Martins pseudopotentials (21), with a plane-wave cutoff of 50 Rydberg. Interaction between molecules is avoided by a super cell approach with a box size of 50 × 50 × 25 Bohr³ and Γ-point sampling of the Brillouin zone. In the iterative procedure we make use of the oversampling method developed from coherent diffraction techniques (22, 23). Thereby, we take advantage of a dense experimental sampling in momentum space 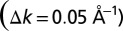which leads to a real-space domain size 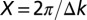much larger than the typical size of molecules. We implement a modified version of the Fineup algorithm (22, 24), as explained in the Iterative Phase Recovery section.