Plakilactones G and H from a marine sponge. Stereochemical determination of highly flexible systems by quantitative NMR-derived interproton distances combined with quantum mechanical calculations of ¹³C chemical shifts

Abstract

In this paper the stereostructural investigation of two new oxygenated polyketides, plakilactones G and H, isolated from the marine sponge Plakinastrella mamillaris collected at Fiji Islands, is reported. The stereostructural studies began on plakilactone H by applying an integrated approach of the NOE-based protocol and quantum mechanical calculations of ¹³C chemical shifts. In particular, plakilactone H was used as a template to extend the application of NMR-derived interproton distances to a highly flexible molecular system with simultaneous assignment of four non-contiguous stereocenters. Chemical derivatization and quantum mechanical calculations of ¹³C on plakilactone G along with a plausible biogenetic interconversion between plakilactone G and plakilactone H allowed us to determine the absolute configuration in this two new oxygenated polyketides.

Introduction

In recent years the quantum mechanical (QM) calculation of NMR parameters [1–6] has been demonstrated to be a valid tool for the stereostructural determination of organic compounds [7–17], especially for high flexible systems. Recently, an additional method has been proposed for the relative configuration assignment based on experimental interproton distances derived from a quantitative and accurate NOEs analysis [18]. These quantitatively measured NOEs have been initially developed for the stereochemical assignments of rigid molecular frameworks, as the NOE analysis is complicated due to equilibriums between multiple conformers, which are present in highly flexible molecules. Recently, the quantitative NOE-based method has been extended to relatively flexible compounds, and the reliability of the approach for the analysis of multiconformational systems was shown [19–20].

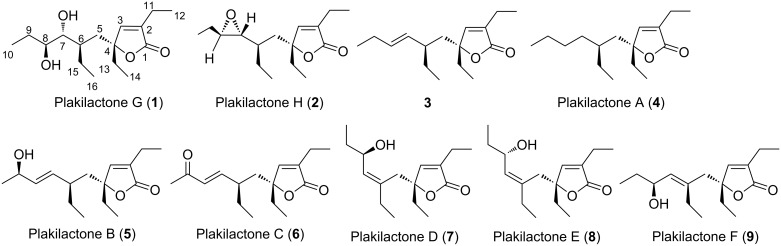
Due to the huge chemical variety of secondary metabolites from natural sources, the identification of the configuration of highly flexible compounds is still a great challenge. We recently demonstrated that an integrated approach combining quantitative NOE-based protocol in parallel with the quantum mechanical calculation of ¹³C chemical shifts leads to a better discrimination of stereochemical configurations of a rigid natural product scaffold [21]. In the present contribution, we propose to extend our integrated approach to the substantially more challenging stereochemical configurations of two new conformationally flexible oxygenated polyketides, plakilactone G (1) and H (2) (Figure 1), isolated from a Fiji collection of the marine sponge Plakinastrella mamillaris.

Figure 1.

Plakilactones G and H, new oxygenated polyketides from Plakinastrella mamillaris, and their congeners previously reported.

Results and Discussion

Isolation and determination of the constitution of plakilactones G and H

The chloroform extract from the Kupchan partitioning procedure [22] on the lyophilized material (171 g) of P. mamillaris Kirkpatrick, 1900 (Homoscleromorpha) afforded plakilactones B–F, previously reported as a new chemotype of PPARγ modulators [23], together with two new oxygenated polyketides, plakilactones G (1) and H (2). As depicted in Figure 1, 1 and 2 share with other members of this family a large portion of their chemical scaffold including the γ-lactone moiety and the ethyl-branched side chain. Even if the absolute configuration at C-4 and C-6 has been previously determined for plakilactone A (4) and notably for the corresponding 7,8-dehydroderivative (3) [23], that is likely the biosynthetic precursor of all side-chain-oxidized derivatives belonging to this family, this information was not considered for the validation of our protocol and all four stereocenters for plakilactones G and H have been investigated.

Plakilactone G (1) was isolated as a colorless oil, [α]_D²⁵ −75.5 (c 0.11, CHCl₃), and had a formula of C₁₆H₂₈O₄ inferred from high resolution mass spectrum (HRMS–ESI). ¹H and ¹³C NMR data (Table 1) indicated the presence of four ethyl groups, one methine, one methylene, one substituted double bond, one quaternary and two secondary oxygenated carbons and one acyl group. The acyl carbon signal at 175.9 ppm (C-1), along with the oxygenated carbon resonance at δ_C 91.9 (C-4) suggested the presence of a lactone. The olefinic methine carbon at δ_C 153.5 (C-3) with the quaternary carbon at δ_C 136.6 (C-2) completed the five-membered α,β-unsaturated lactone ring. The linkage of an ethyl side chain at C-2, suggested by the long range allylic coupling between protons H-3 and H₂-11, was supported by the diagnostic HMBC correlations H-3/C-11 and H₃-12/C-2 (Figure 2). A second isolated ethyl system was linked at C-4 on the basis of the HMBC correlation H₃-14/C-4. Due to the fortuitous coincidence of the chemical shift of some protons in the side chain (e.g. H-7 and H-8; H-6 and H₂-15) and the absence of a detectable homonuclear coupling between H-6 and H-7 protons, the analysis of the COSY spectrum only allowed for the identification of some separated subunits, which were eventually connected on the basis of diagnostic long-range correlations from the HMBC spectrum. In detail, the long range correlation H-7/C-8 implied the C-7/C-8 linkage; the correlation H₃-16/C-6 supported the attachment of an ethyl group at C-6; the correlations H-7/C-15 and C-5 connected C-6 to C-7 (Figure 2). Finally the dihydroxylated C₈ side chain was linked to C-4 on the basis of HMBC correlations H-5/C4 and C-13, leading to the constitution as depicted in Figure 2.

Table 1.

¹H and ¹³C NMR data (500 and 125 MHz, CD₃OD) of plakilactones G (1) and H (2).

	1			2
position	δHa	δC	HMBC	δHa	δC	HMBC
1	–	175.9		–	175.5
2	–	136.6		–	136.6
3	7.11 br t (1.5)	153.5	C1, C2, C4, C11	7.12 br t (1.2)	153.0	C1, C2, C4, C11
4	–	91.9		–	90.7
5	2.04 d (14.7) 1.64 dd (6.0, 14.7)	36.6	C3, C4, C6, C7, C13, C15 C3, C4, C6, C13, C15	1.95 dd (5.2, 14.7) 1.87 ovl	40.0	C3, C4, C6, C7, C13, C15 C3, C4, C6, C7, C13, C15
6	1.43 ovl	37.4		0.91 ovl	39.5	C4, C7
7	3.33b	75.3	C5, C8, C15	2.50 dd (2.0, 8.0)	63.3	C6, C9, C15
8	3.32b	73.9	C7	2.69 ddd (2.0, 5.6, 7.5)	61.6	C9
9	1.76 m 1.34 m	27.4	C10 C8, C10	1.54 m	26.0	C8, C10
10	1.00 t (7.4)	10.1	C8, C9	0.98 t (7.5)	9.9	C8, C9
11	2.28 q (7.5)	19.2	C1, C2, C3, C12	2.26 q (7.5)	19.3	C1, C2, C3, C12
12	1.17 t (7.5)	12.1	C2, C11	1.16 t (7.5)	12.3	C2, C11
13	1.85 m	32.1	C3, C4, C5, C14	1.86 ovl, 1.84 m	31.8	C5, C14
14	0.81 t (7.5)	7.8	C4, C13	0.81 t (7.3)	7.8	C4, C13
15	1.43 ovl	26.2	C6	1.44 m 1.39 m	26.9	C5, C6, C7, C16 C5, C6, C7, C16
16	0.85 t (6.8)	11.6	C6, C15	0.91 t (7.5)	11.8	C6, C15

^aCoupling constants are in parentheses and given in Hertz. ¹H and ¹³C assignments aided by COSY, HSQC and HMBC experiments. ^bOverlapped with solvent signal; ovl: overlapped with other signals.

Figure 2.

COSY connectivities (bold bonds) and selected HMBC (arrows) correlations for plakilactones G (1) and H (2).

Plakilactone H (2) was isolated as a colorless oil, [α]_D²⁵–47.9 (c 0.07, CHCl₃) and showed a molecular formula of C₁₆H₂₆O₃ as deduced by HRMS–ESI analysis. The proton and carbon signals of the 2,4-diethyl γ-lactone were almost identical to those of the corresponding part of plakilactone G (1), whereas differences were observed in the C-8 side chain. Two mutually coupled signals at δ_H 2.50 (dd, J = 2.0 and 8.0 Hz) and 2.69 (ddd, J = 2.0, 5.6, 7.5 Hz), observed in the ¹H NMR spectrum, were found to correlate in the HSQC spectrum with two oxygenated carbons at δ_C 63.3 and 61.6, respectively, and were assigned to an epoxy ring. The localization of the epoxy functionality at C-7 and the structure (Figure 2) of the side chain was easily inferred from the analysis of the COSY spectrum and confirmed by key HMBC correlations (Table 1 and Figure 2). The connection of the side chain to C-4 was established by long-range couplings observed between the two diasterotopic methylene protons at C-5 and the C-3 and C-4 carbons of the lactone ring. Therefore the constitution of plakilactone H (2) was determined as shown in Figure 2.

Determination of the relative configuration of plakilactone H (2)

The better dispersion of proton resonances in the ¹H NMR spectrum of plakilactone H inclined us to first address the configurational assignment of plakilactone H.

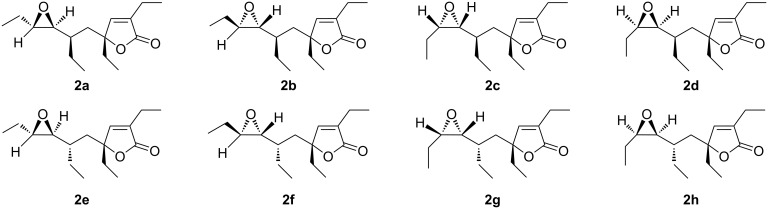
Molecular dynamics and Monte Carlo conformational search calculations were performed on all possible diastereoisomers of 2 (Figure 3) by using the MMFFs [24] force field (MacroModel software package [25]) in the presence of chloroform (continuum model). Over 200 conformers were found for each of the stereoisomers for 2a–h (see Experimental), and their geometries were optimized at the DFT theoretical level by using the MPW1PW91 functional and 6-31G(d) [26] basis set (Gaussian 09 Software Package [27]). From the DFT-optimized geometries interproton distances were calculated, accounting the Boltzmann-weighted average derived from the energies of the single conformers.

Figure 3.

Molecular structure of the eight possible diastereoisomers of plakilactone H (2).

For the analysis, we applied the previously described method [18–21], firstly recording different 1D NOESY spectra, irradiating at diverse resonances. In particular, the NOE coupling between vicinal protons H-15b–H-16 were chosen as the reference NOE for the 1D NOESY data set and the derived distance was adjusted for each stereoisomer in order to get the lowest MAE. To narrow the number of diastereoisomers, we initially analysed the relative configuration of C-7 and C-8, to disclose if the substituents of the epoxide are cis or trans-configured.

The observed absolute differences for calculated versus NOE-derived distances/calculated distances (Table 2) suggested a trans-configuration for the epoxide (MAE of 4.7% vs 20.7% for cis-isomer) ring. The next step was the analysis of the four diastereoisomers 2a,b,e,f endowed with the epoxide moiety in a trans-configuration, by comparing the experimental vs the calculated distances (Table 3). In Table 3 only a subset of all values was used for the stereochemical structure elucidation, more specifically, the values where DFT-calculated interproton distances for 2a,b,e,f differed by more than 0.03 Å (≈ 1%) from each other. The data reported in Table 3 clearly show that the diastereoisomer 2b represents the best fit with the experimentally derived distances (MAE 4.1% and standard deviation (STD) 5.0%). The stereoisomers 2a, 2e and 2f poorly agree with the NOE-derived distances. The maximum error shown by the calculated distances for 2b is 9.4%, whereas the other stereoisomers have at least three calculated distances with an associated error higher than 10%. The largest errors (>10%) are relative to protons around the stereocenters under investigation. For 2a, we observed an error of 25.3% for the distance between H-16–H-8 and 12.2% for the protons H-3–H-13a. The calculated interproton distance H-3–H-6 presents an error of 14.7%, whereas the distance H-15b–H-6 has an error of 11.8%. It is noteworthy that 2a has the key distance between H-6 and H-8 with a quite high error of 9.8%. Concerning the diastereoisomer 2e, largest errors are observed for the distances of H-3 with H-6 (11.3%) and H-14 (17.2%). The H-6–H-15b distance has an error of 12.5%, and H-6 shows a large deviation with H-5b of 11.5%. As for 2a, a huge error (39.7%) for the H-16–H-8 distance was found in diasteroisomer 2f. In addition, H-5b presents large deviations from the experimental about distances with H-6 (19.0%) and H-7 (10.6%) and a deviation >10% for the interproton distances of H-15a–H-8 (13.0%), H-7–H-10 (11.4%) and H-15a–H-16 (10.5%) was also observed.

Table 2.

Comparison of interproton distances determined by NOEs for plakilactone H (2) in CDCl₃ with DFT-calculated values for 2b and 2c. Values in bold were used to calibrate the NOEs.

			2b		2c
proton		exp RNOE (Å)	Rcalcd (Å)	ABS % errora	Rcalcd (Å)	ABS % errora
H16	H15b	2.75	2.75	–	2.75	–
H8	H9	2.68	2.73	1.8%	2.72	1.5%
H8	H10	3.27	3.02	7.9%	2.95	10.1%
H8	H6	2.32	2.44	4.9%	3.80	48.4%
H7	H9	2.65	2.71	2.1%	3.93	38.7%
H7	H10	3.60	3.39	6.1%	4.71	26.8%
H7	H6	2.94	3.03	2.9%	3.07	4.2%
MAEb				4.7%		20.7%
STD				2.9%		17.3%

^a|% error| = |R_calcd − R_NOE|/[(R_calcd + R_NOE)/2], absolute differences for calculated versus NOE-derived distances/calculated distances. ^bMAE = Σ[% error]/n.

Table 3.

Comparison of interproton distances determined by NOEs for plakilactone H (2) in CDCl₃ with DFT-calculated values for 2a,b,e,f. Values in bold were used to calibrate the NOEs.

			2a		2b		2e		2f
proton		exp RNOE (Å)	Rcalcd (Å)	ABS % errora	Rcalcd (Å)	ABS % errora	Rcalcd (Å)	ABS % errora	Rcalcd (Å)	ABS % errora
H16	H15b	2.75	2.75	0.0%	2.75	0.0%	2.71	1.5%	2.72	1.1%
H16	H8	3.32	4.28	25.3%	3.37	1.5%	3.40	2.4%	4.97	39.7%
H3	H11	3.14	3.33	5.9%	3.37	7.1%	3.27	4.1%	3.26	3.9%
H3	H5b	2.90	2.81	3.2%	2.74	5.7%	2.84	2.2%	2.76	5.0%
H3	H13a	2.85	3.22	12.2%	2.86	0.4%	3.00	5.0%	2.89	1.3%
H3	H12	3.20	3.03	5.5%	3	6.5%	3.01	6.3%	3.04	5.2%
H3	H14	3.11	3.08	1.0%	3.3	5.9%	3.70	17.2%	3.43	9.8%
H3	H6	3.22	3.73	14.7%	3.13	2.8%	3.61	11.3%	3.08	4.6%
H8	H9	2.68	2.71	1.1%	2.68	0.0%	2.66	0.7%	2.66	0.7%
H8	H10	3.21	3.03	5.8%	3.09	3.8%	3.00	6.9%	3.01	6.5%
H8	H6	2.32	2.56	9.8%	2.44	5.0%	2.50	7.6%	2.44	5.2%
H7	H5b	2.64	2.77	4.8%	2.79	5.5%	2.68	1.5%	2.37	10.6%
H7	H9	2.65	2.71	2.2%	2.77	4.4%	2.72	2.6%	2.66	0.4%
H7	H15a	2.73	2.97	8.4%	2.59	5.3%	2.82	3.2%	2.90	6.0%
H7	H10	3.54	3.76	6.0%	3.39	4.3%	3.44	2.9%	3.97	11.4%
H7	H16	3.44	3.21	6.9%	3.39	1.5%	3.48	1.1%	3.44	0.1%
H7	H6	2.94	2.69	8.9%	3.03	3.0%	2.91	1.1%	2.94	0.1%
H5b	H13a	2.67	2.82	5.5%	2.52	5.8%	2.75	2.9%	2.54	4.9%
H5b	H6	3.23	2.94	9.4%	2.98	8.1%	2.88	11.5%	2.67	19.0%
H5b	H14	3.04	2.99	1.7%	3.28	7.6%	3.04	0.2%	3.35	9.8%
H15b	H6	2.97	2.64	11.8%	2.91	2.0%	2.62	12.5%	2.69	9.9%
H15a	H8	3.44	3.24	6.0%	3.66	6.2%	3.38	1.8%	3.92	13.0%
H9	H10	2.74	2.75	0.3%	2.75	0.3%	2.71	1.2%	2.72	0.8%
H15a	H16	3.02	2.75	9.4%	2.75	9.4%	2.71	10.9%	2.72	10.5%
H12	H11	2.76	2.75	0.3%	2.75	0.3%	2.71	1.8%	2.72	1.4%
MAEb				6.6%		4.1%		4.8%		7.2%
STD				8.7%		5.0%		6.7%		11.1%

^a|% error| = |R_calcd − R_NOE|/[(R_calcd + R_NOE)/2], absolute differences for calculated versus NOE-derived distances/calculated distances. ^bMAE = Σ[% error]/n.

In previous papers [18–21], describing the accurate measurement of interproton distances from NOE, it was established that the expected MAE and STD are both around 5% or less for rigid and simple flexible molecules, and substantial individual errors of more than 10% are indicative of incorrect assignments. In this more complex, flexible molecule we found a MAE of 4.1% and a STD of 5.0% for 2b, which are in line with correct assignments obtained in our earlier studies. For example, the obtained MAE for 2b is identical to the MAE obtained for the previously reported test case of strychnine in CDCl₃ [18]. On the other hand, the obtained MAE and STD for 2a,e,f are all out of the expected range, although 2e has a nearly acceptable MAE value, the range of error (as represented by an STD of 6.7%) is too wide, and five of the individual distances have errors of ≥10% (underlined values in Table 3).

The results derived from NOE analysis were confirmed by QM calculation of ¹³C chemical shifts. On the refined geometries at the DFT theoretical level for 2a,b,e, and f, ¹³C chemical shift values were calculated by using the MPW1PW91 functional and the 6-31G(d,p) basis set [26] (Gaussian 09 Software Package [27]) and taking into account the Boltzmann-weighted average derived from the energies of the single conformers. The analysis was carried out with linear regression analysis by using values as intercept and slope, which were obtained at the same level of theory for a set of known natural compounds [26]. Moreover, we considered the diagnostic carbons and calculated the difference with the experimental values that were re-acquired and reassigned in CDCl₃ (Supporting Information File 1, Table S1), to avoid the introduction of explicit solvent molecules in the calculations, as required for a polar and protic solvent such as methanol. Comparison of predicted ¹³C chemical shifts for 2a,b,e,f with the experimental values (Table 4) suggests the best fit with the experimental data for stereoisomer 2b. In particular, 2a presents a MAE more than twice the value found for 2b. The MAE of 2e is almost twice the value of 2b. By analysing the |Δδ| for carbon atoms around C-6, we find largest errors for the calculated ¹³C chemical shifts of 2e, except for C-14 (Table 4). In detail, for C-5 and C-13 of 2e the |Δδ| are 1.5 and 2.1, vs 1.1 and 1.0 of 2b. For C-15 and C-16, the |Δδ| are 1.3 and 1.3 for 2e, whereas for 2b they are 1.3 and 0.0, respectively. Moreover, we observe large deviations from the experimental values for C-8 and C-9 of 2e. Indeed, the |Δδ| of C-8 and C-9 are 1.7 and 1.1, compared to 0.1 and 0.7 for 2b. A smaller difference for the MAE values calculated for 2b and 2f is observed. The stereoisomer 2b shows all calculated ¹³C values falling in the proposed error limit of 2 ppm. For 2b, we observed a maximum error of 1.5 ppm. On the other hand, we found a |Δδ| of 2.5 ppm for 2f. Parallel with the MAE and |Δδ| analysis, we compared the calculated ¹³C chemical shifts with the experimental values by using the DP4 probability [28]. This analysis also shows that the best fit with the experimental chemical shifts are found for 2b, which has 78.9% of DP4 probability (Table 4). The 2a, 2e and 2f present low DP4 probability values: 1.5%, 3.9% and 15.7%, respectively (Table 4). The stereostructural analysis by the DFT-NMR approach agrees with the outcomes obtained by the accurate NOE-distance method, confirming the relative configuration of plakilactone H as in diastereoisomer 2b.

Table 4.

Comparison of calculated (in vacuo) vs experimental (in CDCl₃) ¹³C NMR chemical shifts of stereoisomers 2a,b,e and f.

		2a		2b		2e		2f
carbon	δexp	δcalcd	|Δδ|a, ppm	δcalcd	|Δδ|a, ppm	δcalcd	|Δδ|a, ppm	δcalcd	|Δδ|a, ppm
10	9.7	10.8	1.1	9.6	0.1	9.6	0.1	10.8	1.1
9	24.9	25.7	0.7	25.6	0.7	26.0	1.1	25.1	0.2
8	60.9	58.5	2.3	61.0	0.1	59.1	1.7	62.1	1.3
7	62.1	59.5	2.6	60.6	1.5	60.5	1.6	61.1	1.0
6	38.3	36.1	2.2	37.9	0.3	38.8	0.5	36.4	1.8
5	39.2	36.7	2.5	40.3	1.1	40.6	1.5	39.3	0.1
13	31.2	30.7	0.5	32.2	1.0	29.1	2.1	32.6	1.5
14	7.7	7.9	0.1	6.9	0.9	7.4	0.3	6.8	0.9
15	25.8	28.2	2.3	27.1	1.3	27.1	1.3	26.1	0.3
16	11.4	10.0	1.4	11.4	0.0	10.1	1.3	8.9	2.5
MAEb			1.6		0.7		1.2		1.1
DP4c			1.5		78.9		3.9		15.7

^a|Δδ| = |δ_exp − δ_calcd|, absolute differences for experimental versus calculated ¹³C NMR chemical shifts. ^bMAE = Σ[|δ_exp − δ_calcd|]/n. ^cDP4 probabilities were obtained considering all the calculated chemical shifts , as proposed by Smith and Goodman [28].

Determination of the absolute configuration

The 1,2-diol substructure in plakilactone G (1) allowed the configurational assignment of the C-7 and C-8 contiguous stereocenters through chemical derivatization. Thus, plakilactone G (1) was converted to the corresponding 7,8-O-isopropylidene derivative by treatment with 2,2-dimethoxypropane and a catalytic amount of p-TsOH. As reported in the literature [29], the difference in the chemical shifts of the methyl groups in the five membered acetonide is larger for the cis-isomer (Δδ 0.12–0.14) when compared to the trans-isomer (Δδ 0.01–0.04). The observed Δδ value of 0.10 ppm between the two methyl groups in the plakilactone G acetonide (see Experimental) points towards the cis-isomer allowing us to suggest a 7,8-erythro relative stereochemistry.

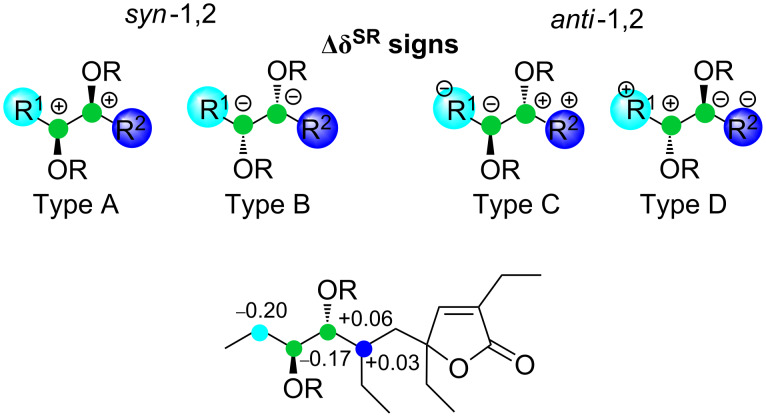
The application of the double derivatization method with a chiral auxiliary reagent developed by Riguera [30] allows for the confirmation of the relative configuration at C-7 and C-8 and the assignment of the absolute configuration at C-7 and C-8. Through theoretical calculation and experimental data, Riguera demonstrated that bisphenylacetic acid ester derivatives of a diol with two asymmetric carbons have a specific and distinctive distribution of Δδ^SR signs, determined by a combined anisotropy effect of the two auxiliares. The Δδ^SR distribution model for a bisMTPA derivative of an acyclic 1,2-diol is shown in Figure 4. Thus, esterification of plakilactone G (1) with (−)- and (+)-MTPACl in pyridine led to bisMTPA derivatives which Δδ^SR distribution is reported in Figure 4. The observed sign distribution model is consistent with anti-1,2-diol type C. Therefore the 7R,8S configuration is assigned. Notably, considering the plausible biogenetic interconversion of an epoxide and a diol, the above absolute configuration at C-7 and C-8 of plakilactone G is in full agreement with the trans-epoxide 2b.

Figure 4.

Δδ^SR sign distribution model for the bisMTPA esters of a 1,2-diol and absolute configuration for C-7–C-8 diol in plakilactone G (1).

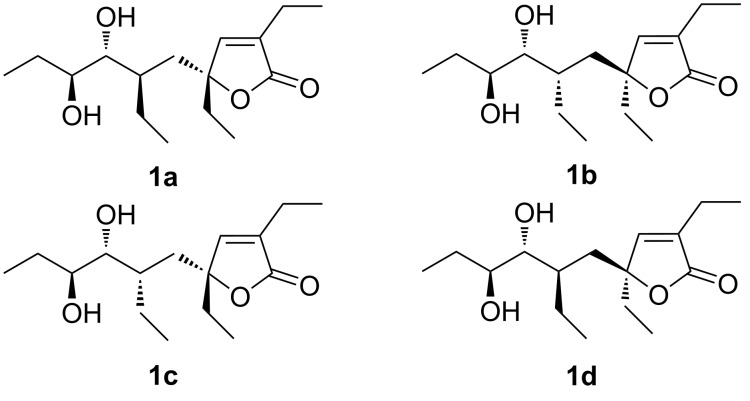
Having assigned the absolute configuration at C-7 and C-8, we tried to elucidate the absolute configuration at C-4 and C-6 on plakilactone G (1). The first step was the conformational search of the four possible diastereoisomers (1a–d in Figure 5), obtained with a fixed 7R,8S configuration, by using molecular dynamics (400, 600 and 800 K) and MonteCarlo Multiple Minimum method (MacroModel package [25], see Experimental).

Figure 5.

Molecular structure of the four possible diastereoisomers of plakilactone G (1).

The geometries of all the significant conformers of 1a–d were subsequently optimised at DFT level by using the MPW1PW91 functional and the 6-31G(d) basis set. Unfortunately, the application of quantitative NOEs method was limited by severe overlapping in many crucial proton resonances (e.g. 1.38–1.52 ppm; 3.46–3.49 ppm, Supporting Information File 1, Table S1) rendering difficult the selective irradiation and the integration of NOE peaks. Thus, many experimental NOE intensities had to be ignored, resulting in MAE and STD values higher than expected for a quantitative NOE-distance investigation of small molecules in our experience. However, the analysis of the limited number of reliable NOEs gave distances (Supporting Information File 1, Table S4) which fitted best with stereoisomer 1a as the structure of plakilactone G (MAE of 6.8% and STD of 8.8%). For 1b–d substantially larger MAE and STD values were observed, in particular for 1c and 1d: 8.1% and 12.5% (1b), 13.8% and 19.9% (1c); 11.3 % and 17.0% (1d).

Due to the lack of a definitive fit for the NOE-distance data we relied more heavily on the QM calculations of the ¹³C chemical shifts in case of the stereostructural investigation of C-4 and C-6 of plakilactone G (1). On the obtained geometries at DFT theoretical level, single point calculation of the ¹³C chemical shifts were performed by using the same functional and the 6-31G(d,p) basis set. The final ¹³C chemical shift values for 1a–d were derived taking into account the Boltzmann weighted average based on the energies of the single conformers for each stereoisomer. The obtained ¹³C chemical shifts were compared with the experimental data by considering the diagnostic carbons and calculating the difference with the experimental values (|Δδ|) and the relative MAE (Table 5).

Table 5.

Comparison of calculated (in vacuo) vs experimental (in CDCl₃) ¹³C NMR chemical shifts of stereoisomers 1a–d.

		1a		1b		1c		1d
carbon	δexp	δcalcd	|Δδ|a, ppm	δcalcd	|Δδ|a, ppm	δcalcd	|Δδ|a, ppm	δcalcd	|Δδ|a, ppm
9	24.0	21.6	2.4	26.0	2.0	27.5	3.5	22.1	1.9
8	73.6	72.4	1.2	74.6	0.9	73.0	0.6	70.7	2.9
7	75.6	76.1	0.5	71.3	4.3	79.1	3.5	76.4	0.8
6	35.6	36.0	0.3	37.3	1.7	34.2	1.4	34.0	1.6
5	36.2	39.2	3.1	36.9	0.8	37.4	1.2	36.8	0.6
4	89.6	87.1	2.5	87.1	2.5	88.8	0.8	87.4	2.2
13	30.9	30.3	0.5	28.0	2.9	32.3	1.4	32.7	1.8
15	25.3	24.2	1.0	22.6	2.7	20.4	4.8	24.5	0.8
16	10.7	9.6	1.1	11.1	0.4	11.7	1.0	10.2	0.5
MAEb			1.4		2.0		2.0		1.5
DP4c			62.9		1.9		5.4		29.7

^a|Δδ| = |δ_exp − δ_calcd|, absolute differences for experimental versus calculated ¹³C NMR chemical shifts. ^bMAE = Σ[|δ_exp − δ_calcd|]/n. ^cDP4 probabilities were obtained considering all the calculated chemical shifts, as proposed by Smith and Goodman [28].

The comparison of ¹³C chemical shifts with the experimental data suggests that 1a presents the best agreement with the experimental values. The stereostructural hypotheses 1b and 1c are unlikely given their substantially larger MAE values, whereas 1a and 1d both show comparable MAE values. We also applied the DP4 probability analysis proposed by Smith and Goodman [28], which strongly suggests that stereoisomer 1a presents the best agreement with the experimental data set. Indeed, 1a has a DP4 probability of 62.9% (Table 5), whereas for 1b–d we found a probability of 1.9%, 5.4% and 29.7% (Table 5), respectively. Isomers 1a and 1d differ only in the configuration at C-4, and considering a putative interconversion between diol 1 and epoxide 2 and a common biogenetic pathway in combination with the chemical shift data and supported by the NOE-distance data, we suggest that the structure of plakilactone G is as depicted in 1a and the absolute configuration of plakilactone H as depicted in 2b.

Conclusion

In this paper two new plakilactones are reported from the marine sponge Plakinastrella mamillaris. Plakilactone H was used as a template to set up the potential application of a combined approach of quantitative NMR-derived interproton distances and QM calculations of ¹³C chemical shifts in defining the stereostructure of highly flexible chemical scaffolds. The two independent methodologies agree and suggest the structure of plakilactone H as depicted in 2b. It is noteworthy that the analysis of accurate NOE-derived distances, up to date, is limited to rigid and relatively flexible molecules and the extension of this methodology to a highly flexible natural product affirms the reliability of this approach to investigate multiconformational chemical systems. Moreover, for the first time, we simultaneously assigned the relative configuration of four stereocenters by using the NOE analysis. In particular, the C-4 stereocenter is not adjacent to the other stereogenic carbons, highlighting that the NOE-based method is useful to investigate the relative configuration of isolated carbons. The absolute configuration of plakilactone G (1) by using a combined approach of chemical derivatization and ¹³C QM calculation, is also reported. Firstly, the absolute configurations at C-7 and C-8 were determined by the double derivatization method with a chiral auxiliary reagent and the results were fully in agreement with the relative configuration of the epoxide moiety on the plakilactone H side chain. Subsequently, the absolute configuration at C-4 and C-6 was obtained through QM calculations of ¹³C chemical shifts, supported by the less satisfactory NOE-distance analysis in this case which failed to give a completely unambiguous solution. Considering the plausible biogenetic epoxide/diol interconversion, the absolute configuration of plakilactone H is also proposed as depicted in 2.

Experimental

Plakinastrella mamillaris Kirkpatrick, 1900 (order Homosclerophorida, family Plakinidae) was processed as previously reported [23]. A portion (5.1 g) of the overall 16.6 g of CHCl₃ extract, rich in plakilactones [23,31–32] and gracilioethers, which was already available in our laboratory, was chromatographed by silica gel MPLC by using a solvent gradient system from CH₂Cl₂ to CH₂Cl₂/MeOH 1:1. Fractions eluted with CH₂Cl₂ (302 mg) were further purified by HPLC on a Nucleodur 100-5 C18 (5 μm; 10 mm i.d. × 250 mm) with 65% MeOH/H₂O as an eluent (flow rate 3.5 mL/min) to give 6.3 mg of plakilactone H (2) (t_R 29.4 min). As described in [31], the purification of fractions eluted with CH₂Cl₂/MeOH 99:1 (2.0 g) furnished 15.4 mg of plakilactone G (1) (t_R 16.5 min).

Characteristic data for each compound

Plakilactone G (1): colorless oil; [α]_D²⁵ −75.5 (c 0.11, CHCl₃); ¹H and ¹³C NMR data in CD₃OD are given in Table 1; ESIMS m/z: [M + Na]⁺ 307.2; HRMS–ESI (m/z): [M + Na]⁺ calcd for C₁₆H₂₈NaO₄, 307.1885; found, 307.1890.

Plakilactone H (2): colorless oil; [α]_D²⁵ −47.9 (c 0.07, CHCl₃); ¹H and ¹³C NMR data in CD₃OD are given in Table 1; ESIMS m/z: [M + Na]⁺ 289.2; HRMS–ESI (m/z): [M + Na]⁺ calcd for C₁₆H₂₆NaO₃, 289.1780; found, 289.1788.

Acetonide derivative from plakilactone G (1). A mixture of 1 (1.1 mg), 2,2-dimethoxypropane (1.0 mL) and a catalytic amount of p-TsOH (4.0 mg) was stirred at room temperature for 4 h. Saturated aqueous NaHCO₃ (1 mL) was then added, and the reaction mixture was extracted with CH₂Cl₂ (3 × 2 mL). The organic solvents were removed under a high vacuum, providing the acetonide derivative in quantitative yield. Selected ¹H NMR (500 MHz, CD₃OD) δ 7.11 (br t, J = 1.5 Hz, 1H, H-3), 3.89 (m, 2H, H-7 and H-8), 2.28 (q, J = 7.5 Hz, 2H, H₂-11), 2.11 (dd, J = 3.9, 14.9 Hz, 1H, H-5a), 1.89 (dd, J = 3.9, 14.9 Hz, 1H, H-5b), 1.41 (s, 3H, Me), 1.31 (s, 3H, Me), 1.18 (t, J = 7.5 Hz, 3H, H₃-12), 0.94 (t, J = 7.5 Hz, 3H, H₃-16), 0.90 (t, J = 7.1 Hz, 3H, H₃-10), 0.82 (t, J = 7.4 Hz, 3H, H₃-14) ppm.

General procedure for the preparation of bis-MTPA esters of plakilactone G (1). As described in [31], plakilactone G (0.5 mg) was dissolved in freshly distilled CH₂Cl₂ and treated with triethylamine (10 μL), (R)- or (S)-α-methoxy-α-(trifluoromethyl)phenylacetyl chloride (MTPACl) (5 μL) and a catalytic amount of 4-(dimethylamino)pyridine to obtain bis-(S)- or bis-(R)-MTPA esters, respectively. The mixture was left to stand at room temperature for 1 h, with the resulting mixture purified by silica gel column.

Bis-(S)-MTPA ester. Selected ¹H NMR (500 MHz, CD₃OD) δ 6.12 (br t, J = 1.7 Hz, 1H, H-3), 5.34 (m, 1H, H-7), 5.09 (m, 1H, H-8), 2.30 (m, 2H, H₂-11), 2.22 (m, 1H, H-5a), 1.67 (m, 1H, H-5b), 1.47 (m, 2H, H₂-9), 1.23 (m, 1H, H-6), 1.18 (t, J = 7.2 Hz, 3H, H₃-12), 0.86 (t, J = 7.5 Hz, 3H, H₃-10) ppm.

Bis-(R)-MTPA ester. Selected ¹H NMR (500 MHz, CD₃OD) δ 6.66 (br t, J = 1.5 Hz, 1H, H-3), 5.28 (m, 1H, H-7), 5.26 (m, 1H, H-8), 2.30 (m, 2H, H₂-11), 1.69 (m, 2H, H₂-9), 1.56 (dd, J = 3.8, 14.7 Hz, 1H, H-5a), 1.42 (dd, J = 3.8, 14.7 Hz, 1H, H-5b), 1.33 (m, 2H, H₂-15), 1.20 (m, 1H, H-6), 1.18 (t, J = 7.3 Hz, 3H, H₃-12), 0.98 (t, J = 7.4 Hz, 3H, H₃-10), 0.91 (t, J = 6.5 Hz, 3H, H₃-16), 0.63 (t, J = 7.5 Hz, 3H, H₃-14) ppm.

NMR experiments

Plakilactone G and H were dissolved in 0.5 mL of CDCl₃ and transferred in 5 mm tubes under air without degassing. NMR experiments were performed at T = 298 K on a Varian 500 MHz VNMRS spectrometer equipped with an H{C,X}, and on a Varian 600 MHz VNMRS spectrometer equipped with an H{C,N} coldprobe. Chemical shifts (δ, ppm) are referenced to CDCl₃ as an internal standard (δ_H 7.26, δ_C 77.2).

For the assignment in CDCl₃ of 1, we performed: 2D-COSY spectrum with 1024 t2 points, 128 t1 points, 0.15 s t2 acquisition time, and 4 scans; 2D-HSQC spectrum was obtained with 2048 t2 points, 256 t1 points, 0.15 s t2 acquisition time, and 4 scans; 2D-HMBC spectrum was obtained with 1024 t2 points, 128 t1 points, 0.15 s t2 acquisition time, and 20 scans. For the assignment in CDCl₃ of 2, we performed: 2D-COSY spectrum with 2048 t2 points, 128 t1 points, 0.3408 s t2 acquisition time, and 16 scans; 2D-HSQC spectrum was obtained with 2048 t2 points, 64 t1 points, 0.0745 s t2 acquisition time, and 16 scans; 2D-HMBC spectrum was obtained with 1024 t2 points, 256 t1 points, 0.1499 s t2 acquisition time, and 16 scans. To determine the interproton distances of 1 and 2, 1D selective transient NOESY spectra were obtained by using 512 (for 1) and 256 (for 2) scans, acquisition time: 3.2768 s for 1, 5.3248 s for 2. For all NOESY spectra of 1 and 2, 500 ms of mixing time and 1 s of relaxation delay were applied. Wurst2i selective shaped pulse was applied for the 1D-NOESY experiments. NMR data were processed by using MestreNova version7.

Computational studies

In order to explore the conformational space of plakilactones G and H (1 and 2), we performed Molecular dynamics and Monte Carlo calculations. Molecular dynamics calculations of 1 and 2 were performed at different temperatures (400 and 600 and 800 K for 5 ns (time-step of 1.5 fs) by using the MMFFs [24] force field (MacroModel software package [25]). During the molecular dynamics, a standard constant temperature velocity–Verlet algorithm was used to integrate the equations of motions [33]. Independently from molecular dynamics, we also applied Monte Carlo Multiple Minimum (MCMM) method (10,000 steps) of the MacroModel module to explore the conformational space of 1 and 2 by using the MMFFs [24] force field. All molecular mechanics calculations were performed in chloroform (continuum model, MacroModel software package [25]). We found 254 major conformers for 1a, 285 for 1b, 574 for 1c and 146 for 1d. We found 209 major conformers for 2a; 400 for 2b; 284 for 2c; 218 for 2d; 225 for 2e; 347 for 2f; 254 for 2g; 183 for 2h.

All the obtained structures from both methods for 1a–d and 2a–h were minimized by using the Polak–Ribiere conjugate gradient algorithm (PRCG, 9 × 10⁷ steps, convergence threshold 0.001 kJ mol⁻¹ Å⁻¹). All the geometries of 1a–d and 2a–h presenting an energy difference ≤13 kJ/mol from the global minimum were retained and used for QM calculations. All the obtained geometries of 1a–d and 2a–h from molecular mechanics methods, were further refined in vacuo at the DFT theoretical level by using MPW1PW91 functional and the 6-31G(d) basis set [26] (Gaussian 09 software package) [27]. The DFT-optimized structures were used for the single-point ¹³C chemical shift calculations (in vacuo) with the same functional and the 6-31G(d,p) basis set. By the same theoretical level (MPW1PW91/6-31G(d,p)) we calculated frequencies for 1. The calculated values of chemical shifts of 1 and 2 were referenced to the theoretical tetramethylsilane ¹³C chemical shift value (previously optimized at the DFT level), computed at the same level of theory.

Supporting Information

File 1

Analytical data.