Brain Organization Underlying Superior Mathematical Abilities in Children with Autism

Abstract

Background

Autism spectrum disorder (ASD) is a neurodevelopmental disorder characterized by social and communication deficits. While such deficits have been the focus of most research, recent evidence suggests that individuals with ASD may exhibit cognitive strengths in domains such as mathematics.

Methods

Cognitive assessments and functional brain imaging were used to investigate mathematical abilities in 18 children with ASD and 18 age-, gender-, and IQ-matched typically developing (TD) children. Multivariate classification and regression analyses were used to investigate whether brain activity patterns during numerical problem solving were significantly different between the groups and predictive of individual mathematical abilities.

Results

Children with ASD showed better numerical problem solving abilities and relied on sophisticated decomposition strategies for single-digit addition problems more frequently than TD peers. Although children with ASD engaged similar brain areas as TD children, they showed different multivariate activation patterns related to arithmetic problem complexity in ventral temporal-occipital cortex, posterior parietal cortex, and medial temporal lobe. Furthermore, multivariate activation patterns in ventral temporal-occipital cortical areas typically associated with face processing predicted individual numerical problem solving abilities in children with ASD but not in TD children.

Conclusions

Our study suggests that superior mathematical information processing in children with ASD is characterized by a unique pattern of brain organization and that cortical regions typically involved in perceptual expertise may be utilized in novel ways in ASD. Our findings of enhanced cognitive and neural resources for mathematics have critical implications for educational, professional, and social outcomes for individuals with this lifelong disorder.

Autism spectrum disorder (ASD), a neurodevelopmental disorder with an estimated prevalence rate greater than 1% (1), is characterized by a complex phenotype that includes social, communicative, and sensorimotor processing deficits (2). Despite the clinical focus on cognitive deficits, it has been noted that the “altered developmental trajectory that defines ASD can also lead to remarkable cognitive strengths” (3) and that children with ASD might present “islets of ability” in various domains (4). One domain in which individuals with ASD often demonstrate exceptional abilities is mathematics. Evidence for greater proficiency in mathematics in ASD has been mostly anecdotal (5) and descriptive (6). It has been shown that scientists score higher than nonscientists on self-administered questionnaires for “autism associated traits” (6) and there is a “three- to seven-fold increase for autism spectrum condition among mathematicians” (7). Furthermore, a recent study in 14- to 16-year-olds with ASD demonstrated a larger discrepancy between IQ and mathematical abilities compared with other abilities such as reading (8).

A seminal theoretical account proposes that systematic, logical, and analogical thinking are enhanced in individuals with ASD (3), suggesting that “hyper-systemizing” may be an adaptive mechanism to reduce environmental variance into a series of regular sets with repeatable rules. Mathematics represents the most concrete instantiation of such abilities, as it is built upon systematic axiomatic procedures. Mathematical skills are essential for educational and professional success and are also crucial in everyday life (9). Thus, mathematics represents an ideal domain to experimentally measure potential cognitive strengths in ASD.

Here, we provide the first simultaneous cognitive and neural characterization of mathematical abilities in children with ASD compared with typically developing (TD) children. We predicted that compared with TD children, children with ASD would show better mathematical abilities, as measured by standardized neuropsychological assessments. We further hypothesized that compared with TD children, children with ASD would show different patterns of brain responses during arithmetic problem solving, with greater reliance on posterior brain areas (10,11). Finally, we hypothesized that neural processes subserving mathematical skills in children with ASD might rely on cortical areas typically devoted to other cognitive abilities.

Methods and Materials

Participants

We studied eighteen 7- to 12-year-old children with ASD (14 male subjects; mean age = 9.60; SD = 1.64) and eighteen TD children (14 male subjects; mean age = 9.59, SD = 1.53). All children in the ASD group were verbal and within an IQ range considered to be high-functioning. Children with ASD received a diagnosis based on scores from the Autism Diagnostic Interview-Revised (12,13) and/or the Autism Diagnostic Observation Schedule (14) (Table 1). Children with ASD were screened through a parental phone interview and excluded if they had other known genetic, psychiatric, or neurological disorders (e.g., fragile X syndrome or Tourette syndrome). Table S1 in Supplement 1 contains additional clinical information on the ASD sample. The TD cohort was selected from a larger sample of children, based on matching of the following parameters: age, full-scale IQ, and gender (Table 1).

Table 1.

Demographic, IQ, and Diagnostic Measures

Measure	ASD (n = 18)	TD (n = 18)	t Test	p Value
Male to Female Ratio	14:4	14:4
Age (Years)	9.60, SD = 1.64	9.59, SD = 1.53	.016	.988
IQ–WASI Scale
Full IQ	113.27, SD = 15.25	113.27, SD = 15.50	−.022	.983
Verbal IQ	112.00, SD = 19.32	112.72, SD = 16.64	−.139	.891
Performance IQ	112.05, SD = 17.88	111.22, SD = 16.65	.145	.886
ADI-R
Social	19.00, SD = 6.66
Communication	15.33, SD = 6.03
Repetitive behavior	5.94, SD = 2.80
ADOSa
Social	8.24, SD = 1.86
Communication	3.41, SD = 1.46
Algorithm	11.65, SD = 3.10

Demographic and mean IQ scores are shown for the ASD and TD groups. Mean ADI-R and ADOS scores are shown for the ASD group only. Note: df = 1,34 for all analyses.

ADI-R, Autism Diagnostic Interview-Revised; ADOS, Autism Diagnostic Observation Schedule; ASD, autism spectrum disorder; TD, typically developing; WASI, Wechsler Abbreviated Scale of Intelligence.

^aMissing score from one participant.

Parental consent and child assent forms were obtained for each child. All protocols were approved by the human participants Institutional Review Board at the Stanford University School of Medicine. All participants were volunteers and were treated in accordance with the American Psychological Association’s Ethical Principles of Psychologists and Code of Conduct.

Neuropsychological and Strategy Assessments

Prior to the functional magnetic resonance imaging (fMRI) scan, each child participated in a neuropsychological assessment session consisting of the Wechsler Abbreviated Scale of Intelligence (15), the Wechsler Individual Achievement Test-Second Edition (WIAT-II) for mathematics (16), and the Working Memory Test Battery for Children (17). On the day of the fMRI scan, children performed a strategy assessment task, outside the scanner, consisting of single-digit addition problems (e.g., 5 + 6 = ?) (18–21). The problems were presented one at a time on a computer screen. There were 18 problems that used random pairs of integers from 2 to 9 and sums ranging from 6 to 17. Children were given explicit examples of strategy use: “just knew it” (i.e., retrieval), “counted on my fingers”, “counted in my head” (i.e., counting), and “broke down the problem, such as 9 + 5 = 9 + (1 + 4) = (9 + 1) + 4 = 10 + 4 = 14” (i.e., decomposition). Subsequently, children were instructed to say the answer out loud as soon as they had it in their head. The experimenter then probed the child on which strategy was used during problem solving. Responses were categorized as retrieval, counting, and decomposition. Trials where the experimenter noted overt signs of counting even when the child reported retrieval were classified as counting and not retrieval or decomposition. Six children (three in each group) did not complete the strategy assessment due to time constraints. For each remaining child, we computed the proportion of correctly answered problems solved by retrieval, counting, or decomposition strategies.

Functional Brain Imaging

Experimental Design

The fMRI experiment consisted of two arithmetic conditions, 1) complex addition and 2) simple addition, and two nonarithmetic conditions, 1) number identification and 2) passive fixation/rest. In the complex addition task, participants were presented with an equation involving two addends and asked to indicate, via a button box, whether the answer shown was correct or incorrect (e.g., 3 + 4 = 8). One operand ranged from 2 to 9 and the other operand ranged from 2 to 5 (tie problems, such as 5 + 5 = 10, were excluded), and answers were correct in 50% of the trials. Incorrect answers deviated by ±1 or ±2 from the correct sum. The simple addition task was identical except that one of the addends was always 1 (e.g., 3 + 1 = 4). In the number identification task, arithmetic symbols were replaced by alternative keyboard symbols (e.g., 4 o 5 @ 7) and participants were asked to assess if the number 5 was among the presented digits. Finally, in the passive fixation task, the symbol * appeared at the center of the screen and participants were asked to focus their attention to it. To aid children’s performance, specific task instructions appeared below each problem. During the complex and simple addition tasks, the word “Solve” was presented below the problem. In the number identification task, the word “Find” appeared on the screen, and during the passive fixation/rest trials, the word “Look” appeared on the screen.

Stimuli were presented in a block fMRI design to optimize signal detection. In each task, stimuli were displayed for 5 seconds with an intertrial interval of 500 milliseconds. There were 18 trials of each task condition, broken up into four blocks of 4 or 5 trials; thus, each block lasted either 22 or 27.5 seconds. The order of the blocks was randomized across participants with the following constraints: in every set of four blocks, all conditions were presented and the complex and simple addition task blocks were always separated by either a number identification or a passive fixation/rest block. All orders of arithmetic and nonarithmetic task conditions were equally likely. The total length of the experiment was 6 minutes and 36 seconds.

The present study focused on group differences in arithmetic complexity by contrasting behavioral and brain responses to the complex and simple addition tasks. Behavioral research in adults suggests that the simple N + 1 addition trials are solved by incremental counting (22) and performance on this task is characterized by higher accuracy and faster reaction times compared with complex addition problems (18,23,24). Moreover, because stimuli in the simple task have the same format as in the complex task, it provides a high-level control for sensory and number processing, as well as decision making and response selection.

fMRI Data Acquisition

Functional brain images were acquired on a 3T GE Signa scanner (General Electric, Milwaukee, Wisconsin). A total of 29 axial slices (4.0 mm thickness, .5 mm skip) parallel to the anterior commissure-posterior commissure and covering the whole brain were imaged using a T2* weighted gradient echo spiral-in/spiral-out pulse sequence with the following parameters: repetition time = 2 sec, echo time = 30 msec, flip angle = 80°, 1 interleave. The field of view was 20 cm, and the matrix size was 64 × 64, providing an in-plane spatial resolution of 3.125 mm. To reduce blurring and signal loss from field inhomogeneity, an automated high-order shimming method based on a spiral acquisition was used before the acquisition of fMRI scans (25).

fMRI Data Analysis

Data were analyzed using the general linear model implemented in SPM8 (http://www.fil.ion.ucl.ac.uk/spm/). The first five volumes were not analyzed to allow for signal equilibration. Images were first realigned to the first scan to correct for motion and slice acquisition timing. Translational movement in millimeters (x, y, z) was calculated based on the SPM8 parameters for motion correction of the functional images in each subject. To correct for deviant volumes resulting from spikes in movement, we used despiking procedures similar to those implemented in Analysis of Functional NeuroImages (AFNI) toolkit maintained by the National Institute of Mental Health (Bethesda, Maryland) (26). Volumes with movement exceeding .5 voxels (1.562 mm) or spikes in global signal exceeding 5% were interpolated using adjacent scans. In the ASD group, the majority of volumes repaired occurred in isolation. The same was true for the TD group. Moreover, the frequency distribution of adjacent repaired scans did not differ between groups (Fisher’s exact test p value = .11). Finally, no participant had maximum scan-to-scan movement of 4.6 mm and no more than 8.5% of volumes were corrected. Crucially, movement parameters did not differ between the groups (Table S2 in Supplement 1). After the interpolation procedure, images were spatially normalized to standard Montreal Neurological Institute space, resampled to 2 mm isotropic voxels, and smoothed with a 6 mm full-width at half maximum Gaussian kernel.

Univariate Analyses

The primary goal of this analysis was to examine group differences in activation related to arithmetic problem complexity. Brain activation related to each task condition (complex addition, simple addition, number identification) was first modeled at the individual subject level using boxcar functions with a canonical hemodynamic response function and a temporal derivative to account for voxel-wise latency differences in hemodynamic response. Voxel-wise contrasts and t statistics images at the group level were then generated by contrasting complex versus simple addition problems. Additional analyses were conducted using contrast images for the simple addition problems versus rest and for the complex addition problems versus rest (Supplement 1).

Differences in brain activation between the ASD and TD groups were compared using t tests on contrast images for complex versus simple addition problems. In both analyses, significant clusters of activation were identified at the whole-brain level using a height threshold of p < .001, with family-wise error (FWE) correction for multiple spatial comparisons at p < .01, computed using Monte Carlo simulations (see Supplement 1 for details).

Multivariate Analyses

Multivariate Pattern Analysis

The primary goal of this analysis was to examine group differences in multivariate activation patterns related to arithmetic problem complexity. Multivariate pattern analysis (MVPA) (18) was used to identify brain regions that discriminated spatial activation patterns to complex versus simple problems between children with ASD and TD children. Additional analyses were conducted using simple addition problems versus rest and complex addition problems versus rest. Machine learning algorithms and cross-validation procedures used in the MVPA are described in detail in Supplement 1. The statistical map corresponding to group differences in multivariate activation patterns was thresholded using the same height threshold as in the univariate analyses (p < .001), with FWE corrections at p < .01 for multiple comparisons computed using Monte Carlo simulations (Supplement 1).

Support Vector Regression Analysis

Support vector regression (SVR) analysis (27,28) was used to assess whether brain activation could predict mathematical abilities in the two groups. Regions of interest were defined for each significant cluster from the MVPA analysis. Within each region of interest, voxel values were used to predict the response variable of interest: performance on the Numerical Operations subtest of the WIAT-II for each group. Details of the SVR analysis are provided in Supplement 1.

Results

Mathematical Ability and Problem Solving Strategies

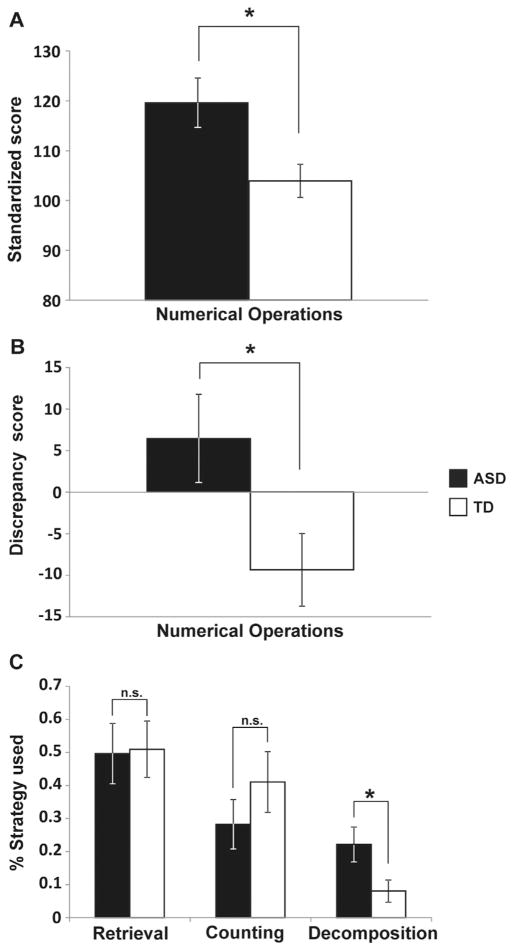
Measures of math ability included two subtests of the WIAT-II (16) and an assessment of strategies used during arithmetic problem solving (18–21). Children in the ASD group scored higher than TD children on the Numerical Operations subscale of the WIAT-II, which assesses basic numerical and arithmetic skills (t₃₄ = 2.638, p = .012) (Figure 1A), while no group differences were found on the Math Reasoning subtest of the WIAT-II (t₃₄ = 1.52, p = .138) (Table S3 in Supplement 1). Discrepancy scores (8), calculated by subtracting full IQ scores from the standardized math measure numerical operations, were higher for the ASD group compared with the TD group (t₃₄ = 2.293, p = .028) (Figure 1B).

Figure 1.

Children with autism spectrum disorder (ASD) show significantly better mathematical abilities and sophisticated strategy use compared with their age-, gender-, and IQ-matched typically developing (TD) peers. (A) Standardized math achievement scores by group. Children with ASD performed better than TD children on the numerical operations subtest of the Wechsler Individual Achievement Test. (B) Discrepancy scores between standardized math measure and full IQ scores by group. Children with ASD displayed a bigger discrepancy score than TD children. (C) Different strategy use in ASD and TD. The groups differed significantly on the percentage of trials in which a decomposition strategy was used. Error bars indicate standard error of the mean. ^*p < .05. n.s., nonsignificant.

Interestingly, compared to the TD group, the ASD group showed greater use of decomposition (t₂₈ = 2.247, p = .033), a more sophisticated strategy for arithmetic problem solving that involves transforming the original problem into two or more simpler subproblems (29) (Figure 1C). No differences in the use of retrieval or counting strategies were found between the groups (p = .917 and p = .288, respectively). Furthermore, the two groups did not differ on any of the four working memory measures of the Working Memory Test Battery for Children (17) (Table S3 in Supplement 1).

Math Performance on Arithmetic Verification Task

Behavioral performance during fMRI scanning was analyzed using a two-way analysis of variance with within-subject factor problem type (complex, simple) and between-subject factor group (ASD, TD). For accuracy, there was a main effect of problem type (F_1,34 = 6.41, p = .016), as complex addition problems were harder than simple addition problems. There was no main effect of group (F_1,34 = .08, p = .774) and no interaction (F_1,34 = 2.04, p = .162). Reaction time also showed a main effect of problem type (F_1,34 = 48.15, p < .001); participants responded faster to simple than complex addition problems. There was no main effect of group (F_1,34 = .01, p = .921) nor an interaction between group and problem type (F_1,34 = .38, p = .847).

Functional Brain Imaging

To identify the brain basis of superior mathematical abilities in children with ASD, we compared fMRI activity between groups during arithmetic problem solving. fMRI data were analyzed at the whole-brain level using both univariate and multivariate approaches.

Univariate Analyses

Between-group t tests showed no significant differences in activation levels between the ASD and TD groups for complex versus simple problems-height threshold p < .001, with FWE correction for multiple spatial comparisons at p < .01. No significant group differences were found on the other two contrasts: simple addition problems versus rest and complex addition problems versus rest (height threshold: p < .001, extent threshold: p < .01).

Multivariate Analyses

Multivariate Pattern Analysis

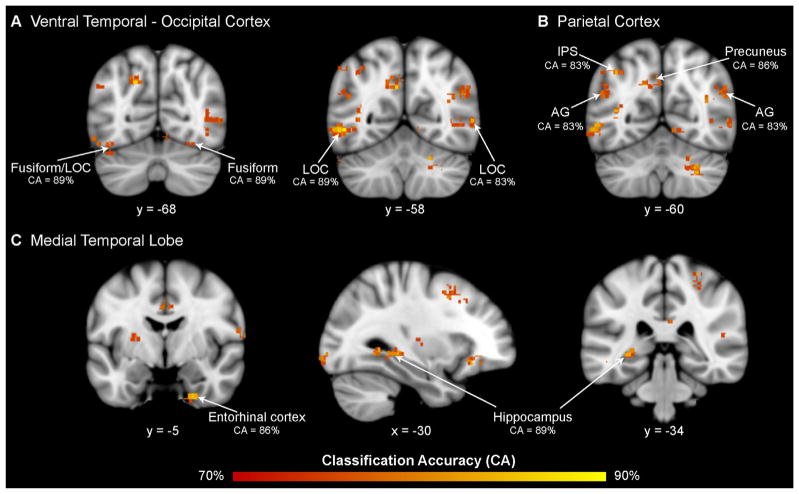
Multivariate pattern analysis highlighted several cortical regions where arithmetic complexity-related activity patterns differed significantly between children with ASD and their TD peers. Notably, high cross-validation classification accuracies (80% to 90%) were found in ventral temporal-occipital cortex (VTOC), including bilateral inferior lateral occipital cortex and fusiform gyrus (Figure 2A; Table 2), as well as posterior parietal cortex, including the left intraparietal sulcus, angular gyrus, and the left precuneus (Figure 2B; Table 2). Medial temporal lobe areas, including the posterior hippocampus and parahippocampal gyrus, as well the entorhinal cortex in the anterior aspects of the medial temporal lobe also showed significant between-group differences in multivariate activity patterns (Figure 2C; Table 2). High classification accuracies were also found in the left dorsolateral prefrontal cortex (DLPFC), the left orbital frontal cortex, the left anterior cingulate cortex, and the right frontal pole, as well as the basal ganglia (Table 2). Additional analyses were conducted to examine whether these differences arose from brain responses to simple addition problems. To address this question, group differences in multivariate activation patterns were examined for simple addition problems contrasted with the rest baseline. No overlap was observed with findings from the arithmetic complexity-related group differences (Figure S1A in Supplement 1).

Figure 2.

Brain activity patterns during arithmetic problem solving distinguish children with autism spectrum disorder from their typically developing peers. Multivariate pattern analysis revealed significant differences in spatial activation patterns between children with autism spectrum disorder and typically developing children in the (A) ventral temporal-occipital cortex: bilateral inferior lateral occipital cortex (LOC) and fusiform gyrus; (B) parietal cortex: left intraparietal sulcus (IPS), bilateral angular gyrus (AG), and left precuneus; and (C) medial temporal lobe: right entorhinal cortex and left hippocampus and parahippocampal gyrus.

Table 2.

Brain Areas that Showed Significant Differences in Multivariate Activation Patterns between ASD and TD Groups During Arithmetic Problem Solving

Region	Cluster Size	Max CA (%)	MNI Coordinates
			X	Y	Z
Ventral Temporal-Occipital Cortex
L lateral occipital cortex	378	89	−50	−58	−4
R fusiform gyrus	131	89	24	−74	−14
L fusiform gyrus	59	83	−46	−72	−18
R lateral occipital cortex	74	86	38	−66	2
L occipital pole	64	86	−32	−94	−6
R lingual gyrus	52	86	8	−66	−10
R occipital pole	80	83	8	−96	−4
R lateral occipital cortex	130	83	58	−58	4
Parietal Cortex
R superior parietal lobule	56	89	32	−38	52
L precuneus	152	86	−6	−58	32
R supramarginal gyrus	183	86	60	−20	20
L intraparietal sulcus	57	83	−38	−60	44
L angular gyrus	87	83	−54	−56	24
R angular gyrus	188	83	42	−52	20
R retrosplenial cortex	59	83	10	−44	20
R posterior cingulate cortex	45	81	2	−26	32
R supramarginal gyrus	48	81	66	−42	14
Medial and Lateral Temporal Lobe
L hippocampus	378	86	−28	−34	−2
R perirhinal cortex	66	86	24	−8	−42
R superior temporal gyrus	54	86	62	−18	−2
L middle temporal gyrus	137	83	−64	−24	−18
R parahippocampal gyrus	90	83	30	−48	−4
Frontal Cortex
L dorsomedial prefrontal cortex	278	86	−2	36	44
L orbitofrontal cortex	47	86	−26	34	−8
L dorsolateral prefrontal cortex	66	86	−4	20	60
R ventromedial prefrontal cortex	82	83	10	62	−2
R dorsomedial prefrontal cortex	69	83	26	26	58
L anterior cingulate cortex	70	81	−4	−10	30
Subcortical Areas
L cerebellum	59	89	−42	−72	−26
R cerebellum	68	86	28	−60	−36
L brain stem	77	83	−2	−26	−26
L putamen	60	83	−28	−16	10
L cerebellum	45	83	−52	−52	−30
R caudate/nucleus accumbens	45	83	12	10	−8

ASD, autism spectrum disorder; CA, classification accuracy; L, left; MNI, Montreal Neurological Institute; R, right; TD, typically developing.

Support Vector Regression Analyses

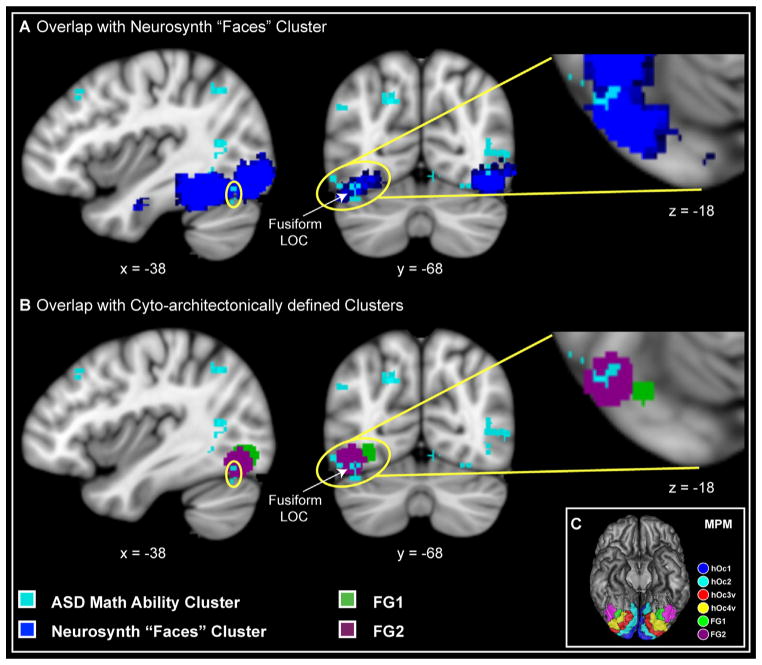
To further investigate neural organization for mathematical problems in children with ASD, we focused on brain areas that distinguished the ASD and TD groups and examined whether multivariate activation patterns in these areas were related to individual differences in math abilities. Specifically, we used SVR (27,28) to examine whether multivariate activity patterns in these areas could predict math abilities assessed using the Numerical Operations subtest of the WIAT-II (16). Our analysis focused on the Numerical Operations subtest because children with ASD showed significantly better performance on this standardized measure of math abilities (Figure 1A), even though they were matched for IQ, age, gender, and working memory abilities (Table 1; Table S3 in Supplement 1). Our SVR analysis revealed that numerical abilities in the ASD group were predicted by the pattern of neural activity in an area of the left VTOC encompassing the left fusiform gyrus and lateral occipital cortex (R² = .69, q = .04, Cohen’s f ² effect size = 2.28, significance of R² was tested nonparametrically with permutation tests, as described in Supplement 1). These voxels show prominent overlap with VTOC face-processing regions identified using Bayesian meta-analysis of 406 studies (www.neurosynth.org) (30) (Figure 3A) and with cytoarchitectonically defined maps of the posterior fusiform gyrus (31) (Figure 3B, C). In the TD group, numerical abilities were predicted by neural activity patterns in the left DLPFC (R² = .64, q = .02, Cohen’s f ² effect size = 1.79, significance of R² was tested nonparametrically with permutation tests, as described in Supplement 1).

Figure 3.

Brain regions predicting numerical problem-solving abilities in children with autism spectrum disorder (ASD) overlap with face processing regions and cytoarchitectonically defined regional maps. Voxels in the left ventral temporal-occipital cortex, encompassing inferior lateral occipital cortex (LOC) and fusiform gyrus (shown in cyan), predicted better numerical abilities (R² = .69, q = .04, Cohen’s f ² effect size = 2.28) in children with ASD. (A) Voxels predicting better numerical abilities in ASD (cyan) showed prominent overlap with ventral temporal-occipital cortex face processing regions identified using Bayesian meta-analysis of 406 studies (blue) (www.neurosynth.org) (30). (B) Voxels predicting better numerical abilities in ASD (cyan) showed prominent overlap with cytoarchitectonically defined maps of the posterior fusiform gyrus, FG1 (green) and FG2 (violet) (31). (C) Maximum probability map (MPM) of the visual cortex. Other cytoarchitectonically delineated areas are abbreviated using the following nomenclature: hOc (human occipital cortex). Ordinal numbers 1 through 4 refer to the cytoarchitectonically defined visual areas moving laterally from the primary visual cortex (Brodmann area 17/primary visual cortex) (32). [Reproduced with permission from Caspers et al. (31)].

Discussion

Building on prior descriptive (6) and anecdotal evidence (5) in adults, our study provides new evidence for numerical problem solving as a domain of cognitive strength in children with ASD (8). Compared with a group of well-matched TD peers, children with ASD showed significantly better abilities on standardized measures of numerical problem solving. Notably, the specific group difference seen on the Numerical Operations, but not on the Mathematical Reasoning, subtest of the WIAT-II, points to an enhanced ability of children with ASD to perform arithmetical computations, while their ability to solve word and language based problems is within the normal range. Critically, there were no differences in IQ and working memory abilities between the groups, pointing to domain-specific strengths independent of general cognitive abilities. Furthermore, compared with their TD peers, children with ASD showed greater reliance on sophisticated analytic strategies when solving single-digit addition problems. The decomposition strategy involves solving problems by breaking them into easier problems. Greater use of this analytic strategy in children with ASD might reflect a better ability to partition arithmetic problems into simpler ones by focusing on the intrinsic details of the equation’s properties, rather than relying on effortful and less efficient strategies. Notably, decomposition strategies are highly successful, even in typical development, as children adopting these strategies tend to be at a more advanced stage of math skill development than their peers who rely on less sophisticated strategies such as finger counting (29).

Our neuroimaging findings provide novel evidence that children with ASD exhibit unique patterns of brain organization for mathematical information processing. Children with ASD engaged similar brain areas as their TD peers, and overall levels of activation did not differ between the two groups. However, they showed different multivariate activation patterns in subregions of the prefrontal, posterior parietal, and ventral temporal-occipital cortices (Figure 2; Table 2) that have been consistently implicated in numerical problem solving (20,23,33). Furthermore, our findings relating standardized measures of numerical abilities with distinct multivariate activation patterns in the two groups provide further evidence for unique patterns of brain organization for numerical information processing in children with ASD.

Although no previous studies have investigated the brain basis of math abilities in children or adults with ASD, greater engagement of posterior brain areas has been posited as a general mechanism underlying the analytical brain in ASD (3,10,11). Accordingly, we hypothesized that posterior brain areas including primary sensory cortex might show heightened activation in children with ASD. However, we found no evidence for differences in activation levels in either extra-striate cortex, visual association, or parietal cortices. Rather, we found that children with ASD engaged these brain areas to the same extent as TD children. However, they showed significantly different activation patterns in these (Figure 2A,B; Table 2), as well as multiple other brain regions (Figure 2C; Table 2).

Of particular interest is our finding of differential multivariate activation patterns between the two groups in the left VTOC. This region showed one of the highest classification rates in distinguishing between the two groups, and it was also the only brain area in which multivariate activation patterns predicted numerical problem solving skills in children with ASD. In contrast, multivariate activation patterns predicted numerical problem solving skills of TD children in the left DLPFC, but not in the VTOC or any other brain region. These results provide further evidence that children with ASD engage posterior brain areas differently than their TD peers. Anatomically, VTOC encompasses multiple divisions of the visual association cortex and has been linked with processing of various types of category-specific information such as words and numbers (33,34), objects (35), and faces (36,37). The versatility of functional specialization in this region suggests that it might be subject to high competition for cortical space (34,38), especially during the earlier stages of development (39). Interestingly, voxels that predicted better numerical problem-solving ability in children with ASD showed prominent overlap with VTOC face processing regions identified using a meta-analysis of 406 brain imaging studies (30) (Figure 3A). Furthermore, these voxels were localized to the cytoarchitectonically defined subdivisions FG1 and FG2 of the fusiform gyrus (31) (Figure 3B, C). These posterior VTOC regions show a high level of expertise-related plasticity (35,40), suggesting that differences in activation patterns could be the consequence of experience with specific types of stimuli (41). VTOC regions, particularly the fusiform gyrus, respond preferentially to classes of objects for which an individual has perceptual expertise (34,35,40). Intriguingly, recent studies suggest that brain activity in these regions can be enhanced through extensive perceptual training (35). Consequently, inadequate attention to faces, a behavioral characteristic of ASD (42), within critical periods of neural plasticity could promote better representations for certain stimulus categories, such as numbers (33,34), over others. Critically, multivariate activation patterns in the left VTOC predicted abilities on standardized tests involving basic numerical operations in the ASD group but not in TD children. These observations suggest that enhanced attention to numbers and the quantities they symbolize may allow specialized neural representations to develop in the VTOC, thereby facilitating numerical problem solving abilities in children with ASD.

Children with ASD also showed significant differences in activation patterns in the hippocampus and entorhinal cortex (Figure 2C). These medial temporal lobe regions are known to play an important role in arithmetic fact retrieval in children (18,43). Notably, in TD children, a recent study demonstrated strategy-related differences in multivariate activation patterns in the same hippocampal region (18). The hippocampus and entorhinal cortex are known to be critical for the formation of new memories, as well as in mediating flexible retrieval and use of these memories (44). These findings suggest that memory processes supported by the medial temporal lobe are engaged differently and play different roles during problem solving in the two groups.

Our study adds to the growing literature suggesting that mathematics is an islet of enhanced cognitive ability in children with high-functioning autism and points to unique patterns of brain organization underlying these abilities in ASD. Further studies are needed to examine low-functioning children with ASD and other potential sources of heterogeneity in this complex disorder. Further studies are also needed to examine other aspects of numerical cognition, such as symbolic and nonsymbolic magnitude and quantity judgment. More broadly, our study highlights the power of multivariate methods in uncovering how children with ASD process academically relevant information differently from their TD peers. Our findings are an important first step toward establishing a new line of research that has the potential to inform not only educators, psychologists, and clinicians, but also parents, about enhanced cognitive abilities in individuals with autism.