TIME INVARIANT MULTI ELECTRODE AVERAGING FOR BIOMEDICAL SIGNALS

Abstract

One of the biggest challenges in averaging ECG or EEG signals is to overcome temporal misalignments and distortions, due to uncertain timing or complex non-stationary dynamics. Standard methods average individual leads over a collection of epochs on a time-sample by time-sample basis, even when multi-electrode signals are available. Here we propose a method that averages multi electrode recordings simultaneously by using spatial patterns and without relying on time or frequency.

1. INTRODUCTION

Extracting relevant parameters from biomedical signals such as EEG or ECG is important. One approach to deal with problems with noise from sources like muscle artifacts, baseline interference or measurement noise its to make repeated observations of the same underlying phenomenon and average. Averaging is usually done over the ensemble of signals at each time point, based on the assumptions that all the observations are time-shifted versions of the same underlying signal perturbed with additive noise. Therefore, with the appropriate alignment, performed manually or automatically [1], equivalent signal features across beats occur at the same sample times. In practice, alignment is not a completely solved problem, and it has been shown that misalignments lead to significant errors in averaging accuracy [2]. Moreover, both in the brain and the heart, the assumption that different observations are all pure shifted versions of the same underlying signal is a strong assumption. Processes like habituation or sensitization in the brain, or heart rate dependent variability, suggest that other factors may cause observations to vary in a manner not consistent with this assumption.

In most settings multiple electrodes are used for EEG or ECG. Although these signals contain different measurements of the same underlying electrical activity, averaging is usually performed on an electrode by electrode basis. We propose here a method that uses multi-electrode recordings to perform averaging by defining similarity in terms of spatial patterns in the across-electrode snapshots without relying on time dependence. Our method avoids explicit alignment and allows robustness to variable temporal dynamics.

Single-lead ensemble averaging has been extended by several approaches, such as optimal weighted averaging [3, 4], but with no added robustness to alignment errors. A number of methods have used signal decompositions (e.g. wavelet transforms [5], empirical mode decomposition [6], filter banks [7], adaptative filtering [8]) or statistical factorizations such as principal or independent component analysis [9, 10]. However, all of these methods rely on thresholding to distinguish between signal and noise. Moreover, many treat individual leads independently. EMD and PCA [11] do not, for example, but the former approach is still being studied and the latter is restricted to linear decomposition of the multidimensional signal.

In a more general setting, this problem has been addressed by time warping multivariate time series prior to averaging. One approach, which comes with a considerable computational burden, has been to use dynamic time warping (DTW) [12] to obtain pairwise time warps. Our method differs from this approach because it avoids explicitly computing pairwise time warps, instead treating all observations jointly.

Specifically we treat each snapshot across all electrodes as a point in the appropriate vector space which traces, as it evolves over the duration of the observation, as a curve in that space. We define similarity of these spatial patterns based on distance in the vector space. As in [13], we assume that the sample trajectories lie near a true underlying continuous trajectory in that space, with no fixed velocity along the path. Rather instantaneous velocities along the path can be different between observations. Our approach is to search for the single curve that explains the set of sample curves, in effect traveling through the middle of the observations, similar to the principal curve concept introduced by Hastie [14]. Although conceptually similar, we will approach the problem differently. In particular since the unknown over which the optimization is performed in principal curves is the continuous curve itself, which is then discretized, whereas we will use an explicit parametric curve.

2. METHODS

We denote the multi-electrode signal as a multi-channel time-varying vector:

$$\mathbf{x}[n]={\left[\begin{array}{cccc}{x}_1[n]& x_2[n]& \cdots & x_N[n]\end{array}\right]}^{\text{T}},$$ (1)

where N is the number of electrodes. We parameterize the desired curve as a piecewise cubic spline in each electrode dimension; the number of knots is fixed but the knot locations are unknown. Because cubic splines also have two extra parameters to specify, we added the derivatives at the first and last knot points to the knot locations as unknown parameters, collecting all parameters into the variable θ. Then we minimize the total distance of the data to the unknown curve as a function of θ in the multidimensional space. Geometrically, we seek to minimize the sum of Euclidean distances squared from all data points to their projection onto the curve. We approximate the projection of a point to the curve by searching over a discrete set of candidate points, regularly sampled from the continuous curve at regular intervals of the curve parameter s. The optimization problem is then:

$$\underset{\theta }{min}\frac{1}{M}\sum _{i=1}^M{\left|\right|\mathbf{x}[i]-\mathbf{c}(s_i,\theta )\left|\right|}^2$$ (2)

$$s.t.s_i=\underset{s\in \mathbf{S}}{min}{\left|\right|\mathbf{x}[i]-\mathbf{c}(s,\theta )\left|\right|}^2,$$ (3)

where c(s, θ) is the parameterized curve, M is the total number of observed data points, s_i is the curve parameter of the curve point onto which x[i] projects, and S the collection of discrete candidate points s_i. We solve this problem using the Nelder-Mead simplex reflection method [15]. We initialize this algorithm by choosing the best fit individual observation after regularly sampling all observations to select knot points, and estimating their end point derivatives using finite differencing. The initialization is thus chosen to be a trajectory going through the middle of the point cloud. The averaged curve is the local minimum found by our optimization algorithm starting from this initialization.

2.1. Denoising individual observations

After solving the optimization problem, our resulting curve is parameterized by a curve parameter which is a warped version of the original observation time domain. In order to recover the original timings of our observations, we project all the samples of each observation to the closest point on our averaged curve, yielding a de-noised version of the observation which preserves its original individual “velocity”. This step can be regarded as a nonlinear filter. Furthermore, the same procedure provides the Time Warping Function, which relates the original time domain in individual observations to the values of the curve parameter s to which the observations get projected onto.

3. EXPERIMENTS

In order to show the performance of the proposed method we report here on two different types of multi-electrode electrocardiogram signals. The first dataset starts with a standard measured 12 lead ECG and synthesizes noisy, misaligned measurements, while the second is a clinically-recorded dataset using a 120 electrode torso array (called a “body surface potential map”).

3.1. 12 electrodes synthetic torso dataset

We used a normal sinus rhythm heartbeat recorded from a healthy patient available from the ECGSIM software package [16]. The sample rate was 1000 Hz. We extracted only the QRS complex q(t) for our study. We generated 20 synthetic heartbeats x_j(t), j = 1, 2, …, 20 from the original data by time-shifting and then adding noise as follows:

$${\overline{\mathbf{x}}}_j(t)=\mathbf{q}(t-{\varphi }_j)\text{where}{\varphi }_j~N(0,2ms)$$ (4)

$${\mathbf{x}}_j(t)={\overline{\mathbf{x}}}_j(t)+\mathbf{n}(\mathbf{t}),$$ (5)

where n(t) is zero-mean additive Gaussian noise whose variance was chosen to match a number of different signal-to-noise ratio (SNR) values.

We note that because we choose the SNR globally across all leads, we mimic a realistic scenario where the amplifier noise is not signal dependent. The effect is that individual signals will have different effective SNRs.

The actual SNR is also affected by the misalignment. Thus we calculate an initial SNR (SNR₀) for x_j(n) as follows:

$${\mathit{SNR}}_0=\frac{{\sum }_{i=1}^{T}q{(i)}^2}{\frac{1}{20}{\sum }_{j=1}^{20}{\sum }_{i=1}^T{(x_j(i)-q(i))}^2}$$ (6)

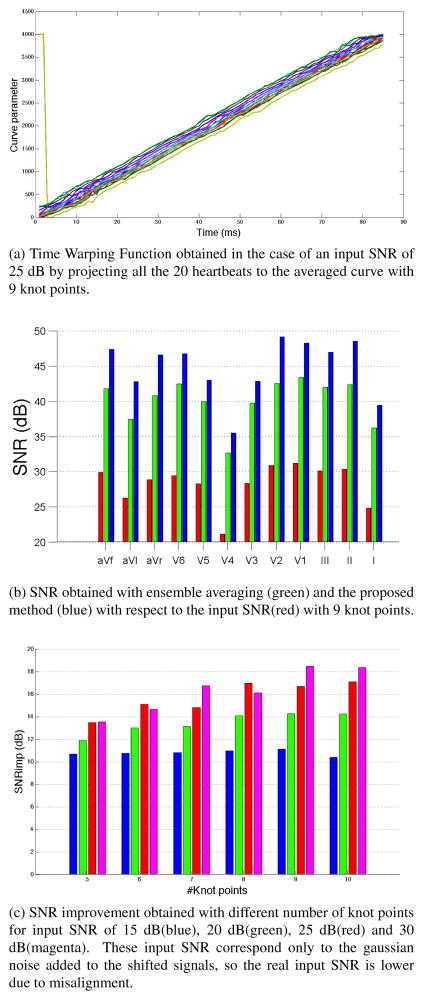
where T is the total number of time samples. We denote the denoised versions of our individual heartbeats as x̂_j(n). In the Fig. 1a we have plotted the Time Warping Functions that we obtained after projecting all the heartbeats with an input SNR of 25 dB onto an averaged curve with 9 knot points. This figure reveals clearly that the only difference in timing between heartbeats is a global shift, shown by the constant translation difference between the curves. We also note that one heartbeat gets projected from the beginning of the beat to the end of our average curve. This is due to the fact that our heartbeats are periodic in space, because they start and end around the baseline. With no timing constraint in the projection step, the nearest neighbor to a point in the beginning of a heartbeat can be in the end of our average curve, and vice versa. To quantify the performance of the proposed method we calculated the SNR improvement in each lead SNRimp_l across all the denoised heartbeats:

$${\mathit{SNRimp}}_l=\frac{{\sum }_{j=1}^{20}{\sum }_{i=1}^T{(x_j(i)-q(i))}^2}{{\sum }_{j=1}^{20}{\sum }_{i=1}^T{({\widehat{x}}_j(i)-{\overline{x}}_j(i))}^2}.$$ (7)

Fig. 1.

Results obtained in the 12 lead synthetic scenario

This measure allows us to compare the performance of our method to the results that were obtained by applying ensemble averaging to all the heartbeats on a lead by lead basis, without performing any time alignment previous to it, as shown in Fig. 1b, using 9 knot points in our method. Our method performs better on all twelve leads. We think it is important to point out that the improvement in this figure includes both the noise removal as well as the overcoming misalignments. Finally we have calculated a scalar measure SNRimp of the performance of our method by averaging SNRimp_l across leads. When we described the mathematical details of our method we mentioned that the number of knot points used to create the splines was fixed, which implies a model order selection step. In Fig. 1c we have used the metric of SNR improvement across leads to study how the proposed method performs for different numbers of knot points and input SNR. We observe that if the level of noise is high, the performance of the method is stable for different numbers of knot points. However, if it is low compared to the amplitude of the signals using more knot points improves performance, presumably because we obtain a more refined version of the average curve.

3.2. 120 electrode torso dataset

In the second study we used body surface potentials recorded from a subject at the Charles University Hospital in the Czech Republic during a clinical procedure. The heart was paced by applying electrical stimuli to the interior wall of the left ventricular blood chamber at multiple sites with the tip of a CARTO ablation catheter. Measurements were recorded at a 2048 Hz sampling rate from 120 torso leads, and two of them were discarded as defective recordings. Again we considered only the QRS complex, and a baseline correction was performed. We present results for 28 heartbeats paced from the mid-anterior part if the left ventricle, although different pacing sites were also studied and all showed similar results. The presence of a “pacing spike” in the data allowed accurate alignment of the beats by a manual procedure. We performed ensemble averaging on a lead by lead basis as well as using our approach.

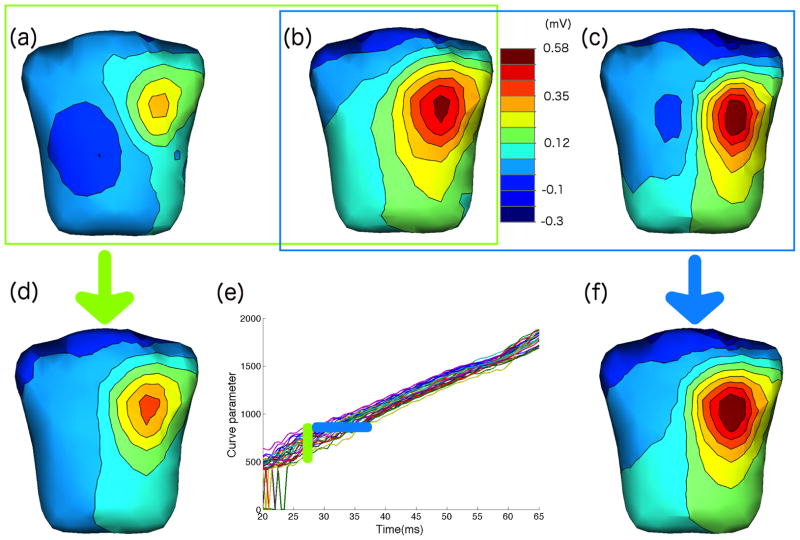
Fig. 2 summarizes these results. We observe that in the resulting Time Warping Function (panel (e)) the translation behavior of the curves for different beats is now time dependent, suggesting that the instantaneous velocities in the different heartbeats vary. To further study the results, we have plotted body surface maps (shown as colormapping of interpolated potential values along with isopotential contour line). We show maps for two heartbeats in the same (real) time instant in panels (a) and (b) along with the result of performing ensemble averaging over all beats in panel (d) (as shown by the vertical green bar in panel (e). In panel (c) we show another map which was recorded at a different sample time, but which was warped to the same time instance as the map in panel (b). Panel (f) shows the spatial average map we obtained by our method (as shown by the horizontal blue bar in panel (e)). The results illustrate that the individual beats chosen indeed reflect different “velocities” during the heartbeat, so that maps at the same time post-stimulus are quite different, but the spatial patterns travel over similar trajectories, so that after time-warping we can average similar maps. Clearly this similarity cannot be seen on a lead-by-lead basis but rather depends on the nature of the trajectories in the higher-dimensional space. Finally we note that in this case we used 10 knot points in our parameterization.

Fig. 2.

Body surface maps of 120 torso leads. From the Time Warping Function extracted from all the heartbeats (e) with 10 knot points we show two body potential maps corresponding to the same time sample in two different heartbeats (figures (a) and (b)), and the result of averaging all the heartbeats across that time sample in figure (d). We have highlighted such process in the Time Warping Function as a vertical grouped heartbeats (blue). Separately, we have highlighted a set of heartbeats that correspond to similar spatial locations with an horizontal group (green) and plotted the body maps of two of them in figures (a) and (c). Finally, the result of the proposed method for such spatial location with 10 knot points is shown in figure (f).

4. DISCUSSION

We have shown that time misalignments, noise, and variability in underlying physiological parameters can lead to significant errors when performing averaging. Our proposed spatial averaging method allows a more coherent averaging and in addition showed improvement in signal to noise ratio both in individual leads (1b) and across them (1c).

Finally, there are several aspects of the method we propose that remain to be studied. For one, we have mentioned that we do not impose any restriction in the projection step that accounts to errors due, for example, to signals that show a periodic pattern. Secondly, as a result of our method we obtain a parametric curve that explains the spatial pattern of our signals, which implies a continuous solution that could be used in prediction or for interpolation purposes. Furthermore, we compress the parametric solution in just several parameters (knot points locations and derivatives in first and last one of them) which could also be explored for compression purposes or increasing computation efficiency.