Abstract
This work introduces molecular nonlinear dynamics (MND) as a new approach for describing protein folding and aggregation. By using a mode system, we show that the MND of disordered proteins is chaotic while that of folded proteins exhibits intrinsically low dimensional manifolds (ILDMs). The stability of ILDMs is found to strongly correlate with protein energies. We propose a novel method for protein thermal uncertainty quantification based on persistently invariant ILDMs. Extensive comparison with experimental data and the state-of-the-art methods in the field validate the proposed new method for protein B-factor prediction.
Protein folding produces characteristic and functional three-dimensional structures from unfolded polypeptides or disordered coils.1, 2, 3, 4, 5 The emergence of extraordinary complexity in the protein folding process poses astonishing challenges to theoretical modeling and computer simulations.6, 7 The present work introduces molecular nonlinear dynamics (MND), or molecular chaotic dynamics, as a theoretical framework for describing and analyzing protein folding. We represent the dynamics of macromolecular particles (i.e., atoms or coarse-grained superatoms) by a set of intrinsically chaotic oscillators. A geometry to topology mapping is employed to create driving and response relations among chaotic oscillators. We unveil the existence of intrinsically low dimensional manifolds (ILDMs) in the chaotic dynamics of folded proteins. Additionally, we reveal that the transition from disordered to ordered conformations in protein folding increases the transverse stability of the ILDM. Stated differently, protein folding reduces the chaoticity of the nonlinear dynamical system, and a folded protein has the best ability to tame chaos. Furthermore, we bring to light the connection between the ILDM stability and the thermodynamic stability, which enables us to quantify the disorderliness and relative energies of folded, misfolded, and unfolded protein states. Finally, we exploit chaos for protein uncertainty quantification and develop a robust chaotic algorithm for the prediction of Debye-Waller factors, or temperature factors, of protein structures.
INTRODUCTION
Protein folding process is one of the most important processes in life. How exactly a random coil of polypeptide chain folds into functional structure or conformation after being translated from a sequence of mRNA remains a mystery. Anfinsen's dogma of sequence-structure-function,8 in which a protein's function depends on its uniquely folded three-dimensional (3D) structure and its structure is determined by the amino acid sequence, is challenged due to the discovery that many partially folded or intrinsically unstructured proteins remain functional despite of the lack of uniquely folded 3D structures.3, 4, 9, 10 Kinetically and thermodynamically regulated competing pathways, including disordered aggregation, degradation, folding and unfolding, convert linear chains of amino acids translated from sequences of mRNA into degraded fragments, protofibrils, amyloid-like fribrils, amyloids, intrinsically disordered proteins, partially disordered proteins, and folded structures.1, 2, 3, 4, 5 The formation of disordered proteins is often exploited by living systems to perform novel and diverse biological functions. Unfortunately, aggregated or misfolded proteins are often associated with sporadic neurodegenerative diseases, such as mad cow disease, Alzheimer's disease, and Parkinson's disease.11, 12 Currently, there is a lack of efficient means for the characterization of disordered aggregation and the quantification of orderliness, which are crucial to the understanding of the molecular mechanism of degenerative diseases.
The emergence of complexity in self-organizing living systems, including protein folding, poses fabulous challenges to their quantitative description and prediction.6, 7 Cyrus Levinthal suggested that there are near 1095 possible conformations for a relatively small polypeptide of 100 residues,13 while an average human protein of 480 residues might have an astronomical number of conformations. The complexity is extraordinary since human proteins are coded by over 20 000 genes. The straightforward sampling of the full conformational space becomes unfeasible for large proteins. It takes many months for molecular dynamics (MD) simulations, the main workhorse of computational protein folding,14 to come up with a very poor copy of what Nature administers perfectly within a tiny fraction of a second. In fact, disordered aggregation, unfolding and folding often occur at slower time scales and involve larger length scales, which are essentially intractable to full atomic simulations.6, 7 Coarse-grained (CG) representations of polypeptides are employed to reduce the number of degrees of freedom, extend molecular modeling, and bridge with experimental observations. An active research topic is how to improve the accuracy of CG models so as to differentiate near degenerate energy landscapes of some conformations generated by the protein folding process. Elastic network models (ENMs), including Gaussian network model (GNM) and anisotropic network model, represent folded proteins as elastic mass-spring networks to investigate its mechanical flexibility and long-time stability beyond the reach of molecular dynamics.15, 16, 17, 18, 19, 20 In general, ENMs can be viewed as a time-independent molecular mechanics derived from their corresponding time dependent molecular mechanics by using the time-harmonic approximation. An underlying assumption adopted in all of the above-mentioned theoretical models is that protein folding, misfolding, and aggregation are to be modeled with some deterministic dynamical systems, which reinforce Anfinsen's dogma and exclude any unpredictability and molecular degradation. However, the existence of degraded fragments, protofibrils, amyloid-like fribrils, amyloids, misfolds, and intrinsically disordered proteins highlights the fundamental limitation of current simulation models.
Chaos is ubiquitous in nature. The discovery of the sensitivity of initial conditions, one of three signatures of chaos, dated to the 1880s by Henri Poincaré.21 However, little attention was paid to chaos until Edward Lorenz's work on nonlinear dynamics and description of butterfly effect in weather forecasting in the 1960s, which underpin the modern theory of deterministic chaos.22 Understanding deterministic chaos is of theoretical and practical importance.23, 24, 25, 26 Some detailed analysis of chaos dynamics can be found in the literature.27, 28 Mathematically, a chaotic dynamics also exhibits dense periodic orbits and topologically mixing of its phase space open sets.27, 28 Chaos has been observed in a vast variety of realistic systems, including Belouzov-Zhabotinski reactions, nonlinear optics, Chua-Matsumoto circuit, Rayleigh-Bénard convention, meteorology, population dynamics, psychology, economics, finance solar system, protein dynamics,29 and heart and brain of living organisms.30 Various chaos control strategies have been proposed.23, 24, 25, 26 However, the natural ability of protein folding in controlling chaos has not been unveiled yet.
Imagine that a folded protein is a Greek chorus where all particles sing with a synchronized voice on the dramatic action, while an unfolded protein is an anharmonic chaotic orchestra where each particle plays its own rhythm with its own instrument. In this work, we propose a method, called MND, to describe this chaotic behavior of a protein. The fundamental assumption of the MND is that each protein configuration (structure) is the direct manifestation of the internal and external interactions of the protein. Protein functions, such as stability and flexibility, are entirely determined by the protein structure or geometry. Therefore, there is no need to resort to protein interactions to predict thermal fluctuations. Our approach has two basic ingredients: the connectivity matrix and the nonlinear oscillator representation of protein particles. The former is constructed by a geometry to topology mapping and the latter describes the relative motions of particles. It is found that this model reveals the role of the protein structure in taming the chaos from two aspects. First, folded protein structures induce the transition from chaos to periodicity. Additionally, the protein folding process restrains high dimensional chaos to achieve synchronization. We also show that MND can be used to successfully predict the Debye–Waller factor, which describes thermal fluctuations of the structure. A comparison with the GNM further validates our approach.
The rest of this paper is organized as follows. Section 2 is devoted to methods and algorithms. The MND method is discussed in detail, including a kernel function representation for the connectivity matrix, the construction of MND from coupled nonlinear oscillators, and the stability analysis of the ILDM. Numerical results are presented in Sec. 3. We demonstrate the protein folding induced control of chaos by using a model system, the Lorenz equation. It is shown that folded protein conformations correspond to the ILDM, while unfolded structures are associated with high-dimensional chaotic dynamics. We further utilize the persistence of the invariant ILDM for protein uncertainty quantification, i.e., analyzing protein thermal fluctuations. The ILDM based flexibility analysis is calibrated with a state-of-the-art method, GNM. Finally, concluding remarks including the limitation and possible improvement are presented.
METHODS AND ALGORITHMS
We assume that the 3D structure or geometry of a protein contains in all the information regarding to protein-protein interactions sits, and most importantly the internal interactions between particles, which can be atom, amino acid, or superatoms within the protein itself. Therefore, the final configuration of the protein is the manifestation of balanced interactions. From another perspective, the distance between two particles is directly associated with their total interaction strength. Additionally, all the protein functions, including thermal fluctuations, are solely determined by the structure. Therefore, functional predictions can be done with the structural information without resorting to the ultimate interactions. We build up a connectivity matrix from the geometry of a protein. Further, we represent the dynamics of each particle by a nonlinear oscillator, and couple particles with the connectivity matrix extracted from the geometry. In this section, we discuss the details of our methods, algorithms, and their further applications to protein folding.
Geometry to topology mapping
Topological relations or connectivities among molecular particles are basic ingredients in MND model. As discussed above, this topological information can be extracted from the geometric properties of a given molecule of interest. Let us consider a molecule of N particles located at , where , where particles are either atoms, amino acids residues, or other superatoms in the molecule. The distance between the ith and jth particles is given by . The connectivity matrix must satisfy the driven and response relation between two dynamics systems Additionally, we assume that all particles are mutually connected and their interactions decay as a function of their distance Aij(dij). The simplest form for the connectivity matrix is the Kirchhoff (or connectivity) matrix generated by cutoff distances
| (1) |
To account for the distance effect in a more realistic manner, it is also convenient to employ smooth and monotonically decreasing radial basis functions or delta sequence kernels of positive type.31 Here, we consider generalized exponential functions
| (2) |
and power-law functions
| (3) |
where are characteristic distances between particles. In the present model, can be used as a set of fitting parameters. Note that some of the above matrix expressions have also been used in other flexibility analysis approaches.19, 32, 33, 34, 35, 36 However, the present construction of these functional forms was based on the driven and response relation of coupled dynamical systems.27
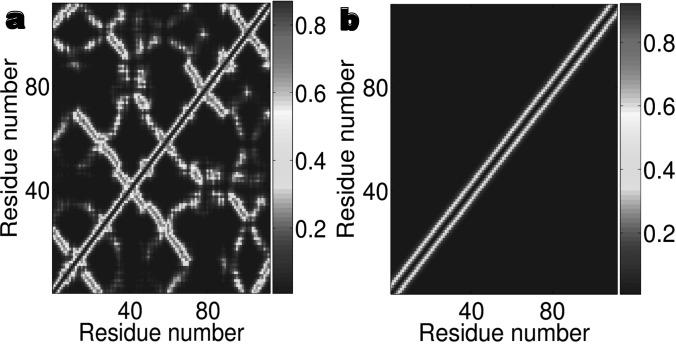
Expressions 1, 2, 3 map a molecular geometry into topological relations or connectivities. The connectivity matrix A is an N × N symmetric, diagonally dominant matrix. Note that elements in the connectivity matrix are not interaction potentials among particles. For simplicity, we set characteristic distances to for all amino acid residues. Figure 1 illustrates the non-diagonal elements of two connectivity matrices, one for the native protein structure of 2mcm and the other for completely unfolded conformation generate from pulling the structure of 2mcm. It is seen that the native protein shows a heterogeneity (or small-world property37) in its connectivity matrix, which contributes to the protein stability. Whereas the connectivity matrix of the completely unfolded conformation has little nonlocal connection.
Figure 1.
The connectivity matrices for two conformations of protein 2mcm generated by using Eq. 2 with k = 2 and . Diagonal elements have been excluded to emphasize non diagonal interactions. (a) The connectivity matrix of the native structure of 2mcm shown in Fig. 3a indicates much nonlocal interactions. (b) The connectivity matrix of a completely unfolded conformation shown in Fig. 3g demonstrates little nonlocal interactions.
Molecular nonlinear dynamics
To introduce the MND, let us consider a folding protein that constitutes N particles and has the spatiotemporal complexity of . Assume that the molecular mechanics of the protein is described by molecular nonlinear dynamics having a set of N nonlinear oscillators of dimension , where n is the dimensionality of a single nonlinear oscillator. Let us consider an n × N-dimensional nonlinear system for N interacting chaotic oscillators
| (4) |
where is an array of state functions for N nonlinear oscillators, is an n-dimensional nonlinear function for the jth oscillator, is an array of nonlinear functions of N oscillators, and . Here, ε is the overall interaction strength, A is the N× N connectivity matrix defined in Sec. 2A, and Γ is an n × n linking matrix. Although it is possible to consider all the physical interactions among protein particles, we feature the importance of the protein distance geometry in this work. As such, we map a protein geometry into a set of topological relations or connectivities.
Stability analysis of the ILDM
We use the protein connectivity matrix to define the driving and response relation of nonlinear chaotic oscillators. Amazingly, an N-time reduction in the spatiotemporal complexity can be achieved, leading to an ILDM of dimension . Formally, the n-dimensional ILDM is defined as
| (5) |
where s(t) is a synchronous state or reference state.
To understand the stability of the ILDM of protein chaotic dynamics, we define a transverse state function as w(t)= u(t)– S(t), where S(t) is a vector of N identical components . Obviously, the invariant ILDM is given by w(t)= u(t)– S(t)= 0. Therefore, the stability of the ILDM can be analyzed by , which can be studied by the following linearized equation:27, 28
| (6) |
where DF(s) is the Jacobian of F.
To further analyze the stability of Eq. 6, we diagonalize connectivity matrix A
| (7) |
where are eigenvectors and are the associated eigenvalues. These eigenvectors span a vector space in which a transverse state vector has the expansion27, 28
| (8) |
Therefore, the stability problem of the ILDM is equivalent to the following stability problem:
| (9) |
where Df (s) is the diagonal component of DF(s). The stability of Eq. 9 is determined by the largest Lyapunov exponent Lmax, namely, , which can be decomposed into two contributions
where Lf is the largest Lyapunov exponent of the original n dimensional chaotic system , which can be easily computed for most chaotic systems. Here, Lc depends on and Γ. The largest eigenvalue equals 0, and its corresponding eigenvector represents the homogeneous motion of the ILDM, and all of other eigenvalues govern the transverse stability of the ILDM. Let us consider a simple case in which the linking matrix is the unit matrix . Then stability of the ILDM is determined by the second largest eigenvalue , which enables us to estimate the critical interaction strength in terms of and Lf,
| (10) |
The dynamical system reaches the ILDM when and is unstable when . The eigenvalues of protein connectivity matrices are obtained with a standard matrix diagonalization algorithm.
NUMERICAL RESULTS
To demonstrate the full strength of the molecular nonlinear dynamics, we present three major results in this work. First, we show that the transition from chaos to periodicity can be induced by protein interactions. Additionally, we demonstrate the correlation between protein randomness and the dimensionality of chaos in the protein MND. Finally, we utilize the persistence of the invariant ILDM for the uncertainty quantification of protein structures due to thermal fluctuations.
In our MND model Eq. 4, the exact expressions of the nonlinear functions F(u) is not specified. Mathematically, it is well known that a double well or triple well function can lead to multiple local minima, which support bistable or multiple stable states. The system becomes unstable or chaotic under certain perturbation. In this paper, for simplicity, we just choose a set of Lorenz attractors22 to illustrate our ideas. The Lorenz equation is three-dimensional ,
| (11) |
where parameters and are to be specified for each given system.
The Lorenz Eq. 11 can be analyzed with the Poincaré section and the first return map.38 Parameter γ has been used to classify certain behavior of the Lorenz Eq. 11. The origin is a fixed point when . When , the system is at the saddle-node bifurcation point. For , there is a pair of fixed points given by
For , the above twin fixed points are stable if
At , the twin fixed points are no longer stable due to the Hopf bifurcation.
By choosing the classical parameter values and , almost all points in the phase space go to a strange attractor—the Lorenz attractor. The Lorenz equations are solved by using the forward Euler scheme and/or the fourth order Runge-Kutta scheme in this work.
Note that the Lorenz oscillators used in the present work do not directly govern the realistic dynamics of protein residues or atoms. Instead, they just provide a simple representation of the protein dynamics. It turns out that such a simple representation is able to capture certain fundamental features of the protein as described below.
Folding induced transition from chaos to periodicity
As a proof of principle, we first demonstrate that folded proteins are able to control chaos. To this end, we consider the MND generated by the coarse-grained representation of bacteriocin AS-48 (protein data bank (PDB) ID: 1e68) by using its 70 amino acid residues. As a comparison, we create a reference dynamical system with 70 weakly coupled Lorenz attractors. In this case, we set E in Eq. 4 as , where B is given by
| (12) |
The linking matrix is given as
| (13) |
In this setting, there is no realistic protein structure information in the connectivity matrix. Consequently, the dynamics of original seventy weakly coupled Lorenz attractors is chaotic as shown in Figs. 2a, 2b. In fact, each chaotic attractor resembles the well-known wings of butterfly as plotted in Fig. 2a. Here, and are used. The Lorenz parameters are set to , and .
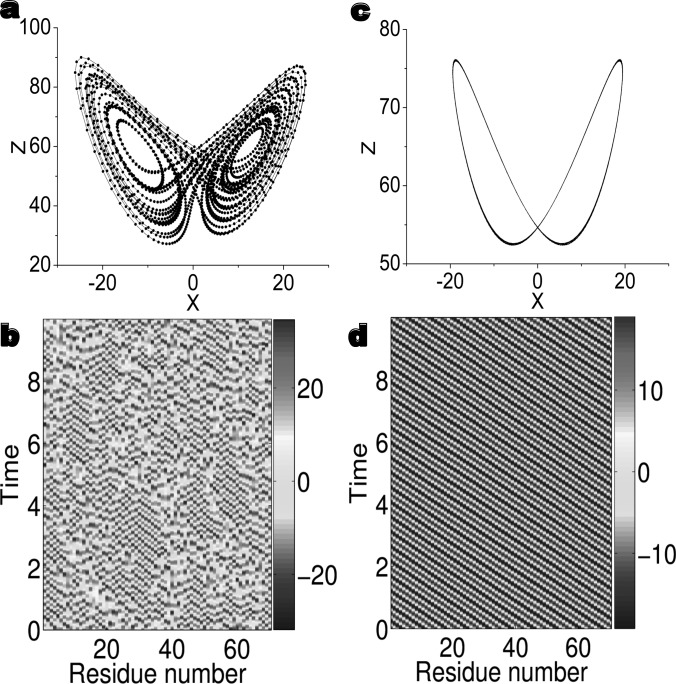
Figure 2.
Transition from chaos to periodicity in the chaotic dynamics model (CDM) of bacteriocin AS-48 (PDB ID 1e68). (a) The butterfly wing pattern for one of 70 chaotic oscillators. (b) The solution of original 70 chaotic oscillators. (c) The periodic orbit of the ILDM for bacteriocin AS-48. (d) Bacteriocin AS-48 induced Hopf bifurcation from chaos. All of 70 nonlinear oscillators are in one lag synchronized periodic orbit.
To appropriately consider protein interactions, we set , where the connectivity matrix A takes the form given in Eq. 2 and . Surprisingly, the MND of bacteriocin AS-48 exhibits a shocking transition from chaos to periodicity as depicted in Figs. 2c, 2d. The chaotic dynamics of each oscillator undergoes a Hopf bifurcation as illustrated in Fig. 2c. It is interesting to note that there is a constant delay in the dynamics of any two adjacent oscillators and there is a lag synchronization in the protein dynamics. As such, the protein dynamics can be described by an dimensional ILDM, which achieves a stunning 70-fold reduction in complexity and dimensionality.
High dimensional chaos associated with unfolding proteins
Having demonstrated the ability of transforming high dimensional chaos to a three-dimensional periodic orbit by a folded protein, we further analyze the dynamics of a set of forty one conformations generated from pulling the structure of macromomycin (PDB ID: 2mcm) with a constant force. It is quite standard to create partially folded and unfolded proteins by a pulling force in computer simulations39 and with experimental means.40 The relation between protein topology and energy was discussed in the literature.39 In Fig. 3, partially folded and unfolded protein conformations are obtained by using the molecular dynamical simulation tool NAMD with a constant pulling velocity. In the protein preparation procedure, a protein structure downloaded from the PDB is first submerged into a box with a layer of 5 Å water in each direction from the atom with the largest co-ordinate in that direction. We use the time interval of 2 ps in our simulations. A total of 15 000 time steps of equilibration is performed with the periodic boundary condition after 10 000 time steps of initial energy minimization.
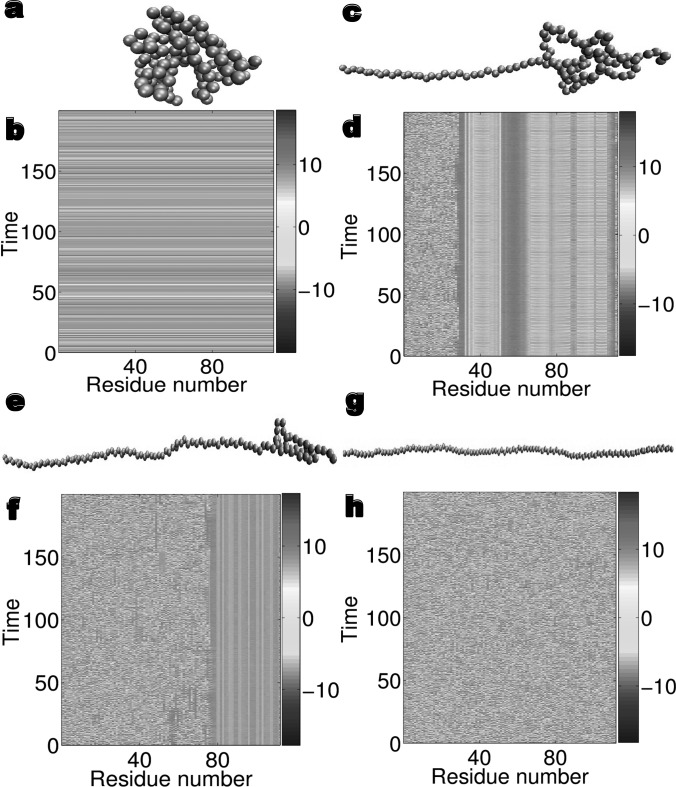
Figure 3.
The spectacular correlation between folded residues and controlled chaos in the dynamics of macromomycin. Forty partially folded or totally unfolded conformations are generated by pulling the folded structure (PBD ID: 2mcm). (a) The atoms of the native folded structure. (b) The synchronous dynamics of a 3D ILDM for the native folded structure. (c) The atoms of partially ordered Conformation 14. (d) The partial ordered chaotic dynamics of Conformation 14. The first 30 residues are unfolded, which leads to the chaotic dynamics in their nonlinear oscillators. The dynamics of the last two residues are also chaotic for the same reason. Interesting synchronized domains occur in the middle for partially folded residues. (e) The atoms of more disordered Conformation 28. (f) The more chaotic dynamics of Conformation 28 showing a higher degree of randomness. Unfolded residues are in their chaotic motions. Compared to the dynamical behavior of Conformation 14, there are fewer synchronized domains and an average synchronized domain involves fewer oscillators. (g) The atoms of completely unfolded Conformation 41. (h) The completely chaotic dynamics of Conformation 41 showing 336-dimensional chaotic motions.
It is no doubt that water molecules are of significant importance for protein folding pathways and biological functions. However, since the purpose of the present work is to reveal the relation between protein structures and their chaotic dynamics, water molecules, and their impact to the protein conformations are somewhat irrelevant to our findings. Therefore, we construct partially folded and unfolded protein conformations by pulling the relaxed protein structures in steered molecular dynamics (SMD) simulations with a constant velocity. Basically, we fix the first atom and apply a constant pulling velocity on the last atom along the direction that connects these two atoms. We set the spring constant as 7 kcal/(mol Å2), while 1 kcal/(mol Å2/) equals 69.74 pN Å. The constant velocity is 0.005 Å per time step. A total of 20 000 simulation steps is integrated in generating 1ubq conformations and a new conformation is extracted after every 500 simulation steps. For proteins 7rsa and 2mcm, a total of 80 000 simulation steps is employed for each protein and new conformations are extracted at the frequency of every 2000 steps.
We make use of the generalized exponential functions given in Eq. 2 to construct the connectivity matrix. Related parameters in the MND are chosen as follows: the characteristic distance , k = 2, and the interaction strength . For parameters in the Lorenz dynamic system, we use , and . Random numbers of range [0,1] are used for as initial conditions for all oscillators. The unit matrix is used for linking matrix in this case and in the rest of this paper. The forward Euler scheme with the time increment of h = 10−2 is used for the time integration.
Our basic results are demonstrated in Fig. 3. Conformation 1, shown in Fig. 3a, is the folded structure obtained by a short period of relaxation of the crystal structure from the PBD, while Conformations 2 to 41 are increasingly less folded due to the increase in the pulling force during their generation, see three typical ones in Figs. 3c, 3e, 3g. The same set of random initial data is assigned to all the nonlinear oscillators in all conformations. Figure 3b shows the occurrence of a stable ILDM, a synchronous chaos, in the dynamics of the folded structure. What spotlights the uniqueness and importance of the native structure is that none of any other conformations that are partially ordered and/or essentially disordered is able to tame chaos in their nonlinear dynamics under the same condition. Indeed, the dynamical systems of Conformations 2 to 41 are unstable, chaotic, and 336-dimensionally complex due to 112 residues. Consequently, they are very sensitive to initial values, simulation algorithms, and time increments. However, it is still possible to extract some useful physical information from their unstable chaotic dynamics with well designed numerical experiments. Figures 3d, 3f indicate synchronized domains in overall non-synchronized chaotic dynamics. Amazingly, there is a miraculous correspondence between synchronized domains and the locations of partially folded amino acid residues, which clearly indicates that protein folding leads to the control of chaos. It is interesting to note that synchronized domains are strikingly persistent over time. They appear to be locked in certain ranges of solution values and show much less fluctuation and volatility than fully chaotic oscillators do. Finally, as shown in Fig. 3h, the dynamics of the completely unfolded conformation is fully chaotic, which reinforces our observation that protein folding tames chaos and induces ILDM.
Transverse stability of the ILDM
To shed light on the mechanism of protein folding induced chaos control and ILDM, we analyze the transverse stability of the synchronous state. It turns out that the stability problem of the n × N-dimensional nonlinear dynamics system is determined by its maximal Lyapunov exponent (MLE). Consequently, the ILDM is invariant with respect to a transverse perturbation if the MLE is smaller than zero. The MLE of a protein dynamics consists of two independent parts, i.e., the contribution from the single nonlinear attractor and that from the connectivity matrix obtained from the protein distance geometry or the negative gradient of the protein interaction potential in general. The MLE of the single nonlinear attractor can be easily analyzed and is all known for the Lorenz attractor used in this work, while the contribution from protein distance geometry depends on the product of the interaction strength and the largest nonzero eigenvalue of the protein connectivity matrix. The latter can be easily computed by a matrix diagonalization. As a result, there is a critical interaction strength for the chaotic dynamics of each protein conformation to arrive at its stable and invariant ILDM.
Protein orderliness
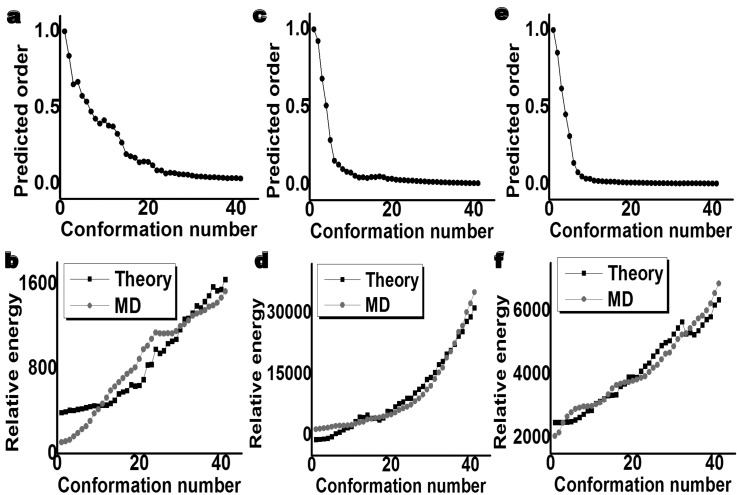
Interestingly, the above ILDM analysis gives rise to a new chaotic dynamics model for the characterization of the disordered aggregation and the quantification of disorderliness in protein confirmations. A more disordered protein conformation requires a larger critical interaction strength to establish the synchronous state; whereas the uniquely folded protein is, in principle, associated with the smallest critical interaction strength. To quantify orderliness and disorderliness in protein conformations, we define an order parameter , where and are the critical interaction strengths of a given conformation and the native conformation, respectively. Therefore, the order of the native protein conformation is 1 and that of a disordered protein is smaller than 1. Figures 4a, 4c, 4e illustrate the order parameters of three sets of conformations generated from ubiquitin (PDB ID: 1ubq), phosphate-free bovine ribonuclease A (PDB ID: 7rsa), and macromomyci (PBD ID: 2mcm). Forty partially folded or unfolded conformations are generated for each protein. Their order parameters exhibit a fast decay as their structures become less folded.
Figure 4.
The orders and energy comparisons of three sets of protein conformations predicted by the stability analysis of the ILDM. All conformations are generated from pulling native protein structures. (a) The predicted orders of 41 conformations for ubiquitin. (b) Comparison of relative energies of 41 conformations for ubiquitin. (c) The predicted orders of 41 conformations for phosphate-free bovine ribonuclease A. (d) Comparison of relative energies of 41 conformations for phosphate-free bovine ribonuclease A. (e) The predicted orders of 41 conformations for macromomycin. (f) Comparison of relative energies of 41 conformations for macromomycin.
Critical interaction strength
It remains to understand why the critical interaction strength in Eq. 10 is able to determine the transverse stability of the chaotic dynamics of a given molecular conformation. It is seen that the critical interaction strength is an inverse function of the second largest nonzero eigenvalue of the molecular connectivity matrix. The latter is a manifestation of the molecular structure. As shown in Fig. 1, the structure of a folded protein gives rise to a “small-world” connectivity network,37 while the structure of completely unfolded conformation has little nonlocal interactions. This implies that the transverse stability of the ILDM of a molecule is ultimately determined by its structure. Since the thermodynamical stability of a molecular structure is characterized by its total energy, there must be a one-to-one correspondence between the critical interaction strength and the total energy. As such, we can estimate the relative energies of protein folding conformations based on their second largest nonzero eigenvalue of their connectivity matrix. To verify this hypothesis, we analyze the nonlinear dynamics of protein structures 1ubq, 7rsa, and 2,mcm. For each structure, we create a set of unfolded confirmations by molecular dynamics. Figures 4b, 4d, 4f show good agreements between energies estimated by using the largest eigenvalues and those obtained from molecular dynamics simulations.
Various procedures of conformation generation are also considered, including using different initial structure preparations, number of integration steps, and pulling velocities, which lead to different sets of conformations. However, our findings presented in Figs. 34 are not affected by these variations.
ILDM based B-factor prediction
In this section, we introduce a new approach for protein flexibility analysis. The proposed method is based on transverse stability of the ILDM for the prediction of atomistic B-factors, or temperature factors of a given molecular structure. B-factor is a measure of the mean-squared atomic displacement due to thermal motion and possible experimental uncertainties. In general, an atom with a larger B-factor implies it is more flexible and atoms with smaller B-factors are relatively rigid. The analysis of B-factors provides insights on the large-scale and long-time functional behaviors of native state macromolecules. This information is complementary to that obtained from atomic detail simulation techniques.
There are many other interesting approaches for the flexibility analysis in the literature. For example, normal mode analysis (NMA) has been proposed to uncover the intrinsic structural flexibility of the protein15, 16, 17, 41, 42 and study biomolecular systems like lysozyme.17, 43 NMA approach has a large number of variations. Tirion proposed ENM by simplifying the interaction potential in the NMA.18 By introducing the idea from polymer science,44 Bahar et al. use GNM to describe protein flexibility.19, 32 They employed the atom representation of proteins based on local packing density and contact topology. Anisotropic fluctuations are considered in anisotropic network model (ANM).33 Parameters in these models are calibrated with Debye-Wallers factor or B-factors. Crystal structures have been also taken into considerations.45, 46, 47, 48 Due to the simplified potential and reduced representation, these coarse-grained based ENM and GNM approaches19, 20, 32, 33, 34, 35, 36 gain popularity and have been applied to the study of macroproteins or protein complexes, such as, hemoglobin,49 F1 ATPase,50, 51 chaperonin GroEL,52, 53 viral capsids,54, 55 and ribosome.56, 57 More applications can be found in a few good review papers.42, 58, 59, 60 Our ILDM based method should be potentially useful for solving these problems as well.
It is interesting to note that the intriguing dynamics of a protein ILDM is exponentially stable and persistently invariant. It will be wonderful if one can take advantage of such properties in practical biophysical studies. To this end, we propose an ILDM based new method for protein rigidity analysis. Our essential idea is to perturb the dynamics of each particle in a macromolecule in the transverse direction. Because of the stability of the ILDM, the nonlinear system must return to its original orbit, just like the free induction decay of the spin dynamics in nuclear magnetic resonance (NMR) experiments. Similar to the T2 and T1 relaxations in an NMR experiment, the total relaxation time after the transverse perturbation, defined as the time used to recover the original state within a factor of 1/e, is a measure of the strength of its particle-particle and particle-environment interactions. For a given particle, stronger interactions with neighboring particles and environment lead to a shorter relaxation time, which translates into higher rigidity and lower B-factor. Therefore, the direct connection between the thermodynamical stability and the ILDM stability enables us to quantitatively estimate atomic temperature factors in a molecule.
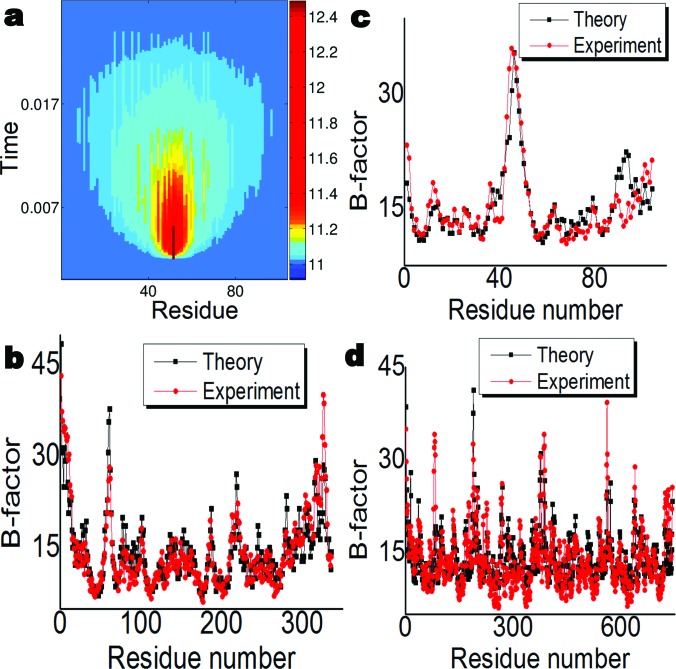
Figure 5a illustrates the relaxation process of a perturbed nonlinear dynamics of protein 2nuh. The instantaneous perturbation is propagated from the nearest neighboring amino acid residues to a wider region over a time period before gradually fades off. By recording the relaxation time, one is able to predict the B-factor of an amino acid residue and compare it to the experimental data given by X-ray crystallography. Figures 5b, 5c, 5d provide such comparisons for three protein structures, namely 2nuh, 1aru, and 4dr8. It is seen that our results obtained from the perturbation of the ILDM are in a very good consistency with those of X-ray data.
Figure 5.
Protein flexibility analysis by the present ILDM method. (a) The impact and relaxation of the transverse perturbation of the ILDM at a given amino acid residue (the 52th ). The residues in horizontal axis are listed in the descending order according to their distances with respect to the perturbed residue. (b)-(d) The experimental B-factors and ILDM predictions for protein 1aru, 2nuh, and 4dr8. The correlation coefficients are respectively 0.913, 0.866, and 0.751 for three predictions.
The parameter details used in our B-factor prediction are as follows. The chaotic dynamical system parameters are chosen as , and . Both forward Euler scheme and the fourth order Runge-Kutta scheme are used in the time integration to validate each other. Appropriate time increment that satisfies the stability requirement under given interaction strength is used. Initially, all oscillators rest in their steady states. A perturbation is then employed on the jth particle: . The perturbation procedure is repeatedly carried out for all particles in the protein to compute their relaxation time values, which are converted to B-factors by linear regressions. For the predictions of B-factors in Figs. 5b, 5c, 5d, is employed for 2nuh, is used for 1aru, and is chosen for 4dr8.
Comparison with GNM
To demonstrate the robustness of the present chaotic dynamics model, a set of 60 protein structures downloaded from the PDB is considered. All the structures are obtained by the X-ray diffraction with resolution about 2.0 Å, and they are free from multiple conformations, which mean that for each protein, all the atomic occupancies equal 1.0. The correlation coefficient Cc is used to measure the consistency between theoretical predictions and experimental data
| (14) |
where are theoretical prediction of B-factors and are a set of experimental B-factors obtained directly from the PDB. Here, and the statistical averages of theoretical and experimental B-factors, respectively.
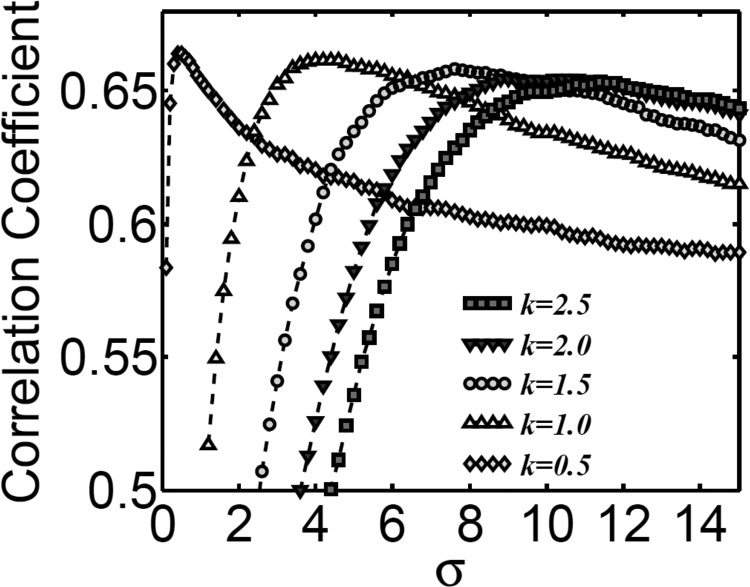
Through the calculation of correlation coefficients averaged over 60 proteins, we search the optimal value of parameter for a set of k values (k = 0.5, 1.0, 1.5, 2.0, 2.5). It is seen from Figure 6 that the best average correlation coefficient is achieved around , except when k = 0.5. Based on this analysis, we create a parameter free version of our MND model by setting and k = 1. This version is employed in all of our comparison with GNM.
Figure 6.
The optimal parameter search for exponential type of probability density estimators in Eq. 2. A set of 60 proteins is used and their correlation coefficients are averaged over the set. The averaged correlation coefficients are plotted with respect to the change of parameter and k. It is seen that except for k = 0.5, all other kernels achieve their maximal correlation coefficient in the range .
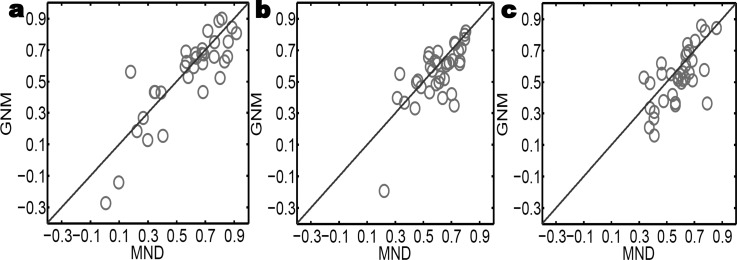
We validate our method by the comparison with the GNM. The code for the GNM is adopted from Jernigan Laboratory (http://ribosome.bb.iastate.edu/software.html). The cutoff distance used is 7 Å and some minor modification is done to enhance its performance on the coarse-grained PDB data. Three sets of protein data utilized by Park, Jernigan, and Wu61 are considered in our work. We careful go through these data to delete the multiple conformations and add in the missing residues. The modified data lead to improved GNM predictions compared to those in the literature.61 Tables 1, 2, TABLE III. list our results for three date sets, respectively. Figure 7 plots the results of the comparison over three data sets. Apparently, the proposed MND method outperforms GNM for most proteins. The average correlation coefficients are listed in Table TABLE IV.. It is seen that the proposed method achieves about 8% improvement over the GNM.
TABLE I.
Comparison of B factor prediction by parameter free MND and Gaussian normal mode (GNM) for small-sized data set.61 The asterisk sign indicates improved prediction with modified protein data.
| PDB ID | N | MND | GNM |
|---|---|---|---|
| 1AIE | 31 | 0.405 | 0.155 |
| 1AKG | 16 | 0.223 | 0.185 |
| 1BX7 | 51 | 0.679 | 0.706 |
| 1ETL | 12 | 0.833 | 0.628 |
| 1ETM | 12 | 0.683 | 0.432 |
| 1ETN | 12 | 0.007 | −0.274 |
| 1FF4 | 65 | 0.676 | 0.674 |
| 1GK7 | 39 | 0.718 | 0.821 |
| 1GVD | 52 | 0.618 | 0.591 |
| 1HJE | 13 | 0.681 | 0.616 |
| 1KYC | 15 | 0.860 | 0.754 |
| 1NOT | 13 | 0.801 | 0.523 |
| 1O06 | 20 | 0.886 | 0.844 |
| 1OB4 | 16 | 0.764 | 0.750* |
| 1OB7 | 16 | 0.637 | 0.652* |
| 1P9I | 29 | 0.569 | 0.625 |
| 1PEF | 18 | 0.915 | 0.808 |
| 1PEN | 16 | 0.267 | 0.270 |
| 1Q9B | 43 | 0.762 | 0.656 |
| 1RJU | 36 | 0.391 | 0.431 |
| 1U06 | 55 | 0.350 | 0.434 |
| 1UOY | 64 | 0.690 | 0.671 |
| 1USE | 40 | 0.097 | −0.142 |
| 1VRZ | 21 | 0.633 | 0.677* |
| 1XY2 | 8 | 0.181 | 0.562 |
| 1YJO | 6 | 0.344 | 0.434 |
| 1YZM | 46 | 0.815 | 0.901 |
| 2DSX | 52 | 0.298 | 0.127 |
| 2JKU | 35 | 0.854 | 0.656 |
| 2NLS | 36 | 0.580 | 0.530 |
| 2OL9 | 6 | 0.565 | 0.689 |
| 2OLX | 4 | 0.794 | 0.885 |
| 6RXN | 45 | 0.559 | 0.594 |
TABLE II.
Comparison of B factor prediction in terms of correlation coefficients by parameter free MND and Gaussian normal mode (GNM) for medium-sized data set.61 The asterisk sign indicates improved prediction with modified protein data.
| PDB ID | N | MND | GNM |
|---|---|---|---|
| 1ABA | 87 | 0.757 | 0.613 |
| 1CYO | 88 | 0.729 | 0.741 |
| 1FK5 | 93 | 0.590 | 0.485 |
| 1GXU | 88 | 0.702 | 0.421 |
| 1I71 | 83 | 0.332 | 0.549 |
| 1LR7 | 73 | 0.684 | 0.620 |
| 1N7E | 95 | 0.451 | 0.497 |
| 1NNX | 93 | 0.761 | 0.631 |
| 1NOA | 113 | 0.601 | 0.615 |
| 1OPD | 85 | 0.315 | 0.398 |
| 1QAU | 112 | 0.665 | 0.620 |
| 1R7J | 90 | 0.365 | 0.368 |
| 1UHA | 83 | 0.709 | 0.638* |
| 1ULR | 87 | 0.612 | 0.495 |
| 1USM | 77 | 0.794 | 0.798 |
| 1V05 | 96 | 0.582 | 0.632 |
| 1W2L | 97 | 0.638 | 0.397 |
| 1X3O | 80 | 0.536 | 0.654 |
| 1Z21 | 96 | 0.545 | 0.433 |
| 1ZVA | 75 | 0.604 | 0.690 |
| 2BF9 | 36 | 0.541 | 0.680* |
| 2BRF | 100 | 0.768 | 0.710 |
| 2CE0 | 99 | 0.619 | 0.529 |
| 2E3H | 81 | 0.663 | 0.605 |
| 2EAQ | 89 | 0.750 | 0.695 |
| 2EHS | 75 | 0.722 | 0.747 |
| 2FQ3 | 85 | 0.720 | 0.348 |
| 2IP6 | 87 | 0.564 | 0.572 |
| 2MCM | 112 | 0.803 | 0.820 |
| 2NUH | 104 | 0.794 | 0.771 |
| 2PKT | 93 | 0.220 | −0.193* |
| 2PLT | 99 | 0.461 | 0.509* |
| 2QJL | 99 | 0.548 | 0.594 |
| 2RB8 | 93 | 0.650 | 0.517 |
| 3BZQ | 99 | 0.484 | 0.466 |
| 5CYT | 103 | 0.440 | 0.331 |
TABLE III.
Comparison of B factor prediction in terms of correlation coefficients by parameter free MND and Gaussian normal mode (GNM) for large-sized data set.61 The asterisk sign indicates improved prediction with modified protein data.
| PDB ID | N | MND | GNM |
|---|---|---|---|
| 1AHO | 64 | 0.617 | 0.562 |
| 1ATG | 231 | 0.606 | 0.497 |
| 1BYI | 224 | 0.464 | 0.552 |
| 1CCR | 111 | 0.562 | 0.351 |
| 1E5K | 188 | 0.751 | 0.859 |
| 1EW4 | 106 | 0.596 | 0.547 |
| 1IFR | 113 | 0.684 | 0.637 |
| 1NKO | 122 | 0.561 | 0.368 |
| 1NLS | 238 | 0.634 | 0.523* |
| 1O08 | 221 | 0.410 | 0.309 |
| 1PMY | 123 | 0.646 | 0.685 |
| 1PZ4 | 113 | 0.859 | 0.843 |
| 1QTO | 122 | 0.378 | 0.334 |
| 1RRO | 108 | 0.334 | 0.529 |
| 1UKU | 102 | 0.650 | 0.742 |
| 1V70 | 105 | 0.409 | 0.162 |
| 1WBE | 204 | 0.531 | 0.549 |
| 1WHI | 122 | 0.407 | 0.270 |
| 1WPA | 107 | 0.542 | 0.417 |
| 2AGK | 233 | 0.687 | 0.512 |
| 2C71 | 205 | 0.662 | 0.560 |
| 2CG7 | 90 | 0.477 | 0.379 |
| 2CWS | 227 | 0.659 | 0.696 |
| 2HQK | 213 | 0.793 | 0.365 |
| 2HYK | 237 | 0.583 | 0.515 |
| 2I24 | 113 | 0.380 | 0.494 |
| 2IMF | 203 | 0.615 | 0.514 |
| 2PPN | 107 | 0.637 | 0.668 |
| 2R16 | 176 | 0.461 | 0.618* |
| 2V9V | 135 | 0.580 | 0.528 |
| 2VIM | 104 | 0.375 | 0.282 |
| 2VPA | 204 | 0.771 | 0.576 |
| 2VYO | 206 | 0.705 | 0.761 |
| 3SEB | 238 | 0.777 | 0.826 |
| 3VUB | 101 | 0.638 | 0.607 |
Figure 7.
The comparison of the B-factor predicted by MND and GNM in terms of correlation coefficients. (a) GNM vs MND for the small-sized protein set. (b) GMA vs MND for the medium-sized protein set. (c) GNM vs MND for the large-sized protein set.
TABLE IV.
The comparison of average correlation coefficients calculated by MND and GNM over three data sets.
| PDB set | MND | GNM | Improvement wrt GNM (%) |
|---|---|---|---|
| Small | 0.580 | 0.541 | 7.21 |
| Medium | 0.603 | 0.555 | 8.65 |
| Large | 0.584 | 0.530 | 10.2 |
Improvement of the flexibility prediction by considering co-factors
Protein structures downloaded from the PBD typically contain many cofactors, i.e., coenzymes and prosthetic groups, which are important for proteins' biological functions. Cofactors also contribute to protein structural rigidity. Therefore, the inclusion of cofactors in the present chaotic dynamics model will improve the prediction of protein B-factor. In the present work, we consider a simple treatment of cofactors in which the nonlinear oscillators of cofactors are used as part of driven sources while those of residues are treated as a response system. This treatment reduces computational cost if the MND is on a stable fixed point, because one does not need to actually compute cofactors' dynamics.
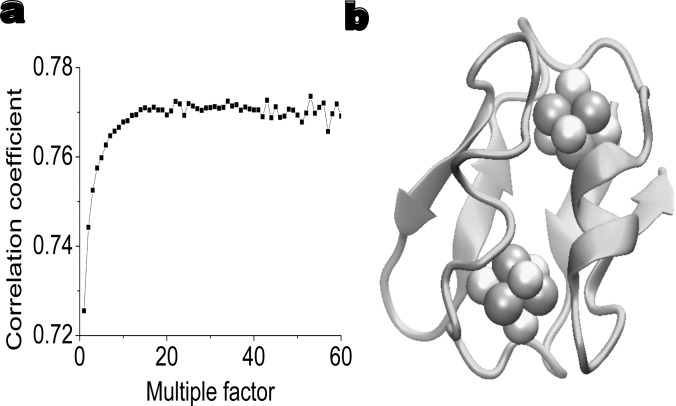
Figure 8 depicts the improvement in the theoretical prediction of protein 1fac B-factors due to the consideration of two metal clusters, i.e., Fe4S4 clusters. We plot the interaction strength of cofactors with respect to the correlation coefficient. Clearly, the consideration of cofactors leads to a five percent improvement in our prediction.
Figure 8.
The improvement of B-factor prediction by considering cofactors. (a) The impact of the interaction strength of two Fe4S4 clusters in 1fca to the predicted correlation coefficient. (b) The structure of ifca showing two Fe4S4 clusters. Amino acid residues are colored according to B-factor values.
CONCLUDING REMARKS
Protein folding and the related structure function relation are of fundamental interest and importance to scientific community. The present work proposes MND to represent the protein folding process and illustrate the structure function relation. We unveil the ability of folded protein structures for controlling the chaos in the underlying MND and show the existence of an ILDM for each folded protein. We demonstrate that protein unfolding leads to high dimensional chaotic states. The orderliness of unfolded protein configurations generated by using steered molecular dynamics simulations directly correlates with the dimensionality of chaotic states. We further utilize the transverse stability of the ILDM for protein uncertainty quantification, i.e., the prediction of protein temperature factors due to thermal fluctuations. By a comparison with cutting edge method in the field, namely, the GNM, it is found that the proposed ILDM based approach works well for protein flexibility analysis.
A discussion of several aspects is in order. First, although the Lorenz system is employed in our study, our findings about the protein control of chaos and the existence of ILDM associated with the folded protein conformation are general and can be regenerated by using other nonlinear dynamical systems. The ability of the ILDM for protein flexibility analysis can also be realized by using other nonlinear dynamical systems because it is the connectivity matrix, rather than the specific dynamical system, that captures the fundamental physics of protein dynamics. Secondly, a simple method for steered molecular dynamics simulations is utilized in the present work to generate partially folded and unfolded protein conformations. However, our findings about the order of unfolded proteins and eigenvalue analysis of protein orderliness are independent of the method used in generating unfolded conformations and protein unfolding pathways. Similar results are obtained by analyzing unfolded protein conformations generated by a different steered molecular dynamics approach. Finally, the prediction of the B-factor can be further improved by the consideration of different types of the residues and the crystal structure of a given protein.
ACKNOWLEDGMENTS
This work was supported in part by NSF Grants DMS-1160352 and IIS-1302285, and NIH Grant R01GM-090208. The authors acknowledge the Mathematical Biosciences Institute for hosting valuable workshops.
References
- Fischer E., “ Einfluss der configuration auf die wirkung den,” Enzyme Ber. Dtsch. Chem. Ges. 27, 2985–2993 (1894). 10.1002/cber.18940270364 [DOI] [Google Scholar]
- Go N., “ Theoretical studies of protein folding,” Annu. Rev. Biophys. Bioeng. 12, 183–210 (1983). 10.1146/annurev.bb.12.060183.001151 [DOI] [PubMed] [Google Scholar]
- Schroder M. and Kaufman R. J., “ The mammalian unfolded protein response,” Annu. Rev. Biochem. 74, 739–789 (2005). 10.1146/annurev.biochem.73.011303.074134 [DOI] [PubMed] [Google Scholar]
- Chiti F. and Dobson C. M., “ Protein misfolding, functional amyloid, and human disease,” Annu. Rev. Biochem. 75, 333–366 (2006). 10.1146/annurev.biochem.75.101304.123901 [DOI] [PubMed] [Google Scholar]
- Uversky V. and Dunker A. K., “ Controlled chaos,” Science 322, 1340–1341 (2008). 10.1126/science.1167453 [DOI] [PubMed] [Google Scholar]
- Bryngelson J. D., Onuchic J. N., Socci N. D., and Wolynes P. G., “ Funnels, pathways, and the energy landscape of protein folding: A synthesis,” Proteins 21, 167–195 (1995). 10.1002/prot.340210302 [DOI] [PubMed] [Google Scholar]
- Dill K. A. and Chan H. S., “ From levinthal to pathways to funnels,” Nat. Struct. Biol. 4, 10–19 (1997). 10.1038/nsb0197-10 [DOI] [PubMed] [Google Scholar]
- Anfinsen C. B., “ Einfluss der configuration auf die wirkung den,” Science 181, 223–230 (1973). 10.1126/science.181.4096.223 [DOI] [PubMed] [Google Scholar]
- Onuchic J. N., Luthey-Schulten Z., and Wolynes P. G., “ Theory of protein folding: The energy landscape perspective,” Annu. Rev. Phys. Chem. 48, 545–600 (1997). 10.1146/annurev.physchem.48.1.545 [DOI] [PubMed] [Google Scholar]
- White S. H. and Wimley W. C., “ Membrane protein folding and stability: Physical principles,” Annu. Rev. Biophys. Biomol. Struct. 28, 319–365 (1999). 10.1146/annurev.biophys.28.1.319 [DOI] [PubMed] [Google Scholar]
- Massi F. and Straub J. E., “ Energy landscape theory for Alzheimer's amyloid beta-peptide fibril elongation,” Protein 42, 217–229 (2001). [DOI] [PubMed] [Google Scholar]
- Massi F., Peng J. W., Lee J. P., and Straub J. E., “ Simulation study of the structure and dynamics of the Alzheimer's amyloid peptide congener in solution,” Biophys. J. 80, 31–44 (2001). 10.1016/S0006-3495(01)75993-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levinthal C., “ How to fold graciously,” in Mossbauer Spectroscopy in Biological Systems: Proceedings of a meeting held at Allerton House, Monticello, Illinois, edited by DeBrunner J. T. P. and Munck E. (University of Illinois Press, 1969), pp. 22–24. [Google Scholar]
- McCammon J. A., Gelin B. R., and Karplus M., “ Dynamics of folded proteins,” Nature 267, 585–590 (1977). 10.1038/267585a0 [DOI] [PubMed] [Google Scholar]
- Tasumi M., Takenchi H., Ataka S., Dwidedi A. M., and Krimm S., “ Normal vibrations of proteins: Glucagon,” Biopolymers 21, 711–714 (1982). 10.1002/bip.360210318 [DOI] [PubMed] [Google Scholar]
- Brooks B. R., Bruccoleri R. E., Olafson B. D., States D. J., Swaminathan S., and Karplus M., “ Charmm: A program for macromolecular energy, minimization, and dynamics calculations,” J. Comput. Chem. 4, 187–217 (1983). 10.1002/jcc.540040211 [DOI] [Google Scholar]
- Levitt M., Sander C., and Stern P. S., “ Protein normal-mode dynamics: Trypsin inhibitor, crambin, ribonuclease and lysozyme,” J. Mol. Biol. 181(3 ), 423–447 (1985). 10.1016/0022-2836(85)90230-X [DOI] [PubMed] [Google Scholar]
- Tirion M. M., “ Large amplitude elastic motions in proteins from a single-parameter, atomic analysis,” Phys. Rev. Lett. 77, 1905–1908 (1996). 10.1103/PhysRevLett.77.1905 [DOI] [PubMed] [Google Scholar]
- Bahar I., Atilgan A. R., and Erman B., “ Direct evaluation of thermal fluctuations in proteins using a single-parameter harmonic potential,” Fold. Des. 2, 173–181 (1997). 10.1016/S1359-0278(97)00024-2 [DOI] [PubMed] [Google Scholar]
- Demerdash O. N. A. and Mitchell J. C., “ Density-cluster NMA: A new protein decomposition technique for coarse-grained normal mode analysis,” Proteins: Structure, Function, and Bioinformatics 80(7 ), 1766–1779 (2012). [DOI] [PubMed] [Google Scholar]
- Poincaré J. H., “ Sur le problme des trois corps et les équations de la dynamique. Divergence des series de m. lindstedt,” Acta Math. 13(1 ), A3–A270 (1890). 10.1007/BF02392506 [DOI] [Google Scholar]
- Lorenz E. N., “ Deterministic nonperiodic flow,” J. Atmos. Sci. 20, 130–141 (1963). [DOI] [Google Scholar]
- Ott E., Grebogi C., and Yorke J. A., “ Controlling chaos,” Phys. Rev. Lett. 64, 1196–1199 (1990). 10.1103/PhysRevLett.64.1196 [DOI] [PubMed] [Google Scholar]
- Pecora L. M. and Carroll T. L., “ Synchronization in chaotic systems,” Phys. Rev. Lett. 64, 821–824 (1990). 10.1103/PhysRevLett.64.821 [DOI] [PubMed] [Google Scholar]
- Wei G. W., Zhan M., and Lai C. H., “ Tailoring wavelets for chaos control,” Phys. Rev. Lett. 89, 284103 (2002). 10.1103/PhysRevLett.89.284103 [DOI] [PubMed] [Google Scholar]
- Ashwin P., “ Nonlinear dynamics - synchronization from chaos,” Nature 422, 384–385 (2003). 10.1038/422384a [DOI] [PubMed] [Google Scholar]
- Pecora L. M., Carroll T. L., Johnson G. A., and Mar D. J., “ Fundamentals of synchronization in chaotic systems, concepts and applications,” Chaos 7, 520–543 (1997). 10.1063/1.166278 [DOI] [PubMed] [Google Scholar]
- Hu G., Yang J. H., and Liu W. J., “ Instability and controllability of linearly coupled oscillators: Eigenvalue analysis,” Phys. Rev. E 58, 4440–4453 (1998). 10.1103/PhysRevE.58.4440 [DOI] [Google Scholar]
- Braxenthaler M., Unger R., Auerbach D., Given J. A., and Moult J., “ Chaos in protein dynamics,” Proteins 29, 417–425 (1997). [DOI] [PubMed] [Google Scholar]
- Boccaletti S., Grebogi C., Lai Y. C., Mancini H., and Maza D., “ The control of chaos: Theory and applications,” Phys. Rep. 329, 103–197 (2000). 10.1016/S0370-1573(99)00096-4 [DOI] [Google Scholar]
- Wei G. W., “ Wavelets generated by using discrete singular convolution kernels,” J. Phys. A 33, 8577–8596 (2000). 10.1088/0305-4470/33/47/317 [DOI] [Google Scholar]
- Bahar I., Atilgan A. R., Demirel M. C., and Erman B., “ Vibrational dynamics of proteins: Significance of slow and fast modes in relation to function and stability,” Phys. Rev. Lett. 80, 2733–2736 (1998). 10.1103/PhysRevLett.80.2733 [DOI] [Google Scholar]
- Atilgan A. R., Durrell S. R., Jernigan R. L., Demirel M. C., Keskin O., and Bahar I., “ Anisotropy of fluctuation dynamics of proteins with an elastic network model,” Biophys. J. 80, 505–515 (2001). 10.1016/S0006-3495(01)76033-X [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinsen K., “ Analysis of domain motions by approximate normal mode calculations,” Proteins 33, 417–429 (1998). [DOI] [PubMed] [Google Scholar]
- Tama F. and Sanejouand Y. H., “ Conformational change of proteins arising from normal mode calculations,” Protein Eng. 14, 1–6 (2001). 10.1093/protein/14.1.1 [DOI] [PubMed] [Google Scholar]
- Li G. H. and Cui Q., “ A coarse-grained normal mode approach for macromolecules: An efficient implementation and application to ca(2+)-atpase,” Biophys. J. 83, 2457–2474 (2002). 10.1016/S0006-3495(02)75257-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watts D. J. and Strogatz S. H., “ Collective dynamics of ‘small-world' networks,” Nature 393, 440–442 (1998). 10.1038/30918 [DOI] [PubMed] [Google Scholar]
- Tucker W., “ A rigorous ODE solver and smale's 14th problem,” Found. Comput. Math. 2, 53–117 (2002). [Google Scholar]
- Paci E. and Karplus M., “ Unfolding proteins by external forces and temperature: The importance of topology and energetics,” PNAS 97(12 ), 6521–6526 (2000). 10.1073/pnas.100124597 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dudko O. K., Hummer G., and Szabo A., “ Intrinsic rates and activation free energies from single-molecule pulling experiments,” Phys. Rev. Lett. 96, 108101 (2006). 10.1103/PhysRevLett.96.108101 [DOI] [PubMed] [Google Scholar]
- Go N., Noguti T., and Nishikawa T., “ Dynamics of a small globular protein in terms of low-frequency vibrational modes,” Proc. Natl. Acad. Sci. U.S.A. 80(12 ), 3696–3700 (1983). 10.1073/pnas.80.12.3696 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma J. P., “ Usefulness and limitations of normal mode analysis in modeling dynamics of biomolecular complexes,” Structure 13, 373–380 (2005). 10.1016/j.str.2005.02.002 [DOI] [PubMed] [Google Scholar]
- Brooks B. R. and Karplus M., “ Normal modes for specific motions of macromolecules: Application to the hinge-bending mode of lysozyme,” Proc. Natl. Acad. Sci. U.S.A. 82(15 ), 4995–4999 (1985). 10.1073/pnas.82.15.4995 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flory P. J., “ Statistical thermodynamics of random networks,” Proc. R. Soc. London, Ser. A 351, 351–378 (1976). 10.1098/rspa.1976.0146 [DOI] [Google Scholar]
- Kundu S., Melton J. S., Sorensen D. C., and G. N.Phillips, Jr., “ Dynamics of proteins in crystals: Comparison of experiment with simple models,” Biophys. J. 83(2 ), 723–732 (2002). 10.1016/S0006-3495(02)75203-X [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kondrashov D. A., Van Wynsberghe A. W., Bannen R. M., Cui Q., and G. N.Phillips, Jr., “ Protein structural variation in computational models and crystallographic data,” Structure 15, 169–177 (2007). 10.1016/j.str.2006.12.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinsen K., “ Structural flexibility in proteins: Impact of the crystal environment,” Bioinformatics 24, 521–528 (2008). 10.1093/bioinformatics/btm625 [DOI] [PubMed] [Google Scholar]
- Song G. and Jernigan R. L., “ vgnm: A better model for understanding the dynamics of proteins in crystals,” J. Mol. Biol. 369(3 ), 880–893 (2007). 10.1016/j.jmb.2007.03.059 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu C., Tobi D., and Bahar I., “ Allosteric changes in protein structure computed by a simple mechanical model: Hemoglobin T < – > R2 transition,” J. Mol. Biol. 333, 153–168 (2003). 10.1016/j.jmb.2003.08.027 [DOI] [PubMed] [Google Scholar]
- Zheng W. J. and Doniach S., “ A comparative study of motor-protein motions by using a simple elastic-network model,” Proc. Natl. Acad. Sci. U.S.A. 100(23 ), 13253–13258 (2003). 10.1073/pnas.2235686100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui Q., Li G. J., Ma J., and Karplus M., “ A normal mode analysis of structural plasticity in the biomolecular motor f(1)-atpase,” J. Mol. Biol. 340(2 ), 345–372 (2004). 10.1016/j.jmb.2004.04.044 [DOI] [PubMed] [Google Scholar]
- Keskin O., Bahar I., Flatow D., Covell D. G., and Jernigan R. L., “ Molecular mechanisms of chaperonin groel-groes function,” Biochemistry 41, 491–501 (2002). 10.1021/bi011393x [DOI] [PubMed] [Google Scholar]
- Zheng W., Brooks B. R., and Thirumalai D., “ Allosteric transitions in the chaperonin groel are captured by a dominant normal mode that is most robust to sequence variations,” Biophys. J. 93, 2289–2299 (2007). 10.1529/biophysj.107.105270 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rader A. J., Vlad D. H., and Bahar I., “ Maturation dynamics of bacteriophage hk97 capsid,” Structure 13, 413–421 (2005). 10.1016/j.str.2004.12.015 [DOI] [PubMed] [Google Scholar]
- Tama F. and C. K.BrooksIII, “ Diversity and identity of mechanical properties of icosahedral viral capsids studied with elastic network normal mode analysis,” J. Mol. Biol. 345, 299–314 (2005). 10.1016/j.jmb.2004.10.054 [DOI] [PubMed] [Google Scholar]
- Tama F., Valle M., Frank J., and C. K.BrooksIII, “ Dynamic reorganization of the functionally active ribosome explored by normal mode analysis and cryo-electron microscopy,” Proc. Natl Acad. Sci. U.S.A. 100(16 ), 9319–9323 (2003). 10.1073/pnas.1632476100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y., Rader A. J., Bahar I., and Jernigan R. L., “ Global ribosome motions revealed with elastic network model,” J. Struct. Biol. 147, 302–314 (2004). 10.1016/j.jsb.2004.01.005 [DOI] [PubMed] [Google Scholar]
- Yang L. W. and Chng C. P., “ Coarse-grained models reveal functional dynamics–I. elastic network models–theories, comparisons and perspectives,” Bioinform. Biol. Insights 2, 25–45 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skjaerven L., Hollup S. M., and Reuter N., “ Normal mode analysis for proteins,” J. Mol. Struct. Theochem. 898, 42–48 (2009). 10.1016/j.theochem.2008.09.024 [DOI] [Google Scholar]
- Cui Q. and Bahar I., Normal Mode Analysis: Theory and Applications to Biological and Chemical Systems (Chapman and Hall/CRC, 2010). [Google Scholar]
- Park J. K., Jernigan R., and Wu Z., “ Coarse grained normal mode analysis vs. refined Gaussian network model for protein residue-level structural fluctuations,” Bull. Math. Biol. 75, 124–160 (2013). 10.1007/s11538-012-9797-y [DOI] [PMC free article] [PubMed] [Google Scholar]