Abstract
The dynamics and energetics of formation of loops in the 46-residue N-terminal fragment of the B-domain of staphylococcal protein A has been studied. Numerical simulations have been performed using coarse-grained molecular dynamics with the united-residue (UNRES) force field. The results have been analyzed in terms of a kink (heteroclinic standing wave solution) of a generalized discrete nonlinear Schrödinger (DNLS) equation. In the case of proteins, the DNLS equation arises from a Cα-trace-based energy function. Three individual kink profiles were identified in the experimental three-α-helix structure of protein A, in the range of the Glu16-Asn29, Leu20-Asn29, and Gln33-Asn44 residues, respectively; these correspond to two loops in the native structure. UNRES simulations were started from the full right-handed α-helix to obtain a clear picture of kink formation, which would otherwise be blurred by helix formation. All three kinks emerged during coarse-grained simulations. It was found that the formation of each is accompanied by a local free energy increase; this is expressed as the change of UNRES energy which has the physical sense of the potential of mean force of a polypeptide chain. The increase is about 7 kcal/mol. This value can thus be considered as the free energy barrier to kink formation in full α-helical segments of polypeptide chains. During the simulations, the kinks emerge, disappear, propagate, and annihilate each other many times. It was found that the formation of a kink is initiated by an abrupt change in the orientation of a pair of consecutive side chains in the loop region. This resembles the formation of a Bloch wall along a spin chain, where the Cα backbone corresponds to the chain, and the amino acid side chains are interpreted as the spin variables. This observation suggests that nearest-neighbor side chain–side chain interactions are responsible for initiation of loop formation. It was also found that the individual kinks are reflected as clear peaks in the principal modes of the analyzed trajectory of protein A, the shapes of which resemble the directional derivatives of the kinks along the chain. These observations suggest that the kinks of the DNLS equation determine the functionally important motions of proteins.
INTRODUCTION
Proteins come in many shapes. However, the number of different folds seems to be quite limited. For example, the structural classification scheme CATH1 has thus far identified around 1300 different topologies while in SCOP2 there are today around 1400 unique folds. These figures have grown very slowly; during the last five years, there have been only nominal changes. Consequently the number of different protein conformations must be relatively limited, and it is possible that the majority have already been found.3, 4
The great success of CATH, SCOP, and other similar approaches such as FSSP5 to classify the structure of proteins is a manifestation that proteins are built in a modular fashion and from a relatively small number of different individual modular elements. It has been proposed6, 7, 8, 9, 10 that, mathematically, the modular building blocks of folded proteins can be described by various parameterizations of a kink, or heteroclinic standing wave solution, of a generalized version of the discrete nonlinear Schrödinger (DNLS) equation.11 The DNLS equation is one of the most fundamental lattice equations. It plays a prominent role in the theories of optical waveguides, photorefractive crystals, Bose-Einstein condensates, particle physics, and string theory.12, 13, 14, 15, 16 The equation describes the stationary points of a Hamiltonian energy function that, in the case of proteins, emerges from general geometric considerations. In fact, it has already been shown that over 92% of high resolution crystals in the Protein Data Bank (PDB)17 can be built by combining together no more than 200 different parameterizations of the kink of the DNLS equation as modular elements.10
Molecular dynamics (MD) simulations have proven to be a very powerful tool for studying dynamics of protein folding.18 The accuracy of such simulations depends on the force field used to describe physical interactions within and between peptide units. Force fields range from atomically detailed, in which interatomic interactions are considered explicitly, to coarse grained, in which a simplified description of a polypeptide chain is used and only the most important interactions are usually considered in a simple approximate form. The more detailed the force field is, the more time it takes to run a simulation. Owing to recent hardware and algorithm development such as construction of dedicated machines,19 use of graphical processing units,20 or massive use of distributed computing,21 it is now possible to run all-atom simulations of ab initio folding of up to 100-residue proteins at the millisecond scale.22 Coarse graining enables us to extend this time scale by 3-4 orders of magnitude.18, 23 It must be noted, though, that the present force fields, both atomically detailed and coarse-grained, are far from being accurate. Even small errors in the description of protein energy surfaces can accumulate over a polypeptide chain to disfigure the correct fold.
In this paper, we propose to consider protein folding from another, complementary point of view. Instead of analyzing individual interactions that contribute to the formation of folded structure, we are looking for model-independent principles which are based on symmetry. We suggest that all the physical forces, no matter how strong or weak they are, combine together to give rise to a particular type of protein dynamics, described by a generalized version of the DNLS equation.6, 7, 8, 9, 10 This approach, to much extent, is motivated by methods developed in quantum fields and string theory, in which gauge symmetry was successfully used to derive Hamiltonians of many fundamental forces.16 We use the united residue (UNRES) force field developed in our laboratory24, 25, 26, 27, 28, 29, 30, 31, 32 to run simulations, to test and confirm our general considerations.
We selected the N-terminal part of the B-domain of staphylococcal protein A as the test case (PDB code: 1BDD). The fold of this protein is a three-α-helix bundle.33 The folding and energy landscape of this protein were subject to a variety of experimental34, 35, 36 and theoretical37, 38, 39, 40, 41, 42, 43, 44, 45 studies. The version of UNRES used in our study folds α-helical proteins in unrestricted folding simulations,27 including protein A. Our extensive studies of the free-energy landscape of this protein44 simulated with the force field used in this study have repeatedly shown that the native three-α-helix bundle is its free-energy minimum and forms a large basin in the free-energy landscape. Another reason to use protein A as the test case was that it was not used in force-field parameterization27 and the force field is, therefore, not biased to reproduce its native structures (as opposed to the Gō-like models, which are constructed to locate the native structure of the protein under study as the global energy minimum).
The article is organized as follows. In Sec. 2A, the geometry of coarse-grained polypeptide chains is defined and new visualization techniques, which are exploited further in the article, are introduced. In Sec. 2B, it is argued that protein secondary structures can be described by a kink of the generalized DNLS equation, similar in shape to the hyperbolic-tangent function. This solution of the DNLS equation is the basic modular element that is used here to describe the geometry of a folded protein. An entire protein loop structure is obtained by joining together several kinks in a modular fashion, one after the other, and in combination with those stationary points of the DNLS Hamiltonian that have a well defined secondary structure (such as α-helices and β-strands). In Sec. 3A, the previously developed technique is used to describe protein A. In Secs. 3B1, 3B2, the kink is studied based on the results of coarse-grained simulations with the UNRES force field. In Sec. 3C, the behavior of side chains is interpreted as that of spins in spin-chain models. In Sec. 3D, mechanisms that cause loop formation are proposed. Finally, in Sec. 3E, the profiles of the kinks are compared to those of the principal modes in principal-component analysis (PCA).
METHODS
Protein backbone geometry and local conformational states
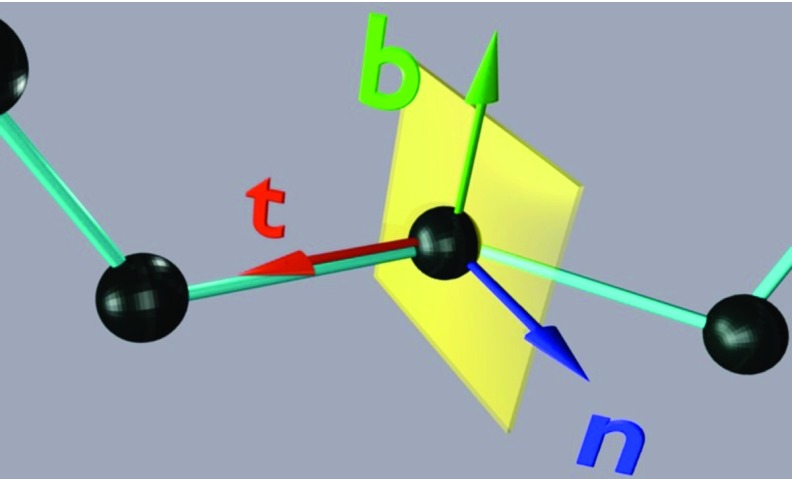
In this paper, protein-backbone geometry is described in terms of Frenet frames.46 The frames depend only on the positions of the Cα carbon coordinates ri where i = 1, …, n labels the residues. At a given residue, the frame is defined by the unit backbone tangent (t), binormal (b), and normal (n) vectors, which are defined by Eqs. 1, 2, 3, respectively; see Figure 1 for graphical illustration:
| (1) |
| (2) |
| (3) |
where is the position of the Cα atom of ith residue.
Figure 1.
Definition of Frenet frame. Vector t (the transversal or tangent vector) points from a given polymer-chain bead to the next bead. Vector n (the normal vector) is perpendicular to t and lies in the plane of the preceding, current, and next polymer-chain bead, pointing towards the preceding bead. Vector b (the binormal vector) forms the right-handed coordinate system with the transversal vector and the normal vector.
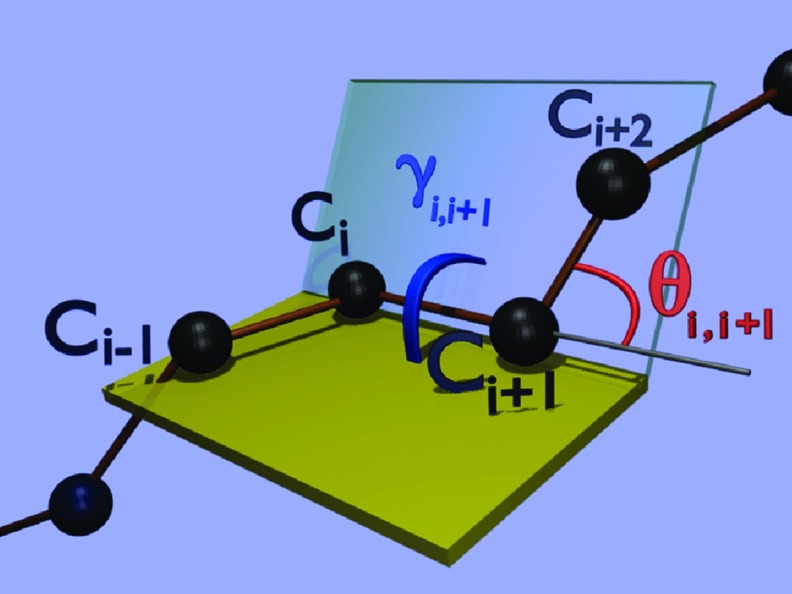
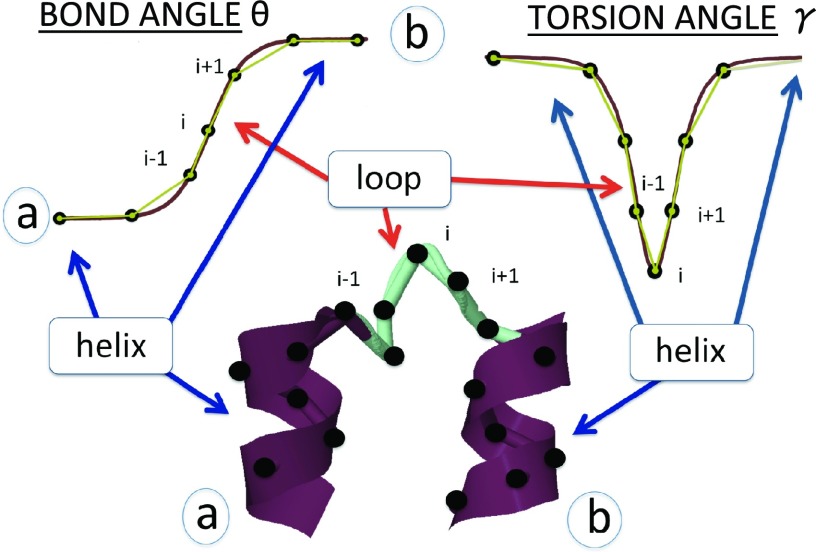
Because the distance between the consecutive Cα atoms is nearly constant so that |ri + 1 − ri| ≈ 3.8 Å for trans peptide groups, the backbone geometry can be described in terms of virtual-bond-valence angles θ and virtual-bond-dihedral (torsion) angles γ. These angles are the discrete versions of the intrinsically geometric curvature and torsion of a continuous space curve. The complements of the angles θ and the angles γ are defined by Eqs. 4, 5, respectively:
| (4) |
| (5) |
with
| (6) |
These angles are also illustrated in Figure 2.
Figure 2.
Definitions of the backbone virtual-bond angle (θi, i + 1) and virtual-bond-torsion angle (γi, i + 1) in terms of the Cα atoms.
The frame vectors can be expressed in terms of the virtual-bond-valence angles θ and virtual-bond-dihedral angles γ by Eq. 7 and then the Cα-trace geometry can be calculated from Eq. 8:
| (7) |
| (8) |
We may assume that the distance between two consecutive Cα atoms is constant, and given by
This is a good approximation, as long as there are no cis-residues.
It should be noted that, unlike the tangent vector ti, the normal and binormal vectors (ni, bi) do not appear in Eq. 8. Therefore, if these vectors are simultaneously rotated around the vector t, they constitute a good reference system. In particular, rotation by π constitutes the discrete gauge transformation [Eq. 9], which was used extensively in our earlier work6, 7, 8, 9, 10, 46 and will also be utilized in this work:
| (9) |
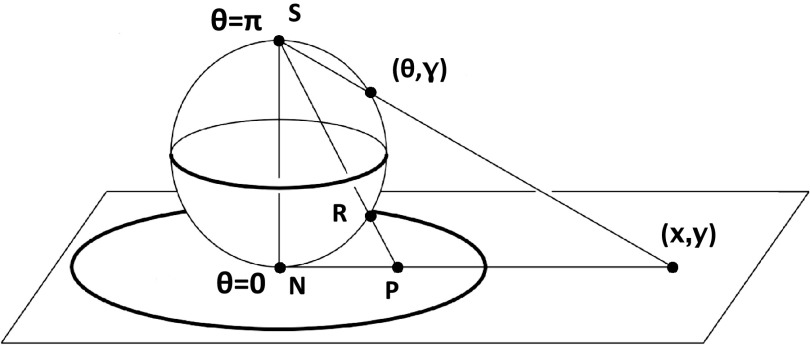
If the (θ, γ) angle pairs are identified with polar coordinates, local conformational states of amino-acid residues can be mapped onto a sphere and then stereographically projected onto a disk, as shown in Figure 3. The stereographic projection is obtained by projecting the (θ, γ) coordinates onto the north-pole tangent plane of the two-sphere. If (x, y) are the coordinates of this tangent plane, the projection is defined by Eq. 10:
| (10) |
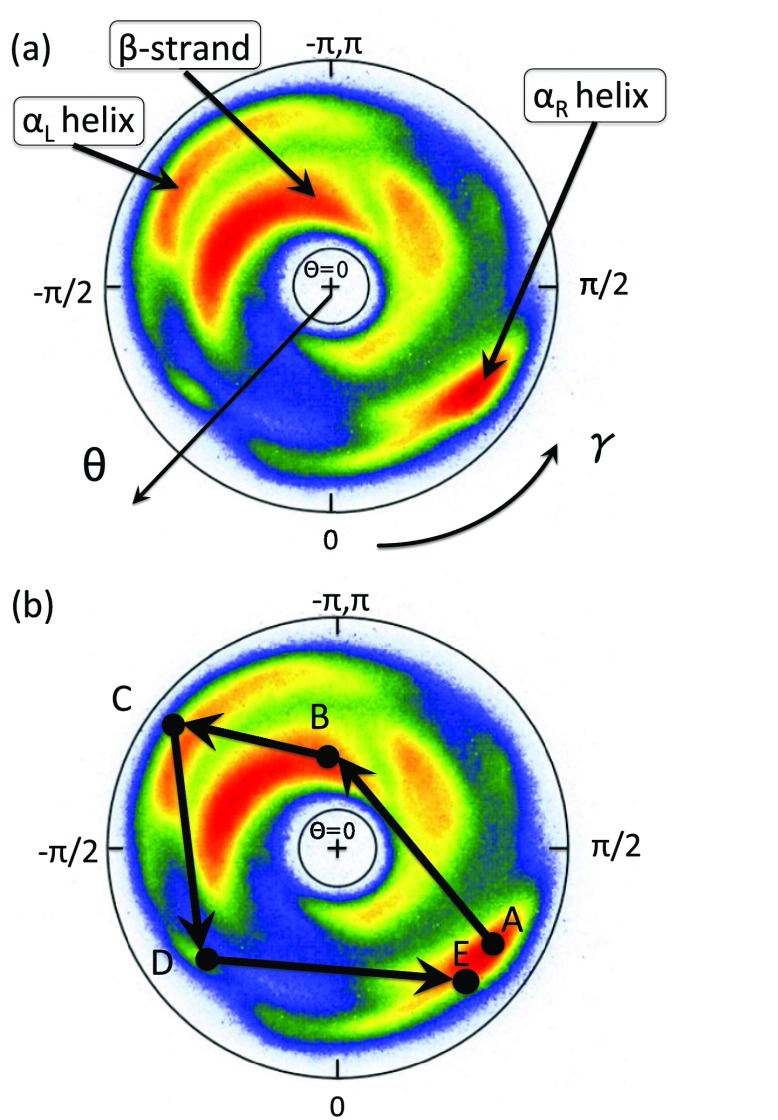
The statistical distribution for all PDB proteins in the stereographically projected two-sphere, for those conformations that have been determined at resolution higher than 2.0 Å is shown in Figure 4. Two regions corresponding to the right-handed α and to the β structure can be distinguished. In Figure 4b, a generic loop is depicted that connects two right-handed α-helical structures. A generic loop is a pathway that connects the adjacent regular secondary structures; the latter corresponds to point-like structures in the map, i.e., constant values of (θi, γi). For example, parameter values (in radians) for which
| (11) |
describe a right-handed α-helix, and parameter values for which
| (12) |
describe a β-strand.
Figure 3.
Two-sphere with its stereographic projection onto the plane. The point (θ, γ) on the surface of the sphere is mapped onto the point (x, y) on the plane, as expressed by Eq. 10. N and S are the north and south poles, respectively.
Figure 4.
(a) The distribution of bond and torsion angles on the stereographically projected two-sphere (θ, γ); see Figure 3 for definition of the projection. The color intensity is (logarithmically) proportional to the number of PDB entries (). (b) An example of a circular path (corresponding to a loop structure), as an oriented trajectory on the stereographically projected two-sphere. The circular path starts from the right-handed α-helical region (A), proceeds to the β-strand region (B), to the left-handed α region (C), followed by steps (D) and (E), and terminates in region of the right-handed α-helical region (A).
A notable property of the trajectory drawn in Figure 4b is that it encircles the north-pole of the two-sphere. It turns out that this kind of encircling is quite generic for loops. Consequently, each loop can be assigned a winding number termed folding index, Indf,47 which is defined by Eq. 14:
| (13) |
| (14) |
where [x] denotes the integer part of x, and Γ is the total rotation angle (in radians) that the projections of the Cα atoms of the consecutive loop residues make around the north pole. The folding index is a positive integer when the rotation is counterclockwise and a negative integer when the rotation is clockwise. The folding index classifies loop structures and entire folded proteins in terms of its values. The value is equal to twice the number of times the ensuing pathway encircles the north-pole in the map of Figure 4.
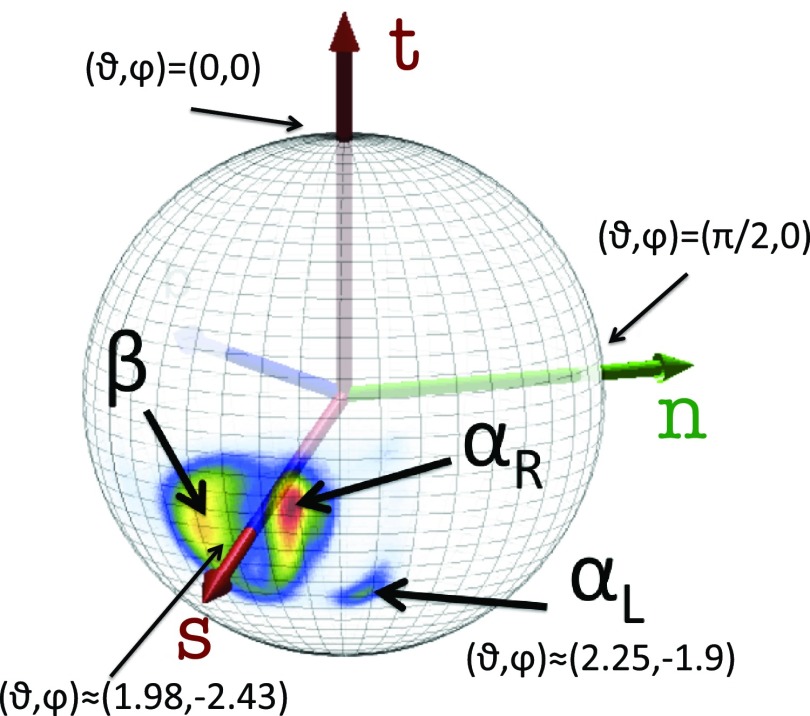
Using the Frenet frame, the Cβ atoms can also be visualized in the unit two-sphere system centered at the Cα atom with the axis t chosen as the polar (z) axis and the axes n and b chosen as the x and y axes, respectively, to define a right-handed coordinate system. The canonical spherical coordinates (ϑi, φi) are introduced, which are essentially the bond angle θ and torsion angle γ, respectively. Like the angle θ, the angle ϑ ∈ [0, π] measures the latitude from the positive z-axis and the angle φ ∈ [0, 2π] now measures the longitude in a counterclockwise direction from the x-axis, i.e., from the direction of n towards that of b. Then the coordinates of a unit vector si pointing from Cα in the direction of Cβ can be computed from Eq. 15:
| (15) |
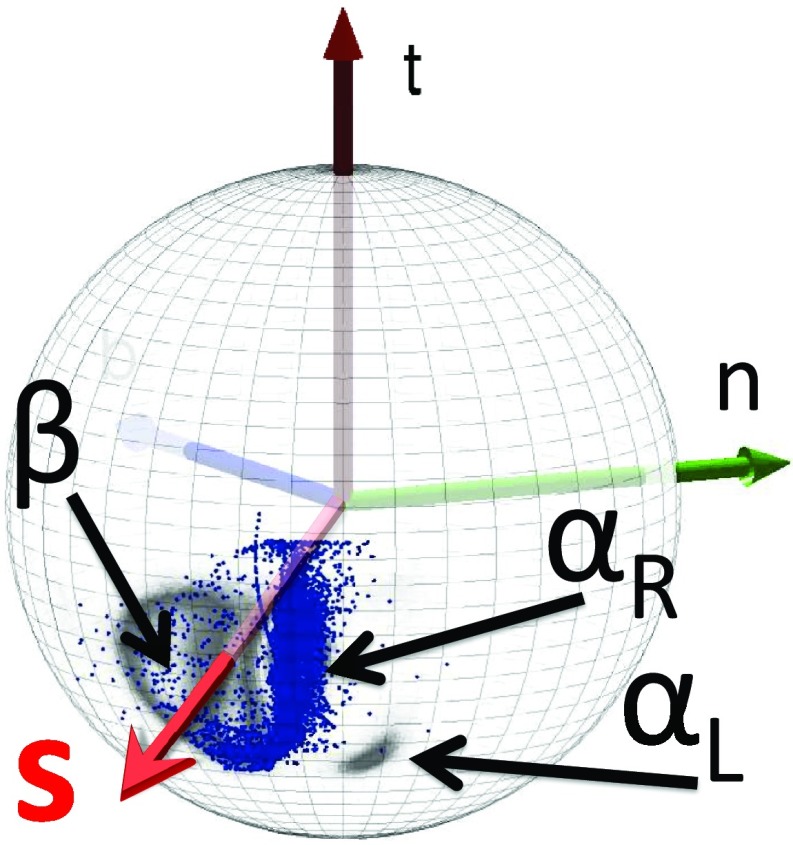
As shown in Figure 5, the direction of the vector si, computed from PDB structures, is quite well defined, with one major and one minor cluster subdivided into regions corresponding to αR and β structures and one minor region corresponding to the left-handed α-helical (αL) structures. For the major cluster, the average latitude angle ϑi is ⟨ϑ⟩ ≈ 1.98 rad and the average value of the longitude angle φ is ⟨φ⟩ ≈ −2.43 rad; these values undergo only small fluctuations. The average values of the spherical angles for the αL region are ⟨ϑ⟩ ≈ 2.25 rad and ⟨φ⟩ ≈ − 1.90 rad, respectively. Thus, the orientation of the Cβ atom is quite well defined in a given frame of three consecutive Cα atoms and, consequently, the positions of Cβ atoms can be determined quite accurately given the Cα trace.
Figure 5.
Statistical distribution of the Cβ direction in the PDB, as seen from the corresponding Cα, located at the center of the sphere. The vector t points towards the next Cα. The regions of right-handed αR-helices, β-sheets, and left-handed αL are displayed, the rest being non-regular structures (including loops). The (average) vector s is also shown.
Kink of the DNLS equation and protein geometry
As noted in Sec. 2A, the Cα trace geometry can be described in terms of the virtual bond and virtual torsion angles [Eqs. 4, 5]. For a coarse-grained description of the side-chain orientations, the vector from the Cα to the ensuing side-chain centroids can be utilized. These variables are present in the UNRES energy function.24, 25, 26, 27, 28, 29, 30, 31, 32 Alternatively, the vector from the Cα atom to its side-chain Cβ atom [vector s of Eq. 15] can be used. As follows from Figure 5, the direction of vector s is essentially constant and independent of amino-acid type. Consequently, the backbone geometry largely determines the side-chain orientations and, thus, the complete geometry of polypeptide chains at the coarse-grained level.
In the case of a protein, the variables θi and γi are mutually connected by the equations of motion, determined by the atomic level interactions along the protein chain. In Refs. 6, 7, 9 and 10 (see also Ref. 48 in the present context), the following Landau energy has been introduced to approximate the Helmholtz free energy F of the protein backbone in terms of the discrete virtual bond and torsion angles:
| (16) |
In addition, the excluded volume (steric) constraint
| (17) |
is imposed, for the distance between the backbone Cα atoms. This condition is well respected by folded protein structures in the PDB. In Eq. 16, λ, q, p, r, and m are parameters. The free energy, Eq. 16, has been derived and motivated in detail in Refs. 6, 7, 9 and 10. Here it suffices to state that this free energy can be shown to relate to the long-distance limit that describes the full microscopic energy of a folded protein in the universal sense of Refs. 49, 50, 51, 52. As such, it does not explain the details of the (sub)atomic level mechanisms that give rise to protein folding.
A Cα backbone conformation is constructed by seeking the minimum of F in Eq. 16.6, 7, 9, 10 The necessary condition for the minimum is to find the zero of the gradient of F in the virtual-bond angles θ and in the virtual-bond dihedral angles γ. The solution of this problem is the solution of a system of 2N − 5 nonlinear equations in 2N − 5 unknowns (where N is the number of residues). In order to obtain this solution, the virtual-bond-dihedral angles γ are first expressed as functions of the virtual-bond angles θ, as given by Eq. 18:
| (18) |
with u = p/r and v = q/r. By inserting Eq. 18 into Eq. 16, the virtual-bond-dihedral angles γ are eliminated and a system of equations 19 for the motion of the virtual-bond angles θ is obtained:
| (19) |
where θ0 = θN + 1 = 0 and
| (20) |
where the structure of the generalized DNLS equation with a double-well potential that describes discrete symmetry, that has been spontaneously broken,15, 16 is recognized.6, 7, 8, 9, 10 The kink solution to Eq. 19 can be constructed numerically by following the iterative procedure of Ref. 7. But its explicit form, until now, has not been found in terms of elementary functions. However, an excellent approximation is obtained by naively discretizing the heteroclinic standing wave solution to the continuum nonlinear Schrödinger equation6, 7, 8, 9, 10
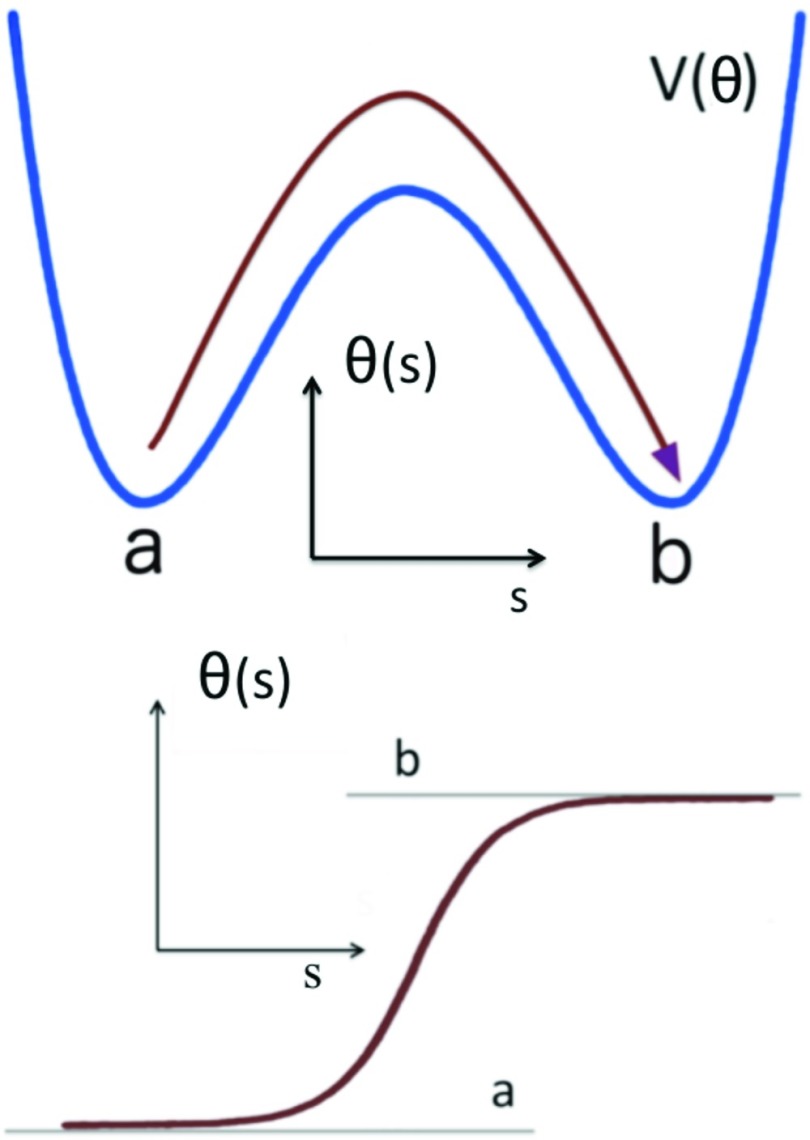
| (21) |
Here s is a parameter that determines the center of the solution. The a, b ∈ [0, π] mod(2π) are parameters which determine the amplitude of the variation of θ and the asymmetry of the inflection regions; they correspond to the two minima of the potential energy contribution V[θ] in Eq. 20. The θ angle profile given by Eq. 21 is like a localized domain wall, which describes the boundary between two neighboring minima of the potential energy.15, 16 The parameters σ1 and σ2 are related to the inverse of the range of the kink. It is notable that, in the case of proteins, the values of a, b are determined entirely by the adjacent helices and strands. Far away from the center of the kink we have (see Figure 6)
and, according to Eqs. 11, 12, the asymptotic values
correspond to the α-helix or β-strand, respectively. A kink corresponding to a loop connecting two α-helices in the helix-turn-helix motif is illustrated in Figure 7. It should be noted that, in the case of proteins, negative values of θi are related to positive values of θi by Eq. 9. Moreover, in the case of proteins, to satisfy the monotonic character of the profile of Eq. 21, the experimentally measured values of θi have to vary monotonically along the amino-acid sequence. Otherwise, a multiple of 2π is added to the experimental values. This does not affect the backbone geometry because θi ′s are defined .
Figure 6.
Top: The potential of mean force (PMF) of θ. Bottom: The kink [Eq. 21] is the boundary between two neighboring local minima s = a and s = b of the PMF.
Figure 7.
Top: Schematic sketches of the profiles of angles θ (left) and γ (right) along the chain. Bottom: The solutions of the generalized DNLS equation are the modular building blocks of folded proteins. They correspond to super-secondary structures such as right-handed-α-helix-loop-right-handed-α-helix (strand-loop-strand).
Finally, only σ1 and σ2 are intrinsically specific parameters for a given loop in Eq. 21. But they specify only the length of the loop, not its shape which is determined by the functional form of Eq. 21 and, as in the case of a and b of Eq. 21, they are combinations of the parameters in Eq. 20.
The corresponding virtual-torsion angles γi, i = 1, 2, …, N − 3, are evaluated in terms of the bond angles using Eq. 18. In Eq. 18 for the virtual-torsion angles, there are only two independent parameters u and v. As a consequence, the profile of γi is determined entirely by the profile of θi, and on the structure of the adjacent regular secondary structures.
It has been shown9 that most protein loop structures from the PDB (over 92% of them) can be described in terms of the explicit profile Eq. 21 in combination with Eq. 18 along with the parameters of these equations, as the elemental modular components, with a root-mean-square-deviation (RMSD) precision which is better than 0.6 Å. This is strong support for the proposal6, 7, 9, 10 that the kink correctly describes the protein structures in the PDB.
At present, we do not consider the kinks in terms of protein-structure prediction but as a convenient tool to describe protein structure. As mentioned in the Introduction, we have already proved that loop geometries of the protein structures present in the PDB can be described in terms of 200 sets of the parameters of the DNLSE.10 Nevertheless, in our earlier work10 we have also demonstrated that, using the kink parameters extracted from the experimental structure of a protein, its folding can be simulated.
Kink analysis seems to handle the description of the conformations that do not occur in the PDB. In our earlier work,48 we studied the AICD/Fe65 complex by means of kink analysis (in that paper referred to as soliton analysis) and coarse-grained simulations with UNRES. The kinks in the AICD part of the complex, when propagated according to the solution of the DNLSE, resulted either in the formation of the compact structure (favorable for the single components) or even more unfavorable partially extended structure that could be amyloid precursor.
Coarse-grained dynamics simulations
To study formation of the structures described by the kink solution of Eq. 19 in proteins, canonical coarse-grained dynamics simulations of the 10-55 fragment of protein A were carried out with the UNRES package developed in our laboratory24, 25, 26, 27, 28, 30, 31, 32 available at http://www.unres.pl. The MD protocol described in our earlier work18, 23, 53 was used. Sixteen parallel trajectories, started from complete right-handed α-helical structures, were run at each of the following temperatures: T = 150, 200, 240, 250, 300, and 310 K. 20 000 000 steps were run for each trajectory with the time step δt = 4.89 fs. This trajectory length corresponds to 98.8 ns UNRES time, but because the time scale in UNRES/MD is distorted at least 1000 times compared to all-atom MD with explicit water,23, 53 the effective duration of simulations was about 0.1 ms. Constant temperature was maintained with the use of the Berendsen thermostat54 with the coupling parameter τ = 48.9 fs. The version of the UNRES force field parameterized with the 1GAB training protein was used;27 this force field is good for simulating the structure and dynamics of α-helical proteins.27
RESULTS AND DISCUSSION
An analysis of the experimental structure of protein A in terms of kinks
We carried out a detailed analysis of protein-loop formation, using the N-terminal segment of the B-domain of staphylococcal protein A as an example. Our analysis relies on quite general, universal concepts and, consequently, it can be argued that the results are generic. The 1BDD experimental structure33 was taken as the reference. This is an average nuclear magnetic resonance (NMR) structure. Of the 60 residues present in the experimental structure, a 46-residue fragment (residues Gln10-Asn55 of the PDB structure) was selected, after removing the unstructured N-terminal and C-terminal residues. In Figure 8, both the full 1BDD backbone and the 46-residue Gln10–Ala55 are shown.
Figure 8.
On the left, the full PDB structure 1BDD, and on the right the 46-residue segment substructure Gln10-Ala55 studied in detail. The dark grey areas in the figure on the left are the unstructured N and C tails that have been removed.
Kink structure of 1BDD
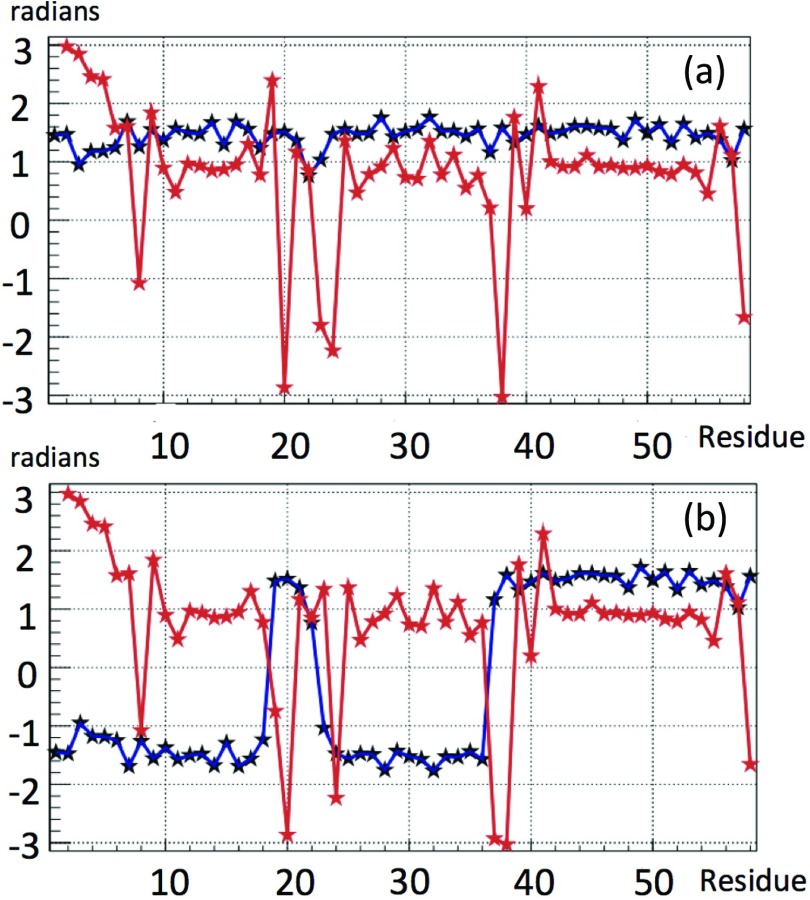
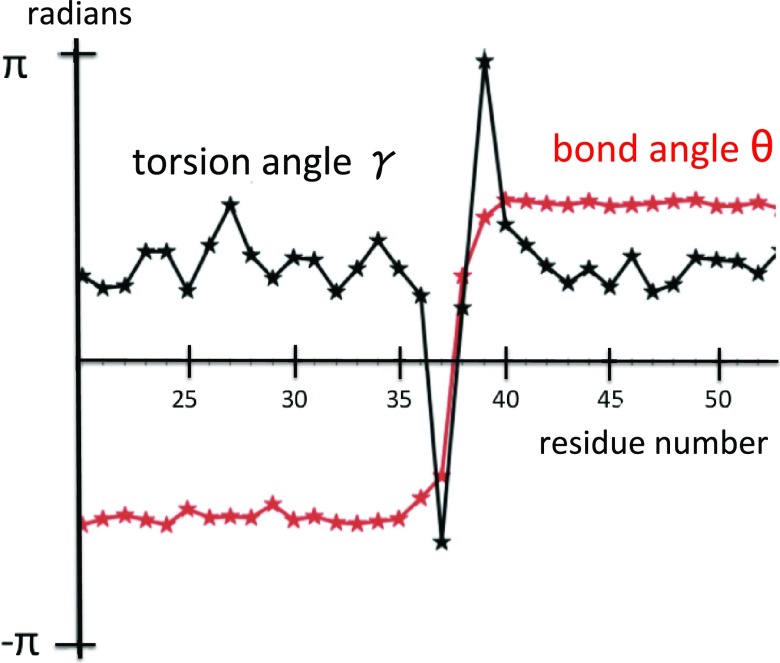
We start by resolving the kink structure of 1BDD, using the explicit profile given by Eq. 21. Variations of the angles θ and γ along the chain are shown in Figure 9a, with the convention that the bond angle is always positive. For the most part, the bond and torsion angles fluctuate in the vicinity of the standard right-handed α-helical values (θ ≈ π/2, γ ≈ 1). However, there are two regions, located between Ile17–Asn24 and Gln33–Ala43, respectively, where in particular the virtual-bond-dihedral angle γi is subject to large fluctuations.
Figure 9.
The virtual-bond θi (black) and torsion γi (red) angle spectra of 1BDD. Figure 9a uses the convention that the bond angle is positive. In Figure 9b, we have introduced the transformation [Eq. 9] to reveal the kink content at the peaks.
In Figure 9b the discrete transformation [Eq. 9] was applied to the data in Figure 9a, to resolve the kink content of the backbone: There is a putative conformation, described by a combination of two kinks of Eq. 21 in succession, located in the segment between PDB Cα sites Ile17 and Asn24. The putative first kink is centered between PDB Cα sites Leu20 and Pro21, and the putative second kink is centered at Asn24–Glu25. Together, these two kinks constitute the first loop structure of 1BDD. The second loop structure consists of a single kink, which is centered between residues Asp38 and Pro39.
The fact that a loop is described by two kinks tells us that it consists of two half-turns, which form roughly an “open rectangle with rounded edges” shape, as opposed to an approximate “U” shape created by one kink (see the blue plot in Figure 9b, in the region of Ile17–Asn24 and Gln33–Ala43, respectively, and the structures corresponding to these regions in Figure 10).
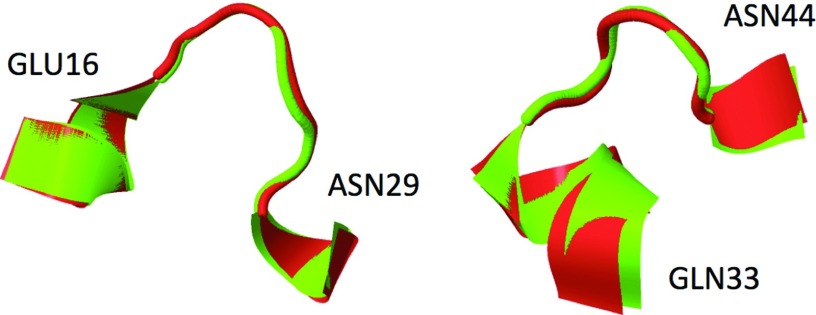
Figure 10.
The kink representation for the two loops of protein A (red) interlaced with the 1BDD structure (green). On the left, the first two kinks, on the right the third kink. The first kink covers sites Glu16-Asn22, the RMSD from the experimental 1BDD structure being 0.12 Å. The second kink covers sites Leu20-Asn29, the RMSD with respect to the experimental 1BDD structure being 0.31 Å. The third kink covers sites Gln33-Asn44, the RMSD from 1BDD being 0.47 Å.
Kink profiles
We have confirmed [Figure 9b] that the interpretation of 1BDD in terms of one kink pair and an isolated kink solution of DNLS equation is correct, by fitting the profile to the discretized form of Eqs. 21, 18. The parameter values are listed in Table 1. Equations 21, 18 describe the first kink with RMSD precision of 0.12 Å, the second kink with RMSD precision 0.31 Å, and the third kink with RMSD precision 0.47 Å. In Figure 10 the ensuing conformations, interlaced with the PDB structure of protein A (1BDD) are displayed. It can be concluded that the interpretation of protein A as a combination of three kinks is fully consistent with Eqs. 18, 19, 20, 21 that we have derived from the Helmholtz free energy of Eq. 16.
Table 1.
Best parameter values for each of the three kinks in protein A.1 Note that the angular variables are dimensionless; thus, these parameters are also dimensionless.
| Parameter | Kink-1 | Kink-2 | Kink-3 |
|---|---|---|---|
| a | −33.0096 | −20.3583 | −45.5178 |
| b | 33.0784 | 20.346 | 45.4973 |
| σ1 | 2.2082 | 2.5755 | 2.9127 |
| σ2 | 2.2064 | 2.5837 | 2.9221 |
| s | 18.4962 | 22.1432 | 37.9139 |
| u | 976012.94 | −311747.469 | −5669135.02 |
| v | −0.00098719 | −0.00158963 | −0.00021636 |
It should be noted that a, b are determined .
Folding index
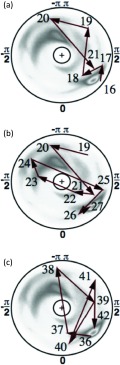
The (θi, γi) trajectories of the three kinks of 1BDD in the stereographically projected hemisphere are shown in Figures 11a, 11b, 11c. The putative first kink (Figure 11a) located at Leu20–Pro21 rotates counterclockwise. But, since it does not extend around the center, there is no contribution to the folding index. The second putative kink at Asn24–Glu25 (Figure 11b) rotates clockwise around the center once, and consequently it contributes −2 to the normalized folding index defined by Eq. 1447 (i.e., the loop makes one turn around the north pole). Finally, for the Asp38-Pro39 region (Figure 11c) the folding index is unstable. A tiny fluctuation of the coordinates of Asp37 or Asp38 to avoid crossing the center causes the normalized folding index either to vanish, or acquire, the value +2. As a consequence, on average, the value of the folding index vanishes.
Figure 11.
The folding index trajectories for the three loop structures of 1BDD identified in Figure 8. The quality of the data of 1BDD is not optimal. But it appears that in (a), a trajectory tries to go around the center once, in a counterclockwise fashion. In (b) and (c), the circulation is once in a clockwise direction. As a consequence, the kink contribution to the folding index of fully folded protein A should be −2.
Except for the second kink, the quality of the experimental structure is not good enough to eliminate the effect of fluctuations in the folding index. But an inspection of Figure 11 proposes that the first kink located at Leu20–Pro21 should have (integer part of) folding index equal to +2 as the vector field rotates once around in a counterclockwise direction. Similarly the third kink should make a contribution of −2 to the folding index, as the vector field makes one full clockwise turn. Consequently, the three kinks should contribute a total of
to the total folding index.
We note that, for the entire chain, including the flexible portions near the N and C tails, we obtain
Thus, the portion of the chain adjacent to the tails that were removed also appears to support (at least one) kinky structure. But the experimental data are not very precise for determining the folding index structure. It should be reminded that the experimental structure of protein A has been determined by NMR as an ensemble of conformations,33 which makes the folding index analysis unprecise.
UNRES analysis of kinks in the backbone of protein A
We have made extensive simulations using the UNRES energy function to study the folding patterns of protein A. In the UNRES effective free-energy function, the effects of water are taken into account implicitly; they are mainly included in the potential of mean force of side chain–side chain interactions.24 To eliminate noise as much as possible, we analyzed trajectories simulated at T = 250 K; this value of temperature was chosen as a compromise between reasonably fast folding and small noise, after analysis of folding pathways at T = 150 K, 240 K, 250 K, 260 K, 300 K, and 310 K. Although the selected simulation temperature is low, the trajectories simulated at physiological temperature are found to be qualitatively similar to those at lower temperatures except that the folding process takes longer. In particular, we have found that various short duration oscillations and random thermal fluctuations affect only the small-scale ruggedness of the energy landscape, with only very little if any relevance to the folding process per se.
The qualitative features of the physical phenomena that we describe in Secs. 3B1, 3B2 are largely UNRES temperature independent. Consequently we expect that our observations capture the essential aspects of the folding process, over a wide range of solvent environments. A movie has been attached as a supplementary material;64 it shows both the evolution of the (ungauged) backbone angles and the corresponding three-dimensional Cα structure.
Third kink
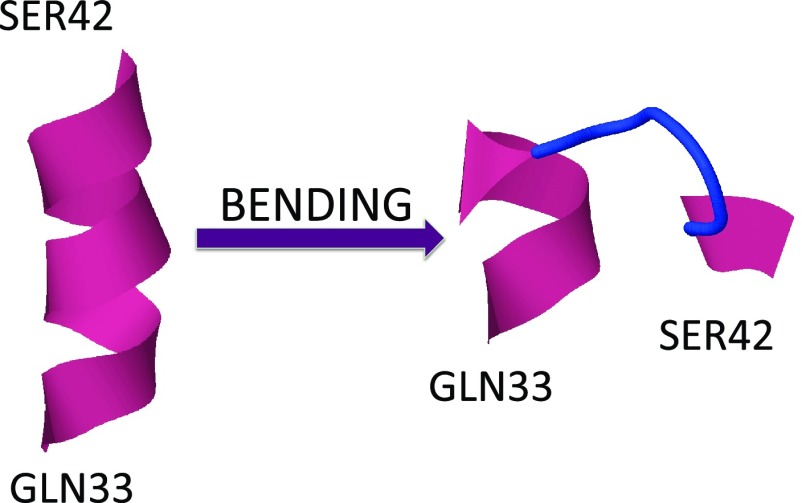
We start our analysis from the third kink which is located at the Gln33–Ser42 segment. We use the conceptual analogy, summarized in Figures 67, between the profile of the kink and a right-handed-α-helix-loop-right-handed-α-helix super-secondary structure. Accordingly, we are interested in studying how the kink, that describes the loop by interpolating between the two pertinent local minima (a and b in Figure 6), emerges from an initial conformation that is one of the two local minima.
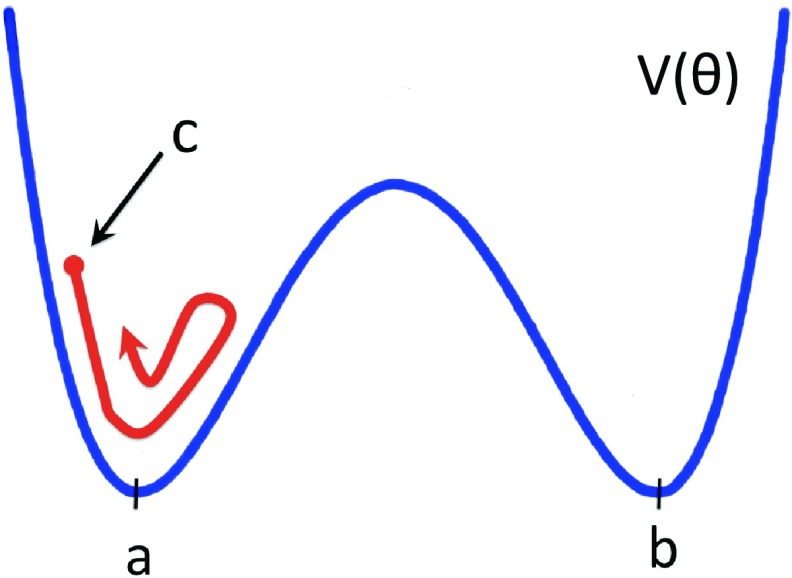
In the present case, a conformation in one of the two local minima corresponds to helical geometry. Consequently, as an initial conformation, we consider the segment Gln33–Ser42 in the right-handed α-helix conformation. We inquire how this becomes deformed into the right-handed-α-helix-loop-right-handed-α-helix conformation of protein A, i.e., how the kink forms. In Figure 12, we show the initial conformation (left) and the kink structure (right); the latter is taken from the PDB. It should be noted that, instead of a monotonous α-helical conformation, we could have started, alternatively, e.g., from a monotonous β-strand or polyproline-II conformation. At the level of the kinks, these latter two possible starting conformations correspond to uniform values of the bond angles which are different from a and b, respectively, using the analogy in Figure 6. This would cause initial oscillations and inhomogeneities around the corresponding values a and b. These are local fluctuations that are equally accounted for by thermal noise and are not directly relevant to the kink formation. A change in starting conformation introduces only some transient initial fluctuations around the minimal energy conformations, as shown schematically in Figure 13.
Figure 12.
The initial and final conformations for the third loop between Gln33 and Ser42. The initial conformation (right-handed α-helix) is like minimum a or b in Figure 6, and the final conformation (third loop) is like the kink that interpolates between a and b, in Figure 6. See the profile of bond angles γi in Figure 9.
Figure 13.
The initial conformation in Figure 12 is a local minimum conformation while the kink, i.e., loop, forms between two such local minima (a and b). If another initial conformation is chosen, for example, polyproline-II, these correspond to unstable states such as conformation c shown in the figure. This will cause initial conformation-specific embryonic fluctuations around the local minimum. But, already during the very early stages of the folding process, these random fluctuations become mingled with thermal fluctuations and lose their relevance in guiding the folding process. In specifying the initial conformations in our simulations, we try to minimize transient random effects.
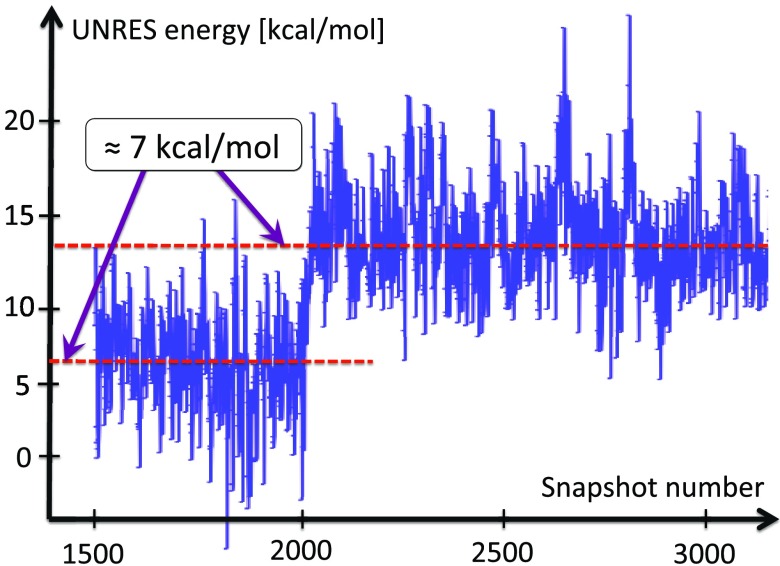
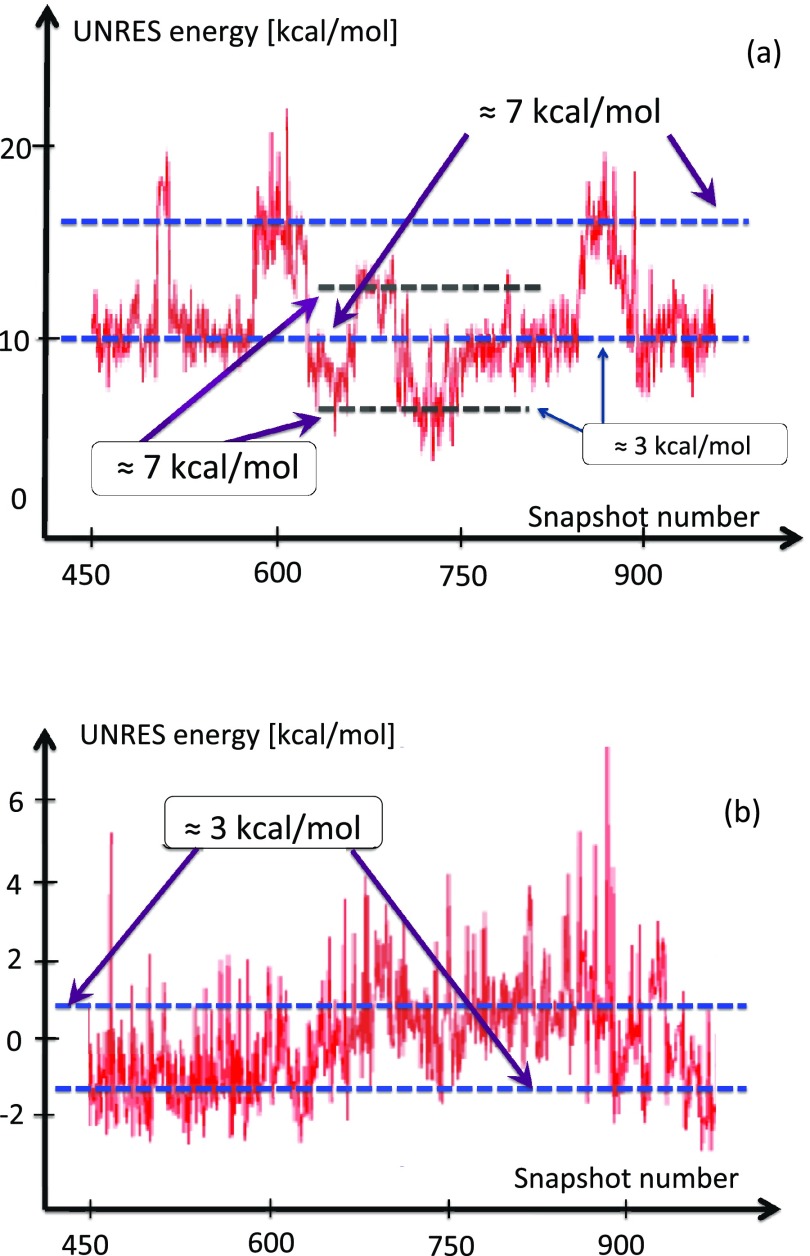
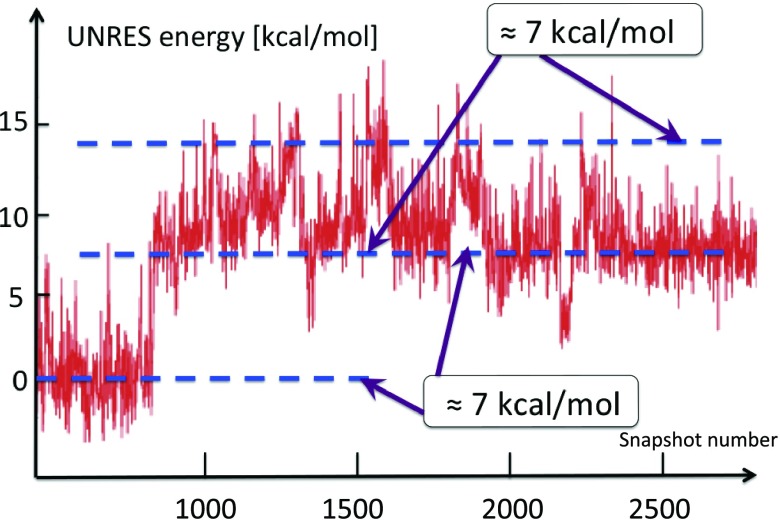
In our extensive UNRES simulations we have found that, typically, the transition between the two conformations in Figure 12 takes place during a very short time period. In Figure 14, it is shown how the free energy of the Gln33–Ser42 segment, computed by using the UNRES effective energy function, which has the sense of a free energy,28 changes when the transition takes place. The red horizontal dashed lines in this figure correspond to the average UNRES energy averaged over “before” and “after” energy jump (from snapshot 1500 to snapshot 2000 and from snapshot 2001 to snapshot 3200, respectively). It can be seen that the free energy over the putative kink region increases by about 7 kcal/mol, when the kink forms. Because the UNRES energy of the chain decreases during the progress of simulations, the unfavorable free-energy change of 7 kcal/mol, that we observe when the kink forms and the right-handed α-helix breaks to form a right-handed α-helical hairpin, must be compensated by long-range hydrophobic interactions between the side chains of the two α-helices adjacent to the segment that turns into a loop; however, the free energy increases by 7 kcal/mol before the contacts are formed. The 7 kcal/mol value can thus be considered the free energy of kink formation. It can be noted that 7 kcal/mol is very close to the Gibbs free energy that is released by cleaving a phosphate (Pi) unit from adenosine triphosphate (ATP) at 1M concentration.55 The coupling of ATP hydrolysis to a change of protein conformations is observed in molecular motors:56
In a future investigation, we propose to clarify whether a connection between kink formation and ATP hydrolysis actually exists.
Figure 14.
The UNRES energy change during the formation of the second loop (3rd kink) of protein A, in a generic UNRES simulation. The energy needed to excite the kink is around 7 kcal/mol. The kink formation takes place very rapidly, during a small number of UNRES steps.
First and second kinks
As follows from Figures 911, the first and second kinks are located very close to each other, namely, at Leu20–Pro21 and at Asn24–Glu25, respectively; these will hereafter be referred to as kink 1 and kink 2, respectively. As follows from Figure 11, these two kinks have opposite contributions to the folding index; the first is oriented counterclockwise, while the second is oriented clockwise. It was found from UNRES simulations that either kink 1 or kink 2 can be formed first. The other kink then emerges close to the first one, and slowly drifts away. Moreover, during the initial formation stage, these kinks may form and then again disappear before they become stabilized. The slow speed of the separation suggests that there is a substantial Peierls-Nabarro barrier57, 58 for the kinks to move. It should also be noted that kink 3 is practically stationary along the backbone, which is presumably due to a Peierls-Nabarro barrier. On the other hand, kinks 1 and 2 fluctuate substantially; in particular their shape and their mutual distances oscillate, even at very low temperatures. These fluctuations are visualized in Figure 15, where diagrams of the kinks in the stereographically projected (θi, γi) plane are shown. The changes in the structure following kink formation are shown in Figure 16.
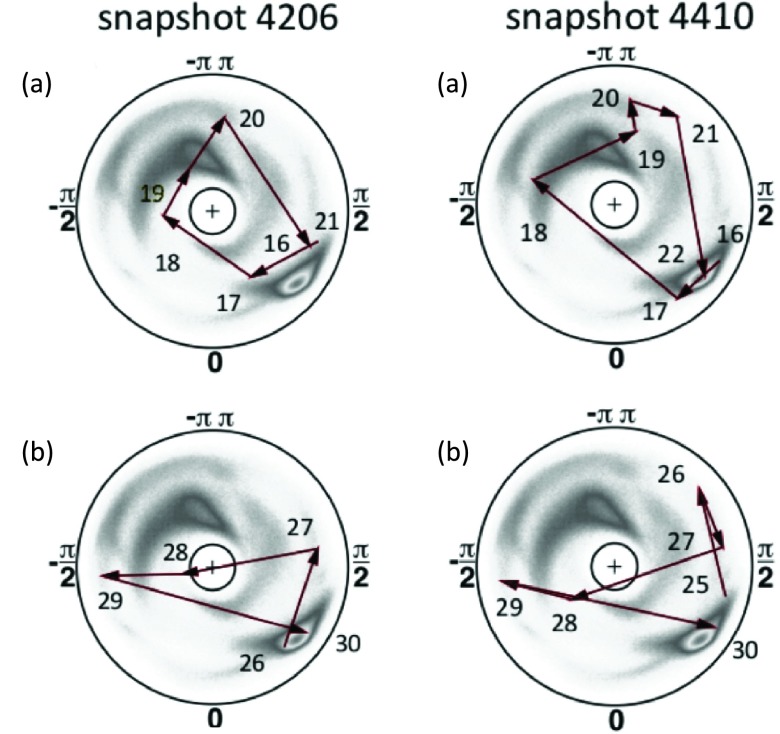
Figure 15.
The trajectories of kink 1 (a) and kink 2 (b), drawn on the stereographically projected (θi, γi) plane, at two different snapshots in the same simulation. Both trajectories of (a) start at site Glu16. Snapshot 4206 ends at Pro21 and snapshot 4410 ends at Asn22. Trajectories of (b) both end at Gly30; in snapshot 4206, it starts at site Glu26 and in snapshot 4410 at site Glu25. The snapshot values are shown only to indicate that the time difference is very short, and the fluctuations are rapid. A more precise determination of the time difference is not meaningful.
Figure 16.
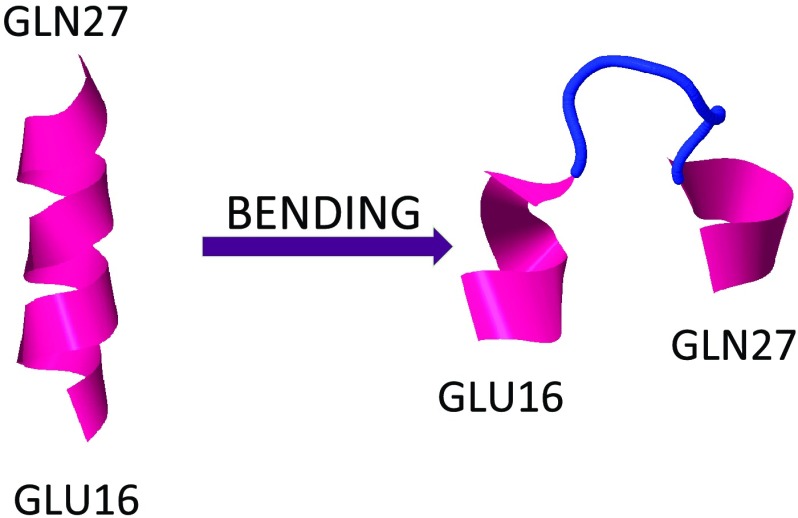
The initial and final conformations for the loop between Glu16 and Gln27. The initial conformation (right-handed α-helix) is like minimum a or b in Figure 6, and the final conformation is like a pair of kinks that each interpolate between a and b, as a kink pair would in Figure 6. See the profile of bond angles γi in Figure 9b.
The kink pairs depicted in Figure 15 both start at the same site, namely Glu16. But at snapshot 4206(a), kink 1 ends one site earlier, i.e., it is shorter. At snapshot 4410(a), the first kink has become extended by one site, towards kink 2. Similarly, the two kinks of pair 2 both end at Gly30. But the second kink at 4410(b) starts one site earlier than the first kink at 4206(b).
It should be noted that the placement of kink 1 at snapshot 4206(a) compares well with the corresponding kink in 1BDD, shown in Figure 9a; there, the first kink extends between sites 17 and 21. However, the orientation is different: In Figure 9a the kink rotates counterclockwise, while in Figure 15a it rotates clockwise. Both kinks in Figure 15 are moved away from the N terminus in comparison to the 1BDD conformation. In Figure 15, these kinks both extend to site 30, while in Figure 9b, kink 1 terminates at site 26. Both kinks 1 and 2 in Figure 15 are also oriented counterclockwise, while in the experimental 1BDD structure the orientation is opposite, i.e., clockwise.
In Figure 17a, the variation of the UNRES energy of the Asn22–Ile32 segment upon formation of the first kink in a typical UNRES simulation is shown. The visible steps, in which the energy changes by around 7 kcal/mol, corresponds to creation and annihilation of the first kink, which can take place a few times in a typical run before the loop settles down. The smaller changes are due to the kink drifting (partially) outside the window, towards the first kink. This can be seen in Figure 17b, in which the energy is computed over the sites that separate these two kinks. The variation in the average energy in Figures 17a, 17b is relatively small, and clearly slower than during the process of kink formation.
Figure 17.
(a) Energy change during formation of the second kink (sites Asn22-Ile32) of protein A in a generic UNRES simulation. The fluctuations in the average value of energy are consistently around 7 kcal/mol. The kink formation takes place very rapidly during a small number of UNRES steps. Between steps ≈ 620 and 800, the second kink drifts towards the first kink, causing the energy to drop on average of about 3 kcal/mol. (b) The average energy between the first two kinks increases by an amount that is comparable to the decrease in average energy in (a). The change is due to oscillation in the distance between the two kinks; the second one drifts towards the first one, causing the energy to increase.
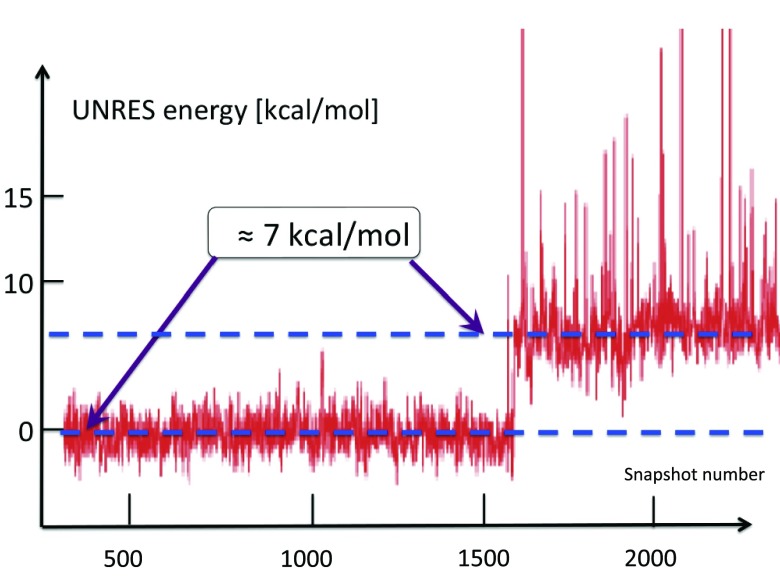
In Figure 18, the evolution of the average energy of kink 2 (between Glu16 and Glu27), over a longer period of time than that covered by Figure 17, is shown. An initial formation of a kink pair near the eventual location of the second kink can be observed. The first kink then drifts towards the N-terminus, with stabilization of the second kink towards its thermodynamic equilibrium with energy again about 7 kcal/mol. Finally, in Figure 19, a typical example of a simulation is shown, in which the first kink emerges and stabilizes towards the equilibrium conformation, with energy again about 7 kcal/mol. The energy is computed over a very narrow segment that covers the kink, and the second kink forms outside of the segment in this particular example.
Figure 18.
The energy change between the initial and final conformations for the loop between Glu16 and Gln27 (the region of the first and the second kink). The initial conformation (right-handed α-helix) is like minimum a or b in Figure 6, and the final conformation is like a pair of kinks that each interpolate between a and b, as in Figure 6. See the profile of the virtual-bond angles θi in Figure 9b.
Figure 19.
The energy change between the initial and final conformations for the loop between Glu16 and Leu20 (the region of the first kink). The initial conformation (right-handed α-helix) is like minimum a or b in Figure 6, and the final conformation is like a pair of kinks that each interpolate between a and b, as in Figure 6. See the profile of the virtual-bond angles θi in Figure 9b.
UNRES analysis of side-chains in protein A
According to Figure 5, the Cα⋯Cβ vector s [Eq. 15] is strongly slaved to the backbone geometry. Conversely, it may be argued that the backbone is slaved to the side chains. In fact, there appears to be a duality between the backbone and the side chains, to the extent that the coordinates of either of these two types of sites may be utilized to describe the folding. Here, the kink (loop) formation is discussed in terms of side-chain geometry, because it provides some visual advantages over the backbone-based description.
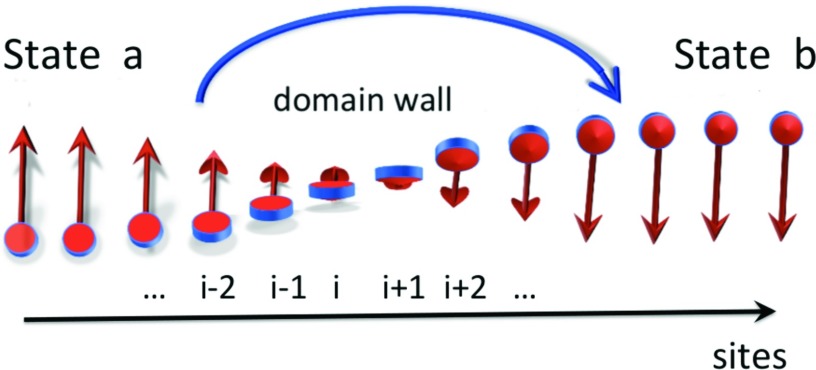
It should be noted that the DNLS equation has a natural interpretation in terms of a (magnetic) spin-chain: The variable γi can be identified as the order parameter for magnetization in a two-state ferromagnet.59 Positive values of γi describe a “spin-up” state, while negative values correspond to a “spin-down” state; the absolute value characterizes the strength of the magnetization. The kink, Eq. 21, can be interpreted as the continuum-chain limit of a (magnetic) Bloch domain wall60 that interpolates between the two (ferromagnetic) spin states. See Figure 20.
Figure 20.
The kink in Figure 6 is the boundary between the two minima a and b. It can be interpreted as a continuum limit of a magnetic Bloch-type domain wall that interpolates between spin-up state (a) and spin-down state (b). Here, we show, as an example, the Bloch wall in the transversal O(2) spin model.
Using an energy-based procedure,61, 62 we converted the coarse-grained trajectories to all-atom trajectories and then computed the unit Cα⋯Cβ vectors s from Eq. 15. The folding pathways were subsequently analyzed in terms of the vectors s. A protein molecule can then be interpreted as a one-dimensional spin chain akin that in Figure 20, with the sites identified as the Cα atoms and the vectors s with Eq. 15. Since these vectors can point in any direction in , this is a variant of the O(3) Heisenberg spin chain59 rather than a two-state Ising spin chain.59
We have investigated in detail how the direction of the vector s of Eq. 15 evolves during the simulated formation of the tertiary structure of protein A. A typical result is shown in Figure 21. The initial conformation in this particular simulation is a linear right-handed α-helix. We find that during the entire collapse simulation, the vectors s of Eq. 15 along the backbone are very strongly coupled to the backbone geometry. The deviations from the background shown in Figure 5 (grey area in Figure 21) are minuscule, during the entire helix-packing transition. This confirms that the direction vectors s of Eq. 15 can indeed be used to describe the transformation of the full-α-helical conformation of protein A into a native-like conformation in UNRES simulations.
Figure 21.
Statistical distribution of Cβ directions during a generic UNRES collapse simulation, in the backbone Frenet frames. The vectors s of Eq. 15 are near parallel to their average values, during the entire collapse transition.
As an illustrative example of our observations, in Figure 22 the bond and torsion angles (θ and γ) of kink 3 (the second loop) are described, as they appear during a generic UNRES run.
Figure 22.
Values of θ and γ of a generic conformation during an UNRES simulation, corresponding to the third kink (second loop) of 1BDD.
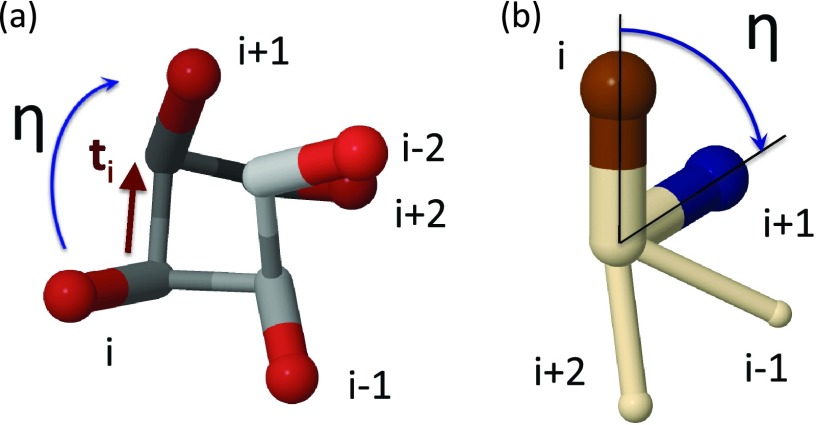
To describe kink formation in terms of the change of the orientation of the Cβ atoms, the dihedral angles η defined by are utilized. These angles are computed as those between the consecutive u vectors, each being computed from the respective vector s by orthogonalization to the transversal t vectors, as defined by Eqs. 22, 23:
| (22) |
| (23) |
The dihedral angle η is the side-chain O(2) order parameter that will be utilized. For regular structures, the value of η is constant along the chain; for example, for a right-handed α-helix, η ≈ 0.75 (rad) and, for a β-strand, η ≈ π (rad). For a single kink, the values of the angle η interpolate between those that correspond to the adjacent regular structures, much as in Figure 6.
In Figure 23a, the vectors si are displayed along one turn of the right-handed α-helix, and in Figure 23b the definition of the angle η in terms of the vectors s of Eq. 15 is illustrated.
Figure 23.
(a) A right-handed α-helix with the vectors s [Eq. 15], viewed along the Cα⋯Cβ axis. (b) Two consecutive vectors s [Eq. 15] along the right-handed α-helix, viewed along the tangent vector ti that connects the successive Cα atoms. The angle of their projection onto the plane, which is normal to the vector ti is given by Eq. 23. The top of the vector is colored blue in (b) to distinguish it from the top of the vector .
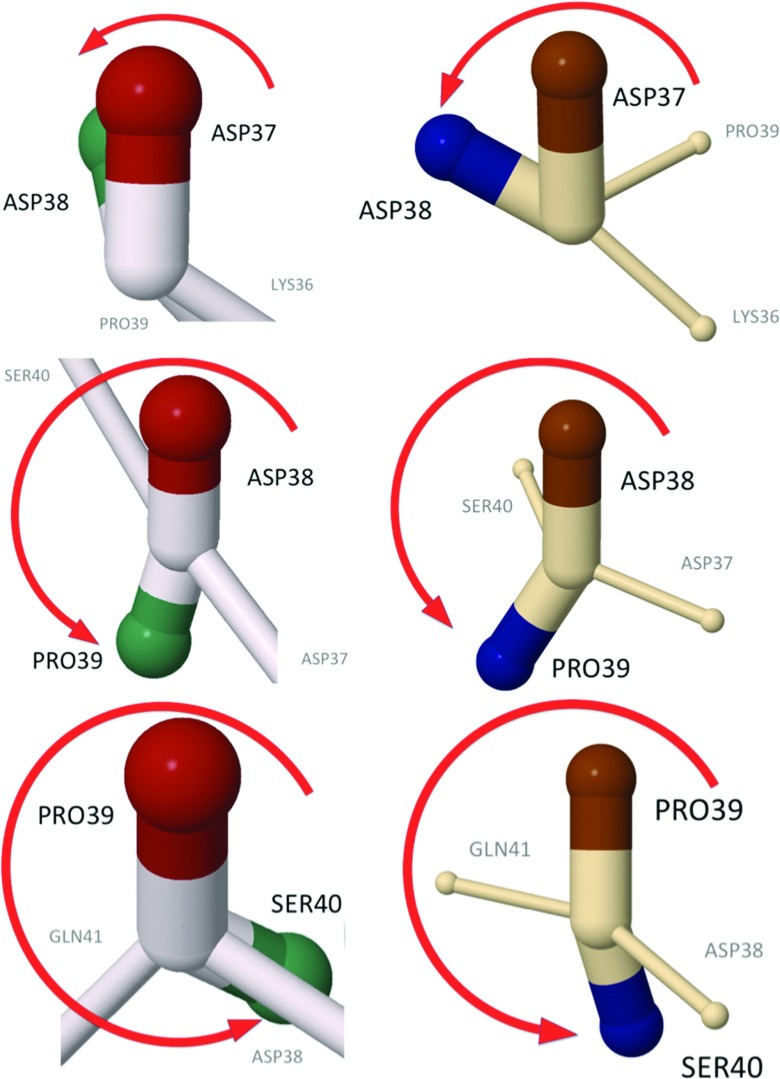
In terms of the side-chain vectors, the loop region, the backbone angles of which are plotted in Figure 22, has the structures shown in Figures 2425.
Figure 24.
The side-chain structure of the second loop in the experimental structure of 1BDD (left) and of the UNRES kink (right) (whose profile is shown in Figure 22). The figures show the evolution of the relative torsional angles [Eq. 23], along the residue number. In both the experimental 1BDD structure and the UNRES kink, the angles η prior to the Asp37-Asp38 bonds are in the right-handed α-helical position, as shown in Figure 23b.
Figure 25.
Continuation of Figure 24, along the 1BDD and UNRES kink backbones. In the UNRES kink, the bond between Gln41 and Ser42 returns back to the initial α-helical position, and in 1BDD, the kink is one step longer. The green and blue colors are used to distinguish side chains that belong to consecutive residues.
In these figures, the side-chain orientations of the vectors of Eq. 15 between two consecutive sites i and i + 1, in the projection to the plane which is normal to the tangent vector ti that connects them are compared. In both the experimental 1BDD structure and the UNRES simulated structure, the side chains rotate once in the clockwise direction as the kink is traversed starting from the Asp37–Asp38 bond, like a Bloch domain wall in a magnetic spin chain. The previous bond (Lys36–Asp37) is in the α-helical state shown in Figure 23 for both experimental and simulated structures. In the UNRES-simulated structures, the side-chain rotation reaches back to the α-helical position at the bond between Gln41 and Ser42, while in 1BDD the kink terminates in the α-helical position between Ser42 and Ala43. In both cases, the loop can be clearly interpreted as a Bloch domain wall akin to the one shown in Figure 20.
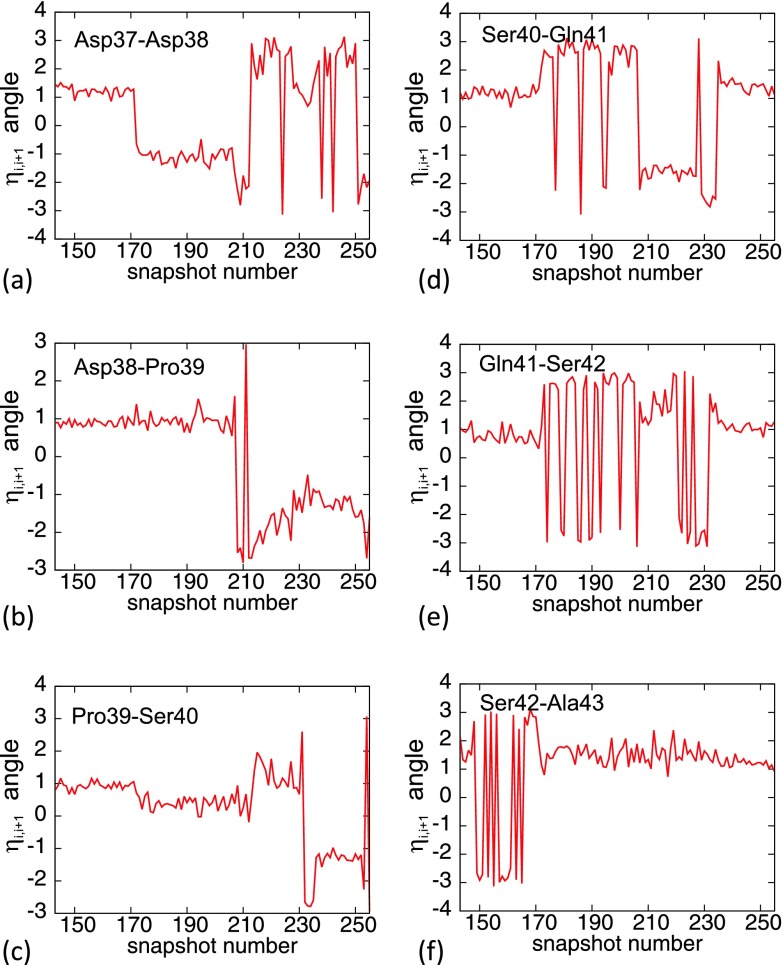
In Figure 26, the time evolution of the angles of Eqs. 23 during a generic UNRES run is shown for the six bonds between Asp37 and Ala43. In the initial conformation, the angles η are all close to the right-handed α-helical values (0.75 rad). It can be observed that the transitions are abrupt, taking place during a very small number of UNRES/MD steps; it should be noted that strong fluctuations between values around ±π, that are seen in each of the figures, are due to the 2π periodicity of the angular variable, whose fundamental range is η ∈ [−π, π). It can also be noted that there are only very few clearly identifiable equilibrium values for η, in decreasing order
This is consistent with the kink structure of the side chain-side chain interaction potential; it appears to have the functional form akin to the torsion angle in the expression for the conformational energy
where Va is a torsional constant, and the loop is a kink conformation that forms the boundary between two neighboring minima of the potential.
Figure 26.
((a)–(f)) Time evolution of the angles ηi, i + 1 of Eq. 23 during a generic UNRES simulation, over the location of the third kink.
UNRES analysis of kink dynamics
We now turn to describe the mechanism that we have identified as the cause of the kink formation, i.e., the transition in which a local oscillation as in Figure 13 becomes converted into a conformation shown in Figure 12. For this transition to take place, the local oscillations such as those portrayed in Figure 13, must exceed the threshold energy that enables them to overcome the potential barrier between the minima a and b. We have confirmed that these oscillations have a thermal origin. For example, in our UNRES simulations at very low temperatures (100 K), we observe that it takes a long time to form a loop from an initial α-helical conformation (data not shown). This is due to the presence of the energy barrier of about 7 kcal/mol for the kinks to form, and at sufficiently low temperatures the thermal oscillations are unable to exceed this threshold value.
Backbone lattice oscillations
The thermal oscillations cause localized bending and twisting deformations in an α-helical segment. The α-helical structure in a protein is stabilized by longitudinal hydrogen bonds, and there are three parallel channels that run along the helix. Each of the channels has the composition ⋯H-N-C=O⋯H-N-C=O⋯H-N-C=O⋯. The three channels can vibrate due to the C=O stretching (amide I vibrations).
It should be noted that, although the whole channel of H-N-C=O groups is treated as a single interaction site in UNRES, and their atoms are not present explicitly, the internal motions of the peptide groups are included implicitly in the UNRES energy function through the second- and higher-order terms of the cumulant expansion for the potential of mean force (restricted free energy) of polypeptide chains.26 The ensuing oscillations are quasiparticles that interact with the phonons of the longitudinal displacements of the amino acids. The three channels are also directly coupled to each other, by nearest neighbor dipole-dipole interactions. There are three different channels and, in addition to a longitudinal compression, a generic backbone Cα-lattice displacement also involves distortions such as bending and twisting of the right-handed α-helix.
We have observed that, in UNRES simulations, wave-like distortions of the Cα-lattice are constantly present. The waves that we observe travel along the protein chain and with a very high speed. The time it takes for a typical distortion to traverse the entire backbone is no more than a few hundreds of picoseconds, in UNRES time. In Figure 27, we show as an example how a thermally excited bending deformation proceeds along a protein A chain in an α-helical initial conformation. In Figure 28, we show an example of a twisting deformation that we have observed. On average, the deformation propagates 6.2 residues (forward or backward) per snapshot (1000 time steps at 4.89 fs UNRES time), which gives 0.030 ns UNRES propagation time from residue to residue. However, because of elimination of fast-moving degrees of freedom, the UNRES time scale is by about 3 orders of magnitude faster compared to the all-atom time scale23, 53 and, therefore, the deformation-propagation time can be estimated to be about 30 ns. This value is by about an order of magnitude greater than the rate of helix propagation in α-helical peptides;63 however, our simulations were run at a low temperature of T = 250 K to reduce the random motion that could disturb the analysis of the kink structure.
Figure 27.
An example of a bending deformation that proceeds along an initial α-helical protein A conformation.
Figure 28.
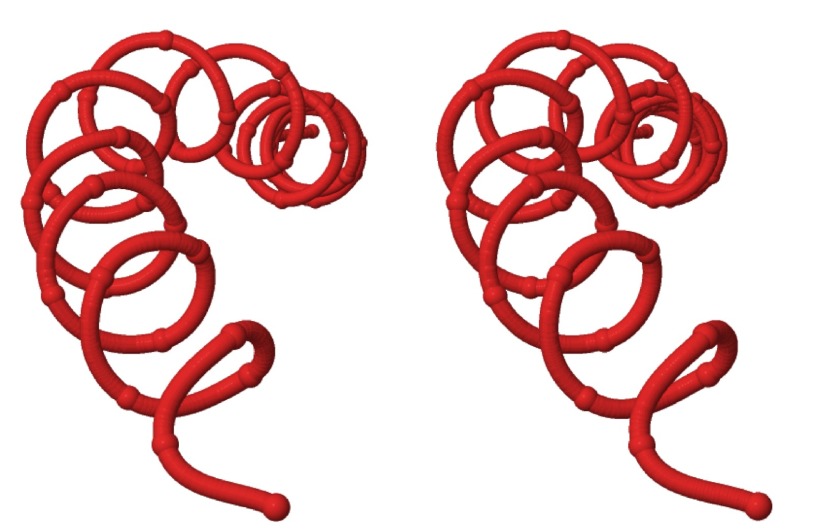
Stereoview of an example of a twisting deformation along an initial α-helical protein A conformation.
In our interpretation, the lattice deformations that we observe are propagating phonon waves due to amide vibrations. Since UNRES is a reduced atom model, we are not able to fully identify their detailed character. For a detailed investigation of the deformations that we observe, all-atom simulations would be necessary.
A movie that displays the propagation of the deformation of the virtual-bond and virtual-bond-dihedral angles during the course of simulation is included in the supplementary material.64
Finally, it is observed that the residues in the loop regions are especially prone to hopping from one minimum of the potential of mean force to the other one. Based on the discussion presented in Sec. 3C, it can be concluded that interactions between the neighboring side chains can trigger kink formation, propagating it as a spin wave.
UNRES, principal component analysis
Principal component analysis, a covariance-matrix-based mathematical technique, is an effective method for extracting important motions from molecular dynamics trajectories.65, 66, 67, 68 PCA rotates the Cartesian or internal coordinate space to a new space with new coordinates, PCs, a few of which are sufficient to describe a large part of the fluctuations of a protein. Here, structural fluctuations of θ and γ angles [mean-square-fluctuations (MSF)] can be decomposed into collective modes by PCA.44, 66, 67, 68 The modes have “frequencies” and directions corresponding to the eigenvalues and eigenvectors of the covariance matrix. The modes with the largest eigenvalues (λi) correspond to the modes which contribute the most to the structural fluctuations of the protein. The contribution of each angle (θn and γn) to a mode i is called the influence, νi, n.
The kinks describe loops, which are flexible, and consequently the kinks certainly correspond to principal modes. But the exact correspondence is not known. In particular, one might inquire whether PCA is sensitive enough for identifying, and possibly analyzing, kinks in the background of generic motions? A good demonstration of this is the movie (see the supplementary material64), which illustrates the evolution of the backbone angles. The peaks which appeared along the backbone angles in the course of time coincide with the peaks that appeared in the principal modes calculated at the corresponding time intervals.
MD trajectories of protein A were analyzed by PCA. The results are displayed in Figure 29 as the contributions of the two main principal modes (with the largest eigenvalues) to the MSF along the θ and γ angles for different trajectory windows. It can be seen that the peaks in the contributions appear exactly in the regions where the kinks are located. There are three peaks in the initial time window (Figures 29a, 29b), the middle of which reflects the traveling kink structure, which is visualized in Figure 27. After 4890 ps UNRES time (Figures 29c, 29d), only two peaks appear which correspond to the stabilization of a folded structure. The bands in Figure 29, corresponding to the contribution from the variation of the virtual-bond angles θ, are unimodal, while those corresponding to the contributions from the γ angles have finer structure; this is similar to the shapes of the kink profiles in the θ and γ angles of the experimental 1BDD structure (Figure 9).
Figure 29.
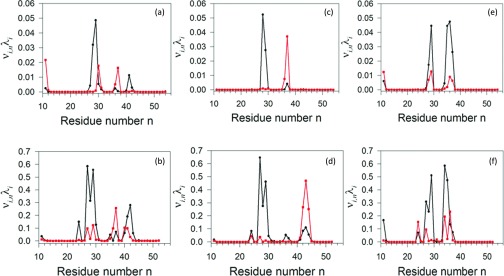
Contributions (νi, n, λi) of principal mode 1 (black) and mode 2 (red) to the mean-square fluctuations along the θ ((a), (c), and (e)) and γ ((b), (d), and (f)) angles, respectively, in the time windows from 0 to 4.89 ns ((a) and (b)), 4.89 to 9.78 ns ((c) and (d)), and from 9.78 to 14.67 ns ((e) and (f)).
It should be noted that MD simulations, in the presented work, were started from the full right-handed α-helix. The principal modes do not exhibit any peaks in kink regions until loops form (not shown). This is because the first principal modes capture the largest fluctuations, which do not come from helices. Once loops are formed (consequently the kinks), which are more flexible and characterized with fluctuations greater than those in the helices, the peaks start to appear in principal modes in kink regions.
It is remarkable that the shapes of the contributions of the principal modes to mean square fluctuations along θ and γ angles resemble those of the squares of the derivatives of the kink profiles. This feature probably arises since the contributions plotted in Figure 29 are variances of the respective θ or γ angles along a given principal component. Following error propagation rules, the variance of a composite quantity is proportional to the square of the derivative of a quantity. Therefore, the more an angle varies along the chain, the greater are its fluctuations.
CONCLUSIONS
The folding pathway of the N-terminal segment of the B-domain of staphylococcal protein A has been simulated in this work with the coarse-grained UNRES force field.24, 25, 26, 27, 28, 30, 31, 32 The analysis demonstrates that the description of protein structure in terms of kinks of the DNLS equation proposed in our earlier work6, 7, 9 can be applied to the description of protein folding pathways and energetics. Intuitively, this feature of protein structure and dynamics is seen to result from the approximate bimodal character of the local potential of mean force of polypeptide chains in backbone virtual-bond angles θ (Figure 6). This can be seen both in the statistic of the PDB (Figure 4; see also Ref. 25) and from the potential of mean force calculated from ab initio energy surfaces of terminally blocked amino-acid residues.69
The present kink structure is, in particular, useful in representing chain-reversal structure which seems to be crucial in initiating nucleation sites, which then enable the formation of long-range contacts between side chains.70, 71 For protein A, the kinks are located in the regions between residues Glu16-Asn22, Leu20-Asn29, and Gln33-Asn44, respectively. The trajectories that were analyzed in this work had been started from a full-α-helical conformation but this starting point had been selected to focus the observation on loop formation instead of on the formation of α-helices from random structure. Moreover, transitions from a long right-handed α helix to a helical hairpin structure is part of functionally important motions of many proteins; e.g., the transition from an open to a closed (substrate-binding) conformation of Hsp70 chaperones;72, 73, 74 it also constitutes a part of folding of many proteins such as, e.g., the engrailed homeodomain.75
Kink analysis enables us to realize the importance of local interactions, specifically the bimodal character of the potential of mean force in virtual-bond angles θ, as the driving force of folding. The Landau Hamiltonian used in this study and in the studies reported in our earlier work6, 7, 8, 9, 10, 48 does not contain any long-range terms. Still, it was usable to simulate folding pathways in our earlier studies10 in a Gō-like manner, using kink parameters derived from the experimental structure of the protein under study. In this regard, the kinks can provide a prediction of local collective motions without MD simulations, while PCA requires MD simulations for this. Moreover, we learned from our current study that the bimodal character of the potentials in the virtual-bond angles θ makes the system jump from state to state, causing conformational transitions.
A remarkable observation made during this study is that the creation of a kink in a full-α-helical protein segment consistently involves a local free energy increase of about 7 kcal/mol. Surprisingly, this is a value which is very close to the dissociation of a phosphate residue from ATP. However, it remains to be clarified in future work, whether the observation, that the energy for the initiation of helix bending in protein A is equal to the elementary energy supply from ATP hydrolysis, is accidental.
Even though bimodality of the potential of mean force in backbone virtual-bond valence angles characterizes all amino-acid residues, some of them are more prone to change their local conformational state. The analysis presented in Sec. 3C suggests that the interactions between neighboring side chains or the side chains and adjacent backbone sites trigger the jump from one local minimum to another one. This process is similar to the formation of a Bloch domain wall in magnetic spin chains. It should be noted that, apart from kink initiation, we also observe very fast-moving wave-like phonon propagation along the chain (Figure 27). For a detailed investigation of these wave-like structures, all-atom simulations should be performed.
Finally, a principal-component analysis of the folding trajectories of protein A in Sec. 3E has shown that the principal modes appear to be clearly correlated with kink formation. As expected, the largest contributions to the most significant principal modes arise from loop regions (Figure 29), and the shapes of the plots of the principal modes along the chain resembles the directional derivative of the solution of the DNLSE (cf. Sec. 3E). But the strong correlation observed here between PCA and kink formation is somewhat unexpected. This observation suggests that kinks can be used to describe principal motions of proteins without having to resort to a posteriori essential dynamics. This line of research is now being followed in our laboratory.
ACKNOWLEDGMENTS
This work was supported by grants from the National Institutes of Health (GM-14312), the National Science Foundation (MCB10-19767), by the Polish National Science Centre (2012/06/A/ST4/00376), by the Carl Tryggers Stiftelse för Vetenskaplig Forskning, by a CNRS PEPS collaboration grant, by a Qian Ren grant at the Beijing Institute of Technology (BIT), by an Égide—Programme Cai Yuanpei collaboration grant, and by a Région Centre research grant. A.L. thanks the Department of Physics and Astronomy at Uppsala University for hospitality during this collaboration. Computational resources were provided by (a) Argonne Leadership Computing Facility at Argonne National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-06CH11357, (b) the National Science Foundation (http://www.nics.tennessee.edu/), and by the National Science Foundation through TeraGrid resources provided by the Pittsburgh Supercomputing Center, (c) the Informatics Center of the Metropolitan Academic Network (IC MAN) in Gdańsk, (d) our 624-processor Beowulf cluster at the Baker Laboratory of Chemistry, Cornell University, and (e) our 184-processor Beowulf cluster at the Faculty of Chemistry, University of Gdańsk.
References
- Orengo C. A., Michie A. D., Jones S., Jones D. T., Swindells M. B., and Thornton J. M., Structure 5, 1093 (1997). 10.1016/S0969-2126(97)00260-8 [DOI] [PubMed] [Google Scholar]
- Murzin A. G., Brenner S. E., Hubbard T., and Chothia C., J. Mol. Biol. 247, 536 (1995). 10.1006/jmbi.1995.0159 [DOI] [PubMed] [Google Scholar]
- Rackovsky S., Proteins Struct. Funct. Genet. 7, 378 (1990). 10.1002/prot.340070409 [DOI] [PubMed] [Google Scholar]
- Skolnick J., Arakaki A. K., Seung Y. L., and Brylinski M., Proc. Natl. Acad. Sci. U.S.A. 106, 15690 (2009). 10.1073/pnas.0907683106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holm L., Ouzounis C., Sander C., Tuparev G., and Vriend G., Protein Sci. 1, 1691 (1992). 10.1002/pro.5560011217 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chernodub M., Hu S., and Niemi A. J., Phys. Rev. E 82, 011916 (2010). 10.1103/PhysRevE.82.011916 [DOI] [PubMed] [Google Scholar]
- Molkenthin N., Hu S., and Niemi A. J., Phys. Rev. Lett. 106, 078102 (2011). 10.1103/PhysRevLett.106.078102 [DOI] [PubMed] [Google Scholar]
- Hu S., Krokhotin A., Niemi A. J., and Peng X., Phys. Rev. E 83, 041907 (2011). 10.1103/PhysRevE.83.041907 [DOI] [PubMed] [Google Scholar]
- Krokhotin A., Niemi A., and Peng X., Phys. Rev. E 85, 031906 (2012). 10.1103/PhysRevE.85.031906 [DOI] [PubMed] [Google Scholar]
- Krokhotin A., Lundgren M., and Niemi A. J., Phys. Rev. E 86, 021923 (2012). 10.1103/PhysRevE.86.021923 [DOI] [PubMed] [Google Scholar]
- In Refs. the epithet topological (dark) soliton was used, but here kink is preferred. This choice highlights that the potential in the DNLS equation displays spontaneous breakdown of a discrete symmetry, and the kink describes the ensuing domain wall; see Refs. . It should be noted that the kink considered here has no direct relationship with the concept of Davydov's soliton Davydov A. S., J. Theor. Biol. 66, 379 (1977): When two kinks collide, their shapes in general change. But when solitons collide, their shapes remain intact. 10.1016/0022-5193(77)90178-3 [DOI] [PubMed] [Google Scholar]
- Faddeev L. D. and Takhtajan L., Hamiltonian Methods in the Theory of Solitons (Springer Verlag, Berlin, 1987). [Google Scholar]
- Ablowitz M. J., Prinardi B., and Trubatch A., Discrete and Continuous Nonlinear Schrödinger Systems (Cambridge University Press, Cambridge, 2004). [Google Scholar]
- Kevrekidis P., The Discrete Nonlinear Schrödinger Equation: Mathematical Analysis, Numerical Computations and Physical Perspectives (Springer-Verlag, Berlin, 2009). [Google Scholar]
- Manton N. and Sutcliffe P., Topological Solitons (Cambridge University Press, Cambridge, 2004). [Google Scholar]
- Weinberg S., The Quantum Theory of Fields, Vol. 2 (Cambridge University Press, 1995). [Google Scholar]
- Bernstein F. C., Koetzle T. F., Williams G. J. B., Meyer E. F. J., Brice M. D., Rodgers J. R., Kennard O., Shimanouchi T., and Tasumi M., J. Mol. Biol. 112, 535 (1977). 10.1016/S0022-2836(77)80200-3 [DOI] [PubMed] [Google Scholar]
- Khalili M., Liwo A., Rakowski F., Grochowski P., and Scheraga H., J. Phys. Chem. B 109, 13785 (2005). 10.1021/jp058008o [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaw D. E., Deneroff M. M., Dror R. O., Kuskin J. S., Larson R. H., Salmon J. K., Young C., Batson B., Bowers K. J., Chao J. C., Eastwood M. P., Gagliardo J., Grossman J. P., Ho C. R., Ierardi D. J., Kolossváry I., Klepeis J. L., Layman T., McLeavey C., Moraes M. A., Mueller R., Priest E. C., Shan Y., Spengler J., Theobald M., Towles B., and Wang S. C., Commun. ACM 51, 91 (2008). 10.1145/1364782.1364802 [DOI] [Google Scholar]
- Friedrichs M. S., Eastman P., Vaidyanathan V., Houston M., Legrand S., Beberg A. L., Ensign D. L., Bruns C. M., and Pande V. S., J. Comput. Chem. 30, 864 (2009). 10.1002/jcc.21209 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pande V. S., Baker I., Chapman J., Elmer S., Kaliq S., Larson S. M., Rhee Y. M., Shirts M. R., Snow C. D., Sorin E. J., and Zagrovic B., Biopolymers 68, 91 (2003). 10.1002/bip.10219 [DOI] [PubMed] [Google Scholar]
- Lindorff-Larsen K., Trbovic N., Maragakis P., Piana S., and Shaw D. E., J. Am. Chem. Soc. 134, 3787 (2012). 10.1021/ja209931w [DOI] [PubMed] [Google Scholar]
- Liwo A., Khalili M., and Scheraga H. A., Proc. Natl. Acad. Sci. U.S.A. 102, 2362 (2005). 10.1073/pnas.0408885102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liwo A., Ołdziej S., Pincus M. R., Wawak R. J., Rackovsky S., and Scheraga H. A., J. Comput. Chem. 18, 849 (1997). [DOI] [Google Scholar]
- Liwo A., Pincus M. R., Wawak R. J., Rackovsky S., Ołdziej S., and Scheraga H. A., J. Comput. Chem. 18, 874 (1997). [DOI] [Google Scholar]
- Liwo A., Czaplewski C., Pillardy J., and Scheraga H. A., J. Chem. Phys. 115, 2323 (2001). 10.1063/1.1383989 [DOI] [Google Scholar]
- Liwo A., Khalili M., Czaplewski C., Kalinowski S., Ołdziej S., Wachucik K., and Scheraga H., J. Phys. Chem. B 111, 260 (2007). 10.1021/jp065380a [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liwo A., Czaplewski C., Ołdziej S., Rojas A. V., Kaźmierkiewicz R., Makowski M., Murarka R. K., and Scheraga H. A., in Coarse-Graining of Condensed Phase and Biomolecular Systems, edited by Voth G. (CRC Press, 2008), Chap. 8, pp. 107–122. [Google Scholar]
- He Y., Xiao Y., Liwo A., and Scheraga H. A., J. Comput. Chem. 30, 2127 (2009). 10.1002/jcc.21215 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kozłowska U., Maisuradze G. G., Liwo A., and Scheraga H. A., J. Comput. Chem. 31, 1154 (2010). 10.1002/jcc.21402 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sieradzan A. K., Scheraga H. A., and Liwo A., J. Chem. Theory Comput. 8, 1334 (2012). 10.1021/ct2008439 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sieradzan A. K., Hansmann U. H. E., Scheraga H. A., and Liwo A., J. Chem. Theory Comput. 8, 4746 (2012). 10.1021/ct3005563 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gouda H., Torigoe H., Saito A., Sato M., Arata Y., and Shimada I., Biochemistry 31, 9665 (1992). 10.1021/bi00155a020 [DOI] [PubMed] [Google Scholar]
- Bai Y. W., Karimi A., Dyson H. J., and Wright P. E., Protein Sci. 6, 1449 (1997). 10.1002/pro.5560060709 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dimitriadis G., Drysdale A., Myers J. K., Arora P., Radford S., Oas T. G., and Smith D. A., Proc. Natl. Acad. Sci. U.S.A. 101, 3809 (2004). 10.1073/pnas.0306433101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato S., Religa T. L., Daggett V., and Fersht A. R., Proc. Natl. Acad. Sci. U.S.A. 101, 6952 (2004). 10.1073/pnas.0401396101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolinski A. and Skolnick J., Proteins Struct. Funct. Genet. 18, 353 (1994). 10.1002/prot.340180406 [DOI] [PubMed] [Google Scholar]
- Lee J., Liwo A., and Scheraga H. A., Proc. Natl. Acad. Sci. U.S.A. 96, 2025 (1999). 10.1073/pnas.96.5.2025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alonso D. O. V. and Daggett V., Proc. Natl. Acad. Sci. U.S.A. 97, 133 (2000). 10.1073/pnas.97.1.133 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghosh A., Elber R., and Scheraga H. A., Proc. Natl. Acad. Sci. U.S.A. 99, 10394 (2002). 10.1073/pnas.142288099 [DOI] [PMC free article] [PubMed] [Google Scholar]
- García A. E. and Onuchic J. N., Proc. Natl. Acad. Sci. U.S.A. 100, 13898 (2003). 10.1073/pnas.2335541100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vila J. A., Ripoll D. R., and Scheraga H. A., Proc. Natl. Acad. Sci. U.S.A. 100, 14812 (2003). 10.1073/pnas.2436463100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khalili M., Liwo A., and Scheraga H., J. Mol. Biol. 355, 536 (2006). 10.1016/j.jmb.2005.10.056 [DOI] [PubMed] [Google Scholar]
- Maisuradze G. G., Liwo A., and Scheraga H. A., Phys. Rev. Lett. 102, 238102 (2009). 10.1103/PhysRevLett.102.238102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maisuradze G. G., Liwo A., Ołdziej S., and Scheraga H., J. Am. Chem. Soc. 132, 9444 (2010). 10.1021/ja1031503 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu S., Lundgren M., and Niemi A. J., Phys. Rev. E 83, 061908 (2011). 10.1103/PhysRevE.83.061908 [DOI] [PubMed] [Google Scholar]
- Lundgren M., Krokhotin A., and Niemi A. J., Phys. Rev. E 88, 042709 (2013). 10.1103/PhysRevE.88.042709 [DOI] [PubMed] [Google Scholar]
- Krokhotin A., Liwo A., Niemi A. J., and Scheraga H. A., J. Chem. Phys. 137, 035101 (2012). 10.1063/1.4734019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Widom B., J. Chem. Phys. 43, 3892 (1965). 10.1063/1.1696617 [DOI] [Google Scholar]
- Kadanoff L. P., Physics 2, 263 (1966). [Google Scholar]
- Wilson K., Phys. Rev. B 4, 3174 (1971). 10.1103/PhysRevB.4.3174 [DOI] [Google Scholar]
- Fisher M. E., Rev. Mod. Phys. 46, 597 (1974). 10.1103/RevModPhys.46.597 [DOI] [Google Scholar]
- Khalili M., Liwo A., Jagielska A., and Scheraga H., J. Phys. Chem. B 109, 13798 (2005). 10.1021/jp058007w [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berendsen H. J. C., Postma J. P. M., van Gunsteren W. F., DiNola A., and Haak J. R., J. Chem. Phys. 81, 3684 (1984). 10.1063/1.448118 [DOI] [Google Scholar]
- Berg J., Tymoczko J. L., and Stryer L., Biochemistry, 6th ed. (W. H. Freeman, New York, 2007). [Google Scholar]
- Thomas N. and Thornhill R. A., J. Phys. D: Appl. Phys. 31, 253 (1998). 10.1088/0022-3727/31/3/002 [DOI] [Google Scholar]
- Peierls R., Proc. Phys. Soc. 52, 34 (1940). 10.1088/0959-5309/52/1/305 [DOI] [Google Scholar]
- Nabarro F. R. N., Proc. Phys. Soc. 59, 256 (1947). 10.1088/0959-5309/59/2/309 [DOI] [Google Scholar]
- Huang K., Statistical Mechanics (Wiley, New York, 1987). [Google Scholar]
- Landau K. D. and Lifshitz E. M., Electrodynamics of the Continuous Media (Pergamon Press, New York, 1960). [Google Scholar]
- Kaźmierkiewicz R., Liwo A., and Scheraga H. A., J. Comput. Chem. 23, 715 (2002). 10.1002/jcc.10068 [DOI] [PubMed] [Google Scholar]
- Kaźmierkiewicz R., Liwo A., and Scheraga H. A., Biophys. Chem. 100, 261 (2003); 10.1016/S0301-4622(02)00285-5 [DOI] [PubMed] [Google Scholar]; Kaźmierkiewicz R., Liwo A., and Scheraga H. A., Biophys. Chem. 106, 91 (2003) (erratum). 10.1016/S0301-4622(03)00245-X [DOI] [Google Scholar]
- Muñoz V. and Ramanathan R., Proc. Natl. Acad. Sci. U.S.A. 106, 1299 (2009). 10.1073/pnas.0812577106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- See supplementary material at http://dx.doi.org/10.1063/1.4855735 for a movie of the folding trajectory of protein A at T=250 K.
- Kitao A., Hirata F., and Gō N., Chem. Phys. 158, 447 (1991). 10.1016/0301-0104(91)87082-7 [DOI] [Google Scholar]
- Mu Y., Nguyen P. H., and Stock G., Proteins 58, 45 (2005). 10.1002/prot.20310 [DOI] [PubMed] [Google Scholar]
- Altis A., Nguyen P. H., Hegger R., and Stock G., J. Chem. Phys. 126, 244111 (2007). 10.1063/1.2746330 [DOI] [PubMed] [Google Scholar]
- Maisuradze G. G., Liwo A., and Scheraga H. A., J. Mol. Biol. 385, 312 (2009). 10.1016/j.jmb.2008.10.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kozłowska U., Liwo A., and Scheraga H. A., J. Phys. Condens. Matter 19, 285203 (2007). 10.1088/0953-8984/19/28/285203 [DOI] [Google Scholar]
- Matheson R. R. and Scheraga H. A., Macromolecules 11, 819–829 (1978). 10.1021/ma60064a038 [DOI] [Google Scholar]
- Lewandowska A., Ołdziej S., Liwo A., and Scheraga H. A., Biophys. Chem. 151, 1 (2010). 10.1016/j.bpc.2010.05.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swain J. F., Dinler G., Sivendran R., Montgomery D. L., Stotz M., and Gierasch L. M., Mol. Cell 26, 27 (2007). 10.1016/j.molcel.2007.02.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mapa K., Sikor M., Kudryatsev V., Waegermann K., Kalinin S., Seidel C. A. M., Neupert W., Lamb D. C., and Mokranjac D., Mol. Cell 38, 89 (2010). 10.1016/j.molcel.2010.03.010 [DOI] [PubMed] [Google Scholar]
- Golas E. I., Maisuradze G. G., Senet P., Ołdziej S., Czaplewski C., Scheraga H. A., and Liwo A., J. Chem. Theory Comput. 8, 1750 (2012). 10.1021/ct200680g [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayor U., Grossman J. G., Foster N. W., Freund S. M. V., and Fersht A. R., J. Mol. Biol. 333, 977 (2003). 10.1016/j.jmb.2003.08.062 [DOI] [PubMed] [Google Scholar]