Abstract
We describe a method based on Rosetta structure refinement for generating high-resolution all-atom protein models from electron cryo-microscopy density maps. A local measure of the fit of a model to the density is used to directly guide structure refinement and to identify regions incompatible with the density that are then targeted for extensive rebuilding. Over a range of test cases using both simulated and experimentally generated data, the method consistently increases the accuracy of starting models generated either by comparative modeling or by hand-tracing the density. The method can achieve near atomic resolution starting from density maps at 4-6Å resolution.
Introduction
Electron cryomicroscopy (cryo-EM) has matured to the point that density maps can regularly be obtained at 4-8Å resolution. Methods have been developed to fit solved structures into such maps, to find locations of secondary structure elements1,2 and determine the topology of these elements3, to select and rethreading homology models using density data4, and to flexibly fit models into density5,6,7,8,9,10,11. These methods generally start with complete all-atom models, rather than the Cα-only models that are often traced through low-resolution density.
The Rosetta structure prediction methodology12 has been successful at predicting structures de novo for small proteins and for refining comparative models to higher resolution. Rosetta uses Monte Carlo sampling to search for the lowest energy structure of the polypeptide chain according to a detailed all atom force field. For small proteins (less than 100 amino acids), Rosetta can in some cases generate atomic-accuracy models with no experimental data. The bottleneck to more consistent de novo prediction is conformational sampling: conformations within 1.5-2Å RMSd of the native structure generally have much lower energies than non-native models, but for larger proteins such models are generated extremely rarely. With even a small amount of data (e.g., NMR chemical shift data13) to guide conformational sampling, Rosetta can consistently build atomic-level models for proteins of 120 amino acids or less. Rosetta's rebuild-and-refinement protocol often improves the accuracy of comparative models, especially distant homologues (<30% sequence identity).
In this paper, we adapt Rosetta to refine comparative models and low-resolution Cα traces using density maps as a guide. The Rosetta energy function is augmented with a term that assesses the agreement of a structure to experimental density data. By optimizing the combination of the fit-to-density term and Rosetta energy, models are generated that are simultaneously low in energy and fit the density. The method can generate models with near-atomic accuracy using 4-8Å density maps.
Results and Discussion
The adaptation of Rosetta to utilize input density maps is described in the METHODS section. We have developed two protocols; the first starts with an alignment to a homologous protein of known structure, the second, with a low resolution Cα trace through the density. In this section we describe application of the two methods to a variety of structure modeling problems using both synthetic and experimentally determined density maps.
Comparative modeling using synthesized density
This test involves the refinement of a set of models built from distant homologues into synthesized low-resolution cryoEM density maps at 5Å and 10Å resolution. For each of eight structures, noise-free maps were constructed using EMAN's mrc2pdb1, at both 5Å and 10Å resolution. The starting models are based on Moulder reference alignments14. Moulder uses a genetic algorithm that simultaneously optimizes a sequence-alignment potential and a potential on the threaded model implied by a particular sequence alignment. The top 300 threaded models according to Moulder's fitness function were refined into density using the protocol outlined in Figure 1 (see METHODS section and supplementary materials for more details).
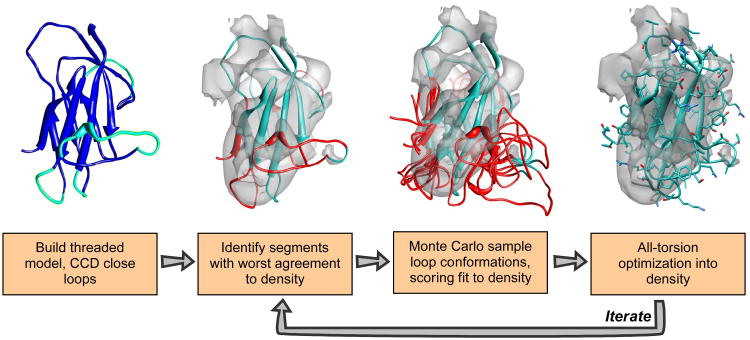
Figure 1.
The comparative modeling into density protocol. We initially build a threaded model from some alignment (blue), using cyclic coordinate descent to close gaps in the alignment (cyan). We then dock this threaded model into density, and identify regions that have a poor local agreement with the density data (red). We aggressively resample the conformations in these regions, scoring each potential conformation with Rosetta's low-resolution energy function together with an agreement-to-density score. Finally, we optimize sidechain rotamers and minimize all backbone and sidechain torsions using Rosetta's high-resolution potential, also augmented with this agreement-to-density score. We iterate over these final three steps until the lowest-energy models converge, at each iteration enriching our population for those models with both favorable Rosetta energy as well as good fit to density.
The results of this refinement are shown in Table 1 and two examples are illustrated in Figure 2. For each of the 8 structures, the refined model is closer to the native structure (in terms of Cα and all-atom RMSd) than the best initial model. In some cases the initial model that was closest to native was not the one highest ranked by Moulder; in some cases it was not even in the top 20. In six of the eight cases at 5Å and four of the eight cases at 10Å, the lowest-energy model was closer than 2Å to the crystal structure. Refinement improved individual starting models from 1-3Å (see Supplementary Figure 1). Several structures at 5Å resolution refined from 2-4Å RMSd to sub-1Å accuracy. These results show that the Rosetta refinement procedure – restricted by a low-resolution density map to focus sampling in relevant regions – can improve homology models, even those that are already quite close to native.
Table 1.
Comparative modeling into synthetic density maps at 5Å and 10Å resolution. In each pair of values in the table, the first is the Cα RMS and the second the all-atom RMS to the crystal structure.
| nres | lowest-RMS starting model | 5Å map | 10Å map | |||
|---|---|---|---|---|---|---|
|
| ||||||
| lowest-energy refined structure | lowest RMS of 10 lowest-energy | lowest-energy refined structure | lowest RMS of 10 lowest-energy | |||
| 1bbh | 127 | 2.48 / 3.41 | 1.76 / 2.47 | 1.60 / 2.31 | 2.31 / 2.98 | 1.78 / 2.57 |
| 1c2r | 115 | 3.45 / 4.15 | 0.54 / 1.12 | 0.54 / 1.12 | 1.61 / 2.43 | 1.37 / 2.40 |
| 1cid | 109 | 3.34 / 4.33 | 1.82 / 2.99 | 1.66 / 2.79 | 1.97 / 3.24 | 1.88 / 3.30 |
| 1dxt | 143 | 2.02 / 2.78 | 0.50 / 1.14 | 0.50 / 1.14 | 1.12 / 1.88 | 1.12 / 1.88 |
| 1lga | 279 | 3.16 / 3.77 | 2.27 / 2.83 | 2.27 / 2.83 | 2.40 / 3.07 | 2.24 / 2.91 |
| 1mup | 152 | 3.49 / 4.47 | 2.19 / 3.25 | 1.35 / 2.68 | 2.67 / 3.77 | 1.99 / 3.23 |
| 1onc | 101 | 2.23 / 2.97 | 0.81 / 1.92 | 0.53 / 1.47 | 1.31 / 2.09 | 1.09 / 1.91 |
| 2cmd | 310 | 2.50 / 3.42 | 1.80 / 2.63 | 1.43 / 2.31 | 2.21 / 3.36 | 2.02 / 3.09 |
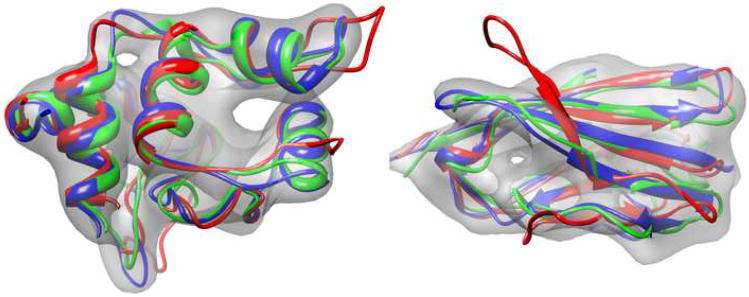
Figure 2.
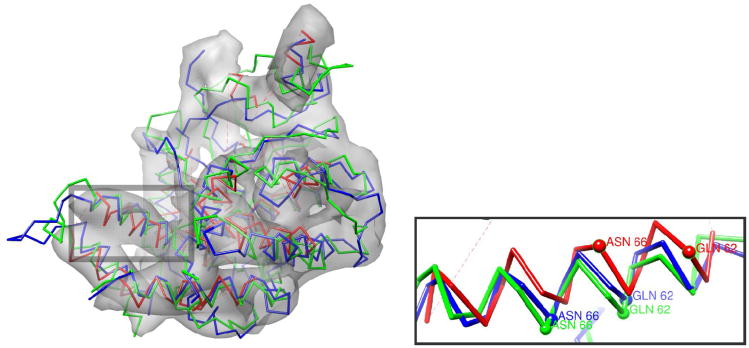
Comparative modeling into density on synthetic 10Å cryoEM maps for 1c2r (left) and 1cid (right). Three hundred homology models were constructed using Moulder. From these models, the best twenty were selected using fit-to-density score; these twenty were then further refined using the protocol outlined in Figure 1. The best Moulder structure is shown in red, while the crystal structure is shown is blue. The lowest-energy Rosetta model is in green.
Benchmark tests on real data
Refining the upper domain of RDV
The rebuilding and refinement-into-density protocol illustrated in Figure 1 was applied to the upper domain (residues 173-292) of the Rice Dwarf Virus (RDV) capsid protein P8. A 6.8Å resolution cryoEM map of this structure has been determined15. The crystal structure of this protein has also been solved (pdb code: 1uf2)16, giving a standard against which to compare. A starting model was generated from an alignment to a structural homologue from Bluetongue Virus17 (coat protein vp7, pdb code: 1bvp) produced by GenThreader18. Details of this alignment are shown in Supplementary Figure 2. The standard Rosetta rebuild-and-relax protocol (without density data) was used to create an initial 10000 models, which were then refined into density as described in the METHODS section.
A superposition of the starting structure, crystal structure, and the lowest-energy model is shown in Figure 3. The model has a Cα RMSd from the native structure of 3.7Å, compared to 5.6Å in the lowest-energy threaded model. As expected, much of the error is in gaps in the initial alignment: the model has an RMSd of 3.2Å over residues aligned in the template. The starting template has an RMS error of 3.8Å over these same residues. The refined model has a correlation with the density better than the crystal structure (see Supplementary Table 1).
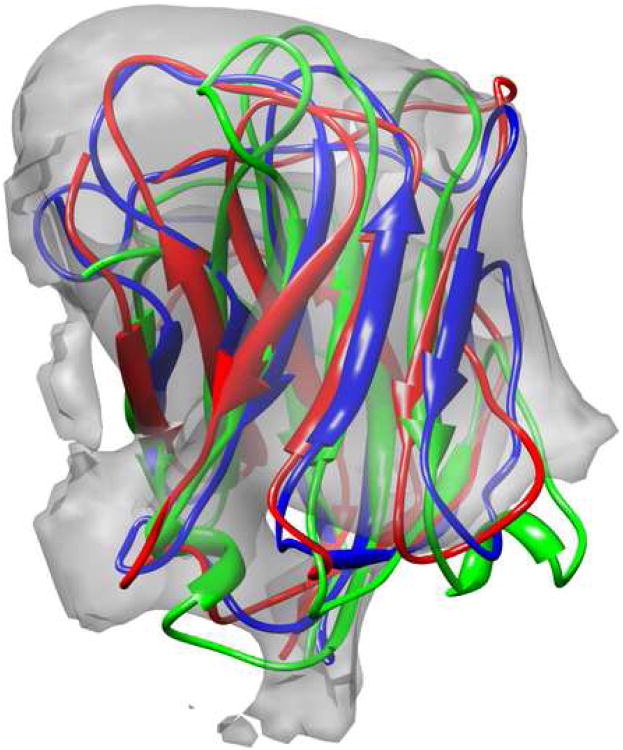
Figure 3.
A comparison of the starting homology model (red), the crystal structure (blue), and the model refined into density (green) for the upper domain of RDV P8 [1uf2, residues 173-292], docked into a 6.8Å cryoEM density map. The predicted model was built using a homology model from bluetongue virus [1bvp], aligned with mGenThreader, which was then iteratively refined using the method from Figure 1. The model has a Cα RMSd of 3.7Å, compared to 5.6Å in Rosetta's lowest-energy threaded model.
Refining the equatorial domain GroEL from a hand-traced model
To test the performance of the protocol for refining a Cα-only model into density, we used the 4.2Å resolution D7 cryoEM map of GroEL19. The starting Cα trace was the hand-traced model produced by Matthew Baker (pdb code: 3cau), shown in Figure 4. The rebuilding focused on the equatorial domain (residues 2-136,410-525). Starting from the Cα-only model of this domain, we applied the protocol described in the METHODS section and illustrated in Figure 5.
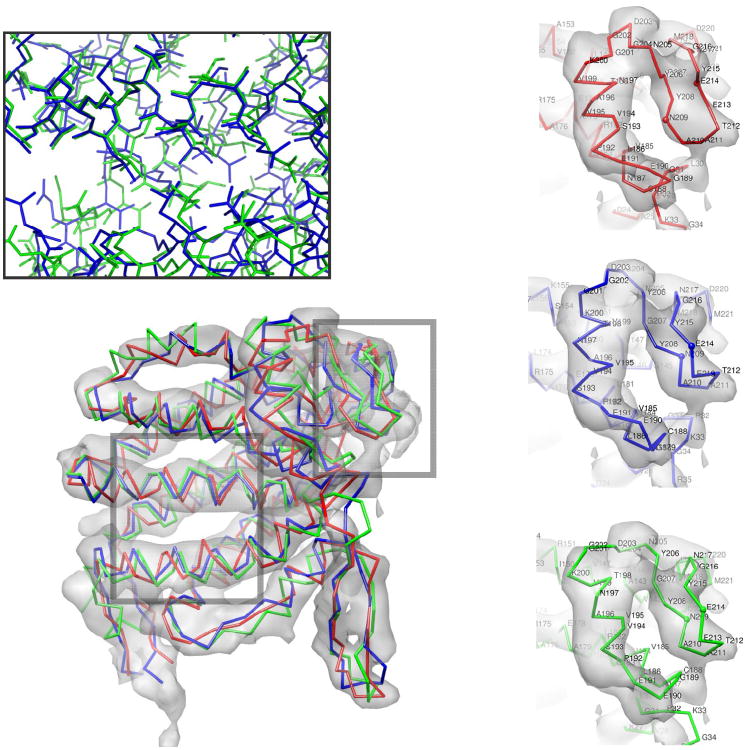
Figure 4.
The hand annotated Cα trace of the equatorial domain of GroEL (red), the model refined into density (green), and the docked crystal structure [1oel, residues 2-136,410-525] (blue) in the 4.2Å cryoEM density. The model has a Cα RMSd of 3.4Å, compared to 3.6Å in the initial trace; however, the error in the core helices is much lower in the predicted model than in the original trace, 2.23 versus 3.41Å. (inset-upper) The lowest-energy refined models converge on near-native core packing. (inset-right) An error in the hand-traced model is corrected by the refinement protocol. The handtraced model (upper) does not have the crystal structure's (center) β pairing between residues 208-210 and 215-213. The refined model (lower) recovers this pairing.
Figure 5.
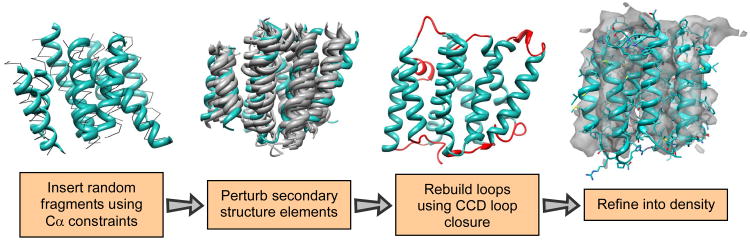
Building a model from a Cα trace. The input trace is segmented into individual secondary structure elements. For each of these segments, a set of fragments is chosen based on both sequence similarity to the target as well as low Cα RMS to the target trace (thin black lines). Then these fragments are perturbed in a Monte Carlo simulation. Harmonic constraints on the original Cα positions from the input trace keep the model from deviating too far. The lowest energy model from each trajectory is chosen and loops are rebuilt using cyclic coordinate descent. Finally, each model is docked into the density and passed through the iterative refinement into density protocol (of Figure 1).
The lowest-energy model generated – superimposed on the crystal conformation – is illustrated in Figure 4. The Cα RMSd over the nine helices in the equatorial domain is only 2.2Å, compared to 3.4Å in the initial trace. The Rosetta model has errors in the termini and loops so the Cα RMSd over all residues is only slightly better than the starting model (3.4Å versus 3.6Å).
An illustration of an error in the initial trace that is corrected in the Rosetta model is highlighted in Figure 4. In this case, the hand-traced Cα-only model does not have the proper beta pairing in residues 206-216 (in the figure). Additionally, the orientation of the adjacent helix (residues 191-201 in the figure) is much closer to native in the model than in the original hand-traced model.
Rebuilding and refining the lower domain of RDV p8 from hand-annotated helices
A second test refining a Cα-only model into density is provided by the lower domain (residues 1-172,293-421) of RDV capsid protein P8. The density data is the same 6.8Å cryoEM map used previously. The initial model – provided by Matthew Baker – consists of a set of helices that were located by the program ssehunter20. The topology of these helices was inferred from a homologous protein in BTV18, and the helices were mapped to the sequence using a consensus secondary structure prediction21. The helices from our initial model, the docked crystal structure, and the lowest-energy model produced from the Figure 5 protocol are shown in Figure 6.
Figure 6.
The starting model – a hand annotated Cα helix-only trace – of the lower domain of RDV P8 (red), the crystal structure [1uf2, residues 1-172,293-421] (blue), and the lowest-energy model refined into density (green), in 6.8Å cryoEM density data. The refined model has an overall Cα RMSd of 4.5Å from native, and an RMSd of 2.7Å in the 10 core helices. The initial Cα trace has an RMSd of 4.7Å over these same helices. (inset) Rosetta properly shifts a helix by two residues.
The lowest-energy Rosetta model has a Cα RMSd to native of 4.5Å. Though several loops are incorrectly placed, and a short helix is unwound in our prediction, the core is mostly correct. The RMSd over the ten core helices is 2.8Å, compared to 4.7Å in the initial hand-traced model. The initial model has several significant register shifts compared to the final model; one that is corrected is highlighted in Figure 6. The refined model has a (Cα-only) correlation with the map higher than does the starting model, but lower than the crystal structure (see Supplementary Table 1).
Contributions to model accuracy
The protocols we have developed involve successive rounds of refinement at each generation enriching for the lowest energy structures that best fit the density. When choosing models to carry over from one generation to the next it is necessary to balance between fit-to-density and energy. In general, the lowest-energy decoys are not the ones that best fit the density and vice versa. The energy difference between native and non-native structures is in general much greater in the core than in loop regions, and indeed we find that the Rosetta energy function better identifies the native structure of the core, while the fit-to-density score does better in identifying t native loop conformations. For example, in the set of models produced after one generation of rebuilding-and-refinement into density with GroEL, the 5 models with lowest Rosetta energy over the core exhibit a median core RMSd of 2.0Å, but a median whole-structure RMSd 5.6Å. In contrast, in the 5 models with best fit-to-density, there is a somewhat worse median core RMSd of 2.3Å, but an improved median whole-structure RMSd of 4.0Å. The selection criterion outlined in the METHODS section aims to strike a balance between the two; however, preferring one term versus the other may be beneficial for some applications.
There are also tradeoffs in the voxel spacing of the sampled density used during the matching of protein fragments into the density map. Coarser sampling requires significantly less time, but can reduce accuracy. We have found that in the resolution range explored in this paper (roughly 4 to 10Å), a grid spacing of 2Å is best. Empirically, model discrimination is about as good using 2Å grid spacing as it is with 1Å grid spacing; beyond that, it deteriorates rapidly. For all experiments in this paper a voxel spacing of 2Å was used.
The protocol for refining Cα-only models consists of both backbone fragment insertions (as in the Rosetta ab initio protocol) and rigid-body perturbation of secondary structure elements (see METHODS for more details). To test the importance of rigid-body moves in this protocol, we repeated the initial round of all-atom model building of GroEL, without allowing rigid body perturbations of the initial structure; initial all-atom models were built just using fragment insertions and loop remodeling. Without rigid-body perturbations, among the lowest-energy 10% (5000) of models, no sampled models are closer than 4Å to native, 1% are with 4.5Å, and 20% are within 5Å. Including rigid-body moves results in about 0.3% of sampled models within 4Å of native, 8% of models within 4.5Å, and 45% of models within 5Å. By enhancing sampling where errors are likely to occur (e.g., translations along helical axes) while minimizing sampling where errors are less like (e.g., movement normal to the helical axis), the rigid-body perturbations significantly improve the RMS distributions of the sampled models.
Materials and Methods
Incorporating Fit-to-Density into Rosetta Modeling
Rosetta12 uses Monte Carlo sampling together with gradient-based minimization to generate an ensemble of low-energy protein structures starting with either an extended chain or a homology model of the protein. To enable rapid searching, sampling and energy function evaluation are first carried out at a low-resolution level – in which sidechains are represented as a single sphere – and subsequently at a high-resolution all-atom level. We incorporate a scoring term into Rosetta that describes how well a particular protein conformation agrees with density data. This density score is the log of the probability of observing a particular correlation between a model's density (computed at some resolution) and the experimental density data. Because we must perform torsion space minimization with this function – and hence must evaluate it – many thousands of times, some approximations must be made to make calculations tractable.
Given a protein conformation X={x1,…,xN}, where each xi describes the location of one atom, and a density map ρo(y) over grid points y in the density map, we compute the expected density ρc(y) by placing a Gaussian sphere of density at each atom:
| (1) |
The parameters C and k are resolution-dependant parameters describing the shape of the Gaussian blob; the parameter a is the mass of atom xi. The fit to density measure we employ is a function of the correlation between ρc and the experimental map over a region specified by a masking function ε. Using a mask is advantageous for several reasons: it minimizes the effect of poor segmentation of the monomer, it makes correlation scores comparable between different maps at the same resolution, and most importantly, it greatly facilitates the calculation of gradients with respect to the atomic positions (see below). The masking function, ε(y), restricts the calculation of the correlation to points in the density map within some distance m of a specified subset of atoms in the protein:
| (2) |
where σ is the sigmoid function, σ(x) = 1(1 + e−x). The parameter m is the masking distance (in our experiments 5Å if every atom is used to compute ρc and 8Å if only Cα's are used to compute ρc); density beyond this distance from any atom will have marginal impact on the fit-to-density score. This mask is used in computation of the correlation coefficient between ρo(y) and ρc(y):
| (3) |
ρ̄o and ρ̄c are the average observed and calculated densities over the mask; so and sc are the standard deviations of the observed and calculated densities, also over the mask.
For scoring, we convert this correlation into a negative log-likelihood. We compute the probability that a particular correlation was generated by random chance, assuming that correlations are distributed normally (this normal distribution is supported empirically; see the supplementary materials), with mean μ and standard deviation σ. Given a correlation S, the score is given as the log of the probability that a correlation greater than S is seen by chance:
| (4) |
Here, Φ is the error function, . The parameters μ and σ are trained for a particular resolution range by matching randomly oriented structures into a generated density map at that resolution. This is similar to the cross-correlation used by Topf et al.11; the key difference is that the density surrounding each residue is scaled independently. This makes refinement sensitive to the shape of the density, rather than the absolute magnitudes, which allows for different levels of contrast in different parts of the map.
Computing first derivatives of the density score (Equation 4) with respect to each atom's movement is straightforward given the derivatives of the masked correlation (Equation 3). Derivative calculation this requires computation of:
The change in the volume covered by the mask, ∂Σy ε(y)/∂xi, as the mask moves in response to an atom's movement (since each atom's mask overlaps the mask of neighboring atoms, compression or expansion of the molecule leads to a change in the mask's total volume).
The change in the mean and variance of the observed density as the mask moves, which require calculation of ∂Σy ε(y)ρo(y)/∂xi and .
The change in the variance of the calculated density as each atom moves, which requires calculation of
The change in the masked product of observed and calculated density, ∂Σy ε(y)ρo(y)ρc(y)/∂xi as the mask and each atom moves.
There are two aspects of the masking function ε (Equation 2) that are important for computing these values. First, the functional form allows for straightforward factoring out of the contribution of each individual atom to the derivatives in (1) and (2) above. Second, the mask smoothly decays to 0, so the derivative is well defined. This allows us to quickly compute each of the derivatives above – for a single atom's movement – by only considering a small neighborhood of density around that atom. These Cartesian-space derivatives are converted to torsion-space derivatives using the recursive relations of Abe et al.22, which allows for torsion-space optimization (via a quasi-Newton minimizer) of the density score and the energy.
The fit to the density is initially computed at low resolution and later in the conformational search at high resolution. For the low resolution score, one Gaussian blob per residue is placed on the Ca atom when computing the expected density ρc(y), with k = (π/(2.4 + 0.8R0))2 and C = (k/π)3/2 (for map resolution R0). The value k is chosen to maximize the correlation between the single-Gaussian approximation and alanine's all-atom Gaussian density. The single Gaussian approximation becomes a better representation as the map resolution becomes worse, approaching 0.95 correlation as the map nears 10Å resolution. For the low-resolution score, the masking function ε(y) is based on the distance to the nearest Cα, and the masking distance is set to 8Å to include all the density associated with the residue. The high-resolution score places a Gaussian placed on each atom, with k = (π/R0)2 and C as before. A separate correlation is computed for each residue, with the mask covering all atoms in the residue and in the two flanking residues on each side; the masking distance is 5Å. This formulation allows us to compute the correlation over a much smaller region, allowing for greater efficiency, while allowing the density score to guide sidechain optimization.
The density score is added to the Rosetta energy function (low or high resolution depending on the stage of the trajectory) with a weight wdens chosen such that the dynamic range (the difference between the worst- and best- scoring models) of this term is approximately 0.5-1 energy units per residue (Rosetta's high-resolution energy function has a dynamic range of roughly 2-3 energy units per residue, the low-resolution function has slightly less). For all experiments in this paper, the weight on the low-resolution term was 0.02 and the weight on the high resolution fit-to-density term 0.2.
Incorporating fit-to-density into Rosetta's rebuilding-and-refinement
Rosetta's rebuilding-and-refinement protocol has been used extensively for comparative modeling from distant (<30% sequence identity) homologues. The approach consists of two main phases. During the first phase, portions of the protein are chosen for aggressive refinement. These portions may be chosen using several different criteria, but in general, given some ensemble of starting structures (either from an NMR ensemble or threadings to multiple templates or even multiple Rosetta simulations from a single starting model), they correspond to regions of high variation in the ensemble most likely to deviate from the native conformation. These high-variance regions are aggressively remodeled using internal loop-building algorithms together with Rosetta's low-resolution score. In the second phase, the endpoints of these trajectories are then subjected to all-atom refinement with respect to all sidechain and backbone degrees of freedom.
In very distant homology cases, it is often necessary to iterate through this process using an evolutionary algorithm. Through successive generations, we want to enrich the population for low-energy models, while maintaining a diverse ensemble of conformations. Thus, Rosetta's rebuilding-and-refinement – when choosing models to propagate to the subsequent generation – alternates between choosing the lowest-energy models (intensification) and choosing a set of structures that explore conformational space (diversification). After each selection round, the two-phase process is repeated; the protocol repeats until successive generations converge to a single structure.
Incorporating the fit-to-density score into the Rosetta rebuilding-and-refinement method is relatively straightforward. The complete protocol – illustrated in Figure 1 – is comprised of three stages:
Coarse fragment rebuilding using Rosetta's low-resolution potential and Cα-only fit-to-density.
All-atom refinement using Rosetta's high-resolution (all-atom) potential and Cα-only fit-to-density.
For the lowest energy models from 2, sidechain repacking and all-torsion minimization using Rosetta's high-resolution potential and all-atom fit-to-density
Refinement iterates over the first two stages for several generations, while the time-consuming third phase is only carried out on a small subset of low-energy models. Though rebuilding-and-refinement in steps one and two use the low-resolution density score, the high-resolution score is used to select the segments to aggressively rebuild, and to select the best-matching structures at each generation.
Selecting regions for aggressive remodeling
Rosetta's standard rebuilding-and-refinement chooses regions to aggressively remodel using the population's positional variation at each residue. When remodeling structures in the presence of density data, a sliding-window fit-to-density score is used to determine which regions of the protein should be aggressively remodeled. At each position in each starting structure, we consider the 9-amino-acid fragment centered at that position. The correlation between the computed density from this 9-amino-acid fragment and the density map – masked in a neighborhood around the fragment – is calculated. A threshold correlation value is chosen, and all residues with local correlation below this value are selected for remodeling. In order to prevent major topology changes, we do not rebuild more than four residues into a helix or more than two residues into a strand. Of the remaining residues, we select a correlation cutoff such that approximately 30% of residues are rebuilt.
Aggressive remodeling
Once regions of potential error have been identified, local sequence information is used to find a set of fragments (that is, backbone segments) with similar local sequence and predicted secondary structure. 200 fragments – three and nine amino acids in length – are selected, centered on each residue in each region. A break is introduced at a random location in the region. Then, fragments are inserted at random into the region. The insertions are made such that all movement is propagated toward the cut using appropriate fold trees23. The insertions will generally open the chain at the cut; thus, these fragment insertions are alternated with “closure moves” that slightly adjust backbone torsions (using cyclic coordinate descent24) to minimize the distance between both sides of the cut. These moves are carried out in a Monte Carlo simulation, and each candidate structure is scored using the Rosetta low-resolution potential function and the low-resolution fit-to-density score. To remodel a segment of length n, 30n fragment insertion and closure moves are made. The probability of making a closure move (versus a fragment-insertion move) starts low, and is increased as the simulation progresses. Multiple regions are remodeled one at a time; in each simulation, the order is randomly chosen.
Repacking and torsion-space minimization with low-resolution density score
After aggressive remodeling, candidate structures are evaluated with the Rosetta all-atom energy function and the low-resolution fit-to-density score. First, the energy is minimized through combinatorial optimization of sidechain rotamer conformations25 with the backbone held fixed. All backbone and sidechain torsion angles are then minimized with respect to the sum of the Rosetta full atom energy and the low-resolution density score. This process is repeated for 18 cycles; the lowest-energy structure encountered over these 18 cycles is chosen.
Model selection
The standard Rosetta rebuilding-and-refinement alternates between selecting a subset of structures optimized for energy (intensification generations) and those optimized for diversity (diversification generations). The fit to density score is also used to select which models are carried over in a subsequent generation. During both intensification and diversification generations, the top 10% of models from the previous generation are chosen using Rosetta energy alone. In intensification generations, the top 20 are selected based on the average per-residue sliding-window correlation score over residues not selected for aggressive remodeling. That is, structures are evaluated based on the fit to density of the parts that will change relatively little during the next refinement round. During diversification generations, these lowest-energy 10% of models are first clustered (to a 3Å radius). The same selection criterion is employed; however, no more than one model is taken from each cluster.
All-atom refinement with high-resolution density score
To generate more accurate and physically realistic models, after several iterations of rebuilding-and-refinement, we perform a final all-atom refinement with the high-resolution density score, with 18 iterations of sidechain rotamer optimization and all-torsion minimization. During this phase we also consider less-common sidechain rotamers at each position: in addition to all rotamers with at least 1% population26, we also consider variants where the sidechain torsions χ1 and χ2 are shifted + and − one standard deviation.
The advantage of this additional step is that the density score – which now includes density contribution from sidechain atoms – now affects sidechain placement and not just torsion-space minimization. Computing correlations over these smaller 5 amino acid windows allows for greater efficiency, making the problem tractable. However, the computational demands are moderately high, requiring several CPU-hours for this final refinement in a 150 amino acid structure.
Refining a Cα-only model
The protocol for generating an ensemble of physically feasible all-atom structures starting with an initial Cα-only model – illustrated in Figure 5 – begins by breaking the protein into individual secondary structure elements. Loops are removed from the structure. Then for each individual secondary structure element, a set of 1000 protein fragments is chosen (from a non redundant subset of the PDB) of the correct secondary structure type that most closely matches the sequence. These 1000 fragments are sorted by Cα RMS to the starting model, and the closest 200 are then chosen. In each attempted move, a secondary structure element is randomly chosen, a random fragment is inserted, the fragment is aligned to the Cα trace, and the entire structure is minimized with respect to the Rosetta low-resolution steric repulsive potential and the Cα constraints. Minimization uses a multistep quasi-Newton optimization algorithm (BFGS). The backbone torsions within each segment as well as the rigid-body orientation of each segment are simultaneously minimized. In each simulation, 100 of these moves are made.
In the second phase of the protocol, we perturb individual secondary structural elements. A random secondary structure element is chosen, and is randomly perturbed by either: (a) a rigid-body move or (b) a sequence-shifting move. For rigid-body moves, three rotational parameters (rotation about the helical axis, two rotations perpendicular to the helical axis) and three translational parameters are chosen from a Gaussian distribution. Parameters are chosen such that the magnitude of motion is generally greater along the helical axis than it is perpendicular to the helical axis (for this paper, the standard deviation of translational motion used is 2Å along the helical axis and 0.1Å perpendicular to the helical axis; for rotational motion these values are 60 degrees and 2 degrees, respectively). For sequence-shifting moves, a direction and magnitude (i ∈ {-2, -1, 1, 2}) are randomly chosen. A transformation is applied to give amino acid n the same Cα position, Cα–C and Cα–N vector as the current amino acid n+i. If n+i extends beyond the secondary structure element the previous position's transformation is applied. In each simulation, 500 of these moves are made. This phase is similar to an approach to folding helical proteins27.
Finally, loops are rebuilt as in comparative modeling, sidechains are placed on the structure, and the entire structure is relaxed with Rosetta's high-resolution energy. Throughout the entire process, harmonic constraints keep Cα positions from deviating too much from their initial positions. The weights on these constraints are chosen such that the majority of models generated are within 4Å of the initial Cα trace. These models are then fed into the refinement protocol outlined in the previous two sections.
Conclusion
With the incorporation of low-resolution density data, Rosetta can accurately refine models threaded from structural homologues and low-resolution Cα-only models. We show that the method improves the accuracy of models on a variety of synthetic and experimental cryoEM density maps from 4-10Å resolution.
As noted in the introduction, flexible fitting models have been developed to refine models in density. Most of the methods have focused on sampling relatively small degrees of freedom, such as hinge regions, rather than the complete set of backbone and sidechain torsion angles, as in our method. Previous approaches have generally started with all-atom models; to our knowledge, ours is the first to refine Cα-only models into density.
It is perhaps surprising that by incorporating density data, Rosetta can achieve accuracy well beyond the resolution of the map. How does a low-resolution map guide the detailed placement of individual atoms in the protein? The answer is that in our approach a map, rather than playing an instructive role in atom placement, instead constrains the search for low-energy states to the small subspace consistent with the density. The Rosetta energy function has sufficient accuracy that native structures nearly always are significantly lower in energy than non-native structures so the primary bottleneck in structure prediction is conformational sampling. A density map focuses Rosetta sampling in the relevant regions of the conformational space, instead of wandering off into unproductive regions. We anticipate the method will prove broadly useful in determining physically realistic and more-accurate models from cryoEM data.
There are several avenues for improvement of the method. First, refinement in the presence of density terms can result in local distortions of secondary structure elements and breaking of hydrogen bonds, and it may be useful to upweight the backbone torsional and hydrogen bond terms in the Rosetta forcefield when EM data is being used. Second, tracing beta-sheet structures can be exceedingly difficult in a low-resolution density map, and it may be possible to use the Rosetta de novo structure prediction methodology to build up beta sheets – loosely constrained by the map – instead of relying on a starting Cα trace.
Code Availability
The fit-to-density scoring functions and code for refining models from a Cα trace will be available in the next release, version 3.1, of Rosetta (see http://www.rosettacommons.org for details) and are also available from the authors. Sample command lines are provided in the supplementary materials.
Supplementary Material
Acknowledgments
This work was supported by NSF IIS-0705474, NIH P41RR02250, and PN2EY016525.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Jiang W, Baker ML, Ludtke SJ, Chiu W. Bridging the information gap: Computational tools for intermediate resolution structure interpretation. J Mol Bio. 2001;308:1033–1044. doi: 10.1006/jmbi.2001.4633. [DOI] [PubMed] [Google Scholar]
- 2.Cowtan K. Modified phased translation functions and their application to molecular fragment location. Acta Cryst D. 1998;54:750–756. doi: 10.1107/s0907444997016247. [DOI] [PubMed] [Google Scholar]
- 3.Abeysinghe S, Ju T, Baker ML, Chiu W. Shape modeling and matching in identifying 3D protein structures. Computer-Aided Design. 2008;40:708–720. [Google Scholar]
- 4.Topf M, Baker ML, Marti-Renoma MA, Chiu W, Sali A. Refinement of Protein Structures by Iterative Comparative Modeling and CryoEM Density Fitting. J Mol Bio. 2006;357:1655–1668. doi: 10.1016/j.jmb.2006.01.062. [DOI] [PubMed] [Google Scholar]
- 5.Trabuco LG, Villa E, Mitra K, Frank J, Schulten K. Flexible fitting of atomic structures into electron microscopy maps using molecular dynamics. Structure. 2008;16:673–683. doi: 10.1016/j.str.2008.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Orzechowski M, Tama F. Flexible fitting of high-resolution X-ray structures into cryoelectron microscopy maps using biased molecular dynamics simulations. Biophys J. 2008;95:5692–5705. doi: 10.1529/biophysj.108.139451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Schröder G, Brunger A, Levitt M. Combining efficient conformational sampling with a deformable elastic network model facilitates structure refinement at low resolution. Structure. 2007;15:1630–1641. doi: 10.1016/j.str.2007.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tama F, Miyashita O, Brooks CL., III Flexible multi-scale fitting of atomic structures into low-resolution electron density maps with elastic network normal mode analysis. J Mol Biol. 2004;337:985–999. doi: 10.1016/j.jmb.2004.01.048. [DOI] [PubMed] [Google Scholar]
- 9.Jolley CC, Wells SA, Fromme P, Thorpe MF. Fitting low-resolution cryo-EM maps of proteins using constrained geometric simulations. Biophys J. 2008;94:1613–21. doi: 10.1529/biophysj.107.115949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Velazquez-Muriel JA, Valle M, Santamaría-Pang A, Kakadiaris IA, Carazo JM. Flexible fitting in 3D-EM guided by the structural variability of protein superfamilies. Structure. 2006;14:1115–1126. doi: 10.1016/j.str.2006.05.013. [DOI] [PubMed] [Google Scholar]
- 11.Topf M, Lasker K, Webb B, Wolfson H, Chiu W, Sali A. Protein structure fitting and refinement guided by cryo-EM density. Structure. 2008;16:295–307. doi: 10.1016/j.str.2007.11.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bradley P, Misura KM, Baker D. Toward high-resolution de novo structure prediction for small proteins. Science. 2005;309:1868–1871. doi: 10.1126/science.1113801. [DOI] [PubMed] [Google Scholar]
- 13.Rohl CA. Protein structure estimation using Rosetta. NMR Meth Enz. 2005;394:244–260. doi: 10.1016/S0076-6879(05)94009-3. [DOI] [PubMed] [Google Scholar]
- 14.John B, Sali A. Comparative protein structure modeling by iterative alignment, model building and model assessment. Nucl Acids Res. 2003;31:3982–3992. doi: 10.1093/nar/gkg460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zhou H, Baker ML, Jiang W, Dougherty M, Jakana J, Dong G, Lu G, Chiu W. Electron cryomicroscopy and bioinformatics suggest protein fold models for rice dwarf virus. Nat Struct Biol. 2001;8:868–873. doi: 10.1038/nsb1001-868. [DOI] [PubMed] [Google Scholar]
- 16.Nakagawa A, Miyazaki N, Taka J, Naitow H, Ogawa A, Fujimoto Z, Mizuno H, Higashi T, Watanabe Y, Omura T, Cheng RH, Tsukihara T. The atomic structure of rice dwarf virus reveals the self-assembly mechanism of component proteins. Structure. 2003;11:1227–1238. doi: 10.1016/j.str.2003.08.012. [DOI] [PubMed] [Google Scholar]
- 17.McGuffin LJ, Jones DT. Improvement of the GenTHREADER method for genomic fold recognition. Bioinformatics. 2003;19:874–881. doi: 10.1093/bioinformatics/btg097. [DOI] [PubMed] [Google Scholar]
- 18.Grimes J, Basak AK, Roy P, Stuart D. The crystal structure of bluetongue virus VP7. Nature. 1995;373:167–170. doi: 10.1038/373167a0. [DOI] [PubMed] [Google Scholar]
- 19.Ludtke SJ, Baker ML, Chen DH, Song JL, Chuang DT, Chiu W. De novo backbone trace of GroEL from single particle electron cryomicroscopy. Structure. 2008;16:441–448. doi: 10.1016/j.str.2008.02.007. [DOI] [PubMed] [Google Scholar]
- 20.Baker ML, Ju T, Chiu W. Identification of secondary structure elements in intermediate-resolution density maps. Structure. 2007;15:7–19. doi: 10.1016/j.str.2006.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bryson K, McGuffin LJ, Marsden RL, Ward JJ, Sodhi JS, Jones DT. Protein structure prediction servers at University College London. Nucl Acids Res. 2005;33:W36–38. doi: 10.1093/nar/gki410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Abe H, Braun W, Noguti T, Gō N. Rapid calculation of first and second derivatives of conformational energy with respect to dihedral angles for proteins general recurrent equations. Comp & Chem. 1984;8:239–247. [Google Scholar]
- 23.Bradley P, Baker D. Improved beta-protein structure prediction by multilevel optimization of nonlocal strand pairings and local backbone conformation. Proteins. 2006;65:922–929. doi: 10.1002/prot.21133. [DOI] [PubMed] [Google Scholar]
- 24.Canutescu A, Dunbrack R., Jr Cyclic coordinate descent: A robotics algorithm for protein loop closure. Protein Sci. 2003;12:963–972. doi: 10.1110/ps.0242703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kuhlman B, Baker D. Native protein sequences are close to optimal for their structures. Proc Natl Acad Sci. 2000;97:10383–10388. doi: 10.1073/pnas.97.19.10383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Dunbrack R, Jr, Karplus M. Backbone-dependent rotamer library for proteins: Application to side-chain prediction. J Mol Biol. 1993;230:543–574. doi: 10.1006/jmbi.1993.1170. [DOI] [PubMed] [Google Scholar]
- 27.Wu GA, Coutsias EA, Dill K. Iterative assembly of helical proteins by optimal hydrophobic packing. Structure. 2008;16:1257–1266. doi: 10.1016/j.str.2008.04.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.