On the Efficiency of Score Tests for Homogeneity in Two-Component Parametric Models for Discrete Data

Summary

In many applications of two-component mixture models for discrete data such as zero-inflated models, it is often of interest to conduct inferences for the mixing weights. Score tests derived from the marginal model that allows for negative mixing weights have been particularly useful for this purpose. But the existing testing procedures often rely on restrictive assumptions such as the constancy of the mixing weights and typically ignore the structural constraints of the marginal model. In this article, we develop a score test of homogeneity that overcomes the limitations of existing procedures. The technique is based on a decomposition of the mixing weights into terms that have an obvious statistical interpretation. We exploit this decomposition to lay the foundation of the test. Simulation results show that the proposed covariate-adjusted test statistic can greatly improve the efficiency over test statistics based on constant mixing weights. A real-life example in dental caries research is used to illustrate the methodology.

1. Introduction

In discrete data, when an observation exhibits an excessive frequency, it is a common practice to use two-component mixture models that combine an atom distribution with a proper distribution. Well known members of this class of models include the so-called zero-inflated models for independent count data first studied by Mullahy (1986), Farewell and Sprott (1988), and Lambert (1992) and their extensions to correlated count data by Hall (2000). Zero-inflated models have been extensively studied in statistical research and applied to data from various disciplines including agriculture, econometrics, medicine, engineering, sociology, and behavioral sciences. Ridout, Demetrio, and Hinde (1998) provide an extensive review of this literature.

Two-component mixture models provide an interesting parametric framework to accommodate heterogeneity in a population. A prevailing concern, however, is whether the inherent heterogeneity is consistent with observed data. Many authors have examined this important issue using two-sided score tests. In a Biometrics paper, van den Broek (1995, pp. 738–748) has developed a two-sidsed score test for homogeneity in zero-inflated models for count data. Others have extended this test to situations where the nondegenerate distribution is a member of the exponential family (Deng and Paul, 2000) and to clustered data (Xiang et al., 2006). The original test by van den Broek (1995) and its extensions were constructed under alternatives to homogeneity that allow for negative mixing weights. Specifically, they were derived under the marginal mixture model that ignores its hierarchical representation. Although this approach uses score functions that are well defined at the null value, it is often unclear how constraints generated from this marginal model are accommodated under the alternative. Most importantly, existing testing procedures typically do not fully exploit the general structure of the mixing weights. A common restriction is that constant mixing weights are often assumed under heterogeneity. This is an important limitation as covariate-dependent mixing weights are typical in real applications of these models. From a technical perspective, tests that rely on constant mixing weights may lack power to detect heterogeneity if both inflation and deflation are present in the population.

The problem of inflation and deflation, typically at zero, arises quite naturally in various applications. A good example is provided by a very unique survey designed to collect oral health information on low-income African American children (0–5 years) and their main caregivers (14+ years), living in the city of Detroit (see Tellez et al., 2006). This article aimed at promoting oral health and reducing its disparities within this community through the understanding of determinants of dental caries. Dental caries were measured using scores which represent the cumulative severity of the disease for each surveyed participants. These scores have well-documented shortcomings regarding their ability to describe dental caries experiences, but they continue to be instrumental in evaluating and comparing the risks of dental caries across population groups (Lewsey and Thomson, 2004). Most importantly, they remain popular in dental caries research for their ability to conduct historical comparisons in population-based studies. Homogeneous models when applied to these data typically reveal an inflation of zeros (few children with no dental caries predicted than observed) for younger children and deflation of zeros (more children with no dental caries predicted than observed) for older children. For these data, an analysis based on constant mixing weights under the alternative may fail to detect heterogeneity in this population.

Health services research is another area of applications where inflation and deflation are often encountered. For example, Hur et al. (2002) presented a study on patients undergoing a partial colectomy operation from 123 Veterans Affairs (VA) medical centers in the National Surgical Quality Improvement Program. The primary goal of this program was to improve surgical care for veteran patients by developing performance measures for surgery in the VA system. One of the primary study outcomes was the number of postoperative complications. It was reported that patients that are relatively healthier before the surgical operation, as measured by the classification from the American Society of Anesthesiologists, will likely have no complications, although their sicker counterparts will be associated with higher numbers of complications. For such data, a homogenous model will exhibit an inflation at zero for relatively healthier patients and a deflation at zero for the sickest patients.

The examples above then draw into question the efficiency of testing procedures which assume constancy of the mixing weights. In this article, we suggest an extension of the score test of homogeneity to covariates. A recent illustration of this approach for zero-inflated models is given by Jansakul and Hinde (2009). These authors related the mixing weights to covariates using an identity link function. A limitation, however, is that the identity link function is seldom used in practice for this class of models. Moreover, the structure of the marginal model is not properly integrated into the testing procedure. As a solution, we formulate and develop a score test of homogeneity based on an intuitive approach that accommodates the features of the marginal model. Specifically, we embed the structural constraints of the marginal model into the procedure. The technique is based on decomposing the mixing weights into terms that have an obvious statistical interpretation. One appealing feature of this decomposition is that it naturally incorporates covariates into the mixing weights. We exploit this decomposition to lay the foundation of the test. We show that this is a natural strategy to adopt when testing is carried out under the marginal model that ignores its hierarchical representation. The proposed test in its current formulation can be naturally used to study heterogeneity at any point of the population and for any nondegenerate parametric distributions that are not necessarily members of the exponential family.

The remainder of this article is organized as follows. In Section 2, we specify the homogeneity hypothesis using composite link functions and develop a score test that accommodates the features of the marginal model. In Section 3, the empirical performance of the proposed test is studied and its real-life applications are illustrated using dental caries counts in young children. Some remaining issues are discussed in Section 4. Additional technical details are contained in a Web supplementary materials file.

2. The Method

2.1 Hypothesis Formulation and Reparameterization

We consider a sample of n independent realizations ${\{y_i\}}_{i=1}^n$, of random variables ${\{Y_i\}}_{i=1}^n$ each drawn from a mixture of an atom distribution at a known point y^* and an unknown nondegenerate discrete distribution G governed by a finite dimensional parameter vector θ,

$$Pr(Y_i=y_i)=\{\begin{array}{ll}{\omega }_i+(1-{\omega }_i)g_i(y^{\ast })\hfill & \text{if}{y}_i=y^{\ast }\hfill \\ (1-{\omega }_i)g_i(y_i)\hfill & \text{if}{y}_i\ne y^{\ast }.\hfill \end{array}$$ (1)

Here ω_i is an unknown mixing weight and g_i (.) is a probability mass associated with G. The mixture model in equation(1) allows for two types of representations, depending on the support of ω_i. Under its hierarchical representation, the mixing weight is a probability mass, requiring the distributional constraints 0 ≤ ω_i ≤ 1, i = 1,…, n. Under the marginal representation, however, the only distributional constraints are that 0 ≤ Pr(Y_i = y_i) ≤ 1, for all i = 1, …, n, under the mixture model equation (1), which result in constraints on mixing weights,

$$-g_i(y^{\ast })/(1-g_i(y^{\ast }))\le {\omega }_i\le 1,i=1,\dots ,n.$$ (2)

The marginal model can then be used to accommodate both inflation (positive ω_i) and deflation (negative ω_i) at y^*, a property not shared by its hierarchical counterpart. The marginal model, however, does not allow any hierarchical interpretation of the mixture model when the mixing weight is negative. For further discussions on the interpretation of these models when y^* = 0, see Heilbron (1994).

Suppose we are interested in evaluating the hypothesis of zero mixing weights. Under the marginal model that allows for negative mixing weights, one is typically interested in the two-sided hypotheses,

$${\mathrm{H}}_0:{\omega }_i=0,\text{for}\text{all}i\text{vs}.{\mathrm{H}}_1:{\omega }_i\ne 0,\text{for}\text{some}i,$$

, where ω_i satisfies constraints in equation (2). To test these hypotheses, we consider a suitable transformation of ω_i that incorporates the constraints in equation (2) into the testing scheme. A natural transformation in light of these constraints is given by,

$${\omega }_i=\frac{{\pi }_i-g_i(y^{\ast })}{1-g_i(y^{\ast })},0\le {\pi }_i\le 1.$$ (3)

Evidently, the lower and upper bounds of ω_i in equation (2) are attained at points 0 and 1 of π_i, respectively. The quantity π_i has an obvious statistical interpretation. To see this, consider a binary version of Y_i denoted δ(Y_i) taking value 1 if Y_i = y^* and 0 otherwise. The term π_i is simply the first moment E{δ(Y_i)} = Pr(Y_i = y^*) under the marginal mixture model equation (1), which can be estimated very well if many independent copies δ(y_i) of δ(Y_i) are available. The transformation as specified in equation (3) then arises from equating the probability mass at y^* as predicted by the mixture model in equation (1) to the first moment of δ(Y_i). That is, E{δ(Y_i)} = ω_i + (1 − ω_i)g_i (y^*), where g_i (y^*) is the probability Pr(Y_i = y^*) under the distribution G.

Based on the parameterization equation (3), we formally state the hypotheses as,

$${\mathrm{H}}_0:{\pi }_i=g_i(y^{\ast }),\text{for}\text{all}i\text{vs}.{\mathrm{H}}_1:{\pi }_i\ne g_i(y^{\ast }),\text{for}\text{some}i.$$

We exploit this reformulation to lay the foundation of the test. We consider a suitable parameterization of π_i and g_i (y^*) that reduces the homogeneity hypothesis above to a problem involving a small number of parameters. For this, we assume that μ_i the mean of Y_i under the nondegenerate parametric distribution G is finite. We express the probability mass at y^* with respect to the distribution G as a function of μ_i, that is g_i (y^*) = g̃(μ_i), where g̃(.) is a bounded function between 0 and 1, which depends on θ and y^*. If the data can be arranged to form strata with a finite, possibly small, number of terms π_i and μ_i, the homogeneity hypothesis naturally reduces to a problem involving a small number of parameters. This stratified approach has its limitations when the number of strata or more generally when the number of covariates is increasing, however. Alternatively, regression techniques relating μ_i and π_i to some observed covariates can be used to address the curse of dimensionality. For this, consider two-column vector covariates x_i and z_i, of dimensions p and q, respectively, that are also observed alongside the responses y_i, i = 1, 2, …, n. We relate μ_i to covariates x_i as follows, $h({\mu }_i)=x_i^{\prime }\beta$, where β is a parameter vector of dimension p × 1 and a subset of θ and h(.) is a monotone, differentiable, and invertible function. Likewise, we relate π_i to covariates z_i as follows, ${\pi }_i=f(z_i^{\prime }\gamma )$, where γ is a parameter vector of dimension q × 1 and f (.) is a differentiable function. We find a suitable function f (.) that translates the homogeneity hypothesis into an equality involving only parameters β and γ. This is summarized in the proposition below.

Proposition

Assuming the model $h({\mu }_i)=x_i^{\prime }\beta$ under the nondegenerate distribution G, a suitable choice for f(.) is given by $f(z_i^{\prime }\gamma )=\stackrel{\sim }{g}\circ h^{-1}(z_i^{\prime }\gamma )$, where ∘ represents the composite function operator, and the homogeneity (null) hypothesis can be reformulated as,

$${\mathrm{H}}_0:\stackrel{\sim }{g}\circ h^{-1}(z_i^{\prime }\gamma )=\stackrel{\sim }{g}\circ h^{-1}(x_i^{\prime }\beta ),\text{for}\text{all}i,$$ (4)

which further reduces to a linear contrast involving only parameters β and γ.

The proof of this proposition is provided in the Web supplementary file. The function f (.) falls in the class of composite link functions which are not always invertible (Thompson and Baker, 1981). Below, we give an explicit expression of this function for commonly used nondegenerate parametric distributions G and link functions h(.). Specific results when y^* = 0 are given in Table 1.

Table 1.

Natural parameterizations relating π_i to linear predictors $z_i^{\prime }\gamma$ for commonly used two-component models and link functions relating μ_i to linear predictors $x_i^{\prime }\beta$ when y^* = 0

Nondegenerate distribution G	Link function h(·) relating μi to $x_i^{\prime }\beta$	Probability gi(0) = g̃(μi)	Parameterization relating πi to $z_i^{\prime }\gamma$
Poisson with mean μi	log{μi}	$exp\{-exp\{x_i^{\prime }\beta \}\}$	$exp\{-exp\{z_i^{\prime }\gamma \}\}$
Binomial with success probability μi and mi trials	logit{μi}	${\{1+exp\{x_i^{\prime }\beta \}\}}^{-m_i}$	${\{1+exp\{z_i^{\prime }\gamma \}\}}^{-m_i}$
	Φ−1(μi)	${\{1+\mathrm{\Phi }(x_i^{\prime }\beta )\}}^{m_i}$	${\{1+\mathrm{\Phi }(z_i^{\prime }\gamma )\}}^{m_i}$
	log{−log{μi}}	${\{1-exp\{-exp\{x_i^{\prime }\beta \}\}\}}^{m_i}$	${\{1-exp\{-exp\{z_i^{\prime }\gamma \}\}\}}^{m_i}$
Negative binomial with mean μi and over dispersion parameter κ	log{μi}	${\{1+\kappa exp\{x_i^{\prime }\beta \}\}}^{-1/\kappa }$	${\{1+\kappa exp\{z_i^{\prime }\gamma \}\}}^{-1/\kappa }$

Note: θ = β for the Poisson and the binomial processes;

θ = {β, κ} for the negative binomial process.

1. The two-component model when G is a Poisson distribution with mean μ_i. Here θ = β and g̃(μ_i) = exp{−μ_i}{μ_i}^y*Γ⁻¹(y^* + 1). Assuming the log link function $log\{{\mu }_i\}=x_i^{\prime }\beta$, a natural parameterization relating π_i to $z_i^{\prime }\gamma$ is, ${\pi }_i=exp\{-exp\{z_i^{\prime }\}\}{\{exp\{z_i^{\prime }\gamma \}\}}^{y^{\ast }}{\mathrm{\Gamma }}^{-1}(y^{\ast }+1)$.

2. The two-component model when G is a binomial distribution with success probability μ_i and planned number of trials m_i. Here θ = β and $\stackrel{\sim }{g}({\mu }_i)=m_i{\mathrm{C}}_{y^{\ast }}{\mu }_i^{y^{\ast }}{\{1-{\mu }_i\}}^{m_i-y^{\ast }}$ with $m_i{\mathrm{C}}_{y^{\ast }}=\frac{\mathrm{\Gamma }(m_i+1)}{\mathrm{\Gamma }(y^{\ast }+1)\mathrm{\Gamma }(m_i-y^{\ast }+1)}$. Assuming the logit link function $log\{{\mu }_i/(1-{\mu }_i)\}=x_i^{\prime }\beta$, a natural parameterization for π_i is then, ${\pi }_i=m_i{\mathrm{C}}_{y^{\ast }}{\{1+exp\{-z_i^{\prime }\gamma \}\}}^{-y^{\ast }}{\{1+exp\{z_i^{\prime }\gamma \}\}}^{y^{\ast }-m_i}$.

3. The two-component model when G is a negative binomial distribution with mean μ_i and overdispersion parameter κ. Here θ = {β, κ} and $\stackrel{\sim }{g}({\mu }_i)=\frac{\mathrm{\Gamma }(y^{\ast }+{\kappa }^{-1})}{\mathrm{\Gamma }({\kappa }^{-1})\mathrm{\Gamma }(y^{\ast }+1)}{\{1+\kappa {\mu }_i\}}^{-1/\kappa }{\{1+{\kappa }^{-1}{\mu }_i^{-1}\}}^{-y^{\ast }}$. For the log link function $log\{{\mu }_i\}=x_i^{\prime }\beta$, a natural parameterization for π_i is then, ${\pi }_i=\frac{\mathrm{\Gamma }(y^{\ast }+{\kappa }^{-1})}{\mathrm{\Gamma }({\kappa }^{-1})\mathrm{\Gamma }(y^{\ast }+1)}{\{1+\kappa exp\{z_i^{\prime }\gamma \}\}}^{-1/\kappa }{\{1+{\kappa }^{-1}exp\{-z_i^{\prime }\gamma \}\}}^{-y^{\ast }}$.

2.2 A Covariate-Adjusted Score Test for Homogeneity

Without any loss of generality, we will develop the test for the case where x_i = z_i, although our method generalizes quite naturally for any x_i and z_i Under this assumption, our homogeneity hypothesis then becomes, H₀ : β = γ. Let C be a selector matrix such that Cθ = β, the homogeneity hypothesis is then equivalent to, H₀ : Cθ = γ. Under the alternative model, the log-likelihood function, given observations ${\{y_i\}}_{i1}^n$, as a function of θ and γ is given by,

$$\ell (\theta ,\gamma )=\sum _{i=1}^n\left(\delta [y_i]log[{\pi }_i]+[1-\delta \{y_i\}]log\left[\frac{\{1-{\pi }_i\}{g}_i\{y_i\}}{1-g_i\{y^{\ast }\}}\right]\right).$$

We assume the following change of variables, α = Cθ − γ, with α = 0 under the null hypothesis. We denote by u(θ, α) the score function ∂ℓ(θ, Cθ − α)/∂(θ, α). To construct the score test statistic and derive its limiting null distribution, we set the following conditions for the arguments in the sequel to be valid.

• C1The support set of (θ, α) is compact.
• C2Assume a nonsingular matrix (θ, α) such that −n⁻¹∂u(θ, α)/∂(θ, α) = (θ, α) + o_p (1).
• C3For all a > 0, sup_||ζ||≤a {n^−1/2[u((θ, α) + n^−1/2ζ) −u(θ, α)] + (θ, α)ζ} = o_p (1), where o_p (1) represents the convergence in probability as n → ∞.

Under Conditions C1–C3, standard asymptotic results give, n^−1/2 u(θ, α) →_d 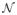(0, 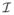(θ, α)), where →_d represents the convergence in distribution as n → ∞ (see Cox and Hinkley, 1974, pp. 311–343, for this large-sample size result). Assume the following decomposition, $u(\theta ,\alpha )={(u_{\theta }^{\prime }(\theta ,\alpha ),u_{\alpha }^{\prime }(\theta ,\alpha ))}^{\prime }$ where the respective entries are the first-order derivatives of the log-likelihood function with respect to θ and α. Let 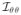(θ, α), 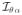(θ, α), and 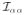(θ, α) be the corresponding blocks in 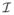(θ, α). The main building block of the test statistic is given by,

$$u_{\alpha }(\theta ,\alpha )=\sum _{i=1}^n\left\{\frac{\delta (y_i)-{\pi }_i}{{\pi }_i(1-{\pi }_i)}\frac{\partial {\pi }_i}{\partial \alpha }\right\}.$$

Note that π_i in this expression depends on both θ and α because of the change of variables. The other building block 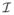(θ, α) is in general tedious to compute. In the Web supplementary file, we give details of these calculations when the component G of the mixture model is a Poisson or a binomial distribution (two well known exponential family members) and assuming y^* = 0.

Let b(θ) define the score function with respect to θ under the null distribution G. We assume the existence of a root-n consistent estimator θ̂ of θ^*, the true value of θ under the null distribution G, such that $n^{1/2}(\widehat{\theta }-{\theta }^{\ast })=n^{-1/2}{\mathcal{I}}_{\theta \theta }^{-1}({\theta }^{\ast },0)b({\theta }^{\ast })+o_p(1)$. The core of the score statistic to evaluate the hypothesis α = 0 is given by û_α = u_α(θ̂, 0). In the Web supplementary file, we give an explicit form for this quantity when the component G is a Poisson or a binomial distribution.

The asymptotic distribution of û_α can be derived by applying a standard Taylor series expansion coupled with the law of large numbers,

$$n^{-1/2}{\widehat{u}}_{\alpha }=n^{-1/2}\sum _{i=1}^n\{u_{i,\alpha }({\theta }^{\ast },0)-{\mathcal{I}}_{\theta \alpha }^{\prime }({\theta }^{\ast },0){\mathcal{I}}_{\theta \theta }^{-1}({\theta }^{\ast },0)b_i({\theta }^{\ast })\}+o_p(1),$$

where u_{i, α}(θ^*, 0) and b_i(θ^*) are, respectively, the random contributions of subject i to the score functions u_α(θ^*, 0) and b(θ^*). The right-hand side of this equation consists of sums of independent random vectors $v_i({\theta }^{\ast })=u_{i,\alpha }({\theta }^{\ast },0)-{\mathcal{I}}_{\theta \alpha }^{\prime }({\theta }^{\ast },0){\mathcal{I}}_{\theta \theta }^{-1}({\theta }^{\ast },0)b_i({\theta }^{\ast })$, i = 1, …, n, for which the central limit theorem applies. That is, n^−1/2û_α →_d 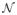(0, Λ(θ^*)), where $\mathrm{\Lambda }({\theta }^{\ast })={lim}_{n\to \infty }{n}^{-1}{\sum }_{i=1}^{n}E(v_i^{\otimes 2}({\theta }^{\ast }))$, with $v_i^{\otimes 2}({\theta }^{\ast })=v_i({\theta }^{\ast })v_i^{\prime }({\theta }^{\ast })$. A straightforward calculation gives $\mathrm{\Lambda }({\theta }^{\ast })={\mathcal{I}}_{\alpha \alpha }({\theta }^{\ast },0)-{\mathcal{I}}_{\theta \alpha }^{\prime }({\theta }^{\ast },0){\mathcal{I}}_{\theta \theta }^{-1}({\theta }^{\ast },0){\mathcal{I}}_{\theta \alpha }({\theta }^{\ast },0)$ for which a consistent estimator is obtained by replacing θ^* by its estimator θ̂. We then construct a score test statistic as,

$$s_n=n^{-1}{\widehat{u}}_{\alpha }^{\prime }{\mathrm{\Lambda }}^{-1}(\widehat{\theta }){\widehat{u}}_{\alpha }{\to }_d{\chi }_r^2\text{under}{H}_0\text{as}n\to \infty ,$$

where r = p = q. The null hypothesis is rejected for large values of s_n.

3. Numerical Studies

3.1 Simulation

The two representations of the mixture model in equation (1) have some technical implications on the data generating mechanism. When ω_i is positive, the mixture model maintains its hierarchical representation and data can then be generated using the usual two-stage process. For negative ω_i, however, the mixture model loses its hierarchical representation and the data can not be generated from the two-stage process. Instead, data are generated directly from the marginal distribution in equation (1) by inverting the cumulative distribution function (CDF) of a uniform distribution on the interval (0, 1).

We conducted a simulation study to evaluate the empirical performances of the proposed covariate-adjusted score test in small to moderate sample sizes. We compared these performances to those of the tests proposed by van den Broek (1995), and Jansakul and Hinde (2009). Throughout our simulations, we generated data from a two-component model with true mixing weights ${\omega }_i^{\ast }$, i = 1, …, n, at y^* = 0, and a nondegenerate Poisson distribution with a simple mean ${\mu }_i^{\ast }=exp\{{\beta }_0^{\ast }-1.45x_i\}$, where the intercept ${\beta }_0^{\ast }$ takes values in the set {−0.75, 0, 0.75} and x_i is a covariate generated from a uniform distribution on the interval (0, 1). Throughout our simulations, we performed the proposed covariate-adjusted score test assuming the working mixing weight model ω_i = {π_i − exp{−μ_i}}{1 − exp{−μ_i}}⁻¹ under the alternative, where π_i = exp{−exp{γ₀ + γ₁x_i}} and μ_i = exp{β₀ + β₁x_i}. The test of van den Broek (1995) was performed assuming ω_i = γ₀, and that of Jansakul and Hinde (2009), assuming ω_i = γ₀ + γ₁x_i. With these parameterizations, the null hypotheses to be evaluated were then given by: H₀ : γ₀ = β₀, γ₁ = β₁, for our formulation; H₀ : γ₀ = 0, for van den Broek’s test; and H₀ : γ₀ = 0, γ₁ = 0, for Jansakul and Hinde’s test. The maximum likelihood estimate β̂ of the true value of β = (β₀, β₁)′ under the null was obtained from a homogeneous Poisson model with mean μ_i = exp{β₀ + β₁x_i}. Finally, all simulations were replicated 1,000 times and for sample sizes 50, 100, and 200.

To investigate the empirical type I error rates of the tests, we generated data from the homogeneous Poisson model. The empirical type I error rates at 5% nominal level are reported in Table 2. All considered score tests have well controlled type I error rates even for a sample size as small as 50 when ${\beta }_0^{\ast }$ is large. However, for smaller values of ${\beta }_0^{\ast }$ (large values of ${-\beta }_0^{\ast }$) these tests tend to be slightly conservative. In other words, when the true mean ${\mu }_i^{\ast }$ nears zero they tend to reject the null hypothesis less often than anticipated and this conservativeness does not diminish with increasing sample sizes.

Table 2.

Empirical size of score test statistics when the null model is a nondegenerate Poisson model with mean ${\mu }_i^{\ast }=exp\{{\beta }_0^{\ast }-1.45x_i\}$, x_i ~ Uniform(0, 1), at 5% significance level

${\beta }_0^{\ast }$	n = 50			n = 100			n = 200
	−0.75	0	0.75	−0.75	0	0.75	−0.75	0	0.75
ω* = 0
vdB test	0.031	0.053	0.051	0.048	0.063	0.059	0.042	0.050	0.066
J&H test	0.033	0.051	0.054	0.038	0.044	0.061	0.036	0.049	0.052
Prop. c-a test	0.036	0.048	0.048	0.040	0.046	0.057	0.033	0.045	0.060

Note: vdB, van den Broek, test with df = 1; J&H, Jansakul and Hinde, test with df = 2; Prop. c-a, Proposed covariate-adjusted, test with df = 2.

We investigated the empirical power of the tests to detect various forms of heterogeneity in the population. First, we generated data from a two-component mixture model with a constant mixing weight fixed at 0.25. For this constant mixing weight model, increasing sample sizes and separation of mixture components improve the power of detecting the alternatives under consideration for all tests considered (see Table 3). The test proposed by van den Broek (1995) appears to be more powerful than the two covariate-adjusted tests, especially when the mixture components are well separated. This is expected as data were generated from a positive and constant mixing weight model, for which the associated marginal model maintains its hierarchical representation. The loss of power was fairly minor for covariate-adjusted tests, however.

Table 3.

Empirical power of score test statistics to detect various forms ${\omega }_i^{\ast }$ of heterogeneity coupled with a nondegenerate Poisson model with mean ${\mu }_i^{\ast }=exp\{{\beta }_0^{\ast }-1.45x_i\}$, x_i ~ Uniform(0, 1), at 5% significance level

${\beta }_0^{\ast }$	n = 50			n = 100			n = 200
	−0.75	0	0.75	−0.75	0	0.75	−0.75	0	0.75
${\omega }_i^{\ast }=0.25$
vdB test	0.060	0.096	0.313	0.086	0.147	0.578	0.122	0.294	0.895
J&H test	0.069	0.087	0.249	0.094	0.118	0.481	0.123	0.238	0.851
Prop. c-a test	0.071	0.086	0.247	0.094	0.122	0.478	0.124	0.241	0.849
${\omega }_i^{\ast }=0.45+0.15x_i$
vdB test	0.100	0.221	0.698	0.156	0.388	0.960	0.219	0.684	1.000
J&H test	0.102	0.190	0.623	0.178	0.362	0.927	0.237	0.608	0.999
Prop. c-a test	0.105	0.191	0.617	0.179	0.363	0.933	0.235	0.603	0.999
${\omega }_i^{\ast }=\frac{exp\{-1.2+1.1x_i\}}{1+exp\{-1.2+1.1x_i\}}$
vdB test	0.059	0.109	0.373	0.090	0.213	0.704	0.124	0.343	0.953
J&H test	0.080	0.112	0.318	0.103	0.192	0.662	0.136	0.297	0.929
Prop. c-a test	0.087	0.112	0.317	0.105	0.194	0.655	0.135	0.292	0.924
${\omega }_i^{\ast }=\frac{{\pi }_i^{\ast }-exp\{-{\mu }_i^{\ast }\}}{1-exp\{-{\mu }_i^{\ast }\}},{\pi }_i^{\ast }=exp\{-exp\{1.3-2.4x_i\}\}$
vdB test	0.166	0.293	0.257	0.295	0.395	0.413	0.392	0.612	0.590
J&H test	0.236	0.454	0.386	0.383	0.628	0.544	0.506	0.847	0.731
Prop. c-a test	0.710	0.845	0.957	0.944	0.981	0.997	0.997	1.000	1.000
${\omega }_i^{\ast }=\frac{exp\{-15+30x_i\}}{1+exp\{-15+30x_i\}}$
vdB test	0.026	0.067	0.095	0.039	0.079	0.131	0.051	0.090	0.189
J&H test	0.054	0.107	0.166	0.082	0.141	0.271	0.090	0.180	0.448
Prop. c-a test	0.068	0.151	0.430	0.122	0.238	0.758	0.131	0.431	0.967
${\omega }_i^{\ast }=\mathrm{\Phi }(-15+30x_i)$
vdB test	0.042	0.070	0.099	0.045	0.069	0.153	0.057	0.083	0.221
J&H test	0.051	0.097	0.160	0.075	0.114	0.278	0.104	0.167	0.465
Prop. c-a test	0.062	0.142	0.485	0.095	0.222	0.739	0.142	0.409	0.962

Note: vdB, van den Broek, test with df = 1; J&H, Jansakul & Hinde, test with df = 2; Prop. c-a, Proposed covariate-adjusted, test with df = 2.

Second, we allowed the true mixing weight to depend on covariates using the linear, the logistic, and the proposed transformation (mixing weight models in rows 2, 3, and 4 of Table 3). Overall, the power of the three score tests improves with the sample size, regardless of the true mixing weight. When the true mixing weight is a linear or a logistic function of the covariates, all considered tests appear to have comparable powers. But the power deteriorates as the mean of the non-degenerate Poisson model nears zero. This is not surprising as the true mixing weights in these schemes are bounded between 0 and 1, a condition for the marginal mixture model to maintain its hierarchical representation. When the true mixing weights allow for negative values (mixing weight model in row 4 of Table 3), the proposed score test statistic appears to be more powerful than the other tests. The deterioration of power appears to be greater for the test proposed by van den Broek (1995). This is expected as the constant mixing weight test averages the mixing weights over the space of covariates, which may greatly affect power if both deflation and inflation are present in the population.

From the previous simulation results, one referee was concerned that the proposed covariate adjusted test outperforms the other competitors only when the simulated data are generated from a model that allows for negative mixing weights. Following this referee’s suggestion, we conducted further simulation studies in which data were generated from a two-component mixture model with positive covariate dependent weights ${\omega }_i^{\ast }={\{1+exp\{15-30x_i\}\}}^{-1}$ and ${\omega }_i^{\ast }=\mathrm{\Phi }(-15+30x_i)$, i = 1, …, n, where Φ(·) is the CDF of a standard normal variable. For these simulation schemes, the proposed test outperforms the other two competitors, especially when the two mixture components are well separated (see the last two simulation schemes in Table 3). Here the test proposed by Jansakul and Hinde (2009) adjusts for the covariate x_i in modeling the mixing weight ω_i, but fails to provide an adequate functional relationship between ω_i and x_i. In general, we expect this test to perform well when linearity holds and poorly otherwise. Following another referee’s suggestion, another simulation study was conducted to compare the three tests when covariates x_i and z_i are not equal. Findings from this article (results where x_i is a subset of z_i are shown in Table 5, Web supplementary file) were similar to those that assume x_i = z_i.

In sum, incorporating covariates in the score tests for homogeneity can greatly improve efficiency. But this efficiency gain highly depends on the prespecified working model of the mixing weight and the behavior of the tests under model mis-specification. When the true mixing weight does not depend on covariates, our test may not be as efficient as the constant mixing weight test. However, given that the true model is usually unknown to the analyst, a general approach that assumes covariate dependent mixing weights appears to be the most conservative data analytic strategy.

3.2 Dental Caries Data

To illustrate our methodology, we considered children dental caries data from the Detroit study. We focused on scores representing the number of tooth surfaces that show signs of clinically detectable enamel lesions comprising both noncavitated and cavitated lesions. Using this stringent dental caries definition, three different outcomes were derived. These outcomes represent the number of decayed surfaces (DS), the number of decayed and filled surfaces (DFS), and the number of decayed, missing, and filled surfaces (DMFS). Although this survey is longitudinal in nature, our numerical computations are based on cross-sectional data of 897 children surveyed in the first wave of examinations conducted between 2002 and 2003. Covariates considered include Age (the child’s age in years), SI (the child’s sugar intake), and their multiplicative interaction Age * SI. A more detailed description of the study can be found elsewhere (see, for example, Tellez et al., 2006).

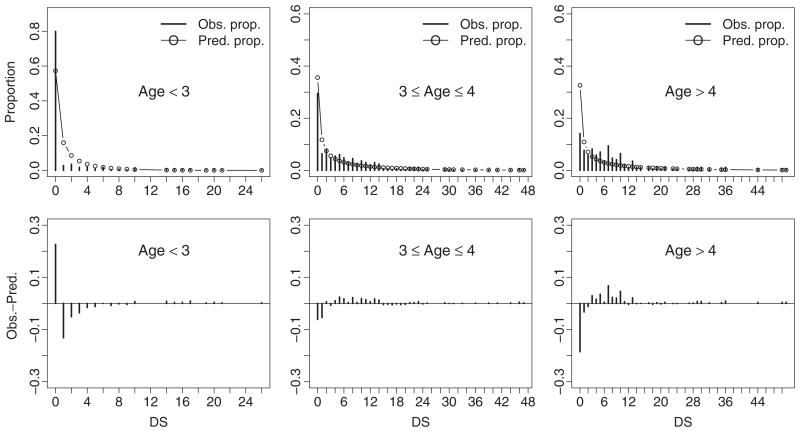
It is a common practice to use zero-inflated models to characterize dental caries scores (see, for example, Böhning et al., 1999). In addition, it is well known that dental caries data often exhibit overdispersion in addition to zero inflation. For low-income children, however, it is possible that both zero inflation and deflation may be present, even when overdispersion is accounted for. To investigate this, as a simple analysis we discretized the age variable (Age < 3, 3 ≤ Age ≤ 4, and Age > 4) and fit a homogeneous negative binomial model with age group specific means and a common overdispersion parameter to DS. Figure 1 presents an informal assessment of this model by comparing the observed proportions to the predicted probabilities for each age group. In this population, there is an inflation of zeros for children under the age of 3 and a deflation for children above the age of 4 (Bottom panel of Figure 1). A constant mixing weight test by averaging out the mixing weights over the age groups, may fail to detect heterogeneity in this population.

Figure 1.

Observed and predicted proportions (Top panel) and observed–predicted proportions (Bottom panel) of the number of decayed surfaces (DS) for each age group. Fitted model is a negative binomial distribution with age group specific means.

We evaluated the homogeneity hypothesis using the proposed covariate-adjusted score test. Specifically, we considered a two-component mixture model for which the nondegenerate distribution is a negative binomial model with mean μ_i = exp{β₀ + β₁Age_i + β₂SI_i + β₃Age_i * SI_i} and overdispersion parameter κ and the mixing weight ω_i is given by equation (3) with π_i = (1 + κ exp{γ₀ + γ₁Age_i + γ₂SI_i + γ₃Age_i * SI_i})^−1/κ. For comparison, the score test with constant mixing weight ω_i = γ₀ of van den Broek (1995) and that proposed by Jansakul and Hinde (2009) with mixing weight ω_i = γ₀ + γ₁Age_i + γ₂SI_i + γ₃Age_i * SI_i were also performed. With these parameterizations, the null hypotheses to be evaluated were then giving by: H₀ : γ_j = β_j, j = 0, 1, 2, 3, for our formulation; H₀ : γ₀ = 0, for van den Broek’s test; and H₀ : γ_j = 0, j = 0, 1, 2, 3, for Jansakul and Hinde’s test. All these tests were conducted by replacing the nuisance parameter β by its maximum likelihood estimate under the null distribution. Results of this analysis are presented in Table 4.

Table 4.

Score test statistics, degrees of freedom, and associated p-values for heterogeneity in dental caries data when the null model is a nondegenerate negative binomial distribution

Response	van den Broek test			Jansakul & Hinde test			Proposed cov.-adj. test
	df	statistic	p-value	df	statistic	p-value	df	statistic	p-value
DS	1	0.0164	0.8980	4	128.1512	<0.001	4	151.8566	<0.001
DFS	1	0.0083	0.9274	4	123.2241	<0.001	4	148.8391	<0.001
DMFS	1	0.0009	0.9759	4	126.7810	<0.001	4	151.8784	<0.001

Our test statistic and that of Jansakul and Hinde (2009) reject the homogeneity hypothesis for all outcomes at 5% significance level, supporting the hypothesis of heterogeneity. But our test provides a stronger evidence for heterogeneity in this population in view of the p-values. The constant mixing weight test, however, fails to reject the null for all outcomes. The observed value of the constant mixing weight test statistic is almost zero, suggesting that inflation and deflation at zero appear to be of the same magnitude, taking into account the random variation. This is a good example where the score test based on constant mixing weights is not powerful enough to capture heterogeneity in the data. But when adjusted by covariates, the score test greatly improves efficiency in detecting heterogeneity.

It is worth noting that failure to reject homogeneity does not give evidence that the zero-inflated negative binomial model provides a best fit for the data. Instead, such rejection only gives grounds for the zero-inflated negative binomial model to be further evaluated. As a final investigation, we then compared the zero-inflated negative binomial model to the zero-inflated Poisson model. A one-sided test (Silvapulle and Silvapulle, 1995; Ridout, Hinde, and Demetrio, 2001) of the overdispersion parameter of the negative binomial model was highly significant at 1% significance level, revealing a strong evidence for overdispersion in addition to zero inflation. This confounding of mixtures with overdispersion is not uncommon in practice as recognized by Lindsay and Roeder (1992) and Böhning et al. (1999).

4. Discussion

The goal of this article was not to argue for or against the marginal model, but rather to show how to conduct inferences for the mixing weights in this class of models. Although score tests for evaluating homogeneity in two-component models for discrete data have been well discussed in the literature, existing methodologies have relied primarily on restrictive assumptions. One common restriction is that constant mixing weights are often assumed. From a practical perspective, this is an important limitation as covariates dependent mixing weights are typical in real applications of two-component regression models. More generally, limitations of existing methodologies result from the structure of the marginal model being simply ignored or at best not properly integrated into the testing procedures. In this article, we formulated and developed a score test of homogeneity based on an intuitive approach that accommodates the features of the marginal model. Specifically, our proposed test adopted a novel parameterization that allows the structural constraints of the mixing weight to be embedded in the testing scheme. Most importantly, this parameterization naturally incorporates covariates in the mixing weights. We showed that this is a natural strategy to adopt when testing is carried out under the marginal model that ignores its hierarchical representation.

The proposed test can be extended to refine the model specification. We generally conduct the test of homogeneity because it is easy to control its type I error. However, if the null hypothesis is rejected, one is typically interested in evaluating composite hypotheses. For example, one may be interested in testing for equality of some coefficients of the binary regression model and corresponding coefficients of the nondegenerate regression model. Although the details to evaluate such composite hypotheses warrant a separate investigation, the results presented here can be used to evaluate these specific hypotheses with a proper adjustment of the type I error. It is noteworthy that rejecting the homogeneity hypothesis against a specific two-component model does not necessarily imply that the latter model is appropriate. Instead, we advocate that such rejection only gives grounds for the two-component model to be further investigated. It is therefore crucial to study how plausible are inferences with respect to a candidate model under consideration that are of major substantive interest from the observed data standpoint.